|
|
|
发布时间: 2019-04-10 |
|
|
|
|
收稿日期: 2018-10-01
基金项目: 国家自然科学基金(41672114, 41702148);上海市自然科学基金(16ZR1413200)
中图法分类号: TM9;TM6
文献标识码: A
文章编号: 1006-4729(2019)02-0149-04
|
摘要
由于风力发电受天气条件的影响, 所以其输出功率难以预测。将风力发电功率与气象数据依据一定的排列规则整理为三维图像, 通过FILTERSIM算法对训练数据图像降维并提取其特征, 然后在已知的气象数据组成的验证点集上预测风力发电功率。试验结果与验证数据的对比表明, 该方法能有效预测风电的发电功率。
关键词
风力发电; 预测; FILTERSIM; 过滤器
Abstract
Due to the impact of wind power from the weather conditions, the nonlinear characteristics of the output power is difficult to accurately capture.The wind power and meteorological data are arranged into three-dimensional images according to certain arrangement rules.The training data images are reduced in dimension and their characteristics are extracted by FILTERSIM algorithm.Then the wind power is predicted on the verification point set of known meteorological data.By comparing the experiment results with the validation data, it is shown that the method can effectively predict wind power generation.
Key words
wind power generation; forecast; FILTERSIM; filter
目前, 风电作为一种可再生能源, 在我国的电力系统中扮演着越来越重要的角色, 而准确地预测风电发电功率对有效缓解电网调度压力、减少备用电力容量配置、提高电力系统的稳定性等具有重要的意义[1]。
根据风力发电功率预测模型的不同, 目前主要有物理学方法、统计学方法、智能计算方法以及以上3种方法的组合方法[2]。物理学方法的优势主要是只需要少量的观察数据, 适用于投产不久的新风电厂, 对其进行初期预测; 不足之处是模型复杂, 需要精准的天气数据, 数据的微小误差容易导致误差累积效应, 影响预测精度。相比物理学方法, 统计学方法更易建模, 但由于风电数据具有自相关性等统计性特征, 预测误差会随着时间的变长而增加, 且无法面对突变情况, 因此统计学方法更适用于短期预测。智能计算方法是学习自然界中的规律, 找出训练数据中的非线性关系, 其常见的方法有支持向量机、深度学习、神经网络等。智能计算方法仅仅需要输入训练数据便可以建立短期和长期预测模型, 但容易出现过拟合和欠拟合的问题。目前, 世界各国的风电功率预报系统的平均表现为短期预测误差在15%左右, 超短期预测误差在10%以内, 而随着时间幅度的变长, 其精准度的可靠性越低[3]。
FILTERSIM算法属于多点地质统计学的分支, 目前多应用于地质结构预测、矿藏分布预测等领域[4]。该算法通过一些线性滤波器扫描训练图像, 并对其打分, 再通过分值对图像特点进行分类。在模拟期间, 这些线性滤波器扫描给出预测条件数据, 确定与其分值最接近的先前分类, 从中提取出一个“粘贴”回待预测图像, 以完成预测[5]。本文采用晋北某风电场数据进行试验, 并与传统的风电功率预测方法进行比较。结果表明, 利用FILTERSIM算法可以有效提高预测的准确率。
1 FILTERSIM算法概述
1.1 训练模式分类
训练模式分类是依据过滤器的打分来决定的。通过指定3个方向边长分别为(nx, ny, nz)的一个三维搜索模板τ来搜索训练图像; 由于随后的分数记录在中心位置u, 所以nx, ny, nz要求均为正奇数。假定有F个不同的过滤器{fk(hj); j=1, 2, 3, …, n; k=1, 2, 3, …, F}, 每个过滤器与搜索模板τ大小一致, 都包含n个像素。训练图像中一个以u为中心的局部图像的第k个过滤器分数定义为
| $\begin{aligned} S_{\tau, k}^{\mathrm{T}}(u) &=\sum\limits_{f=1}^{n} f_{k}\left(h_{j}\right) T\left(u+h_{j}\right) , \\ k &=1,2,3, \cdots, F \end{aligned}$ | (1) |
式中:T(u+hj)——训练图像在u+hj位置的属性值。
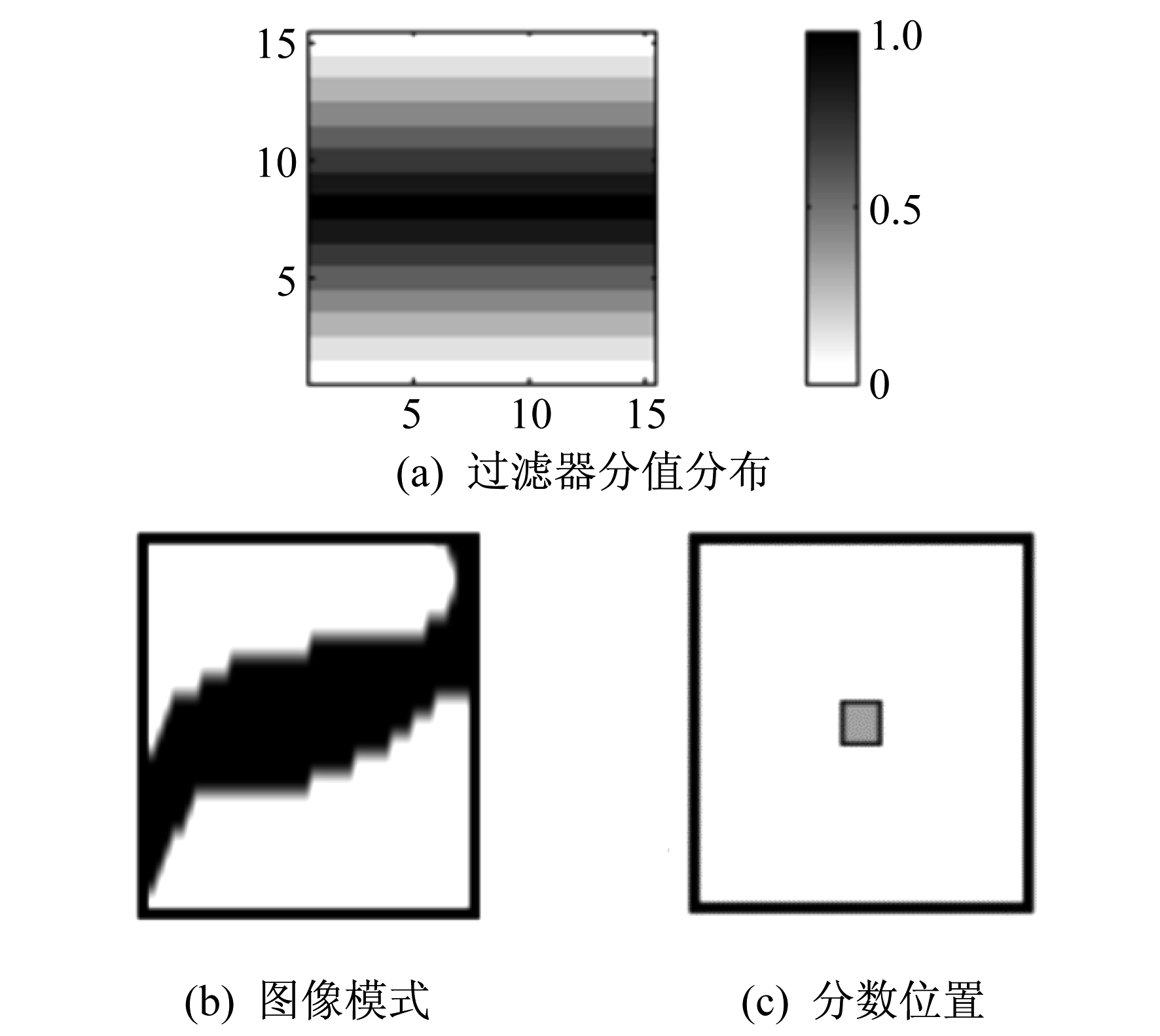
过滤器可以是二维或者三维的。其打分流程如图 1所示。其中, 图 1(a)表示一个15×15大小的像素矩阵组成的二维过滤器, 反映的是对应的分值分布, 其中间的分值最高, 逐渐向上下递减; 图 1(b)表示需要打分的图案; 图 1(c)表示分数被赋予了中心像素[6]。
对于训练图像的某个局部图案而言, 过滤器打分显示了其在该过滤器下的模式特征。为了更好地表现训练图像的特征, 需要定义F个过滤器来表现其不同的特征, 针对某个局部图案, 这F个过滤器对其打出的分值则为一个F维的向量, 从原来的多个像素点的特征降低为F维特征。
文献[5]提出了在三维情况下包含9个过滤器的默认过滤器组, 分别用来度量不同方向的均值、梯度和曲率。ni是i方向的搜索模板大小(i表示的是x, y, z 3个方向); mi=(ni-1)/2; ai为过滤器中心点在i方向的偏移量, ai=-mi, …, +mi。默认过滤器定义如下。
(1) 均值过滤器
| $ \left(\alpha_{i}\right)_{1}=1-\frac{\left|\alpha_{i}\right|}{m_{i}} \in[0,1] $ | (2) |
(2) 梯度过滤器
| $ \left(\alpha_{i}\right)_{2}=\frac{\left|\alpha_{i}\right|}{m_{i}} \in[-1,1] $ | (3) |
(3) 曲率过滤器
| $ \left(\alpha_{i}\right)_{3}=\frac{2\left|\alpha_{i}\right|}{m_{i}}-1 \in[-1,1] $ | (4) |
将F个过滤器对K个训练图像进行扫描, 可以得到F×K个分数图, 特征相似的图像会得到差不多的分数, 因此可以用分数对训练图像进行分类, 每一类别称为模式原型(prototype), 记为prot, 其计算公式为
| $\begin{aligned} p_{\text {rot }}\left(h_{i}\right) &=\frac{1}{c} \sum\limits_{j=1}^{c} T\left(u_{j}+h_{i}\right) \\ i &=1,2,3, \cdots, n \end{aligned}$ | (5) |
式中:c——原型分类的训练重复次数。
分类策略有交叉分割与K-mean聚类分割两种。前者分割速度很快, 但很粗糙; 后者是最简单的非监督学习算法之一, 分割效果很好, 但比交叉分割慢许多[7]。本文选择交叉分割的方法。
1.2 图像模拟运行流程
基于FILTERSIM算法的图像模拟运行流程如下:
过滤器组扫描图像获得过滤器打分
在得分空间进行模式分类
在模拟网格G中定位采样点
在模拟网格上定义一条随机路径
for随机路径上每个节点u, do
提取以u为中心节点的条件数据集dev
搜索距离dev最近的父型prot, p
if prot, c含有子型集, then
搜索距离dev最近的子原型prot, c
从prot, c中随机抓取一个模式pat
else
从prot, c中随机抓取一个模式pat
end if
将pat粘贴到已经模拟的节点中, 并锁定中心点及附近点的值
end for
2 风力发电功率模拟
在风力发电功率预测环节, 风速是影响风机输出功率的重要因素之一。此外, 风向、环境温度、湿度等环境因素对其也有不同程度的影响[8]。构建风电发电功率训练图像的基本向量V=(风速, 风向, 环境温度, 湿度, 电网频率, 风机功率), 时间间隔为1 min。利用真实采集到的晋北某风电场数据进行试验, 时间为2016年10月, 其中训练图像中包含8 900条数据, 验证图像包含2 500条数据。
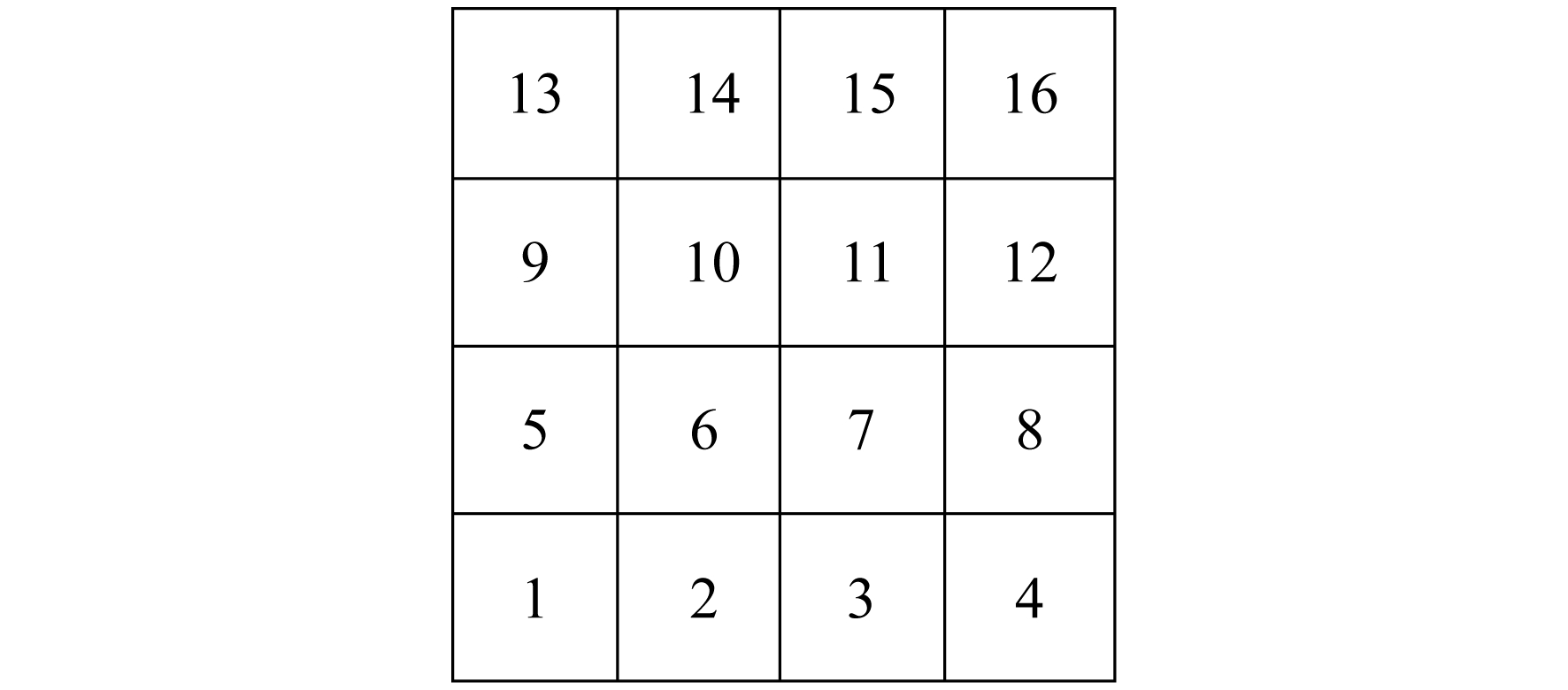
训练图像以向量V为单位根据时间顺序先后排列, 风速、风向、环境温度等每个数据值占据训练图像的一个像素点。数据的排列从原点开始, 沿x轴正方向排列, 直至提前设定好的网格大小的x值, 随后向y轴正方向平移一个单位后继续沿x轴正方向排列数据, 以此类推, 直至网格排满数据为止。图 2给出了一个4×4的笛卡尔网格例子。图 2中的标号按顺序排列, 三维数据则是在一个平面排满数据后向z轴正方向延伸。
风速、风向、环境温度、湿度、电网频率、风机功率这6种数据的取值范围均不同, 其中风机功率的数值远大于其他5种。因为风机功率数值太高, 使得其他数值很小的几个属性值看起来没有任何的变化, 导致在一幅图中用同一个图例表示数据的可视化效果极差, 因此试验中将功率的数值缩小了40 000倍。试验数据中除温度有负数取值外, 其他数据均为正数。为了使数据更为直观, 试验中笛卡尔网格的x轴大小均选择6的倍数。搜索模板大小为11×11×3。试验依据上述FILTERSIM算法流程, 首先利用三维数据模板扫描训练图像并对其进行打分分类, 然后在验证点集的基础上, 根据之前学习到的结构特征对空白位置即发电功率进行合理预测, 最后将预测结果与验证数据进行对比[9]。
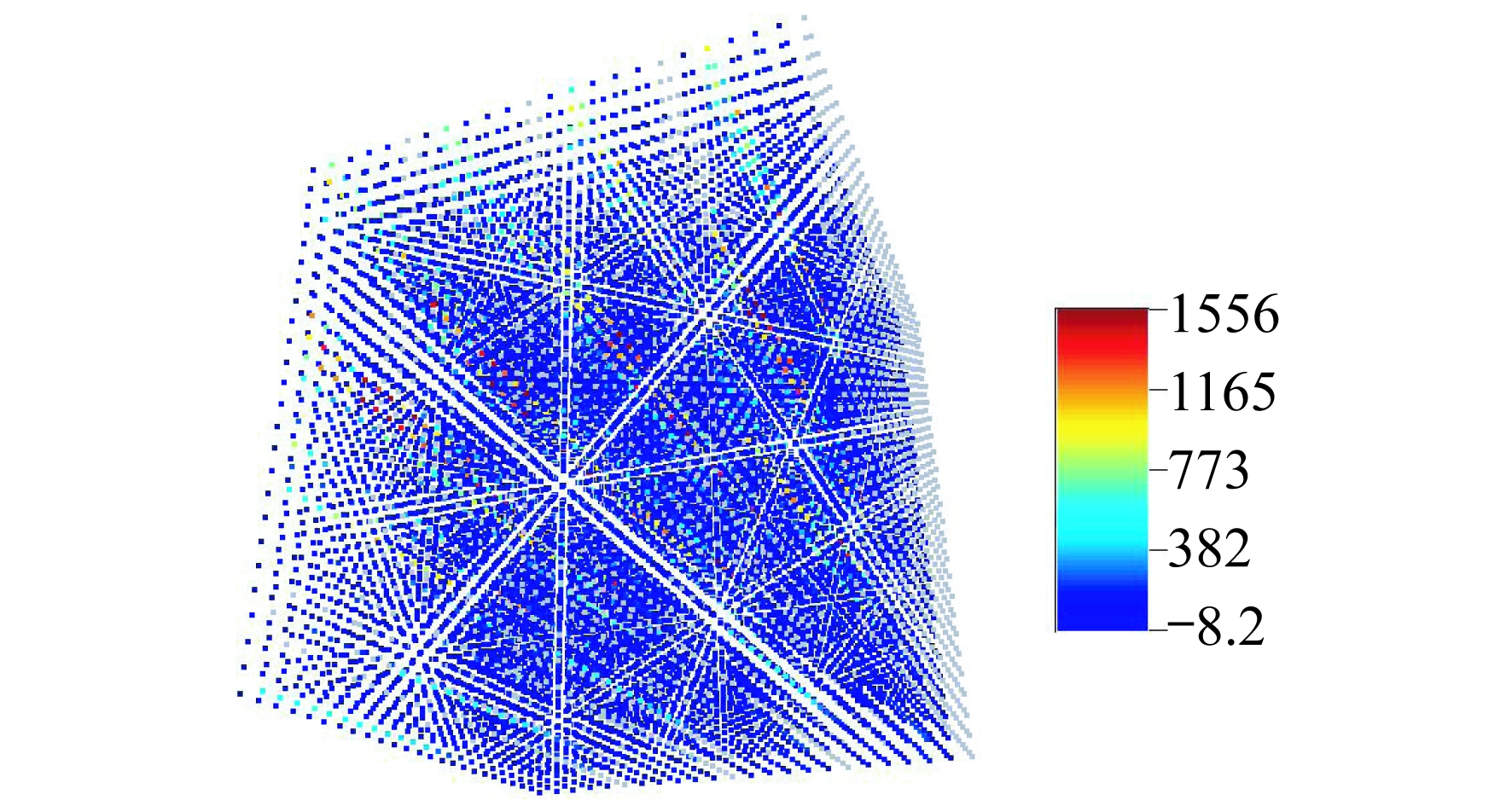
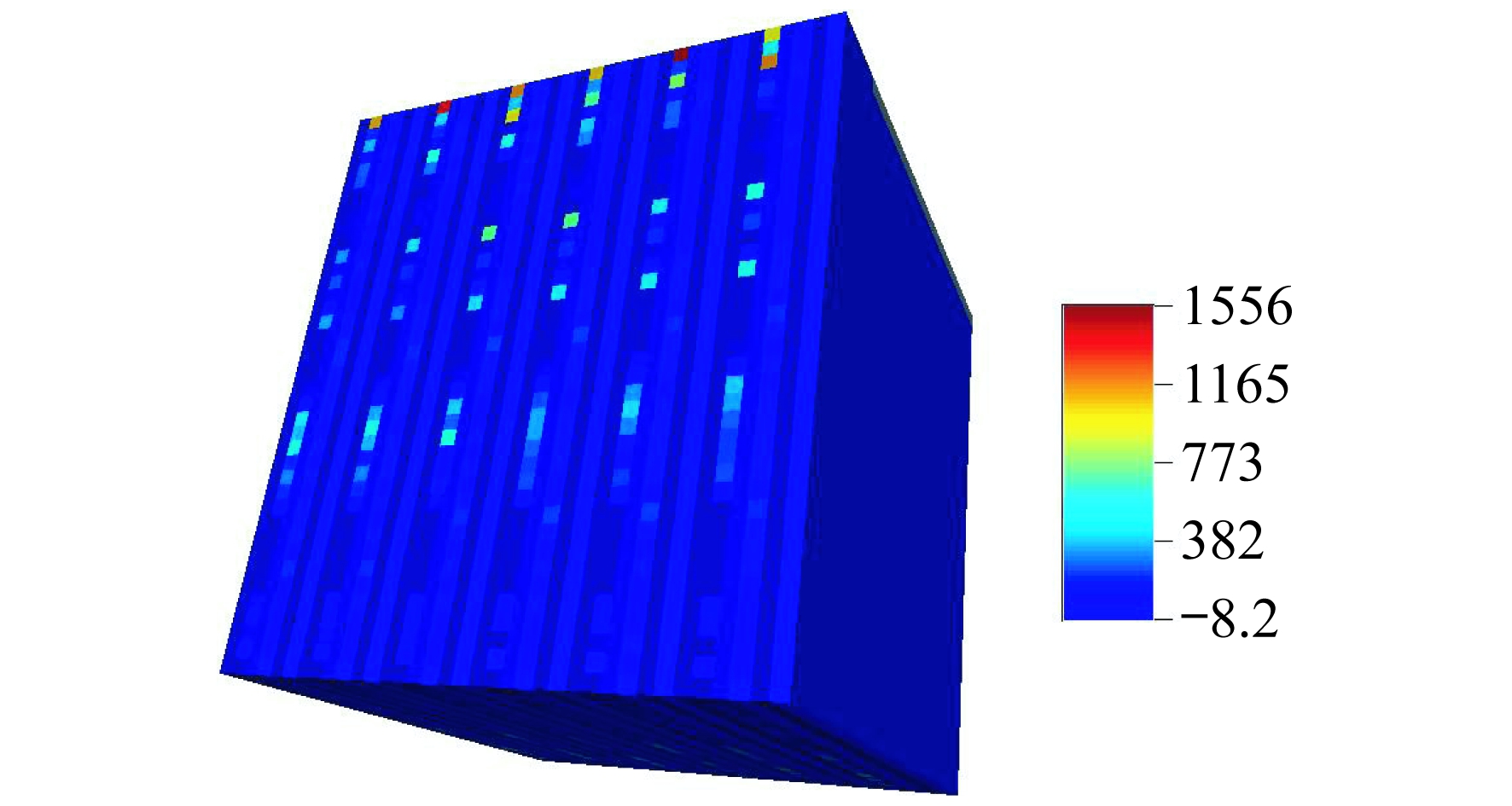
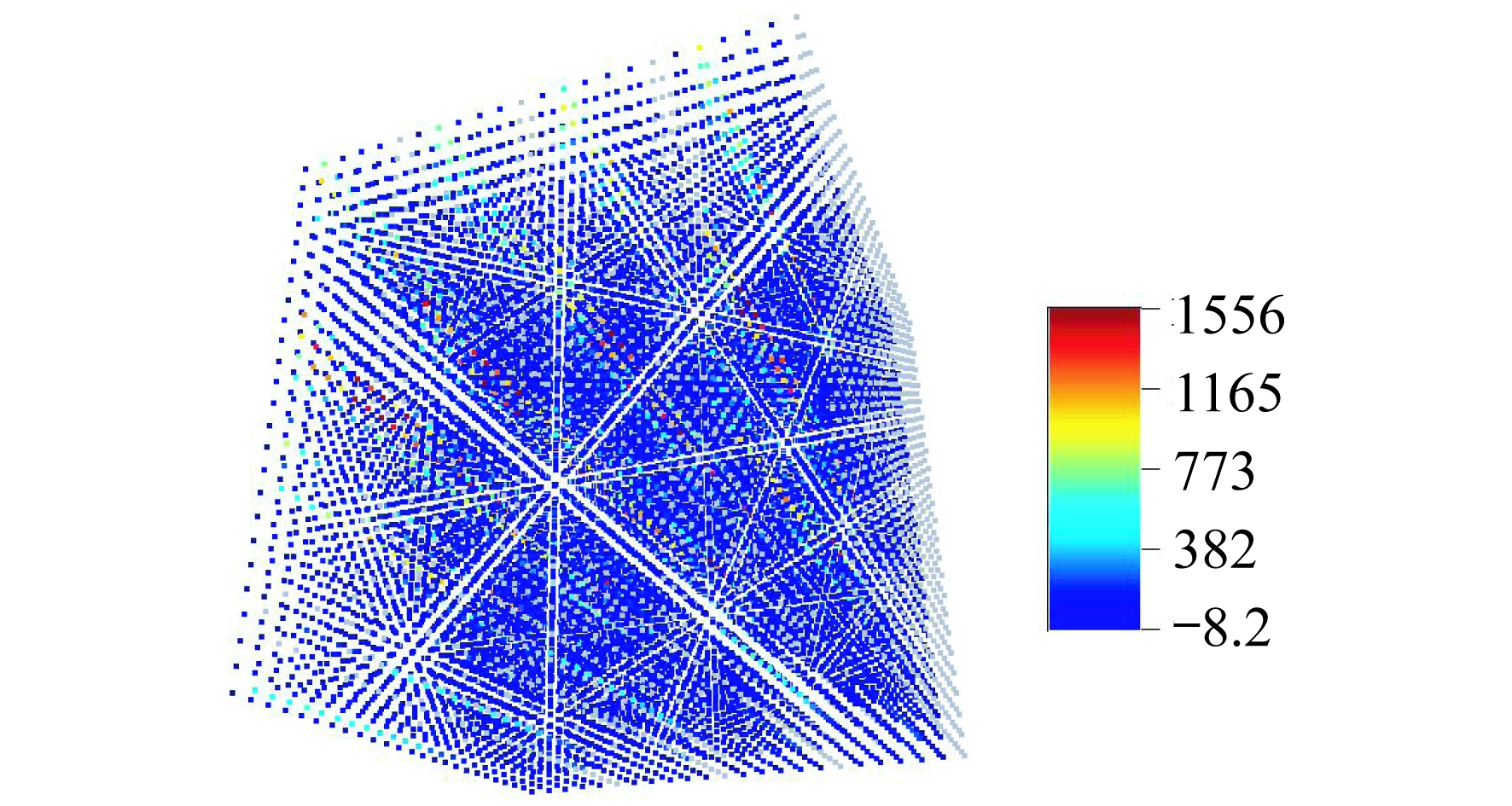
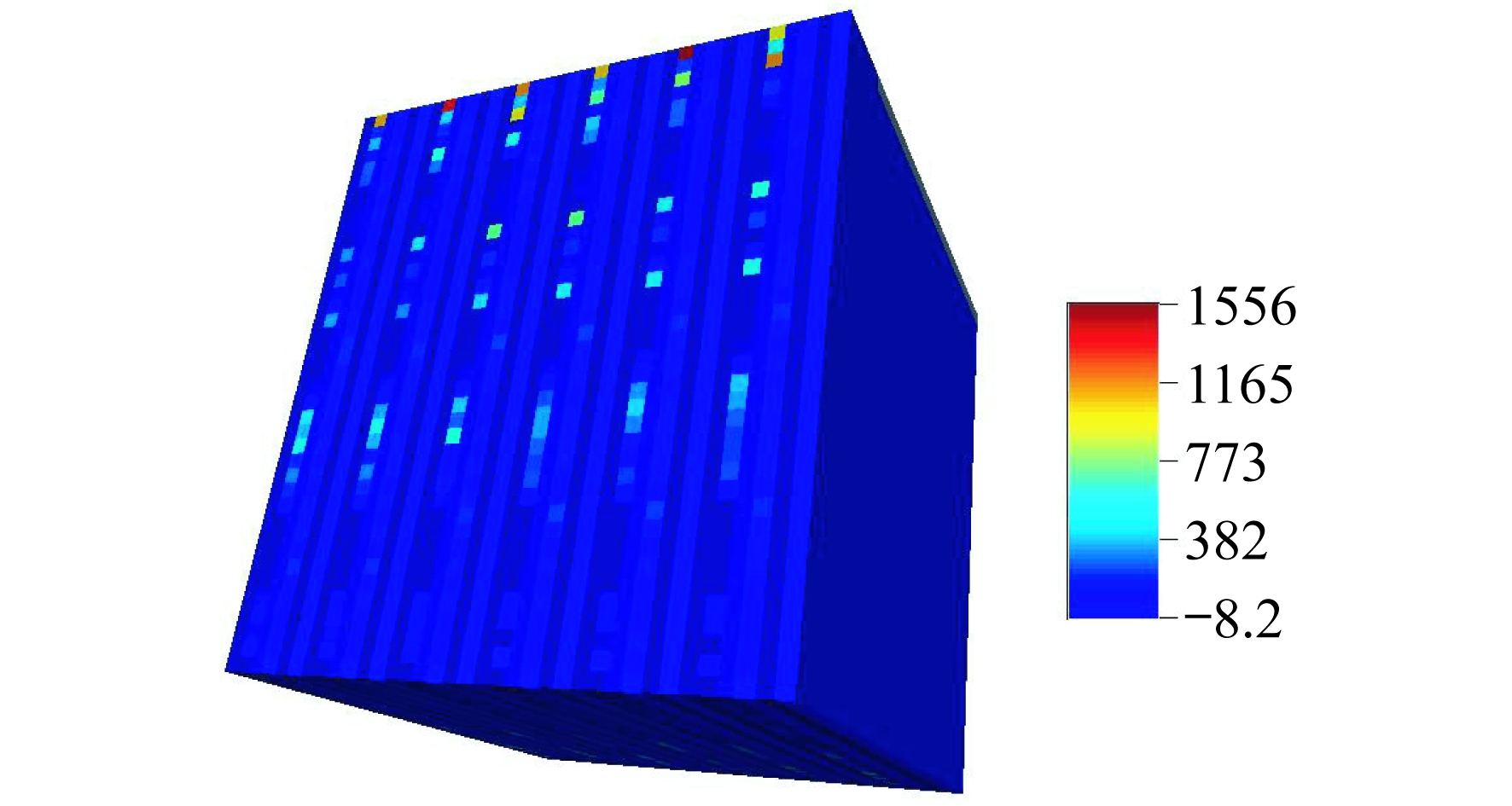
验证点集为在验证数据的基础上将风机功率作为空数据的点阵数据集, 大小为24×25×25, 如图 3所示。图 3中, 灰色点即为空数据。图 4为由历史数据构成的训练图像, 大小为36×38×40。图 5为通过FILTERSIM算法在图 3的基础上模拟得到的预测数据图像, 大小为24×25×25。图 5实现了对于图 3中缺失的发电功率值的模拟预测。图 6为验证数据图像, 为同一风机的与训练数据不同时间段的数据, 大小为24×25×25。
表 1为FILTERSIM算法预测功率的数据结果(图 5)与验证集(图 6)的均值与方差对比。由表 1可以看出, 无论是在图像相似度、均值还是方差上, 功率的预测结果与验证集都十分接近。
表 1
FILTERSIM算法功率试验结果与验证集的均值与方差
| 参数 | 均值 | 方差 |
| 预测结果 | 127.078 | 35484 |
| 验证集 | 124.693 | 35258 |
对试验结果进行进一步的定量分析, 选择均方根误差(Root Mean Squared Error, RMSE)[3]计算FILTERSIM模型的风电功率预测误差, 其公式为
| $e_{\mathrm{RMSE}}=\frac{1}{\sqrt{n}} \sqrt{\sum\limits_{t=1}^{n}\left(\frac{p_{t}-p_{t}^{\mathrm{r}}}{p_{t}}\right)^{2}} \quad t=1,2,3, \cdots, n$ | (6) |
式中:pt——实际风电功率;
 预测风电功率;
预测风电功率;
n——风电数据条数。
根据式(6)计算得到模型的风电预测误差为4.791%, 表明误差得到了明显的降低。
3 结语
FILTERSIM算法能有效提取训练数据所构成图像的特征, 在获得有效天气数据下可对目标风机的发电功率进行有效预测。本文将电力数据整理为图像形式, 运用FILTERSIM算法在已知部分气象数据的情况下对特定风机的发电功率进行预测。该模型有效地建立了环境因素与风电功率之间的映射关系, 降低了风电功率预测的误差。
参考文献
-
[1]考虑预报风速与功率曲线因素的风电功率预测不确定性估计[J]. 电网技术, 2014, 38(2): 463-468.
-
[2]风电功率预测技术研究综述[J]. 现代电力, 2017, 34(3): 1-11. DOI:10.3969/j.issn.1007-2322.2017.03.001
-
[3]KHALID M, SAVKIN A V. A method for short-term wind power prediction with multiple observation points[J]. IEEE Transactions on Power Systems, 2012, 27(2): 579-586. DOI:10.1109/TPWRS.2011.2160295
-
[4]多点地质统计学在河流相储层建模中的应用[J]. 地质科技情报, 2008, 27(3): 68-72. DOI:10.3969/j.issn.1000-7849.2008.03.010
-
[5]ZHANG T. Filter-based training pattern classification for spatial pattern simulation[D]. Palo Alto: Stanford University, 2006.
-
[6]LU D T, ZHANG T, YANG J Q, et al. A reconstruction method of porous media integrating soft data with hard data[J]. Chinese Science Bulletin, 2009, 54(11): 1876-1885.
-
[7]基于人工神经网络的风电功率预测[J]. 中国电机工程学报, 2008, 28(34): 118-123. DOI:10.3321/j.issn:0258-8013.2008.34.019
-
[8]短期风电功率预测误差分布研究[J]. 电力系统保护与控制, 2013(12): 65-70. DOI:10.7667/j.issn.1674-3415.2013.12.011
-
[9]WU J, BOUCHER A, ZHANG T. A SGeMS code for pattern simulation of continuous and categorical variables: FILTERSIM[J]. Computers & Geosciences, 2008, 34(12): 1863-1876.