DC-DC变换器将直流电转换为另一固定电压或可调的直流电, 是一个用开关调节方式控制电能的变换电路, 已被广泛应用于各种开关电源、燃料电池、光伏发电和分布式电源系统中。随着其应用范围的增加, 对DC-DC变换器的控制性能要求也逐渐提高, 就要求对DC-DC变换器有更好的控制算法。

近年来, 随着现代控制理论的发展, 研究者们设计了一系列的DC-DC变换器控制方法, 进一步提高了DC-DC变换器系统的控制性能。文献[1-3]针对DC-DC变换器, 通过模糊控制规则对PID控制器进行了增益调节。该算法超调量小, 改善了系统的动态特性和静态特性, 但由于其信息处理简单且缺乏系统性, 导致控制精度降低和动态品质变差, 不利于实际应用。文献[4]将神经网络控制策略引入DC-DC变换器, 基于BP神经网络构造了一种新型控制方法。该系统具有更好的动态响应性能, 但由于学习速率是固定的, 所以网络收敛速度较慢, 需要较长的训练时间。文献[5-6]通过建立DC-DC变换器模型, 选取线性切换函数和指数趋近律, 设计了滑模变结构控制器。该控制策略具有良好的动态调节性能和稳态误差调节特性, 但变结构本身存在着抖动问题, 给实际应用带来了一大障碍。文献[7]通过建立DC-DC变换器的欧拉-拉格朗日(Euler-langrange, EL)模型, 配置系统能量耗散方程中的无功力迫使系统总能量跟踪预期的能量函数, 使系统的电压渐近收敛至参考值, 设计的一种无源控制器存在稳态直流电压误差。文献[8]针对Buck型DC-DC变换器, 利用采样降维观测器, 设计了采样输出反馈控制器, 可以控制输出电压收敛至期望值, 取得了比PID方法更快的跟踪速度。但该方法的设计目标只是将系统电压输出跟踪并稳定至期望值, 没有显式包含“以尽可能快的速度驱动Buck型DC-DC变换器电压输出跟踪期望值”这一速度要求。如果能以电压输出尽快到达期望值为设计目标, 将有效提升Buck变换器输出的控制性能, 因此该方法的控制效果还有进一步提升的空间。本文选择以驱动电压输出尽快到达期望值作为优化目标, 将从优化角度出发, 设计算法来优化电压输出的收敛速度, 以期进一步有效改善电压输出控制效果。

由于预测控制可以方便地处理各种约束问题, 因此从问世以来就受到工业界和学术界的关注, 并在工业过程控制中得到了广泛应用和推广。本文针对Buck型DC-DC变换器对象, 引入预测控制优化思想, 基于线性矩阵不等式技术(Linear Matrix Inequalities, LMIs), 通过半正定规划方法优化Buck变换器的无穷时域性能, 以提高Buck变换器的系统控制性能。

在电流连续型(Continuous Conduction Mode, CCM)工作模式下, 通过机理建模建立连续系统数学模型。

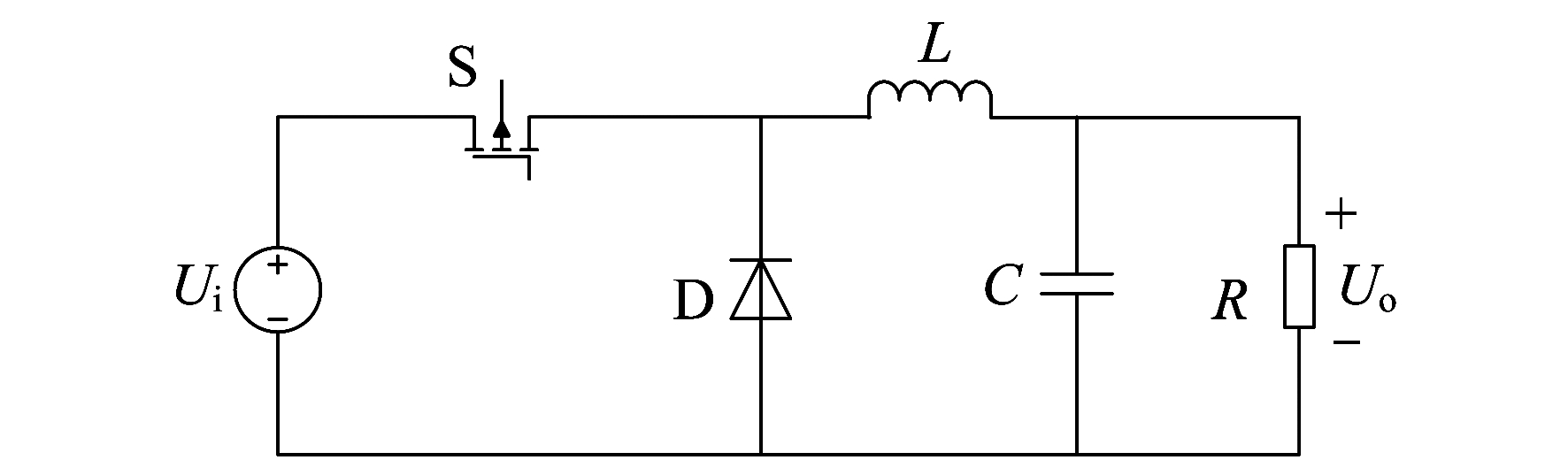
Buck变换器在CCM工作模式时, 有两种工作模态。如图 1所示, 开关S导通时, 电源U_i向负载供电, 二极管D承受反向电压而截至, 电感L充电, 电流持续增加; 开关管S关断时, 二极管D导通续流, 电感L放电, 电流减小, 直到一个开关周期结束为止。

本文选取控制性能指标:

$ \begin{aligned} \min J=\int_{0}^{\infty}\left\|U_{\mathrm{o}}-U_{\mathrm{s}}\right\|_{W}^{2}+\\ \left\|u-u_{\mathrm{s}}\right\|_{M}^{2} \mathrm{d} t \end{aligned} $

(1)

式中:U_o, U_s——输出电压和期望输出电压;

u, u_s——占空比和期望占空比;

W, M——性能指标中的加权矩阵。

经分析可知, 当电压输出达到期望值, 即U_o=U_s时, 则有:电感电流i_L=U_s/R; u_s=U_s/U_i(U_i为输入电压)。

根据基尔霍夫电压电流定律得到系统的i_L和U_o满足以下关系

$ \left\{\begin{array}{l} L \frac{\mathrm{d} i_{L}}{\mathrm{d} t}=-U_{\mathrm{o}}+u U_{\mathrm{i}} \\ C \frac{\mathrm{d} U_{\mathrm{o}}}{\mathrm{d} t}=i_{L}-\frac{U_{\mathrm{o}}}{R} \end{array}\right. $

(2)

选取状态变量x₁为电感电流, x₂为输出电压, u为输入变量, 则系统状态方程为

$\dot{x}=A x+B u$

(3)

其中:

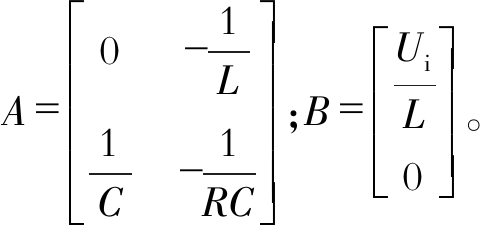
占空比输入量的约束条件为0≤u≤1。

根据式(3)的解析表达式

$x(t)=e^{A t} x(0)+\int_{0}^{t} e^{A(t-\tau)} B u(\tau) \mathrm{d} \tau$

(4)

式中:e^A(t-τ)——状态转移矩阵。

对式(3)进行精确离散化处理, 得到

$x\left((k+1) T_{\mathrm{s}}\right)=G\left(T_{\mathrm{s}}\right) x\left(k T_{\mathrm{s}}\right)+ \\ H\left(T_{\mathrm{s}}\right) u\left(k T_{\mathrm{s}}\right)$

(5)

式中:T_s——采样周期;

u(kT_s)——系统第k时刻的占空比, 且满足

0≤u(kT_s)≤1;

G(T_s)=e^AT_s;

H(T_s)= 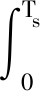e^Atdt·B。

定义将x和u作变量替换, 通过坐标平移

$ \left\{\begin{array}{l} \zeta\left(k T_{\mathrm{s}}\right)=x\left(k T_{\mathrm{s}}\right)-x_{\mathrm{s}} \\ v\left(k T_{\mathrm{s}}\right)=u\left(k T_{\mathrm{s}}\right)-u_{\mathrm{s}} \end{array}\right. $

(6)

将式(6)代入式(5)中, 经变换后, 得到一个以原点为平衡点的状态方程

$ \begin{aligned} \xi\left((k+1) T_{\mathrm{s}}\right)=& G\left(T_{\mathrm{s}}\right) \xi\left(k T_{\mathrm{s}}\right)+\\ & H\left(T_{\mathrm{s}}\right) v\left(k T_{\mathrm{s}}\right) \end{aligned} $

(7)

进一步简记为

$\xi(k+1)=G\left(T_{\mathrm{s}}\right) \xi(k)+H\left(T_{\mathrm{s}}\right) v(k)$

(8)

$-u_{\mathrm{s}} \leqslant v(k+i \mid k) \leqslant 1-u_{\mathrm{s}}$

(9)

构建Buck变换器的优化问题, 具体描述为

$ \begin{aligned} \min J_{\infty}(k)=& \sum_{i=0}^{\infty}\|\xi(k+i)\|_{W}^{2}+\\ & \|v(k+i)\|_{M}^{2} \\ & \text { s. t. }(8)(9) \end{aligned} $

(10)

针对Buck变换器, 设计预测控制优化算法, 对受控系统的控制性能进行滚动优化, 从而优选出Buck变换器的占空比输入量, 驱动Buck变换器输出量快速地收敛至其期望输出值, 进而有效提高Buck变换器的电压输出质量。

对于优化问题, 其控制输入序列为

V(k) [v(k|k), v(k+1|k), …, v(∞|k)]^T

考虑Buck变换器系统式(8), 将式(9)进一步收缩为如下关于原点对称的约束条件:

$|v(k+i)| \leqslant \min \left\{u_{\mathrm{s}}, 1-u_{\mathrm{s}}\right\} \\ i=1, 2, 3, \cdots, \infty$

(11)

通常无穷时域预测控制在线优化问题可表示为

$ \begin{aligned} \min _{v(k+i k), i \geq 0} J_{\infty}(k)=& \sum_{i=0}^{\infty}\left(\|\xi(k+i \mid k)\|_{W}^{2}+\right.\\ & \left.\|v(k+i \mid k)\|_{M}^{2}\right) \\ & \text { s.t. }(11) \end{aligned} $

(12)

由于式(12)涉及到求解未来无穷多时刻的控制变量v(k+i|k), i=1, 2, 3, …, ∞, 将导致寻优计算量繁重, 难以实现。为了解决这一问题, 本文针对Buck变换器系统, 引入控制不变集优化技术^[9-10]构造并优化目标函数J(k)上界来优选出占空比输入量, 进而将原来的优化问题转化为半正定规划问题, 具体如下。

对于式(8), 首先定义二次函数Ψ(i, k)=ζ(k+i|k)^TP(k)ζ(k+i|k), P(k) > 0, 且强制要求其满足如下稳定性约束

$\Psi(i+1, k)-\Psi(i, k) \leqslant \\ -\left[\|\zeta(k+i \mid k)\|_{W}^{2}+\|v(k+i \mid k)\|_{M}^{2}\right]$

(13)

在控制系统稳定的情况下, ζ(∞|k)=0, Ψ(∞, k)=0。将式(13)从i=0叠加到i=∞, 可得其无穷时域性能指标上界: J_∞(k) ≤Ψ(0, k), 定义矩阵P=γQ^-1, 其中标量γ > 0为寻优变量, 则

$J_{\infty}(k) \leqslant \Psi(0, k) \leqslant \gamma$

(14)

令矩阵X∈R^2×2, Y∈R²为LMIs变量, 记F=YQ^-1, 利用LMIs的Schur补性质, 可将式(13)和式(14)转化为如下LMIs^[9]

$\left[\begin{array}{cccc}Q & Q G^{\mathrm{T}}+Y^{\mathrm{T}} H^{\mathrm{T}} & Q W^{\frac{1}{2}} & Y^{\mathrm{T}} M^{\frac{1}{2}} \\ G Q+H Y & Q & 0 & 0 \\ W^{\frac{1}{2}} Q & 0 & \gamma I & 0 \\ M^{\frac{1}{2}} Y & 0 & 0 & \gamma I\end{array}\right] \geqslant 0$

(15)

$\left[\begin{array}{cc}1 & \xi^{\mathrm{T}}(k) \\ \xi(k) & Q\end{array}\right] \geqslant 0$

(16)

输入约束同样可以转化为如下LMIs

$\left[\begin{array}{cc}X & Y \\ Y^{\mathrm{T}} & Q\end{array}\right] \geqslant 0, X_{j j} \leqslant\left\{\min \left\{u_{\mathrm{s}}, 1-u_{\mathrm{s}}\right\}\right\}^{2} , \\ j=1, 2, 3, \cdots, m$

(17)

因此将式(11)转化为下列LMIs求解问题

$\min\limits_{\gamma, Q, X, Y} \gamma \\ \mathrm{s.t.} (15) \sim(17)$

(18)

集合ε(Q)={ξ∈R²|ξ^TQ^-1ξ≤1, Q > 0}即为式(8)的椭圆不变集, 其对应的反馈控制律为v(k)=F(k)ζ(k)。

综上所述, Buck变换器的预测控制问题已被转化为半正定规划问题, 可将Buck变换器的预测控制优化算法归纳如下。

(1) 测量当前时刻系统的状态ζ(k)=ζ(k|k)。

(2) 适当选择对称正定加权矩阵W和M。

(3) 求解具有LMIs约束的优化问题式(17), 得到最优解γ, Q, X, Y。

(4) 计算得到状态反馈预测控制器增益矩阵F(k)=YQ^-1。

(5) 通过计算得到k时刻的控制反馈律u(k)=F(k)ζ(k|k)+u_s, 并将其施加于被控系统。

(6) 令k=k+1, 返回(1), 重复优化过程。

定  理  对于式(8), 如果在k时刻, 对于系统状态ζ(k|k), 本文算法有可行解, 则本文算法所设计的预测控制算法可以使该系统渐近稳定。

证  明  设k时刻本文算法是可行的, 优化问题的最优解为

Γ^*(k)=[γ^*, Q^*, X^*, Y^*]

其中, F(k)=Y^*(Q^*)^-1。

首先证明可行性。需要证明在k+1时刻, 对于系统状态ζ(k+1)=ζ(k+1|k+1), 式(15)~(17)仍然可行, 即可证明可行性。为证明可行性, 需构造k+1时刻优化问题的可行解, 即Г(k+1)=[αγ^*, αQ^*, αX^*, αY^*]。

其中

$ \alpha=\frac{U(k+1)}{\gamma^{*}(k)} $

(19)

并且F(k+1)=αY^*(αQ^*)^-1, 即F(k+1)=Y^*(Q^*)^-1, 可推出Γ(k+1)满足式(15)和式(17)。

由式(16)可推得

$\Psi(k+1) \leqslant \gamma^{*}(k)$

(20)

进而推得0 < α≤1。由式(19)可得

$\zeta(k+1)^{\mathrm{T}}\left(\alpha Q^{*}(k)\right)^{-1} \zeta(k+1)=1$

(21)

所以Γ(k+1)满足式(16)。

综上, αγ^*, αQ^*, αX^*, αY^*满足式(15)~(17), 因此Γ(k+1)是k+1时刻的可行解。

由于0 < α≤1, 可推得

$\gamma^{*}(k+1) \leqslant \gamma(k+1)=\alpha \gamma^{*}(k) \leqslant \gamma^{*}(k)$

(22)

因此, 闭环系统是渐近稳定的。

仿真验证控制算法的有效性, 考虑如下系统:

$ \left[\begin{array}{c} \dot{x}_{1} \\ \dot{x}_{2} \end{array}\right]=\left[\begin{array}{cc} 0 & -\frac{1}{L} \\ \frac{1}{C} & -\frac{1}{R C} \end{array}\right]\left[\begin{array}{l} x_{1} \\ x_{2} \end{array}\right]+\left[\begin{array}{c} U_{\mathrm{i}} \\ \hline L \\ 0 \end{array}\right] u $

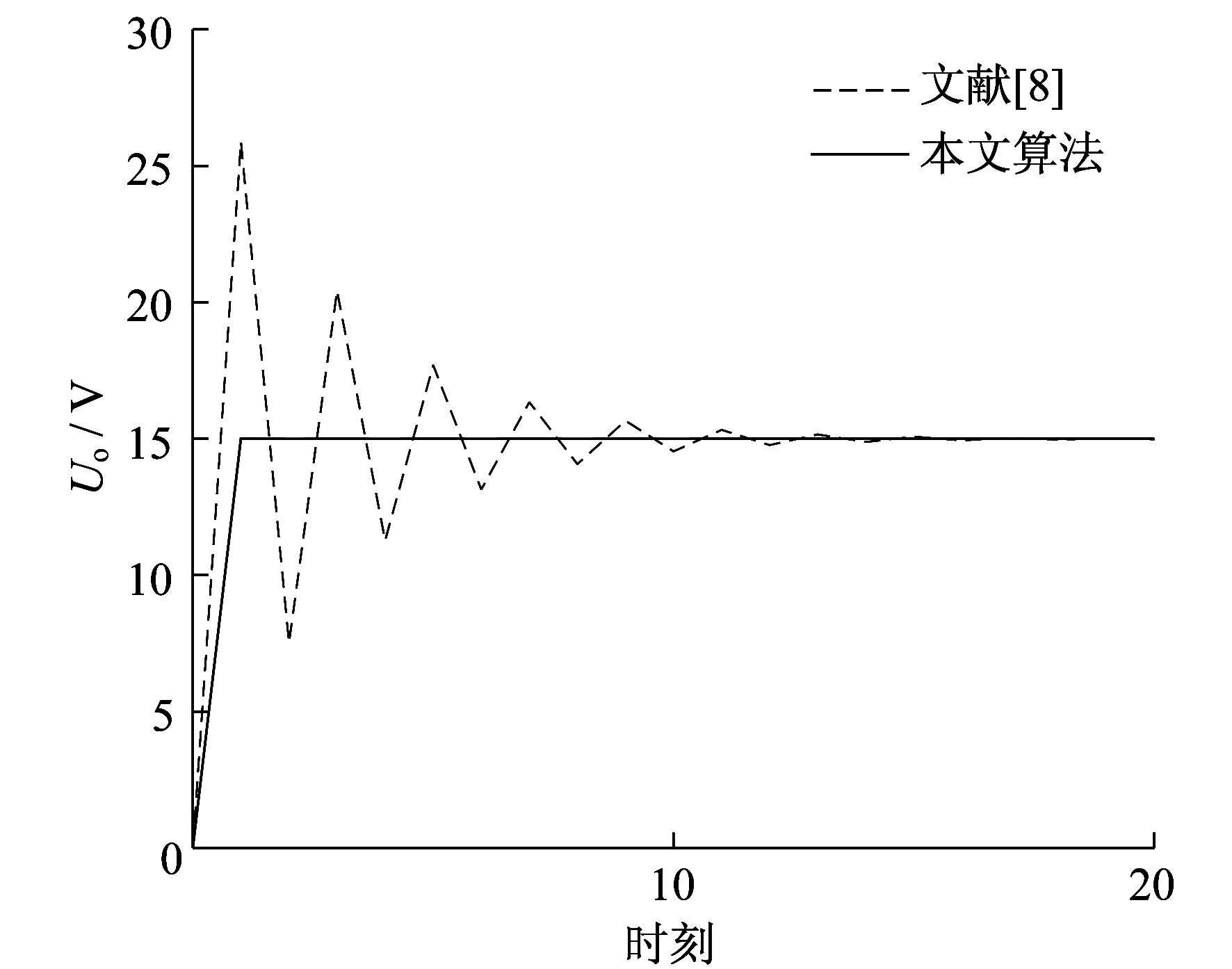
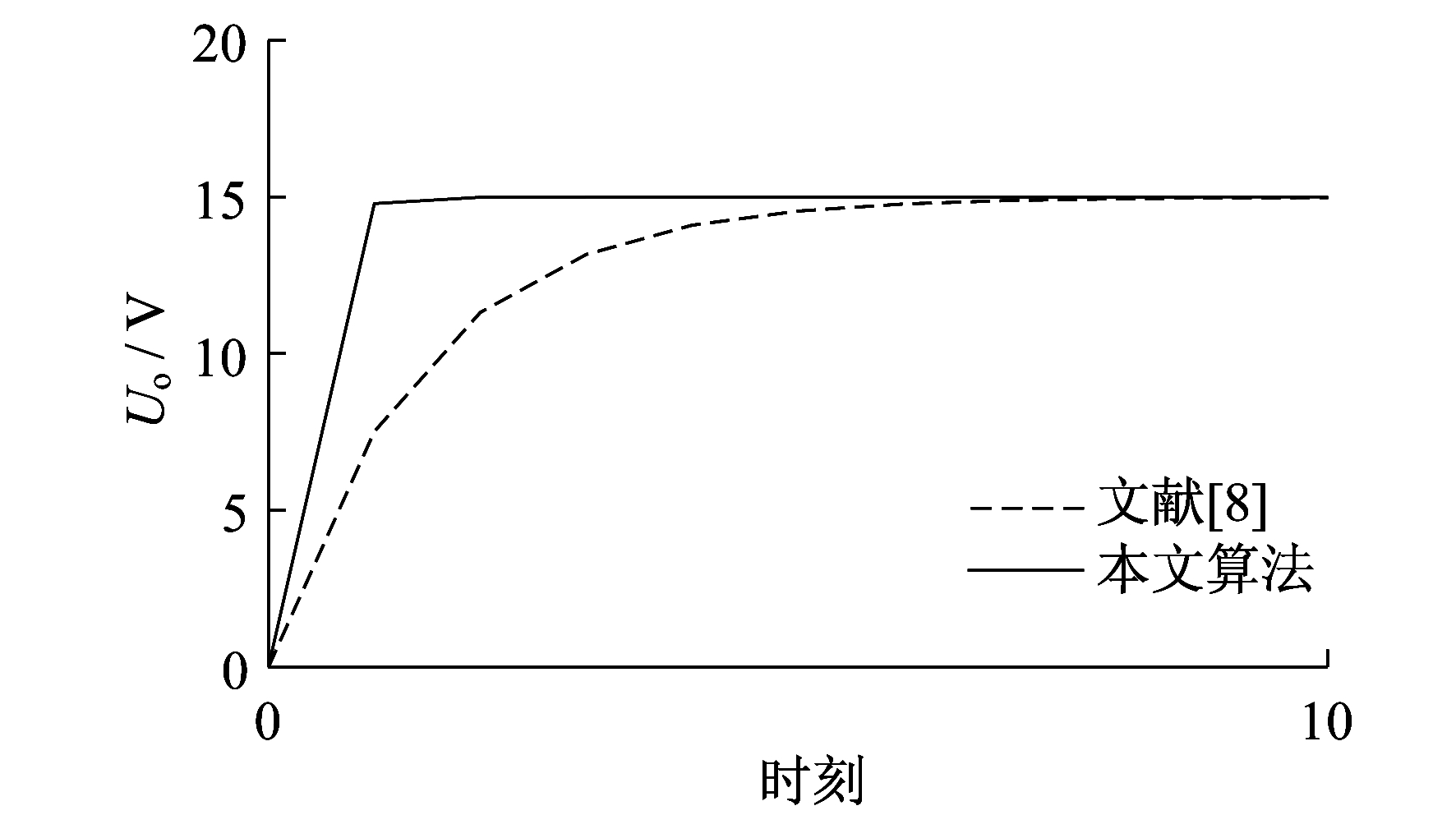
系统参数如下:输入电压U_i=30 V, 输出电压U_o=15 V, 负载R=10 Ω, 电感L=4.7 mH, 电容C=1 000 μF; 并且, 输入约束|u|≤1, 选取控制性能指标如式(10)所示, 其中加权矩阵W=diag(1, 1), M=1, 初始状态x(0)=[0, 0]^T, 分别基于T_s=0.05 ms, T_s=0.25 ms, T_s=0.5 ms 3个不同的采样周期对系统进行MATLAB仿真, 并与文献[8]方法进行仿真效果对比。

采用本文算法和文献[8]方法, 基于3个采样周期进行仿真, 得到的系统输出电压波形分别如图 2~图 4所示。由图 2~图 4可知, 与文献[8]方法相比, 本文算法可以驱动Buck型变换器电压输出以更快的速度收敛于期望值。

本文算法和文献[8]方法的控制性能和收敛时间如表 1所示。

由表 1可知, 本文算法取得了比文献[8]更优的控制性能和更快的收敛速度。

本文针对Buck型DC-DC变换器系统电压跟踪问题, 通过将Buck变换器连续模型转化为离散模型, 引入不变集方法将Buck变换器的跟踪控制问题转化为半正定规划问题, 设计了预测控制算法。仿真结果表明, 在该预测控制算法下, Buck变换器电压输出以更快的速度收敛于期望值, 获得了更优的控制性能。

本文方法在取得优异控制效果的同时, 也存在在线计算负担较重的缺点。后期研究将采取“离线设计、在线综合”的设计方法来加以改进, 通过将部分在线优化计算量转移至离线设计, 以期进一步降低在线计算负担。