种群竞争模型的研究一直备受关注^[1-6]。文献[1-2]研究了一般的种群竞争模型, 并对平衡点进行了稳定性分析, 文献[2]分析了平衡点的局部稳定性和全局稳定性。文献[3]研究了一类捕食与被捕食的食物链系统的关系, 研究了系统平衡点的稳定性和极限环的存在性, 得到了不同条件下两物种生存之间的变化关系。他们使用的模型都是常微分方程组, 通过分析特征根(或者说特征根实部)的符号来分析平衡点的稳定性, 进而得到种群的生存或死亡的结论。在自然界中, 有些种群向另一个种群的生存区域入侵时, 入侵种群的生存区域是随时间变化的(通常被称为“自由边界”), 所以我们考虑的是自由边界问题, 使用的是反应扩散方程组。

本文考虑的是两种种群竞争模型, 假设A种群在半空间中生存, B种群从一侧入侵A种群, 研究何种状态下B种群能在A种群的生存空间中存活, 以及此时B种群的生存区域, 也分析何种状态下B种群入侵失败。

本文主要研究带有自由边界条件的反应扩散方程组解的渐近行为, 即

$ \left\{\begin{array}{c} u_{t}-u_{x x}=u\left(a_{1}-b_{1} u-c_{1} v\right) \\ t \gt 0,0 \leqslant x \lt h(t) \\ v_{t}-v_{x x}=v\left(a_{2}-b_{2} u-c_{2} v\right) \\ t \gt 0,0 \leqslant x \lt \infty \\ u_{x}(t, 0)=v_{x}(t, 0), u(t, x)=0 \\ t \gt 0, h(t) \leqslant x \lt \infty \\ h^{\prime}(t)=-u_{x}(t, h(t)), \quad t \gt 0 \end{array}\right. $

(1)

式中:h(t)——自由边界, h(0)=h₀ > 0;

u(t, x)——种群A的密度;

v(t, x)——种群B的密度;

a₁, a₂——两种群的内增长率;

c₁, b₂——内部竞争系数;

b₁, c₂——外部竞争系数。

对于自由边界h(t), [0, h(t)]为种群A在t时刻所占领的区域。种群A的初始密度为u(0, x)=u₀(x), x∈[0, h₀]; 种群B的初始密度为v(0, x)=v₀(x), x∈(0, ∞), 种群B的生存区域为半空间(0, +∞), 现在种群A向半空间中传播, 我们主要考虑种群A是否能传播成功。

定理1  式(1)存在唯一解且一致有界, 即对所有t > 0, 存在两个常数M₁和M₂, 使得

$ \begin{array}{l} 0 \lt u(t, x) \leqslant M_{1}, \quad t \gt 0,0 \lt x \lt h(t) \\ 0 \lt v(t, x) \leqslant M_{2}, \quad t \gt 0,0 \lt x \lt \infty \end{array} $

另外, 存在与t无关的常数M₃ > 0, 使得

0 < h′(t)≤M₃

证  明  设u₁(t)是式(2)的解, 即

$ \left\{\begin{array}{l} \frac{\mathrm{d} u}{\mathrm{d} t}=u\left(a_{1}-b_{1} u\right), \quad t \gt 0 \\ u(0)=\left\|u_{0}\right\|_{\infty} \end{array}\right. $

(2)

则由常微分方程的知识可知

$u_{1}(t)=\frac{a_{1}}{b_{1}} \mathrm{e}^{\frac{a_{1}}{b_{1} }t}\left(\mathrm{e}^{\frac{a_{1}}{b_{1} }t}-1+\frac{a_{1}}{b_{1}\left\|u_{0}\right\|_{\infty}}\right)^{-1}$

由比较原理得到

u(t, x)≤u₁(t), t > 0, 0 < x < h(t)

于是

$u(t, x) \leqslant M_{1}:=\sup\limits_{t>0} u_{1}(t)$

又因为v(t, x)满足

$\left\{\begin{array}{l}v_{t}-v_{x x} \leqslant v\left(a_{2}-c_{2} v\right), \quad t>0,0<x<\infty \\ v(0, x)=v_{0}(x) \geqslant 0, \quad 0<x<\infty\end{array}\right.$

所以

$v(t, x) \leqslant \max \left\{\left\|v_{0}\right\|, \frac{a_{2}}{c_{2}}\right\}=: M_{2}$

最后, 构造二次函数

U(t, x)=M₁[2M(h(t)-x)-M ²(h(t)-x)²]

直接计算可以得到

U_t=2M₁M(1-Mh(t)+M)

U_xx=-2M₁M²

$U\left(t_{1}, h(t)-\frac{1}{M}\right)=M_{1} \geqslant u\left(t_{1}, h(t)-\frac{1}{M}\right)$

U(t, h(t))=0=u(t, h(t))

取M充分大, 可以证明

u(t, x)≤U(t, x), t > 0,

$ h(t)-\frac{1}{M} \lt x \lt h(t) $

由数学分析知识可知, 对所有的t≥0有

-u_x(t₁, h(t))≤-U_x(t, h(t))=2MC

所以, h′(t)=-u_x(t, h(t))≤2MC, t > 0。

这里主要考虑种群A是弱竞争者的情形, 即假设

$\frac{a_{1}}{a_{2}}<\min \left\{\frac{b_{1}}{b_{2}}, \frac{c_{1}}{c_{2}}\right\}$

(3)

下面证明若竞争者传播失败, 原来的种群B战胜竞争者而永远生存下去。

定理2  若式(3)成立且v₀≠0, 则

$\lim\limits_{t \rightarrow \infty}(u(t, x), v(t, x))=\left(0, \frac{a_{2}}{c_{2}}\right), \quad x \in[0, \infty)$

证  明  首先, 由上述分析可知

$ \lim\limits_{t \rightarrow \infty} \sup u(t, x) \leqslant \frac{a_{1}}{b_{1}}, \quad x \in[0, \infty) $

同样的, 可证

$ \lim\limits_{t \rightarrow \infty} \sup v(t, x) \leqslant \frac{a_{2}}{c_{2}}, \quad x \in[0, \infty) $

(4)

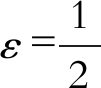
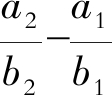
令 , 则由式(4)可知存在t₁, 当t > t₁且x∈[0, ∞)时,

$ u(t, x) \leqslant \frac{a_{1}}{b_{1}}+\varepsilon_{1} $

从而v(t, x)满足

$ \left\{\begin{array}{l} v_{t}-v_{x x} \geqslant v\left(b_{2} \varepsilon_{1}-c_{2} v\right), \quad t \gt t_{1}, 0 \leqslant x \lt \infty \\ v_{x}(t, 0)=0, \quad t \gt t_{1} \\ v\left(t_{1}, x\right) \gt 0, \quad 0 \leqslant x \lt \infty \end{array}\right. $

令v₁(t, x)为式(5)的解, 即

$\left\{\begin{array}{l}w_{t}-w_{x x}=w\left(b_{2} \varepsilon_{1}-c_{2} w\right), \quad t>t_{1}, 0 \leqslant x<\infty \\ w_{x}(t, 0)=0, \quad t>t_{1} \\ w\left(t_{1}, x\right)=v\left(t_{1}, x\right), \quad 0<x<\infty\end{array}\right.$

(5)

则有

$ \lim\limits_{t \rightarrow \infty} v_{1}(t, x)=\frac{b_{2} \varepsilon_{1}}{c_{2}} $

根据比较原理可知, 当时间很大时, 存在t₂, 当t > t₂时,

$ v(t, x) \geqslant v_{1}(t, x) \geqslant \frac{b_{2} \varepsilon_{1}}{c_{2}} $

此时, u和v满足

$\left\{\begin{array}{l}u_{t}-u_{x x}=u\left(a_{1}-b_{1} u-c_{1} v\right), \quad t>t_{2}, 0<x<h(t) \\ v_{t}-v_{x x}=v\left(a_{2}-b_{2} u-c_{2} v\right), \quad t>t_{2}, 0<x<\infty \\ v_{x}(t, 0)=u_{x}(t, 0)=0, \quad t>t_{2} \\ u(t, x) \leqslant \frac{a_{1}}{b_{1}}+\varepsilon, v(t, x) \geqslant \frac{b_{2} \varepsilon_{1}}{2 c_{2}}, \quad t>t_{2}\end{array}\right.$

考虑由式(6)来构造上解和下解, 进而分析解的渐近行为, 即

$ \left\{\begin{array}{l} z_{t}=z\left(a_{1}-b_{1} z-c_{1} w\right), \quad t \gt 0 \\ w_{t}=w\left(a_{2}-b_{2} u-c_{2} v\right), \quad t \gt t_{2} \\ z(0)=\frac{a_{1}}{b_{1}}+\varepsilon, w(0)=\frac{b_{2} \varepsilon_{1}}{2 c_{2}}, \quad t \gt 0 \end{array}\right. $

(6)

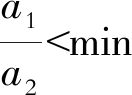
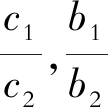
因为 , 由常微分方程组的知识可知

$(z, w) \rightarrow\left(0, \frac{a_{2}}{c_{2}}\right)$

再由比较原理可知

u(t, x) < z(t, x), v(t, x)≥w(t, x)

因此

$ \lim\limits_{t \rightarrow \infty} u(t, x)=0, \lim\limits_{t \rightarrow \infty} v(t, x)=\frac{a_{2}}{c_{2}} $

这里主要考虑种群A入侵种群B, 但种群A是强竞争者, 即

$\frac{a_{1}}{a_{2}}>\max \left\{\frac{b_{1}}{b_{2}}, \frac{c_{1}}{c_{2}}\right\}$

(7)

与以往常微分方程组描述的竞争模型不同的是, 这里得到的都是二分性(二择一)的结论。

定理3  设式(7)成立, (u, v, h)是式(1)的解, 且v₀≠0, 则有下面的二分性结果:

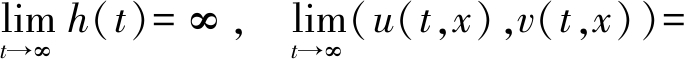
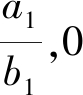
(1) 传播   , x∈(0, +∞);

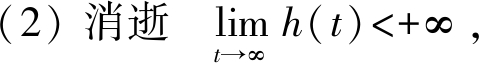且 。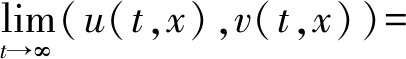

证  明  一是传播现象的证明。由定理1可知

$ \lim\limits_{t \rightarrow+\infty} \sup u(t, x) \leqslant \frac{a_{1}}{b_{1}}, x \in[0, \infty) \\ \lim\limits_{t \rightarrow+\infty} \sup v(t, x) \leqslant \frac{a_{2}}{c_{2}}, x \in[0, \infty)$

(8)

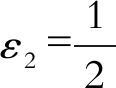
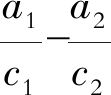
令 , 则存在t₂ > 0, 使得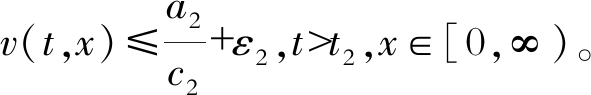于是u满足

$ \left\{\begin{array}{l} u_{t}-u_{x x} \geqslant u\left(c_{1} \varepsilon_{2}-b_{1} u\right), \quad t \gt t_{2}, 0 \leqslant x \lt h(t) \\ u_{x}(t, 0)=0, u(t, h(t))=0, \quad t \gt t_{2} \\ h^{\prime}(t)=-u_{x}(t, h(t)), \quad t \gt t_{2} \\ u\left(t_{2}, x\right) \gt 0, \quad 0 \leqslant x \lt h(t) \end{array}\right. $

从而可知, 对于充分大的正常数L, 存在t_L > t₂, 使得

$ u(t, x) \geqslant \frac{c_{1} \varepsilon_{2}}{2 b_{1}}, \quad t \geqslant t_{L}, 0 \lt x \lt L $

于是u和v满足

$\left\{\begin{array}{l}u_{t}-u_{x x}=u\left(a_{1}-b_{1} u-c_{1} v\right), \quad t>t_{L}, 0<x<L \\ v_{t}-v_{x x}=v\left(a_{2}-b_{2} u-c_{2} v\right), \quad t>t_{L}, 0<x<L \\ u_{x}(t, x)=v_{x}(t, x)=0, \quad t>t_{L} \\ u(t, x) \geqslant \frac{c_{1} \varepsilon_{2}}{2 b_{1}}, v(t, x) \leqslant \frac{a_{2}}{c_{2}}+\varepsilon, \quad t>t_{L}, 0<x<L\end{array}\right.$

为了分析u和v的渐近行为, 先考虑一个常微分方程组

$ \left\{\begin{array}{l} u_{t}=u\left(a_{1}-b_{1} u-c_{1} v\right), \quad t \gt t_{L} \\ v_{t}=v\left(a_{2}-b_{2} u-c_{2} v\right), \quad t \gt t_{L} \\ u_{x}(t, 0)=v_{x}(t, 0), \quad t \gt t_{L} \end{array}\right. $

则

u(t, x)≥z(t), v(t, x)≤w(t)

而由经典的常微分方程竞争模型可知

$ \lim\limits_{t \rightarrow \infty} z(t)=\frac{a_{1}}{b_{1}}, \lim\limits_{t \rightarrow \infty} w(t)=0 $

再结合式(8)得到

$ \lim\limits_{t \rightarrow 0} u(t, x)=\frac{a_{1}}{b_{1}}, \lim\limits_{t \rightarrow \infty} v(t, x)=0 $

二是消逝现象的证明。由文献[5]可知, 当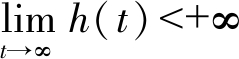时, 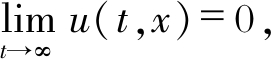故任意ε > 0在充分大的时间T, 当t > T时, u(t, x) < ε。将此结果代入式(1)中的第2个方程, 可得

$\left\{\begin{array}{l}v_{t}-v_{x x} \geqslant v\left(a_{2}-b_{2} \varepsilon-c_{2} v\right), \quad t>0,0<x<\infty \\ v(0, x)=v_{0}(x)>0, \quad 0<x<\infty\end{array}\right.$

先考虑常微分方程

$ \left\{\begin{array}{l} \frac{\mathrm{d} w}{\mathrm{d} t}=w\left(a_{2}-b_{2} \varepsilon-c_{2} v\right), \quad t \gt 0 \\ w(0) \gt 0 \end{array}\right. $

可知

$ \lim\limits_{t \rightarrow \infty} w(t)=\frac{a_{2}-b_{2} \varepsilon}{c_{2}} $

再由比较原理可知, v(t, x)≥w(t)。

结合ε的任意性可知

$ \lim\limits_{t \rightarrow \infty} v(t, x) \geqslant \lim\limits_{t \rightarrow \infty}=\frac{a_{2}}{c_{2}} $

(9)

由式(8)和式(9)可知

$ \lim\limits_{t \rightarrow \infty} v(t, x)=\frac{a_{2}}{c_{2}} $

本文利用带有自由边界条件的反应扩散方程研究了种群的强竞争和弱竞争现象。结果表明, 无论种群的初始密度有多小, 种群都会生存且生存区域不变, 显然本文的结论更符合实际现象。