2016年6月14日, 国家能源局正式启动灵活性改造示范试点项目。根据国家发展和改革委员会、国家能源局印发的《可再生能源调峰机组优先发电试行办法》的专项行动措施意见等相关文件要求, 燃煤电厂需进行相应的灵活性改造, 以提高机组的深度调峰能力。通常, 机组在低负荷运行时, 锅炉的NO_x排放量普遍较高, 加上深度调峰负荷波动频繁, 如何对NO_x排放量进行有效的预测, 以及如何在减少或者不进行就地试验的情况下去完成这项任务就显得十分重要。

相关文献介绍了锅炉燃烧优化技术的研究成果。周建新等人^[1]分析了从20世纪90年代至今, 电站锅炉燃烧优化技术的发展历程。近年来, 人工智能在燃烧优化中的作用日益显著。神经网络属于人工智能方法的主要手段之一, 其相关研究较为多见。比如, 周昊等人^[2-3]对燃煤锅炉氮氧化物燃烧特性的神经网络预报进行了研究, 模型采用反向传播(Back Propagation, BP)算法, 显示的结果与实际情况吻合良好, 模型给出了详细的输入节点、隐节点等重要参数。方海泉等人^[4]采用贝叶斯神经网络遗传算法对锅炉进行了燃烧优化, 实现了锅炉热效率和NO_x排放浓度两个目标的同时优化预报。顾燕萍等人^[5]采用最优MVs决策模型, 对电站锅炉燃烧进行了优化, 其与全局寻优结果接近, 且算法复杂度低、稳定性高, 适用于在线实时优化和自适应更新。王淅芬等人^[6]在上述研究的基础上, 将炉内温度分布, 尤其是炉膛断面最高温度作为新增的输入参数加入BP神经网络算法模型, 提升了NO_x排放预报的准确性。王子杰等人^[7]进一步推进了人工智能在锅炉燃烧中的应用, 不仅采用BP算法得出了模型, 而且利用遗传算法实现了全局寻优。吴智群等人^[8]则采用径向基神经网络模型建模和遗传算法寻优对某600 MW机组锅炉的燃烧进行了优化, 实现了人工智能的良好应用。薛阳等人^[9]利用神经网络控制方法对单神经元比例-积分-导数(Prposration Integral Differential, PID)控制器和BP神经网络PID控制器的汽温控制进行了研究, 结果表明, 神经网络PID控制结构简单, 有较强的鲁棒性, 取得了较好的控制效果。

随着计算机技术的深入发展, 人工智能算法日益模块化。王渡等人^[10]提出了基于改进的BP神经网络的方法, 并引入附加动量项和自适应学习率进行实际建模。计算结果表明, 该模型能够较好地对循环流化床的床温进行预测, 可以反映主要参数变化时循环流化床床温的动态特性, 验证了该建模方法的可行性。徐齐胜等人^[11]利用MATLAB软件对锅炉燃烧基于神经网络的遗传算法进行了优化, 其预报及优化的值是锅炉效率, 结果表明MATLAB软件能够有效处理类似的优化问题。

由于电厂每天的深度调峰低负荷运行时间累计只有几个小时, 而且波动频繁, 在低负荷下的燃烧优化以及就地测试等工作难以参考常规负荷下的相关测试数据。因此, 利用MATLAB软件对低负荷运行时的NO_x排放值(以下简称“NO_x值”)预报建模的研究非常有意义, 可以快速准确地获取选择性催化还原(Selective Catalytic Reduction, SCR)装置入口的NO_x值。本文对NO_x值的预测进行了深入研究, 利用MATLAB软件自带的神经网络工具箱对锅炉在低负荷运行时的NO_x值进行了预报。

锅炉燃烧优化涉及较多的输入量, 比如给煤量、氧量、入炉煤热值、二次风门挡板开度等。本文采用的输入模型数据参考文献[2-3], 一共12个工况, 每个工况29组参数对NO_x值进行预报, 输出量为1个NO_x值, 将隐节点数量从30调整至32, 模块示意图如图 1所示。

图 1 输入、隐节点和输出模块

每次调整训练若干次, 直到误差(均方误差小于0.000 01)以及拟合结果满意为止, 由此来验证MATLAB自带的神经网络方法的预测精确性。再结合笔者采集的某330 MW机组锅炉在深度调峰时低负荷的燃烧侧主要运行数据, 对该机组锅炉在深度调峰时低负荷下的NO_x值进行预报。

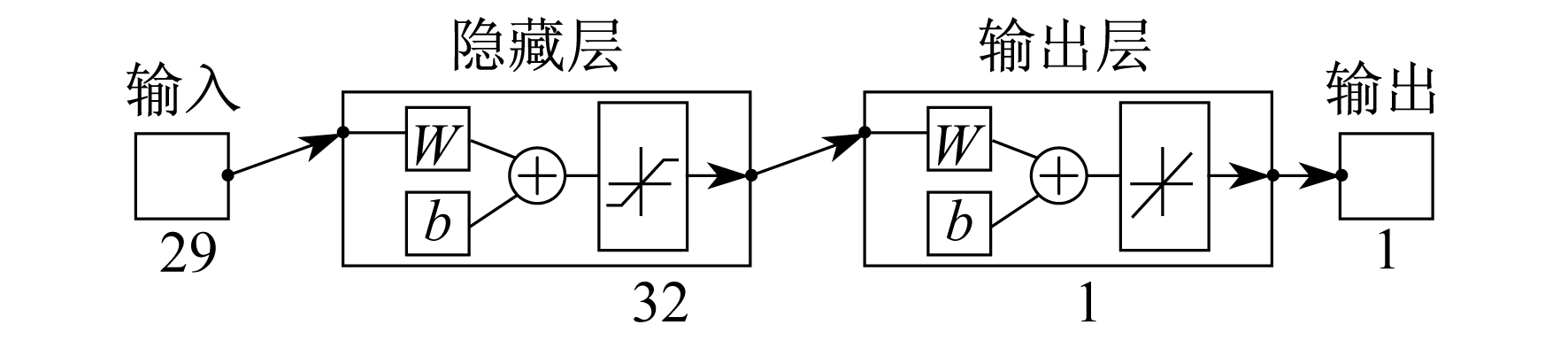
启动MATLAB软件后, 选择神经网络拟合模块, 依次读入作为输入参数的数据矩阵和输出数据矩阵; 采用系统默认的莱文贝格-马夸特(Levenberg-Marquardt)训练算法, 这是一种非线性最小二乘算法, 利用梯度求最大(小)值, 具有梯度法和牛顿法的优点。作为输入的样本数据会被随机地分为训练数据(Training)、验证数据(Validation)和测试数据(Test)。其中, Training数据一般占50%以上, 而另外两个可以调整比例。在本模型中, 3种数据都是从样本中随机选取的。

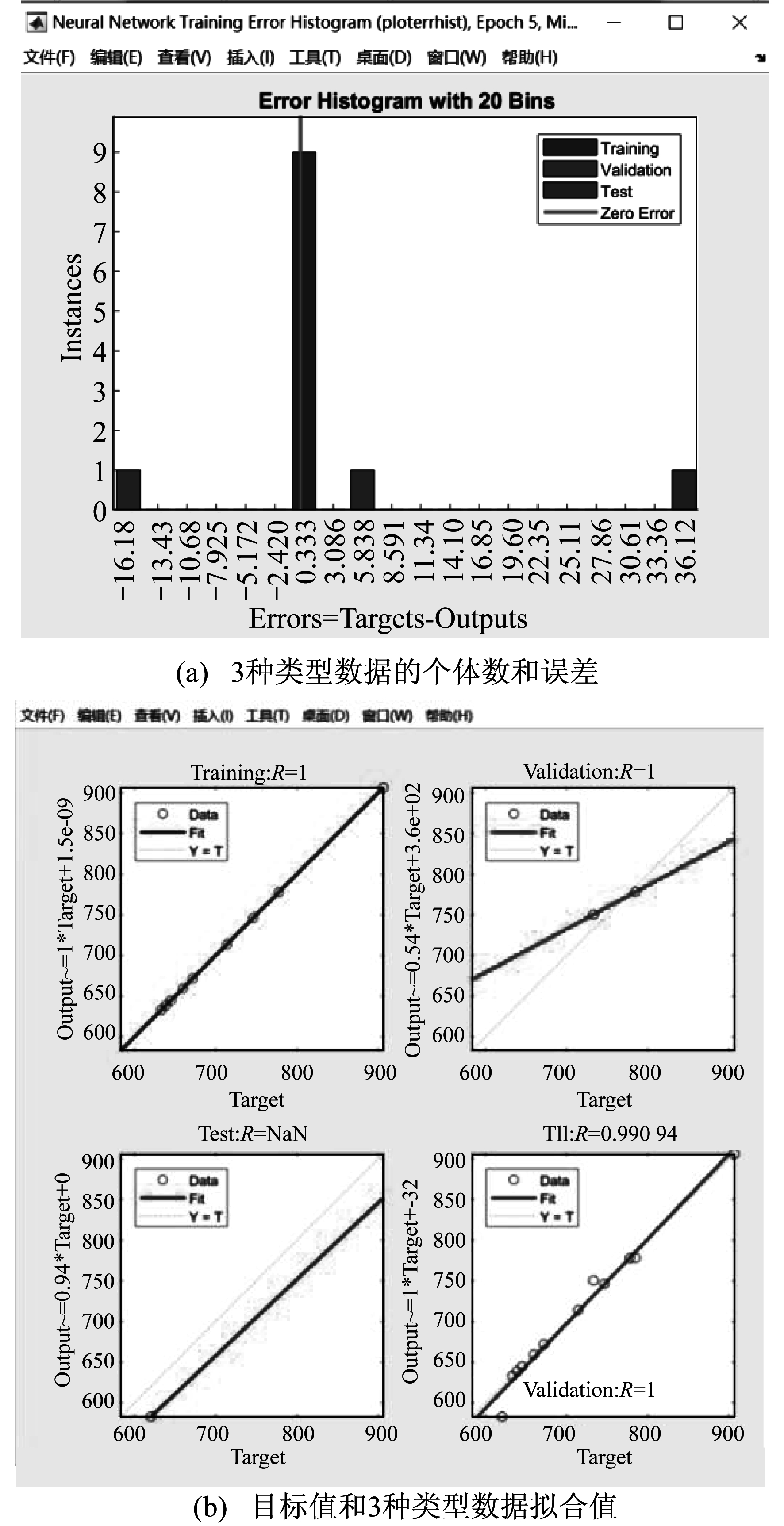
图 2是对文献[2]的训练结果, Traing占50%, Validation和Test各占25%。图 2(a)中, 训练数是9个, 验证数是2个, 测试数是1个, 样本数一共12个, 横坐标为目标值和输出值的差, 即误差值, 纵坐标为样本数, 每个样本中个体数据是29个。图 2(b)是目标值与Training, Validation, Test分别拟合的结果, 其中第4个图表示综合的拟合值, 其R值越接近1, 说明预报效果越好。

图 2 利用文献[2]数据对目标值的训练和拟合结果

由图 2可以看出, 绝大多数训练结果的误差接近于零, 满足输出结果的要求。此时点击MATLAB Function, 可以在主界面编辑器里的代码中找到Layer1和Layer2中的两个矩阵并储存下来。其中, Layer1中的b1和IW1_1, Layer2中的b2和IW2_1;它们分别是图 1中隐藏层和输出层中的W值和b值(W是权重值, b是截距值)。除此以外, 在输出模块中可以找到输出值, 此时的输出值为620.11, 与文献[2-3]中输入数据的NO_x最小值620.17最为接近。综上说明, MATLAB具有神经网络预报的模块化能力, 每一次训练就可以实现自适应地修改各个Layer中的W值和b值, 最终使得输出值与目标值非常接近。

某330 MW亚临界机组的锅炉采用摆动式垂直浓淡煤粉燃烧器, 共有5层, 四角切圆燃烧方式。制粉系统采用一次冷风机正压直吹式制粉系统, 每台锅炉配置5台中速磨煤机, 燃烧设计煤种时, 4台运行, 1台备用。磨煤机型号为HP863型中速磨煤机, 采用动态分离器。

对机组在深度调峰低负荷运行时, 在SCR入口进行NO_x值测试, 需要较多的人员根据相关试验规程, 携带仪器利用网格法进行测试。若在试验数据的基础上, 利用神经网络方法进行训练, 可以对NO_x值进行预报, 减少人力物力的投入, 达到预期的目的。

采用26个物理量(如实发功率、主蒸汽压力等)作为输入参数, 分析49个工况的运行情况, 由于篇幅有限, 这里只罗列15个工况的数据。运行数据采集于机组DCS表盘, 试验数据只有1个, 即在SCR入口处所测得的NO_x值(实测), 每5 min记录一次, 具体如表 1所示。

表 1 部分运行数据和NO_x测试值

下载CSV

工况	机组实 发功率/ MW	一次冷风总管压力/ kPa			空预器后送风温度/ ℃			二次风流量/ (t·h-1)			空预器入口烟气含氧量/ %			给煤机煤量/(t·h-1)				磨煤机入口总风量/(t·h-1)				磨煤机分离器风粉混合物温度/℃				主蒸汽压力设定/MPa	总燃料量/ (t·h-1)	过热器出口蒸汽温度/℃			再热器出口蒸汽温度/℃			空预器入口烟气温度/℃		SCR入口实测 NOx值/ (mg·m-3)
		A侧	B侧		A侧	B侧		A侧	B侧		A侧	B侧		2#	3#	4#		2#	3#	4#		2#	3#	4#				右	左		右	左		A侧	B侧
1	110.13	7.00	7.3		300.28	307.73		92.66	76.93		6.34	6.04		27.47	24.34	25.67		105.83	89.56	107.35		70.02	69.96	71.57		11.27	76.90	511.71	541.75		474.33	484.50		319.37	322.91	835.13
2	108.48	7.01	7.3		300.16	307.63		93.09	76.55		6.29	5.98		27.00	24.15	25.43		105.49	89.34	107.46		69.96	69.92	71.50		11.27	77.03	512.24	542.25		474.59	484.92		319.38	322.74	841.66
3	107.27	7.02	7.3		300.05	307.54		94.40	76.86		6.27	5.93		27.11	24.09	25.33		106.21	88.52	107.56		69.91	69.89	71.44		11.27	77.15	512.77	542.76		474.85	485.33		319.40	322.56	767.95
4	106.83	7.02	7.3		299.94	307.45		90.10	75.08		6.24	5.92		27.28	24.30	25.55		104.97	90.39	107.67		69.87	69.85	71.37		11.27	77.28	513.29	543.26		475.11	485.74		319.41	322.38	797.65
5	107.16	7.03	7.3		299.83	307.35		91.64	75.36		6.25	5.92		27.44	24.51	25.77		105.66	89.45	107.50		69.82	69.81	71.30		11.27	77.41	513.82	543.36		475.37	486.16		319.43	322.20	818.04
6	107.25	7.04	7.3		299.71	307.26		92.04	80.89		6.29	5.98		27.61	24.72	25.99		105.96	88.88	107.27		69.78	69.78	71.23		11.27	77.53	514.35	543.17		475.63	486.57		319.44	322.02	841.07
7	107.72	7.04	7.3		299.60	307.17		96.46	75.30		6.32	6.01		27.49	24.57	25.83		105.25	89.44	107.17		69.74	69.74	71.17		11.27	77.66	514.87	542.98		475.88	486.98		319.46	321.84	788.14
8	106.41	7.08	7.3		299.49	307.07		93.68	78.63		6.32	5.98		27.10	24.18	25.34		105.79	90.41	107.35		69.69	69.70	71.10		11.27	77.04	515.40	542.80		476.14	487.40		319.47	321.66	770.50
9	106.09	7.12	7.3		299.38	306.98		92.75	73.22		6.34	5.98		26.86	23.98	25.20		106.33	90.80	107.54		69.65	69.67	71.03		11.27	76.39	515.92	542.61		476.40	487.81		319.49	321.49	754.65
10	106.60	7.12	7.3		299.27	306.89		90.81	76.49		6.34	6.01		27.00	24.11	25.33		106.20	90.09	107.63		69.60	69.63	70.96		11.27	76.12	516.45	542.42		476.66	488.22		319.50	321.31	810.43
11	106.85	7.12	7.3		299.15	306.79		90.89	77.65		6.32	6.01		27.14	24.24	25.46		106.17	89.43	107.64		69.56	69.59	70.90		11.27	76.54	516.98	542.23		476.92	488.64		319.52	321.13	844.66
12	106.89	7.11	7.3		299.04	306.70		94.28	78.42		6.34	6.04		27.27	24.37	25.59		105.52	89.65	107.66		69.51	69.56	70.83		11.27	76.95	517.50	542.04		477.18	488.79		319.53	320.95	818.24
13	106.75	7.10	7.3		298.93	306.61		92.24	78.65		6.34	6.07		27.41	24.50	25.73		104.67	89.91	107.67		69.47	69.52	70.76		11.27	77.37	518.03	541.85		477.44	488.92		319.55	320.77	784.80
14	106.54	7.11	7.3		298.82	306.51		93.86	74.69		6.36	6.10		27.55	24.63	25.86		105.61	89.72	107.68		69.43	69.48	70.69		11.27	77.78	518.55	541.66		477.69	489.06		319.56	320.87	772.09
15	107.72	7.13	7.3		298.71	306.42		92.91	76.67		6.39	6.13		27.73	24.79	26.02		105.69	90.14	107.69		69.38	69.44	70.63		11.27	78.20	519.08	541.47		477.95	489.20		319.58	321.00	762.47

由表 1可以看出, 15个工况中, 已知运行参数为26个, 试验测试数据为1个(SCR入口NO_x值)。低负荷下, 锅炉投运2^#, 3^#, 4^#共3台磨煤机, 负荷逐步降低, 最低达到32.4%。

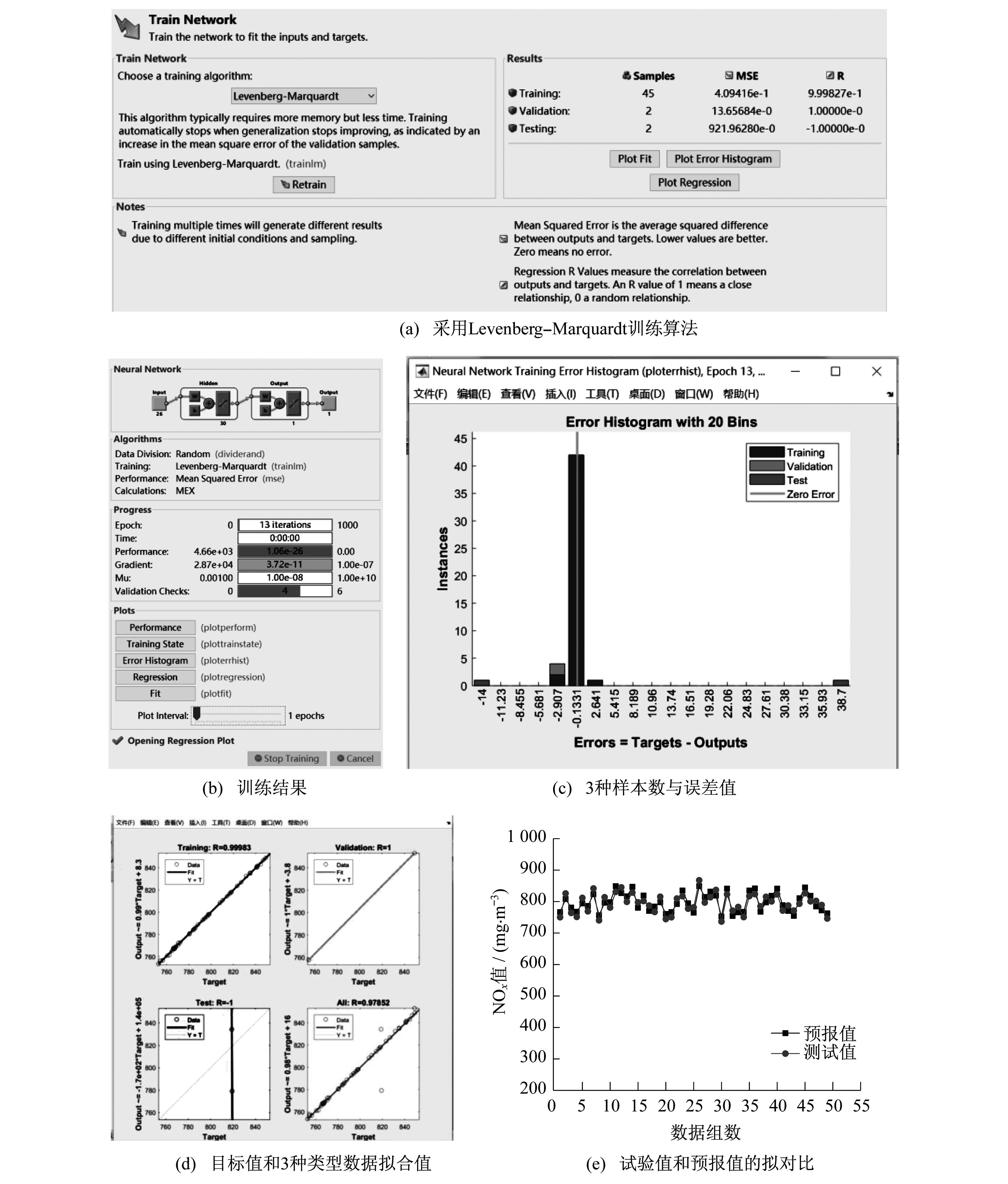
以预报NO_x值为目的, 利用MATLAB软件对数据进行神经网络算法的训练。确定隐节点为30个, Training占90%, Validation占5%, Test占5%, 训练结果如图 3所示。

图 3 训练过程和结果

图 3(a)中, 选择了Levenberg-Marquardt算法, 3种数据在样本中的划分是随机的。图 3(b)中, 3种数据经过13次迭代就可达到所需的效果。由图 3(c)和图 3(d)可以看出, Training数据样本为45个, Validation和Test各2个, 其中Test值是选取的误差最大值和最小值(分布在最左侧、最右侧); 在图 3(d)中, 总的拟合值与目标值的R值为0.978, 拟合精度较好。生成的Function代码中可以看到最小值是752.70, 与第9组的754.65相当接近, 记录下Layer1和Layer2中W值和b值, 进而利用这些数值作为权重值和截距值, 对49组输入数据的NO_x值进行预报, 结果如图 3(e)所示。由图 3(e)可以看出, 预报值十分接近测试值, 这是因为经过不断的训练, 目标值与输出值的拟合R值接近0.98。综合拟合值R越接近1, 说明预报结果与目标值越接近, 故可以认为预报值能在实际运行过程中代表测试值。

本文利用MATLAB软件首先对某文献中罗列的锅炉燃烧优化数据进行了神经网络算法的校核, 采用多次训练, 得到了与文献中较为接近的结果。然后对某330 MW机组锅炉在深度调峰低负荷运行时, 进行了5 min 1组数据的NO_x值的实测, 结合神经网络算法, 对NO_x值进行了预报, 经过多次训练, 得出了较好的结果。最终模型的输出值与目标值的拟合R值接近0.98, 认为在日常机组运行过程中, 尤其是灵活性深度调峰期间, 可以采用神经网络算法来进行NO_x值的预报, 以达到降低工作量、减少成本的目的。