|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-04-02
基金项目: 国家自然科学基金青年科学基金(51607111);上海市科学技术委员会地方院校能力建设项目(15160500800);上海市高校青年教师培养资助计划(ZZsdl15142)
中图法分类号: TM734;TM721
文献标识码: A
文章编号: 1006-4729(2019)05-0503-07
|
摘要
发展区域综合能源系统是提高能源利用率、缓解可再生能源消纳问题及改善环境的重要途径。对区域综合能源系统各类设备进行了建模, 以经济性最优及一定环保性为目标, 建立了区域综合能源系统优化调度模型, 然后采用混合整数线性规划模型对实例问题进行求解, 并以夏季典型日为例, 分析说明了优化调度结果, 以验证模型和优化算法的可行性和经济性。
关键词
区域综合能源系统; 优化调度; 混合整数线性规划; 实时互补; 经济环保
Abstract
The development of regional integrated energy system is an important way to improve energy efficiency, alleviate the problem of renewable energy consumption and improve environment.The various types of equipment in the regional integrated energy system are modeled, and the regional integrated energy system optimization scheduling model is established with the aim of economical optimality and certain environmental protection.Then the mixed integer linear programming model is used to solve the example problem and the typical days of summer is taken as an example to illustrate the optimization of the scheduling results and verify the feasibility and economy of the model and optimization algorithm.
Key words
regional integrated energy system; optimized scheduling; mixed integer linear programming; real-time complementary; economic and environmental protection
在能源危机和环境污染的双重压力下, 区域综合能源系统(Regional Integrated Energy System, RIES)得到了发展[1], 集气、电、冷、热多种能源于一体, 形成了复杂的能源结构。因此, 发展RIES对于实现多能互补、提高能源利用率具有重要意义[2]。
目前国内外已有不少关于RIES能量优化调度方面的研究。文献[3]引入能源集线器(Energy Hub, EH)描述了RIES中气、电、冷、热不同形式能源之间的关系, 并采取分层优化的方法进行了优化求解; 文献[4]考虑了RIES中热力管道传输延迟、热损失动态特性以及用户的供需柔性, 建立了管道储热模型, 提升了系统的灵活性; 文献[5]从提高经济效益角度出发, 在RIES中配置了冷、热、电混合储能并进行了双层优化求解。
本文综合考虑了RIES中气、电、冷、热资源, 以经济性和一定环保性为目标, 建立了混合整数线性规划模型, 并通过算例分析验证了所建模型的正确性和经济性。
1 RIES设备建模
1.1 微型燃气轮机
在RIES中, 微型燃气轮机(Micro Turbine, MT)通过燃烧天然气生产电能和热能, 在联供模式运行下MT的能源利用效率可达80%。它是实现冷热电三联供的核心设备。本文涉及的MT数学模型主要考虑功率输出与消耗成本, 其模型表达式为
| $ \left\{\begin{array}{l} Q_\mathrm{MT}(t)=\frac{P_\mathrm{MT}(t)\left(1-\eta_\mathrm{MT}-k\right)}{\eta_\mathrm{MT}} \\ Q_{\mathrm{wh}}(t)=Q_\mathrm{MT}(t) C_{\mathrm{OP}} \\ Q_{\mathrm{sh}}(t)=Q_\mathrm{MT}(t) C_{\mathrm{OP}} \eta_{\mathrm{wh}} \\ C_\mathrm{MT}(t)=\frac{\sum\left[Q_{\mathrm{l}}(t)-Q_{\mathrm{sh}}(t)\right] \Delta t}{C_{\mathrm{OP}} \lambda \mathrm{L}} C_{\mathrm{gas}}(t) \end{array}\right. $ | (1) |
式中:QMT(t), PMT(t)——MT在任意t时刻的产热功率和产电功率, kW;
ηMT——MT发电效率, %;
k——MT散热损失系数, 取值为0.03;
Qwh(t), Qsh(t)——MT在任意t时刻的余热产热功率和排烟产热功率, kW;
COP——MT的制热系数, 取值为1.2;
ηwh——MT的余热回收率, %;
CMT(t)——任意t时刻时MT燃料消耗成本, 元;
Ql(t)——任意t时刻时MT的负荷量, kW;
Δt——机组运行的一个采样周期, h;
λ——燃料燃烧的效率值, %;
L——燃料燃烧的低热值, 如天然气可取9.7 Wh/m3;
Cgas(t)——任意t时刻燃料价格, 元/m[6]。
1.2 太阳能发电设备
光伏发电技术在近10年来得到了快速发展。光伏发电系统具有清洁环保、太阳能资源充沛、开发便捷、建设周期短等优点。本模型采取简易模型简化计算, 只考虑光照强度和温度两个主要因素的影响, 模型表达式为
| $ P=\frac{P_{0} G\left[1+k\left(T-T_{0}\right)\right]}{G_{0}} $ | (2) |
式中:P——光伏输出功率, kW;
P0——理想状态下光伏最大功率, kW;
G, G0——实际光照强度和标准光照强度, Lx[7];
k——实际温度, ℃;
T0——参考温度, ℃。
1.3 燃气锅炉
燃气锅炉通过燃烧天然气获取热能, 其热能转换效率可达90%, 是一种运行稳定的清洁能源利用形式。在一定负荷条件下, 可认定其输入输出是稳定的线性关系, 模型表达式为
| $L_{\mathrm{GB}}(t)=\eta_{\mathrm{GB}} \lambda_{\mathrm{gas}} P_{\mathrm{GB}}(t)$ | (3) |
式中:LGB(t)——任意t时刻燃气锅炉输出的热功率, kW;
ηGB——燃气锅炉的供热效率, %;
λgas——燃气锅炉的转换效率, %;
PGB(t)——任意t时刻燃气的消耗速率, kW[8]。
1.4 热泵
热泵可以将土壤、工业废热中的低品位热输送至高位热源, 是一种高效节能装置。根据其制热(冷)特性, 模型表达式为
| $ \left\{\begin{array}{l} Q_{\mathrm{PH}}=E_{\mathrm{P}} C_{\mathrm{OP}, \mathrm{P}} \\ Q_{\mathrm{PC}}=E_{\mathrm{P}} C_{\mathrm{OP}, \mathrm{P}} \end{array}\right. $ | (4) |
式中:QPH, QPC——热泵系统的制热量和制冷量, kWh;
EP——热泵系统的耗电量, kWh;
COP, P——热泵系统的性能系数。
1.5 吸收式制冷机组
吸收式制冷机组利用能源生产设备产生的余热进行制冷, 可以提高系统的整体能源利用率, 是联供系统的重要组成部分。模型表达式为
| $Q_{\mathrm{Br}, \mathrm{c}}=Q_{\mathrm{Br}, \mathrm{h}} C_{\mathrm{OP}, \mathrm{Br}}$ | (5) |
式中:QBr, c, QBr, h——吸收式制冷机组的制冷量和余热吸收量, kWh;
COP, Br——吸收式制冷机组的制冷系数, 取值为0.8[9]。
1.6 电制冷机组
电制冷机组以电制冷, 一般作为联供系统中的补冷装置, 通常在电价效益高时进行制冷作业。这样不仅能提升能源的综合利用效率, 也能提升系统整体的经济运行水平。其模型表达式为
| $Q_{\mathrm{ec}}=E_{\mathrm{ec}} C_{\mathrm{OP}, \mathrm{ec}}$ | (6) |
式中:Qec, Eec——电制冷机组的制冷量和耗电量, kWh;
COP, ec——电制冷机组的制冷系数[10]。
1.7 储电装置
储电装置不仅能缓解系统对供需瞬时平衡的要求, 还能改善电能质量, 维护系统平稳, 实现削峰填谷。本文对其工作模式进行了研究, 模型表达式为
| $E_{\mathrm{s}}(t+1)=\left\{\begin{array}{l}E_{\mathrm{s}}(t)+\Delta t \frac{p_{\mathrm{c}, t}}{\eta_{\mathrm{c}}}, \text { 充电模式 } \\ E_{\mathrm{s}}(t)-\Delta t \frac{p_{\mathrm{d}, t}}{\eta_{\mathrm{d}}}, \text { 放电模式 }\end{array}\right.$ | (7) |
| $\left\{\begin{array}{l}E_{\mathrm{s}, \mathrm{in}}=\frac{1}{\eta_{\mathrm{c}}} \int_{\Delta t-1}^{\Delta t} p_{\mathrm{c}, t} \mathrm{d} t \\ E_{\mathrm{s}, \mathrm{out}}=\frac{1}{\eta_{\mathrm{d}}} \int_{\Delta t-1}^{\Delta t} p_{\mathrm{d}, t} \mathrm{d} t\end{array}\right.$ | (8) |
式中:pc, t, pd, t——t时刻储电装置的充放电功率, kW;
ηc, ηd——储电装置的充放电效率;
Es(t)——t时刻的电量, kWh;
Es, in, Es, out——Δt时间内储电装置的存储电量和释放电量, kWh。
1.8 储冷和储热装置
在综合能源系统中, 储冷和储热装置可以对系统内产生的多余的冷量和热量进行储存。储冷和储热是一种灵活的能量转换方式, 用于满足区域内负荷种类的变化需求。本文对其工作模式进行了研究。由于储冷与储热模式相似, 所以可使用相同的模型, 模型表达式为
| $ \left\{\begin{array}{c} \begin{aligned} Q_{d(h+1), \mathrm{sc}}=& \eta_{\mathrm{sc}} Q_{d h, \mathrm{sc}}+B_{d h, \mathrm{sc}, \mathrm{in}} Q_{d h, \mathrm{sc}, \mathrm{in}}-\\ & B_{d h, \mathrm{sc}, \text { out }} Q_{d h, \mathrm{sc}, \mathrm{out}} \end{aligned} \\ \begin{aligned} Q_{(d+1) 1, \mathrm{sc}}=& \eta_{\mathrm{sc}} Q_{d 24, \mathrm{sc}}+B_{d h, \mathrm{sc}, \mathrm{in}} Q_{d 24, \mathrm{sc}, \mathrm{in}}-\\ & B_{d h, \mathrm{sc}, \mathrm{out}} Q_{d 24, \mathrm{sc}, \mathrm{out}} \end{aligned} \\ \begin{aligned} B_{\mathrm{sc}, \mathrm{in}}+B_{\mathrm{sc}, \mathrm{out}} \leqslant 1 \end{aligned} \end{array}\right. $ | (9) |
式中:d——天, d=1, 2, 3, …, 364;
h——小时, h=1, 2, 3, …, 24;
Qsc——储冷装置/储热装置当前存储的冷量和热量, kWh;
Qdh, sc, in, Qdh, sc, out——存储和释放的冷量和热量, kWh;
ηsc——储冷装置和储热装置的存储效率;
Bsc, in, Bsc, out——储冷装置/储热装置的储放标志, 取值0或1, 0为关, 1为开。
2 RIES优化调度模型
2.1 目标函数
本模型考虑在满足系统内用户需求的同时达到经济性最优的目的, 并且保证具有一定的环保性。目标函数构造如下。
(1) 系统日运行费用为
| $ \begin{aligned} C_{\mathrm{W}}=& \sum_{h=1}^{24}\left(Q_{d h, \mathrm{gas}} C_{\mathrm{gas}}+E_{d h, \mathrm{grid}} C_{\mathrm{e}}-\right.\\ & \left.E_{d h, \text { solar }} C_{\text {solar }}\right) \end{aligned} $ | (10) |
式中:CW——系统日能耗成本, 元;
Qdh, gas——天然气消耗量, kWh;
Cgas——天然气价, 元/kWh;
Edh, grid——综合能源系统与大电网的交换电量, Edh, grid > 0时表示从大电网购电, Edh, grid < 0时表示向大电网卖电(此时产生的经济效益可以抵消能耗成本), kWh;
Ce——大电网电价, 元/kWh;
Edh, solar——光伏的发电量, kWh;
(2) 系统碳排放成本为
| $ C_{\mathrm{a}}=\sum\limits_{h=1}^{24}\left(Q_{d h, \mathrm{gas}} \lambda_{\mathrm{gas}}+M_{d h, \mathrm{coal}} \lambda_{\mathrm{coal}}\right) $ | (11) |
式中:Ca——系统日碳排放总量, g;
λgas——天然气碳排放系数, g/kWh;
Mdh, coal——从电网购电折合的标煤消耗量;
λcoal——标煤碳排放系数, g/kWh。
表 1
碳排放成本
| 系统碳排放系数 | 电网购电碳排放系数 | 治理费用/(元·g-1) |
| (g·kWh-1) | ||
| 0.225 | 0.321 | 0.00467 |
2.2 约束条件
基于上述系统中各设备模型的表达式, 从能量平衡角度提出以下3种约束。
(1) 冷平衡约束。系统中的制冷装置主要是吸收式制冷机组、电制冷机组、热泵装置和储冷装置。区域冷平衡约束可以表示为
| $Q_{\mathrm{Br}, \mathrm{c}}+Q_{\mathrm{ec}}+Q_{\mathrm{pc}}+Q_{\mathrm{sc}, \text { out }}=Q_{\mathrm{c}}+Q_{\mathrm{sc}, \mathrm{in}}$ | (12) |
式中:Qsc, out——蓄冷装置的放冷量, kWh;
Qc——区域冷负荷的需求量, kWh;
Qsc, in——蓄冷装置的储冷量, kWh[14]。
(2) 热平衡约束。系统中的制热装置主要是微型燃气轮机、燃气锅炉、热泵以及储热装置。区域热平衡约束可以表示为
| $Q_{\mathrm{MT}}+Q_{\mathrm{GB}}+Q_{\mathrm{ph}}+Q_{\mathrm{sh}, \text { out }}=Q_{\mathrm{h}}+Q_{\mathrm{sh}, \mathrm{in}}$ | (13) |
式中:QGB——燃气锅炉的制热量, kWh;
Qsh, out, Qsh, in——蓄热装置的放热量和储热量, kWh[15-16];
Qh——区域热负荷的需求量, kWh。
(3) 电平衡约束。系统中的供电装置主要是光伏、微型燃气轮机、大电网电量交换以及储电装置, 涉及到的耗电装置是热泵和电制冷机组。区域电平衡约束可以表示为
| $E_{\mathrm{MT}}+E_{\mathrm{solar}}+E_{\mathrm{s}, \mathrm{out}}+E_{\mathrm{grid}}= \\ E+E_{\mathrm{p}}+E_{\mathrm{ec}}+E_{\mathrm{s}, \mathrm{in}}$ | (14) |
式中:EMT——MT的发电量, kWh;
Esolar——光伏的发电量, kWh;
Egrid——从电网购得的电量, kWh;
E——区域电负荷的需求量, kWh;
Ep——热泵机组的耗电量, kWh;
Eec——电制冷机组的耗电量, kWh。
2.3 求解方法
RIES的优化调度问题是一个混合整数线性规划模型求解问题。采用优化模型求解的标准形式为
| $ \left\{\begin{array}{l} \min C^{\mathrm{T}} x \\ \mathrm{s} . \mathrm{t} . A x=b \\ x_{\mathrm{min}} \leqslant x \leqslant x_{\max } \end{array}\right. $ | (15) |
式(15)中, 优化变量x包括各能源输入量、各类设备的出力及电网购电量; 等式约束表示系统功率平衡约束条件; 不等式表示系统中各变量约束情况, 包括设备容量约束、设备出力等约束条件。本文在GAMS(General Algebraic Modeling System)上采用混合整数线性规划模型编写相关优化程序进行求解[17-18]。
3 RIES优化调度算例分析
3.1 算例系统概况
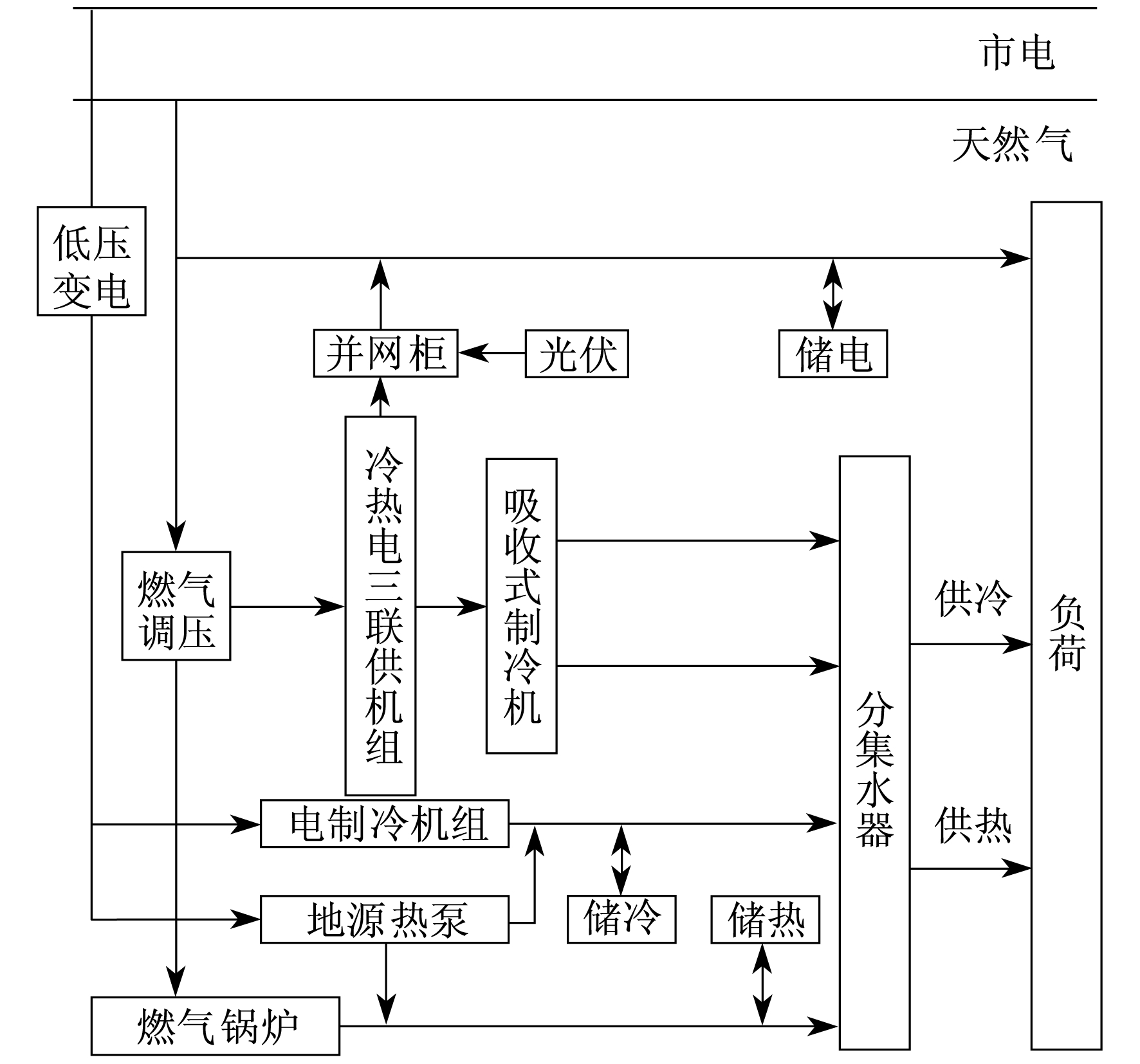
以某RIES项目为例, 系统由燃气三联供机组、电制冷机组、燃气锅炉、光伏以及相应储能设备组成, 各设备模型与上文描述一致。利用调度策略实现区域能量供需平衡, 以达到系统优化的目标。
该系统以微型燃气轮机为核心, 在产电的同时, 高温烟气进入热交换装置进行供热, 烟气余热进入吸收式制冷机进行供冷。此外, 加装的燃气锅炉和电制冷机组分别满足用户侧的热、冷高峰需求, 并配套了地源热泵机组在必要时进行补冷或补热; 基于项目所在地的光照资源, 系统还加装了光伏发电单元。系统结构如图 1所示。
该系统设备列表及设备具体参数如表 2所示。
表 2
供能设备参数
| 设备名称 | 参数名称 | 数值 |
| 微型燃气轮机 | 最大发电功率/kW | 1 000 |
| 最小发电功率/kW | 80 | |
| 发电效率 | 0.33 | |
| 运行维护费/(元·kWh-1) | 0.008 | |
| 吸收式制冷机 | 制冷能效比 | 0.8 |
| 最大输出功率/kW | 500 | |
| 运行维护费/(元·kWh-1) | 0.008 | |
| 电制冷机组 | 制冷能效比 | 3.0 |
| 最大输出功率/kW | 800 | |
| 运行维护费/(元·kWh-1) | 0.002 | |
| 地源热泵 | 制冷能效比 | 5.0 |
| 制热能效比 | 4.0 | |
| 运行维护费/(元·kWh-1) | 0.007 6 | |
| 燃气锅炉 | 最大输出功率/kW | 800 |
| 供热效率 | 0.9 | |
| 运行维护费/(元·kWh-1) | 0.02 | |
| 光伏电池 | 最大发电功率/kW | 150 |
| 运行维护费/(元·kWh-1) | 0.003 2 |
本文研究的RIES优化调度模型的调度周期为24 h, 调度间隔为1 h。下面以夏季典型日优化结果为例进行分析。
系统中3种能量形式的储能设备的具体参数如表 3所示。分时电价及时段划分如表 4所示。天然气价格为3.50元/kWh。
表 3
储能设备参数指标
| 设备 | 充能功率/kW | 充能效率 | 放能效率 | 自损耗系数 | |
| 最大 | 最小 | ||||
| 储电装置 | 800 | 80 | 0.85 | 0.85 | 0.003 |
| 蓄冷装置 | 500 | 50 | 0.80 | 0.80 | 0.002 |
| 蓄热装置 | 500 | 50 | 0.80 | 0.80 | 0.002 |
表 4
分时电价及时段划分
| 价格类型 | 单价/(元·kWh-1) | 时段 |
| 峰时电价 | 0.972 | 12:00~15:00; 19:00~22:00 |
| 平时电价 | 0.674 | 08:00~12:00; 15:00~19:00 |
| 谷时电价 | 0.378 | 22:00~08:00 |
3.2 优化结果分析
根据算例设定参数, 按照电能优先运行、冷热优先运行及实时互补运行策略进行调度结果求解, 并对结果进行分析对比。
电能优先运行策略和冷热优先运行策略的系统方案具体如下。
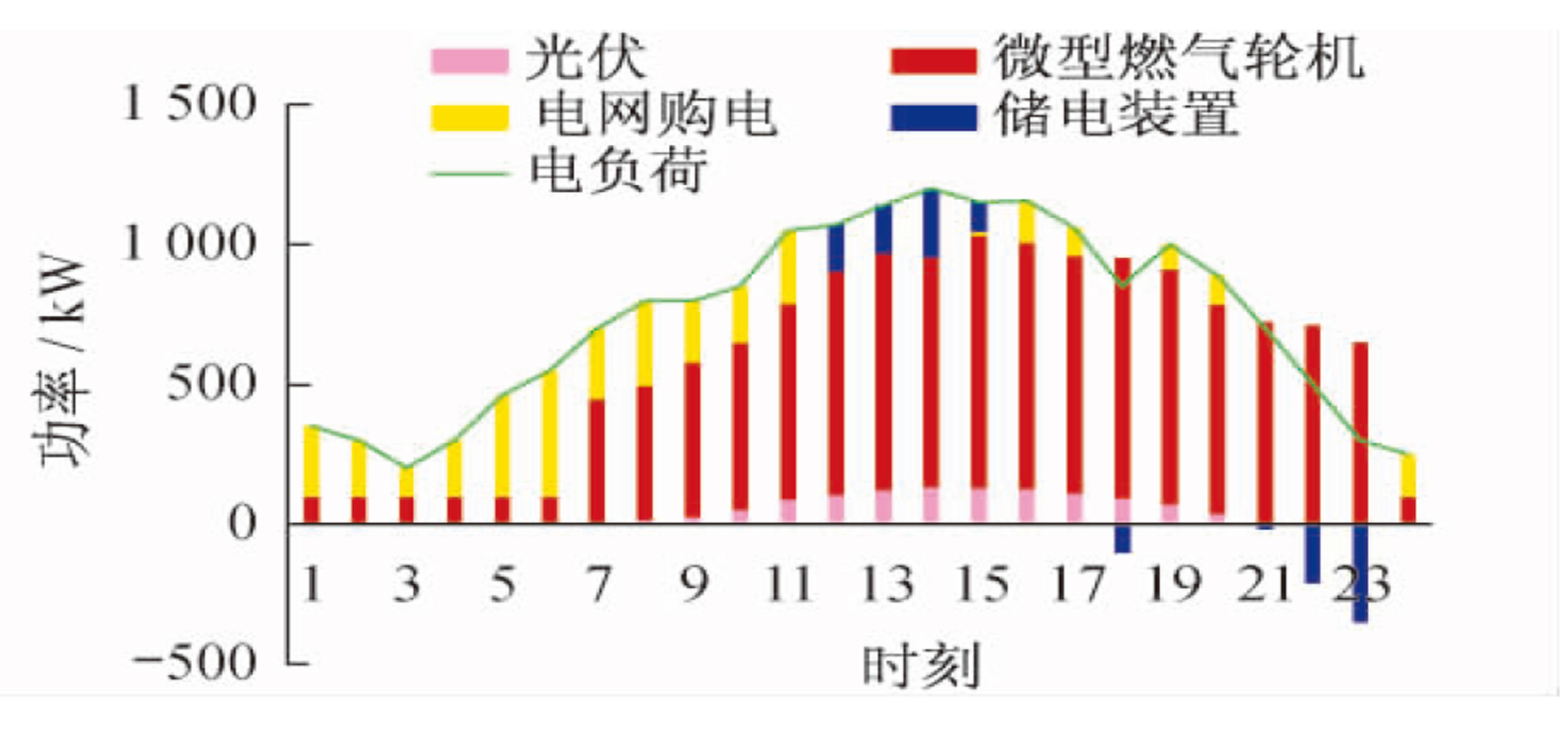
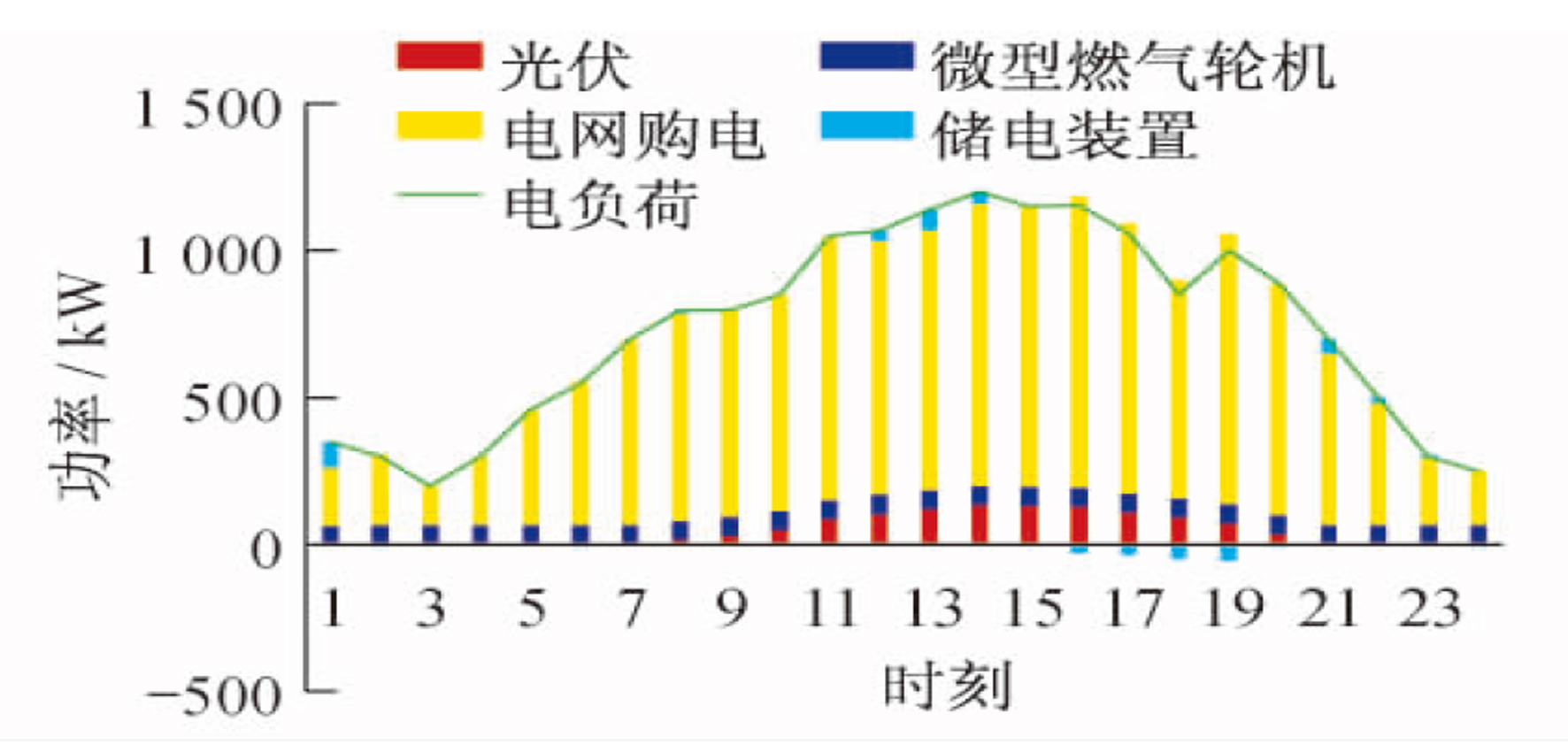
(1) 供电工况下, 在电价谷时段, 从电网购电最具有经济效益。考虑厂区日负荷需求的稳定性, 系统中MT一直处于运行状态, 但在谷时段, MT以满足基本负荷需求的最低出力功率运行。考虑储能装置的使用寿命, 此时并没有选择进行谷时段充电, 否则会造成一定的成本对冲行为。在电价平时段, 随着厂区负荷需求的递增, 同时满足冷热负荷的需求变化, MT机组进入正常运行状态, 此时MT的发电效益与电网购电相当。此时光伏出力可以补充少部分的电力需求。考虑到峰时电价不进行购电, 平时段燃气轮机在个别时间间隔运行时产生的多余电量通过储电装置进行储存, 由此时储存的电量对部分峰时段的负荷进行差额补充。电负荷电能优先调度结果如图 2所示。
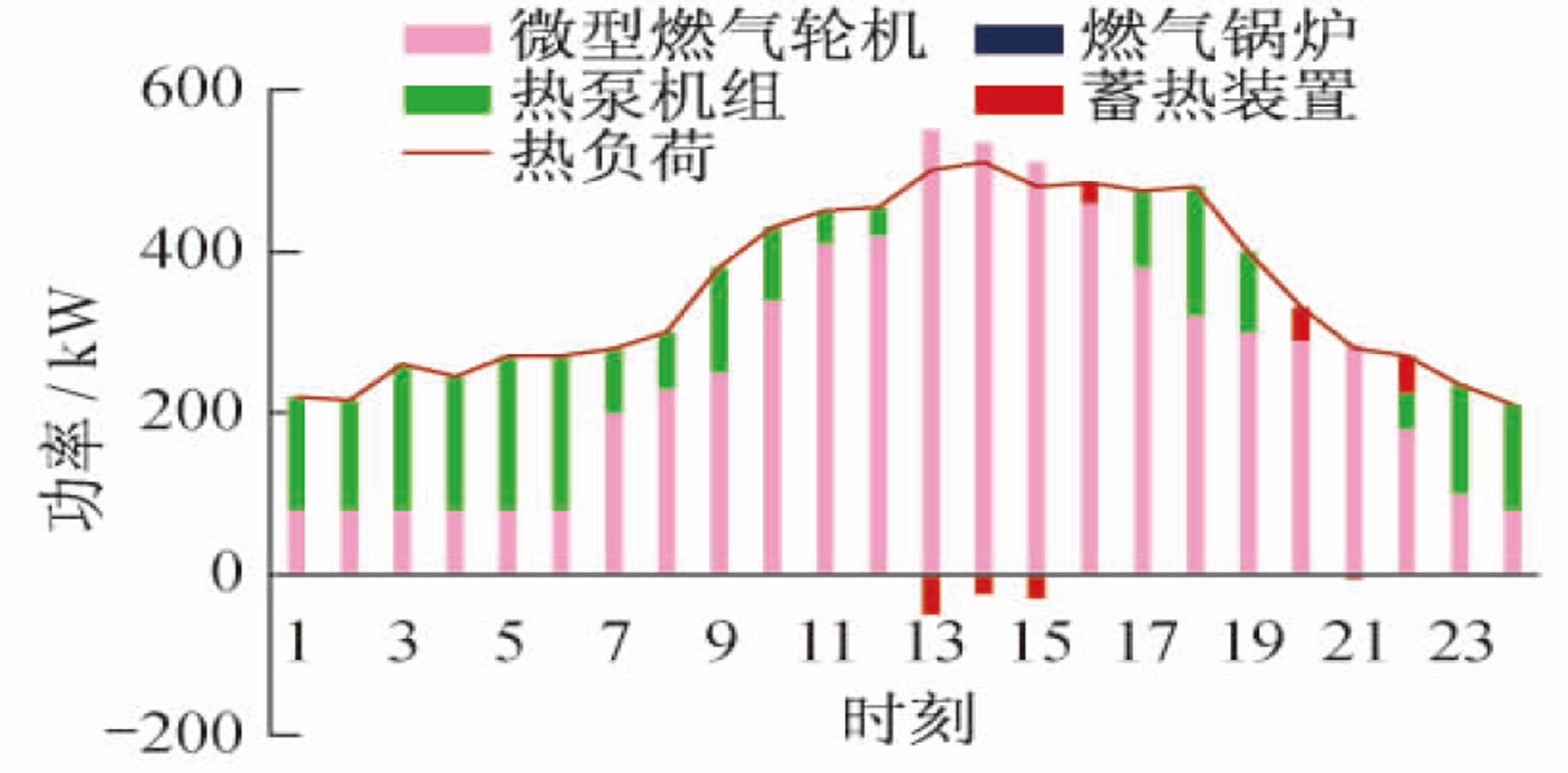
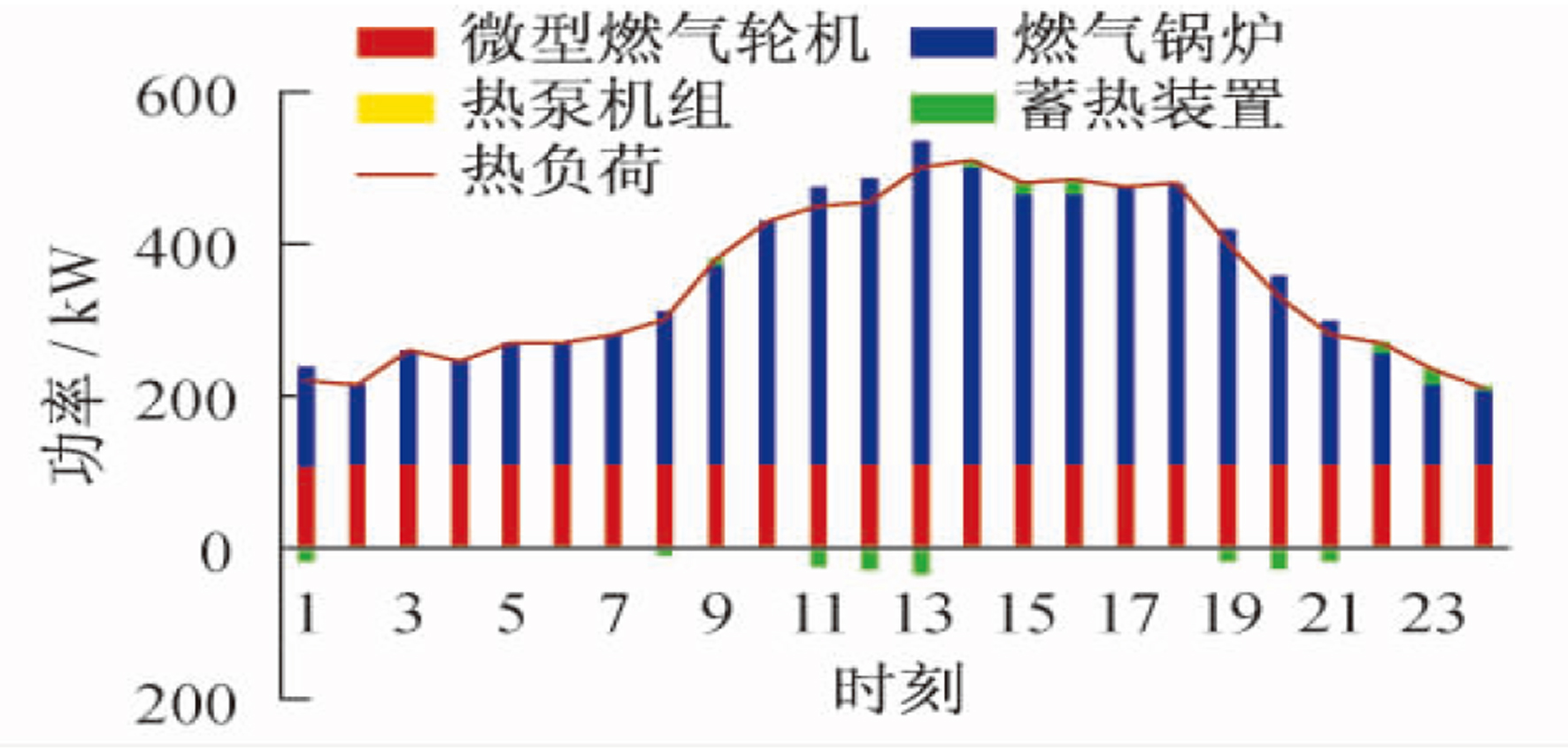
(2) 供热工况下, 夏季厂区的热负荷主要来自生产的基本需求, 负荷量偏低, 负荷曲线走势与电负荷差别不大。同样在谷时段, 微型燃气轮机的运行状态产热功率不足以满足热负荷需求, 此时开启热泵机组, 利用低电价进行补充供热, 峰平时段由微型燃气轮机正常运行产生的多余热量进入蓄热装置, 用以补充个别时段的差额。热负荷冷热优先调度结果如图 3所示。
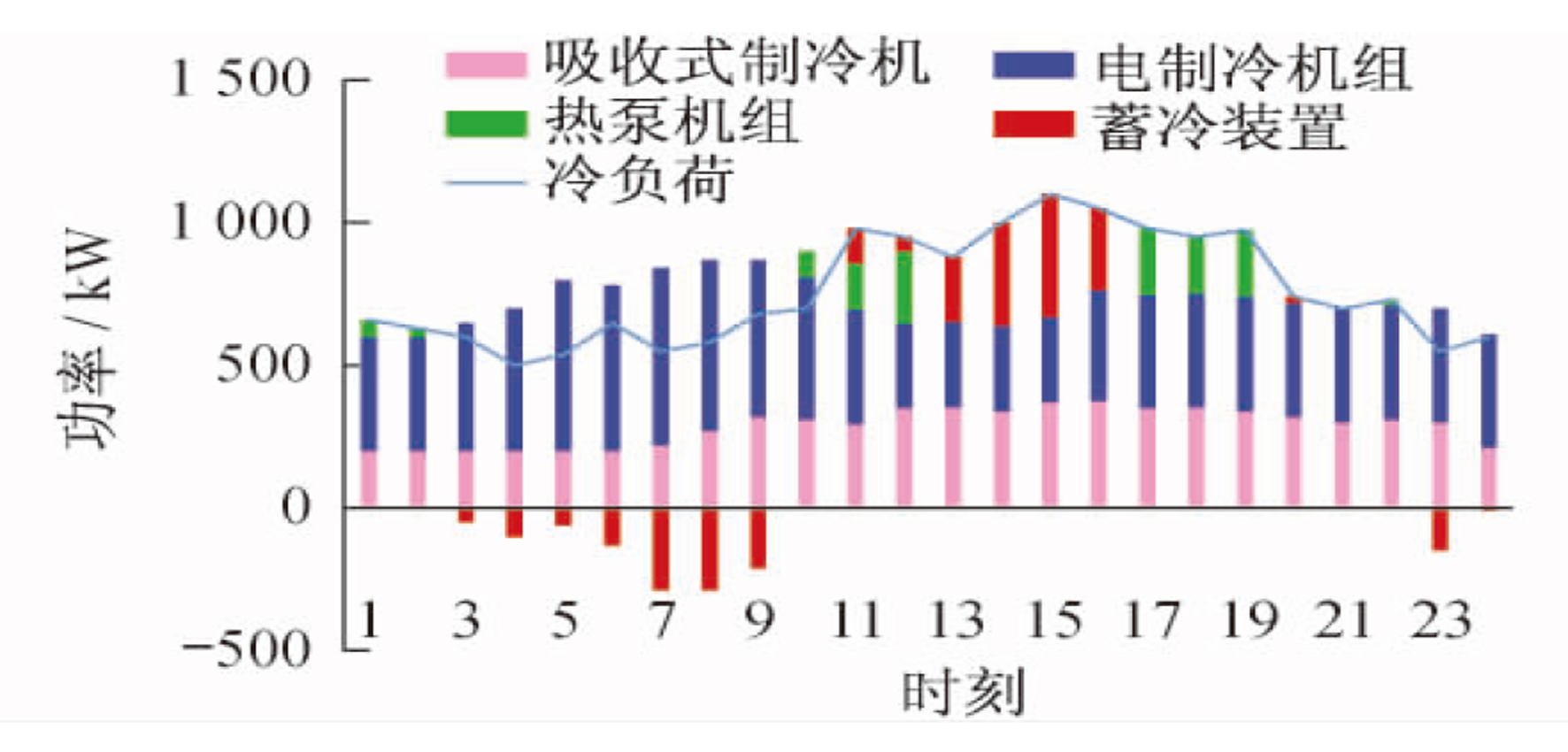
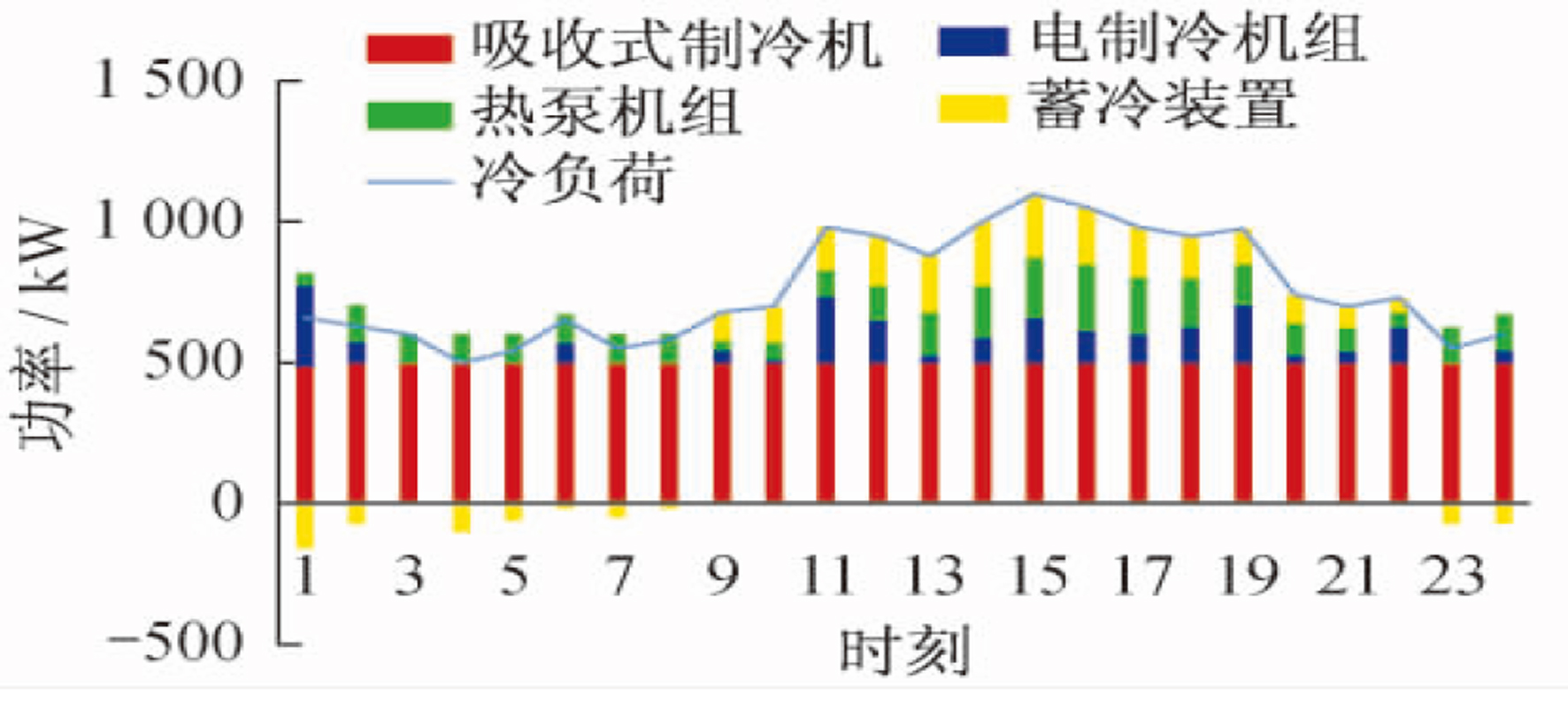
(3) 供冷工况下, 夏季厂区冷负荷需求整体较高, 微型燃气轮机配套的吸收式制冷机在各个时段运行时产生的制冷量都不能满足需求, 此时开启电制冷机满发供冷, 便于及时满足冷负荷。针对个别时段差额部分, 同时开启热泵机组进行制冷, 谷时段满发供冷的多余冷量进入蓄冷装置储存, 在电价峰平时段, 电制冷机组非满发运行状态下, 由蓄冷装置进行差额补冷。冷负荷冷热优先调度结果如图 4所示。
实时互补运行策略的系统方案具体如下。
结合分时电价和天然气价, 系统内设备全运行, 按不同时段选择性搭配开启, 以达到经济性最优的目的。此时, 供电工况中电负荷的大部分由电网购得, 另一部分由光伏和微型燃气轮机供应, 在经济性最大的情况下, 微型燃气轮机以低功率(约为65 kW)稳定运行。供冷工况下, 考虑到夏季冷负荷需求较大, 为最大效率优先满足冷负荷, 当日地源热泵机组选择全部供冷, 不提供热负荷, 大部分冷负荷由微型燃气轮机配套的吸收式制冷机对热量进行利用制冷。因电价限制, 电制冷机组和地源热泵机组选择性开启补冷。供热工况下, 因为同时段系统内设备全运行供应3种负荷, 微型燃气轮机同时段产生的热量不能满足需求, 此时开启燃气锅炉作为主要热力来源。3种蓄能装置的自损耗系数及充放效率加入约束条件后, 与前两种调度策略的运行方式的区别在于启停次数和充放容量大大减少。考虑24个小时段气、电输入成本的实时变化, 在成本最优的前提下, 优化调度后的结果如图 5、图 6、图 7所示。
两种调度策略成本对比如表 5所示。
表 5
调度策略成本对比元
| 调度策略 | 系统运行成本 |
| 电能优先运行和冷热优先运行 | 56738.450 |
| 实时互补运行 | 38548.343 |
由表 5可知, 电能优先运行和冷热优先运行两种策略累加下的成本达到了56 738.45元, 究其原因, 是因为要满足某一时段的一种负荷需求, 策略决定当前出力最大的设备进行供应但忽视了成本约束, 当满足当前负荷需求后, 再启动另一种负荷需求下的机组设备, 没有根据实时电价进行策略同步更换; 而实时互补运行策略是在一个调度周期的每个小时段内所有设备共同出力的情况下, 对两种能量优先策略进行实时更换, 达到了成本最优, 但因为结合实时电价而从电网大量购电的行为造成了环境成本高于前两种能量优先运行策略。因此, 总体来说, 不同策略下系统设备整体出力均达到了完全消纳, 未出现能源废弃或电网倒送, 而且实时互补运行策略考虑了系统内每个设备的运行约束, 达到了最佳的冷热电优化调度。
4 结语
本文以经济性及一定环保性为目标, 建立了RIES混合整数线性规划模型, 并以夏季典型日为例将电能优先运行策略、冷热优先运行策略以及实时互补运行策略下的设备优化调度情况进行了对比。结果表明, 基于供需互动的实时调度策略能够充分利用能源网络的耦合关系, 有效提高能源响应效率及效果, 且实时互补策略下的系统运行成本最低。
参考文献
-
[1]基于能源互联网的新能源及微电网接入对电网的影响[J]. 上海电力学院学报, 2018, 34(6): 581-585.
-
[2]多能互补分布式能源系统优化设计研究进展[J]. 上海电力学院学报, 2018, 34(3): 229-235.
-
[3]基于能源集线器的区域综合能源系统分层优化调度[J]. 电力自动化设备, 2017, 37(6): 171-178.
-
[4]考虑供热网储热特性的电-热综合能源系统优化调度[J]. 电力系统自动化, 2018, 42(21): 45-55. DOI:10.7500/AEPS20170908013
-
[5]考虑多能互补的区域综合能源系统多种储能优化配置[J]. 电力自动化设备, 2019, 39(1): 118-126.
-
[6]陈志彤.多能流型区域综合能源系统经济调度优化运行[D].西安: 西安理工大学, 2018.
-
[7]太阳能冷热电联供系统在城市建筑中的适用性分析[J]. 上海电力学院学报, 2018, 34(2): 147-151.
-
[8]吕凯文.多源互补城市供热系统负荷调度实时优化研究[D].杭州: 浙江大学, 2018.
-
[9]何仲潇.多能协同的综合能源系统协调调度方法研究[D].杭州: 浙江大学, 2018.
-
[10]冷热电联供型多微网主动配电系统日前优化经济调度[J]. 电网技术, 2018, 42(6): 1726-1735.
-
[11]基于智能电网调度控制系统基础平台的新能源优化调度[J]. 电力系统自动化, 2015, 39(1): 159-163. DOI:10.7500/AEPS20141008018
-
[12]冷热电联供型微电网系统多目标日前优化调度[J]. 自动化仪表, 2018, 39(2): 1-6.
-
[13]曾艾东.冷热电混合能源联合优化运行与调度策略研究[D].南京: 东南大学, 2017.
-
[14]基于冷热电联供的多园区博弈优化策略[J]. 电力系统自动化, 2018, 42(13): 68-75. DOI:10.7500/AEPS20170914005
-
[15]基于冷热电多能互补的工业园区互动机制研究[J]. 电力自动化设备, 2017, 37(6): 260-267.
-
[16]基于模型预测控制的冷热电联供型微网动态优化调度[J]. 中国电机工程学报, 2017, 37(24): 7174-7184.
-
[17]计及可平移负荷的分布式冷热电联供系统优化运行[J]. 电网技术, 2018, 42(3): 715-721.
-
[18]考虑能量梯级利用的工厂综合能源系统多能协同优化[J]. 电力系统自动化, 2018, 42(14): 123-130. DOI:10.7500/AEPS20170825006