|
|
|
发布时间: 2020-04-10 |
|
|
|
|
收稿日期: 2019-04-02
中图法分类号: TK16;TK325;TK-9
文献标识码: A
文章编号: 2096-8299(2020)02-0105-06
|
摘要
由于高炉煤气燃气机组的燃料特性和受热面的不同, 使得传统的性能计算方法不再适用, 因此对试验规程中的性能计算方法进行改进, 得到了适用于高炉煤气燃气机组直流锅炉的方法。采用二变量Pearson分析法对直流锅炉的效率进行分析, 其结果可为电站人员提供技术和理论支撑。
关键词
高炉煤气燃气机组; 直流锅炉; 性能计算; Pearson分析法
Abstract
Due to the different fuel characteristics and heating surface of the blast furnace gas unit, the traditional performance calculation is no longer applicable.Therefore, the performance calculation method for the blast furnace gas-fired gas unit DC boiler is improved by the performance calculation method in the test procedure, and the efficiency of the DC boiler is analyzed by the two-variable Person analysis method.The analysis results can provide technical and theoretical support for power station personnel.
Key words
blast furnace gas unit; direct current boiler; performance calculation; Pearson analysis
目前, 用于计算锅炉效率的方法主要有3种, 分别来源于GB 10184—1988《电站锅炉性能试验规程》、ASME PTC 4.1《锅炉机组性能试验规程》以及一些相关教材。由于高炉煤气燃气机组的锅炉为直流锅炉, 燃料主要是高炉煤气(Blast Furnace Gas, BFG)、焦炉煤气(Coke Oven Gas, COG)、转炉煤气(Linz Donawitz Gas, LDG)、轻油(Light Fuel Oil, LFO)、天然气(Natural Gas, NG)等, 故上述传统方法均不适用。与汽包锅炉不同, 直流锅炉在加热、蒸发和过热过程之间没有明确的界线。直流式锅炉的概念可以简单地定义为仅有一个管的锅炉[1]。根据直流锅炉燃料的性质和特点, 对GB 10184—1988《电站锅炉性能试验规程》中的方法进行改进来计算锅炉效率, 各个燃料的参数均可为锅炉燃烧系统提供计算依据。
1 直流锅炉计算方法
1.1 锅炉构造
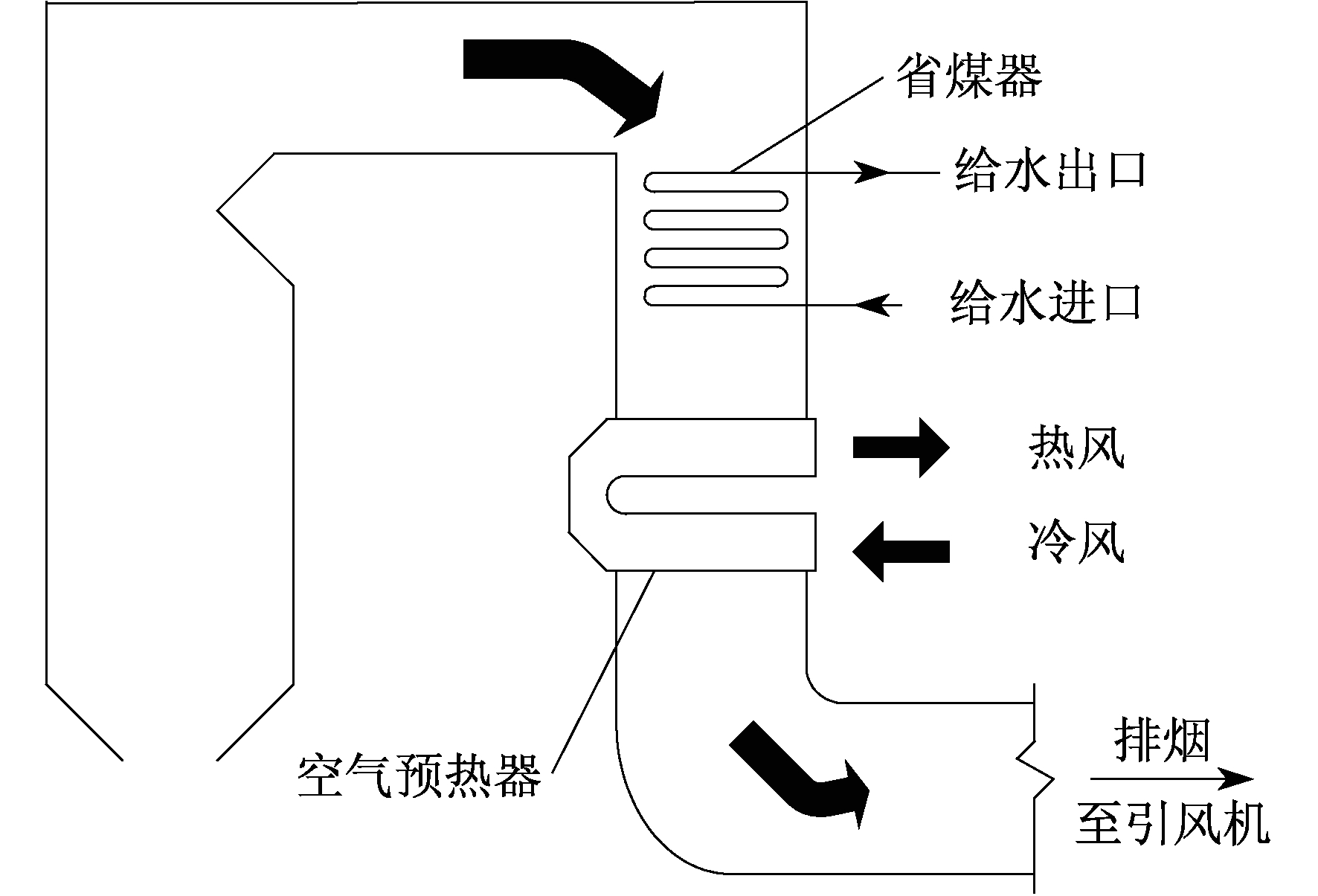
主烧BFG燃气直流锅炉如图 1所示。
1.2 锅炉燃料及空气中常用参数的选取
此高炉煤气燃气机组燃料主要为BFG, COG, LDG, NG, LFO。通常情况下, 可单独燃烧BFG, 在稳定的工况下也可以主燃BFG, 并适量掺烧COG和LDG。由于NG属于高热值燃料, 故在掺烧时NG的质量流量值比COG和LDG的要小, 在机组点火时需适量加入LFO助燃[2]。各燃料常用的计算参数如表 1所示。
表 1
各燃料计算参数
| 参数 | 含量 |
| BFG中C元素含量/% | 16.769 |
| BFG中H元素含量/% | 0.535 |
| BFG中O元素含量/% | 36.898 |
| BFG中N元素含量/% | 45.797 |
| 干BFG中H2摩尔含量/% | 3.300 |
| 干BFG中O2摩尔含量/% | 1.100 |
| 干BFG中CO摩尔含量/% | 21.200 |
| 干BFG中CO2摩尔含量/% | 22.000 |
| 干BFG中N2摩尔含量/% | 50.500 |
| 干COG中H2摩尔含量/% | 53.500 |
| 干COG中CH4摩尔含量/% | 28.500 |
| 干COG中CO摩尔含量/% | 7.500 |
| 干COG中CO2摩尔含量/% | 2.000 |
| 干COG中N2摩尔含量/% | 5.000 |
| 干LDG中CO摩尔含量/% | 56.500 |
| 干LDG中CO2摩尔含量/% | 18.000 |
| LFO比热/[kJ·(kg·K)-1] | 1.9 |
| LFO密度/(kg·m-3) | 544 |
| LFO在15 ℃时的密度/(kg·m-3) | 863 |
| LFO在25 ℃时的密度/(kg·m-3) | 849 |
| LFO中C元素含量/% | 84.320 |
| LFO中H元素含量/% | 13.830 |
| LFO中O元素含量/% | 1.850 |
| LFO中N元素含量/% | 0 |
| LFO中S元素含量/% | 0.020 |
| LFO中Ash元素含量/% | 0 |
| NG中C元素含量/% | 87.500 |
| NG中H元素含量/% | 4.300 |
| NG中O元素含量/% | 5.650 |
| NG中N元素含量/% | 1.500 |
根据高炉煤气燃气直流锅炉的具体特点, 其效率计算公式为
| $ \begin{aligned} \eta_{\mathrm{B}}=& 1-\frac{Q_{\mathrm{Ltot}}}{Q_{\mathrm{Ztot}}}=\\ & 1-\frac{Q_{\mathrm{G}}+Q_{\mathrm{CO}}+Q_{\mathrm{RC}}}{Q_{\mathrm{F}}+Q_{\mathrm{Fs}}+Q_{A}+Q_{\mathrm{AS}}+Q_{\mathrm{EI}}} \end{aligned} $ | (1) |
式中:QLtot——总热损失;
QZtot——总输入热;
QG——烟气带走的热损失, MW;
QCO——CO未完全燃烧热损失, MW;
QRC——辐射对流热损失, MW;
QF——燃料化学输入热, MW;
QFs——燃料物理显热, MW;
QA——燃烧用空气物理显热, MW;
QAS——雾化蒸汽物理显热, MW;
QEI——锅炉辅机电机驱动带入的物理显热, MW。
1.3 各热损失的计算模型
根据式(1)可知, 被计测的热损失有烟气带走的热损失、CO未完全燃烧热损失和辐射对流热损失; 输入热有燃料化学输入热、燃料物理显热、燃烧用空气显热、雾化蒸汽物理显热和辅机电机驱动带入的物理显热[3]。其中, 烟气带走的热损失是指在最终热交换器后排出烟气时所带走的物理显热占输入热量的百分比, 是由尾部烟气的排烟温度高于外部环境温度引起的, 其所占份额最大, 约为总热量损失的4%~8%。其公式为
| $ Q_{\mathrm{G}}=m_{\mathrm{GAHo}}\left(\vartheta_{\mathrm{GAHo}} t_{\mathrm{GAHo}}-\vartheta_{0} t_{0}\right) $ | (2) |
式中:mGAHo——空气预热器出口烟气量, kg/s;
ϑGAHo——0 ℃到空气预热器出口烟气温度之间的烟气比热, kJ/(kg·K);
tGAHo——空气预热器出口温度, ℃;
ϑ0——0 ℃到基准温度之间的烟气比热, kJ/(kg·K);
t0——基准温度, ℃。
在主燃BFG的燃气机组中, 主要的未完全燃烧成分为CO[4]。CO未完全燃烧热损失为
| $Q_{\mathrm{CO}}=N_{\mathrm{CV}, \mathrm{CO}} \times m_{\mathrm{GAHo}} \times \varphi_{\mathrm{CO}}$ | (3) |
式中:NCV, CO——CO热值, MJ/m3;
φCO——空气预热器出口CO含量, %。
辐射对流热损失为
| $Q_{\mathrm{RC}}=C_{\mathrm{rg}} Q_{\mathrm{N}}^{0.7}$ | (4) |
式中:Crg——燃气锅炉系数;
QN——锅炉输出热, MW。
燃料化学输入热为
| $ Q_{\mathrm{F}}=\frac{N_{\mathrm{CV}, \mathrm{rl}}}{m_{\mathrm{rl}}} $ | (5) |
式中:NCV, rl——燃料的低位发热量, MJ/m3;
mrl——燃料的标准流量, m3/s。
燃料物理显热为
| $Q_{\mathrm{FS}}=C_{\mathrm{r}}\left(t_{\mathrm{r}}-t_{0}\right)$ | (6) |
式中:QFS——燃料的物理显热, kJ/kg;
Ct——燃料的比热, kJ/(kg·K);
tr——燃料温度, ℃。
燃烧用空气中物理显热为
| $Q_{A}=m_{A}\left(\vartheta_{A} t_{A}-\vartheta_{0} t_{0}\right)$ | (7) |
式中:mA——空气流量, kg/s;
ϑA——0~A ℃之间平均湿空气比热, kJ·K/kg;
tA——空气温度, ℃;
ϑ0——0 ℃到基准温度之间平均湿空气比热, kJ·K/kg。
雾化蒸汽显热为
| $Q_{A S}=m_{A S}\left(h_{A S}-h_{0}\right)$ | (8) |
式中:mAS——雾化蒸汽流量, kg/s;
hAS——雾化蒸汽焓, kJ·K/kg;
h0——参考温度下的雾化蒸汽焓, kJ·K/kg。
由于锅炉辅机电机驱动带入的物理热值非常小, 对最后的锅炉效率几乎没有影响, 故在计算时忽略不计[3]。从电厂中分布式控制系统(Distributed Control System, DCS)和安全仪表系统(Safety Instrumented System, SIS)中取得大量历史数据, 并选取较为典型的20个工况, 每个典型工况取两小时数据, 一分钟为一个点, 共120个点。最后取其平均值进行上述公式的计算。其锅炉效率主要热损失部分计算数据如表 2所示。
表 2
锅炉效率部分计算数据
| 参数 | 工况1 | 工况2 | 工况3 | 工况4 | 工况5 | … | 工况19 | 工况20 |
| 负荷/MW | 210 | 270 | 240 | 180 | 180 | … | 210 | 270 |
| BFG流量/(m3·s-1) | 717.962 | 610.495 | 466.988 | 644.017 | 780.667 | … | 506.25 | 648.753 |
| COG流量/(m3·s-1) | 0 | 0 | 0 | 9 | 0 | … | 0 | 0 |
| LDG流量/(m3·s-1) | 15.823 | 10.413 | 0.242 | 0 | 9.830 | … | 20.120 | 10.182 |
| NG流量/(m3·s-1) | 0 | 0 | 3.740 | 0 | 0 | … | 2.140 | 0 |
| LFO流量/(m3·s-1) | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 |
| 总输入热/MW | 1 539.28 | 2 125.77 | 2 591.19 | 1 677.23 | 2 147.44 | … | 1 525.6 | 2 589.52 |
| 烟气带走热损失/MW | 102.570 | 166.161 | 231.130 | 124.365 | 149.85 | … | 123.45 | 231.13 |
| 未完全燃烧热损失/MW | 0.004 | 0.004 | 0.002 | 0.007 | 0.008 | … | 0.007 | 0.001 |
| 辐射对流热损失/MW | 0.296 | 0.371 | 0.389 | 0.341 | 0.394 | … | 0.388 | 0.388 7 |
| 锅炉效率/% | 93.317 | 92.166 | 91.065 | 92.564 | 93.003 | … | 91.894 | 91.061 |
| 修正后锅炉效率/% | 93.474 | 92.358 | 91.244 | 92.898 | 93.328 | … | 92.207 | 91.224 |
由表 2可以看出, CO未完全燃烧热损失非常小, 说明气体燃料在锅炉内燃烧比较充分; 辐射对流热损失占整个锅炉热损失的一小部分; 对锅炉效率影响最大的热损失之一是烟气带走的热损失。对于BFG中混有COG, LDG, NG的工况, 随着燃料的增加, 烟气带走的热损失减少, 与燃煤机组的锅炉效率随燃料量的变化趋势相反。对于掺烧LOF的工况, 随着燃料的增加, 烟气带走的热损失增大, 但此变化趋势相对较弱。综上, 燃气锅炉的热效率不但与气体燃料的消耗量有关, 还与该燃料的发热量关系密切[5]。
2 锅炉效率的修正计算
此高炉煤气燃气机组的直流锅炉修正项目及具体修正公式以厂家给出的修正曲线为准。其主要修正项目为送风温度、给水温度、再热器进口蒸汽温度、LFO温度、BFG增压风机进口温度和空气湿度。根据厂家提供的修正曲线, 通过拟合得到修正性能计算公式如下。
送风温度修正曲线为
| $y=0.028 x-0.784$ | (9) |
给水温度修正曲线为
| $y=0.012\;95x-3.73$ | (10) |
再热器进口蒸汽温度修正曲线为
| $y=\left\{\begin{array}{l}-0.009\;4x+3.496\;8, \quad x \leqslant 372 \\ -0.004x+1.488, \quad x>372\end{array}\right.$ | (11) |
LFO温度修正曲线为
| $y=-0.000\;133 x+0.003\;3$ | (12) |
BFG增压风机进口温度修正曲线为
| $y=0.008\;7x-0.330\;6$ | (13) |
空气湿度修正曲线为
| $y=\left\{\begin{array}{l}-0.005\;89x+0.051\;478\;6, \quad x \leqslant 8.74 \\ -0.006x+0.054, \quad x>8.74\end{array}\right.$ | (14) |
3 电厂运行数据的二元相关性分析
涉及到一个独立变量和一个因变量之间的相关性, 称为二元变量相关性分析[6]。二元相关性分析是对两个变量之间相关程度的分析, 所用的指标称为单相关系数, 又称为Pearson相关系数[7]。
Pearson相关性系数的数学表达式为[8]
| $ \rho(X, Y)=\frac{\operatorname{Cov}(X, Y)}{\sqrt{\operatorname{Var}(X) \operatorname{Var}(Y)}} $ | (15) |
式(15)中, Cov(X, Y)是随机变量X和Y的协方差, 公式为
| $\operatorname{Cov}(X, Y)=\sum\limits_{i = 1}^n {({x_i} - \bar X)({y_i} - \bar Y)} $ | (16) |
Var(X)和Var(Y)分别为变量X和Y的方差, 公式为
| $\sqrt{\operatorname{Var}(X) \operatorname{Var}(Y)}=\\ \sqrt{\sum\limits_{i = 1}^n {{{({x_i} - \bar X)}^2}} } \sqrt {\sum\limits_{i = 1}^n {{{({y_i} - \bar Y)}^2}} } $ | (17) |
由相关性系数的定义可知, |ρ(X, Y)|≤1。对于随机变量X和Y, 当X与Y无关时, |ρ(X, Y)|的值为零; 当X与Y线性相关时, |ρ(X, Y)|的值为1。相关性系数ρ(x, y)用来表示相关程度的大小。当两变量在同一增减趋势上变化时, 即为正相关; 在相反的增减趋势上变化时, 即为负相关; 无变化即为不相关。相关性系数ρ(x, y)的取值范围为(-1, +1), +1表示完全正相关, -1则表示完全负相关, 0表示不相关[9]。
在统计学研究领域, 相关性强度划分如表 3所示。
表 3
相关性强度划分表
| 范围 | 相关性强度 |
| $0.8 < |r| \leqslant 1$ | 高度相关 |
| $0.6 < |r| \leqslant 0.8$ | 强相关 |
| $0.4 < |r| \leqslant 0.6$ | 中等程度相关 |
| $0.2 < |r| \leqslant 0.4$ | 弱相关 |
| $|r| \leqslant 0.2$ | 极弱相关 |
通过计算样本Pearson相关性系数, 可以基本了解各参数之间的影响强度。
3.1 锅炉效率性能指标Pearson分析
通过上海某钢铁企业自备电厂4#燃气机组的SIS系统与DCS系统, 选择2018年9月1日00:00至2018年9月7日00:00的数据, 每10 min取一个点, 共得到842个时刻的运行数据, 运行参数部分数据如表 4所示。
表 4
高炉煤气燃气机组运行参数
| 序号 | BFG流量/ (m3·s-1) |
BFG温度/ ℃ |
BFG压力/ MPa |
… | 排烟温度/ ℃ |
排烟氧量/ % |
给水温度/ ℃ |
| 1 | 706.557 | 27.198 | 6.576 | … | 135.0 | 1.834 118 | 257.801 2 |
| 2 | 706.578 | 27.156 | 6.309 | … | 135.2 | 1.719 601 | 257.186 6 |
| 3 | 706.511 | 27.499 | 6.256 | … | 135.5 | 1.909 909 | 257.189 8 |
| 4 | 604.809 | 27.316 | 6.211 | … | 135.3 | 1.855 887 | 256.696 7 |
| 5 | 604.888 | 27.655 | 6.332 | … | 134.9 | 1.796 446 | 257.189 1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 840 | 705.434 | 28.188 | 6.765 | … | 135.0 | 1.791 549 | 260.150 8 |
| 841 | 705.445 | 28.613 | 6.409 | … | 135.2 | 1.687 408 | 259.355 1 |
| 842 | 705.400 | 29.166 | 6.019 | … | 135.4 | 1.908 508 | 259.991 7 |
以表 4中数据为基础, 进行Pearson相关性分析, 可以得知有一部分锅炉原始量与锅炉效率有关联性, 相关分析结果如表 5所示。
表 5
相关性分析结果
| 参数 | 相关系数 | 范围 | 相关性强度 |
| BFG流量 | 0.85 | 0.8 < |r|≤1 | 高度相关 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 排烟温度 | -0.82 | 0.8 < |r|≤1 | 高度相关 |
| 排烟氧量 | 0.41 | 0.4 < |r|≤0.6 | 中等程度相关 |
| 大气温度 | -0.74 | 0.6 < |r|≤0.8 | 强相关 |
| 大气压力 | 0.43 | 0.4 < |r|≤0.6 | 中等程度相关 |
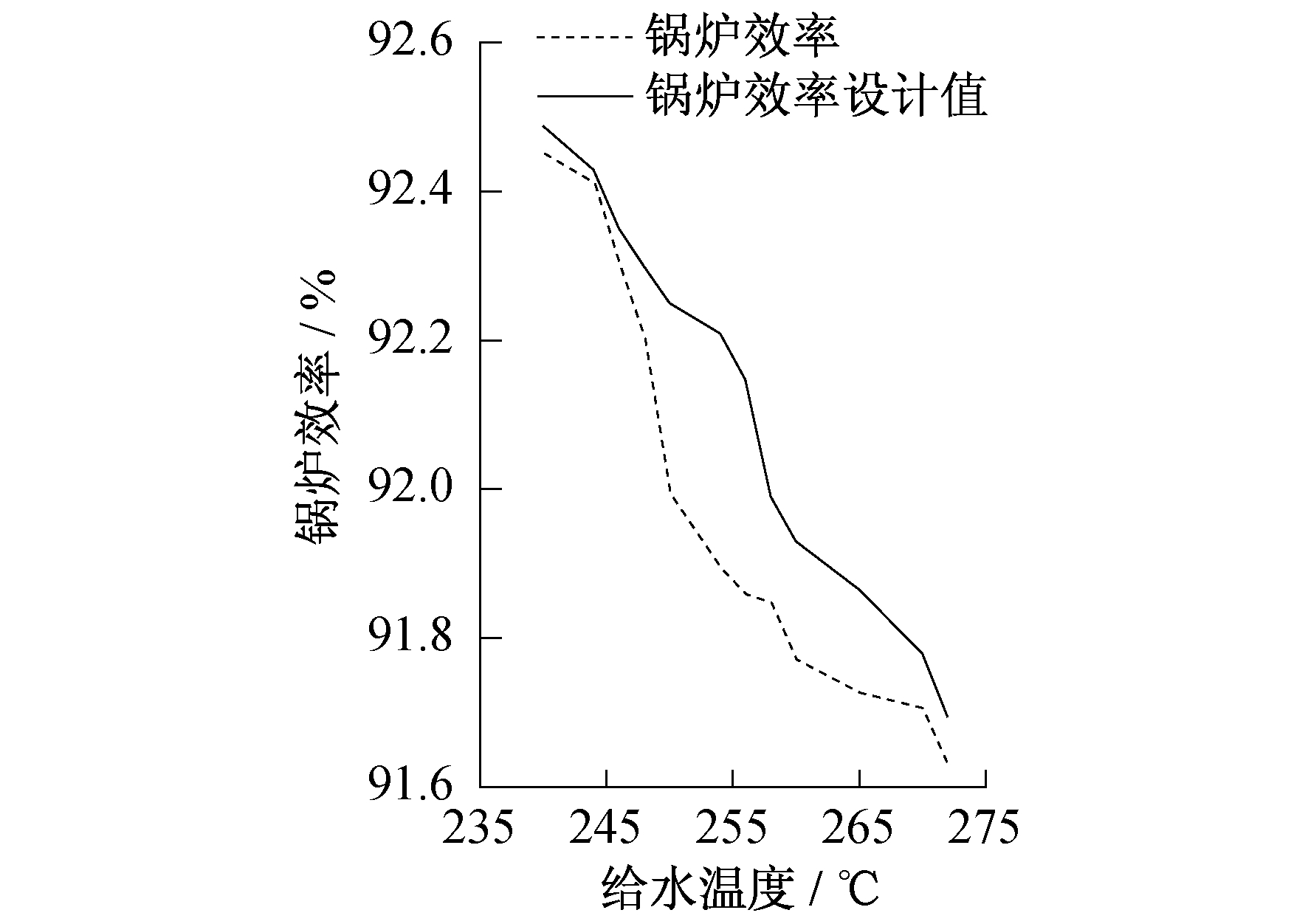
| 给水温度 | -0.62 | 0.6 < |r|≤0.8 | 强相关 |
3.2 锅炉效率性能指标机理分析
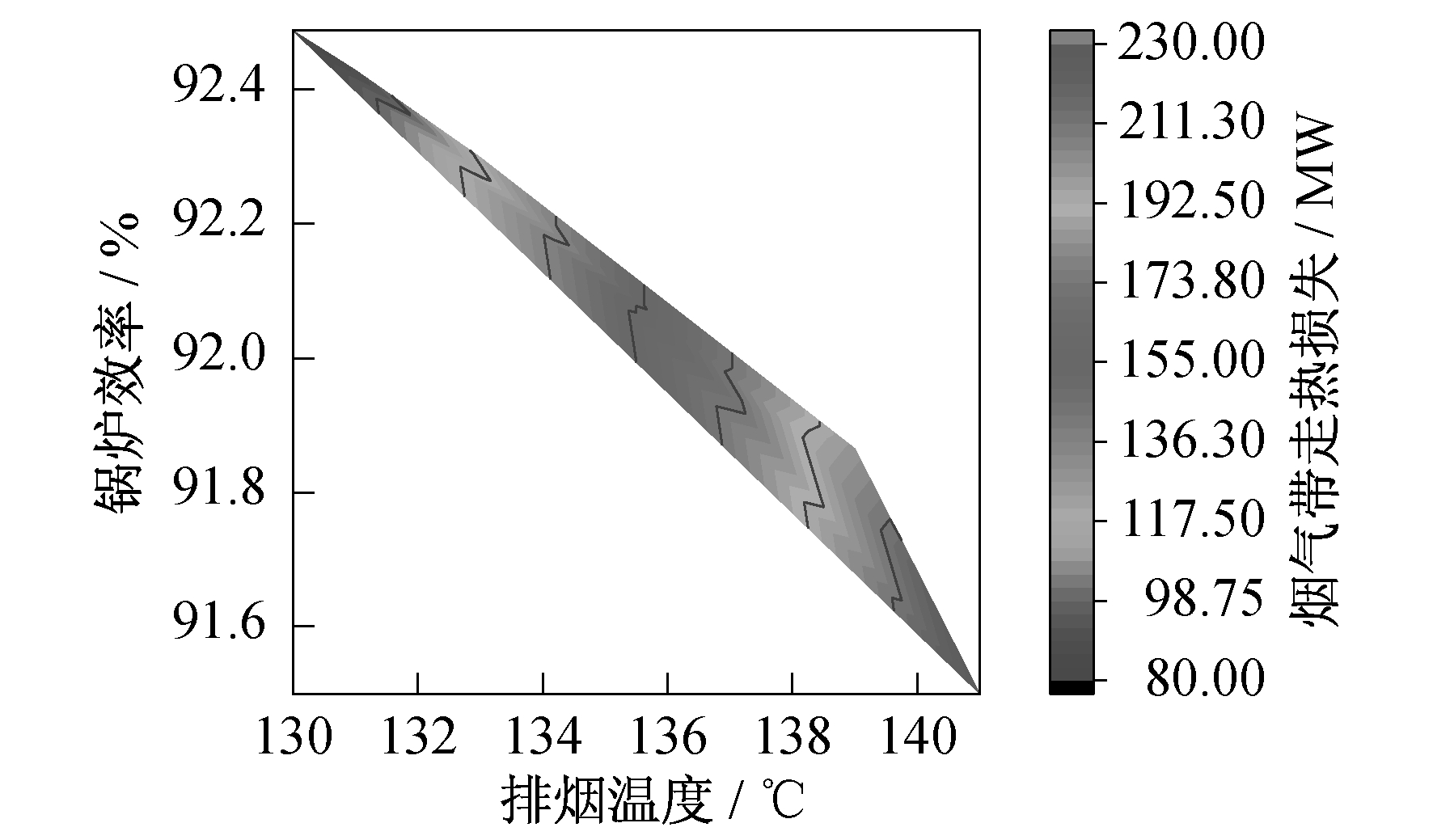
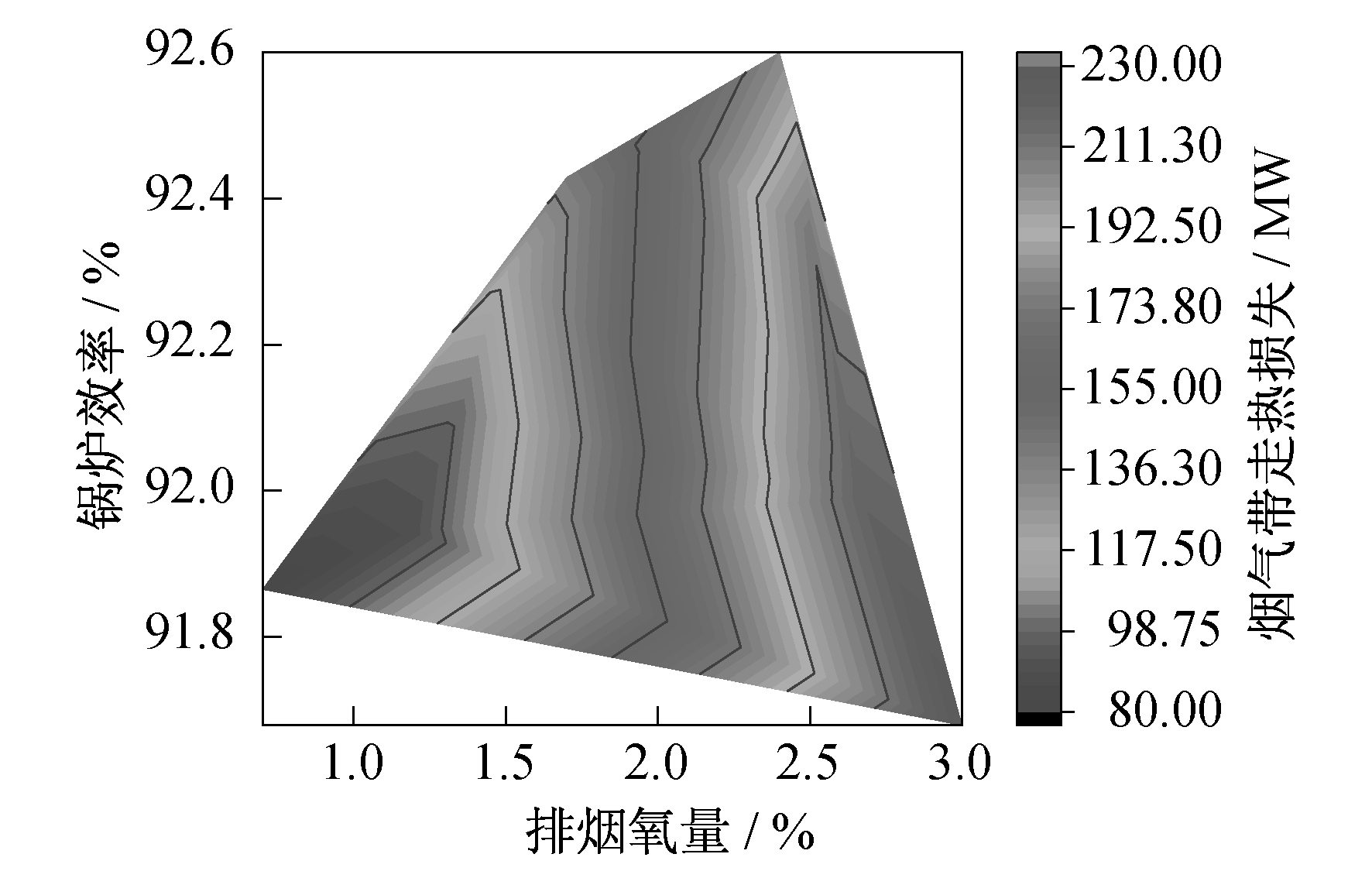
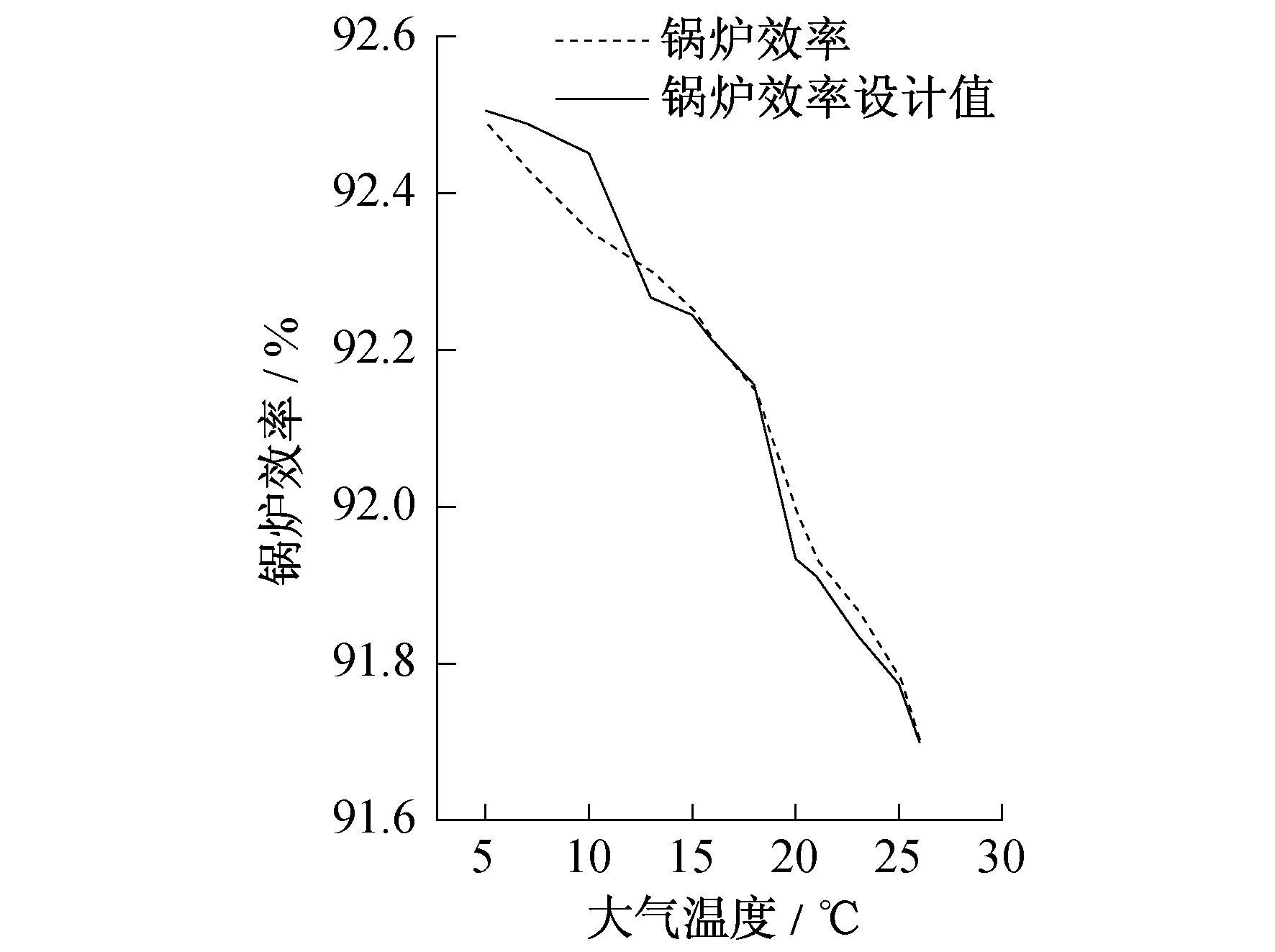
由表 5可知, 锅炉效率与BFG流量呈高度正相关, 故BFG流量的增加会导致锅炉效率增加; 锅炉效率与大气温度呈强负相关, 故大气温度上升, 锅炉效率会显著下降。现对排烟温度、排烟氧量、大气温度、给水温度参数进行分析, 具体如下。
3.2.1 排烟温度
3.2.2 排烟氧量
3.2.3 大气温度
3.2.4 给水温度
4 结语
为了研究高炉煤气燃气机组直流锅炉的性能计算方法, 本文对锅炉效率公式进行了改进, 采取适用于高炉煤气燃气机组的性能计算方法来计算锅炉效率。计算完成后, 通过Pearson二变量分析法对直流锅炉效率进行分析, 研究了排烟温度、排烟氧量、大气温度和给水温度对锅炉效率的影响, 对高炉煤气燃气机组的发展有一定的借鉴意义。
参考文献
-
[1]燃煤烟气余热和水分综合利用技术研究[J]. 上海电力学院学报, 2019, 35(1): 36-42.
-
[2]LAGUNA M F, RISAU-GUSMAN S. Correction of lice and math: using models to understand and control populations of head lice.[J]. PLoS ONE, 2018, 6(8): 48-52.
-
[3]掺烧高炉煤气对锅炉传热特性影响的研究[J]. 华北电力大学学报, 2013, 21(1): 66-70.
-
[4]吕政.基于数据的高炉煤气系统建模与调度应用研究[D].大连: 大连理工大学, 2016.
-
[5]煤粉与高炉煤气混烧锅炉空气预热器漏风率计算方法[J]. 热力发电., 2016, 45(5): 88-93.
-
[6]张磊.关联规则在电站锅炉大数据挖掘及优化运行中的应用研究[D].上海: 上海发电设备成套设计研究院, 2018.
-
[7]汪安明.基于数据分析的电站运行优化研究[D].北京: 华北电力大学, 2016.
-
[8]高炉煤气锅炉与CCPP的发电经济性比较[J]. 冶金能源, 2018, 37(6): 11-14. DOI:10.3969/j.issn.1001-1617.2018.06.003
-
[9]运行中电站锅炉入炉煤元素组成的理论计算[J]. 热能动力工程, 2016, 31(12): 109-115.