|
|
|
发布时间: 2020-04-10 |
|
|
|
|
收稿日期: 2019-09-23
基金项目: 上海市“科技创新行动计划”地方院校能力建设专项项目(19020500700);上海市科学技术委员会工程技术研究中心项目(14DZ2251100);上海市青年科技英才扬帆计划(16YF1404700)
中图法分类号: TM474
文献标识码: A
文章编号: 2096-8299(2020)02-0123-08
|
摘要
针对传统智能诊断方法使用的浅层模型难以准确挖掘信号特征量与对应故障原因之间复杂的映射关系, 导致故障诊断精度不高的问题, 提出了一种基于深度信念网络(DBN)的燃气轮机故障诊断方法。采用Apriori关联度分析法分析燃气轮机故障模式与故障特征向量之间的关系, 生成关联度矩阵; 根据关联结果筛选出满足精度的特征向量作为输入, 同时结合遗传算法(GA)对深度信念网络的结构参数进行优化, 建立了基于GA-DBN的燃气轮机故障诊断模型。最后通过诊断实例验证了所提方法的有效性。
关键词
燃气轮机; 故障诊断; 深度信念网络; 遗传算法; Apriori算法
Abstract
The shallow model used in the traditional intelligent diagnosis method is difficult to accurately mine the complex mapping relationship between the signal feature quantity and the corresponding fault cause, resulting in low fault diagnosis accuracy.This paper proposes a method based on deep belief network (DBN) gas turbine fault diagnosis.The Apriori correlation analysis method is used to analyze the relationship between the gas turbine failure mode and the fault feature vector, and the correlation degree matrix is generated.The feature vector satisfying the accuracy is selected as the input according to the correlation result, and the structure of the deep belief network is combined with the genetic algorithm (GA).The parameters are optimized to establish a GA-DBN based gas turbine fault diagnosis model.A diagnostic example verifies the effectiveness of the method.
Key words
gas turbine; fault diagnosis; deep belief network; genetic algorithm; Apriori algorithm
燃气轮机作为燃气-蒸汽联合循环机组的核心动力装备, 工作于高温、高压、高转速状态, 极易发生故障。对燃气轮机的状态监测及故障诊断不仅可以大幅提高机组运行的可靠性, 而且还可以降低检修成本。文献[1]应用时域和频域特征训练深度信念网络(Deep Belief Network, DBN), 准确识别出多种气阀故障, 同时给出了DBN的内部结构和训练过程。文献[2]提出了一种振动信号与DBN结合的故障诊断方法, 与支持向量机(Support Vector Machine, SVM)比较得到了较好的诊断结果, 为DBN与燃气轮机故障诊断提供了新的思路。文献[3]提出了一种通过随机森林算法训练分类器对燃气轮机进行故障诊断的方法, 但随机森林是弱分类器, 在构建和决策过程中易产生过拟合, 诊断准确率不高。文献[4]提出了D-S证据理论决策层融合算法对燃气轮机典型故障进行诊断, 但D-S证据理论的证据冲突问题尚未得到完整的解决办法, 决策层无法进一步提高诊断方法的容错性。
专家系统、数据挖掘等方法需要从大量的原始数据中提取出故障特征, 燃气轮机运行时极少产生故障数据, 数据库的搭建面临极大的问题[5]; SVM对参数的选取是一个难题, 参数选取不恰当会使分类的准确率大大下降[6]; 浅层神经网络模型难以准确挖掘出故障特征向量与众多故障模式之间复杂的映射关系, 最终导致分类器诊断准确率不高[1]。对于燃气轮机故障诊断面临的问题, 本文提出了一种基于遗传算法(Genetic Algorithm, GA)优化的DBN燃气轮机故障诊断模型(GA-DBN模型)。DBN是一种深层网络模型, 具有更好处理高维、非线性数据的能力, 同时能更快找出故障特征向量与故障模式之间复杂的非线性关系[7-9]。燃气轮机自身结构的复杂性使得引起故障的原因多种多样, 若将大量特征向量直接输入模型进行诊断, 会使无关的特征向量影响诊断结果, 造成诊断准确率下降, 而且巨大的数据量会使模型诊断时间变长, 效率变低。对于DBN的, 结构参数选择合适与否对模型性能的影响很大, 一般DBN的初始结构参数为随机生成, 经过逆向微调得到调整, 但会增加系统的运行时间。本文采用Apriori算法对原始特征向量进行处理, 挖掘不同故障特征向量与故障类型间的规律, 刻划每类故障特征向量对不同故障模式的影响程度, 去除无关特征向量, 划分训练样本和测试样本。采用GA计算得到DBN的结构参数。
1 关联规则的建立
由于燃气轮机自身结构极为复杂, 部件繁多, 因此引起燃气轮机故障的原因多种多样[10]。目前研究的大部分诊断方法仅依靠故障特征向量参数来诊断故障原因, 虽然对识别故障种类有较高的准确度, 但对故障产生原因及产生部位的识别效果较差。为了提高诊断精度, 在建立故障诊断模型前, 需要使用相关性分析准确刻划每类故障特征向量对不同故障模式的影响程度, 区分主次影响因素[11]。
Apriori算法适用于样本数据有限、复杂且具有不确定性问题的分析与评价[12-13]。设元素Am称为项, A={A1, A2, A3, …Am}为项的集合, Ym称为目标项, Y={Y1, Y2, Y3, …Ym}为目标项的集合。D是项与目标项的集合, D={Am, Ym}, 即D是一个知识数据库。一个关联规则形如A→Y的映射关系式(A∈D, Y∈D且A∩Y=F)。规则A→Y的支持度定义为项A和Y同时发生的概率就称为关联规则的支持度, 记Sup(A→Y), 规则A→Y的置信度定义为A发生, 则Y发生的概率就称关联规则的置信度, 记Conf(A→Y), 即
| $ \operatorname{Sup}(A \rightarrow Y)=\frac{\operatorname{Sup}_{-} \operatorname{count}(A \cup Y)}{\operatorname{Total}_{-} \operatorname{count}(D)} $ | (1) |
| $ \operatorname{Conf} (A \rightarrow Y)=\frac{\operatorname{Sup}_{-} \operatorname{count}(A \cup Y)}{\operatorname{Sup}_{-} \operatorname{count}(A)} $ | (2) |
挖掘关联规则实质上是寻找满足最小置信度和最小支持度。燃气轮机发生压气机叶片磨损记为Y, 故障征兆可能是压气机发生较大幅度的振动, 导致低压压气机转速变化量等特征量的变化, 则将发生变化的特征量称为故障征兆, 记为:A1, A2, A3, …, Am, 而A和Y是故障集D的子集。Apriori算法是一种基于多维的关联规则, 以最小支持度、最小置信度和分析目标作为条件, 若所有规则均不满足条件, 则重新调整模型参数, 否则输出关联规则。
2 深度信念网络
DBN是一种非监督深层网络结构特征学习模型, 由多个受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)堆叠而成[14]。
2.1 受限玻尔兹曼机
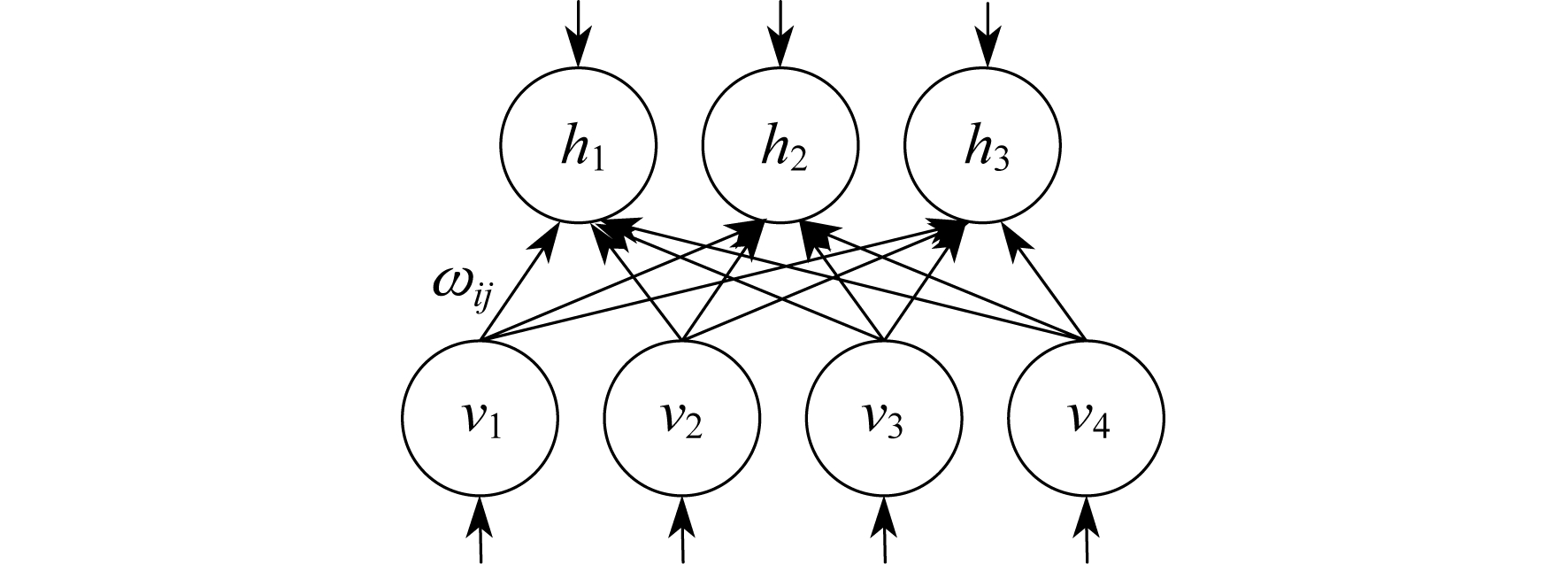
RBM是DBN的基本组成单元, 本质是一种概率生成模型。RBM由可视层(v)和隐含层(h)组成。可视层的偏置量为ci, 隐含层的偏置量为bj。v与h之间通过权值ωij连接, v与h内部单元之间不连接, 属于独立个体, 是一种层外有连接、层内无连接的网络结构[15]。RBM的结构如图 1所示。
在一组确定的RBM中, 用vi和hj分别表示可视层神经元和隐含层神经元的状态。定义可视层神经元与隐含层神经元之间的联合组态能量, 即一个RBM所具备的能量为
| $ E(v, h \mid \theta)= - \sum\limits_{i = 1}^V \sum\limits_{j = 1}^H v_{i} h_{j} \omega_{i j}- \sum\limits_{i = 1}^V v_{i} c_{i}-\sum\limits_{j = 1}^H h_{j} b_{j} $ | (3) |
式中:θ——RBM的结构参数, θ={ωij, ci, bj};
ωij——可视层神经元与隐含层神经元之间的连接权重;
V——可视层神经元个数;
H——隐含层神经元个数。
由于RBM中v层与h层各个神经元都是独立的状态, 所以当给定隐含层状态时可视层神经元的激活概率为
| $ P\left(v_{i} \mid h, \theta\right)=\xi\left(c_{i}+\sum\limits_j \omega_{i j} h_{j}\right) $ | (4) |
式中:ξ(·)——激活函数, 一般选用sigmoid函数。
当给定可视层状态时, 隐含层神经元的激活概率为
| $ P\left(h_{j} \mid v, \theta\right)=\xi\left(b_{j}+\sum\limits_i \omega_{i j} v_{i}\right) $ | (5) |
式(4)表示由特征变量数据重构后输入数据的逆向学习过程, 式(5)表示RBM将高维空间的输入数据转换为低维特征变量的正向学习过程。在这一过程中, RBM中的ωij得到了更新, 即
| $\Delta \omega_{i j}=\alpha\left[E_{\mathrm{obj}}\left(v_{i} h_{j}\right)-E_{\mathrm{model}}\left(v_{i} h_{j}\right)\right]$ | (6) |
式中:a——学习率;
Eobj(vihj)——训练集的目标;
Emodel(vihj)——训练模型的输出。
2.2 深度信念网络的训练过程
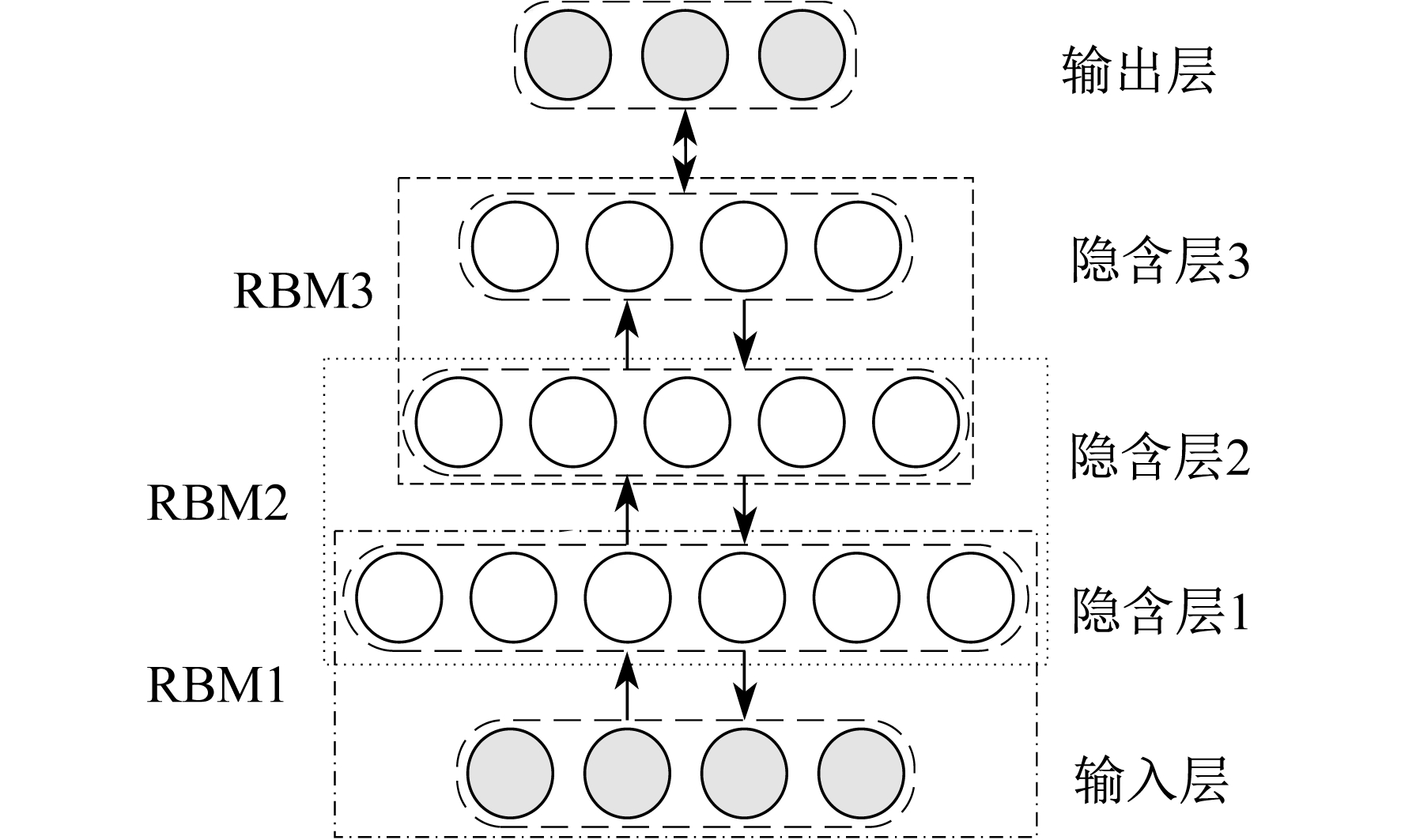
一个DBN由两个或两个以上的RBM堆叠形成。相邻的两个RBM中, 底层RBM的输出为高层RBM的输入。图 2为包含3个RBM的一个DBN结构图。RBM1的可视层和隐含层分别为DBN的输入层和隐含层。最后一层为输出层, 即softmax层。由DBN结构可知, RBM1的隐含层即为RBM2的可视层, 以此类推。
基于DBN的燃气轮机故障分类器模型是通过两个步骤训练得到的:一是根据非监督式学习机制, 自输入层经过隐含层到输出层对每一个RBM进行独立充分训练, 确定DBN初始结构参数; 二是采用有监督式反向传播算法(BP算法)自上而下整体对DBN的结构参数进行微调。
在第一步中, 充分且独立训练每一个RBM的目的是得到最优化参数θ*。它是整个DBN分类器模型建立的关键, 即
| $ \theta^{*}=\arg \mathop {\max }\limits_\theta \sum\limits_{m = 1}^M \log P\left(v^{(m)} \mid \theta\right) $ | (7) |
式中:M——染色体个数。
根据文献[7]提出的对比散度, 得到ωij, ci, bj的更新准则为
| $ \omega_{i j}^{(1)}=\omega_{i j}^{(0)}+\varepsilon\left(\left\langle v_{i}^{(0)} h_{j}^{(0)}\right\rangle-\left\langle v_{i}^{(1)} h_{j}^{(1)}\right\rangle\right) $ | (8) |
| $ c_{i}^{(1)}=c_{i}^{(0)}+\varepsilon\left(\left\langle v_{i}^{(0)}\right\rangle-\left\langle v_{i}^{(1)}\right\rangle\right) $ | (9) |
| $ \mathrm{b}_{j}^{(1)}=\mathrm{b}_{j}^{(0)}+\varepsilon\left(\left\langle\mathrm{h}_{j}^{(0)}\right\rangle-\left\langle\mathrm{h}_{j}^{(1)}\right\rangle\right) $ | (10) |
在完成RBM的训练后, 采用有监督式的BP算法对整体DBN网络结构参数进行反向微调。微调的目的是进一步优化结构参数, 减小训练误差, 提高分类器的精度。训练误差的定义为
| $ \mu(\theta)=\frac{1}{M} \sum\limits_{m = 1}^M \left(\left\|L_{m}-Y_{m}\right\|^{2}\right) $ | (11) |
式中:Lm——训练样本; Ym——分类器输出。
2.3 GA-DBN结构及原理
DBN结构参数的选取对模型的整体性能有较大的影响。RBM中, θ(θ={ω, c, b})作为DBN结构参数对整个DBN故障分类器能否准确区分故障种类起着决定作用。由于最大似然估计方法的局限性, 使θ极易陷入局部最优值, 不容易得到全局最优值。本文提出了一种基于GA对θ优化的DBN模型, 将ωij, ci, bj进行数据重构, 组成串结构数据, 随机生成N个串结构数据, 每一个串结构数据作为一个染色体, 与群体内其他染色体进行选择、交叉、变异, 以及适应度评价、保优等操作, 得到最优染色体, 即θ*。将θ*重新配置到DBN中, 计算DBN的适应度, 满足终止条件后输出分类结果。
GA模拟自然界生物的遗传机制形成的过程搜索最优解算法, 具有原理简单且全局搜索能力强的特点, 在智能诊断领域有着极为广泛的应用[16]。因此, 本文采用GA对DBN结构参数进行优化。优化步骤分为以下3步。
(1) 初始化DBN结构参数, 将θ重构为串数据, 即为一条染色体。随机生成一个初始种群, 种群中包含M条染色体。
(2) 从种群中任意选择一条染色体替代初始θ, 训练DBN, 并计算适应度函数。适应度函数定义为Yt/Ytotal。其中, Yt为分类正确样本数, Ytotal为总样本数。
(3) 利用第1代种群中适应度大于a(a为一常数)的染色体, 经选择、交叉、变异和保优4步衍生出第2代新种群。重复第2步, 计算新结构参数下DBN的适应度函数。
2.4 算法实现
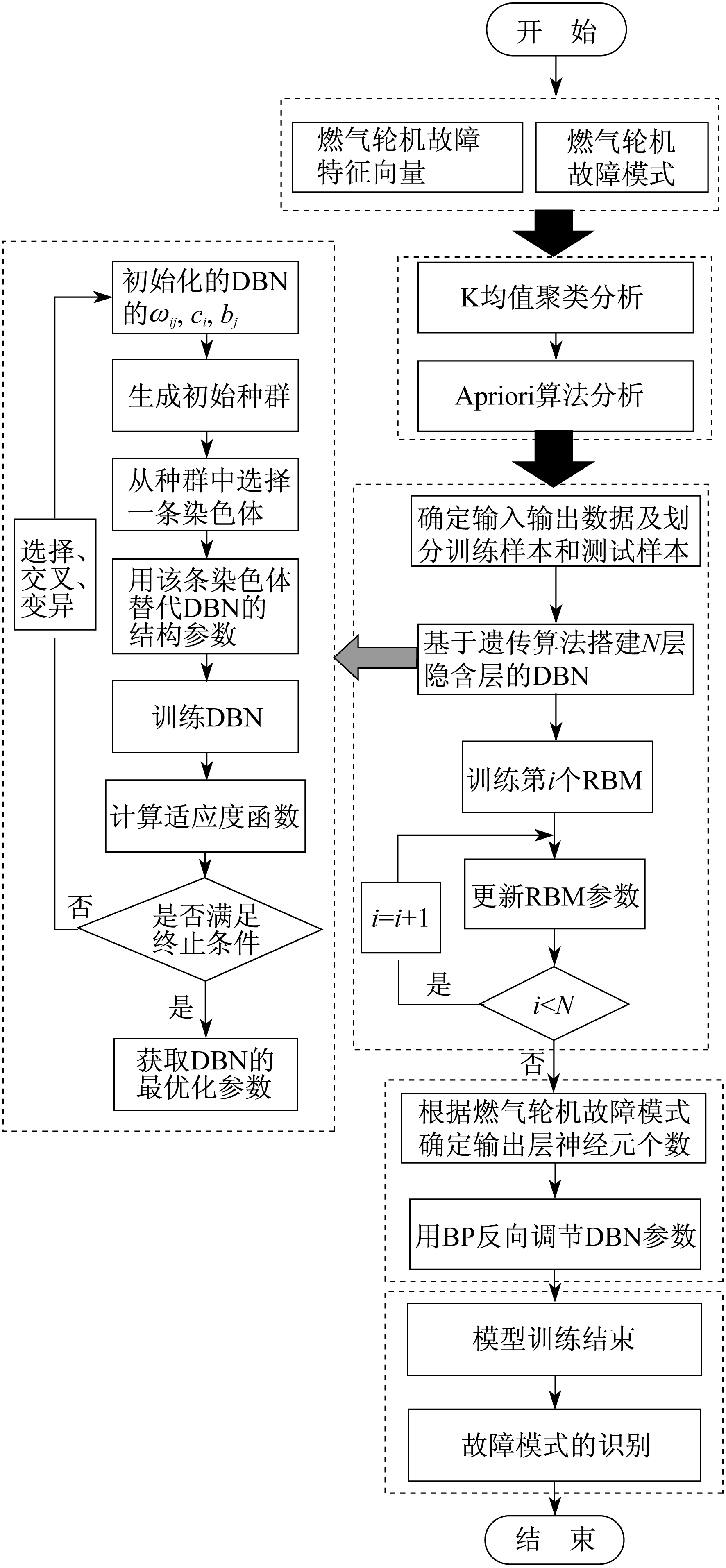
本文设计了一种经GA对DBN网络结构参数优化后的燃气轮机故障诊断模型, 即GA-DBN模型。其总体流程如图 3所示。
由上述分析可知, DBN训练过程分为非监督式正向学习过程和监督式逆向学习过程。在搭建DBN模型时, 文献[17]提出了一个相对通用的原则用于搭建DBN结构:网络后一层单元数小于前一层单元数, 这样设置的目的是为了在训练过程中训练数据可以被逐层压缩, 得到较好的准确率。本文中DBN的输入节点为5, 等于每一类故障特征向量的维度。隐含层层数选定4层, 即3个RBM堆叠的DBN网络。由于隐含层节点数的选择上没有相应的定理和规律, 主要根据设置不同节点数计算训练误差, 因此本文对3个RBM逐个进行最优隐含层神经元个数的选取, 以最小训练误差作为神经元个数的选取准则。输出节点对应故障模式0-1矩阵维数。训练参数主要包括正向学习的训练学习率和迭代训练次数。因为每个RBM的隐含层节点数不尽相同, 而每个RBM学习率的选取方法与RBM隐含层神经元最优个数的选取方法相同, 因此以训练误差为衡量标准, 选取训练误差最小的学习率作为单个RBM中的最优学习率。对于迭代次数, 一般过大会使诊断模型产生过拟合现象, 过小会使诊断模型产生欠拟合现象, 所以迭代次数需要不断调整得到。
3 实例分析
为验证本文所提方法的有效性, 针对压气机叶片积垢、压气机顶端间隙、压气机叶片磨损、压气机叶片机械损伤、涡轮叶片热腐蚀、涡轮叶片积垢、涡轮叶片磨损、涡轮叶片机械损伤、燃烧室故障9种故障模式及正常状态进行诊断分析。分别用A~E表示部分故障特征向量, 具体如表 1所示。分别用H1~H10表示9种故障模式及正常状态, 具体如表 2所示。
表 1
燃气轮机故障特征符号及其向量
| 符号 | 故障特征向量 |
| $\mathrm{A}$ | 低压压气机转速变化量$\left(\boldsymbol{S}_{1}\right)$ |
| $\mathrm{B}$ | 高压压气机转速变化量$\left(\boldsymbol{S}_{2}\right)$ |
| $\mathrm{C}$ | 低压压气机压缩比变化量$\left(\boldsymbol{S}_{3}\right)$ |
| $\mathrm{D}$ | 高压压气机压缩比变化量$\left(\boldsymbol{S}_{4}\right)$ |
| $\mathrm{E}$ | 燃油流量变化量$\left(\boldsymbol{S}_{5}\right)$ |
表 2
故障模式和正常模式的符号及状态
| 符号 | 故障状态 | 符号 | 故障状态 |
| H1 | 压气机叶片积暫 | H6 | 浴轮叶片积暫 |
| H2 | 压气机顶端间隙 | H7 | 浴轮叶片磨损 |
| H3 | 压气机叶片磨损 | H8 | 浴轮叶片机械损伤 |
| H4 | 压气机叶片机械损伤 | H9 | 燃烧室故障 |
| H5 | 浴轮叶片热腐蚀 | H10 | 正常模式 |
由于故障特征向量数据分布并不是均匀分布且故障特征向量所对应的故障模式尚未清楚, 因此不可用均分的方法对不同类别的故障特征向量进行分组。选取K均值聚类算法对特征向量进行自动区间划分, 得到每类故障特征向量离散表, 具体如表 3所示。
表 3
故障特征向量离散表
| 符号 | S1 | 符号 | S2 | 符号 | S3 | 符号 | S4 | 符号 | S5 |
| A1 | [-4.71, -3.51) | B1 | [-2.1, -1.1) | C1 | [-3.40, -2.18) | D1 | [-2.66, -1.98) | E1 | [-0.3, 0.05) |
| A2 | [-3.51, -3.13) | B2 | [-1.1, -0.6) | C2 | [-2.18, -1.34) | D2 | [-1.98, -1.38) | E2 | [0.05, 0.14) |
| A3 | [-3.13, 0.10) | B3 | [-0.6, -0.3) | C3 | [-1.34, -0.48) | D3 | [-1.38, -0.98) | E3 | [0.14, 0.42) |
| A4 | [0.10, 1.37) | B4 | [-0.3, 0) | C4 | [-0.48, 0.02) | D4 | [-0.98, -0.80) | E4 | [0.42, 0.72) |
| A5 | [1.37, 2.30) | B5 | [0, 0.14) | C5 | [0.02, 1.24) | D5 | [-0.80, -0.64) | E5 | [0.72, 1.31) |
| A6 | [2.30, 3.18) | B6 | [0.14, 1.03) | C6 | [1.24, 1.71) | D6 | [-0.64, -0.52) | E6 | [1.31, 1.95) |
| A7 | [3.18, 4.09) | B7 | [1.03, 1.43) | C7 | [1.71, 2.28) | D7 | [-0.52, -0.05) | E7 | [1.95, 2.77) |
| A8 | [4.09, 5.30) | B8 | [1.43, 2.11) | C8 | [2.28, 3.29) | D8 | [-0.05, 2.17) | E8 | [2.77, 3.49) |
| A9 | [5.30, 7.23) | B9 | [2.11, 2.99) | C9 | [3.29, 5.25) | D9 | [2.17, 2.78) | E9 | [3.49, 4.94) |
| A10 | [7.23, 7.99) | B10 | [2.99, 3.32) | C10 | [5.25, 6.57) | D10 | [2.78, 3.52) | E10 | [4.94, 6.54) |
设置模型的最小支持度和最小置信度, 通过Apriori算法对离散化特征向量进行分析, 将模型的最小支持度和最小置信度以及故障模式作为条件, 设置最小支持度为5%, 最小置信度为55%。由于关联结果较多, 限于篇幅, 本文取第一类故障为例, 关联结果如表 4所示。
表 4
第一类故障(H1)的关联结果
| 范围标志 | (支持度, 置信度) |
| A1 | $(10 \%, 78.9474 \%)$ |
| B2 | $(6.6667 \%, 90.9091 \%)$ |
| B6 | $(3.3333 \%, 71.4286 \%)$ |
| A4, C5 | $(10 \%, 93.75 \%)$ |
| C5, D8 | $(10 \%, 100 \%)$ |
| A4, D8, E1 | $(6.6667 \%, 100 \%)$ |
| A4, C5, D8, E1 | $(6.6667 \%, 100 \%)$ |
隐含层节点个数选取参数设置如表 5所示。表 5中, hbest和hbest_2分别为RBM1和RBM2的最优个数。最优学习率参数选取设置如表 6所示。
表 5
隐含层节点个数参数选取设置
| RBM | 隐含层节点初始个数/个 | 步长 | 隐含层节点个数最大值 |
| RBM1 | 1 | 2 | 120 |
| RBM2 | 1 | 1 | hbest |
| RBM3 | 1 | 1 | hbest_2 |
表 6
最优学习率参数选取设置
| RBM | 初始学习率 | 步长 | 学习率最大值 |
| RBM1 | 0.010 | 0.010 | 1.5 |
| RBM2 | 0.010 | 0.010 | 1.0 |
| RBM3 | 0.001 | 0.001 | 0.2 |
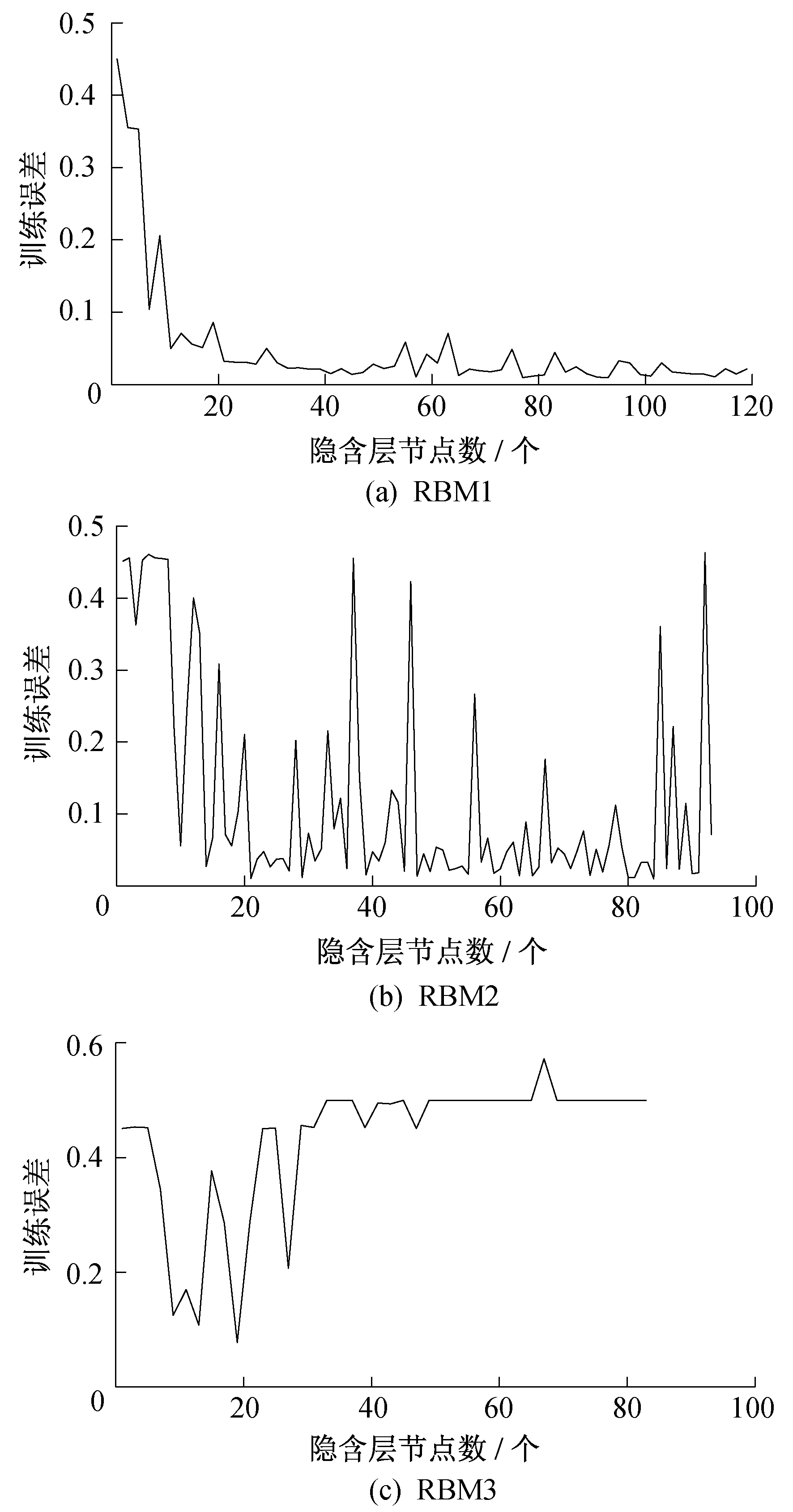
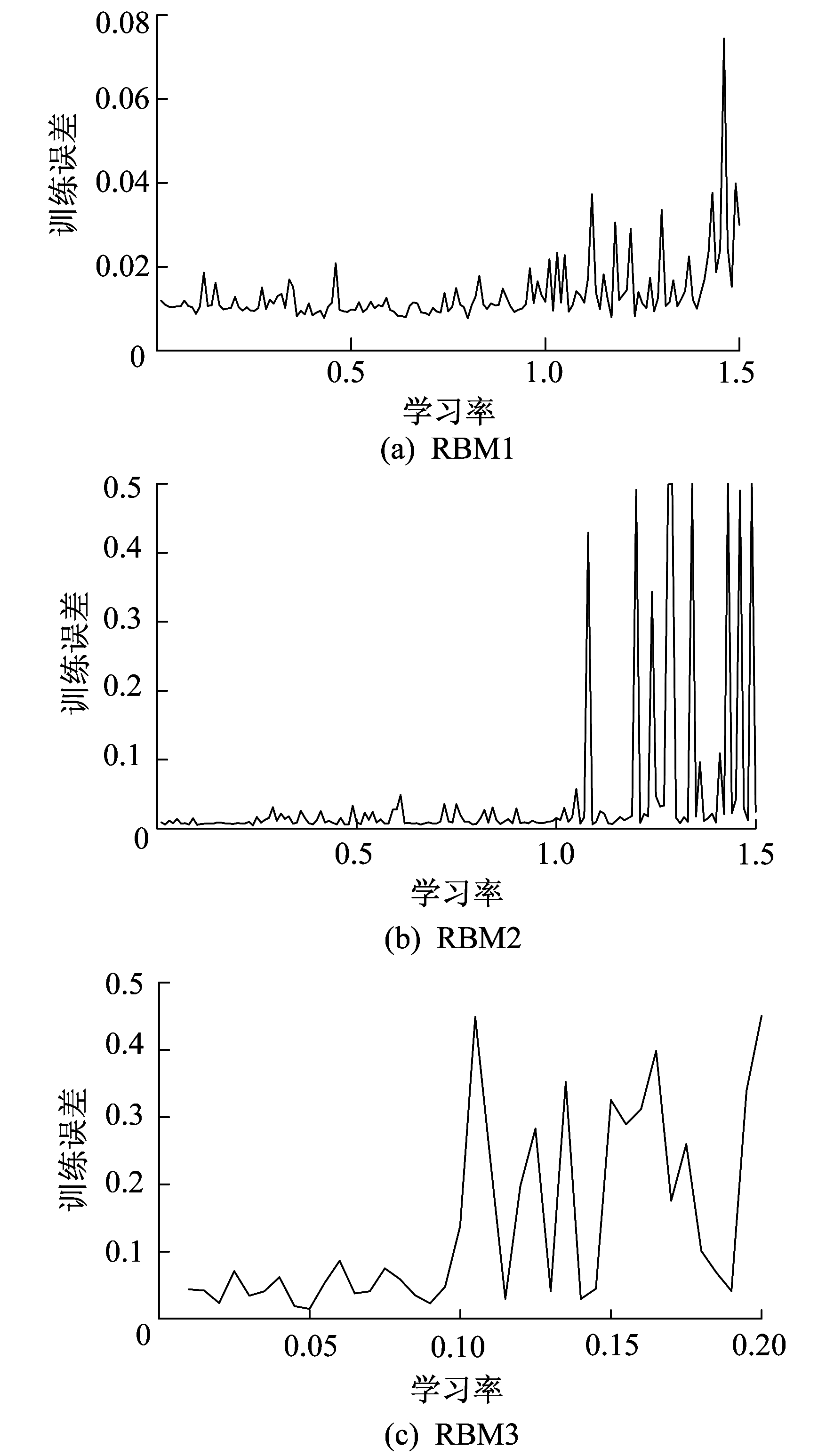
不同隐含层节点个数及学习率对应训练误差如图 4和图 5所示。
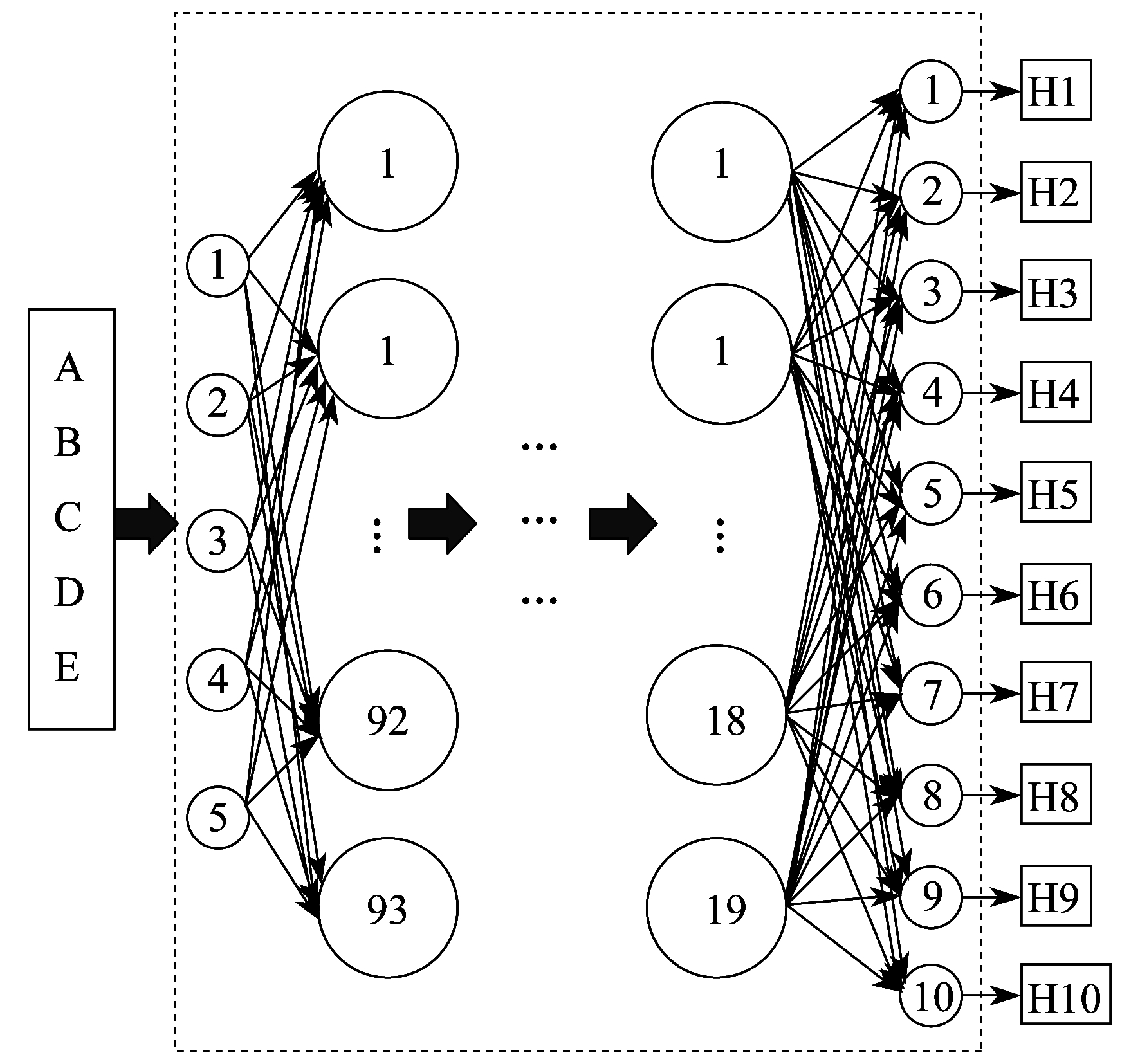
经过迭代计算最终确定3个RBM最优隐含层节点个数和最优学习率, 如表 7所示。即DBN为5-93-43-19-10结构, 将3个RBM最优学习率作为DBN学习率送入网络训练, 最终得到DBN模型, 如图 6所示。
表 7
最优个数及学习率
| RBM | 最优隐含层节点个数/个 | 最优学习率 |
| RBM1 | 93 | 0.80 |
| RBM2 | 43 | 0.24 |
| RBM3 | 19 | 0.05 |
DBN诊断模型的全部参数配置如表 8所示。
表 8
DBN全部参数配置
| DBN参数 | 参数值 | DBN参数 | 参数 |
| 输入节点/个 | 5 | 最大进化代数/次 | 20 |
| 输出节点/个 | 10 | 正向学习迭代/次 | 100 |
| 隐含层数/个 | 4 | 逆向学习迭代/次 | 200 |
| 初始偏置 | 0 | 遗传交叉概率 | 0.7 |
| 最小学习 | $1.0 \times 10^{-4}$ | 遗传变异概率 | 0.1 |
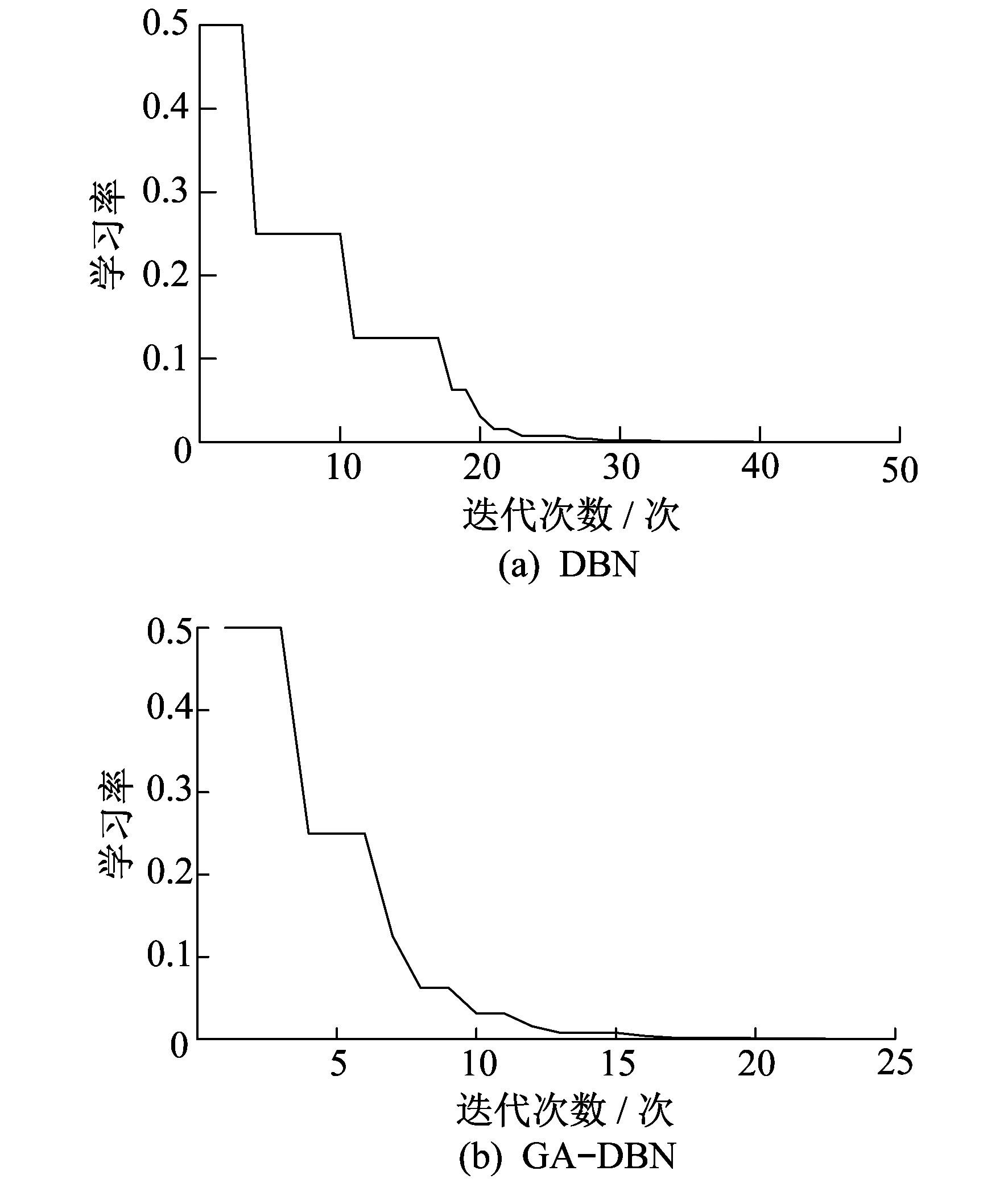
同时选取DBN模型、LM神经网络模型与GA-DBN模型做对比。DBN与GA-DBN中RBM1的学习率对比如图 7所示。
标准DBN设置初始学习率为0.5, 学习率最小值为0.001, 当适应度小于上一代最优适应度时, 学习率减半, 直到小于最小值时结束循环; GA-DBN则采用最优学习率。
由图 7可以看出, 标准DBN在第43次学习率达到最小值; GA-DBN经过遗传算法寻优的结构参数使得适应度值以较快速度减小, 在第25次学习率达到最小值, 所以GA-DBN有着更快、更少的迭代次数和更快的迭代速度。
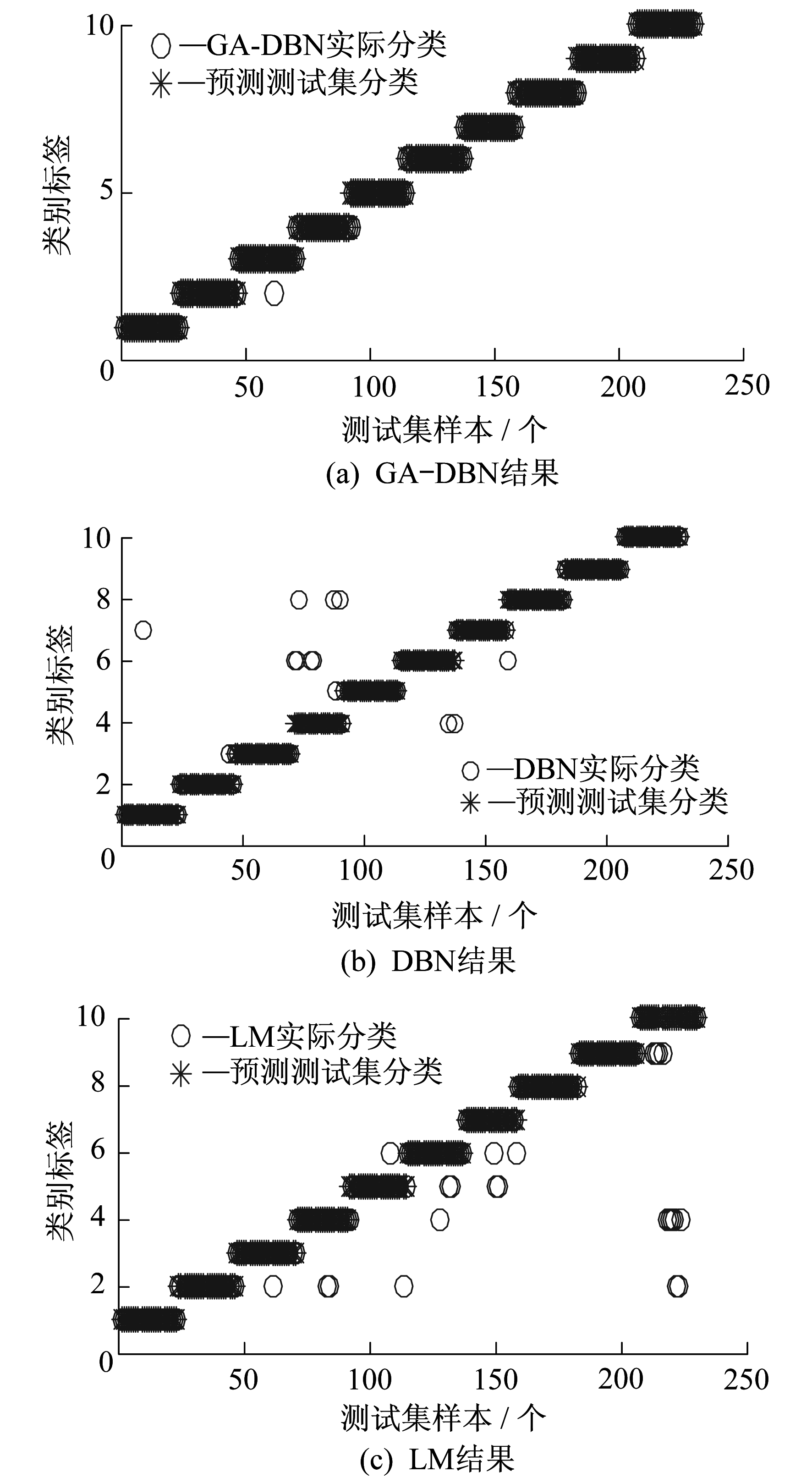
图 8为3种算法故障诊断结果的比较。
此外, 在230个测试数据中, GA-DBN误诊个数为3, 整体准确率可以高达98.696%。在相同的测试数据中, 标准DBN模型误诊个数为13, 整体准确率94.348%; LM神经网络模型误诊个数为30, 整体准确率86.957%。由此可知, 与传统浅层智能诊断方法相比, 本文提出的方法能更加稳定地诊断出燃气轮机的故障模式, 且准确率更高。
4 结语
本文通过Apriori算法筛选出满足最小支持度和最小置信度的故障特征向量进行关联度分析及分类, 将处理好的数据作为DBN的输入数据, 同时结合GA对DBN结构参数进行优化, 建立了基于DBN的非监督式燃气轮机故障诊断模型GA-DBN模型。与DBN模型和LM神经网络模型相比, 本文所提方法的故障准确率有明显提升, 多次实验准确率均可达到98%以上, 在3种模型中准确度最高。
参考文献
-
[1]VAN TUNG T, FAISAL A, ANDREW B. An approach to fault diagnosis of reciprocating compressor valves using Teager-Kaiser energy operator and deep belief networks[J]. Expert Systems With Applications, 2014, 41(9): 4113-4122. DOI:10.1016/j.eswa.2013.12.026
-
[2]胡应兰.基于D-S证据理论的多Agent辩论谈判策略研究[D].北京: 北京工业大学, 2014.
-
[3]基于随机森林的燃气轮机故障诊断检测方法研究[J]. 电工技术, 2018(22): 144-145. DOI:10.3969/j.issn.1002-1388.2018.22.059
-
[4]基于改进D-S证据理论的燃气轮机滑油系统故障诊断[J]. 燃气轮机技术, 2018, 31(2): 17-22.
-
[5]浅析故障诊断专家系统[J]. 内燃机与配件, 2019(6): 123-124. DOI:10.3969/j.issn.1674-957X.2019.06.059
-
[6]基于人工蜂群算法优化支持向量机的燃气轮机故障诊断[J]. 热能动力工程, 2018, 33(9): 39-43.
-
[7]HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527
-
[8]HINTON G E. Training products of experts by minimizing contrastive divergence[J]. Neural Computation, 2012, 14(8): 1771-1800.
-
[9]基于自适应深度信念网络的变电站负荷预测[J]. 中国电机工程学报, 2019, 39(14): 4049-4061.
-
[10]发电厂燃气轮机的检修及运行策略[J]. 化工设计通讯, 2018(8): 97. DOI:10.3969/j.issn.1003-6490.2018.08.087
-
[11]人工智能技术在云计算数据中心能量管理中的应用与展望[J]. 中国电机工程学报, 2019, 39(1): 31-42.
-
[12]基于Apriori算法的二次设备缺陷数据挖掘与分析方法[J]. 电力系统自动化, 2017, 41(19): 147-151. DOI:10.7500/AEPS20170306017
-
[13]基于MapReduce改进的Apriori算法及其应用研究[J]. 计算机科学, 2017, 44(6): 250-254.
-
[14]DBN网络的深度确定方法[J]. 控制与决策, 2015, 30(2): 256-260.
-
[15]基于深度置信网络的电力系统暂态稳定评估方法[J]. 中国电机工程学报, 2018, 38(3): 735-743.
-
[16]ERNOULT M, GROLLIER J, QUERLIOZ D. Using memristors for robust local learning of hardware restricted boltzmann machies.[J]. Scientific Reports, 2019, 9(1): 1851. DOI:10.1038/s41598-018-38181-3
-
[17]HINTON G E. Learning multiple layers of representation.[J]. Trends in Cognitive Sciences, 2007, 11(10): 428-434. DOI:10.1016/j.tics.2007.09.004