|
|
|
发布时间: 2020-04-10 |
|
|
|
|
收稿日期: 2019-11-08
中图法分类号: TP301
文献标识码: A
文章编号: 2096-8299(2020)02-0195-06
|
摘要
为了解决樽海鞘群算法(SSA)在收敛速度和求解精度方面存在的问题, 提出了一种改进的樽海鞘群算法。通过在原算法中引入天体运动更新机制来提高算法的收敛速度和收敛精度。用7个常见的测试函数对改进算法进行仿真验证, 同时将结果与现有的灰狼算法(GWO)、粒子群算法(PSO)和蚁狮算法(ALO)进行对比。结果表明, 引入天体运动更新机制的樽海鞘群算法具有更优的性能, 证明了改进方案的有效性。
关键词
樽海鞘群算法; 函数优化; 天体运动更新机制; 平均绝对误差
Abstract
In order to make up for the shortcomings such as the salp swarm algorithm in the convergence speed and the low accuracy of the solution, an improved salp swarm algorithm is proposed.The convergence speed and convergence precision of the algorithm are increased by introducing the celestial motion update mechanism on the original algorithm.The improved algorithm is verified by seven common test functions, and the results are compared with the existing gray wolf algorithm, particle swarm optimization and ant lion algorithm.The results show that the salp swarm algorithm with celestial motion update mechanism has better performance and proves the superiority of the improved scheme.
Key words
salp swarm algorithm; function optimization; astrophysics; mean absolute error
樽海鞘群算法(Salp Swarm Algorithm, SSA)是2017年由MIRJALILI S等人[1]提出的一种新的智能算法。作为一种元启发式算法, SSA具有收敛速度快、设定参数少、简单易懂等优点, 但也存在易陷入局部极值点、收敛精度不高等问题。目前, 已有学者对该算法进行了改进并应用于相关研究。文献[2]引入了评估移动策略来增强算法的开发能力, 并成功用于永磁同步电机的多参数辨识; 文献[3]通过引入levy飞行机制来提高算法的全局搜索能力, 并用于多阈值图像分割时的优化; 文献[4]结合了混沌精英质心拉伸机制, 有效地提高了SSA的收敛速度和收敛精度; 文献[5]用Tent映射来初始化种群个体, 并在食物源的位置中加入“疯狂”算子, 提高了算法的开发能力。本文在SSA中引入天体运动算子来提高算法的开发能力, 并通过7个常用的算法测试函数验证改进算法的有效性。
1 樽海鞘群算法
1.1 基本原理
SSA的思想来源于樽海鞘聚集成一条链式的行为, 即前后个体之间相互影响。将樽海鞘群中的个体划分为领导者和追随者, 其中领导者在链的前端, 对周围的环境有更好的判断。SSA的具体运算步骤如下[6]。
1.1.1 种群的随机初始化
设种群总数为N, 其中领导者个数为Nl, 追随者个数为Nf, 解空间维数为D维, 搜索空间的上限和下限分别为:ub=[ub1 ub2 ub3…ubD]和lb=[lb1 lb2 lb3…lbD], 那么樽海鞘个体的位置可以表示为xi=[x1 x2 x3 …xD]。
1.1.2 领导者的位置更新
对第i个领导者在第j维上的位置进行更新, 表达式为
| $ x_{j}=\left\{\begin{array}{ll} F_{j}+c_{1}\left[\left(u_{\mathrm{b} j}-1_{\mathrm{b} j}\right) c_{2}+1_{\mathrm{b} j}\right] & c_{3} \geqslant 0.5 \\ F_{j}-c_{1}\left[\left(u_{\mathrm{b} i}-1_{\mathrm{b} j}\right) c_{2}+1_{\mathrm{b} i}\right] & c_{3} \lt 0.5 \end{array}\right. $ | (1) |
| $ c_{1}=2 e^{-\left(\frac{4 t}{t_{\max }}\right)^{2}} $ | (2) |
式中:Fj——目标食物的位置;
c2, c3——随机产生的数, 范围均为[0, 1];
t, tmax——当前迭代次数和最大迭代次数。
参数c1的值对于算法的开发和探索能力的平衡起着至关重要的作用。由式(2)可以看出c1的值由2递减到0。
1.1.3 追随者的位置更新
对第i个追随者在第j维上的位置进行更新, 表达式为
| $ x_{j}=\frac{1}{2} a t_{0}^{2}+v_{0} t_{0} $ | (3) |
式中:a——加速度;
t0——时间;
v0——初始速度。
在SSA中, 时间t0就是当前迭代数与上一迭代数之差, 即t0=1;而初始速度v0往往设为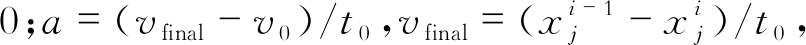 那么xj的最终更新公式为
那么xj的最终更新公式为
| $ x_{j}=\frac{1}{2}\left(x_{j}^{i}+x_{j}^{i-1}\right) $ | (4) |
1.2 算法改进
天体运动更新的思想来自于天体物理学中行星绕太阳运动的轨迹[7]。本文将这一思想与SSA结合, 得到天体运动更新的樽海鞘群算法(Astrophysics-inspired Salp Swarm Algorithm, ASSA)。其具体改进方法如下。
从N个种群中随机选择k个樽海鞘个体, 让这k个个体围绕当前种群中最优的个体来更新位置, 其更新表达式为
| $Y_{i, \text { new }}=Y_{\text {best }}+R_{i, \text { best }} U(-2,2)$ | (5) |
式中:Yi, new——被选择的个体更新后的位置;
Ybest——当前最优个体;
Ri, best——个体i与最优个体间的距离;
U(-2, 2)——区间[-2, 2]内的随机数, 与参数c1的变化相对应。
同时, 最优个体也更新其自身位置, 更新公式为
| $Y_{\text {best }, \text { new }}=Y_{\text {best }} U(-2,2)$ | (6) |
将更新后的位置与原位置相比, 选择适应度较好的作为最终更新位置, 即
| $ Y_{i}^{\prime}=\left\{\begin{array}{ll} Y_{i, \text { new }} & f\left(Y_{i, \text { new }}\right) \lt f\left(Y_{i}\right) \\ Y_{i, \text { else }} & \text { 其 他} \end{array}\right. $ | (7) |
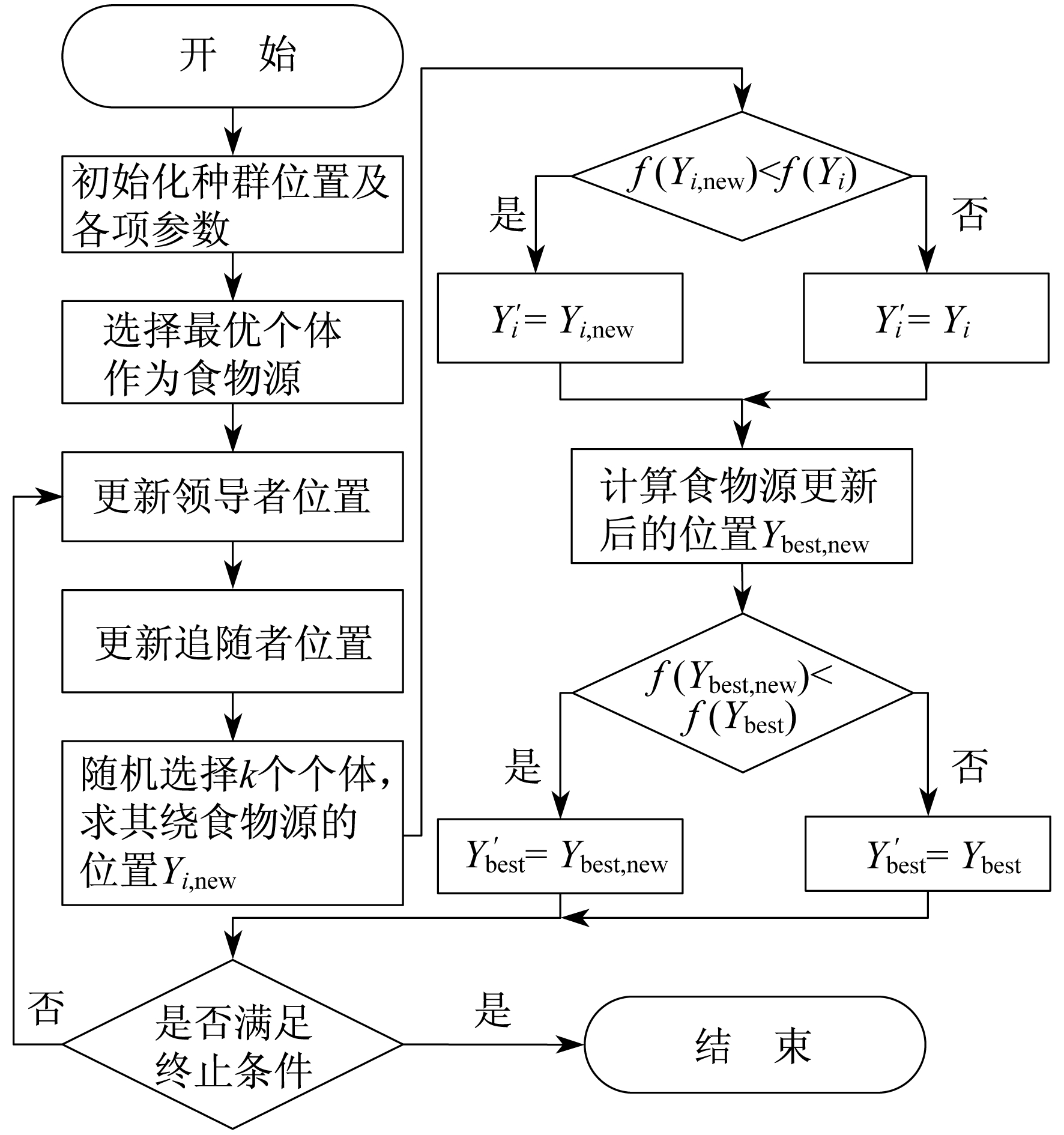
改进后的樽海鞘群算法流程如图 1所示。
2 实验分析
文献[4-5]中为了验证所提出的改进算法的有效性, 将其与其他智能算法对基准函数进行了多次独立重复实验, 并最终比较了各个算法的最佳值(Best)、平均值(Mean)、标准差(Standard Deviation, Std), 以及算法的成功率(Success Rate, SR)。为了验证本文所提出的ASSA的有效性, 对7个常用的测试函数进行最小值寻优仿真, 并将结果与SSA、蚁狮算法(Ant Lion Optimization, ALO)[8-9]、灰狼优化算法(Gray Wolf Optimization, GWO)[10-11]、粒子群优化算法(Particle Swarm Optimization, PSO)进行比较, 测试函数的详细信息如表 1所示。其中, U表示单峰, M表示多峰, S表示可分, N表示不可分。
表 1
测试函数信息
| 序号 | 函数 | 维数 | 特征 | 区间 | 最优值 |
| $f_{1}$ | Sphere | 30 | $\mathrm{US}$ | [-100, 100] | 0 |
| $f_{2}$ | Schwefel 2.22 | 30 | $\mathrm{UN}$ | [-10, 10] | 0 |
| $f_{3}$ | Schwefel 1.2 | 30 | $\mathrm{UN}$ | [-100, 100] | 0 |
| $f_{4}$ | Schwefel 2.21 | 30 | $\mathrm{US}$ | [-100, 100] | 0 |
| $f_{5}$ | Rastrigin | 30 | $\mathrm{MS}$ | [-5.12, 5.12] | 0 |
| $f_{6}$ | Ackley | 30 | $\mathrm{MN}$ | [-32, 32] | 0 |
| $f_{7}$ | Griewank | 30 | $\mathrm{MN}$ | [-600, 600] | 0 |
为了避免单次测试带来的偶然性影响, 对每个函数进行30次独立实验, 比较每种算法结果的最佳值、平均值、标准差和算法的成功率。判断每次试验是否成功的公式为
| $\left\{\begin{array}{l}\frac{\left|F_{\mathrm{A}}-F_{\mathrm{T}}\right|}{F_{\mathrm{T}}}<1.0 \times 10^{-3} \quad F_{\mathrm{T}} \neq 0 \\ \left|F_{\mathrm{A}}-F_{\mathrm{T}}\right|<1.0 \times 10^{-3} \quad F_{\mathrm{T}}=0\end{array}\right.$ | (8) |
式中:FA——每次实际求解最佳值;
FT——测试函数理论最佳值。
算法参数设置如下:上述4种算法的种群数N=30;最大迭代次数tmax=200; PSO算法的惯性权重和学习因子分别为w=1, c1, PSO=c2, PSO=1.5[4]; SSA和ASSA中领导者个数Nl和追随者个数Nf设成Nl=Nf[2-12-13], 且Nl=Nf=N/2=15; ASSA中k=15%×N≈5。
表 2为5种算法的实验结果。其中, 最优值和平均值这两个指标能够很好地反映算法的收敛精度, 而收敛精度的高低在很大程度上决定了算法的优劣。由表 2可以看出, 对于单峰函数f1~f4, ASSA的收敛精度非常高, 达到了1.0×10-50以上, 而SSA对这4种函数的寻优最优值均较大, 其中对函数f3的寻优值甚至超过890, 具有较大的误差。由此可见, ASSA能够改善SSA存在的收敛精度不高的问题。对于多峰函数f6, ASSA的收敛精度达到了1.0×10-16, 远高于其他4种算法(GWO的收敛精度为1.0×10-5, PSO为2.7, SSA为5, ALO为8), 满足了算法的精度要求。对于多峰函数f5和f7, ASSA收敛到了理论上的最优值零, 这是其他算法所不能比拟的。
表 2
各个算法的结果对比
| 函数 | 指标 | ASSA | SSA | ALO | GWO | PSO |
| f1 | Best | 6.94×10-105 | 8.65 | 1.09×10-4 | 1.01×10-9 | 1.55 |
| Mean | 3.60×10-67 | 42.52 | 32.52 | 9.18×10-9 | 3.41 | |
| Std | 1.93×10-66 | 28.92 | 106.85 | 1.39×10-8 | 0.83 | |
| SR | 100 | 0 | 53.33 | 100 | 0 | |
| f2 | Best | 1.37×10-59 | 2.68 | 35.34 | 2.16×10-6 | 4.51 |
| Mean | 1.32×10-28 | 7.83 | 91.68 | 5.17×10-6 | 8.04 | |
| Std | 7.10×10-28 | 2.62 | 31.62 | 2.11×10-6 | 1.09 | |
| SR | 100 | 0 | 0 | 100 | 0 | |
| f3 | Best | 1.58×10-106 | 895.55 | 4.99×103 | 0.16 | 4.03 |
| Mean | 5.23×10-64 | 3.55×103 | 8.32×103 | 4.78 | 8.48 | |
| Std | 2.81×10-63 | 1.77×103 | 2.56×103 | 9.45 | 3.14 | |
| SR | 100 | 0 | 0 | 0 | 0 | |
| f4 | Best | 1.71×10-53 | 8.82 | 10.45 | 0.008 8 | 0.463 |
| Mean | 1.73×10-34 | 15.71 | 17.44 | 0.034 | 0.719 | |
| Std | 8.75×10-34 | 3.58 | 3.94 | 0.025 | 0.123 | |
| SR | 100 | 0 | 0 | 0 | 0 | |
| f5 | Best | 0 | 22.82 | 45.77 | 2.90×10-4 | 1.51×102 |
| Mean | 0 | 53.92 | 71.67 | 11.64 | 2.02×102 | |
| Std | 0 | 16.54 | 20.52 | 5.69 | 22.31 | |
| SR | 100 | 0 | 0 | 3.33 | 0 | |
| f6 | Best | 8.88×10-16 | 3.15 | 1.65 | 6.47×10-6 | 1.92 |
| Mean | 8.88×10-16 | 5.23 | 8.34 | 1.63×10-5 | 2.77 | |
| Std | 0 | 1.47 | 3.43 | 6.15×10-6 | 0.33 | |
| SR | 100 | 0 | 0 | 100 | 0 | |
| f7 | Best | 0 | 1.063 | 0.011 | 2.29×10-9 | 0.064 |
| Mean | 0 | 1.39 | 0.45 | 0.014 | 0.136 | |
| Std | 0 | 0.35 | 0.52 | 0.026 | 0.048 | |
| SR | 100 | 0 | 0 | 66.67 | 0 |
标准差和成功率能够反映算法的稳定性。ASSA的标准差远小于其他4种算法, 采用ASSA优化的7个基准函数的标准差基本保持在1.0×10-30, SSA的标准差在1~200, GWO的标准差最好的也只有1.0×10-8。由此可以看出, ASSA对于不同函数的运算结果的稳定性比其他算法要好。对7个基准测试函数, 在规定的200次迭代次数内, ASSA优化结果的成功率都是100%, 而其他算法如GWO在对函数f3~f5时均难以达到100%, PSO和SSA的成功率甚至为零。
以上是基于30次独立运行的平均值、标准差的对比实验, 无法反映每一次运行时各个算法之间的差异。文献[14]提出, 应该对改进的算法进行统计性检验, 以验证其是否具有明显优势。
因此, 本文在5%显著性水平下进行了Wilcoxon秩和检验。在7个基准测试函数下, 5种算法在Wilcoxon秩和检验中求得的p-value值如表 3所示。将每个函数的最佳算法的值标记为N/A, 以符号“+, =, -”分别表示ASSA的性能优于、等于和劣于相比较的算法。
表 3
7个基准函数下5种算法的Wilcoxon秩和检验的p-value值
| 函数 | ASSA | SSA | ALO | GWO | PSO |
| $f_{1}$ | $\mathrm{N} / \mathrm{A}$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ |
| $f_{2}$ | $\mathrm{N} / \mathrm{A}$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ |
| $f_{3}$ | $\mathrm{N} / \mathrm{A}$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ |
| $f_{4}$ | $\mathrm{N} / \mathrm{A}$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ | $3.02 \times 10^{-11}(+)$ |
| $f_{5}$ | $\mathrm{N} / \mathrm{A}$ | $1.21 \times 10^{-12}(+)$ | $1.21 \times 10^{-12}(+)$ | $1.21 \times 10^{-12}(+)$ | $1.21 \times 10^{-12}(+)$ |
| $f_{6}$ | $\mathrm{N} / \mathrm{A}$ | $1.21 \times 10^{-12}(+)$ | $1.21 \times 10^{-12}(+)$ | $1.21 \times 10^{-12}(+)$ | $1.21 \times 10^{-12}(+)$ |
| $f_{7}$ | $\mathrm{N} / \mathrm{A}$ | $1.21 \times 10^{-12}(+)$ | $1.21 \times 10^{-12}(+)$ | $1.21 \times 10^{-12}(+)$ | $1.21 \times 10^{-12}(+)$ |
文献[14]指出, p-value值小于0.05就可以被认为是拒绝秩和假设。由表 3可以看出, 与其他算法相比, ASSA的p-value值均小于0.05, 可以认为在统计上ASSA比其他算法更具优越性, 即ASSA具有更高的收敛精度。
文献[15]提出了一个有效并且可行的判别算法性能的指标, 即为平均绝对误差(Mean Absolute Error, MAE)。其计算公式为
| $ \operatorname{MAE}=\frac{\sum\limits_{i=1}^{N_{\mathrm{b}}}\left|m_{i}-o_{i}\right|}{N_{\mathrm{b}}} $ | (9) |
式中:mi——算法多次独立测试后得到的最优结果的平均值;
Nb——测试函数的个数;
oi——测试函数的理论最优值。
本文同样用MAE来鉴别5种算法的优劣性, 其结果如表 4所示。
表 4
5种算法的MAE排名
| 算法 | MAE | 排名 |
| AS | $1.27 \times 10^{-16}$ | 1 |
| SA | 524.66 | 4 |
| SSA | $1.22 \times 10^{3}$ | 5 |
| ALO | 2.35 | 2 |
| GWO | 32.22 | 3 |
由表 4可以看出, ASSA的MAE值最小, 几乎为零, 远远小于SSA算法的MAE值524, 再一次验证了ASSA算法的优越性。
图 2是5种算法对不同基准测试函数的平均收敛曲线。其中, ASSA在函数f5和函数f7的寻优过程中达到了最优值为零, 故ASSA曲线的后面部分没有显示。
由图 2可以看出, 对于7个基准函数, ASSA的收敛速度很快, 并且在200次的迭代中并没有出现陷入局部极值点的现象。其他4种算法的收敛速度远远不及ASSA, 并且在迭代后期曲线平缓, 下降速度慢, 容易陷入局部极值点。对于函数f1, 函数f3和函数f4, ASSA均以非常快的速度收敛, 而SSA, GWO, ALO的收敛速度十分缓慢, PSO则容易陷入局部极值点; 对于函数f2, PSO, SSA, ALO分别在迭代到18次、20次和100次左右便陷入局部极值; 对于函数f5和f7, ASSA经不到100次迭代就达到了理论最优值, 而其他3种算法依旧收敛速度缓慢, 且最终精度也不高。
不论是针对单峰还是多峰函数, ASSA的收敛速度都很快, 且收敛精度高。
3 结语
本文在SSA的基础上, 随机选取部分个体围绕全局最优个体进行位置更新, 以探索最优个体附近的区域。通过7个基准测试函数对ASSA的性能进行检验, 结果表明, ASSA的最优值、平均值、标准差等各项指标都十分优异, 与SSA算法相比, 其性能有了极大的提高。
参考文献
-
[1]MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017(6): 163-191.
-
[2]基于改进樽海鞘群算法的PMSM多参数辨识[J]. 系统仿真学报, 2018, 30(11): 4284-4297.
-
[3]邢致恺, 贾鹤鸣, 宋文龙.基于莱维飞行樽海鞘群优化算法的多阈值图像分割[J/OL].自动化学报. [2019-02-19]. http://kns.cnki.net/kcms/detail/11.2109.TP.20190219.1551.004.html. DOI: 10.16383/j.aas.c180140
-
[4]陈忠云, 张达敏, 辛梓芸, 等.混沌精英质心拉伸机制的樽海鞘群算法[J/OL].计算机工程与应用. [2019-08-15]. http://kns.cnki.net/kcms/detail/11.2127.TP.20190815.1534.017.html. DOI: 10.3778/j.issn.1002-8331.1905-0048.
-
[5]张达敏, 陈忠云, 辛梓芸, 等.基于疯狂自适应的樽海鞘群算法[J/OL].控制与决策. [2019-01-03].https://doi.org/10.13195/j.kzyjc.2019.0012. DOI: 10.13195/j.kzyjc.2019.0012.
-
[6]基于樽海鞘群算法的无源时差定位[J]. 电子与信息学报, 2018, 40(7): 1591-1597.
-
[7]VIJAY K A, KUMAR D. An astrophysics-inspired grey wolf algorithm for numerical optimization and its application to engineering design problems[J]. Advances in Engineering Software, 2017(5): 231-254.
-
[8]MIRJALILI S. The ant lion optimizer[J]. Advances in Engineering Software, 2015, 83(1): 80-98.
-
[9]尹洪红, 杨晓文, 刘佳鸣, 等.一种基于蚁狮优化的极限学习机[J].计算机应用与软件, 36(8): 230-234.
-
[10]MIRJALILI S, MIRJALILI S M, LEWIS A, et al. Grey wolf optimizer[J]. Advances in Engineering Software, 2014(3): 46-61.
-
[11]模糊函数主脊切面特征提取的灰狼优化方法[J]. 计算机应用与软件, 2018, 35(8): 279-285. DOI:10.3969/j.issn.1000-386x.2018.08.051
-
[12]基于改进樽海鞘群算法的四旋翼飞行器姿态优化控制[J]. 农业机械学报, 2019, 50(10): 243-250. DOI:10.6041/j.issn.1000-1298.2019.10.028
-
[13]部分遮蔽下改进樽海鞘群算法的光伏系统最大功率跟踪[J]. 控制理论与应用, 2019, 36(3): 339-352. DOI:10.7641/CTA.2019.80899
-
[14]DERRAC J, GARCIA S, MOLINA D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm & Evolutionary Computation, 2011(1): 3-18.
-
[15]EMAD N. A modified flower pollination algorithm for global optimization[J]. Expert Systems with Applications, 2016, 57(9): 192-203.