|
|
|
发布时间: 2020-08-30 |
|
|
|
|
收稿日期: 2020-03-18
中图法分类号: TP399
文献标识码: A
文章编号: 2096-8299(2020)04-0341-10
|
摘要
风电功率的准确预测是减少风电并网对电网造成冲击的有效手段之一。利用深度学习算法中的长短期记忆网络(LSTM)对中期风电功率出力进行了预测,综合考虑功率数据、气象数据等多维特征,采用LSTM算法和随机森林(RF)算法搭建预测模型,预测风电场1~7日的风电功率出力。基于某风电场2014年1月到2016年12月的实际发电数据,通过实验对比BP神经网络、支持向量机(SVM)和自回归积分滑动平均模型(ARIMA)等算法可知,提出的预测方法在较为突变的天气状况下仍能保持较高的预测精度,能为风电并网和电网调度提供辅助支撑。
关键词
风电功率预测; 长短期记忆网络; 随机森林算法
Abstract
The accurate prediction of wind power is one of the effective means to reduce the impact of wind power grid on the power grid.The article uses the long and short-term memory neural network (LSTM) in the deep learning algorithm to predict the mid-term wind power output.The model comprehensively considers multi-dimensional features such as power data and meteorological data.The article uses the LSTM algorithm and the random forest algorithm to build a prediction model to predict the wind power output of the wind farm in 1~7 days.Based on the actual power data from January 2014 to December 2016, comparing the BP neural network, SVM and ARIMA models, the method proposed in this paper obtains a better result in the special weather condition, so it can provide support for the wind power integration and the network dispatching.
Key words
wind power prediction; long and short-term memory; random forest
从2010年起, 我国的风机装机容量, 无论是总装机容量还是新增装机容量, 都已跃升为世界第一[1]。但随着装机容量的日渐增大, 部分地区的弃风现象开始变得严重起来。2017第一季度的弃风现象虽有减缓, 但仍不容乐观。一般来说, 风电功率预测可划分为超短期、短期和中长期3个时间尺度。超短期的预测是指超前0~3 h的预测, 时间分辨率不小于15 min, 用于风电实时的调度; 短期预测是预测未来1~3日的数据, 时间分辨率为0.5~1 h; 而中长期的预测, 时间分辨率多为24 h, 超前72 h以上预测发电量。超短期和短期的风电出力预测能够为风电并网和实时调度提供技术性的参考指标; 而中长期的风电预测, 能够协助风电的资源评测, 方便风电场的机组检修安排, 从宏观上也能减少弃风, 提高风电场的发电量和容量系数, 为风电的长期发展以及电网的建设调度提供辅助支撑。
目前, 根据预测原理, 风电发电量预测模型主要分为统计模型和物理模型两类[2]。前者可以细分为时序外推法和人工智能法。时序外推法一般使用发电量的历史数据对未来值进行预测, 一般使用自回归积分滑动平均(Auto Regressive Integrated Moving Average, ARIMA)模型和卡尔曼滤波法[3]; 而人工智能法多采用神经网络[4]和支持向量机(Support Vector Machine, SVM)[5], 利用数值天气预报(Numerical Weather Prediction, NWP)的历史数据和未来的预测数据, 寻找历史输入与输出的对应关系。
单一的输入数据和方法难以满足精度要求日渐严苛的风电预测[6], 因此不少研究者提出了组合的预测方式。文献[7]结合物理模型和统计模型, 提出了混合预测的方法。文献[8]提出了多气象变量模型的组合预测方法, 利用多个气象的变量历史和未来预测数据, 但NWP的预测数据往往与风电场的实测数据存在一定的偏差, 不加处理会造成不必要的误差。另外, 文献[9]指出, 历史和当前的气象状态决定了未来的大气运动趋势, 所以必须结合历史气象数据对未来数值进行预测。目前的风电功率预测研究大多集中于短期或超短期的预测方面, 在中长期的预测方面相对偏少。
此外, 虽然研究者们对风电预测的方法提出了不少改进之处, 但涉及的算法也仅限于BP神经网络和SVM等浅层的学习方法。这些学习方法对输入的处理能力有限[10], 在处理较为复杂的分类和回归任务时, 泛化能力不佳。目前, 深度学习已经在图像识别[11]、视频分类、自然语言处理[12]等应用上取得了十分喜人的效果, 而在电力自动化领域的应用研究仍然处于起步阶段, 在风电功率预测领域的应用更少。近年来, 随着计算机计算能力的大幅度提高以及深度学习算法的飞速发展, 将为风电预测的方案开辟出一条新的道路[13]。常用的深度学习模型有卷积神经网络、深度置信网络、堆栈自动编码器、长短期记忆网络(Long Short-Term Memory, LSTM)等, 其中, LSTM专门用于处理时间序列性的数据, 能够学习到输入序列的元素之间的关系。
本文将深度学习算法应用于风电功率预测, 提出了一个基于LSTM和随机森林(Random Forest, RF)的中长期风电预测的模型。通过风电场的实测数据对该方法进行误差评估和分析, 对比BP神经网络及SVM和ARIMA模型, 基于LSTM和RF的组合风力预测模型从多个评价指标上均显示出较好的精度, 能够很好地满足国家对风电预测要求的标准, 能够为电网调度提供辅助支撑。
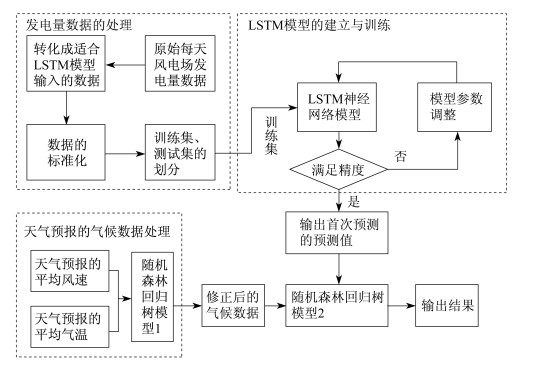
1 方法框架
本文所提方法具体步骤如下。
步骤1 整理原始数据, 获得每一天风电场所对应的总发电量、平均风速、平均温度, 以及天气预报的平均风速和平均温度等数据。
步骤2 对原始数据进行预处理, 使其满足LSTM模型所对应的输入需求。
步骤3 按照任务的需求, 采用不同的归一化方法去归一化原始数据。
步骤4 训练LSTM模型, 并输出训练集的迭代曲线, 优化LSTM的参数。
步骤5 输入测试集, 输出预测结果, 并按照不同的评价标准, 对比不同的预测模型, 对输出结果进行分析。
步骤6 采用RF算法对NWP数据进行修正, 并将修正后的气候特征和LSTM首次预测的值输入到新的RF模型中, 进行二次预测。
步骤7 输出测试结果并进行误差分析。
步骤8 得出结论。
其总体框架如图 1所示。
2 基于LSTM的风电功率预测
2.1 时间序列预测的一般操作与不足
一般的时间序列回归分析预测使用的是自回归模型(Auto Regression Model, AR模型)、滑动平均模型(Moving Average Model, MA模型)或者是ARIMA模型, 其中ARIMA模型的应用较为广泛。一个确定的ARIMA(p, d, q)模型需要确定3个系数, 其中:p为自回归项, d为时间序列成为平稳时所作的差分次数, q为移动平均项数。确定这3个系数一般要对时间序列数据进行平稳性的判断, 非平稳性序列一般要对其进行差分处理, 平稳化后一般会根据Box - Jenkins的模型识别方法[14], 对序列的自相关和偏自相关函数进行判断, 根据其截尾性和拖尾性判断序列所属的类型。模型类型确定后, 根据对应的准则函数, 对所选模型的阶数进行确定。因此, 使用时序外推法利用ARIMA模型对风电场的历史数据进行建模, 需要对原始数据进行相对复杂的预处理, 而且模型的选择需要对序列的自相关函数的图像和偏相关函数的图像进行观察, 会存在一定的主观因素, 且精度不高。使用历史发电数据的基于BP神经网络和SVM的人工智能预测方法, 需要固定一个“观察窗口”, 即使用t时刻的前k步作为输入, 去预测t时刻的输出。此外, 当前的输入仅与观察窗口输入的数据相关, 与观察窗口外的历史数据无关, 就会把影响输出的某些历史数据忽略掉, 从而影响预测结果。此外, 需要对k值的选择进行反复的测试才能达到较好的效果。另外, 使用NWP数值人工智能预测方法, 通过NWP的历史数据建立气象数据和风电输出之间的映射, 受训练样本集影响较大, 鲁棒性较差。
2.2 LSTM神经网络简介
LSTM网络模型属于循环神经网络(Recurrent Neural Networks, RNN)的一种, 是一个循环的网络结构, 具有保留历史信息的能力。一般的RNN, 权重矩阵
| $ {\nabla _W}E = \sum\limits_{k = 1}^t {{\nabla _{Wk}}E} $ | (1) |
式中:
与
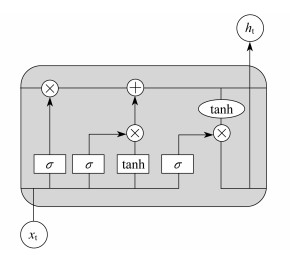
LSTM网络通过一个“门”的结构来对记忆单元(下称“单元”)的状态量, 进行信息的增加和删减操作。单个时间点的LSTM基本结构如图 2所示。
一般的LSTM网络有3种门结构, 分别是遗忘门、输入门和输出门。
遗忘门的作用是决策出一个遗忘系数ft(介于0和1之间的数或者向量)来决定要遗忘单元中的哪些信息。具体的运算公式为
| $ {\rm{ }}{f_t} = \sigma (\mathit{\boldsymbol{ W}}{_{\rm{f}}}\cdot[{h_{t - 1}}, {x_t}] + \mathit{\boldsymbol{ b}}{\mathit{\boldsymbol{}}_{\rm{f}}}) $ | (2) |
式中:
输入门是根据前一时间点的输出
| $ {i_t} = \sigma ({\rm{ }}\mathit{\boldsymbol{W}}{_{\rm{i}}}\cdot[{h_{t - 1}}, {x_t}] + {\rm{ }}\mathit{\boldsymbol{b}}{_{\rm{i}}}) $ | (3) |
| $ \widetilde C{_t} = {\rm{tanh}}({\rm{ }}\mathit{\boldsymbol{W}}{{\rm{}}_{\rm{C}}}\cdot[{h_{t - 1}}, {x_t}] + \mathit{\boldsymbol{ b}}{\mathit{\boldsymbol{}}_{\rm{C}}}) $ | (4) |
| $ {C_t} = {f_t}\cdot{C_{t - 1}} + {i_t}\cdot{\widetilde C_t} $ | (5) |
式中:
最后的输出门取决于
| $ {o_t} = \sigma ({\rm{ }}\mathit{\boldsymbol{W}}{_{\rm{o}}}[{h_{t - 1}}, {x_t}] + \mathit{\boldsymbol{ b}}{\mathit{\boldsymbol{}}_{\rm{o}}}) $ | (6) |
| $ {h_t} = {o_t} \times \tanh \left( {{C_t}} \right) $ | (7) |
式中:
2.3 随机森林回归树
随机森林是集成学习中的一种基于Bagging算法的改良算法。集成学习通过建立多个基学习器去完成学习的任务, 本质上是通过组合多个弱的学习器, 形成一个强的学习器, 来完成学习任务, 多用于分类和回归的任务中。标准的Bagging算法只是通过从原始样本中进行n次的Bootstrap重采样, 通过样本的差异实现单个基学习器的“多样性”。与标准的Bagging算法不同的是, RF加入了来自属性的扰动, 即从原始的T个属性中选取t个属性(t < T), 一般地, 取t=log2T[16], 然后再从t个属性中选取最优的分裂点, 从而增大了机器学习之间的差异程度, 提高了泛化能力, 也加快了收敛的速度。
使用随机森林作为第二次预测的学习器, 能够减少学习模型参数的调节, 而且训练速度也较快, 便于最后作输入特征的修正和拟合。
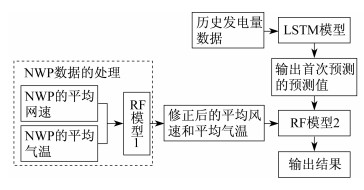
2.4 LSTM和RF的组合模型
3 算例分析
3.1 数据集说明
本文以我国某风电场(总装机容量1.5×105 kW)从2014年1月1日—2016年12月31日的实测数据作为模型训练和测试的样本。具体的数据如表 1所示。
表 1
风电场实测数据部分样例
| 日期 | 发电量/ 104 kWh | 平均风速/ (m·s-1) | 平均气温/℃ |
| 2014-01-01 | 86.967 37 | 9.06 | 6 |
| 2014-01-02 | 26.970 16 | 7.74 | 12 |
| 2014-01-03 | 93.912 64 | 9.15 | 9 |
| 2014-01-04 | 122.489 60 | 12.58 | 11 |
| 2014-01-05 | 96.084 86 | 10.67 | 6 |
3.2 数据预处理
由于神经网络中存在激活函数, 所以一般在数据的预处理上都需要对输入数据进行归一化或标准化处理, 本质上是对数据的一种尺度变换。一般神经网络的激活函数是sigmoid函数, 但sigmoid函数存在两个缺陷:一是函数的两个尾部陷入饱和, 容易导致梯度弥散问题; 二是函数不以零为中心。因此, 本文采用比sigmoid函数性质要好的tanh函数, 因为tanh以零为中心, 能够更快地进行收敛, 而且tanh活跃的区间在[-1, 1], 故本文利用式(8)将原始数据放缩到[-1, 1]之间。
| $ {\rm{ }}{y_i} = {\rm{ }}\frac{{{x_i} - {x_{{\rm{min}}}}}}{{{x_{{\rm{max}}}} - {x_{{\rm{min}}}}}} \times 2 - 1 $ | (8) |
式中:
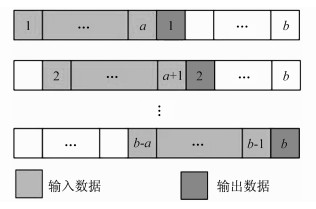
此外, 归一化后, 作为神经网络的输入, 还需要对归一化的序列数据进行转换, 以满足LSTM的输入要求。以LSTM的输入为例, 数据集的输入实际上是一个张量, 如样本数、时间步、输入维度等。输入维度根据考虑的内外因素的个数确定, 如只考虑历史数据, 则输入维度为1, 如同时考虑历史数据和平均风速的话, 则输入维度为2, 以此类推。假设原始序列中一共有a+b个数据点, 输入的时间步为a步, 那么经过转换后的数据共有b条数据, 如图 4所示。
3.3 模型的评价指标
对于回归预测问题, 一般会结合几种不同的评价指标, 综合评价所建立模型的优劣。常用的模型评价标准有MAE(Mean Absolute Error)、RMSE(Root Mean Squared Error)、MAPE(Mean absolute Percentage Error)等。具体计算公式为
| $ {\rm{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{{\widehat p}_i} - {p_i}} \right|} $ | (9) |
| $ {\rm{RMSE}} = \sqrt {\frac{1}{N}{{\sum\limits_{i = 1}^N {\left( {{{\hat p}_i} - {p_i}} \right)} }^2}} $ | (10) |
| $ {\rm{MAPE}} = \frac{1}{N}\sum\limits_{i = 1}^N {\frac{{\left| {{{\widehat p}_i} - {p_i}} \right|}}{{{p_i}}}} \times 100\% $ | (11) |
式中:
MAE与RMSE类似, 都是衡量预测值和实际值之间的绝对误差, 对于两个不同容量的风电场(假设风电场1的容量是风电场2的10倍), 同样的MAE值和RMSE值, 风电场2的发电量预测值误差就要比风电场1大很多, 以此来评价模型的优劣是不妥当的。MAPE是衡量预测值和实际值之间的相对误差, 但是, 当实际值
| $ {\rm{NMAE}} = \frac{1}{N}\sum\limits_{i = 1}^N {\frac{{\left| {{{\widehat p}_i} - {p_i}} \right|}}{{{p_{{\rm{installed}}}}}}} \times 100\% $ | (12) |
| $ {\rm{CC}} = \frac{{{\rm{cov}}(\hat p,p)}}{{\delta \left( {\hat p} \right),\delta \left( p \right)}} $ | (13) |
式中:
除了纵横的两个评价指标外, 在后面的章节还会加入对误差值分布的评价方法。
另外, 根据国家能源局发布的《风电场功率预测管理暂行办法的通知》给出的预测预报要求, 准确率
| $ {r_1} = {\rm{ }}\left( {1{\rm{ }} - \sqrt {{\rm{ }}\frac{{1{\rm{ }}}}{N}{\rm{ }}\sum\limits_{k = 1{\rm{ }}}^N {\left( {\frac{{{P_{{\rm{M}}k}} - {P_{{\rm{P}}k}}}}{{{C_{{\rm{ap}}}}}}} \right)} } {\rm{ }}} \right) \times 100\% $ | (14) |
式中:
合格率
| $ {r_2} = {\rm{ }}\frac{{1{\rm{ }}}}{N}\sum\limits_{{\rm{ }}k = 1{\rm{ }}}^N {{B_k} \times 100\% } $ | (15) |
式中:
其中,
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {1 - \frac{{{P_{{\rm{M}}k - }}{P_{{\rm{P}}k}}}}{{{C_{{\rm{ap}}}}}}} \right) \times 100 \ge 75\% \;\;\;\;\;{B_k} = 1}\\ {\left( {1 - \frac{{{P_{{\rm{M}}k - }}{P_{{\rm{P}}k}}}}{{{C_{{\rm{ap}}}}}}} \right) \times 100 \le 75\% \;\;\;\;\;{B_k} = 0} \end{array}} \right. $ | (16) |
3.4 网络的构建与训练
训练样本选取了2014年1月到2016年6月的数据。使用预测日前14日的数据作为输入向量, 预测方法采用单点滑动窗口预测方法, 即先用前14日的数据预测第15日的发电量, 然后输入向量的窗口向后滑动1日, 把预测出来的第15日的发电量加入输入向量, 把最先的1日的发电量数据从输入向量中删除, 预测第16日, 如此类推, 一共预测7日。
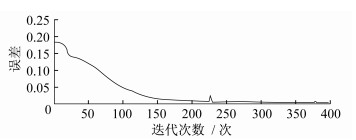
本文采用的LSTM模型是3层的LSTM层加上1层的神经网络全连接层。LSTM层的激活函数为tanh函数, 全连接层采用的liner函数, 采用Adam算法进行网络的训练, 各层的神经元个数分别是14, 30, 8, 1。批训练样本个数为75, 模型的训练迭代次数为400。图 5为模型的迭代与误差示意。
3.5 测试集的选取
选取2016年7月3日到8月17日(下称“时间段1”)和2016年9月21日到2016年11月5日(下称“时间段2”)两个时间段的发电量数据作为模型的测试集。两个时间段发电量的分布指标如表 2所示。
表 2
测试样本的发电量分布指标
| 时间段 | 均值 | 标准差 | 最小值 | 25%分位数 | 50%分位数 | 75%分位数 | 最大值 |
| 1 | 86.57 | 64.41 | 3.28 | 29.02 | 78.42 | 124.66 | 229.81 |
| 2 | 60.07 | 61.07 | 1.38 | 25.58 | 36.91 | 71.85 | 309.91 |
这两个时段的发电量的大小所覆盖的范围都比较广, 而且时间段1和时间段2的发电量的分布也存在较大的不同, 时间段1的发电量均值比时间段2大, 但极差和标准差均比时间段2小, 而时间段2中既有日发电量大于3.0×106 kWh的样本, 也有因为天气原因导致发电量连续在3.0×106 kWh以下的样本。因为这两个时间段的发电量各有特点, 所以测试的结果更能够体现出模型的泛化能力。
3.6 单LSTM的预测结果及对比分析
将时间段1和时间段2对应的数据输入已经训练好的LSTM神经网络中, 输出从第1日预测到第7日预测的结果, 并根据式(12)和式(13)计算NMAE和CC值, 具体数据如表 3所示。
表 3
LSTM中不同日数的预测结果
| 预测日数/日 | NMAE1/% | CC1 | NMAE2/% | CC2 |
| 1 | 4.69 | 0.84 | 5.26 | 0.83 |
| 2 | 4.40 | 0.85 | 6.49 | 0.71 |
| 3 | 4.99 | 0.84 | 7.45 | 0.65 |
| 4 | 5.43 | 0.82 | 8.38 | 0.55 |
| 5 | 6.82 | 0.62 | 9.31 | 0.52 |
| 6 | 7.75 | 0.58 | 10.98 | 0.46 |
| 7 | 8.81 | 0.47 | 11.34 | 0.48 |
由表 3可以看出, LSTM神经网络在时间段1上的预测精度比时间段2的高, 而且时间段1从第1日到第4日的预测值与实际值的CC值都大于0.8, 显示出很强的相关性; 但对比第5日到第7日的预测, 虽然LSTM神经网络在时间段1上的精度依然比时间段2高, 但时间段2中随着时间的推移, 精度的下降幅度小于时间段1, 也体现出LSTM网络结构中记忆门和遗忘门在处理较长历史依赖方面的优势。
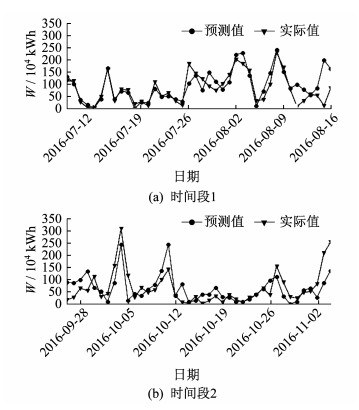
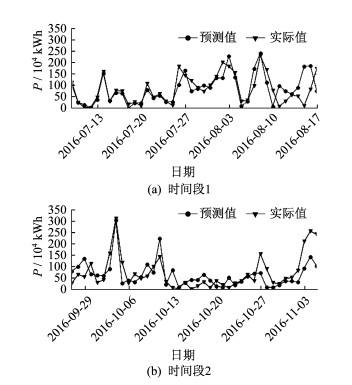
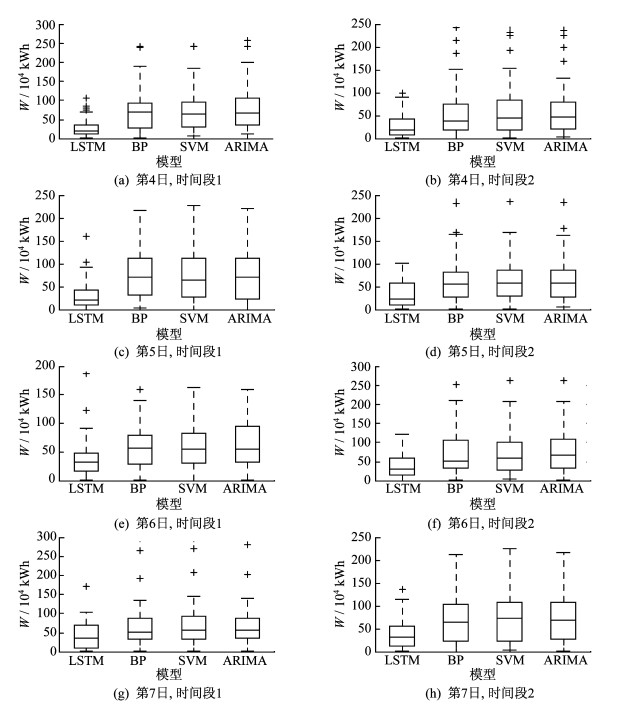
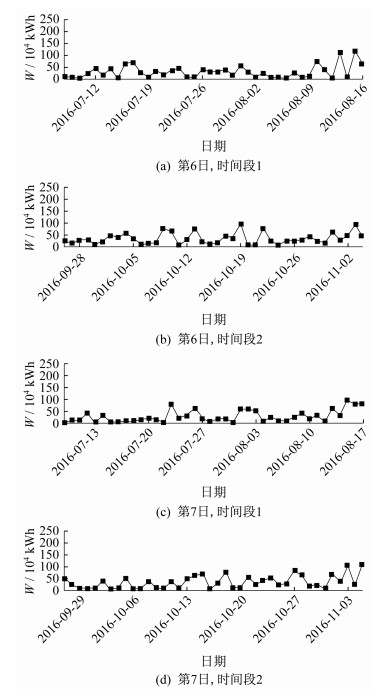
由于篇幅原因, 本文只给出预测第6日和第7日的实际值和预测值的折线图, 如图 6和图 7所示。
由图 6和图 7可以看出, 对于第6日和第7日的预测, LSTM的预测值和实际值的大小以及变化趋势也是比较吻合的, 尤其是时间段1中前半部分的预测结果。
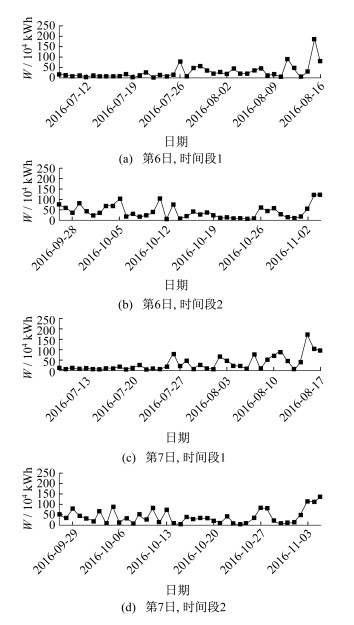
图 8为第6日和第7日两个时间段预测值的误差值。
结合图 6~图 8可以看出, 在相邻日期出现较大发电量偏差的部分日期中, 误差值较其他时段大。经过查阅对应点的气候数据, 发现误差较大的原因很可能是由于气候因素的影响导致误差的增大。
另外, 可以通过描述误差分布的盒状图来比较LSTM与BP神经网络、SVM和ARIMA(1, 2, 5)模型的预测精度。由于篇幅问题, 本文只给出第4日到第7日的误差分布盒状图, 如图 9所示。由图 9可知, 虽然LSTM也会出现误差较大的几个异常点, 但无论从误差的各四分位数的大小或误差分布范围去考虑模型的预测精度, LSTM在只根据历史数据建模后的精度都高于其他3个模型。
3.7 LSTM和RF组合模型的预测结果
针对图 8中出现的部分时间点误差值过大的情况, 加入对应日期的气候数据。由于监测点与风电场现场的地理位置有一定距离, 故需要对输入的气候数据进行修正。本文使用随机森林回归树模型(树的个数为150)对包括当前预测日的未来7日的平均风速和平均气温作修正, 并将修正后的数据经式(8)归一化处理后输入到新建立的随机森林回归树模型中, 并输出结果。对于时间段1和时间段2(以第6日和第7日的预测为例), 修正后的误差曲线如图 10所示。
对比图 8可知, 加入气候特征的新模型, 其预测误差分布更为平均。不同模型纵横指标对比如表 4所示。由表 4可知, 随着预测天数的增加, LSTM和RF组合模型的纵横指标全面领先单LSTM和SVM模型, 而且随着预测时间的增加, 组合模型精度下降的幅度都比单LSTM模型和SVM模型要小, 由此可见组合模型在预测结果上的优越性。
表 4
不同模型纵横指标的对比
| 预测日数/ d | 单LSTM | LSTM和RF组合模型 | SVM | |||||||||||
| NMAE/ % | CC | 准确率/ % | 合格率/% | NMAE/ % | CC | 准确率/ % | 合格率/ % | NMAE/ % | CC | 准确率/ % | 合格率/ % | |||
| 1 | 5.26 | 0.83 | 94.74 | 100.00 | 5.20 | 0.84 | 94.80 | 100.00 | 5.40 | 0.79 | 94.60 | 100.00 | ||
| 2 | 6.49 | 0.71 | 93.51 | 97.50 | 5.88 | 0.81 | 94.12 | 100.00 | 6.95 | 0.68 | 93.05 | 92.50 | ||
| 3 | 7.45 | 0.65 | 92.55 | 97.50 | 6.35 | 0.76 | 93.65 | 100.00 | 8.69 | 0.54 | 91.31 | 90.00 | ||
| 4 | 8.38 | 0.55 | 91.62 | 97.50 | 6.73 | 0.70 | 93.27 | 97.50 | 10.03 | 0.52 | 89.97 | 87.50 | ||
| 5 | 9.31 | 0.52 | 90.69 | 92.50 | 7.43 | 0.66 | 92.57 | 97.50 | 12.53 | 0.42 | 87.47 | 80.00 | ||
| 6 | 10.98 | 0.46 | 89.02 | 85.00 | 8.03 | 0.59 | 91.97 | 95.00 | 14.38 | 0.35 | 85.62 | 77.50 | ||
| 7 | 11.34 | 0.48 | 88.66 | 85.00 | 8.37 | 0.56 | 91.63 | 92.50 | 15.38 | 0.33 | 84.62 | 77.50 | ||
另外, 准确率衡量的是模型的总体平均水平, 而合格率衡量的是预测值与实际值偏差是否过大。从表 4可以看出, 组合模型的准确率和合格率依然比单LSTM和SVM模型高, 而且在预测前3日的合格率达到100%, 即没有出现误差绝对值大于开机容量25%的情况; 而以SVM为代表的浅层模型, 在合格率方面, 虽然在前2日的精度与单LSTM模型和LSTM与RF的组合模型相距不大, 但在后几日的合格率精度上, 差距与其他两个模型逐渐拉大, 体现了LSTM的深层结构在预测时间延长时所展现出的优势。
3.8 实验结果分析
采用滑动窗口单点预测的方法, 利用LSTM网络对风电场单日的发电量历史数据进行风电场的中长期出力预测。凭借LSTM网络结构中的记忆门和遗忘门的作用, 解决了对较长期历史数据的记忆和使用问题, 对比BP神经网络及SVM和ARIMA(1, 2, 5)模型, 在预测未来7日发电量的任务上, LSTM模型的预测误差值分布较其他3个模型集中, 各四分位数也均小于其他3个模型。
在加入修正后的气候特征后, 模型的预测精度进一步提高, 在单一历史数据输入情况下的某些异常点预测误差过大的情况也得以缓解, 精度有所提升。
4 结语
准确的中长期风电功率预测能够辅助风电场制订检修维护计划, 减少因停运检修造成的发电量损失。目前国内中长期的风电功率预测研究并不多, 关于风电功率预测的模型基本上是一些浅层模型, 难以学习到较为复杂的问题。本文提出了一种通过LSTM和RF组合模型来对未来7日的风电场发电量进行预测, 采用了风电场的历史发电量数据对LSTM模型进行训练学习, 再利用RF对NWP预测日的平均风速和平均气温进行修正并再次预测。实验结果表明, 对比BP神经网络、SVM和ARIMA模型, 本文所提方法的预测结果更为准确, 预测值和实际值的误差分布更为集中, 对应的NMAE和CC值也更准确, 而且提前7日的预测精度也满足国家的相关标准, 能够在天气突变的情况下, 减小预测误差。本文提出的方法, 能够为全面考虑影响风电场发电量的一些非直接影响因素, 如机组的故障时间及可运行的机组台数等的研究提供相关参考。
参考文献
-
[1]夏冬.基于时间序列分析的大型风电场功率预测方法研究[D].北京: 北京交通大学, 2012.
-
[2]MONTEIRO C, BESSA R, MIRANDA V, et al.Wind power forecasting: state-of-the-art 2009[R].Argonne National Laboratory (ANL), Argonne, 2009.
-
[3]潘迪夫, 刘辉, 李燕飞. 基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型[J]. 电网技术, 2008(7): 82-86.
-
[4]范高锋, 王伟胜, 刘纯. 基于人工神经网络的风电功率短期预测系统[J]. 电网技术, 2008(22): 72-76.
-
[5]杨锡运, 孙宝君, 张新房, 等. 基于相似数据的支持向量机短期风速预测仿真研究[J]. 中国电机工程学报, 2012, 32(4): 35-41.
-
[6]赵坤, 张挺, 杜奕. 基于FILTERSIM算法的风力发电功率预测[J]. 上海电力学院学报, 2019, 35(2): 149-152.
-
[7]周淑贞, 张如一, 张超. 气象学与气候学[M]. 北京: 高等教育出版社, 1997: 250-356.
-
[8]欧阳庭辉, 查晓明, 秦亮, 等. 中长期风电功率的多气象变量模型组合预测方法[J]. 电网技术, 2016(3): 847-852.
-
[9]COUTO A, COSTA P, RODRIGUES L, et al. Impact of weather regimes on the wind power ramp forecast in Portugal[J]. IEEE Transactions on Sustainable Energy, 2015, 6(3): 934-942. DOI:10.1109/TSTE.2014.2334062
-
[10]BENGIO Y.Learning deep architectures for AI[J/OL].Foundations and trends in Machine Learning, 2009.[2020-03-10] https: //dl.acm.org/doi/10.1561/2200000006.
-
[11]KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[J]. Advances in Neural Information Processing Systems, 2012, 25(2): 1097-1105.
-
[12]COLLOBERT R, WESTON J, BOTTOU L, et al. Natural language processing (almost) from scratch[J]. Journal of Machine Learning Research, 2011, 12(8): 2493-2537.
-
[13]彭彤宇, 茅大钧, 韩万里. 基于改进ARMA的电厂风机状态预测[J]. 上海电力学院学报, 2019, 35(6): 535-538.
-
[14]BOX G E P, JENKINS G M, REINSEL G C, et al. Time series analysis:forecasting and control[M]. Hobeken: John Wiley & Sons, 2015.
-
[15]GRAVES A, LIWICKI M, FERNÁNDEZ S, et al. A novel connectionist system for unconstrained handwriting recognition[J]. IEEE transactions on Pattern Analysis and Machine Intelligence, 2009, 31(5): 855-868. DOI:10.1109/TPAMI.2008.137
-
[16]BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32.
-
[17]徐曼, 乔颖, 鲁宗相. 短期风电功率预测误差综合评价方法[J]. 电力系统自动化, 2011, 35(12): 20-26.