|
|
|
发布时间: 2020-08-30 |
|
|
|
|
收稿日期: 2019-04-08
基金项目: 国家自然科学基金(41672114,41702148)
中图法分类号: TP399
文献标识码: A
文章编号: 2096-8299(2020)04-0364-05
|
摘要
岩石的内部结构复杂,虽然利用扫描电镜可获得精确的高分辨率页岩孔隙结构,但是实验成本高,耗时长,不便于大规模运用。针对这一问题,提出了基于无监督卷积神经网络的页岩重构方法,结合页岩图像软数据,进行了页岩重构。实验证明该方法只需要少量的真实页岩数据即可获得较好的重构结果;与经典的数值重构方法Snesim和Filtersim方法相比,该方法耗时更少,具有一定优势。
关键词
重构; 页岩; 卷积神经网络
Abstract
The internal structure of the rock is complex.Although accurate high-resolution shale pore structure can be obtained by scanning electron microscopy, the experiment is expensive, time-consuming and inconvenient for large-scale application.A shale reconstruction method based on unsupervised convolutional neural network is proposed, which combines shale image soft data to reconstruct shale.This method only needs a small amount of real shale data to obtain better reconstruction results.Compared with the Snesim and Filtersim methods for shale reconstruction, this method has advantages.
Key words
reconstruction; shale; convolutional neural network
国民经济的飞速发展刺激了能源的需求, 页岩气作为新型天然气资源越来越受到重视[1]。为了评价页岩的含气性并对其勘探开发, 研究页岩气储层的孔隙结构变得尤为重要[2-5]。直接获取页岩真实孔隙结构的方法分为两大类:物理实验法和数值重构方法。物理实验法包括连续切片法、扫描电镜法、X射线CT扫描、纳米CT[6-10]等。这些物理实验法可以得到高分辨率的真实页岩孔隙结构模型, 但是这类方法成本高, 实验过程繁琐, 需要大量处理时间, 不便于大规模应用。因此基于实际样品数据进行数值重构的方法成为页岩孔隙重构的重要手段。
数值重构方法是从真实岩石样本模型中提取对孔隙结构和分布有直接影响的关键信息, 建立相似的孔隙结构, 从而实现页岩图像重构。数值重构方法包括以下3种:一是过程法, 模拟自然界岩石沉积胶结过程的重构方法; 二是随机法, 通过选取合适的岩石薄片图像的统计量来描述孔隙空间形态特性; 三是多点地质统计法, 使用多点统计信息进行重构, 来获得岩石微观孔隙结构。
上述传统的数值重构方法需要大量的训练数据, CPU运行负荷大, 运行时间较长, 重构效果随机性强。近年来, 深度学习算法兴起, 卷积神经网络(Convolutional Neural Network, CNN)作为其重要分支在图像和视频处理领域得到广泛运用[10], 但未应用于重构页岩微观结构的实验中。因此, 本文提出利用CNN结合页岩软数据进行页岩内部结构重构, 得到页岩的孔隙结构。
1 无监督CNN总体架构
由于CNN对于数据具有强大的学习能力, 能学习到数据更高维的特征, 因此被广泛应用于图像处理。CNN的基础架构中, 输入层直接获取图像数据, 各节点不进行数学运算。隐藏层可以只有一层, 也可以有很多层, 数据在隐藏层中会经历加权求和, 经过传输函数最终传递给输出层。输出层计算出最终结果。CNN的隐藏层并不全是全连接, 各层神经元只连接到前一层的部分神经元。此外, 同一层神经元之间连接的权值是共享的, 这样可以在不影响学习效果的前提下, 减少了参数的数量。
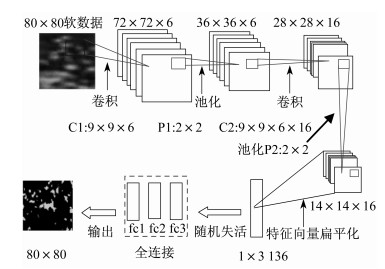
重构过程中, 使用硬数据作为重构的输入数据。硬数据是随机截取的部分点的值, 即部分空间值是空白的, 这一情况无法对硬数据直接进行CNN的重构, 因此使用可以反映页岩孔隙空间变化的软数据进行填充, 以此作为输入数据重构页岩图像, 最小化重构图像与目标图像的重构损失来优化模型参数。图 1为网络模型的架构图。以80×80的软数据为例, 首先经过6个大小为9×9的卷积核C1, 以1为步长滑动, 得到72×72×6的特征图。然后经过2×2大小的随机池化P1, 对卷积特征降维。接着经过第二层卷积C2和随机池化P2得到14×14×16的局部特征, 再将矩阵形式的特征映射扁平化为1×3136大小, 加入随机失活(dropout)以防过拟合, 输入fc1, fc2, fc3 3层全连接层获得全局信息。最后经输出层得到80×80页岩数据。
1.1 卷积层
卷积层是由若干个卷积核连接起来的特征平面。这些特征平面中的所有神经元均以矩阵形式排列, 卷积核以已知尺寸的随机数矩阵的形式进行卷积, 对特征图组合进行局部感知, 为后续更高层的全局信息的整合提供局部信息, 这样可以在保留有用信息的同时有效减少网络的负荷。因为页岩图像某些部分包含相似的特征, 提取特征时就可以将一部分已经学习到的特征用在另一部分上, 意味着提取的特征与位置无关, 可以在类似的位置上使用同样的学习特征, 所以卷积核是权值共享的。这样可以降低模型复杂度, 极大地提高CNN的运行速度。本次实验使用9×9大小的滤波器进行卷积, 提取局部特性。对于卷积层的每一种输出的特征图有
| $ a_j^l = f\left( {\sum\limits_{i \in {M_j}} {a_j^{l - 1} \times w_{ij}^l + b_j^i} } \right) $ | (1) |
式中:
1.2 子采样层
子采样也叫作池化, 基于局部相关性原理压缩数据和参数数量, 但池化操作仅是对图像大小压缩, 不改变特征的尺度, 具有特征不变性。池化过程通常和卷积过程组合出现, 池化层的每个特征映射都连接到其前一个卷积层的相应特征映射。池化过程与卷积过程类似, 可视为一种不带权重的池化函数, 以子采样层使用的特征映射区块尺寸从输入特征图的左上角开始按一定步长从左向右、从上到下进行池化操作。为了降低出现过拟合的概率, 同时可以相对完整地保存局部特征信息, 使用最大值池化和平均值池化组合的混合池化方法。最大值池化选取领域内的最大值, 可以直接获取最显著特征, 避免特征值的偏移, 实际应用偏多。平均值池化对特征映射区域内的值求平均, 用以保留图像的背景信息。对于混合池化的特征映射
| $ \begin{array}{l} {y_{i, j, k}} = {\rm{ }}\lambda \;{\rm{ma}}{{\rm{x}}_{\left( {m, n} \right) \in R}}_{_{i, j}}\left( {{a_{m, n, k}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{1 - \lambda }}{{\left( {\left| {{R_{i, j}}} \right|} \right)\left( {{a_{m, n, k}}} \right)}}{\rm{ }} \end{array} $ | (2) |
式中:
1.3 全连接层
经过以上的卷积和池化操作后, 岩石图像的局部特征已经被提取出来, 接着还需要将局部特征全局化。全连接层即是每层每个神经元都与其上一层所有神经元进行连接, 用以整合局部特征获取全局信息。这一部分使用了以下两个函数。
(1) Sigmoid激活函数 其取值范围为0~1, 公式为
| $ \sigma \left( x \right) = {\rm{ }}\frac{1}{{1 + {{\rm{e}}^x}}}{\rm{ }} $ | (3) |
(2) Tanh激活函数 其取值范围为-1~1, 公式为
| $ \sigma \left( x \right) = \frac{{{{\rm{e}}^x} - {{\rm{e}}^{ - x}}}}{{{{\rm{e}}^x} + {{\rm{e}}^{ - x}}}} $ | (4) |
1.4 参数优化
在训练任务中, 给定样例集
| $ \begin{array}{l} {\rm{loss}}\left( {\;\;\;} \right) = - y\;{\rm{lg}}\left( {y\_} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1 - y)\;{\rm{lg}}(1 - y\_) \end{array} $ | (5) |
为了更好地进行模型的自主学习, 训练过程中对学习率进行了动态设定, 使用了Adam算法[11]为参数设计独立的自适应性学习率。当目标函数震荡不收敛时, 降低学习率; 当目标函数收敛速度过慢时, 增加学习率。
2 基于无监督CNN的页岩孔隙重构实验
2.1 数据预处理
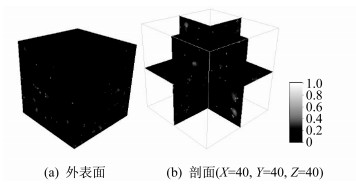
本次实验使用真实情况下页岩的三维图像作为训练样品。原始样品图像是圆柱状, 从中截取了80×80×80体素的页岩图像作为目标图像。目标图像是指模拟者希望模拟实现的图像, 实验时用作与计算结果进行对比的参照数据, 从而验证模型参数的正确性。图 2是目标图像。
重构页岩图像时, 从截取的目标图像中随机采集了4%的点作为卷积神经网络输入使用的原始硬数据。这些点随机分布在三维立体空间中, 无法保证一个卷积核大小的区域内点的个数相同且分布一致。为了便于CNN的运行, 对硬数据使用简单克里金算法进行插值, 插值得到的实际上是页岩数据分布情况的估计值, 是一种80×80×80体素的“孔隙概率立方体”软数据。软数据是页岩图像中孔隙空间的概率值, 取值范围是0~1的小数。这些数据总体能够比较准确地体现页岩孔隙空间的变化趋势。将得到的软数据作为CNN的输入。图 3是硬数据图, 图 4是软数据图。
2.2 实验结果
实验机器配置如下:处理器Intel(R) Core(TM) i5 - 3230M 2.60GHz, 内存12G, 操作系统Windows 7。设计实验模型为2层卷积层、2层池化层和3层全连接层的无监督CNN, 输入页岩软数据重构页岩图像, 输出重构结果, 对重构结果进行二值化处理, 阈值为0.5, 最后得到二值化后的页岩重构图像。在重构实验中, 常用外表面图、剖面图、孔隙结构图、孔隙度、变差函数和运行速率作为衡量指标。下面分别针对这几个衡量指标对本文方法与经典的多孔介质数值重构方法Snesim和Filtersim方法进行对比。
2.2.1 重构图像
2.2.2 孔隙度
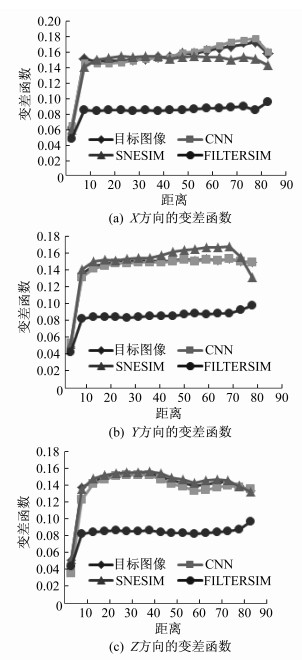
2.2.3 变差函数
2.2.4 CPU重构时间
3 结语
本文提出了一种结合软数据对页岩进行重构的无监督CNN模型。该模型的优势是权值共享减少了参数个数, 使神经网络结构具有更强的适应性, 并且减轻了内存负担, 有效提高了重构速度。此外, 该模型先对数据进行特征提取, 基于特征向量对页岩进行重构, 重构结果比较稳定。将该模型与传统经典多孔介质数值重构方法在孔隙度、变差函数、对内存的需求和CPU运行时间等方面进行了对比, 证明了该算法能够较好地重构页岩图像。
参考文献
-
[1]张珺瑶.基于LBM和数字岩心的页岩基质渗透率计算研究[D].大庆: 东北石油大学, 2016.
-
[2]潘仁芳, 龚琴, 鄢杰, 等. 页岩气藏"甜点"构成要素及富气特征分析——以四川盆地长宁地区龙马溪组为例[J]. 天然气工业, 2016, 36(3): 7-13.
-
[3]张晋言, 李淑荣, 王利滨, 等. 低阻页岩气层含气饱和度计算新方法[J]. 天然气工业, 2017, 37(4): 34-41.
-
[4]庞伟. 采用多点地质统计法重构页岩的数字岩心[J]. 天然气工业, 2017, 37(9): 71-78.
-
[5]董大忠, 王玉满, 李新景, 等. 中国页岩气勘探开发新突破及发展前景思考[J]. 天然气工业, 2016, 36(1): 19-32.
-
[6]张挺, 卢芳芳. 基于纳米CT数据的页岩岩样三维重构[J]. 上海电力学院学报, 2017, 33(5): 477-479.
-
[7]JAVADPOURF, MORAVVEJ M, AMREIN M. Atomic force microscopy (AFM) a new tool for gas shale characterization[J]. Journal of Canadian Petroleum Technology, 2012, 51(4): 236-243. DOI:10.2118/161015-PA
-
[8]LOUCKS R G, REED R M, RUPPEL S C, et al. Spectrum of pore types and networks inmudrocks and a descriptive classification for matrix-related mudrock pores[J]. AAPG Bulletin, 2012, 96(6): 1071-1098. DOI:10.1306/08171111061
-
[9]BLUNTM J, BIJELJIC B, DONG H, et al. Pore-scale imaging and modeling[J]. Advances in Water Resources, 2013(51): 197-216.
-
[10]张玉麒, 陈加, 叶立志, 等. 基于改进卷积神经网络的单幅图像物体重建方法[J]. 计算机应用与软件, 2019(6): 190-195.
-
[11]张峰逸, 彭鑫, 陈驰, 等. 基于深度学习的代码分析研究综述[J]. 计算机应用与软件, 2018(6): 9-17.
-
[12]张挺.基于多点地质统计的多孔介质重构方法及实现[D].合肥: 中国科学技术大学, 2009.