|
|
|
发布时间: 2020-10-25 |
智慧用能 |
|
|
|
收稿日期: 2020-05-27
基金项目: 基于多储能调节的多源直流微电网鲁棒协调控制及稳定性研究(61873159)
中图法分类号: TM734
文献标识码: A
文章编号: 2096-8299(2020)05-0421-10
|
摘要
针对含电-热-冷-气子系统的综合能源系统中潜在的可调度资源,基于能源集线器,构建了包含燃气轮机发电系统、储能、需求侧响应模型在内的社区综合能源管理系统数学模型。该模型根据电、热、冷、气负荷需求特性的不同,分别建立相应需求响应模型。从社区能源运营商的角度出发,以包含系统运行成本和环境成本的系统总成本最低为目标函数,建立社区综合能源系统日前优化调度模型,采用Yalmip工具箱和Cplex求解器对算例进行求解,得到各个设备的最佳出力。仿真结果表明,对比未考虑需求侧协同响应的场景,电、热、冷、气需求侧响应参与调度可以优化负荷曲线,降低系统能耗,减少CO2排放,并使系统经济性达到最优。
关键词
社区综合能源系统; 能源集线器; 需求侧协同响应; 低碳经济调度
Abstract
Aiming at the potential schedulable resources in the integrated energy system containing electricity, heating, cooling and gas subsystems, a mathematical model of a community integrated energy management system including gas turbine power generation system, energy storage and demand response model is built based on the energy hub.According to the different energy demand characteristics of electricity, heating, cooling and gas loads, demand response model are established respectively.From the perspective of community energy operators, taking the lowest total system cost including system operating cost and environmental cost as the objective function, and establishing day-ahead optimal dispatch model of community integrated energy system.The Yalmip toolbox and Cplex solver are used to solve the example, and the best output of each equipment is accepted.Simulation results show that, compared with scenarios where demand response is not considered, the participation of demand response can optimizes the load curve, reduce energy consumption, reduce carbon dioxide emissions and optimize system economy.
Key words
community integrated energy system; energy hub; demand side cooperative response; low-carbon economic dispatch
随着多能源网络融合的不断加深以及能源转化设备的进步[1], 综合能源系统(Integrated Energy System, IES)可挖掘潜力越来越大。同时, 工业、商业和居民用户需要的能源形式越来越多, 然而目前这些能源系统大多是分开运行的[2]。电、热、冷、气各个能源系统单独运行导致系统灵活度低, 能源利用率低, 弃风弃光现象严重。电热冷气联合调度优点明显, 例如能够提高整个系统的运行效率, 减少不同能源的浪费, 降低系统的运营成本, 提高系统的稳定性和灵活性, 减少污染物排放等[3]。作为提高能源利用率的有效措施, 近年来, IES发展迅速[4]。IES有多种方式的能源供应, 例如电网(Power Grid, PG)、天然气(Natural Gas, NG)、光伏发电(Photovoltaic, PV)、风能(Wind Turbine, WT)、废热和其他类型的能源。IES结合了这些不同的资源和先进的技术以更高的整体系统能效为用户提供冷、热、电和气等负荷[5]。在实际应用中, IES被视为统一能源系统, 并且系统中的进程彼此交互建立系统的独特功能。
在不同的系统结构和优化目标下针对IES需求侧管理的研究已有很多。文献[6-7]最早提出了能源集线器的概念并用于IES优化调度。文献[8]研究了电热联供的能源集线器模型, 并建立了电、热柔性负荷特性, 但其缺乏对于电、热、冷、气柔性负荷的研究。文献[9]以包含电、热、冷系统的综合能源系统为对象进行了研究, 但针对电、热、冷柔性负荷的建模方式单一, 未能考虑到负荷间用能特性的区别。文献[10]采用电热冷联供方式并考虑了可平移负荷在削峰填谷、降低IES运营成本上的作用, 但文中的柔性负荷分类方式较为单一。文献[11]研究了包含电、热柔性负荷的区域综合能源系统优化调度, 根据电、热负荷特性的不同分别建立了柔性负荷模型, 并将其用于储能容量的优化配置, 但其未涉及冷、气等负荷种类, 且未考虑到综合能源系统的环境效益。文献[12]建立了建筑和能量枢纽优化模型, 提出了楼宇冷热电气能量转换和存储设备的优化配置方法, 以实现楼宇能量枢纽综合经济成本最优, 但其对于柔性负荷的研究仅限于热、冷负荷, 忽略了电柔性负荷研究。文献[13]搭建了天然气和电能峰谷分时价格及热能负荷响应数学模型, 以运行成本最低为目标函数, 证明了电热气联合响应优于独立响应, 但对于热负荷温度与供热功率之间的关系并未开展研究。文献[14]以区域综合能源系统为研究对象, 同时考虑经济性和环保性, 但并未研究需求响应对系统运营的影响。
针对以上问题, 本文以IES总运营成本最小为目标, 供给侧和需求侧柔性负荷协调配合, 根据电、热、冷、气负荷需求特性的不同, 分别建立相应的柔性需求响应模型; 通过算例分析了需求侧协同响应在削峰填谷、降低运营成本和减少碳排放中的作用; 通过不同场景对比验证了本研究的合理性和有效性。
1 IES架构与需求响应模型
1.1 IES架构
图 1为IES架构。
IES可用能源集线器来描述, 包括能源输入、转化、存储、输出4个模块。IES能源输入包括光伏、风电机组、大电网、天然气网; 能源转化包括电锅炉(Electric Boiler, EB)、电制冷机(Electric Cold, EC)、电转气设备(Power to Gas, P2G)、燃气轮机(Gas Turbine, GT)、燃气锅炉(Gas Boiler, GB)、溴化锂机组(Lithium Bromide Refrigerator, LBR); 储能包括蓄电池、蓄热槽、蓄冷槽、储气罐; 能源消耗包括电、热、冷、气负荷。
1.2 电力负荷模型
本文中, IES电力负荷分为基础电负荷和柔性电负荷:基础电负荷在用电时间和用电量上不可变动; 柔性电负荷分为可平移、可转移、可削减负荷。
1.2.1 可平移电负荷
可平移电负荷如洗衣机、消毒柜等, 负荷供电时间可以变动, 负荷需要整体平移, 用电时间不能中断且持续时间固定。设单位调度时段为1 h, 对于可平移负荷Lshift, 其参与调度前的功率分布向量Lshift0为
| $ { \mathit{\boldsymbol{L}}^0}_{{\rm{shift}}} = (0, \ldots P_{_{{t_{\rm{s}}}}}^{^{{\rm{shift}}}}, P_{_{{t_{\rm{s}}}} + 1}^{^{{\rm{shift}}}}, \ldots , P_{_{{t_{\rm{d}}}}}^{^{{\rm{shift}}}}, \ldots , 0) $ | (1) |
式中:ts——起始时段;
Ptsshift——起始时段可平移负荷功率;
td——终止时段;
Ptdshift——终止时段可平移负荷功率。
设可平移时段区间为[tsh-, tsh+], 用0-1变量∂表示Lshift某一时段τ的平移状态; ∂=1表示平移, ∂=0表示不平移。平移后的功率分布向量Lshift为
| $ {\mathit{\boldsymbol{L}}_{{\rm{shift}}}} = (0, \ldots P_{_\tau }^{^{{\rm{shift}}}}, P_{_{\tau + 1}}^{^{{\rm{shift}}}}, \ldots , P_{_{\tau + {t_{\rm{d}}} - {t_{\rm{s}}}}}^{^{{\rm{shift}}}}, \ldots , 0) $ | (2) |
式中:Pτshift——平移后初始阶段可平移负荷功率。
可平移负荷用户可以得到的经济补偿为
| $ {\mathit{\boldsymbol{F}}_{{\rm{shift}}}} = F_{{\rm{cost}}}^{{\rm{shift}}}P_{{\rm{sum}}}^{{\rm{shift}}}\sum\limits_{t = {t_{{\rm{sh - }}}}}^{{t_{{\rm{sh + }}}} - {t_{\rm{d}}} + 1} {{\partial _t}} $ | (3) |
式中:Fcostshift——单位功率负荷平移的补偿价格;
Psumshift——平移负荷用电功率总和。
1.2.2 可转移电负荷
可转移电负荷如电动汽车, 负荷供电时间可以变动, 且可以中断, 但需满足调度周期内总用电量不变。设可转移负荷转移Ltran时段区间为[ttr-, ttr+], 用0-1变量β表示Ltran某一时段τ的转移状态, βt=1表示在时段τ功率Ptranτ发生转移。转移功率上下限约束为
| $ {\beta _t}P_{{\rm{min}}}^{{\rm{tran}}} \le P_\tau ^{{\rm{tran}}} \le {\beta _t}P_{{\rm{max}}}^{{\rm{tran}}} $ | (4) |
式中:Pmintran, Pmaxtran——可转移负荷功率的最小值和最大值。
为了防止设备频繁启停, 需要对转移负荷的持续时间进行约束, 即
| $ \sum\limits_{\tau = t}^{t + T_{{\rm{min}}}^{{\rm{tran}}} - 1} {{\beta _t}} \ge T_{{\rm{min}}}^{{\rm{tran}}}({\beta _t} - {\beta _{t - 1}}) $ | (5) |
式中:Tmintran——转移负荷最小持续时间。
转移后需补偿给用户的费用为
| $ {F_{{\rm{tran}}}} = T_{{\mathop{\rm cost}\nolimits} }^{{\rm{tran}}}\sum\limits_{t = {t_{{\rm{tr - }}}}}^{{t_{{\rm{tr}}}} + } {({\beta _t}{P_t}^{{\rm{tran}}})} $ | (6) |
式中:Fcosttran——单位功率负荷转移的补偿价格。
1.2.3 可削减电负荷
可削减电负荷例如空调, 负荷供电量可按一定比例削减。用0-1变量r表示可削减负荷Lcut某一时段τ的削减状态, rτ=1表示Lcut在τ时段被削减, 调度后τ时段的功率为
| $ {P_t}^{{\rm{cut}}} = (1 - {\theta _\tau }{r_\tau }){P_t}^{{\rm{cut0}}} $ | (7) |
式中:θτ——τ时段负荷削减系数;
Ptcut0——参与调度前τ时段的功率。
考虑到用户的满意度, 需要对削减持续时间和削减次数进行约束, 削减最小持续时间约束、削减最大持续时间约束、削减次数约束分别为
| $ \sum\limits_{t = t}^{t + T_{{\rm{min}}}^{{\rm{cut}}} - 1} {{r_t}} \ge T_{\min }^{{\rm{cut}}}({r_t} - {r_{t - 1}}) $ | (8) |
| $ \sum\limits_{t = 1}^{t + T_{{\rm{max}}}^{{\rm{cut}}} + 1} {(1 - {r_t})} \ge 1 $ | (9) |
| $ \sum\limits_{t = 1}^T {{r_t}} \le {r_{\max }} $ | (10) |
式中:Tmincut——最小连续削减时间;
Tmaxcut——最大连续削减时间;
rmax——最大削减次数。
削减后补偿用户的费用为
| $ {F_{{\rm{cut}}}} = F_{{\rm{cost}}}^{{\rm{cut}}}\sum\limits_{t = 1}^T {{\beta _t}(P_t^{{\rm{cut}}} - P_t^{{\rm{cut0}}})} $ | (11) |
式中:Fcostcut——单位功率负荷转移的补偿价格。
1.3 热负荷模型
热水负荷和电负荷不同, 由于热惯性的存在, 其响应速度很慢; 同时热负荷用户的用热需求不同于电负荷, 将热负荷温度控制在一定范围内即可。热水负荷供热来源包括电锅炉、燃气轮机、燃气锅炉3个设备。储水箱中的热水需要随时供应, 因此一定量的热水消耗后需等量冷水注入。根据文献[9]得到热水温度与相关参数计算公式为
| $ {\rm{ }}\theta _{{\rm{t + 1}}}^{{\rm{wat}}} = \frac{{V_t^{{\rm{cold}}}({\theta _{{\rm{cw}}}} - \theta _{\rm{t}}^{{\rm{wat}}})}}{{{V_{\rm{w}}}}} + \frac{{\theta _{\rm{t}}^{{\rm{wat}}}}}{{{c_{\rm{w}}}}} + \frac{{h_t^{{\rm{wat}}}\Delta t}}{{{\rho _{\rm{w}}}{V_{\rm{w}}}{c_{\rm{w}}}}} $ | (12) |
式中:Vcoldt——t时段注入水箱的冷水体积, 其与消耗的热水体积相等;
θwatt——水箱内水温;
θcw——注入冷水的温度;
ρw, Vw, cw——水的密度、储水箱容量和水的比热容;
htwat——t时段供热总功率。
考虑到用户的满意度, 热水负荷需要保持热水的温度约束为
| ${\rm{ }}\theta _{{\rm{min}}}^{{\rm{wat}}} \le \theta _t^{{\rm{wat}}} \le \theta _{\max }^{{\rm{wat}}} $ | (13) |
式中:θminwat, θmaxwat——水箱内水温最低值和最高值。
1.4 冷负荷模型
与热水负荷类似, 室内空气负荷温度控制在一定范围内即可。以普通建筑为例, 室内空气热负荷模型建立过程如下。
考虑建筑物的热阻系数, 室内空气温度和室外空气温度关系式为
| $ \theta _t^{{\rm{out}}} - \theta _t^{{\rm{in}}} = {q_t}R $ | (14) |
式中:θtout, θtin——t时段室外和室内的温度;
qt——t时段室内从室外吸收的热量;
R——建筑材料的热阻。
以夏季供冷为例, 室内温度低于室外温度, IES向室内提供的热量为htg, 因此单位时段室内空气温度变化量和提供热量的关系式为
| $ \Delta \theta _t^{{\rm{in}}} = \frac{{{q_t} - h_t^g}}{{{c_{{\rm{air}}}}}} $ | (15) |
式中:cair——空气的比热容。
将式(15)离散化处理可得到室内空气温度公式为
| $ \theta _{t + 1}^{{\rm{in}}} = \theta _t^{{\rm{in}}}{{\rm{e}}^{ - \frac{1}{{R{C_{{\rm{air}}}}}}}} + \\\;\;\;\;\;\;\;\;(Rh_t^g + \theta _t^{{\rm{out}}})(1 - {{\rm{e}}^{ - \frac{1}{{R{C_{{\rm{air}}}}}}}}) $ | (16) |
考虑到人体的舒适度, 室内温度的约束条件为
| $ T_{\min }^{{\rm{air}}} \le T_t^{{\rm{air}}} \le T_{\max }^{{\rm{air}}} $ | (17) |
式中:Tminair, Tmaxair——用户要求的室内温度最低值和最高值。
1.5 天然气负荷
本文的气负荷为社区天然气负荷, 包括天然气灶和天然气汽车等。天然气汽车为可平移负荷, 部分的天然气灶为可削减负荷。可平移负荷和可削减负荷建模过程类似于电负荷, 在此不再赘述。
2 能源转换设备模型
2.1 电转气设备P2G
| $ {Q^{{\rm{p2g}}}} = \frac{{{\varphi ^{{\rm{p2g}}}}}}{{{P^{{\rm{p2g}}}}{H_{{\rm{gas}}}}}} $ | (18) |
式中:Qp2g——P2G设备产生的天然气量, kg/s;
φp2g——P2G设备转化效率;
Pp2g——P2G设备消耗的电能;
Hgas——标准天然气热值, kJ/m3。
2.2 燃气轮机
燃气轮机通过燃烧天然气提供电能和热能。其发电功率和输出热功率公式分别为
| $ {P_{{\rm{mt}}}}\left( t \right) = {\eta _{{\rm{mt}}}}{G_{{\rm{mt}}}}\left( t \right){L_g} $ | (19) |
| $ {P_{{\rm{mt}}, {\rm{r}}}}\left( t \right) = {C_{{\rm{mt}}}}{P_{{\rm{mt}}}}\left( t \right) $ | (20) |
式中:Pmt(t)——t时段发电功率;
Pmt, r(t)——t时段供热功率;
ηmt——燃气轮机发电效率;
Cmt——燃气轮机热电比;
Gmt(t)——t时段消耗的天然气量;
Lg——天然气热值。
燃气轮机出力约束为
| $ 0 \le {P_{{\rm{mt}}}}\left( t \right) \le P_{{\rm{mt}}}^{\max } $ | (21) |
2.3 燃气锅炉
燃气锅炉通过燃烧天然气提供热功率。其输出热功率和输入天然气量的关系式为
| $ {Q_{{\rm{gb}}}}\left( t \right) = {\eta _{{\rm{gb}}}}{G_{{\rm{gb}}}}\left( t \right){L_{\rm{g}}} $ | (22) |
式中:Qgb(t)——t时段燃气锅炉输出热功率;
ηgb——燃气锅炉热效率;
Ggb(t)——t时段燃气锅炉输入天然气量。
2.4 储能设备
本文的储能设备包括蓄电池、蓄热槽、蓄冷槽和储气罐。储能设备的动态模型可以表示为
| $ {S_i}\left( t \right) = (1 - {\varepsilon _i}){S_i}\left( {t - 1} \right) + \\\;\;\;\;\;\;\;\;\;\;\;\;({\mu _i}{P_{i, c}}\left( t \right) - \frac{{{P_{i, d}}\left( t \right)}}{{{\mu _i}}})\Delta t $ | (23) |
式中:Si(t)——储能设备i在t时段的储能量;
εi——储能设备损耗系数;
μi——储能设备充放能损耗系数;
Pi, c(t), Pi, d(t)——t时段储能设备充/放能量。
3 IES优化模型
3.1 目标函数
本文在所建立的电、热、冷、气柔性负荷模型的基础上, 通过优化各机组出力来实现IES总运行成本最优的目标。IES一个调度周期内总运行成本包括用能成本、柔性负荷补偿成本和碳排放惩罚成本, 即
| $ {\rm{min}}{F_{{\rm{EH}}}} = {F_{{\rm{en}}}} + {F_{{\rm{bu}}}} + {F_{{\rm{fa}}}} $ | (24) |
| $ \begin{array}{l} {F_{{\rm{en}}}} = \sum\limits_{t = 1}^T {\left[ {{K_{{\rm{wt}}}}{P_{{\rm{wt}}}}\left( t \right) + {K_{{\rm{pv}}}}{P_{{\rm{pv}}}}\left( t \right) + } \right.} \\ \left. \;\;\;\;\;\;\;\;\;{{K_{{\rm{gird}}}}{P_{{\rm{gird}}}}\left( t \right) + {K_{{\rm{gas}}}}{P_{{\rm{gas}}}}\left( t \right)} \right] \end{array} $ | (25) |
| $ {F_{{\rm{bu}}}} = {F_{{\rm{shif}}t}} + {F_{{\rm{cut}}}} + {F_{{\rm{tran}}}} $ | (26) |
| $ \begin{array}{l} {F_{{\rm{fa}}}} = \sum\limits_{t = 1}^T {{K_c}} ({\delta _1}{P_{{\rm{grid}}}}\left( t \right) + {\delta _2}{P_{{\rm{mt}}}}\left( t \right) + \\ \;\;\;\;\;\;\;\;{\delta _3}{Q_{gb}}\left( t \right)) \end{array} $ | (27) |
式中:Fen——用能成本, 包括光伏发电成本、风电成本、向电网购电成本和消耗天然气成本;
Fbu——柔性负荷的补偿成本;
Ffa——碳排放惩罚成本;
Kwt, Pwt(t)——风机发电成本系数和发电量;
Kpv, Ppv(t)——光伏发电成本系数和发电量;
Pgrid(t)——向电网购电量;
Pgas(t)——天然气用量;
Qgb(t)——燃气锅炉供热功率;
Kgrid, Kgas——购电电价、天然气价;
Kc——单位CO2排放的惩罚系数;
δ1, δ2, δ3——传统燃煤电厂输出单位电功率、MT输出单位电功率和GB输出单位热功率的CO2的排放系数, 元/kg。
以上机组CO2的排放系数及惩罚成本见文献[16]。
3.2 约束条件
(1) 电功率平衡约束
| $ {P_{{\rm{wt}}}}\left( t \right) + {P_{{\rm{pv}}}}\left( t \right) + {P_{{\rm{gird}}}}\left( t \right) + {P_{{\rm{mt}}}}\left( t \right) = \\\;\;\;\;\;\;\;\;{P_{{\rm{load}}}}\left( t \right) + {P_{{\rm{bat}}}}\left( t \right) + {P_{{\rm{echg}}}}\left( t \right) $ | (28) |
式中:Pload(t)——用电总负荷, 包括基础电负荷和柔性电负荷;
Pbat(t)——蓄电池出力, 蓄电池充电为正, 放电为负;
Pechg(t)>——电能转化为热、冷、气的功率。
(2) 热功率平衡约束
| ${P_{{\rm{mth}}}}\left( t \right) + {Q_{{\rm{gb}}}}\left( t \right) + {Q_{{\rm{eb}}}}\left( t \right) = \\\;{H_{{\rm{wat}}}}\left( t \right) + {H_{{\rm{air}}}}\left( t \right) + {H_{{\rm{bat}}}}\left( t \right) $ | (29) |
式中:Pmth(t), Qeb(t)——燃气轮机和电锅炉的供热功率;
Hwat(t), Hair(t), Hbat(t)——热水负荷、室内空气负荷、蓄热槽充放热功率。
(3) 冷功率平衡约束
| $ {P_{{\rm{lbr}}}}\left( t \right) + {Q_{{\rm{ec}}}}\left( t \right) = {C_{{\rm{air}}}}\left( t \right) + {C_{{\rm{bat}}}}\left( t \right) $ | (30) |
式中:Plbr(t), Qec(t)——溴化锂机组和电制冷机组的供冷功率;
Cair(t), Cbat(t)——空气冷负荷、蓄冷槽充放冷功率。
(4) 气功率平衡约束
| $ {P_{{\rm{netg}}}}\left( t \right) + {P^{{\rm{p2g}}}}\left( t \right) = {G_{{\rm{gas}}}}\left( t \right) + {G_{{\rm{bat}}}}\left( t \right) $ | (31) |
式中:Pnetg(t), Pp2g(t)——向天然气网购气量和P2G设备出气量;
Ggas(t), Gbat(t)——气负荷和储气罐充放气量。
(5) 与电网交换功率约束
| $ {P_{{\rm{gird, min}}}} \le {P_{{\rm{gird}}}}\left( t \right) \le {P_{{\rm{gird, max}}}} $ | (32) |
式中:Pgird, min, Pgird, max——与电网交互功率最小值和最大值。
(6) 向天然气网购气量约束
| $ 0 \le {P_{{\rm{netg}}}}\left( t \right) \le {P_{{\rm{netg, max}}}} $ | (33) |
式中:Pnetg, max——天然气网每个调度时段最大供气量。
(7) 储能设备约束
| $ {S_{{\rm{min}}}} \le {S_i}\left( t \right) \le {S_{{\rm{max}}}} $ | (34) |
| $ {S_{\rm{s}}} = {S_{\rm{d}}} $ | (35) |
| $ {P_{{\rm{chu, min}}}} \le {P_{{\rm{chu}}}}\left( t \right) \le {P_{{\rm{chu, max}}}} $ | (36) |
| $ {P_{{\rm{cha}}}}\left( t \right){P_{{\rm{dis}}}}\left( t \right) = 0 $ | (37) |
式中:Smin, Smax——储能设备储能最小和最大值;
Ss, Sd——储能设备始、末荷能状态;
Pchu, min, Pchu, max——储能设备一次充放能最小值和最大值;
Pcha(t), Pdis(t)——储能设备的储能值和放能值。
考虑到频繁的充放能会减少储能设备的使用寿命, 故应限制其充放能次数, 即
| $ \sum\limits_{t = 1}^T {\left| {X\left( t \right)} \right|} \le {M_1} $ | (38) |
| $ \sum\limits_{t = 1}^T {\left| {Y\left( t \right)} \right|} \le {M_2} $ | (39) |
式中:X(t), Y(t)——储能设备的充能状态和放能状态, 为0-1变量;
M1, M2——储能设备最大充放能次数。
3.3 求解方法
本文的IES模型为0-1型混合整数线性规划问题, 求解模型的标准形式为
| $ \left\{ \begin{array}{l} \min F\left( x \right)\\ {\rm s.t.}{P_i}\left( x \right) = 0\;\;\;\;\;i = 1, 2, 3, \ldots , m\\ \;\;\;\;\;{D_j}\left( x \right) \le 0\;\;\;\;\;j = 1, 2, 3, \ldots , n\\ {x_{\rm min}} \le x \le {x_{\rm max}}\\ {x_k} \in \left\{ {0, 1} \right\} \end{array} \right. $ | (40) |
式中:F(x)——目标函数;
x——待优化变量;
Pi(x)=0——等式约束;
Dj(x)≤0——不等式约束;
m, n——等式和不等式约束个数;
xmin, xmax——变量x上下限;
xk——状态变量。
本文采用商业软件MATLAB中的Yalmip工具箱和Cplex求解器进行模型程序的编写和求解。其整体求解原理框图如图 1所示。
4 算例分析
4.1 基础数据
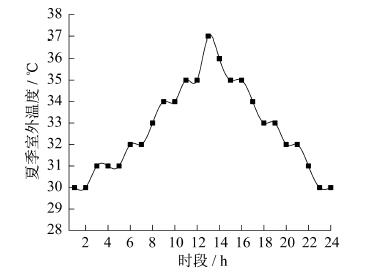
选取某社区的一个夏季典型日进行算例分析。一个调度周期为24 h, 单位调度时间为1 h。该地区根据分时电价将一日分为6个时间段进行分析, 峰时段为10:00~15:00, 18:00~21:00, 电价为0.82元/kWh; 平时段为7:00~10:00, 15:00~18:00, 21:00~24:00, 电价为0.53元/kWh; 谷时段为0:00~7:00, 电价为0.25元/kWh。天然气价格取1.0元/m3, 天然气低燃值取9.7 kWh/m3。Smin取0, Smax取0.95, 充放能效率取0.9, 自放能损耗系数取0.001, 充放能次数各限制为8次。夏季某典型日室外温度曲线如图 3所示, 一日中的热水负荷如图 4所示。
IES能源出力约束参数如表 1所示, 热、冷负荷运行参数和电、气柔性负荷参数如表 2和表 3所示。
表 1
IES能源出力功率约束参数
| 类别 | Pmin | Pmax |
| 大电网 | -650 | 650 |
| 燃气轮机 | 0 | 150 |
| 燃气锅炉 | 0 | 600 |
| 电锅炉 | 0 | 200 |
| 电制冷机 | 0 | 400 |
| 电转气设备 | 0 | 300 |
| 余热回收设备 | 0 | 368 |
| 天然气网 | 0 | 1 000 |
| 溴化锂制冷机 | 0 | 368 |
表 2
IES热、冷负荷运行参数
| 参数 | 数值 |
| R/(℃·kW-1) | 18 |
| θminwat/℃ | 69 |
| θmaxwat/℃ | 71 |
| Tminair/℃ | 24 |
| Tmaxair/℃ | 28 |
| θcw/℃ | 10 |
| Cair/(kWh·℃-1) | 0.525 |
| Cw/[kWh/(kg·℃)-1] | 1.166 7×10-3 |
| Vw/L | 3.0×104 |
| ρw/(kg·m-3) | 103 |
表 3
IES电、气负荷运行参数
| 参数 | ts~td | tsh-~tsh+ | Fcostshift /[元·(kWh-1)] |
||||
| 可平移电负荷 | 18:00~22:00 | 5:00~21:00 | 0.2 | ||||
| 可平移气负荷 | 18:00~22:00 | 0:00~17:00 | 0.1 | ||||
| 参数 | Pmintran~Pmaxtran | ttr-~ttr+ | Fcosttran/ [元·(kWh-1)] |
||||
| 可转移电负荷 | 48~160 | 4:00~22:00 | 0.2 | ||||
| 参数 | Tmincut | rmax | Fcostcut/ [元·(kWh-1)] |
||||
| 可削减电负荷 | 2 | 8 | 0.4 | ||||
| 可削减气负荷 | 2 | 8 | 0.2 | ||||
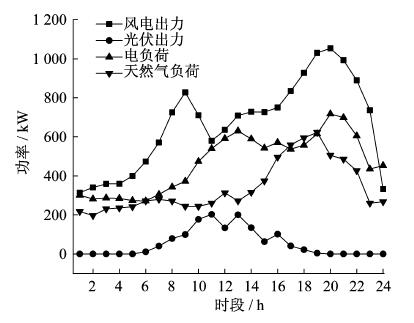
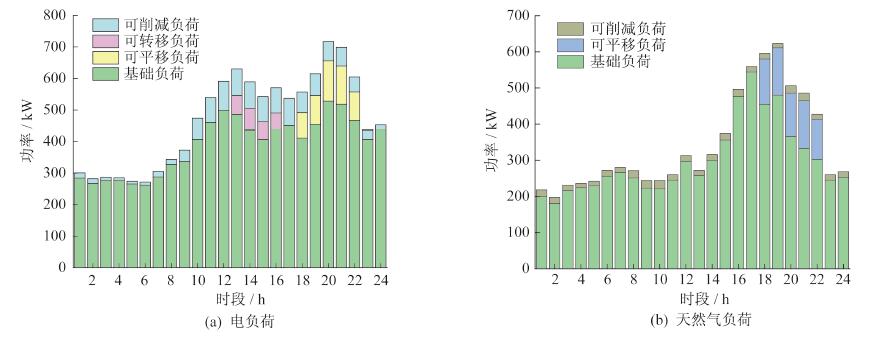
图 5为风机、光伏出力及电、气负荷情况。图 6为优化前电、气负荷分布情况。
为验证本文所建优化模型的合理性和有效性, 建立以下3种场景:
场景1 不计及电、气柔性负荷模型, 热、冷负荷温度取固定值, 热水温度为70 ℃, 室内温度为26 ℃, 进行IES调度;
场景2 计及电、气柔性负荷模型, 热、冷负荷温度取固定值, 热水温度为70 ℃, 室内温度为26 ℃, 进行IES调度;
场景3 计及电、气柔性负荷模型, 并考虑热、冷柔性负荷, 热、冷负荷温度取舒适度范围, 热水温度为69~71 ℃, 室内温度为24~28 ℃, 进行IES调度。
4.2 仿真结果分析
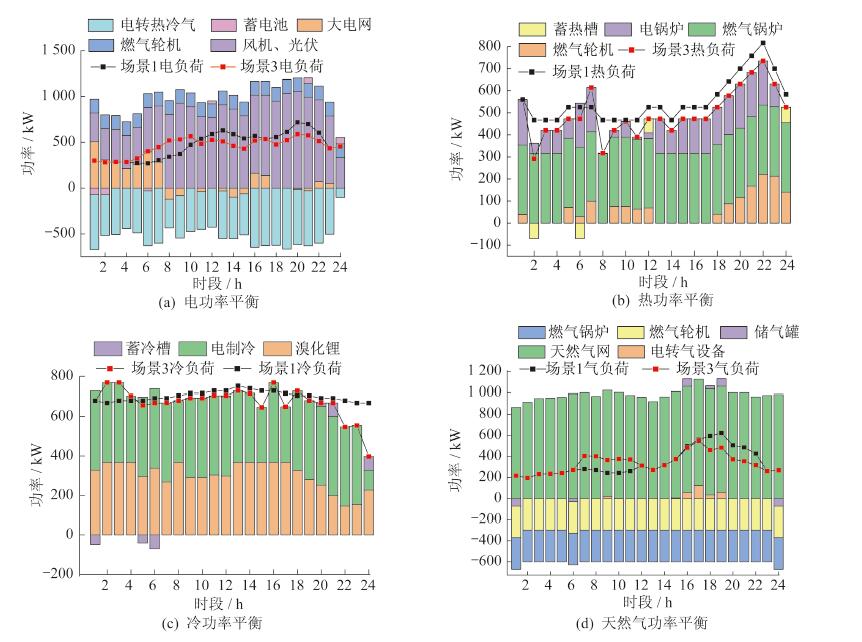
通过MATLAB进行最优求解, 可以得到3种场景下的优化结果。场景3各能源出力情况如图 7所示。
由图 7(a)可以看出, 对于电负荷, 在0:00~7:00时段, 电价处于谷时段, 主要由电网供电。在10:00~15:00和18:00~21:00时段, 分布式能源充沛, 购电成本较高, 可充分利用风光资源; 在00:00~02:00和06:00~07:00电价较低时段, 蓄电池充电, 并在11:00~12:00, 20:00~21:00, 23:00~24:00时段放电。由图 7(b)可以看出, 主要的供热设备为燃气锅炉, 在01:00~02:00和05:00~06:00时段, 热负荷较低, 蓄热槽蓄热; 在11:00~12:00和23:00~24:00时段, 供热压力大, 蓄热槽放热。由图 7(c)可以看出, 场景3的冷负荷明显降低, 主要由溴化锂机组和电制冷机组供冷。在17:00~24:00时段, 溴化锂机组的出力明显减少, 只是由于该时段热负荷达到峰值, 燃气轮机的余热主要用于热负荷, 所以提供给溴化锂机组的功率大大降低, 电制冷机组需要增加功率输出。由图 7(d)可以看出, 天然气能量全部来源于天然气网, 大量消耗于燃气轮机和燃气锅炉, 在14:00~19:00时段, 电转气设备有少量的功率输出, 这是由于该时段电负荷较低, 且光伏出力较大, 因此多余电量通过电转气设备转化为天然气, 同时也缓解了天然气负荷较大的压力。综上所述, 经过优化调度, 各个负荷曲线得到了明显的优化, 峰谷差减小, 削峰填谷效果明显。
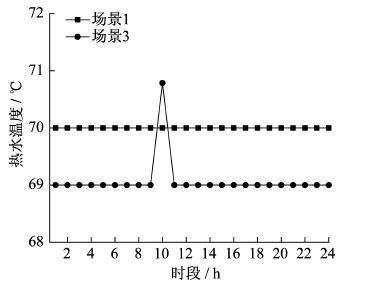
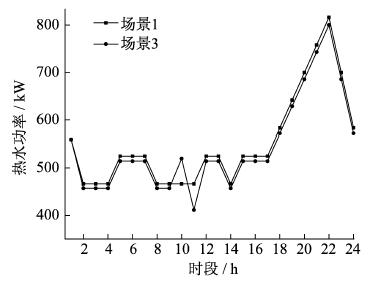
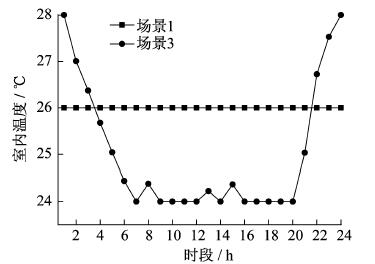
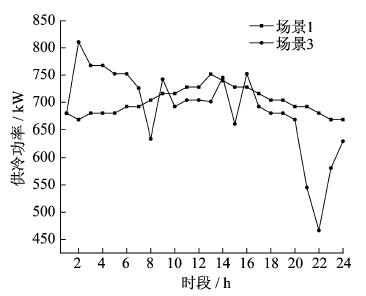
不同场景下热水温度曲线、供热功率曲线、室内温度曲线和供冷功率曲线如图 8~图 11所示。由于场景2的热冷负荷曲线与场景1一致, 故图中不再显示。
由图 8~图 11可知, 在场景1和场景2中, 不考虑热、冷负荷的柔性特征, 热水和室内温度都固定在最舒适温度下。场景3考虑了人体对于温度感知的模糊性, 在满足人体舒适度的前提下, 热水温度和室内温度在一定范围内波动, 为了降低系统总运营成本, 热、冷负荷供能功率也随之改变; 考虑了热、冷柔性负荷后, 供能功率明显降低。热水温度并没有维持在温度范围中的最低温度, 并且在时段10时温度大幅升高, 图 9中对应的供热功率也有所升高, 这是由于热水负荷热惯性较强, 可以在用能成本较低时段增加供热功率, 以此来降低用能成本较高时段的供热功率, 从而达到降低IES总运营成本的目的。室内温度并没有一直保持在最高温度, 而是在温度范围内不断变化, 这是由于室内空气和建筑物有较强的热惯性, 下一时段的室内温度与上一时段的温度有关, 因此IES在用能成本较低时段增大输出功率, 依靠空气和建筑物的热惯性来降低用能成本较高时的输出功率。
表 4给出了3种场景下的运营成本对比。
表 4
不同场景下各种成本对比
| 场景 | 用能成本 | 补偿成本 | 碳排放惩罚成本 | 总运营成本 |
| 1 | 12 565 | 0 | 847 | 13 412 |
| 2 | 11 633 | 172 | 772 | 12 577 |
| 3 | 10 507 | 172 | 702 | 11 381 |
由表 4可知:场景1和场景2对比的结果验证了电、气负荷中可平移、可削减、可转移负荷模型可以降低IES总运营成本, 从13 412元降低到12 577元; 场景2和场景3对比, 体现了热、冷柔性需求响应带来的经济收益, 使得IES总运营成本从12 577元降低到11 381元; 而且在降低总运营成本的同时, 碳排放惩罚成本也在逐步降低, 说明IES的碳排放得到了有效降低。
5 结语
在多能源网络深度融合与能源利用技术大力发展的背景下, 根据电、热、冷、气负荷需求特性的不同, 提出了各能源需求侧响应模型, 并基于能源集线器建立了包含电、热、冷、气子系统的综合能源系统。在达到IES总运营成本最低的同时, 考虑到碳排放惩罚成本, 实现了经济和环境效益的最大化。3种场景算例分析结果表明, 仅考虑电、气需求侧响应, IES总运营成本降低835元; 仅考虑热、冷需求侧响应, IES总运营成本降低1 196元; 考虑电、热、冷、气负荷需求侧协同响应, IES总运营成本降低2 031元, 由此表明本文所提模型具有一定的实际工程意义。但是风光和电、气负荷的不确定性会增加IES优化调度的复杂程度, 后续将围绕风光和电、气负荷的不确定性展开研究。
参考文献
-
[1]张华一, 文福拴, 张璨, 等. 计及舒适度的家庭能源中心运行优化模型[J]. 电力系统自动化, 2016, 40(20): 32-39.
-
[2]吴福保, 刘晓峰, 孙谊媊, 等. 基于冷热电联供的多园区博弈优化策略[J]. 电力系统自动化, 2018, 42(13): 68-75.
-
[3]薛开阳, 楚瀛, 凌梓, 等. 考虑柔性负荷的综合能源系统低碳经济优化调度[J]. 可再生能源, 2019, 37(8): 1206-1213.
-
[4]ZHU S, LIU H, XU J, et al. Study on the day-ahead co-operation strategy of regional integrated energy system including CCHP[J]. The Journal of Engineering, 2019(18): 5219-5223.
-
[5]WANG Y, WANG Y, HUNG Y, et al. Optimal scheduling of the regional integrated energy system considering economy and environment[J]. IEEE Trans Sustain Energy, 2019, 10(4): 1939-1949. DOI:10.1109/TSTE.2018.2876498
-
[6]GEIDL M, KOEPPEL G, FAVRE-PERROD P, et al. Energy hubs for the future[J]. IEEE Power and Energy Magazine, 2007, 5(1): 24-30. DOI:10.1109/MPAE.2007.264850
-
[7]GEIDL M, ANDERSSON G. Optimal power flow of multiple energy carriers[J]. IEEE Transactions on Power Systems, 2007, 22(1): 145-155.
-
[8]刘蓉晖, 李子林, 杨秀, 等. 考虑用户侧柔性负荷的社区综合能源系统日前优化调度[J]. 太阳能学报, 2019, 40(10): 2842-2850.
-
[9]江岳春, 曾诚玉, 郇嘉嘉, 等. 计及人体舒适度和柔性负荷的综合能源协同优化调度[J]. 电力自动化设备, 2019, 39(8): 254-26.
-
[10]胡荣, 张宓璐, 李振坤, 等. 计及可平移负荷的分布式冷热电联供系统优化运行[J]. 电网技术, 2018, 42(3): 715-721.
-
[11]许周, 孙永辉, 谢东亮, 等. 计及电/热柔性负荷的区域综合能源系统储能优化配置[J]. 电力系统自动化, 2020, 44(2): 53-63.
-
[12]范成围, 陈刚, 熊哲浩, 等. 考虑室内体感舒适度的城市楼宇型能量枢纽优化配置与定容应用分析[J]. 全球能源互联网, 2020, 3(3): 291-300.
-
[13]杨海柱, 李梦龙, 江昭阳, 等. 考虑需求侧电热气负荷响应的区域综合能源系统优化运行[J]. 电力系统保护与控制, 2020, 48(10): 30-37.
-
[14]李良余, 马守达, 盛晏. 基于经济性和环保性的区域综合能源系统优化调度研究[J]. 上海电力学院学报, 2019, 35(5): 503-509.
-
[15]马腾飞, 吴俊勇, 郝亮亮. 含冷热电三联供的微能源网能量流计算及综合仿真[J]. 电力系统自动化, 2016, 40(23): 22-27.
-
[16]吴耀文, 马溪原, 孙元章, 等. 微网高渗透率接入后的综合经济效益评估与分析[J]. 电力系统保护与控制, 2012, 40(13): 49-54.