|
|
|
发布时间: 2020-10-25 |
智慧用能 |
|
|
|
收稿日期: 2020-03-24
中图法分类号: TM714
文献标识码: A
文章编号: 2096-8299(2020)05-0436-05
|
摘要
随着智能电网和大数据技术的发展,用电器的识别和检测对规划用电器使用和参与需求响应具有越来越重要的意义。针对用电器识别,提出了一种基于FFT与遗传算法的用电器识别方法。分析了典型用电器负荷的电流波形频谱,并以其谐波作为负荷识别的最优特征参量,通过快速傅里叶变换对波形数据进行处理,以欧式距离最小作为优化指标,采用遗传算法搜寻最优解,最终实现对用电器类别的精确识别。在MATLAB/Simulink中搭建用电器识别模型,并以TI公司的TMS320F28335数字控制器为核心搭建了硬件系统,进行了实验验证。仿真结果与实际测试表明,该算法能够准确识别用电器的类别。
关键词
负荷识别; 特征参量; 快速傅里叶变换; 欧式距离; 遗传算法
Abstract
With the development of smart grid and big data technology, the identification and detection of electrical appliances have become more and more important for planning the use of electrical appliances and participating in demand response.This paper proposes a method for identifying consumers based on FFT and genetic algorithm.The current waveform spectrum of a typical electrical appliance load is analyzed, and its harmonics were used as the optimal characteristic parameters for load identification.The waveform data is processed by fast Fourier transform, taking the minimum Euclidean distance as the optimization indicator, and the genetic algorithm is used to search for the optimal solution, and finally the precise identification of the consumer category is achieved.An electrical appliance identification model is built in MATLAB/Simulink, and a hardware system is built with TI's TMS320F28335 digital controller as the core for actual verification.Simulation and practical tests show that the algorithm can accurately identify the type of consumer electronics.
Key words
load identification; characteristic parameters; fast fourier transform; euclidean distance; genetic algorithm
火灾事故的危害性大, 特别是在人口密集区。对大功率、高发热用电器的使用进行识别和监控, 能避免很多悲剧的发生。文献[1-2]分别提出了通过负载瞬态特征和欧式距离来识别用电器类型的方法, 但该方法只是单纯依靠瞬态特征或欧式距离进行种类繁多的用电器分类, 不同类别用电器数据与样本数据之间的匹配阈值较难确定, 可操作性不强。文献[3]提出了基于遗传算法的神经网络分类识别方法, 结合负载功率、瞬态、稳态电流波形等电路参数进行识别, 对家庭用电智能化具有一定的推动作用, 但是数据采集困难且对硬件设备要求较高。文献[4]以电流波形的15次谐波系数作为系统的输入, 通过样本数据对神经网络模型进行训练获得分类网络, 实现对负载的分类识别, 但是神经网络运算量过大, 对控制器的要求过高。
通过以上分析可知, 从时域的角度进行用电器的识别较为困难。为了降低实际应用中对硬件的要求, 尽可能对多种用电器进行分类识别, 本文从频域出发, 通过快速傅里叶变换(Fast Fourier Transform, FFT)得到信号的频谱[5], 根据用电器的频域特性, 采用遗传算法对当前投入使用的用电器组合进行搜索, 达到用电器识别的目的。
1 用电器特征参量
本文提出的用电器识别算法的核心是, 得到当前电网侧总负荷曲线与各种标准用电器负荷曲线之间的对应关系, 以此得到当前接入的用电器类型, 完成电器类别的判定。因此, 需要选取用电器的特征电能参数, 作为判定依据, 根据文献[6]得到常用的用于用电器识别的特征参量。
1.1 电流特性
周期性变化的电流信号的有效值及其离散化公式为
| $ I\left( t \right) = {I_{\rm m}}{\rm sin}\omega t = 2\sqrt 2 I{\rm sin}\omega t $ | (1) |
| $ {I_{{\rm{rms}}}} = \sqrt {\frac{1}{M}\sum\limits_{n = 0}^{M - 1} {{i^2}\left( n \right)} } $ | (2) |
式中:I(t)——瞬时电流值;
Im——电流峰值;
ω——角频率;
I——有效值;
Irms——电流的均方根;
M——采样点数;
i(n)——电流离散值。
1.2 功率特性
瞬时功率的公式为
| $ P\left( n \right) = u\left( n \right)i\left( n \right) $ | (3) |
式中:P(n)——瞬时功率;
u(n)——电压离散值。
1.3 谐波特性
电流总谐波含有率为
| $ H = \sqrt {\frac{{\sum\limits_{i = 2}^h {{I^2}_i} }}{{\sum\limits_{i = 1}^{h1} {{I^2}_i} }}} $ | (4) |
式中:Ii——电流作傅里叶变换后的第i次谐波幅值;
h——分离谐波的次数。
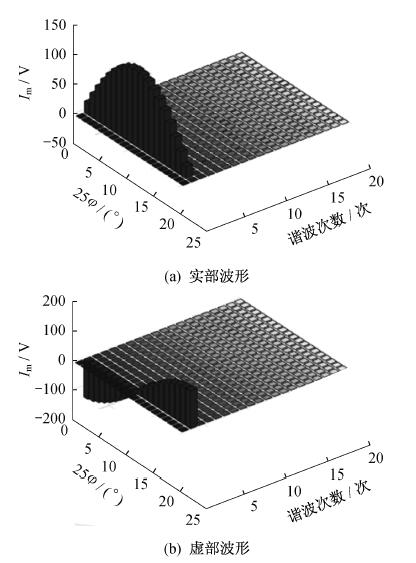
由于用电器的电压、瞬时功率具有局限性, 不符合负荷识别的要求, 而电流谐波特性, 经过FFT变换后各负荷的奇次谐波含有率具有明显特征, 可作为负荷识别的主要指标, 因此选取电流谐波含量作为负荷识别的特征参量。
2 电能参数预处理
3 基于FFT与遗传算法的用电器识别
3.1 FFT的性质
FFT是离散傅里叶变换(Discrete Fourier Transform, DFT)的快速算法, 两者具有相同性质。DFT变换后的数据公式[7]为
| $ \begin{array}{l} X\left( k \right) = \sum\limits_{n = 0}^{N-1} {x\left( n \right){{\rm e}^{-j\frac{{2\pi }}{N}nk}}} \\ k = 0, 1, 2, \ldots , N-1 \end{array} $ | (5) |
式中:x(n)——采样的模拟信号;
N——变换点数。
由式(5)不难推出DFT变换公式为
| $ {\rm{DFT}}[a{x_1}\left( n \right) + b{x_2}\left( n \right)] = a{X_1}\left( k \right) + b{X_2}\left( k \right) $ | (6) |
式中:a, b——常数。
由式(6)可得, 两个时域叠加的信号, 经过DFT变换后的实部与虚部的值与两个信号独立DFT变换后得到的实部与虚部分别相加的值, 对应相等。即
| $ \begin{array}{*{20}{l}} {\left\{ {\begin{array}{*{20}{l}} {{\rm{DFT}}[a{x_1}\left( n \right) + b{x_2}\left( n \right)] = {x_{{\rm{real}}}} + {x_{{\rm{imag}}}}}\\ {{\rm{DFT}}[a{x_1}\left( n \right)] = {x_{{\rm{1real}}}} + {x_{{\rm{1imag}}}}}\\ {{\rm{DFT}}[b{x_1}\left( n \right)] = {x_{{\rm{2real}}}} + {x_{{\rm{2imag}}}}} \end{array}} \right. \Rightarrow }\\ {\left\{ {\begin{array}{*{20}{l}} {{x_{{\rm{real}}}} = {x_{{\rm{1real}}}} + {x_{{\rm{2real}}}}}\\ {{x_{{\rm{imag}}}} = {x_{{\rm{1imag}}}} + {x_{{\rm{2imag}}}}} \end{array}} \right.} \end{array} $ | (7) |
式中:xreal, ximag——叠加信号的实部与虚部;
x1real, x2real, x1imag, x2imag——独立信号的实部与虚部。
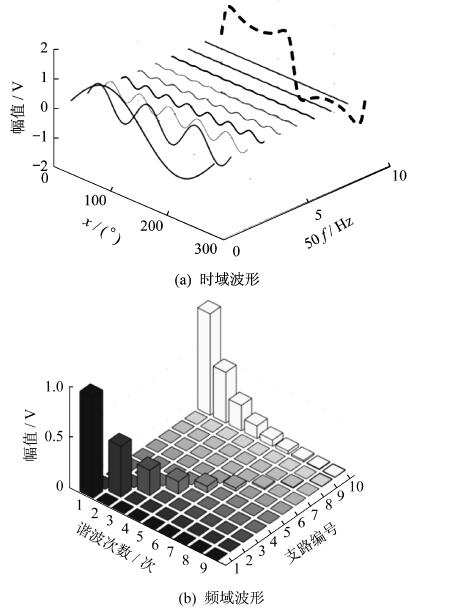
不同频率及叠加信号的时域与频域波形如图 2所示。图 2(a)中实线部分表示9种不同频率信号的时域波形, 虚线部分为所有不同频率信号的时域叠加波形; 图 2(b)为其频域波形, 其中10号支路表示叠加波形的频域柱状图, 1~9号支路表示不同频率信号的频域柱状图。由图 2可知, 1~9号支路频域信号的叠加与10号支路的各次谐波对应相等。
因此, 将时域的电流谐波特征转化为频域的实部、虚部特征, 并将总负荷的谐波频域特征与标准用电器的谐波频域特征对比, 即可达到识别用电器的目的。
3.2 FFT的特点
与DFT相比, FFT的运算量小得多, N点的FFT需要做(N/2)log2N次乘法运算, 而N点的DFT需要做N2次乘法运算, 其运算量是FFT的2N/log2N倍。在实际应用中, 由于DSP芯片厂家会针对FFT运算进行优化, 使程序更简单, 运算效率更高, 运算时间也更短, 所以本文采用FFT得到用电器的频谱特性。
3.3 遗传算法
针对以上对DFT特性的分析, 应用在实际用电器识别系统时, 识别系统需要根据当前总负荷电流的谐波频域特征和不同类型用电器的谐波频域特征组合方式进行对比, 由此得到当前投入的用电器类型。
识别系统可以采用简单的循环方式, 遍历所有可能的标准用电器谐波频域特征, 然后与当前接入的总负荷谐波频域特征进行比较, 得到最为接近的当前用电器接入方式。但是此种方式在电器数量过多时, 消耗的时间较长, 实际中常采用模拟退火、遗传算法、粒子群等智能搜索算法, 通过模拟自然过程, 快速寻找到最优解, 但是同时大多存在局部最优解的问题。遗传算法仅使用由目标函数值变换来的适应度函数值就可确定进一步的搜索范围, 而且该算法的初始种群包含多个个体的信息, 在搜索中可以避免陷入局部最优, 逐步逼近全局最优解, 因此本文采用遗传算法进行最优搜索。
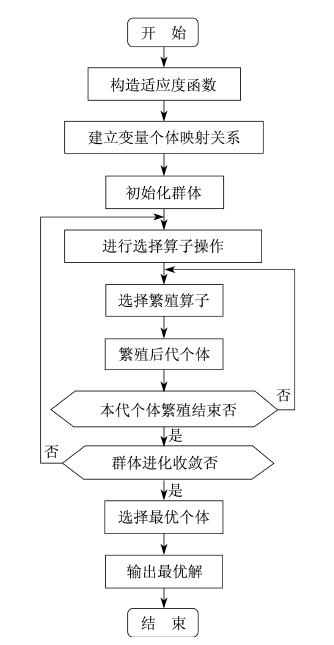
遗传算法是把问题参数编码为染色体, 在利用迭代的方式选择、交叉、变异等运算来交换种群中染色体的信息, 最终生成符合优化目标的染色体[8]。在遗传算法中, 染色体对应的是数据或数组, 通常由一维的串结构数据来表示, 串上各个位置对应基因的取值。基因组成的串就是染色体(个体), 一定数量的个体组成了群体。各个个体对环境的适应程度叫做适应度。遗传算法流程如图 3所示。
由于本文的最终目标是根据当前总负荷电流的谐波频域特征, 得到投入的标准用电器组合方式, 因此可以将各种不同组合方式的谐波频域特征与总负荷的谐波频域特征进行比较, 得到最接近的组合方式, 即为最优值。本文采用欧氏距离最小作为优化目标, 可表示为
| $ {\rm{min}}F = \sqrt {{k_1}^2 + {k_2}^2 + {k_3}^2 + \ldots + {k_i}^2} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{k_i} = {A_{{\rm{real}}\_i}} - {D_{{\rm{real}}\_i}} $ | (8) |
式中:Areal_i——当前电网侧电流经FFT后第i次谐波的实部幅值;
Dreal_i——标准用电器的电流经过不同叠加方式得到的总电流, 再FFT后第i次谐波的实部幅值;
i——谐波次数。
通过遗传算法得到符合式(8)要求时, 此时的标准用电器叠加方式即为最优。
4 仿真分析与实验验证
4.1 仿真分析
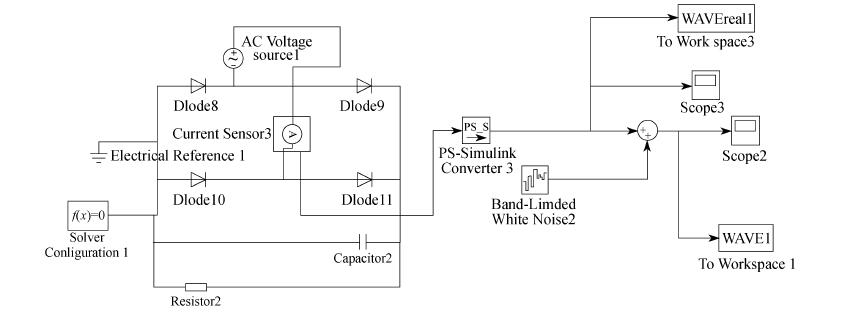
利用MATLAB/Simulink搭建电器识别模型, 模拟10路开关电源负荷电路。模拟标准用电器模型如图 4所示。通过修改电阻和电容的值模拟不同的开关电源负荷。设定模拟电器投入状态的标志为“1”, 切出状态的标志为“0”。因此, 10路模拟标准用电器的1 024种投入切出组合可表示为[(0, 0, 0, 0, 0, 0, 0, 0, 0, 0), (0, 0, 0, 0, 0, 0, 0, 0, 0, 1), (0, 0, 0, 0, 0, 0, 0, 0, 1, 0), ……, (1, 1, 1, 1, 1, 1, 1, 1, 1, 1)]。在Simulink环境下, 改变模拟电器的投入与切出组合, 得到总负荷曲线; 并在MATLAB工作界面获取模拟标准用电器与总负荷曲线数据, 经FFT变换后, 采用遗传算法进行搜索。经过前期的调试结果与标准组合对比, 最终确定遗传算法每一代选取3个个体, 遗传500代, 变异率为0.1。
图 5为遗传算法的迭代图。由图 5可以看到模型最后误差趋向于零, 算法收敛。仿真分析结果如表 1所示。由表 1可得, 遗传算法搜索得到的投入组合与模拟投入组合一致, 算法理论可行且识别精度较高。
表 1
仿真结果
| 序号 | 模拟投入组合 | 算法仿真结果 |
| 1 | (0, 0, 0, 0, 0, 0, 0, 0, 0, 0) | (0, 0, 0, 0, 0, 0, 0, 0, 0, 0) |
| 2 | (0, 0, 0, 0, 0, 0, 0, 0, 0, 1) | (0, 0, 0, 0, 0, 0, 0, 0, 0, 1) |
| 3 | (0, 0, 0, 0, 0, 0, 0, 0, 1, 0) | (0, 0, 0, 0, 0, 0, 0, 0, 1, 0) |
| . . . |
. . . |
. . . |
| 1 023 | (1, 1, 1, 1, 1, 1, 1, 1, 1, 0) | (1, 1, 1, 1, 1, 1, 1, 1, 1, 0) |
| 1 024 | (1, 1, 1, 1, 1, 1, 1, 1, 1, 1) | (1, 1, 1, 1, 1, 1, 1, 1, 1, 1) |
4.2 实验验证
为进一步验证算法的实际可行性, 以TI公司的TMS320F28335数字控制器为核心搭建硬件实验平台。此款DSP时钟周期为150 MHz, ADC位数为12位。实验中设定ADC采样频率为12.8 kHz, FFT点数为256点。实验平台如图 6所示。
电压采样第1级为差分电路, 隔离控制电路
与主电路; 第2级为运放搭建的电压跟随器, 主要作为阻抗匹配; 电流采样使用TBC15DS_3.3霍尔电流传感器, 其输出的电压经过低通滤波抑制高频信号的干扰, 阻抗匹配之后, 可以直接输入到TMS320F28335控制器的AD采样端口上; 初始相角的定位通过电压比较器实现过零比较。
实验过程中, 依次将标准用电器接入插线板, 在DSP中保存其频域特征; 然后以任意的组合方式将标准用电器接入插线板, 识别系统通过遗传算法, 搜索出最优的解, 作为最终识别出的用电器接入组合, 并与实际投入组合进行比较。多次实验后, 查看实验结果。
一共对5种用电器的32种不同投入组合进行了验证。表 2展示了部分实验结果。
表 2
实验结果
| 序号 | 实际投入组合 | 实验结果 |
| 1 | (1, 0, 0, 0, 0) | (1, 0, 0, 0, 0) |
| 2 | (1, 1, 0, 0, 0) | (1, 1, 0, 0, 0) |
| 3 | (1, 1, 1, 0, 0) | (1, 1, 1, 0, 0) |
| . . . |
. . . |
. . . |
| 31 | (1, 1, 1, 1, 0) | (1, 1, 1, 1, 0) |
| 32 | (1, 1, 1, 1, 1) | (1, 1, 1, 1, 0) |
由表 2可知, 只有在用电器全部投入时, 系统出现了识别错误, 这是由于其中一种用电器的功率与其余4种用电器的功率相差较大, 投入与否对总负荷的影响较小, 导致识别结果出现误差。但是系统的识别正确率依然在97%左右, 表明该算法实际可行, 且识别精度较高。
5 结语
由于实际用电器识别过程中存在识别系统硬件要求过高, 且不同各类阈值难以确定等问题, 本文提出基于FFT与遗传算法的用电器识别方法, 在频域中对信号进行处理, 以欧式距离最小作为优化指标, 采用遗传算法进行寻优,完成用电器类别的准确识别。仿真与实验结果表明:本文提出的方法可以达到用电器识别的效果; 随着检测数量的提升, 检测系统能够保持较高的正确率。
参考文献
-
[1]高云, 杨洪耕. 基于暂态特征贴近度匹配的家用负荷识别[J]. 电力系统自动化, 2013, 37(9): 54-59.
-
[2]赵云, 钱斌, 王科, 等. 基于特征相似度的非侵入式用电负荷识别模型研究[J]. 电气应用, 2015, 34(增刊1): 199-203.
-
[3]张荣宝, 张建. 家庭用户端负载的非侵入式电能监测系统研究[J]. 机电元件, 2015, 35(3): 12-15.
-
[4]朱桂川, 周磊. 基于BP神经网络的用电器分类识别技术的研究[J]. 杭州电子科技大学学报(自然科学版), 2016, 36(6): 5-9.
-
[5]金攀, 雷景生. 基于快速傅里叶变换和db小波变换的谐波检测[J]. 上海电力学院学报, 2017, 33(4): 337-340.
-
[6]韩笑.基于信号分解的居民用户非侵入负荷辨识技术[D].北京: 华北电力大学, 2019.
-
[7]胡广书. 数字信号处理理论、算法与实现[M]. 3版. 北京: 清华大学出版社, 2012: 124-127.
-
[8]于艾清, 刘滔. 基于自适应量子遗传算法的电力系统机组组合问题[J]. 上海电力学院学报, 2015, 31(1): 24-28.