电力变压器是组成复杂电网以及较大电力系统不可或缺的重要设备, 其安全运行对电网安全具有重大意义。大型电力变压器的故障主要分为内部故障和外部故障2种。内部故障主要分为绕组故障、铁心故障、分接开关故障及其他故障, 是变压器的主要故障方式。其中绕组故障所占比例很高^[1], 如2004年全国110 kV及以上电压等级的变压器事故中有约70%事故的原因为绕组故障^[2]。

根据电网事故统计分析可知, 出口短路故障是导致大多数变压器故障的原因。在短路电流的冲击下, 绕组会产生松动及变形, 而随着冲击次数的不断累加, 其变形程度也在不断增加。这将导致绕组在振动加剧的同时, 机械性能不断下降。当短路事故再次发生时, 其机械性能下降导致抗短路性能下降, 最终导致故障的发生^[3]。在这种情况下, 压紧线圈是变压器维修的主要方式^[4]。

变压器的安全性能影响其可靠性、电能质量和经济成本。电力变压器发生灾难性故障可能会对环境造成严重影响, 如火灾、变压器漏油等。因此, 对变压器进行在线监测以及故障诊断十分必要。电力变压器绕组状态监测系统的开发能够在整个电力变压器生命周期内降低成本, 提高电力变压器的可用性和可靠性。故障诊断后采取技术措施可延长其使用寿命, 从而保障电网的安全。由于变压器故障的主要原因是因绕组变形、绕组和铁心压紧松动等引起的机械故障, 因此开展变压器绕组故障诊断研究具有十分重要的意义。

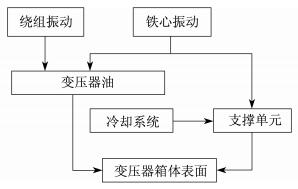
变压器振动方式主要有本体振动、冷却系统振动以及其他方式等, 其中本体振动研究较多, 主要包括绕组振动和铁心振动。图 1为变压器本体振动来源及传播途径示意^[5]。

绕组是变压器发生故障较多的部位, 因此许多学者对变压器振动的产生机理进行了研究。汲胜昌等人^[6]认为, 绕组振动是变压器在短路过程中的主要振动方式。朱叶叶等人^[2]指出, 变压器绕组在经受负载载荷时会产生电磁力, 电磁力是引起绕组振动的主要原因。徐志等人^[7-8]认为, 变压器绕组在电流和磁场的共同作用下产生了令绕组强制振动的驱动力, 并传递至变压器不同部件。几乎所有类型的故障都会引起电力系统电流的突然增大, 从而导致电力系统的故障和已安装设备运行不一致, 严重影响变压器的绝缘性能。

绕组之间产生的不同方向的作用力使得其发生变形。陆杨^[3]认为, 带有相反电流的绕组之间产生排斥力后, 由于实际的绕组结构的高度不对称, 必然会产生轴向分力使绕组之间的高度差继续增大。李树卿等人^[9]认为, 由于变压器有纵向和横向的作用力且高压和低压绕组中的电流方向相反, 使得高压绕组受到横向向外的拉伸力, 低压绕组受到指向绕组内部的横向压缩力, 造成绕组在电磁力作用下发生了不可恢复的变形, 而变形又向着增大且不对称的方向发展, 最终导致绕组变形的不断累积。汲胜昌等人认为, 变压器在短路状态下的振动信号可以用来监测绕组线圈的状态是否发生变形或松动。张友强等人^[10]认为, 绕组振动是一个复杂的机电耦合过程, 变压器绕组所处漏磁场可近似为一个时变函数, 漏磁场在空间的分布随绕组振动及导线位置的变化而发生变化。

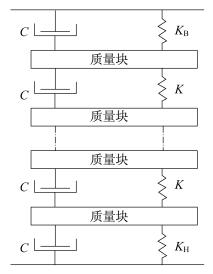
变压器绕组的振动模型主要由等效力学模型和运动方程组成。文献[7]将绕组视为由质量为m的质量块组成的系统, 绕组间的阻尼系数为C, 且之间有绝缘垫块隔开, 用弹性系数为K的弹簧表示, 压紧装置以弹性系数K_B和K_H的弹簧来代替^[7]。图 2表示的是绕组建模的物理模型。此模型将每一部分都用相同的系数代替, 为最简易的模型之一。

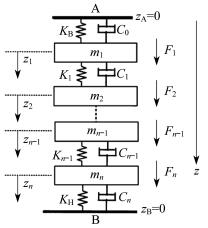
文献[11]建立的绕组等效系统模型如图 3所示。其中A和B处位移为零, 即z_A=z_B=0;各线饼间垫块的弹性系数为K₁, K₂, K₃, …, K_n－1, K_B, K_H为绕组与绝缘垫块的弹性系数, 假设线饼状态相同K_B=K₁=K₂=…=K_n－1=K_H; C₁, C₂, C₃, …, C_n为各线饼的阻尼系数; m₁, m₂, m₃, …, m_n为线饼的等效质量。F₁, F₂, F₃, …, F_n为各线饼所承载的电磁力; 假设线饼只有z₁, z₂, z₃, …, z_n为轴向位移分量。此模型与图 2模型相比, 串联的每一部分都用不同的系数代替, 但A和B处位移为零。

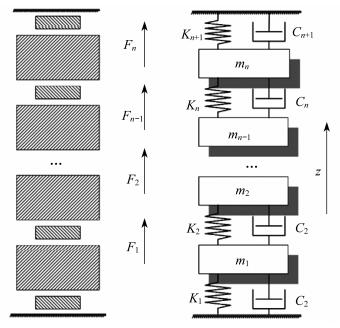
根据绕组的结构特点设置的绕组振动模型如图 4所示。在图 4中, 左侧将绕组等效为集中的质量块, 其中铁心的刚度为无穷大, 右侧为等效力学模型, 其中A和B端固定, 弹性系数用不同的系数表示, 具体为K₁, K₂, K₃, …, K_n。z为轴向位移分量。线饼的振动系统具有n个自由度。线饼之间绝缘垫块的力学性能是非线性的, 其刚度会随着压力的变化而变化。该模型可以通过比较在不同预紧力下特定线饼的振动幅值的实测值和分析值, 较为准确地反映振动特性。

根据牛顿第二运动定律, 将绕组看作一个整体质量块的运动, 并将绕组所受电磁力代入, 得各线圈单元的运动方程^[7]为

$ \begin{array}{l} M^\prime \frac{{{d^2}z}}{{d{t^2}}} + C^\prime \frac{{dz}}{{dt}} + K^\prime z = b(I_{_0}^2 + 12I_{_m}^2) + \\ M^\prime g + 2b{I_0}{I_m}cos\;nwt + \\ \frac{1}{2}bI_{_m}^2cos\;2nw \end{array} $

(1)

式中:M′——绕组质量;

z——线圈单元的相对位移;

C′——振动的阻尼系数;

K′——刚度系数;

b——磁感应强度;

I₀——直流分量;

I_m——最大电流;

g——重力加速度;

w——电网频率。

$C^\prime = \sum C, K^\prime = {K_{\rm B}} + {K_{\rm H}}, M = Nm$, 其中, M, C′为常数, 此时假设绕组忽略压紧力对振动变化产生的影响, 但K′根据压紧力的变化而变化, 故不是常数。

求得绕组因所受电动力作用而引起的振动加速度的幅值为^[3]

$ A = 4{w^2}G = \frac{{4{w^2}b{I^2}_m}}{{\sqrt {{{({K^\prime } - 4M{w^2})}^2} + 4{C^\prime }^2{w^2}} }} $

(2)

式中:A——振动加速度;

G——特解系数。

利用广义坐标形式下的拉格朗日方程可得其微振动方程为^[11]

$ {M}{{z}^{\prime \prime }} + {C}{{z}^\prime } + {K z}{\rm{ = }}{Q}(t) $

(3)

式中:z——各线饼的位移, ${z} = {\left[ {{z_1}\;\;{z_{\rm{2}}}\;\;...\;\;{z_n}} \right]^{\rm{T}}}$;

Q——各线饼所受稳态电磁力, ${Q} = {\left[ {{F_1}\;\;{F_{{2}}}\;\;...\;\;{F_n}} \right]^{\rm{T}}}$;

M——系统的质量矩阵, M=diag[m_i];

C——系统的阻尼矩阵, C=trid[c_i];

K——系统的刚度矩阵, K=trid[k_i]。

其中C和K可通过测量或模态计算获得。

假设垫块弹性系数保持不变, 并遵从胡克定律, 为了方便计算, 省去阻尼项最终得到的振动模型为

$ \begin{array}{l} m{z^{\prime \prime }}_1 + ({k_1} + {k_2}){z_1} - {k_2}{z_2} = {f_1}\\ m{z^{\prime \prime }}_2 - {k_2}{z_1} + ({k_2} + {k_3}){z_2} - {k_3}{z_3} = {f_2}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ m{z^{\prime \prime }}_n - {k_n}{z_{n - 1}} + ({k_n} + {k_{n + 1}}){z_n} = {f_n} \end{array} $

(4)

用矩阵可以表示为

$ {MZ}'' + {KZ} = {F} $

(5)

曹辰等人^[8]提出的绕组振动的动力学方程为

$ {M z}\left( t \right){^\prime} {^\prime} + {C z}\left( t \right)^\prime + {K z}\left( t \right) = {F}\left( t \right) $

(6)

$ \begin{array}{l} {C} = {c_0}\left[ \begin{array}{l} 1 \;\;- 1\\ - 1\;\;1 \end{array} \right]\\ {K} = {k_0}\left[ \begin{array}{l} 1 \;\;- 1\\ - 1\;\;1 \end{array} \right] \end{array} $

式中:z(t)″, z(t)′, z(t)——变压器绕组振动的位移、速度及加速度;

k₀——结构刚度系数;

c₀——结构阻尼系数;

F(t)——绕组受力。

变压器绕组是一个典型的复杂多自由度机械系统, 而绕组轴向振动是电磁力激励下的强迫振动, 满足的动力学方程^[12]为

$ {M}s{\left( s \right)^{\prime \prime }} + {C}s{\left( t \right)^\prime } + {K}s\left( t \right) = {F}\left( t \right) $

(7)

式中:s(t), s(t)′, s(t)″——模型节点处的位移、速度和加速度。

若将绕组视为自由振动, 即F(t)=0, 忽略阻尼影响, 则式(9)可简化为

$ {M}s{\left( t \right)^{\prime \prime }} + {K}s\left( t \right) = 0 $

(8)

现有在线监测电力变压器的方法主要有振动法和噪声法, 相比噪声法, 振动法在线监测电力变压器更为可行。振动法工作原理是通过振动传感器在线监测绕组或铁心状况, 通过吸附在变压器箱体上的加速度传感器, 测得变压器受短路电流冲击时的加速度量幅值来间接反映绕组的状态。加速度量幅值的大小变化, 可以根据振动速度总振级和振动速度烈度指数来反映。该方法不需要电气连接, 更加安全可靠, 具有更高的测量灵敏度, 可以敏锐地反映变压器绕组状态的变化^[13]。

研究表明, 电磁力与绕组所受电流的平方成正比。当电磁力频率达到100 Hz时能判别绕组变形和松动故障^[14]。电磁力与负载电流的平方呈线性关系。电磁力的大小决定着绕组振动加速度的大小。电磁力越大, 绕组的振动加速度也越大。负载电流的平方与绕组振动加速度成正比。

徐志等人^[7]利用自制的变压器振动监测系统, 进行了变压器器身的对称以及不对称负载的振动测试试验, 探究了变压器偏磁振动特征。研究发现, 偏磁电流与绕组的振动幅度有关, 在负载情况一样时, 绕组的振动幅度与偏磁电流的关系成正比; 在有相同的偏磁电流时, 变压器在负载情况下的振动比空载情况下的振动大。POPOV M^[15]发现, 最大谐振过电压与励磁持续时间和谐振频率有关。

洪凯星等人^[1]通过在变压器绕组上施加1~10 MPa的压强发现, 在工频电流下的电磁力的频率为100 Hz, 且呈上下分布。赵宏飞等人^[16]在变压器低压绕组短路的情况下, 通过变压器高压侧的电压调节使得通过低压侧的电流变动, 模拟了变压器在额定运行工况下大电流的情况, 证明了基于振动法的短路试验的研究意义, 为在线监测提供了参考。陆杨^[3]提出的变压器绕组振动烈度检测方法具有较高的灵敏度, 且能判别连续冲击电流下的绕组状态。RAHMATIAN M等人^[17]提出了串联故障和分流故障下的两种绝缘失效定位方案, 在故障监测中获得了较好的结果。文献[18]设计了基于变压器油中溶解气体分析方法和粗糙集方法的故障自动诊断系统, 具有直观、方便、可扩展性好等特点, 测试结果验证了该系统的有效性。

洪凯星等人^[1]发现绕组的固有频率与绕组的压紧力成正比, 所提出的模型能反映变压器绕组的实际振动特性, 为电力变压器振动在线监测与故障诊断提供了一个有效的方法。谢坡岸等人^[4]证明了变压器箱壁上的振动加速度随着内部绕组的压紧状态的变化产生较为明显的波动。陆杨^[3]分析了预紧力与绕组振动加速度之间的关系, 认为要保证绕组的固有振动频率远离电动力的强迫振动频率需要有足够的预紧力, 但由于碰撞等原因, 绕组实际的预紧力会减小。曹辰等人^[8]通过有限元的仿真模拟以及负载试验, 对绕组4种预紧力情况下的振动特性进行了分析, 发现随着绕组预紧力的减小, 绕组振动加速度增大。由此证明了监测振动信号可以判别绕组的松动情况。

徐晨博等人^[14]利用变压器振动在线监测系统和信息模型, 实现了变压器振动在线监测系统的数据传输工作。该模型最终在某电力公司500 kV变电站中投入使用。POPOV M^[15]对变压器绕组的谐振效应进行了深入的研究和分析, 利用一种基于变压器绕组阻抗矩阵的精确方法来确定谐振。该方法通过测试线圈进行了验证。

绕组故障是电力变压器安全运行的一大隐患, 因此对变压器绕组进行故障检测十分必要。振动监测法可以研究变压器在不同绕组状态下的振动特性, 具有一定的适用性。但目前振动监测法还存在一定的不足, 期待后续研究在变压器诊断领域能有进一步的发展。