核电站压水堆堆芯冷却剂平均温度控制系统的性能会直接影响二回路产生的蒸汽质量以及功率调节性能, 因此对压水堆堆芯冷却剂平均温度控制的要求越来越高^[1-2]。

文献[3]设计了一种冷却剂平均温度模糊控制器, 并与传统的棒速程序控制的控制效果进行对比, 结果表明, 模糊控制器在一定程度上减少了冷却剂平均温度跟踪时间, 但隶属函数和模糊推理规则等参数的确定依赖人的主观经验, 控制精度较低, 动态品质较差。文献^[4]提出将对角神经网络(Diagonal Recurrent Neural Networks, DRNN)应用于冷却剂平均温度控制, 并证明了DRNN的鲁棒性。文献^[5]利用冷却剂平均温度的脉冲响应建立非参数模型, 设计了内膜控制器, 系统的响应速度得到了提升, 但出现了较大的超调。

预测控制是近年来被提出的一种适用于过程控制的先进控制算法, 可适用于核电站冷却剂平均温度这类大惯性及较强非线性的过程。预测控制包含多种算法, 例如:动态矩阵控制(Dynamic Matrix Control, DMC)、模型算法控制(Model Algorithm Control, MAC)、广义预测控制(Generalized Predictive Control, GPC)等。基于冷却剂温度控制难题, 文献^[6]利用MAC算法, 将非线性堆芯方程在固定工况点附近线性化, 建立了基于状态空间模型的预测控制器, 具有良好的控制效果, 但这种线性化的状态空间模型不能完整反映非线性系统的特性。文献^[7-8]通过读取仿真平台实时数据的方式, 方便快捷地建立了R棒棒位和冷却剂平均温度的非参数模型, 然后搭建了一种无需辨识被控对象的DMC控制器, 但没有对棒速与冷却剂平均温度的关系进行直接建模。

棒速信号输入下的冷却剂平均温度的变化是一种非自衡过程, 然而DMC算法无法直接控制非自衡过程, 会产生截断误差。为了改进这一点, 许多文献提出了解决方法。文献^[9-10]根据带积分环节的被控对象其阶跃响应值线性递增这一特点, 修改了DMC算法的预测模型部分, 使得控制结果不产生截断误差。但这一控制方法的品质优劣对截断点的选择很敏感。

本文根据压水堆冷却剂平均温度被控系统的非自衡特性及响应需求, 设计了一种带反馈环节的DMC控制器。首先利用MATLAB仿真平台建立了冷却剂平均温度非自衡被控对象的机理模型, 然后通过加入负反馈环节的手段使其变为自衡被控对象, 进行DMC控制器的设计, 求解出实际送入执行机构的棒速控制信号, 最后将改进的DMC控制效果与PI控制的效果进行对比, 以验证其控制的优越性。

联合中子物理模型、堆芯热力学模型和温度反馈模型, 得到堆芯冷却剂平均温度模型。代入相关参数, 利用MATLAB仿真平台求解该方程组, 以实现棒速R_s输入下的堆芯冷却剂平均温度T_m的建模。

温度反馈模型为

$ \begin{array}{l} \rho \left( t \right) = \left\{ {{\rho _{{\rm{rod}}}}\left( 0 \right) + \left[ {\sum\limits_{i = 1}^t {\left( {{R_{\rm{s}}} \times \Delta t} \right)} } \right] \times {\rho _{\rm{I}}}} \right\} + \\ \;\;\;\;\;\;\;\;\;\;\left[ {{\rho _{{\rm{fuel}}}}\left( {t - 1} \right) + {\alpha _{\rm{f}}} \times \Delta {T_{\rm{f}}}} \right] + \\ \;\;\;\;\;\;\;\;\;{\rho _{\rm{m}}}\left( {t - 1} \right) + {\alpha _{\rm{m}}} \times \Delta {T_{\rm{m}}} \end{array} $

(1)

式中:ρ——反应性;

ρ_rod——控制棒反应性;

ρ_I——R棒组的微分价值;

ρ_fuel——燃料温度反馈反应性;

α_f——燃料温度反馈系数;

ΔT_f——燃料平均温度变化量;

ρ_m——冷却剂温度反馈反应性;

α_m——冷却剂温度反应性系数;

ΔT_m——冷却剂温度变化量。

核反应堆的反馈作用极为复杂, 本文主要考虑燃料温度和慢化剂温度变化引起的反应性变化, 即ρ_fuel和ρ_m。根据文献[11], 常规压水堆α_f的经验范围为－4×10^－5~－1×10^－5, α_m的经验范围为－50×10^－5~－8×10^－5, 这里取α_f=－1×10^－5, α_m=－8×10^－5。实际工程应用时, ρ_I随着插入的深度而改变, ρ_I取均一化近似值3.5 pcm^[2]。

中子物理模型为

$ \left\{ \begin{array}{l} \frac{{{\rm{d}}n\left( t \right)}}{{{\rm{d}}t}} = \frac{{\rho \left( t \right) - \beta }}{l}n\left( t \right) + \sum\limits_{i = 1}^6 {{\lambda _i}{C_i}\left( t \right)} \\ \frac{{{\rm{d}}{C_i}\left( t \right)}}{{{\rm{d}}t}} = \frac{{{\beta _i}}}{l}n\left( t \right) - {\lambda _i}{C_i}\left( t \right)\\ i = 1, 2, 3, \cdots , 6 \end{array} \right. $

(2)

式中:n——堆芯热功率;

l——中子代时间;

β_i——第i组缓发中子有效份额;

λ_i——第i组缓发中子衰变常数;

C_i——先驱核衰变功率。

本文考虑6组缓发中子的瞬态响应。假设堆芯在无源条件下, l的近似取值为2×10^－5 s。对于以²³⁵U作燃料的常规压水堆来说, β=$\sum\limits_{i = 1}^6 {{\beta _i}}$=0.0065^[11]。6组缓发中子常数的近似取值^[12]如表 1所示。

堆芯热力学模型为

$ \left\{ \begin{array}{l} {c_1}\frac{{{\rm{d}}{T_{\rm{f}}}\left( t \right)}}{{{\rm{d}}t}} + \frac{{{T_{\rm{f}}}\left( t \right) - {T_{{\rm{cd}}}}\left( t \right)}}{{{R_1}}} = {\rm{ \mathsf{ π} }}r_{\rm{f}}^2{q_{\rm{v}}}\\ {c_2}\frac{{{\rm{d}}{T_{{\rm{cd}}}}\left( t \right)}}{{{\rm{d}}t}} + \frac{{{T_{{\rm{cd}}}}\left( t \right) - {T_{\rm{m}}}\left( t \right)}}{{{R_2}}} = \\ \;\;\;\;\;\;\;\frac{{{T_{\rm{f}}}\left( t \right) - {T_{{\rm{cd}}}}\left( t \right)}}{{{R_1}}}\\ \frac{1}{2}{c_{{\rm{pm}}}}M\frac{{{\rm{d}}{T_{{\rm{out}}}}\left( t \right)}}{{{\rm{d}}t}} = \left( {1 - F} \right)n\left( t \right) + \\ \;\;\;\;\;\;\;h{A_{{\rm{cs}}}}\left[ {{T_{{\rm{cd}}}}(t) - {T_{\rm{m}}}\left( t \right)} \right] - \\ \;\;\;\;\;\;\;{c_{{\rm{pm}}}}\dot m\left[ {{T_{{\rm{out}}}}\left( t \right) - {T_{{\rm{in}}}}} \right] \end{array} \right. $

(3)

式中:c₁——单位长度燃料芯块比热容, c₁=πr_fρ_fc_f;

T_f——燃料平均温度;

T_cd——包壳平均温度;

R₁——芯块与包壳之间的等效热阻, 若考虑气隙导热, 则R₁=1/8πλ_f+1/2πr_fh_g;

r_f——燃料芯块半径;

q_v——燃料的体积释热率, q_v=Fn/V;

c₂——单位长度包壳比热容, c₂=2πr_cdρ_cdC_cdδ_cd;

T_m——冷却剂平均温度;

R₂——包壳与冷却剂之间的等效热阻, R₂=1/2πr_csh;

c_pm——冷却剂比热容;

M——堆芯冷却剂装量;

T_out, T_in——冷却剂出入口温度;

F——燃料元件释热比;

h——对流换热系数;

A_cs——总传热面积;

${\dot m}$——堆芯质量流量。

将反应堆内核燃料产生的热量输出到堆外, 一般要经历3个过程:燃料及原件包壳的热传导; 原件壁面与冷却剂之间的对流传热; 冷却剂将热量传到堆外的输热。式(3)分别对应这3个传热过程。其中, 冷却剂平均温度为冷却剂进口温度和冷却剂出口温度的平均值, 即T_m=(T_in+T_out)/2, 冷却剂入口温度T_in为292 ℃^[13]。

在代入数据求解微分方程组之前, 需要确定T_f, T_cd, T_out, T_m, C_i的初始值。在堆芯处于满功率稳定状态下, T_f, T_cd, T_out, T_m处于平衡状态, C_i也处于平衡状态, 即:

$ \left\{ \begin{array}{l} n\left( t \right) = {n_0}\\ \frac{{{\rm{d}}{T_{\rm{m}}}\left( t \right)}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{T_{{\rm{out}}}}\left( t \right)}}{{{\rm{d}}t}} = 0\\ \frac{{{\rm{d}}{T_{{\rm{cd}}}}\left( t \right)}}{{{\rm{d}}t}} = 0\\ \frac{{{\rm{d}}{T_{\rm{f}}}\left( t \right)}}{{{\rm{d}}t}} = 0\\ {\left. {\frac{{{\rm{d}}{C_i}\left( t \right)}}{{{\rm{d}}t}}} \right|_{t = 0}} = 0\;\;i = 1, 2, 3, \cdots , 6 \end{array} \right. $

(4)

将式(4)代入式(3), 即可得T_f, T_cd, T_out, T_m, C_i的初值。

本文以与秦山二期核电站相关的参考文献[13-17], 整理得到式(1)~式(4)中涉及的堆芯热工水力参数如表 2所示。根据常规压水堆特性, 对流换热系数与流动区间、流型、流量、热流密度等诸多因素有关, 气隙等效导热系数与燃耗有关, 燃料元件释热比也与燃料元件结构有关。为了简化计算, 以上参数本文均取工程经验值。

MATLAB求解微分方程组有多种不同的算法, 如ode45, ode23, ode15s等。其中, ode15s是基于1~5阶数值微分公式的可变步长、可变阶次求解器, 常用于解微分代数方程(Differential Algebraic Equations, DAE)^[18]。由于中子物理模型方程组、堆芯传热方程组是刚性方程组, 故本文选择求解刚性方程组的ode15s算法, 以实现棒速输入条件下的堆芯冷却剂平均温度被控对象的建模。

设仿真总时间为60 s, 初始时间为0 s, 仿真步数为1 s。当引入棒速信号为1步/s的阶跃信号时, 启动MATLAB仿真, 冷却剂平均温度实时值与初始值相比的增量变化曲线如图 1所示。

由图 1可知, 当棒速信号u_c为阶跃信号时, ΔT_m呈线性增长趋势, 故棒速控制下的冷却剂平均温度系统是非自衡系统。若在开环系统加入适当的反馈值K时, 则这种带有反馈环节的被控对象是稳定的。本文取反馈系数K=1, u(k)=1步/s。

DMC算法是一种基于被控对象阶跃响应的预测控制算法, 适用于渐进稳定的系统。只有被控对象的阶跃响应值趋于稳定的情况下, 才能采集稳定区域内的数据点, 构建模型向量^[19]。本文利用上述构建自衡被控对象的方法, 加入反馈通道, 将冷却剂平均温度非自衡模型转化为自衡模型。基于DMC预测算法的冷却剂平均温度控制系统结构图如图 2所示。

首先, 完成自衡化被控对象的建立; 然后, 将预测控制理论应用到自衡化被控系统中, 求得预测控制量u; 最后, 由u计算出实际送入控制棒驱动机构的棒速信号u_c, 完成非自衡系统预测控制器的设计。

DMC算法的计算流程分为离线准备和在线计算。在线计算包括初始化和实时控制两部分。在初始化阶段确定系统采样周期、预测时域、控制时域和校正向量, 用来离线计算控制向量; 然后进入实时控制阶段, 检测当前实际输出值y作为预测初始值${\mathop y\limits^ \wedge _0}$; 由计算误差e进行校正得到校正后的预测输出值${\mathop y\limits^ \wedge _0}$, 从而得到新的预测初始值${\mathop y\limits^ \wedge _0}$, 计算对应的控制量u, 得到u作用下的预测输出并用于下一步的实时控制。整个DMC算法由预测值计算、滚动优化以及反馈矫正3部分循环交替进行。

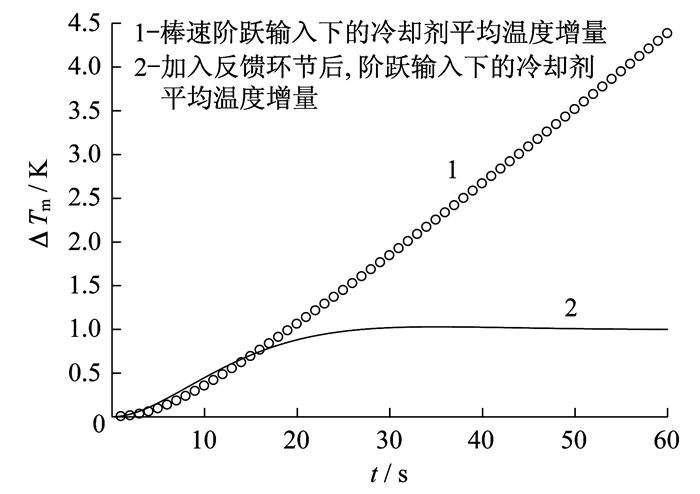
由图 1中曲线2取采样周期为1 s的离散值, 并取预测时域为180 s, 得到自衡化冷却剂平均温度被控系统的阶跃响应。离散化模型记为A₁=[a₁, a₂, a₃, …, a_N]^T, 即为非参数模型的值, 如表 3所示。

选择预测时域P和控制时域U两个参数, 本文取U为1 s。假定k时刻冷却剂平均温度的初始预测值为${\mathop y\limits^ \wedge _0}$(k+i|k), i=1, 2, 3, …, N, 则下一控制时刻冷却剂平均温度的预测值为${\mathop y\limits^ \wedge _1}$(k+i|k)=${\mathop y\limits^ \wedge _0}$(k+i|k)+a_iΔu(k)。

在每一时刻k, 需要确定从该时刻起的U个控制增量即R棒棒速变化量, 使得在其作用下未来P个时刻的冷却剂平均温度预测值${\mathop y\limits^ \wedge _M}$(k+i|k)尽可能地接近平均温度期望值ω(k+i), i=1, 2, 3, …, P。控制过程中, 往往希望控制增量Δu(k)变化过程平稳, 因此可在性能优化指标中加入软约束, 即

$ \begin{array}{l} \min J\left( k \right) = \sum\limits_{i = 1}^P {{q_i}\left[ {\omega \left( {k + i} \right)} \right.} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {\;{{\mathop y\limits^ \wedge }_M}\left( {k + i\left| k \right.} \right)} \right]^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^M {{r_j}\Delta {u^2}\left( {k + j - 1} \right)} \end{array} $

(5)

式中:q_i, r_j——误差加权系数和控制加权系数, 分别表示对跟踪误差和控制作用变化的抑制。

通过约束条件J(k)的极值导数为零这一条件, 可求得最优控制增量Δu(k)。

由于模型失配、环境干扰(如负荷变化或堆芯反应性扰动)等因素可能导致输出产生误差, $e\left( {k + 1} \right) = y\left( {k + 1} \right) - {\mathop y\limits^ \wedge _1}\left( {k + 1\left| k \right.} \right)$, 并且算法对误差的产生缺乏因果性描述, 故误差预测只能采用时间序列法, 引入校正向量并采用加权方式来修正输出预测向量。

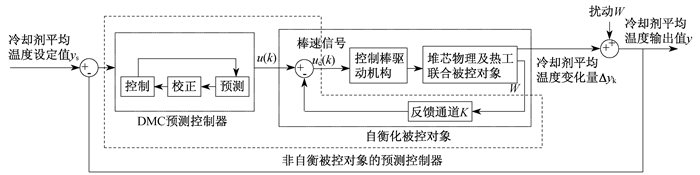
由于冷却剂平均温度为非自衡被控对象, 上述控制量u仅为作用于自衡化模型的控制信号, 因此还需求解出直接作用于控制棒驱动程序的实际棒速控制信号u_c。由被控对象自衡化过程可得如下结构关系

$ \begin{array}{l} {u_c}\left( k \right) = u(k - 1) + \Delta u\left( k \right) - K\Delta y\left( k \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;u(k - 1) + \Delta u\left( k \right) - \Delta y\left( k \right) \end{array} $

(6)

其中, K=1。

由式(6)可以直接解得u_c。

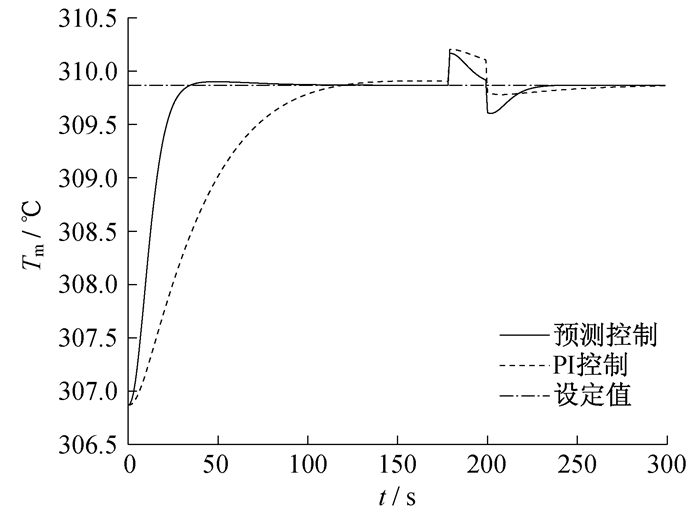
本文基于MATLAB仿真平台, 搭建冷却剂平均温度DMC预测算法控制回路, 并通过与PI控制进行对比, 以验证本文所提出的非自衡系统预测控制方法对被控对象控制性能的改善。设冷却剂平均温度T_m的初始值为306.9 ℃, 在t=0 s时给定冷却剂平均温度设定值为309.9 ℃。由于核反应堆二回路负荷变化会对冷却剂平均温度产生扰动, 故在180~200 s加入+0.3 K的阶跃信号, 用以检测系统的抗扰性能。

设预测算法采样周期T_s为1 s, 建模时域N为180 s, 预测时域P为10 s, 控制时域U为1 s。利用DMC预测控制算法离线计算出控制量u, 再解得R棒棒速控制信号u_c。

PI控制是工业应用中的一种基本控制方法, 控制原理是根据设定值309.9 ℃与实际输出值y构成控制偏差e, 将偏差e的比例和积分通过线性组合构成控制量u_c, 达到消除系统的稳态误差的目的, 从而实现对被控对象的控制。本文通过人工调节PI参数, 得到控制效果最佳的一组控制参数为k_p=0.1, k_i=0.2。

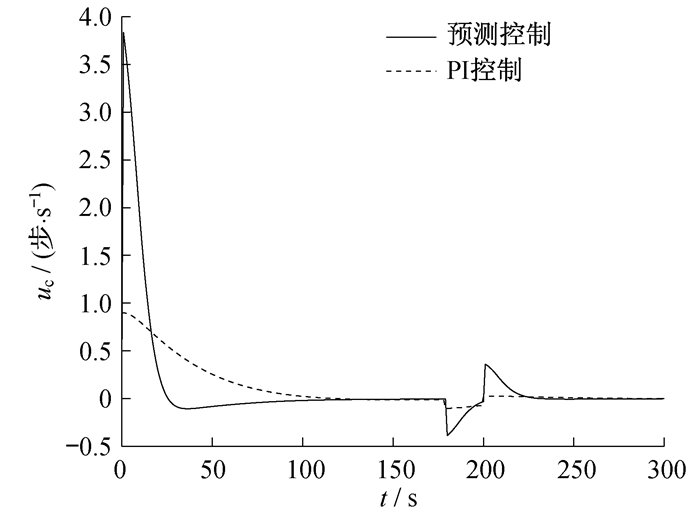
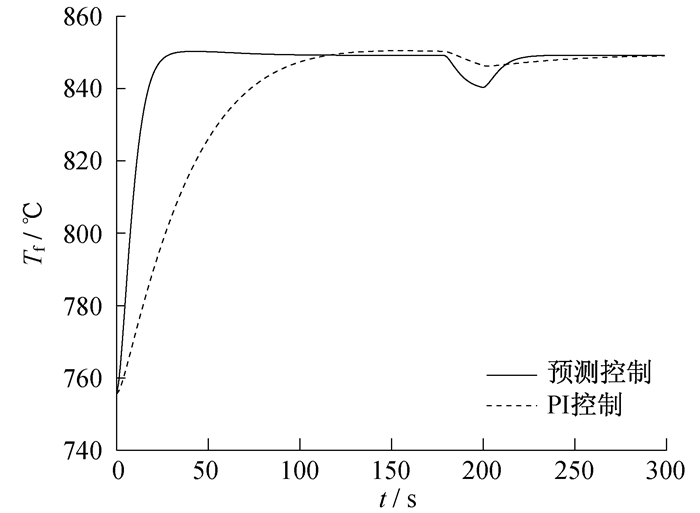
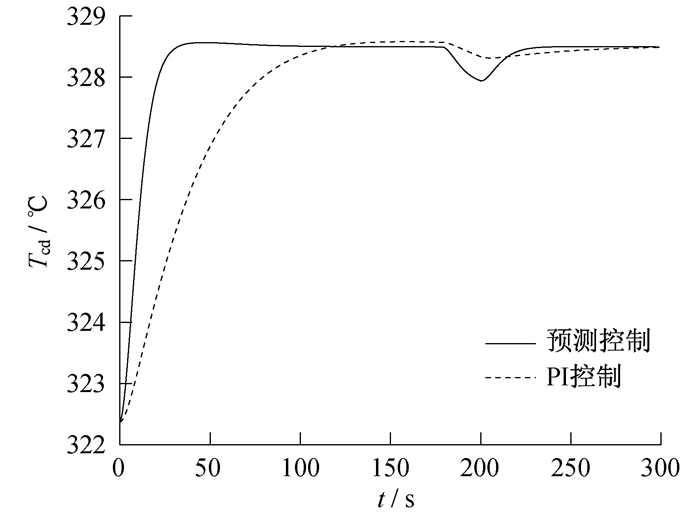
启动MATLAB仿真后, 两种控制算法下, R棒棒速控制信号u_c的变化曲线对比如图 3所示。燃料平均温度T_f的对比如图 4所示, 包壳平均温度T_cd的对比如图 5所示, 冷却剂平均温度T_m的对比如图 6所示。

由上述仿真曲线可知:预测控制下冷却剂平均温度在60 s左右到达稳定, 而PI控制下冷却剂平均温度在100 s左右到达稳定; 在+0.3 K的阶跃输出扰动测试下, 预测控制比PI控制能更快地使系统冷却剂平均温度恢复设定值。仿真结果表明, 将DMC算法应用于棒速控制下的冷却剂平均温度系统, 能够较为快速、稳定地使系统达到设定值, 有效缩短了系统的响应时间, 并使系统具有更好的抗扰能力, 在一定程度上改善了系统的控制性能。

针对压水堆冷却剂平均温度系统具有较强的刚性、开环不稳定性、复杂非线性等特点, 本文提出了一种带反馈环节的DMC预测控制算法, 对冷却剂平均温度进行了控制。首先, 利用MATLAB的ode15s算法, 求解压水堆堆芯热工水力刚性方程组, 建立冷却剂平均温度被控对象模型。然后, 为了弥补DMC算法的控制局限性, 加入反馈环节将非自衡被控对象自衡化, 进行DMC预测控制器设计, 最终求解出作用于R棒的实际棒速控制信号。此外, 本文还将经典PI控制器的控制结果与DMC预测控制器的控制结果进行了对比, 在300 s的仿真时间内, 控制效果对比表明, 加入DMC预测控制器的冷却剂平均温度被控系统的响应速度更快, 对冷却剂平均温度设定值的跟踪能力更强, 具有良好的控制性能。在后续的研究中还可以考虑压水堆核电站二回路对冷却剂平均温度的影响, 以及这种预测控制器对小型核反应堆等其他堆型的控制效果。