|
|
|
发布时间: 2020-06-25 |
|
|
|
|
收稿日期: 2019-04-02
中图法分类号: X701.3
文献标识码: A
|
摘要
火电厂烟气中SO2对环境的污染比较严重,且当前电厂脱硫控制环节的自动化程度和控制精度都比较低,因此为了控制SO2排放,建立良好的控制策略至关重要。在某电厂湿法烟气脱硫系统的辨识结果基础上,分别以浆液pH值和出口SO2浓度为研究对象,建立了对应的前馈-反馈复合控制系统模型,给出了基于多容惯性过程(Multiple Capacity Process,MCP)标准传递函数模型的PID控制器参数整定方法。仿真结果验证了MCP-PID整定方法的适用性和准确性。该方法为电厂脱硫控制环节优化提供了数学模型基础,为多变量连续系统控制策略选择提供了新的思路。
关键词
湿法脱硫; 前馈控制; PID参数整定; 系统辨识
Abstract
Due to the serious environmental pollution caused by SO2 in the flue gas of thermal power plants and the low degree of automation and control precision of the current desulfurization control link of power plants, in order to optimize the desulfurization control link of power plants, the establishment of accurate system model is an important prerequisite for the control of SO2 emissions.In this paper, based on the identification results of a wet flue gas desulfurization system in a power plant, a feedforward and feedback compound control system model corresponding to the slurry pH value and outlet SO2 concentration is established, and a PID controller parameter tuning method based on Multiple Capacity Process(MCP) standard transfer function model is presented.The simulation results verify the applicability and accuracy of the MCP-PID tuning method.This method provides the mathematical model basis for the desulfurization control link optimization of power plant and provides a new idea for the control strategy selection of multivariable continuous system.
Key words
wet desulphurization; feedforward control; PID parameter setting; system identification
近年来, 随着电力行业的快速发展, 我国火电机组装机容量不断增长, 燃煤电厂的SO2排放量已经超过我国排放总量的一半, 并且呈现出逐年递增的趋势。由此可见, 减少火电厂SO2排放是控制SO2排放总量的重点。电厂污染物减排改造是我国环境保护和节能减排中的重要环节, 为此国家先后颁布了《火电厂大气污染物排放标准》和《煤电节能减排升级与改造行动计划(2014—2020年)》等相关政策法规, 要求燃煤电厂的SO2排放浓度控制在35 mg/m3以下, 达到超低排放的标准。目前, 大多数电厂脱硫环节仍然采用手动控制, 自动化程度较低, 控制精度和泛化能力不高, 很难达到脱硫环节的最优化控制。因此, 如何更有效地降低SO2排放浓度, 如何更高效地优化SO2控制环节, 成为当前研究的重点和难点[1-6]。
我国建成投产机组中有90%以上采用的是石灰石-石膏湿法烟气脱硫系统。该方法通过喷洒石灰石浆液, 与烟气中的SO2反应, 最后生成的石膏可供再次使用。在此反应过程中, 对吸收塔浆液pH值的控制对整个脱硫过程影响极大。目前, 燃煤电厂对于浆液pH值的控制主要有两种方法:一是人工操作; 二是PID控制。人工操作需要电厂职工具有丰富的工作经验, 并且对浆液阀门开度的掌控也比较到位, 对人员要求较高, 同时也费时费力; 而PID控制在一定程度上提高了浆液pH值控制的自动化水平, 并且降低了电厂的人工成本。当前大多数电厂均采用PID控制。但是, 对于具有非线性、时变性和大惯性等特点的被控对象, 利用PID控制可能会造成其参数难调、自适应较差, 进而影响控制精度。所以人工控制和常规PID对控制复杂的烟气脱硫过程都是困难的[7-10]。
本文基于火电厂厂级监控信息系统中存储的电厂历史运行数据, 采用实验建模方法, 辨识出较为精确的石灰石-石膏湿法烟气脱硫系统模型; 然后, 设计了前馈-反馈复合结构的脱硫控制系统, 并采用多容惯性过程(Multiple Capacity Process, MCP)标准传递函数控制方法整定了PID控制器的参数; 最后, 分别以浆液pH值和出口SO2浓度为研究对象, 验证了所设计控制系统的性能。
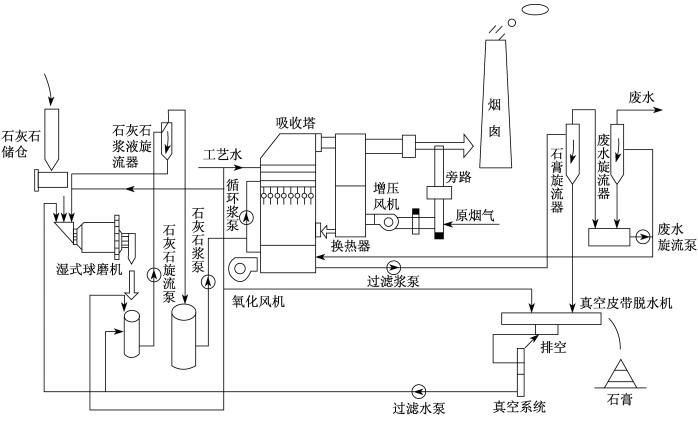
1 电厂湿法脱硫系统工艺流程
石灰石-石膏湿法烟气脱硫系统主要利用SO2和石灰石浆液的酸碱中和反应去除SO2。相比其他脱硫方法, 该方法具有效率高、适应性强、成本低和环保性较强等特点, 市场使用率达到90%以上, 具有很高的研究价值。在电厂大数据和电厂智能化的发展大趋势下, 针对燃煤火电机组的湿法脱硫系统研究, 变得更加迫切和需要。
1.1 工艺原理
在石灰石-石膏烟气湿法脱硫系统中, 首先将石灰石磨成粉状, 调制好石灰石浆液。含有大量污染物的烟气从炉膛进入吸收塔之后, 石灰石浆液中的CaCO3和烟气中的SO2在空气充足的情况下发生反应, 生成可二次利用的石膏, 剩余烟气继续经过后续相应处理排向大气。
为了使反应更加充分, 带有大量污染物的烟气从吸收塔下侧进入, 与吸收塔中的石灰石浆液进行逆流混合, 反应更加彻底[11-13]。
这两个过程的化学反应方程式如下
| $ \begin{array}{*{20}{c}} {2{\rm{CaC}}{{\rm{O}}_3} + {{\rm{H}}_2}{\rm{O}} + 2{\rm{S}}{{\rm{O}}_2} \to }\\ {2{\rm{CaS}}{{\rm{O}}_3} \cdot \frac{1}{2}{{\rm{H}}_2}{\rm{O}} + 2{\rm{C}}{{\rm{O}}_2}} \end{array} $ | (1) |
| $ \begin{array}{*{20}{c}} {2{\rm{CaS}}{{\rm{O}}_3} \cdot \frac{1}{2}{{\rm{H}}_2}{\rm{O}} + {{\rm{O}}_2} + 3{{\rm{H}}_2}{\rm{O}} \to }\\ {2{\rm{CaS}}{{\rm{O}}_4} \cdot 2{{\rm{H}}_2}{\rm{O}}} \end{array} $ | (2) |
该工艺采用吸收法来净化烟气,包含物理和化学两个过程。物理过程主要包括烟气从气相进入液相的吸收过程,符合薄膜理论;化学过程主要包括酸碱中和反应, 液相中的反应加快了物质交换,反应效率变高。
1.2 工艺流程
2 基于改进差分进化算法的系统辨识
2.1 辨识算法
2.1.1 变异策略
标准算法采用的是固定变异因子的变异策略。在算法迭代初期, 种群个体差异大, 若所选的变异因子过大, 则会错过最优解; 在算法迭代后期, 种群个体差异小, 若所选的变异因子过小, 种群多样性就会降低。因此, 本文采用非线性递增的变异因子替换固定的变异因子, 公式如下
| $ F = {F_{\min }} + 0.5(1 - \cos \frac{{{\rm{ \mathsf{ π} }}t}}{G})({F_{\max }} - {F_{\min }}) $ | (3) |
式中: Fmin, Fmax——变异因子的最小值和最大值; G——最大迭代次数。
2.1.2 变异策略
标准算法采用的是固定的交叉概率。经过验证, 较大的交叉概率有利于加快收敛, 较小的交叉概率有利于提高种群多样性。因此, 本文采用非线性渐变的交叉概率替换固定的交叉概率, 公式如下
| $ \begin{array}{*{20}{l}} {{P_{{\rm{CR}}}} = {P_{{\rm{CR}},\min }} + 0.5\left( {1 - \cos \frac{{{\rm{ \mathsf{ π} }}t}}{G}} \right) \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({P_{{\rm{CR}},\max }} - {P_{{\rm{CR}},\min }})} \end{array} $ | (4) |
式中: PCR, min, PCR, max——交叉概率的最小值和最大值。
2.1.3 变异策略
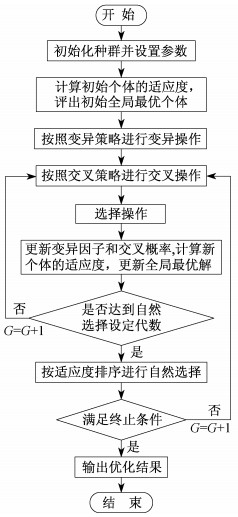
在标准算法迭代后期, 个体间的差异很小, 算法收敛变慢。本文在算法后期引入"自然选择机制", 每次迭代用适应度好的个体替代适应度差的个体, 加快算法收敛, 提高算法对全局最优解的搜索能力。
改进后的差分进化算法流程如图 2所示。
2.2 辨识数据
以浆液pH值为研究对象时, 本文选取某电厂600 MW机组SIS系统历史数据库中300~400 MW之间的两组由稳态到暂态再到稳态过程的历史数据, 包含锅炉负荷、锅炉送风量、原烟气温度、吸收塔给浆流量、吸收塔给浆密度、FGD进口烟气SO2浓度、FGD进口烟气流量、FGD进口烟气氧量和脱硫塔浆液pH值。采样周期都是1 s, 第1组数据长度为10 000 s, 第2组数据长度为12 000 s。其中, 第1组数据作为训练数据, 第2组数据作为验证数据。
以出口SO2浓度为研究对象时, 数据选取规则与上述一致。
2.3 辨识结果
将上述数据经过粗大值处理、滤波和最优变量组选择等预处理, 再利用改进的差分进化算法, 得到相关的辨识结果。
以浆液pH值为研究对象时, 得到的辨识结果为
| $ \begin{array}{*{20}{c}} {{y_1}(s) = \frac{{ - 0.051{\kern 1pt} {\kern 1pt} 2{{\rm{e}}^{ - 85.690{\kern 1pt} {\kern 1pt} 8s}}}}{{(225.260{\kern 1pt} {\kern 1pt} 5s + 1)(41.547{\kern 1pt} {\kern 1pt} 6s + 1)}}{x_1}(s) + }\\ {\frac{{0.003{\kern 1pt} {\kern 1pt} 8{{\rm{e}}^{ - 18.077{\kern 1pt} {\kern 1pt} 0s}}}}{{486.108{\kern 1pt} {\kern 1pt} 7s + 1}}{x_2}(s) + }\\ {\frac{{0.019{\kern 1pt} {\kern 1pt} {\kern 1pt} 4{{\rm{e}}^{ - 7.427{\kern 1pt} {\kern 1pt} 3s}}}}{{(496.257{\kern 1pt} {\kern 1pt} 2s + 1)(444.686{\kern 1pt} {\kern 1pt} 4s + 1)}}{x_3}(s)} \end{array} $ | (5) |
式中: y1(s)——输出变量为pH值;
x1(s)——输入变量为给浆流量;
x2(s)——输入变量为锅炉负荷;
x3(s)——输入变量为给浆密度。
以出口SO2浓度为研究对象时, 得到的辨识结果为
| $ \begin{array}{*{20}{c}} {{y_2}(s) = \frac{{1.417{\kern 1pt} {\kern 1pt} 3{{\rm{e}}^{ - 54.624{\kern 1pt} {\kern 1pt} 5s}}}}{{(145.121{\kern 1pt} {\kern 1pt} {\kern 1pt} 8s + 1)(152.146{\kern 1pt} {\kern 1pt} 4s + 1)}}{x_4}(s) + }\\ {\frac{{0.068{\kern 1pt} {\kern 1pt} {\kern 1pt} 5}}{{(578.415{\kern 1pt} {\kern 1pt} {\kern 1pt} 1s + 1)(681.969{\kern 1pt} {\kern 1pt} 2s + 1)}}{x_5}(s) + }\\ {\frac{{ - 0.049{\kern 1pt} {\kern 1pt} {\kern 1pt} 5{{\rm{e}}^{ - 115.666{\kern 1pt} {\kern 1pt} 8s}}}}{{(132.159{\kern 1pt} {\kern 1pt} 4s + 1)(500s + 1)}}{x_6}(s) + }\\ {\frac{{0.021{\kern 1pt} {\kern 1pt} {\kern 1pt} 7{{\rm{e}}^{ - 171.930{\kern 1pt} {\kern 1pt} 5s}}}}{{(183.915{\kern 1pt} {\kern 1pt} {\kern 1pt} 5s + 1)(500s + 1)}}{x_7}(s)} \end{array} $ | (6) |
式中:y2(s)——输出变量为出口SO2浓度;
x4(s)——输入变量为给浆流量;
x5(s)——输入变量为进口SO2浓度;
x6(s)——输入变量为锅炉负荷;
x7(s)——输入变量为进口烟气流量。
经过模型误差验证, 辨识得到的模型能够较为准确地反映系统的运行特性。
3 前馈-反馈复合控制系统设计
所谓前馈控制, 即测量干扰变化并通过控制克服干扰影响的控制系统。前馈的概念由来已久, 但是直到信息行业和仪表装置的广泛运用, 才为前馈系统的普及奠定了基础。在反馈控制的基础上, 前馈控制可以与之联立组成前馈-反馈复合控制系统, 已成功应用在锅炉、换热器和精馏塔等设备上。
本节在辨识出的石灰石-石膏湿法烟气脱硫系统模型的基础上, 建立针对脱硫塔浆液pH值和出口SO2浓度的前馈-反馈复合控制系统。
3.1 控制系统设计参数
从作用上来说, 反馈控制是"滞后补偿", 可针对系统全部干扰进行补偿; 前馈控制是"超前补偿", 只针对某种特殊干扰进行补偿。在实际应用中, 干扰的情况往往比较复杂, 采用单纯的反馈控制或者前馈控制难以满足系统对精度的要求。因此, 常将反馈控制和前馈控制结合起来使用, 构成前馈-反馈复合控制系统, 满足控制过程的高精度要求。
在前馈-反馈复合控制系统中, 设定值X(s)和干扰F(s)对输出Y(s)的共同影响为
| $ \begin{array}{*{20}{l}} {Y(s) = \frac{{{G_{\rm{c}}}(s){G_{\rm{v}}}(s){G_{\rm{o}}}(s)}}{{1 + {G_{\rm{c}}}(s){G_{\rm{v}}}(s){G_{\rm{o}}}(s)}}X(s) + }\\ {\frac{{{G_{\rm{f}}}(s) + {G_{\rm{o}}}(s){G_{\rm{v}}}(s){G_{\rm{b}}}(s){G_{\rm{m}}}(s)}}{{1 + {G_{\rm{c}}}(s){G_{\rm{v}}}(s){G_{\rm{o}}}(s)}}F(s)} \end{array} $ | (7) |
式中:Gc(s)——反馈控制器, 这里采用PID控制器;
Gv(s)——调节阀传递函数, 一般取1;
Go(s)——控制通道传递函数;
Gb(s)——前馈控制器传递函数;
Gf(s)——干扰环节传递函数;
Gm(s)——扰动检测环节传递函数, 一般取1。
前馈补偿要实现对干扰的完全补偿, 式(7)的第2项应该为零, 则有
| $ {G_{\rm{f}}}(s) + {G_{\rm{o}}}(s){G_{\rm{v}}}(s){G_{\rm{b}}}(s){G_{\rm{m}}}(s) = 0 $ | (8) |
即
| $ {G_{\rm{b}}}(s) = - \frac{{{G_{\rm{f}}}(s)}}{{{G_{\rm{o}}}(s){G_{\rm{v}}}(s){G_{\rm{m}}}(s)}} $ | (9) |
由式(9)可知, 由于反馈回路的存在, 使干扰F(s)对输出的影响要比开环前馈控制的情况下小[1+Gc(s)Gv(s)Go(s)]倍。在系统的通频带内, 控制通道往往有很大的放大倍数, 即
| $ |1 + {G_{\rm{c}}}(s){G_{\rm{v}}}(s){G_{\rm{o}}}(s)| \gg 1 $ | (10) |
由式(10)可知, 经过开环补偿后, 干扰F(s)对被控参数的影响已经很小, 再经过反馈控制进一步减小[1+Gc(s)Gv(s)Go(s)]倍。这就充分反映了前馈-反馈复合控制的优越性。
由式(7)可知, 前馈-反馈复合控制系统的特征方程为
| $ 1 + {G_{\rm{c}}}(s){G_{\rm{v}}}(s){G_{\rm{o}}}(s) = 0 $ | (11) |
在设计前馈-反馈复合控制系统时, 可先按照闭环控制进行设计, 暂不考虑前馈过程, 使系统满足一定的过渡要求。然后加入前馈控制器, 消除干扰影响。最后将闭环和前馈整合起来, 组成前馈-反馈复合控制系统[18]。
3.2 实例分析
3.2.1 以浆液pH值为研究对象
以给浆流量作为输入变量, 以锅炉负荷和给浆密度作为双扰动变量。
控制通道传递函数为
| $ {G_{\rm{o}}}(s) = \frac{{ - 0.051{\kern 1pt} {\kern 1pt} {\kern 1pt} 2{{\rm{e}}^{ - 85.690{\kern 1pt} {\kern 1pt} 8s}}}}{{(225.260{\kern 1pt} {\kern 1pt} {\kern 1pt} 5s + 1)(41.547{\kern 1pt} {\kern 1pt} 6s + 1)}} $ | (12) |
干扰环节传递函数为
| $ \begin{array}{*{20}{c}} {{G_{\rm{f}}}(s) = \frac{{0.003{\kern 1pt} {\kern 1pt} {\kern 1pt} 8{{\rm{e}}^{ - 18.077{\kern 1pt} {\kern 1pt} 0s}}}}{{486.108{\kern 1pt} {\kern 1pt} {\kern 1pt} 7s + 1}} + }\\ {\frac{{0.019{\kern 1pt} {\kern 1pt} 4{{\rm{e}}^{ - 7.427{\kern 1pt} {\kern 1pt} 3}}}}{{(496.257{\kern 1pt} {\kern 1pt} 2s + 1)(444.686{\kern 1pt} {\kern 1pt} 4s + 1)}}} \end{array} $ | (13) |
然后, 根据式(9)求得前馈控制器的传递函数为
| $ \begin{array}{*{20}{l}} {{G_{\rm{b}}}(s) = - \frac{{{G_{\rm{f}}}(s)}}{{{G_{\rm{o}}}(s){G_{\rm{v}}}(s){G_{\rm{m}}}(s)}} = - \frac{{{G_{\rm{f}}}(s)}}{{{G_{\rm{o}}}(s)}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 189.453{\kern 1pt} {\kern 1pt} {\kern 1pt} 1 \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{9359.003{\kern 1pt} {\kern 1pt} {\kern 1pt} 2{s^2} + 266.808{\kern 1pt} {\kern 1pt} {\kern 1pt} 1s + 1}}{{220678.828{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{s^2} + 940.943{\kern 1pt} {\kern 1pt} {\kern 1pt} 6s + 1}}{{\rm{e}}^{ - 78.263{\kern 1pt} {\kern 1pt} 5}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 89.062{\kern 1pt} {\kern 1pt} {\kern 1pt} 5 \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{9359.003{\kern 1pt} {\kern 1pt} {\kern 1pt} 2{s^2} + 266.808{\kern 1pt} {\kern 1pt} {\kern 1pt} 1s + 1}}{{486.100{\kern 1pt} {\kern 1pt} {\kern 1pt} 0s + 1}}{{\rm{e}}^{ - 67.613{\kern 1pt} {\kern 1pt} 8s}}} \end{array} $ | (14) |
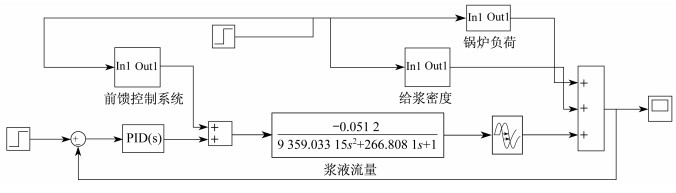
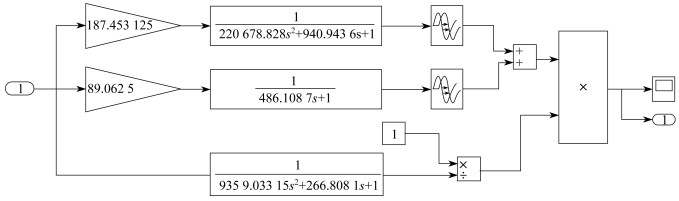
可以得到以浆液pH值为研究对象时, 前馈-反馈复合控制系统框图在MATLAB/Simulink中的结构如图 3所示。
图 3中, PID控制环节的参数待整定。
3.2.2 以出口SO2浓度为研究对象
考虑到前馈控制系统应为因果系统, 因此以给浆流量作为输入变量, 以锅炉负荷和进口烟气流量作为双扰动变量, 结合图 3给出的前馈-反馈复合控制框图, 可以得到控制通道传递函数为
| $ {G_{\rm{o}}}(s) = \frac{{1.417{\kern 1pt} {\kern 1pt} 3{{\rm{e}}^{ - 54.624{\kern 1pt} {\kern 1pt} 5s}}}}{{(145.121{\kern 1pt} {\kern 1pt} {\kern 1pt} 8s + 1)(152.146{\kern 1pt} {\kern 1pt} 4s + 1)}} $ | (15) |
干扰环节传递函数为
| $ \begin{array}{*{20}{l}} {{G_{\rm{f}}}(s) = \frac{{ - 0.049{\kern 1pt} {\kern 1pt} {\kern 1pt} 5{{\rm{e}}^{ - 115.666{\kern 1pt} {\kern 1pt} 8s}}}}{{(132.159{\kern 1pt} {\kern 1pt} {\kern 1pt} 4s + 1)(500s + 1)}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{0.021{\kern 1pt} {\kern 1pt} {\kern 1pt} 7{{\rm{e}}^{ - 171.930{\kern 1pt} {\kern 1pt} 5s}}}}{{(183.915{\kern 1pt} {\kern 1pt} {\kern 1pt} 5s + 1)(500s + 1)}}} \end{array} $ | (16) |
然后, 根据式(9)可以求得前馈控制器的传递函数为
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{G_{\rm{b}}}(s) = - \frac{{{G_{\rm{f}}}(s)}}{{{G_{\rm{o}}}(s){G_{\rm{v}}}(s){G_{\rm{m}}}(s)}} = - \frac{{{G_{\rm{f}}}(s)}}{{{G_{\rm{o}}}(s)}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1.455{\kern 1pt} {\kern 1pt} {\kern 1pt} 2 \cdot } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\frac{{22{\kern 1pt} {\kern 1pt} {\kern 1pt} 079.759{\kern 1pt} {\kern 1pt} 4{s^2} + 297.268{\kern 1pt} {\kern 1pt} 2s + 1}}{{66079.700{\kern 1pt} {\kern 1pt} 0{s^2} + 6321.159{\kern 1pt} {\kern 1pt} 4s + 1}}{{\rm{e}}^{ - 61.036{\kern 1pt} {\kern 1pt} 8s}} + }\\ {0.255{\kern 1pt} {\kern 1pt} {\kern 1pt} 2 \cdot }\\ {\frac{{22079.759{\kern 1pt} {\kern 1pt} 4{s^2} + 297.268{\kern 1pt} {\kern 1pt} 2s + 1}}{{91957.750{\kern 1pt} {\kern 1pt} 0{s^2} + 683.915{\kern 1pt} {\kern 1pt} {\kern 1pt} 5s + 1}}{{\rm{e}}^{ - 117.306{\kern 1pt} {\kern 1pt} 5s}}} \end{array} \end{array} $ | (17) |
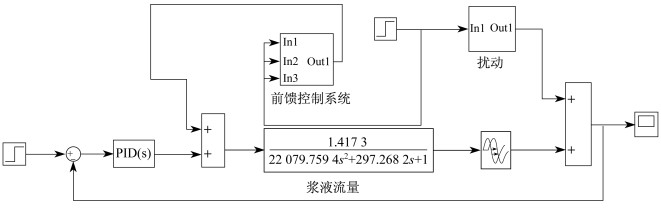
可以得到以出口SO2浓度为研究对象时, 前馈-反馈复合控制系统框图在MATLAB/Simulink中的结构如图 4所示。
图 4中, PID控制环节的参数待整定。
4 基于MCP标准传递函数控制方法的PID参数整定
4.1 MCP标准传递函数模型
MCP是由多个惯性单元串联而成的系统, 其系统极点由各个惯性单元的极点组成。一般而言, 各个惯性单元的极点可以互不相同, 但是, 为了分析和设计的简单性, MCP常假定为多个相同的惯性单元串联而成。
以最简单的情况为例, 型次为1并且增益也为1的MCP的标准传递函数形式为
| $ {G_{{\rm{MCP}}1 - n}}(s) = \frac{1}{{{{(1 + Ts)}^n}}} $ | (18) |
式中: T——惯性单元的时间常数;
n——系统阶数。
由式(18)可知, 最简MCP标准传递函数的参数很少, 只有T和n两个参数。该系统的稳态增益设为1, 若将其传递函数的分母由因式积的形式转换为首1多项式形式, 则有
| $ \begin{array}{*{20}{c}} {{G_{{\rm{MCP}}1 - n}}(s) = \frac{1}{{{{(1 + Ts)}^n}}} = }\\ {\frac{{{\beta _0}}}{{{s^n} + {\beta _{n - 1}}{s^{n - 1}} + \cdots + {\beta _1}s + {\beta _0}}} = }\\ {\frac{{{\beta _0}}}{{{s^n} + \sum\limits_{i = 0}^{n - 1} {{\beta _i}} {s^i}}}} \end{array} $ | (19) |
式中: βi——多项式的系数。
根据二项式定理可得
| $ \begin{array}{*{20}{l}} {\frac{1}{{{{(1 + Ts)}^n}}} = }\\ {\frac{{\frac{1}{{{T^n}}}}}{{{s^n} + \frac{{{\lambda _{n - 1}}}}{T}{s^{n - 1}} + \cdots + \frac{{{\lambda _1}}}{{{T^{n - 1}}}}s + \frac{1}{{{T^n}}}}}} \end{array} $ | (20) |
式中:系数λi(i=1, 2, 3, …, n-1)具体数值由杨辉三角形数阵中不含1的内核部分获得。
比较式(19)和式(20), 可得
| $ \left\{ {\begin{array}{*{20}{l}} {{\beta _0} = \frac{1}{{{T^n}}}}\\ {{\beta _i} = \frac{{{\lambda _i}}}{{{T^{n - i}}}},i = 1,2,3, \cdots ,n - 1} \end{array}} \right. $ | (21) |
根据基本的控制理论, 控制系统的稳态准确性取决于控制系统的型次。若要使某控制系统在阶跃输入下无稳态误差, 则要求该系统的型次至少大于零; 若要使系统在斜坡输入下也无稳态误差, 则要求系统的型次至少要大于1。所以, 表述控制系统的标准传递函数应该有不同的系统型次之分。
| $ \begin{array}{*{20}{c}} {{G_{{\rm{MCPM}} - n}}(s) = \frac{{{\beta _{M - 1}}{s^{M - 1}} + \cdots + {\beta _1}s + {\beta _0}}}{{{s^n} + {\beta _{n - 1}}{s^{n - 1}} + \cdots + {\beta _1}s + {\beta _0}}} = }\\ {\frac{{\sum\limits_{j = 0}^{m = M - 1} {{\beta _j}} {s^j}}}{{{s^n} + \sum\limits_{i = 0}^{n - 1} {{\beta _i}} {s^i}}}} \end{array} $ | (22) |
由式(22)可知,MCP标准传递函数的多项式系数并不随系统型次的改变而改变。因此, 一旦系统阶数n和惯性单元时间常数T确定, MCP标准传递函数的多项式系数也就确定了, 并且与系统型次M值无关。
4.2 PID参数整定公式推导
以双容时滞过程为例,进行MCP-PID参数整定公式的推导。
被控过程模型可近似为
| $ \begin{array}{*{20}{c}} {{G_p}(s) = \frac{K}{{({T_1}s + 1)({T_2}s + 1)}}{{\rm{e}}^{ - \tau s}} \approx }\\ {\frac{K}{{({T_1}s + 1)({T_2}s + 1)(\tau s + 1)}} = }\\ {\frac{{\frac{K}{{{T_1}{T_2}\tau }}}}{{{s^3} + \left( {\frac{1}{\tau } + \frac{1}{{{T_1}}} + \frac{1}{{{T_2}}}} \right){s^2} + \left( {\frac{1}{{{T_1}{T_2}}} + \frac{1}{{{T_2}\tau }} + \frac{1}{{{T_1}\tau }}} \right)s + \frac{1}{{{T_1}{T_2}\tau }}}}} \end{array} $ | (23) |
4.2.1 P控制器整定
P控制器模型如下
| $ {G_{\rm{c}}}(s) = {K_{\rm{p}}} $ | (24) |
则该控制系统的开环传递函数为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {G_{\rm{c}}}(s){G_{\rm{p}}}(s) = \\ \frac{{\frac{{K{K_{\rm{p}}}}}{{{T_1}{T_2}\tau }}}}{{{s^3} + \left( {\frac{1}{\tau } + \frac{1}{{{T_1}}} + \frac{1}{{{T_2}}}} \right){s^2} + \left( {\frac{1}{{{T_1}{T_2}}} + \frac{1}{{{T_1}\tau }} + \frac{1}{{{T_2}\tau }}} \right)s + \frac{1}{{{T_1}{T_2}\tau }}}} \end{array} $ | (25) |
该系统的特征多项式为
| $ \begin{array}{*{20}{c}} {{P^*}(s) = {s^3} + \left( {\frac{1}{\tau } + \frac{1}{{{T_1}}} + \frac{1}{{{T_2}}}} \right){s^2} + }\\ {\left( {\frac{1}{{{T_1}{T_2}}} + \frac{1}{{{T_1}\tau }} + \frac{1}{{{T_2}\tau }}} \right)s + \frac{1}{{{T_1}{T_2}\tau }} + \frac{{K{K_{\rm{p}}}}}{{{T_1}{T_2}\tau }}} \end{array} $ | (26) |
该系统的特征多项式系数与MCP标准传递函数的特征多项式系数相对等的联立方程式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\beta _2} = \frac{3}{\varphi } = \frac{1}{\tau } + \frac{1}{{{T_1}}} + \frac{1}{{{T_2}}}}\\ {{\beta _1} = \frac{3}{{{\varphi ^2}}} = \frac{1}{{{T_1}\tau }} + \frac{1}{{{T_2}\tau }} + \frac{1}{{{T_1}{T_2}}}}\\ {{\beta _0} = \frac{1}{{{\varphi ^3}}} = \frac{1}{{{T_1}{T_2}\tau }} + \frac{{K{K_{\rm{p}}}}}{{{T_1}{T_2}\tau }}} \end{array}} \right. $ | (27) |
最终得到MCP-PID参数整定公式和适用条件为
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{\rm{p}}} = \frac{1}{K}\left( {\frac{{{T_1}{T_2}\tau }}{{{\varphi ^3}}} - 1} \right)}\\ {\varphi = \frac{1}{\tau } + \frac{1}{{{T_1}}} + \frac{1}{{{T_2}}}}\\ {0 < \varphi < \sqrt[3]{{{T_1}{T_2}\tau }}} \end{array}} \right. $ | (28) |
4.2.2 PI控制器整定
PI控制器模型如下
| $ {G_{\rm{c}}}(s) = {K_{\rm{p}}}\left( {1 + \frac{1}{{{T_{\rm{i}}}s}}} \right) = \frac{{{K_{\rm{p}}}}}{s}\left( {s + \frac{1}{{{T_{\rm{i}}}s}}} \right) $ | (29) |
按照如上方法, 得到MCP-PID参数整定公式和适用条件为
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{\rm{p}}} = \frac{1}{K}\left( {\frac{{4{T_1}{T_2}\tau }}{{{\varphi ^4}}} - 1} \right)}\\ {{T_{\rm{i}}} = \frac{{{\varphi ^4}}}{{{T_1}{T_2}\tau }}\left( {\frac{{4{T_1}{T_2}\tau }}{{{\varphi ^3}}} - 1} \right)}\\ {\varphi = \frac{4}{{\frac{1}{\tau } + \frac{1}{{{T_1}}} + \frac{1}{{{T_2}}}}}}\\ {0 < \varphi < \sqrt[3]{{4{T_1}{T_2}\tau }}} \end{array}} \right. $ | (30) |
4.2.3 PID控制器整定
PID控制器模型如下
| $ {G_{\rm{c}}}(s) = \frac{{{K_{\rm{p}}}{T_{\rm{d}}}}}{s}\left( {{s^2} + \frac{1}{{{T_{\rm{d}}}}}s + \frac{1}{{{T_{\rm{d}}}{T_{\rm{i}}}}}} \right) $ | (31) |
按照如上方法, 得到MCP-PID参数整定公式和适用条件为
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{K_{\rm{p}}} = \frac{1}{K}\left( {\frac{{4{T_1}{T_2}\tau }}{{{\varphi ^3}}} - 1} \right)}\\ {{T_{\rm{i}}} = \frac{{K{K_{\rm{p}}}{\varphi ^4}}}{{{T_1}{T_2}\tau }} = \frac{{{\varphi ^4}}}{{{T_1}{T_2}\tau }}\left( {\frac{{4{T_1}{T_2}\tau }}{{{\varphi ^3}}} - 1} \right)} \end{array}\\ \begin{array}{*{20}{l}} {{T_{\rm{d}}} = \frac{1}{{K{K_{\rm{p}}}}}\left( {\frac{{6{T_1}{T_2}\tau }}{{{\varphi ^2}}} - {T_1} - {T_2} - \tau } \right) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\frac{{6{T_1}{T_2}\tau }}{{{\varphi ^2}}} - {T_1} - {T_2} - \tau }}{{\frac{{4{T_1}{T_2}\tau }}{{{\varphi ^3}}} - 1}}}\\ {\varphi = \frac{5}{{\frac{1}{\tau } + \frac{1}{{{T_1}}} + \frac{1}{{{T_2}}}}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 < \varphi < \min \left( {\sqrt {\frac{{6{T_1}{T_2}\tau }}{{{T_1} + {T_2} + \tau }}} ,\sqrt[3]{{4{T_1}{T_2}\tau }}} \right)} \end{array} \end{array} \right. $ | (32) |
单容惯性过程、双容惯性过程、单容时滞过程等其他惯性过程和时滞过程都可以通过类似的推理过程得到其相应的MCP-PID参数整定公式。
4.3 实例分析
4.3.1 以浆液pH值为研究对象
以给浆流量作为输入变量, 以锅炉负荷和给浆密度作为双扰动变量, 进行前馈-反馈复合控制模型的建立与PID参数整定。
当没有干扰接入时, 控制系统框图如图 5所示。
加入前馈控制时, 前馈系统部分的框图如图 6所示。
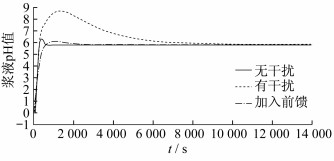
按照惯性时滞过程MCP-PID的参数整定方法, 并经过参数微调, 以上文中系统辨识的训练数据为系统输入, 分别得到无干扰、有干扰、有干扰且加入前馈控制时的仿真结果对比如图 7所示。
由图 7可知:3种情况下, pH值基本稳定在5.8, 比较符合实际运行要求; 加入干扰后, 系统稳定时间非常长, 且超调量较大, 需要通过前馈控制进行修正; 加入前馈后, 相比有干扰且没有加入前馈的情况, 加入前馈后超调量明显降低了很多, 且稳定时间远远小于没有前馈的情况, 对加入扰动后的系统具有明显的修正作用, 具有很高的精确性。由图 7分析可知, MCP-PID整定方法非常适用于该系统模型。
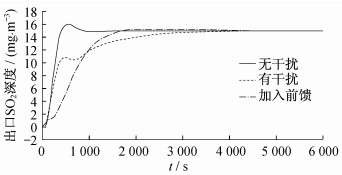
4.3.2 以出口SO2浓度为研究对象
5 结语
(1) 在石灰石-石膏湿法烟气脱硫系统的建模仿真中引入差分进化算法, 经过实际分析对算法进行优化。通过某电厂的运行数据辨识, 本文提出的算法得到了更加精确的辨识结果, 具有很好的适用性和可拓展性。
(2) 给出了前馈-反馈复合控制系统的设计方法和步骤, 并且着重描述了控制系统的设计参数, 分别以浆液pH值和出口SO2浓度为研究对象, 在以改进的差分进化算法的辨识结果基础上, 得到了其相对应的前馈-反馈复合控制系统的MATLAB/Simulink模型。
(3) 介绍了基于MCP标准传递函数模型的PID控制器参数整定方法, 分别以浆液pH值和出口SO2浓度为研究对象, 验证了MCP-PID整定方法的适用性和准确性。另外, 通过对比仿真结果发现, 前馈-反馈复合控制系统的精确度最高、稳定时间最短、超调量最低, 非常适用于石灰石-石膏湿法烟气脱硫系统辨识出的传递函数模型, 为多变量连续系统的模型辨识提供了新思路, 为电厂脱硫控制环节的优化提供了参考, 为大型燃煤机组的实际运行提供了理论支撑。
参考文献
-
[1]王浩.火电厂石灰石-石膏湿法脱硫系统建模与优化[D].北京: 华北电力大学, 2013.
-
[2]乔宗良.石灰石/石膏湿法烟气脱硫系统优化技术研究[D].南京: 东南大学, 2015.
-
[3]苏晖.火力发电厂石灰石-石膏湿法脱硫技术运行优化研究[D].北京: 华北电力大学, 2012.
-
[4]环境保护部, 国家发展改革委员会, 国家能源局. 全面实施燃煤电厂超低排放和节能改造工作方案[J]. 节能与环保, 2016(1): 32.
-
[5]史文峥, 杨萌萌, 张绪辉, 等. 燃煤电厂超低排放技术路线与协同脱除[J]. 中国电机工程学报, 2016, 36(16): 4308-4318.
-
[6]郑婷婷, 周月桂, 金圻烨. 燃煤电厂多种烟气污染物协同脱除超低排放分析[J]. 热力发电, 2017, 46(4): 10-15.
-
[7]于沙家.基于模糊神经网络的热电厂脱硫系统建模与控制研究[D].青岛: 青岛科技大学, 2016.
-
[8]侯鹏飞.石灰石湿法脱硫性能指标在线监测与控制策略的优化设计[D].太原: 山西大学, 2011.
-
[9]孙成富, 胡炜, 胡翔, 等. 基于先进控制的燃煤机组超低排放指标优化控制技术[J]. 浙江电力, 2017, 36(7): 37-42.
-
[10]郑晅. 火电厂烟气脱硫控制策略研究[J]. 电子设计工程, 2009, 17(10): 93-97.
-
[11]RIGATOS G G. Adaptive fuzzy control for field-oriented induction motor drives[J]. Neural Computing and Application, 2012, 21(1): 9-23.
-
[12]李波.DCS在火力发电厂烟气脱硫控制系统的应用及实施[D].北京: 华北电力大学, 2014.
-
[13]MATTEI M. Multivariable PID control for linear parameter varying systems[J]. Automatica, 2001, 37(12): 1997-2003.
-
[14]杨平, 翁思义, 郭平. 自动控制原理:理论篇[M]. 北京: 中国电力出版社, 2009.
-
[15]YANG M, LI C, CAI Z, et al. Differential evolution with auto-enhanced population diversity[J]. IEEE Transactions on Cybernetics, 2015, 45(2): 302-315.
-
[16]陈皓.族群进化算法及其在全局函数优化和电力经济负荷分配中的应用研究[D].西安: 西安理工大学, 2009.
-
[17]张经纬, 归一数, 康英伟, 等. 基于改进粒子群算法的锅炉再热蒸汽温度模型辨识[J]. 热力发电, 2017, 46(7): 72-78.
-
[18]王再英, 刘淮霞, 陈毅静. 过程控制系统与仪表[M]. 北京: 机械工业出版社, 2016: 221-225.
-
[19]杨平, 陈式跃. 无超调不限阶数的M型次多容惯性标准传递函数[J]. 中国测试, 2013, 39(2): 14-18.
-
[20]杨平. 多容惯性标准传递函数控制器——设计理论及应用技术[M]. 北京: 中国电力出版社, 2013: 30-49.
-
[21]杨平, 黄伟, 孙宇贞, 等. PID参数整定的MCP标准传递函数法公式[J]. 上海电力学院学报, 2014, 30(1): 40-46.
-
[22]杨平, 邓亮, 徐春梅, 等. PID控制器参数整定[M]. 北京: 中国电力出版社, 2016: 34-55.
-
[23]雷晓春, 杨平. 双容时滞过程的MCP-PID控制[J]. 工业仪表与自动化装置, 2014(5): 22-36.
-
[24]GOODWIN G C, GRAEBE S F, SAIGADO M E. Control system design[M]. 北京: 清华大学出版社, 2002.
-
[25]苏隽成, 杨平. 过热汽温串级MCP-PID控制[J]. 自动化仪表, 2014, 35(11): 5-8.
-
[26]王燕, 杨平. 主汽温控制系统的MCP-PID控制[J]. 石油化工自动化, 2014, 50(5): 34-37.
-
[27]李昀, 杨平, 贺帅鹏. 恒压供水系统的MCP-PID控制[J]. 自动化仪表, 2013, 34(5): 19-23.
-
[28]BEQUETTE B W. Process Control[M]. Beijing: World Publishing Corp, 2008.