发布时间: 2021-06-25
摘要点击次数:
全文下载次数:
DOI: 10.3969/j.issn.2096-8299.2021.03.005
2021 | Volume 37 | Number 3

智能电网

基于经验模态分解的时间序列预测方法

刘丹丹

上海电力大学电子与信息工程学院, 上海 200090

收稿日期: 2020-03-24

中图法分类号: TM715;TP301.6

文献标识码: A

文章编号: 2096-8299(2021)03-0231-04

摘要

时间序列预测方法广泛应用于各个领域。对非平稳非线性时间序列预测方法进行了研究，利用经验模态分解法将此类序列分解为平稳时间序列，然后选择合适的步长，应用机器学习算法对各个平稳子序列进行预测，各个子序列的预测值之和即为原序列的预测值。将该方法应用于楼宇等电能能耗数据，实验结果表明，基于经验模态分解方法的时间序列预测方法精度较高，适用于预测非线性非平稳时间序列。

关键词

时间序列; 经验模态分解; 建筑能耗; 能耗预测

The Method for Time Series Prediction Based on Empirical Mode Decomposition

LIU Dandan

School of Electronics and Information Engineering, Shanghai University of Electric Power, Shanghai 200090, China

Abstract

Time series prediction methods were widely used in various fields.The prediction method for non-stationary and nonlinear time series was studied in this paper.This method decomposed such series into stationary time series using empirical mode decomposition method.And then an appropriate time-step was chosen and machine learning algorithm was applied to predict each stationary sub-sequence.The sum of predicted values was the forecasting results for the original sequence.The method was applied to electrical energy consumption dataset.The experimental results showed that the combined algorithm of machine learning and empirical mode decomposition method had higher accuracy and was suitable for predicting non-linear and non-stationary time series.

Key words

time series; empirical mode decomposition; building energy consumption; energy prediction

时间序列就是将不同时间上的某个指标的不同数值按照时间顺序排列而成的数列, 是一种现实生活中常见的数据形式。研究时间序列的发展趋势能够帮助人们合理规划生活需求, 如研究某栋大楼的能耗发展趋势, 可以为楼宇节能管理提供理论依据; 研究金融数据时间序列的发展趋势, 有助于人们把握宏观市场的运营规律。各行各业的运行数据几乎都可以被视为时间序列, 因此建立准确有效的时间序列预测模型一直是相关领域的研究热点。

经典的时间序列预测模型以随机过程理论和数理统计学为理论基础, 主要包括自回归滑动平均模型(Auto-Regressive Moving Average model, ARMA)和自回归积分滑动平均模型(Auto Regressive Integrated Moving Average model, ARIMA)。这两种经典的时间序列预测方法在很多领域取得了较好的预测效果^[1-5]。然而, 有一些文献指出, 经典方法用于线性、平稳的时间序列时, 预测精度较高, 但不适用于非线性非平稳时间序列。因此, 近年来, 一些研究将机器学习算法应用于非线性非平稳时间序列预测领域, 取得了更好的效果^[6-8]。这些方法多利用神经网络算法、支持向量机(Support Vector Machine, SVM)算法等, 建立有效的时间序列预测模型, 其中又以SVM算法效果最为良好, 在各个领域都得到了广泛的验证^[9]。

在实际应用中, 针对一些非线性非平稳时间序列来建立预测模型时, 以SVM为代表的机器学习算法仍然难以满足人们对预测精度的要求^[10]。因此, 研究人员提出使用经验模态分解法(Empirical Mode Decomposition, EMD)对序列进行预处理, 而后再使用机器学习算法, 可以获得更高的预测精度^[11-14]。基于此, 本文建立了基于EMD-SVM联合算法的时间序列预测模型, 同时针对能耗时间序列的特点, 构建了模型输入输出数据集, 从而获得了较好的预测效果。

1 算法研究

1.1 经验模态分解算法

EMD方法由HUANG N E等人^[15]于1998年提出。该方法在对信号进行分解时无需设定基函数, 完全根据数据自身的时间尺度特征处理信号。因此, EMD方法在理论上适用于任何类型的信号分解, 尤其是处理非平稳非线性时间序列数据。该方法一经面世, 即在不同工程领域得到了有效的应用。EMD方法分解序列的基本步骤如下。

假设信号x(t), 确定该信号的所有极值。在最小值(最大值)之间进行差值计算, 得到包络s_min(t)(s_max(t)), 且计算包络的均值为

$ m_{1}(t)=\frac{s_{\max }(t)+s_{\min }(t)}{2} $

(1)

计算本征模函数(Intrinsic Mode Function, IMF)c₁(t)为

$ c_{1}(t)=x(t)-m_{1}(t) $

(2)

根据IMF的计算结果迭代残差r₁(t)为

$ r_{1}(t)=x(t)-c_{1}(t) $

(3)

重复以上步骤, 直到分解结果满足停止条件。此时, 原始序列被分解为多个IMF和一个对应残差。该原始序列可表示为

$ x(t)=\sum\limits_{i=1}^{N} c_{i}(t)+r_{N}(t) $

(4)

这里, 残差r_N(t)可以表示为

$ \left\{\begin{array}{c} r_{1}(t)-c_{2}(t)=r_{2}(t) \\ r_{2}(t)-c_{3}(t)=r_{3}(t) \\ \vdots \\ r_{N-1}(t)-c_{N}(t)=r_{N}(t) \end{array}\right. $

(5)

由分解过程可知, 与短时傅立叶变换、小波分解等方法相比, EMD分解过程较为简单、直观。同时, 由于这种方法是基于信号序列时间尺度的局部特性进行分解, 因此具有自适应性。

1.2 支持向量机算法

SVM算法由VAPNIK V^[16]提出, 是一种机器学习方法, 已广泛应用于各个领域。当SVM应用于数据建模和预测时, 被称为支持向量回归(Support Vector Regression, SVR)。核函数和优化器算法是SVM的两个重要部分。使用非线性函数可以将非线性数据从原始的特征空间映射至更高维的希尔伯特空间(Hilbert space), 并使其线性可分; 而优化器算法用于解决优化问题。SVM算法基于结构风险最小化(Structural Risk Minimization, SRM)原理, 因此它力求将由训练误差和置信度之和组成的泛化误差的上限最小化, 优于仅将训练误差最小化的训练模型。

1.3 EMDSVR时间序列预测算法

EMD-SVR联合算法的基本原理主要包括3个部分: 利用EMD算法, 将非线性非平稳原始数据序列分解为各个子序列; 针对各个子序列, 重构数据集, 建立SVR时间序列预测模型, 计算预测结果; 计算子序列预测和, 即为原始序列预测结果。

2 实验方法及结果分析

2.1 数据集重构方法

假设一个时间序列为y={y₁, y₂, y₃, …, y_n}, 定义y_i={(x_i, z_i)} 为重构数据集, 其中x_i为SVM预测模型的输入, z_i为SVM预测模型的输出。

x_i的具体表达形式为

$ \overline{\boldsymbol{x}}_{i}=\left[\begin{array}{cccc} y_{1} & y_{2} & \cdots & y_{d} \\ y_{2} & y_{3} & \cdots & y_{d+1} \\ \vdots & \vdots & \vdots & \vdots \\ y_{n-d} & y_{n-d+1} & \cdots & y_{n-1} \end{array}\right] $

(6)

式中: d——步长。

z_i的具体表达形式为

$ \bar{\boldsymbol z}_{i}=\left[\begin{array}{c} y_{d+1} \\ y_{d+2} \\ \vdots \\ y_{n} \end{array}\right] $

(7)

2.2 预测精度验证标准

一般使用均方误差(Mean Square Error, MSE)及决定系数R²评价预测模型的优劣。这两个参数的总体目标为测量预测值与实际值之间的距离, 比如R²越接近于1, 同时MSE越小, 则证明模型的预测结果越精确。其公式分别为

$ \mathrm{MSE}=\frac{1}{l} \sum\limits_{i=1}^{l}\left(f\left(x_{i}\right)-y_{i}\right)^{2} $

(8)

$ \begin{array}{*{20}{l}} {\;\;\;\;\;\;{R^2} = }\\ {\frac{{{{\left( {l\sum\limits_{i = 1}^l f \left( {{x_i}} \right){y_i} - \sum\limits_{i = 1}^l f \left( {{x_i}} \right)\sum\limits_{i = 1}^l {{y_i}} } \right)}^2}}}{{\left[ {l\sum\limits_{i = 1}^l f {{\left( {{x_i}} \right)}^2} - \left[ {\sum\limits_{i = 1}^l {{{\left. {f\left( {{x_i}} \right)} \right)}^2}} } \right]\left[ {l\sum\limits_{i = 1}^l {y_i^2} - {{\left( {\sum\limits_{i = 1}^l {{y_i}} } \right)}^2}} \right]} \right.}}} \end{array} $

(9)

式中: l——时间序列中的数据个数;

f(·)——时间序列的预测值。

2.3 算法流程

整个算法的完整流程描述如下。

(1) 使用EMD算法将原始时间序列分解为一些子序列。

(2) 对于每个子序列, 假设预测步长为d, 根据序列特性确定d。如建筑能耗数据多以24 h为一个周期, 则对于此类序列d可取2~24之间的数值;

(3) 重构子序列的SVR预测模型的输入及输出分别为x_i和z_i。设置数据集中3/4的数据为训练集, 1/4的数据为测试集。

(4) 应用SVR算法建立子序列预测模型, 并计算MSE及R²。

(5) 重复步骤(2)到步骤(4), 根据MSE及R²的计算结果选取最佳步长d, 记录该子序列的最佳预测结果。

(6) 对每个子序列重复步骤(2)到步骤(5)。

(7) 将各个子序列的预测结果之和作为最终预测结果。

若序列步长可以确定, 则可以省去搜索最佳步长的步骤, 大大减小算法的复杂程度。一般来说, 可选择使MSE较小, 而R²更接近1的步长值。同时, 选择步长d时, 应综合考量测试集和训练集的预测精度, 在针对训练集预测精度差异不大的情况下, 应优先选择针对测试集预测精度更高的步长值。

2.4 实验结果

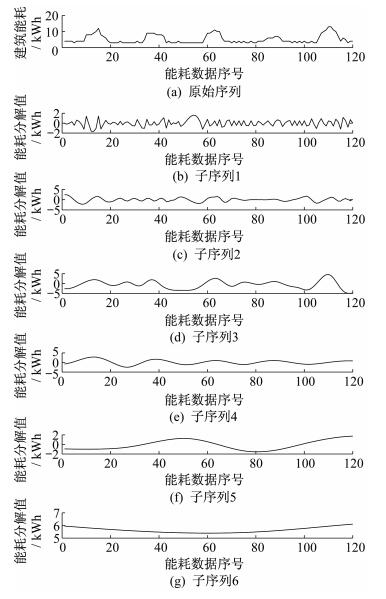
将算法应用于某幢楼的能耗数据。随机选择某周工作日的能耗数据共120个。使用单位根检验法检验后, 确认其为非平稳时间序列。经过EMD分解后的原始序列与平稳子序列如图 1所示。

图 1 EMD算法分解后的子序列示意

对每个子序列建立基于SVR算法的预测模型。选取步长d为(2, 9)之间的整数, 根据MSE及R²的计算结果选取最优步长。同时, 对原始序列针对不同步长直接使用SVR算法建立预测模型, 并对比EMD-SVR算法和SVR算法的预测精度。不同步长时两种算法的MSE和R²值对比结果如表 1所示。由表 1可以看出, 选择任意步长值时EMD-SVR算法针对非平稳时间序列的预测结果都明显优于SVR算法。此外, 综合EMD-SVR算法对测试集和训练集的预测结果可选取步长8作为最优步长, 选择该步长的情况下训练集的R²值为0.967 739, 测试集的R²值为0.926 781。

表 1 不同步长下两种算法的预测性能

下载CSV

步长	算法	训练集		测试集
步长	算法	MSE	R²	MSE	R²
2	EMD-SVR	0.530 675	0.913 070	0.878 166	0.925 873
2	SVR	1.598 363	0.750 836	2.138 498	0.803 233
3	EMD-SVR	0.512 562	0.919 767	0.946 673	0.933 244
3	SVR	0.836 06	0.881 915	1.864 691	0.864 803
4	EMD-SVR	0.478 254	0.926 598	0.919 914	0.939 352
4	SVR	0.838 541	0.876 550	2.067 069	0.851 158
5	EMD-SVR	0.439 302	0.933 324	1.218 089	0.919 094
5	SVR	1.404 345	0.777 708	1.728 945	0.853 921
6	EMD-SVR	0.438 203	0.937 444	1.355 833	0.914 509
6	SVR	1.341 689	0.791 525	1.827 736	0.851 094
7	EMD-SVR	0.292 286	0.966 373	1.039 772	0.928 052
7	SVR	1.346 008	0.793 713	1.732 235	0.851 317
8	EMD-SVR	0.286 934	0.967 739	1.085 487	0.926 781
8	SVR	0.678 652	0.900 490	1.942 448	0.877 158
9	EMD-SVR	0.290 050	0.970 343	1.078 373	0.924 212
9	SVR	0.626 512	0.918 451	2.170 768	0.850 444

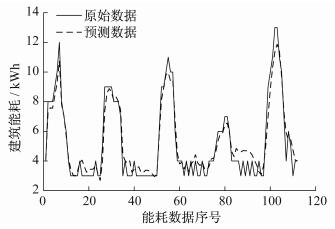
步长为8时, EMD-SVR算法的能耗序列预测结果如图 2所示。其中, 序列数据总数为120, 算法将预测序列中第9到第120共112个数据。由图 2可以看出, 预测数据与原始数据非常接近, 可以满足用户对于预测精度的要求。

图 2 EMDSVR联合算法在数据集上的预测结果

3 结语

本文以非线性非平稳能耗数据时间序列为研究对象, 重点研究了EMD-SVR联合算法在建立能耗数据预测模型上的应用。首先, 将能耗数据视为时间序列数, 使用EMD算法将非平稳时间序列分解为不同频率分量的平稳时间子序列; 然后, 根据能耗数据的特点选择合适的步长, 构建适合算法的数据集; 最后, 应用SVR算法建立子序列预测模型, 子序列模型预测结果之和即为EMD-SVR算法对该时间序列的预测结果。从实验结果可以看出, 预测非平稳时间序列时EMD-SVR算法较SVR算法的精度更高。

参考文献

[1]

周明, 严正, 倪以信, 等. 含误差预测校正的ARIMA电价预测新方法[J]. 中国电机工程学报, 2004, 24(12): 63-68. DOI:10.3321/j.issn:0258-8013.2004.12.013

[2]

丁藤, 冯冬涵, 林晓凡, 等. 基于修正后ARIMA-GARCH模型的超短期风速预测[J]. 电网技术, 2017, 41(6): 1808-1814.

[3]

李鹏辉, 崔承刚, 杨宁, 等. 基于ARIMALSTM组合模型的楼宇短期负荷预测方法研究[J]. 上海电力学院学报, 2019, 35(6): 573-579.

[4]

WANG Q, LI S Y, LI R R, et al. Forecasting U.S.shale gas monthly production using a hybrid ARIMA and metabolic nonlinear grey model[J]. Energy, 2018, 160: 378-387. DOI:10.1016/j.energy.2018.07.047

[5]

ROUNAGHI M M, ZADEH F N. Investigation of market efficiency and financial stability between S & P 500 and London stock exchange: monthly and yearly forecasting of time series stock returns using ARMA model[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 456: 10-21. DOI:10.1016/j.physa.2016.03.006

[6]

MOHAPATRA U M, MAJHI B, SATAPATHY S C. Financial time series prediction using distributed machine learning techniques[J]. Neural Computing and Applications, 2019, 31(8): 3369-3384. DOI:10.1007/s00521-017-3283-2

[7]

CHEN S S, MIHARA K, WEN J X. Time series prediction of CO₂, TVOC and HCHO based on machine learning at different sampling points[J]. Building and Environment, 2018, 146: 238-246. DOI:10.1016/j.buildenv.2018.09.054

[8]

LI Z, YE L, ZHAO Y N. Short-term wind power prediction based on extreme learning machine with error correction[J]. Protection and Control of Modern Power Systems, 2016, 1(1): 1-8. DOI:10.1186/s41601-016-0016-y

[9]

SAPANEVYCH N, SANKAR R. Time series prediction using support vector machines: a survey[J]. Computational Intelligence Magazine, 2009, 4(2): 24-38. DOI:10.1109/MCI.2009.932254

[10]

SHIU M C, WEI L Y, LIU J W, et al. A hybrid one-step-ahead time series model based on GA-SVR and EMD for forecasting electricity loads[J]. Journal of Applied Science and Engineering, 2017, 20(4): 1-8.

[11]

XIN Y F, JIANG Y Y, ZHANG X M. Gas outburst prediction model based on empirical mode decomposition and extreme learning machine[J]. Recent Advances in Electrical & Electronic Engineering, 2015, 8(1): 50-56.

[12]

YASLAN Y, BICAN B. Empirical mode decomposition based denoising method with support vector regression for time series prediction: a case study for electricity load forecasting[J]. Measurement, 2017, 103: 52-61. DOI:10.1016/j.measurement.2017.02.007

[13]

WANG Z Y, QIU J, LI F F. Hybrid models combining EMD/EEMD and ARIMA for long-term stream flow forecasting[J]. Water, 2018, 10(7): 1-12.

[14]

景亚兵, 刘昌文, 毕凤荣, 等. 基于EMD-SVM的小型发电机组物理声源灵敏度分析[J]. 天津大学学报(自然科学与工程技术版), 2017, 50(10): 1077-1083.

[15]

HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454: 903-995. DOI:10.1098/rspa.1998.0193

[16]

VAPNIK V. The nature of statistical learning theory[M]. New York, USA: Springer, 1995: 65-118.