|
|
|
发布时间: 2021-06-25 |
光电技术 |
|
|
|
收稿日期: 2020-01-22
中图法分类号: TN29
文献标识码: A
文章编号: 2096-8299(2021)03-0247-06
|
摘要
介绍了光纤振动传感器的定义及其类别。对相位生成载波(PGC)技术、3×3耦合器解调算法和数字正交解调算法3种光纤振动传感器相位解调算法进行了对比和分析,指出后期相位解调算法仍然有很多改进的方面。最后介绍了未来在实际中有望得到更广泛的应用的情况。
关键词
光纤振动传感器; PGC解调算法; 3×3耦合器解调算法; 正交解调算法
Abstract
First, the definition of fiber optic vibration sensors and types are introduced.Second, the principles of each demodulation algorithm are analysized which mainly includes: phase generation carrier(PGC) technology, 3×3 coupler demodulation algorithm, digital orthogonal demodulation algorithm.Finally, the advantages and disadvantages are compared and summarized, which pointed out that there are still many improvements in the phase demodulation algorithm in the later stage, and it is expected to obtain wide application in the future.
Key words
fiber optic vibration sensor; phase generation carrier demodulation algorithm; 3×3 coupling demodulation algorithm; quadrature demodulation algorithm
光纤是光导纤维的简称, 因为光的全反射效应, 使得光信号在光纤中传输时损耗非常低, 所以在进行长距离的信息传输时, 光纤逐渐成为人们的第一选择。由此, 以该介质制成的传感器在各个领域中得到了广泛应用[1]。光纤传感器包括点式、准分布式和分布式3种。其分类标准依据的是传感器在实际应用中可以测量的范围的大小。其中检测一点的物理量变化是点式传感器, 光纤光栅传感器是此类传感器的代表; 准分布式传感器通过多种形式的串行和并行连接, 连接多个光纤光栅传感器, 以实现多点监视测量[2]; 分布式光纤传感器能够持续稳定地进行大范围数据的测量, 故其在光纤传感技术中发挥着无法替代的作用。
在日常生活中振动现象无处不在, 而当振动的频率、次数、范围等发生异样时, 往往预示着某种事件的发生, 因此可以通过对振动进行监测来实现各类异常事件的警示, 如地震、海啸等。目前振动监测已成为光纤传感技术中较为重要的研究领域和未来研发的方向。分布式光纤振动传感技术根据原理分为两种, 即干涉型和瑞利散射型。其中: 干涉型主要用于监测干涉光信号, 光纤干涉仪对光相位的变化非常敏感, 当光的相位发生变化时, 可以通过解调相位来检测振动; 瑞利散射型针对的是反向瑞利散射光信号, 其散射强度会受到外界振动的影响, 相位、频率等特性也会因此受到影响[3]。在光纤振动传感系统中, 如何将待测信号解调出的解调技术是重中之重, 而能否实时准确地解调出信号, 与解调方法密切相关, 本文针对不同的调制解调原理, 分析了不同的解调方法。
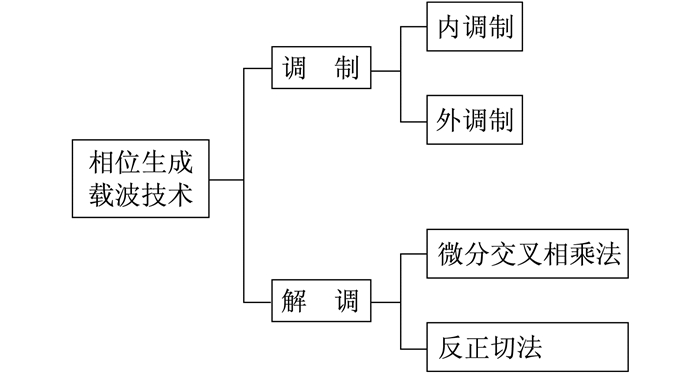
1 光纤调制机制
光纤传感的实质是: 当外界的某一物理量, 如应力等发生变化时, 会导致光纤内传播过程中的光波发生某种变化, 可以通过检测这种变化, 进而实现传感的功能。干涉式光纤传感技术主要是利用外部的参数造成光波的变化, 进而导致相位变化来实现感测, 再通过后期的解调得到相应的相位值。其中, 引起光纤中光波相位变化的因素主要包括应力-应变效应和温度-应变效应, 在光纤振动传感器中主要应用的是应力-应变效应。
光纤应力-应变效应是指光波在传感光纤上的传播。当光纤受到外力作用时, 光波的相位发生某种变化, 这种变化称为应力-应变效应, 可表示为
| $ \varphi = \frac{{{\rm{2 \mathsf{ π} }}}}{{{\lambda _0}}}nL $ | (1) |
式中: φ——光波的相位;
n——光纤的折射率;
L——传感光纤的长度;
λ0——真空中的波长。
如果传感光纤受到外力影响, 即当力作用在传感光纤的轴向上时, 光纤的长度会发生变化, 从L改变为L+ΔL。这将导致光纤中光波的光程差在光路中发生变化, 进而导致输出的相位发生变化, 可表示为
| $ \Delta \varphi = \frac{{{\rm{2 \mathsf{ π} }}}}{{{\lambda _0}}}n\Delta L $ | (2) |
通过式(2)可以得出, 光波相位的变化量Δφ和光纤长度的拉伸量ΔL成正比关系。
光纤振动传感器的相位解调算法原理就是基于应力-应变效应得到相位变化, 通过解调相位, 判定相位变化位置, 以实现振动定位, 并可从相位变化趋势还原外界振动的特征。该相位解调算法主要包括相位生成载波(Phase Generation Carrier, PGC)技术、3×3耦合器解调算法和数字正交解调算法3种算法。
2 PGC解调算法
2.1 PGC调制
内部调制方式是对光源进行直接调制, 同时生成调制载波信号。该方式主要通过改变光源的驱动电流, 使得光波场频率达到相应值。内部调制方式无需在整个光纤系统中加入其他元件, 仅需光源和光纤即可, 实现思路简单, 在信号监测方面具有高度灵敏性, 能够实现较精准的测量[6]。
外部调制方式是在光路外部直接对参考臂光纤施以外力。该外力具体表现为: 将光纤在压电陶瓷换能器(Piezoelectric Ceramic Transducer, PZT)上缠绕多圈, 然后在计算机中引入一个具有周期特性的调制信号。其目的是根据PZT的电致伸缩效应, 在PZT上产生一个周期性的电压, 此时PZT的直径也会发生变化。因此, 该外力会使光纤产生形变, 进而使得光纤中持续传播的光波相位也发生变化, 从而实现外部调制[7]。
在干涉型光纤振动系统中, 以上两种方法都能够实现引入调制信号的目的, 但最常用的方法还是外调制方式。该方法在物理上更易实现。
2.2 PGC解调
对于干涉型光纤振动传感系统, 其最常用的解调方法主要分为微分交叉相乘解调方法和反正切解调方法两种[8]。
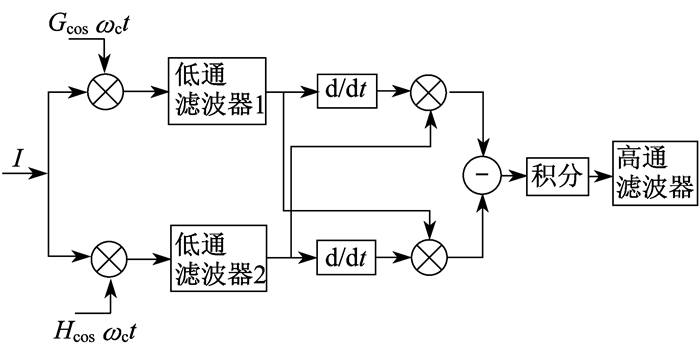
2.2.1 微分交叉相乘解调方法
微分交叉相乘解调方法原理如图 2所示。
在外界引入调制信号, 其调制信号的角频率为ωc, ωc=2πf, 干涉仪的输出信号I可表示为[9]
| $ I = A + B\cos \left( {C\cos \left( {{\omega _{\rm{c}}}t + \varphi (t)} \right)} \right) $ | (3) |
式中: A——直流量的强度;
B——干涉信号的幅值;
C——调制深度;
φ(t)——待测信号。
利用三角函数和Bessel函数展开干涉信号, 并通过相乘、低通滤波器、微分交叉相乘、差分、积分、高通滤波可得
| $ I = D{B^2}GH{J_1}(C){J_2}(C)D\cos \left( {{\omega _{\rm{s}}}t} \right) $ | (4) |
式中: D——需检测的振动信号的幅值;
G, H——外加载波信号的幅值;
J1(C), J2(C)——1阶和2阶贝塞尔函数;
ωs——待解调信号频率。
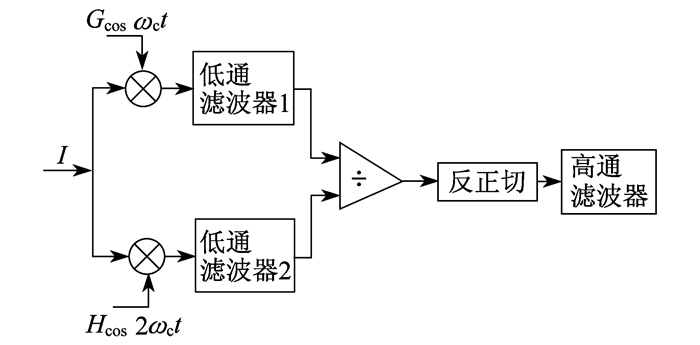
2.2.2 反正切解调方法
3 3×3耦合器解调算法
3.1 3×3耦合器解调原理
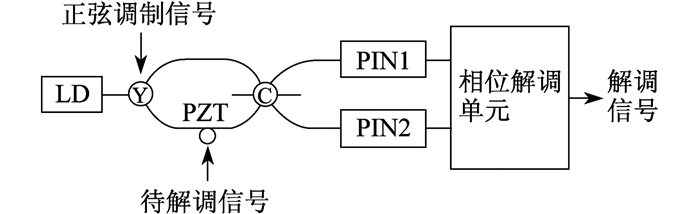
3×3耦合器解调原理主要是指在其构成的干涉仪中, 相邻的两个干涉臂具有120°的相位差, 利用该特点直接对光电探测器接收到的3路信号进行交叉微分相乘, 最终得到相位解调的结果[11]。图 4为基于Mach-Zehnder干涉仪的3×3耦合器系统。
图 4中, 最左端的LD为激光器, 右边的器件Y为Y波导, 中间部分的器件C为3×3耦合器, 右端的PIN1和PIN2为两个光电探测器, 最中间的器件为PZT, 其中中间部分的3个器件和光纤共同组成了光纤Mach-Zehnder干涉仪。该信号解调的过程为: 由LD激光器发射的光波进入到Y波导中, 然后被平均分为2路输入到干涉仪中, 一路直接输入到耦合器中, 另一路经过PZT再输入到耦合器中。同时, 在Y波导上加载了一个频率为f0的正弦调制信号, 而且PZT上被缠绕了多圈光纤, 该光纤为干涉仪的探测臂光纤, 再将周期性的电压加至PZT上, 从而使PZT产生形变, 该形变进而会导致光纤的拉伸, 最终形成光波相位的变化。此相位变化即为待解调的相位信号[12]。在3×3耦合器的3路输出中, 选取2路输出信号, 输入到两个光电探测器中, 然后将光信号变换为电信号, 最后同时输入到相位解调单元, 完成相应的相位解调。
3.2 3×3耦合器解调
与PGC解调算法相同, 均是在干涉仪上加一个调制信号后, 干涉仪的输出信号I有
| $ I=A+B \cos \left(C \cos \left(\omega_{\mathrm{c}} t+\phi\right)\right) $ | (6) |
式中: ϕ——相位差, ϕ=φ(t)+θ。
将式(6)用Bessel函数展开, 再乘以cos(ωct)后经过低通滤波得
| $ I=B J_{1}(C) \cos \phi $ | (7) |
3×3耦合器的2路输出可以表示为
| $ I_{1}=B_{1} J_{1}(C) \cos \left(\varphi(t)+\theta_{1}\right) $ | (8) |
| $ I_{2}=B_{2} J_{1}(C) \cos \left(\varphi(t)+\theta_{2}\right) $ | (9) |
在实际应用中, 3×3耦合器不能保证2个光路的输出能够严格地均分, 故有B1≠B2, 而且2路输出有着一定的相位差, 即θ1-θ2≠0。将式(8)和式(9)分别进行微分运算, 再进行交叉相乘、差分操作后得到
| $ I_{1}^{\prime}=-B_{1} J_{1}(C) \sin \left(\varphi(t)+\theta_{1}\right) \varphi^{\prime}(t) $ | (10) |
| $ I_{2}^{\prime}=-B_{2} J_{1}(C) \sin \left(\varphi(t)+\theta_{2}\right) \varphi^{\prime}(t) $ | (11) |
由式(10)和式(11)可知, 只要sin(θ1-θ2)≠0, 即θ1-θ2≠kπ, k= 0, 1, 2, …时, 式(10)和(11)积分可得到φ(t)。
3×3耦合器相位解调算法原理如图 5所示。
图 5中, 光电探测器PIN1和PIN2分别输出2路电信号, 可将该信号作为相位解调单元的2路输入信号; 经过移除直流分量、A/D转换器转换成数字信号; 然后经过混频处理、低通滤波处理、微分处理、交叉相乘、差分及积分处理等; 最终再通过一个高通滤波器滤除有可能存在的低频成分, 得到待解调的相位信号[13]。
4 数字正交解调算法
4.1 数字正交解调原理
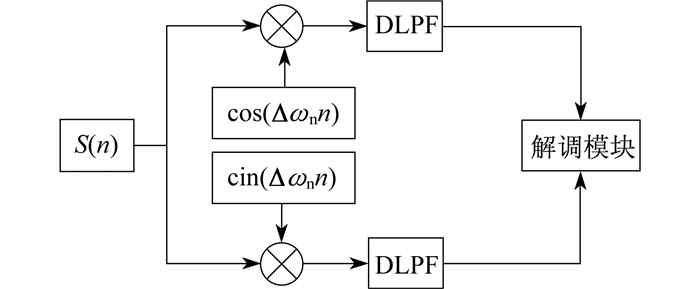
数字正交解调算法是将瑞利散射光信号经过数学算法之后, 形成两路正交信号, 再将这两路信号交由解调模块进行相位的解调[14]。数字正交解调流程如图 6所示。
图 6中, 整个数字正交解调算法包括3个模块。
第1模块是将瑞利散射信号变换为两路正交信号, 即将采集到的S(n)信号分别和两个同频率的正交信号相乘, 两信号分别为cos(Δωnn)和sin(Δωnn), 相乘后产生的两路混频信号可表示为
| $ \begin{aligned} I^{\prime} &=S(n) \cos \left(\Delta \omega_{\mathrm{n}} n\right)=\\ & \frac{1}{2} E_{\mathrm{s}}(n) E_{0}(n)\left(\cos \left(2 \Delta \omega_{\mathrm{n}} n+\varphi_{\mathrm{s}}(n)\right)+\right.\\ &\left.\cos \varphi_{\mathrm{s}}(n)\right) \end{aligned} $ | (12) |
| $ \begin{aligned} Q^{\prime} &=S(n) \sin \left(\Delta \omega_{\mathrm{n}} n\right)=\\ & \frac{1}{2} E_{\mathrm{s}}(n) E_{0}(n)\left(\sin \left(2 \Delta \omega_{\mathrm{n}} n+\varphi_{\mathrm{s}}(n)\right)-\right.\\ &\left.\sin \left(\varphi_{\mathrm{s}}(n)\right)\right) \end{aligned} $ | (13) |
式中: φs(n)——待解调相位;
Es(n)——待测信号振幅;
E0(n)——本地光的振幅。
从式(12)和式(13)可以看出, 混频信号S(n)分别与正交信号相乘, 产生了高频分量cos(2Δωnn+φs(n)), sin(2Δωnn+φs(n))。
若想解调出相应的相位φs(n), 则需要将高频成分滤除, 故第2个模块为滤波模块, 即滤出高频成分, 去除额外的噪声, 保证信号稳定传输, 最后得到I和Q两路信号[15]。
| $ I \propto E_{\mathrm{s}}(n) E_{0}(n) \cos \left(\varphi_{\mathrm{s}}(n)\right) $ | (14) |
| $ Q \propto-E_{\mathrm{s}}(n) E_{0}(n) \sin \left(\varphi_{\mathrm{s}}(n)\right) $ | (15) |
得到I和Q两路信号后, 可以通过式(14)和式(15)分别得到S(n)信号的振幅和相位, 即
| $ {{E_{\rm{s}}}(n){E_0}(n) \propto \sqrt {{I^2} + {Q^2}} } $ | (16) |
| $ {{\varphi _{\rm{s}}}(n) = - \arctan (Q/I) + 2k{\rm{ \mathsf{ π} }}} $ | (17) |
式(17)中k为整数, 该式实现了反正切函数的值域扩展功能, 可得到待解调信号的相位值[16]。
4.2 相位解调
相位的提取过程如图 7所示, 可分为3个部分, 将Q和I信号的比值进行反正切、值域扩展, 最后得到后向瑞利散射光的相位[17]。
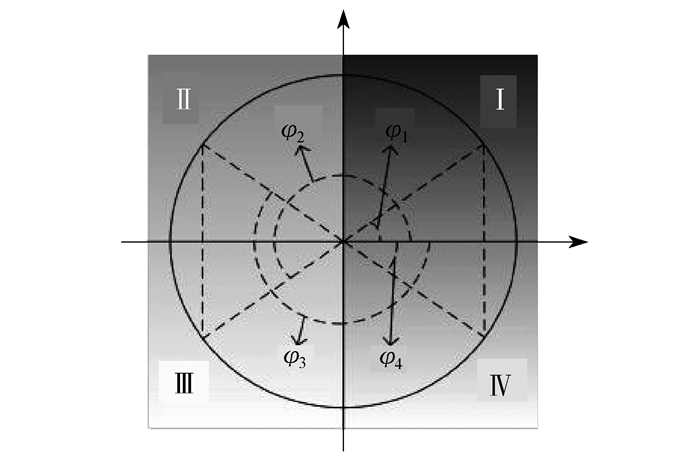
反正切函数的值域为(-π/2, π/2), 实际相位的值在(-2π, 2π)之间, 所以此时相位的值有可能不在该函数的值域范围内。因此, 解调结果不再是正确的相位值, 需要扩展值域的范围[18]。三角函数象限图如图 8所示。
图 8中, 相位φ1=-φ4, φ2=φ1+π, φ3=φ4-π, 则tanφ3=tanφ4。所以, 在利用反正切函数求解相位值时, tanφ3与tanφ4的反正切结果相同, 但实际值与解调值存在不相符的问题。
值域扩展的方法是将反正切函数的范围扩展到(-π, π)之间, 即将原始反正切函数的范围加上2kπ, 使其在扩展的范围内。但在实际解调过程中, 实现值域扩展后, 相位解调的结果还会出现相位从-π到π或是π到-π的跳跃, 相邻的两相位之间变化不连续。为解决此问题, 可以设定相应的阈值, 即设为π。首先计算相邻采样点的相位差的绝对值|ϕ(z_(n+1))-ϕ(z_n)|, 如果该绝对值超过π, 则再次判断ϕ(z_(n+1))-ϕ(z_n); 如果该值大于π, 则在点z_(n+1) 之后的每一点的值均减去2π。同理, 如果比-π小, 则加上2π[19]。
5 算法分析
PGC解调算法是将需要检测信号的频谱搬移到频率较高的频带上, 人为地实现与低频率成分的隔离, 以避免噪声对解调结果产生的影响, 而且能够更好地避免因相位的衰落而产生的影响, 实现相位生成载波的目的。传统的PGC解调方法会受干涉信号光强、调制深度、混频阶数等因素的影响, 文献[8]提出了基频混频及微分自相乘解调算法, 有效解决了调制深度、光源扰动等对解调结果的影响。相位解卷绕算法的实现解决了反正切解调方法检测的动态范围小且相位跳变的问题。PGC算法适用于噪声大的光线振动传感器应用场合, 通过高频带调制, 避免受噪声影响。
3×3耦合器解调方法实现结构简单, 成本低, 但是基于以下3个理想条件, 其解调的效果才可以达到最佳: 一是3路信号中满足两两的相位差值均为120°; 二是直流分量的幅值严格相等; 三是交流分量的幅值严格相等。但是, 在实际的应用过程中, 上述3个条件在工程制作中无法实现, 需要借助其他器件如滤波器、放大器等。干涉仪的偏振态会存在不稳定的情况, 此时需要增加控制器以恢复稳定的干涉效果, 达到预期结果。由于3×3耦合器解调算法的结构较为简单, 光路的搭建物理可实现性强, 因此应用很广泛。
数字正交解调算法利用了后向瑞利散射光对于相位变化高度敏感的特性, 能够实现更大范围的监测。此外, 该方法能够准确地得到振动信息, 监测精度高, 能够实现比上述两种方法更为长距离的监测, 且实现时硬件要求低, 物理结构较为简单; 缺点是存在振动定位滞后的现象, 而且在空间域和时间域上存在相位模糊, 也会出现相位跳变、不连续的问题。通过值域扩展及相位解卷绕算法能够解决这一问题, 因此, 该算法在振动检测、实现振动定位方面应用更广泛。
6 结语
光纤振动传感作为新一代传感技术, 在众多领域中发挥了无可替代的作用, 而光纤振动传感技术实现的核心是能够成功地解调出待测信号。本文概述了光纤振动传感技术的PGC相位解调算法、3×3耦合器解调算法和数字正交解调算法3种相位解调算法, 并对未来算法的改进提供了思路, 以期为实际应用奠定更好的基础。
参考文献
-
[1]高安平. 光纤传感器的研究及应用研究[J]. 科技视界, 2016(17): 13. DOI:10.3969/j.issn.2095-2457.2016.17.008
-
[2]李闯. 基于光纤声传感器的管道泄漏检测技术[D]. 北京: 国防科学技术大学, 2012.
-
[3]于淼. 基于双重同源外差相干检测的Φ-OTDR系统的研究及应用[D]. 长春: 吉林大学, 2017.
-
[4]夏东明, 娄淑琴, 温晓栋, 等. 干涉型光纤传感器相位载波解调技术研究[J]. 光电技术应用, 2011, 26(5): 47-50. DOI:10.3969/j.issn.1673-1255.2011.05.014
-
[5]王旭. 分布式光纤振动传感系统相位解调方法的研究与改进[D]. 长春: 吉林大学, 2018.
-
[6]高文智. 基于光纤振动传感技术的相位解调方法研究及硬件实现[D]. 长春: 吉林大学, 2018.
-
[7]宫经宽, 刘樾. 光纤传感器及其应用技术[J]. 航空精密制造技术, 2010, 46(5): 49-53. DOI:10.3969/j.issn.1003-5451.2010.05.014
-
[8]张爱玲, 王恺晗, 郝彬, 等. 干涉型光纤传感器PGC解调算法的研究[J]. 光电技术应用, 2013, 28(6): 53-56. DOI:10.3969/j.issn.1673-1255.2013.06.011
-
[9]刘腾飞, 赵海增. 用于干涉型光纤传感器的相位生成载波解调技术研究进展[J]. 河南科技, 2018(2): 45-47. DOI:10.3969/j.issn.1003-5168.2018.02.026
-
[10]CHANG T Y, LANG J P, SUN W, et al. Phase compensation scheme for fiber-optic interferometric vibration demodulation[J]. IEEE Sensors Journal, 2017, 17(22): 7448-7454. DOI:10.1109/JSEN.2017.2750725
-
[11]CHEN J D, GAO W Z, CHANG T Y, et al. Method for determining the resonance frequency of a fiber optic interferometric accelerometer[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 67(3): 698-705.
-
[12]王恺晗. 基于双M-Z干涉型光纤振动传感器及其PGC解调技术的研究[D]. 天津: 天津理工大学, 2015.
-
[13]宋美杰, 于廷宽. 一种基于3×3耦合器的光纤相位解调算法[J]. 光通信技术, 2019, 43(5): 55-57.
-
[14]王旭, 刘珉含, 于淼, 等. 相位敏感光时域反射系统数字正交解调算法分析及改进研究[J]. 中国激光, 2017, 44(12): 269-275.
-
[15]LU X, SOTO M A. Temperature-strain discrimination in distributed optical fiber sensing using phase-sensitive optical time-domain reflectometry[J]. Optics Express, 2017, 25(14): 16059-16071. DOI:10.1364/OE.25.016059
-
[16]HE X, XIE S, LIU F, et al. Multi-event waveform-retrieved distributed optical fiber acoustic sensor using dual-pulse heterodyne phase-sensitive OTDR[J]. Optics Letters, 2017, 42(3): 442-445. DOI:10.1364/OL.42.000442
-
[17]邹捷, 王宇, 张建国, 等. 一种基于相干光时域反射的分布式光纤振动传感系统研制[J]. 中国测试, 2019(6): 114-120.
-
[18]孙韦, 于淼, 常天英, 等. 相位生成载波解调方法的研究[J]. 光子学报, 2018, 47(8): 227-234.
-
[19]何毅, 刘德明, 孙琪真. 基于Labview的光纤传感器相位解调技术[J]. 信阳师范学院学报(自然科学版), 2006(1): 94-97.