随着常规油气资源的日益枯竭, 页岩气等非常规油气能源的勘探与开发越来越受到人们的重视。目前我国页岩气的主要产区是涪陵、长宁、威远等地, 较多资源埋深超过3 500 m, 地质条件复杂, 了解和掌握页岩储层的内部结构是开采页岩气的基础^[1]。页岩储层结构复杂, 其岩石组成包含有机质、黏土矿物、石英等脆性矿物以及碳酸盐矿物, 并含有一定量的长石、云母、方解石、白云石、黄铁矿等矿物。对页岩储层内部结构的评价存在着诸多问题, 如孔隙和裂缝结构非常复杂、非均质性强、物性变化大等。目前可以通过CT成像的方式观察页岩内部结构, 但CT成像需要专用且昂贵的设备, 且通常只能获取所研究岩石样本的小范围图像, 难以重建较大区域的页岩结构。为了评估页岩储层, 必须进行大量物理实验, 以获得更大范围的分布情况, 成本较大^[2]。空间数据建模已被广泛用于岩石重构。原始的空间数据建模方法依赖两点概率函数度量空间变异性, 使用训练图像作为样本特征提取的方式是目前空间数据建模方法的主流^[3-5]。通常假定这些训练图像具有平稳的特征分布, 并依赖学习训练图像特征来重构空间数据。

深度学习具有很强的提取特征能力, 可以用于提取训练图像的结构特征, 而生成对抗网络(Generative Adversarial Networks, GANs)是深度学习的一个重要分支。深度卷积生成对抗网络(Deep Convolutional Generative Adversarial Networks, DCGANs)是GANs的一种主要变体, 整体结构与GANs基本相同, 是一种无监督机器学习方法, 可在给定一组训练图像的情况下重构未知图像。本文提出了一种基于DCGANs重建页岩的新方法, 虽然DCGANs的训练要确定一组相对稳定的超参数, 但是用于生成图像的参数集可以在训练后存储, 从而可以快速生成新的重构样本。

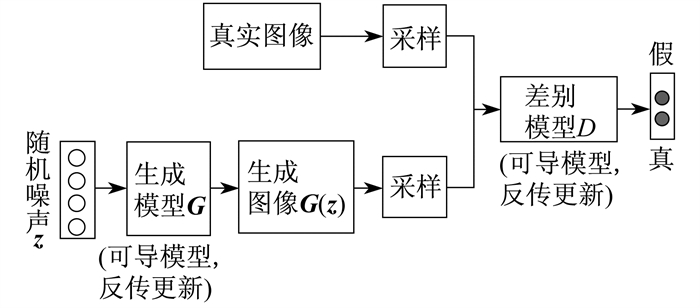
GANs是在深度学习的背景下提出的, 是一种从训练图像中学习高维概率分布表示的方法^[6]。训练图像呈现了图像空间中表示概率分布的代表性样本。GANs包含两个可区分的函数: 鉴别器D和生成器G。生成器G将随机变量从随机噪声z映射到图像空间得到生成图像G(z)。z通常由正态分布p_z的独立实数随机组成, 代表生成器的随机输入。鉴别器D的作用是计算随机样本来自“真实”数据的概率分布p_data。鉴别器尝试正确标记每个样本, 而生成器尝试“欺骗”鉴别器, 标记生成图像G(z)作为真实数据分布的一部分, 即实现D(G(z))接近1。GANs结构如图 1所示^[7-8]。

根据鉴别器输出结果, 得到GANs的损失。通常情况下把最小化GANs的损失函数当作最小化-最大化问题, 即

$ \begin{array}{l} \mathop {\min }\limits_G \mathop {\max }\limits_D \left\{ {{{\mathbb{E}}_{X \sim {p_{{\rm{data }}}}(X)}}[\lg (D(\mathit{\boldsymbol{X}}))] + } \right.\\ \;\;\;\;\;\left. {{{\mathbb{E}}_{\mathit{\boldsymbol{z}} \sim {p_\mathit{\boldsymbol{z}}}(\mathit{\boldsymbol{z}})}}[\lg (1 - D(\mathit{\boldsymbol{G}}(\mathit{\boldsymbol{z}})))]} \right\} \end{array} $

(1)

式中: ${{\mathbb{E}}_{\mathit{\boldsymbol{X}} \sim {p_{{\rm{data}}}}(X)}}$——鉴别器输入在图像X符合真实图像概率分布p_data的数学期望;

${{\mathbb{E}{}}_{\mathit{\boldsymbol{z}} \sim {p_\mathit{\boldsymbol{z}}}\left(\mathit{\boldsymbol{z}} \right)}}$——生成器的输入向量z符合正态分布p_z的数学期望。

该优化问题的解决方案为纳什均衡^[7], 其中每个参与者就其参数而言达到其损失函数的局部最小值。利用可梯度下降的优化方法训练的卷积神经网络来表示G和D。训练分两个步骤。

首先训练鉴别器函数使其最大化, 即

$ \begin{array}{l} {J^{(D)}} = {{\mathbb{E}}_{X \sim {p_{{\rm{data}}}}(X)}}[\lg (D(\mathit{\boldsymbol{X}}))] + \\ \;\;\;\;\;\;\;\;\;\;\;{{\mathbb{E}}_{\mathit{\boldsymbol{z}} \sim {p_\mathit{\boldsymbol{z}}}(\mathit{\boldsymbol{z}})}}[\lg (1 - D(\mathit{\boldsymbol{G}}(\mathit{\boldsymbol{z}})))] \end{array} $

(2)

然后固定生成器的参数。通过从100维正态分布的隐藏空间中抽取向量z来生成向量G(z), 并训练生成器函数以使其最大化, 即

$ {J^{(G)}} = {{\mathbb{E}}_{\mathit{\boldsymbol{z}} \sim {p_\mathit{\boldsymbol{z}}}}}[\lg (1 - D(\mathit{\boldsymbol{G}}(\mathit{\boldsymbol{z}})))] $

(3)

保持鉴别器参数固定, 通过式(3)的生成器来“欺骗”鉴别器, 使其认为样本G(z)是真实数据样本, 使生成器尽可能接近实际数据分布p_data(X)的分布p_g(X), 其中p_g(X)表示生成器所生成图像的概率分布。当达到收敛p_g(X)=p_data(X)时, 鉴别器的值变为0.5, 无法再区分两者。由于最初鉴别器D的性能明显优于生成器, 训练生成器的梯度接近于零, 因此保证lg(D(G(z)))最大化优于保证生成器的lg(1-D(G(z)))最小化^[7]。GANs需要进行反复训练才能找到最佳的超参数集, 以实现稳定的训练。目前许多改进方法可以加速GANs训练^[8]。

DCGANs是GANs的一种主要变体, 整体结构与GANs类似, 只是DCGANs的鉴别器和生成器都使用了卷积神经网络来替代GANs中的多层感知机, 同时为了使整个网络可导, 采用全卷积神经网络, 避免在卷积层之后使用全连接层。在生成器和鉴别器中都添加了批量归一化操作^[9]。同时, 生成器的输出层使用Tanh激活函数, 其他层使用ReLU激活函数。鉴别器的所有层都使用LeakyReLU激活函数^[10-11]。

步骤1  首先初始化生成器G和鉴别器D的超参数。

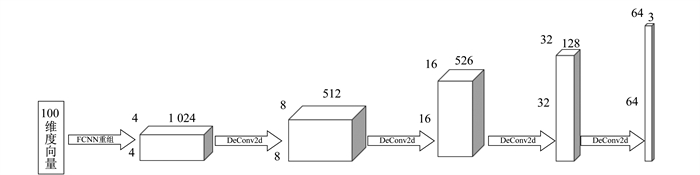
步骤2  由100维随机噪声向量z通过全连接层学习, 变形成4×4×1 024的矩阵输出, 之后通过4个反卷积层操作, 重构生成64×64×3的岩石图像。生成器结构如图 2所示, 其中全卷积神经网络(Fully Convolutional Networks, FCNN)表示全连接神经网络, DeConv2d表示反卷积。

步骤3  鉴别器输入64×64像素的图像, 经过4次卷积, 将分辨率降低为4×4像素, 借用此功能来确定此图像是来自真实图像还是来自生成器。利用鉴别器反向传播更新超参数, 提高鉴别器鉴别真实图像与“假”图像的能力。

步骤4  当鉴别器具有较高鉴别能力时, 固定鉴别器的超参数, 并不断更新生成器超参数促使生成图像的质量逐渐接近于真实图像。这样鉴别器就难以区分真实图像和生成图像, 即生成器达到“欺骗”鉴别器的效果。

步骤5  重复步骤3和步骤4, 直至生成器G和鉴别器D达到纳什平衡, 模型收敛。

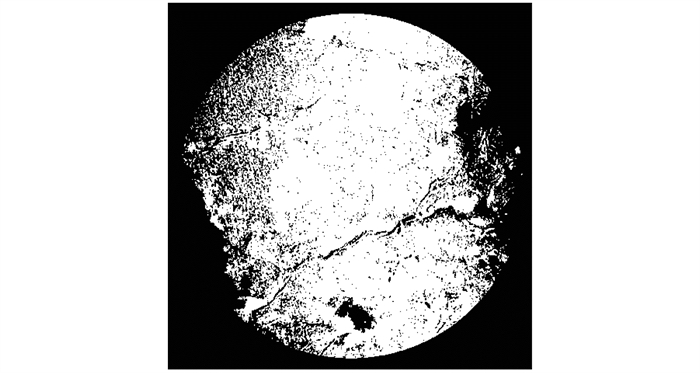
本文实验数据来自纳米CT扫描获取得到的真实页岩图像数据。图 3是一幅大小为1 016×1 024像素的二值化页岩截面, 分辨率为每像素65 nm。图像边缘四周的黑色部分作为无效数据进行剔除, 白色表示页岩的骨架。

页岩内部结构复杂, 很难定量描述其内部特征。对页岩重构质量进行评价主要是考察其结构特征是否得到重构, 而并非在相同的位置具有相同的状态值, 即要求重构数据可以体现出训练图像的结构特征。本文采取变差函数和孔隙度两个岩石主要属性对重构质量进行评价^[12]。

变差函数用于描述数据值的空间相关性。数据点在空间上的距离越远, 相关性就变得越小。变差函数的定义为: 区域化变量Z(x)和Z(x+h)表示两点之差的方差之半, 其中x表示空间位置向量值, h表示空间向量值, 具体含义可参见文献[13]。孔隙度是指岩石中所有孔隙空间体积之和与岩石总体积的比值, 以百分数表示。变差函数与孔隙度是页岩重要的特征参数, 利用变差函数和孔隙度对重构质量进行评估, 可有效地对页岩重构质量进行评估。

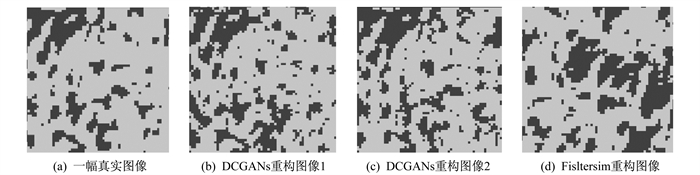
本文利用页岩截面作为训练图像进行DCGANs训练, 实现网络能够自行生成符合真实页岩结构特征的重构图像。通过CT扫描获取1 021幅二值化页岩截面图像, 从每幅图中的相同(x, y)位置截取大小为64×64像素的图像, 作为实验所需的页岩训练图像, 可得到1 021幅64×64像素的二值化真实图像。真实图像与重构图像比较如图 4所示, 其中, 蓝色部分表示孔隙, 白色表示骨架。对比Filstersim^[14]重构得到的页岩图像图 4(d), 可以发现DCGANs与真实图像结构特征的相似性更高。

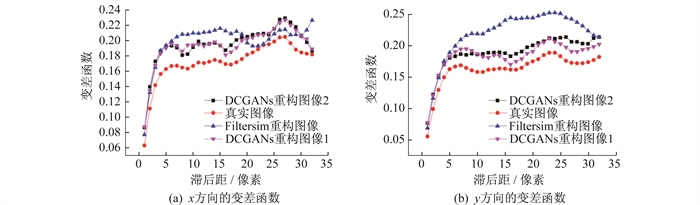
图 5所示为重构图像与真实图像的平均变差函数。相较于Filstersim重构图像, DCGANs重构图像在x和y方向平均变差函数与真实图像更加接近。

表 1为真实图像和DCGANs及Filstersim重构图像的孔隙度。由表 1可以发现, 重构图像与真实图像孔隙度均较为接近。DCGANs训练结束后, 由于超参数可以保存以避免再次训练参数, 因此后继重构页岩时将无需再次进行模型训练。这是DCGANs的一个优势。

本文提出了一种基于DCGANs的二维页岩图像重构方法, 即利用DCGANs生成与原始页岩结构特征相似的重构图像。实验证明, DCGANs可以提取页岩图像中的结构特征, 重构图像与训练图像的变差函数和孔隙度相似。由于DCGANs网络的超参数可以保存, 因此这些参数可以多次重复使用, 较传统方法具有一定的优势。