随着计算机软硬件的高速发展, 以及一系列新兴电子数码设备的普及, 人们对于计算机视觉的处理逐渐由二维平面转向三维立体空间。相较于二维图像, 三维模型可以提供更多的信息及视觉冲击。3D电影、虚拟现实^[1]、城镇建模、医疗模型, 以及高速发展的3D打印技术等都离不开3D模型的制作。目前的主流方法是通过三维重建技术获取人们所需的模型, 作为计算机视觉的一个重要研究方向, 其已具备一系列较为成熟的理论方法^[2]。

TOMASI C等人^[3]于1992年最先提出基于图像运动结构的三维重建方法, 从多幅未标定图像中提取匹配特征, 通过最小化投影误差求解物体和相机参数, 进行模型的重建。马颂德和张正友^[4]于1998年使用棋盘标定板提高相机标定精度^[5]。SNAVELY N等人^[6]在2008创建了Bundler增量式重建系统。FURUKAWA Y等人^[7]于2010年在前者的基础上提出了基于面片的多视图三维重建, 通过重建、扩散、滤波等操作, 在一定程度上解决了点云空洞问题。史利民等人^[8]于2011年利用空间几何信息改进了PMVS算法, 缩短了重建时间, 并提高了重建精度。PIZZOLI M等人^[9]于2014年提出了一种融合贝叶斯估计的单目稠密算法REMODE。中科院自动化所完成的CV Suite, 只需3张图像就可以实现对目标物体的重建, 但精度、效率都有待进一步的改善。

根据建模时所依赖的数据来源, 三维重建可分为主动获取式和被动获取式。主动获取式主要通过激光或雷达等一系列主动发出信号的设备, 近距离对物体进行扫描, 从而获得物体的形状和纹理等参数^[10]。该方法可以生成精度较高的模型, 实时性较好, 但由于其重建场景有限(适用于较小物体或场景, 对于大规模的场景并不适用), 且设备昂贵, 所以很难普及或用于一般性的研究。如今随着手机像素的不断提高, 我们仅通过手机就可以获得质量较高的, 甚至4 K超清的图像, 足够用于三维模型的重建。相对于激光扫描设备, 手机在价格上优惠许多, 且便于携带, 能够满足实际应用需求。本文实现了基于单目图像的三维重建工作, 利用手机的针孔摄像头拍摄物体周围一圈不同角度的图片, 通过尺度不变特征变换(Scale-Invariant Feature Tranfrom, SIFT)^[11]算法进行特征点检测与匹配, 由SFM(Structure From Motion)生成稀疏点云, 再通过PMVS(Patch - based Multi - View Stereo)算法生成稠密点云, 最后得到3D纹理网格模型的全部过程^[12]。通过对点云阵列的修剪与过滤, 保证了最终模型的生成与后续应用。

拍照是将空间中的三维坐标点投影转换为图片中的二维像素点的过程。首先需要确定该点在世界坐标系中的位置, 设为(X_w, Y_w, Z_w)。该点是在基准坐标系下的坐标点。在图片重建中需要使用相机围绕物体拍不同角度和位置的图片, 物体上的同一点在相机不同角度下的位置是不同的, 所以需要将空间点转换为对应相机坐标系下的点。同一相机通过旋转、平移后可以得到不同位置的图像, 即

$ \left[\begin{array}{c} X_{\mathrm{c}} \\ Y_{\mathrm{c}} \\ Z_{\mathrm{c}} \\ 1 \end{array}\right]=\left[\begin{array}{cc} R & t \\ 0^{\mathrm{T}} & 1 \end{array}\right]\left[\begin{array}{c} X_{\mathrm{w}} \\ Y_{\mathrm{w}} \\ Z_{\mathrm{w}} \\ 1 \end{array}\right]=\boldsymbol{M}_{1}\left[\begin{array}{c} X_{\mathrm{w}} \\ Y_{\mathrm{w}} \\ Z_{\mathrm{w}} \\ 1 \end{array}\right] $

(1)

式中: [X_c, Y_c, Z_c, 1]^T——对应相机坐标的齐次形式;

R——对应于坐标的旋转;

t——平移向量;

M₁——刚体变换过程方阵。

在得到对应相机坐标后, 将其投影到对应的归一化像平面上。此时将会损失图像的深度信息Z_c, 其数学表达式为

$ \left[ {\begin{array}{*{20}{l}} x\\ y\\ 1 \end{array}} \right] = \frac{1}{{{Z_{\rm{c}}}}}\left[ {\begin{array}{*{20}{l}} {{x_{\rm{c}}}}\\ {{y_{\rm{c}}}}\\ {{z_{\rm{c}}}} \end{array}} \right] $

(2)

此时得到的(x, y)为归一化像平面坐标, 需要再次转换为物理像平面坐标, 即相机实际成像平面。为了方便建模与计算, 通常将原点转移到图像的左上角, 此过程的数学表达式为

$ \left[ {\begin{array}{*{20}{l}} u\\ v\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{f_\alpha }}&0&{{u_0}}\\ 0&{{f_\beta }}&{{v_0}}\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} x\\ y\\ 1 \end{array}} \right] $

(3)

式中: f——相机焦距, f_α=f_β=f;

(u, v)——转换后的像素坐标;

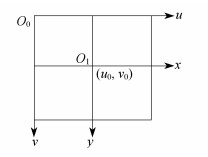
(u₀, v₀)——图像的中心点坐标。

图像坐标系如图 1所示。

此时, 将世界坐标系中的点转换成对应相机的像素坐标的数学模型基本完成, 然后通过逆向求解得到图像的三维坐标点。

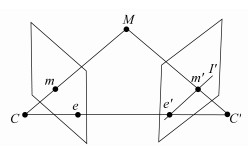
同一场景不同角度的图像之间存在一定的制约关系。这种联系可以作为模型重建计算的约束条件。对极几何是两幅视图之间内在的射影几何, 与所拍摄的场景无关, 仅仅与相机本身的参数和拍摄时的相对位姿有关。对极几何关系如图 2所示。

M为三维空间中一点, m和m′分别为点M在相机C与相机C′中成像平面上的投影点, 两相机光心CC′称为基线, C, C′, M的3点所构成的平面称为极平面, 基线与两成像的交点是极点, 即图 2中的e和e′。直线Mm在另一相机平面上的投影作为点m的极线, 对应于图中的I′。

基础矩阵是两幅图像间对极几何关系的代数形式, 反映了同一空间点在不同的图像坐标系间的对应关系。设三维坐标点M在相机C中成像的齐次坐标为m=[u, v, 1], 在另一相机C′成像的齐次坐标为m′=[u′, v′, 1], 则有

$ m \boldsymbol{F} m^{\prime}=0 $

(4)

式中: F——基础矩阵。

要保证F有唯一解, 则两幅图像间至少需要找到8对匹配点, 否则无法求出。

首先使用相机在物体的周围进行不同角度图像的采集, 尽可能保证能够拍到物体的所有细节; 相邻图像间需要存在重叠部分, 重建物体在图片中需要占绝大部分, 以减少外点对重建结果的影响。基于图像的三维重建的基本流程如图 3所示。

作为三维重建的第一步, 图像的质量对后续的处理计算至关重要。通过手机相机拍摄的图像可能存在模糊和残缺等情况, 直接影响后续特征点的匹配和点云的重建。将这些图像滤除掉能够提高后续的处理速度, 提高模型的生成质量。通过对图像进行高斯平滑处理, 可以去除阶跃函数对特征点求解的影响。

通过对图像的预处理后, 进行不同图像间的特征点匹配。这些特征点应该具有一定的梯度差异, 并在不同视角中多次出现, 一般选择角点或灰度差异较大的点。

SIFT是一种广泛使用的特征点检测方法, 具有仿射不变性。物体在不同视角下, 形状、亮度、大小可能发生变化, 而SIFT特征点能够很好地适应这些变化, 所以广泛用于不同角度图像特征匹配。LOWE G^[11]提出了LoG近似等价于相邻尺度的高斯差分(DoG), 定义如下:

$ \begin{array}{l} D(x,y;\sigma ) = (G(x,y;k\sigma ) - G(x,y;\sigma ))I(x,y) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;L(x,y;k\sigma ) - L(x,y;\sigma ) \end{array} $

(5)

式中: k——尺度伸缩因子;

σ——尺度;

G——高斯核函数;

L——尺度空间函数。

通过高斯差分求得极值点后, 设定阈值去除响应值过小的点和边缘点, 然后进行梯度计算, 以确定像素块的主方向和描述子, 从而得到具有旋转不变性的特征匹配点。

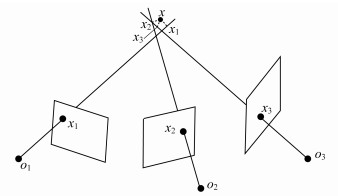
SFM^[13]是一种相机标定方法, 可分为增量式(incremental/sequential)、全局式(global)和混合式(hybrid)等。增量式SFM是在之前重建的数据基础上进行追加, 鲁棒性高, 但容易造成累计误差, 需要反复的捆绑调整, 效率不高。全局式SFM没有累计误差, 且执行效率最高。混合式SFM相较于全局式鲁棒性更强, 但融合了增量式所以效率不高。本文使用全局式SFM, 通过输入序列图像改进其鲁棒性不足的缺点。在相机一系列参数已知的情况下, 可以根据三角测量原理, 依据不同视角的图像从而推断出匹配点的空间三维坐标, 并通过投影矩阵将其转换成图像坐标。若要确定空间中一个点的位置, 至少需要两条射线, 在实际情况中, 由于误差的存在, 这些射线往往不会汇聚于一点, 如图 4所示。

此时通过最小二乘法, 求解出距离这些射线距离最小的点(如图 4中的x)作为这些投影点在世界坐标系中的三维坐标点。由于本实验中相机的参数并不知晓, 所以通过求解单应矩阵^[14], 利用图像中的匹配点计算出投影矩阵, 反推出相机参数。两相机间基线越长, 误差影响效果越小。因此在进行参数估计时, 本文选择基线长、匹配点多的两个相机视角, 再重复上述求三维点坐标的流程, 即可获取稀疏点云。

基于面片的PMVS算法是目前基于多视图的三维稠密重建算法中公认效果最佳的算法之一^[15]。本文在该算法框架下对稀疏点云进行处理, 实验选取5×5像素大小的面片。首先, 通过沿极线进行搜索找到匹配的特征点, 进行种子面片的生成。该特征点与相机中心的连线作为该面片的法向量, 通过计算NCC(Normalized Cross Correlation)的值, 进行特征点的筛选。NCC值过小, 表示该特征点在其他相机中存在遮挡或光度变化过大, 应将其去除。然后, 进行面片扩张, 将三维面片投影到图像上, 若相邻位置没有面片投影且深度连续的情况下, 则将该面片复制到相邻位置进行扩张。最后, 对一些噪声点进行滤除, 将一些在投影空间中相邻、在空间邻域内不相邻的面片去除, 从而得到稠密点云重建。

在得到稠密点云后, 往往存在点云分布不均和空洞现象。本文通过曲面拟合推断未知平面。常见的曲面表述法有参数平面表述法和隐式平面表述法。隐式曲面通过函数f(x, y, z)的零水平集, 即{(x, y, z)|f(x, y, z)=0}所代表的曲面来确定物体表面的空间位置。相较于参数平面, 隐式平面更加灵活, 适合描述结构比较复杂的物体。本文结合了全局拟合法和局部拟合法的优点, 将隐函数问题转化为求解泊松方程的解, 利用模型指示函数与表面采样的有向点集之间的内在关系构建泊松方程^[16], 然后对泊松方程进行求解, 以得到网格模型。

本实验采用Inter(R)Core(TM)i5 - 6300CPU 2.30 GHz, 8 GB内存, Windows 10操作系统, C++编程语言。通过小米MIX3自带相机对玩偶进行不同角度的图像采集, 共拍摄了玩偶的一组55张图像, 将这些图像作为原始输入数据, 如图 5所示。

原始图像进行预处理后, 进行特征点的检测与匹配。通过SFM算法获取玩偶的稀疏点云(其中的蓝色锥形代表相机的位置), 在稀疏点云的基础上通过PMVS算法进行稠密点云的重建, 利用非均匀的空间划分, 通过泊松重建最终得到3D网格模型, 如图 6所示。

相较于增量式SFM, 全局式SFM效率更高且没有累计误差对结果的影响, 如图 7所示。图 7(a)为增量式SFM处理后的稠密点云, 图 7(b)为经过全局式SFM处理后的稠密点云, 相比较而言, 图 7(b)的重建效果较好, 增量式SFM的累计误差在图 7(a)中表现得较为严重。

玩偶的3D模型建立好后, 若需要进行3D打印, 可通过格式转化工具, 将其转化成3D打印常用的STL格式, 如图 8所示。

本文实现了一种通过手机相机拍摄图片, 通过坐标点的转换, 实现三维逆向建模的过程。相比传统正向建模方式, 本文所用方法速度更快, 操作门槛低, 为非专业人员进行三维重建提供了一种可行途径。但基于图像的三维重建仍存在许多问题需要解决, 目前对于透明的、非静止的、反光等物体的重建并没有很好的解决方法, 实验中玩偶头部的透明吸盘重建效果并不理想。下一步的工作将针对这些问题结合深度学习算法作进一步的研究。