Print

发布时间: 2022-02-28
摘要点击次数:
全文下载次数:
DOI: 10.3969/j.issn.2096-8299.2022.01.011
2022 | Volume 38 | Number 1




    计算机与信息科学    




  <<上一篇 




  下一篇>> 




秘密共享的发展与应用综述
expand article info 田秀霞a, 张悦a, 颜赟成b
1. 上海电力大学 计算机科学与技术学院, 上海 200090;
2. 上海电力大学 能源与机械工程学院, 上海 200090
收稿日期: 2020-03-27
基金项目: 国家自然科学基金面上项目(61772327);国家自然科学基金重点项目(61532021)
中图法分类号: TN918.4;TP393
文献标识码: A
文章编号: 2096-8299(2022)01-0066-09

摘要

秘密共享方案为解决信息安全和密钥管理问题提供了一个崭新的思路。秘密共享可应用于数据的安全存储和加密等领域, 保障了传输信息的安全性和准确性。综述了秘密共享方案, 介绍了秘密共享的概念, 归纳总结了多秘密共享技术、可验证秘密共享技术、无分发者秘密共享技术、可安全重构秘密共享技术、主动式秘密共享技术的发展历程及其特点。此外, 列举了秘密共享技术在电子投票、数字图像、生物特征等方面的应用。

关键词

隐私保护; 秘密共享; 加密技术

A Review of the Development and Application of Secret Sharing
expand article info TIAN Xiuxiaa, ZHANG Yuea, YAN Yunchengb
1. School of Computer Science and Technology, Shanghai University of Electric Power, Shanghai 200090, China;
2. School of Energy and Mechanical Engineering, Shanghai University of Electric Power, Shanghai 200090, China

Abstract

The secret sharing scheme provides a new way to solve the problem of information security and key management.Secret sharing can be applied in secure storage and encryption of data, which ensures the security and accuracy of transmitted information.This paper is a review of the secret sharing scheme, introducing the concept of secret sharing, and it also summarizes the development process and the characteristics of much secret sharing technology such as the multi-secret sharing, verifiable secret sharing, non-distributor secret sharing, security reconfigurable secret sharing, and proactive secret sharing technology.Additionally, the applications of secret sharing technology in the field of electronic voting, the field of digital image and the field of biological feature are also listed in this paper.

Key words

privacy protection; secret sharing; encryption technology

随着计算机互联网技术的发展和大数据时代的到来, 人们在生活和工作中的数据越来越重要, 与此同时信息泄露问题也日趋增多。近期自新型冠状病毒肺炎疫情爆发以来, 为了能够更好地控制疫情, 多家企业上线了与疫情相关的大数据产品, 各级政府部门也同时组织摸排和收集返乡人员的信息和资料。在此过程中, 个人信息存在着被非法收集、泄露和传播的风险, 而且恶意攻击者泄露通信数据的案例比比皆是。这些问题严重影响了人民生活并且危害了国家安全。为了解决这些问题, 很多研究者通过研究发现, 秘密共享(Secret Sharing)技术可以有效解决这些问题, 高效保护隐私数据和提高网络安全。

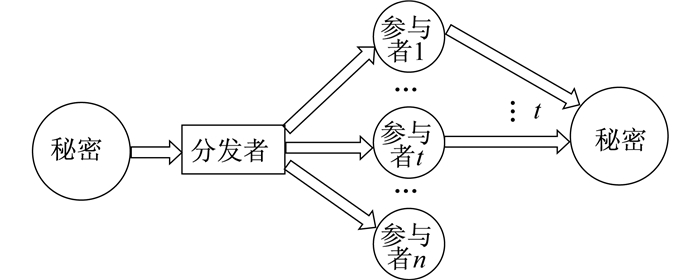
秘密共享技术包括参与者、分发者、秘密3个部分, 对于正整数t和n(t≤n), 规定有n个参与者, 至少t个参与者参与重构秘密。分发者将秘密分发给各个参与者, 参与者拿到各自的秘密份额后, 至少t个参与者的秘密份额参与秘密重构, 方可重构秘密, 否则不能得到秘密。制定秘密共享方案时, 要考虑效率和安全性。分发多个秘密时, 重复共享方案会降低方案的安全性, 而每次分发秘密更新秘密份额, 虽然可以提高安全性, 但会降低秘密分享效率。因此, 针对不同的应用场景需要构建不同的秘密共享方案。本文通过查阅大量文献, 归纳总结了秘密共享方案的发展过程及其应用。

1 秘密共享发展

随着计算机在电子邮件、电子资金转移和信息存储等领域的普及, 保护隐私信息不被泄露、重要信息不被破坏等问题变得更加重要。1979年, 文献[1]和文献[2]分别提出了一种不同类型的保护方案——阈值方案, 一种针对公钥密码的方案。阈值方案的基本思想是创建消息的“阴影”(秘密), 有一定数量的阴影(称为阈值)可用, 然后可以检索消息, 表示为(m, n)阈值方案, 其中m为阈值, n为阴影的数量。秘密共享方案基本原理如图 1所示。



图 1 秘密共享方案的基本原理

1979年, 文献[1]提出了秘密共享方案。该方案基于多项式内插法: 设定S为秘密值的集合S={s1, s2, s3, …, sn}, 设f为秘密共享函数, f(x)=a0+a1x+…+ak-1xk-1, 使得f(0)=s, 计算s1=f(1), s2=f(2), …, sn=f(n), 然后将(i, si)(i=1, 2, 3, …, n)分给n个不同的参与者, 当掌握了任意t对(i, si)时, 就可以确定f(x)的系数, 从而确定秘密S; 当所掌握的(i, si)的数对少于t对时, 则无法确定S。

通常密钥是解密唯一的钥匙, 但如果密钥因为不可抗拒的原因, 出现消失或损坏, 那么就不能访问秘密S。然而, 通过秘密共享方案, 可以很好地解决这一问题。选取合适的t, 将其分散放置在每个参与者手中, 只要有大于或等于t个参与者共同参与访问秘密S, 那么秘密就可以被访问。但需要注意的是, 在使用文献[1]方法时要选择合适的t值。

与此同时, 文献[2]也提出了基于线性投影几何的秘密共享方案。它是一种概率性方法。文献[1]和文献[2]的方案奠定了门限方案的基础。

1.1 多秘密共享

1992年, 文献[3]提出了多秘密共享的应用场景: 有很多枚导弹, 每枚导弹都有自己的发射密码, 通过管理每枚导弹的发射密码, 使得导弹能够安全发射, 最简单的方案就是每枚导弹都进行一次秘密共享。该方案的缺点是, 参与者需要储存大量的秘密份额, 同时由于秘密份额的数量过多, 不方便管理。其优点是可以安全有效地管理导弹发射问题。但是秘密共享一次只能重构一个秘密, 当需要同时发射多枚导弹时, 会导致重构秘密效率太低。1994年, 文献[4]提出了基于单向函数的多阶段秘密共享方案(Multistage Secret Sharing Scheme), 解决了同时发射多枚导弹的问题, 可以—次共享多个秘密, 并且每个参与秘密重构的参与者只需要存储一个秘密份额。但使用该方案时, 重构秘密的顺序不能改变。为了优化上述方案, 1995年, 文献[5]提出了多秘密共享方案(Multi - secret Sharing Scheme), 重构秘密顺序可以发生改变, 分发者的秘密份额可以重复使用, 由此提高了共享秘密的效率。多秘密共享方案是秘密共享方案的改进。在一个秘密共享过程中共享多个秘密时, 最初的秘密共享就不能在此场景中使用。该方案也存在一些安全性问题。同一时间, 文献[6]提出了一种可验证秘密共享方案。该方案可交互且使用的是离散对数难解性算法, 实现了对秘密份额的验证, 提高了方案的安全性。2000年, 文献[7]提出了一种基于系统分组码的(t, n)门限多秘密共享方案。其优点是可以同时重构p(p>1)个秘密, 因此该方案一经提出, 便得到了广泛应用。在使用的过程中, 人们发现该方案计算量大, 需要解(n+p-t)联立方程, 而且秘密泄露问题频繁出现。2002年, 文献[8]提出了防欺骗的多秘密共享方案。该方案的结构是通过映射F: GF(pt)n→GF(pt)m定义的。该方案考虑了两种作弊策略以及两种不同的场景, 并计算出成功作弊的概率, 由此构造了防欺骗的多秘密共享方案。2004年, 文献[9]提出了一种基于文献[1]秘密共享的替代方案, 需要重构(t-1)或(p-1)次拉格朗日插值多项式。因此, 它比文献[7]的方案更容易计算。

2005年, 文献[10]提出的方案采用离散对数难解性算法进行秘密份额的验证, 提高了方案的安全性。2006年, 文献[11]提出了可验证的多重秘密共享方案, 参与者可以自己选择自己的秘密份额, 提高了秘密共享的效率, 因此该方案可以运用于更广泛的场景。2007年, 文献[12]提出了改进的多秘密共享方案, 继承上述方案的优点, 而且在共享秘密的过程中不需要安全传输信道, 其安全性得到了大幅度提升, 实际应用十分广泛。2008年, 文献[13]提出了一种新的基于文献[1]的门限多秘密共享方案。在该方案中, 为了共享p个秘密, 只需要t次拉格朗日插值多项式, 因此该方案比上述方案更容易计算, 特别是当p或n很大时。同年, 文献[14]提出了基于椭圆曲线的多秘密共享方案, 利用椭圆曲线上自配对的特点审查了方案的安全性; 文献[15-16]提出了可验证秘密共享方案, 将RSA加密技术应用到方案中, 以保护交互信息。

近年来, 文献[17]提出了基于同态性质的多秘密共享方案。该方案构造了一个(t-1)次的多项式, 使得n个参与者能够共享t个秘密。每个参与者只持有一份各自的秘密份额, 并使用自己的秘密份额按顺序恢复秘密, 利用同态性分享多个秘密并保证单个秘密不被泄露。文献[18]提出了加权门限多秘密共享方案, 设定了门限条件, n个参与者随机生成各自的秘密份额, 利用中国剩余定理(Chinese Remainder Theorem, CRT)计算出秘密份额的影子信息并验证其正确性即可恢复秘密。该方案极大地提高了秘密份额的安全性, 可以防止参与者利用其进行欺诈并使攻击者无法伪造。

各多秘密共享方案比较如表 1所示。

表 1 多秘密共享方案比较

下载CSV
方案 优点 缺点
基于单向函数的多阶段秘密共享方案[4] 一次共享多个秘密, 每个参与者存储一个秘密份额 恢复秘密顺序不可更改
基于单向函数的多秘密共享方案[5] 秘密份额可重复使用, 恢复秘密顺序无需固定 安全性不高
防欺骗的多秘密共享方案[8] 安全性较高 非动态秘密共享
门限多秘密共享方案[9] 高效地实现一次分享多个秘密 安全性不高
可验证多秘密共享方案[10] 避免份额欺骗 应用场景有限
可验证多重秘密共享方案[11] 应用场景广泛, 参与者可自行选择秘密份额, 秘密份额无需更新 传输信道安全性低
基于同态性质的多秘密共享方案[17] 多个秘密共享过程中单个秘密的保密性高 模型应用范围有限, 容错性低, 系统可用性低
加权门限多秘密共享方案[18] 秘密恢复过程中安全保密性高 计算量庞大

1.2 可验证秘密共享

可验证秘密共享(Verifiable Secret Sharing, VSS)是针对不诚实的参与者的。不诚实的参与者存在两种欺骗现象: 一种是恶意分发者分发不合法的秘密份额给参与者, 造成无法重构秘密; 另一种是恶意参与者提供非法的秘密份额, 破坏秘密恢复[19]。1985年, 文献[20]提出了可验证秘密共享方案的概念, 构造了一种新型认证算法。该算法具有交互式特点, 能够让所有人(包括未参与重构秘密的参与者)都可以对分发者分发的秘密份额进行验证, 提高了方案的安全性, 避免了恶意分发者泄露秘密。但是因为每个参与秘密重构的参与者都要与分发者信息交互以验证秘密份额是否合法, 因此该方案的效率较低[21]。1987年, 文献[22]提出了非交互式秘密共享方案, 但该方案是基于离散对数难解性设计的, 分发者会发布一个承诺信息, 而该承诺信息是一个藏有秘密的多项式, 每个参与秘密重构的人只需要验证该承诺信息即可, 这样就验证了份额的合法性。但是承诺信息一旦被泄露, 这个秘密将会被泄露。1992年, 文献[23]基于ElGarnal签名技术提出了高效安全的非交互式可验证秘密共享方案: 假设不诚实的分发者在不确定的多项式时间内分配不一致的秘密份额, 那么该方案就不会泄露任何关于秘密的信息。1996年, 文献[24]提出了基于ElGamal密码系统的可公开验证秘密共享方案。该方案解决了重构秘密效率低的问题, 提高了秘密分发者和参与重构秘密的人的安全性, 但缺点是秘密分发者存在欺骗导致不能重构秘密, 秘密份额不能实现更新。2011年, 文献[25]优化了该方案, 运用双线性变换的知识提出了可验证、可更新的秘密分享方案, 将验证密钥用于验证份额并更新秘密份额, 分发秘密的人分发秘密份额和密钥, 参与重构秘密的人验证秘密份额, 保证了秘密份额的安全性。经过验证, 该方案改进了以往方案的不足, 可以实现安全有效的秘密重构。

近年来, 有很多技术应用到秘密共享方案中, 例如基于离散对数、基于椭圆曲线加密(Elliptic Curve Cryptography, ECC)、基于CRT、基于RSA加密技术和单向加密、基于线性几何加密的方案等。

可验证秘密共享方案比较如表 2所示。

表 2 可验证秘密共享方案比较

下载CSV
方案 优点 缺点
交互式可验证秘密共享方案[20] 防止份额欺骗 效率低
非交互式可验证秘密共享方案[22] 效率高 承诺信息易被窃取
安全高效的非交互式可验证多秘密共享方案[23] 秘密重构效率高且安全性高 是否能够分享秘密取决于假设
可公开验证的秘密共享方案[24] 分发者和参与重构秘密的人无需安全信道, 可验证秘密份额的合法性 秘密分发者欺骗导致不能重构秘密, 秘密份额不能实现更新
可验证、可更新的秘密共享方案[25] 定期更新参与者的秘密份额并避免欺诈行为 初始阶段计算量大, 更新参与者复杂

1.3 无分发者秘密共享

在最初的秘密共享方案中, 包含分发者、参与者和秘密3个部分。分发者持有秘密并且可以决定每个参与者的秘密份额, 因此很容易受到恶意行为的危害。1985年, 文献[26]首次提出了无秘密分发者秘密共享(Dealer - free Secret Sharing), 但只提出了相关概念, 没有提出可实施的方案。1995年, 文献[27]提出了一种协议来构造秘密共享方案, 实现了任何访问结构, 而不需要经销商的帮助。简而言之, 在文献[27]的协议中, 制定一个公有的秘密共享方案共同使用, 再制定私有方案用于其他参与者之间共享信息。因此, 文献[27]方案也称为“民主秘密共享计划”。该方案持有份额的人无需分发者就可以生成秘密份额。民主的秘密共享只允许在参与者之间共享一个“随机”的秘密, 而在传统的秘密共享方案中, 经销商可以共享任何他想共享的秘密。1991年, 文献[28]提出了一种基于门限密码系统的无需分发者的门限秘密共享方案。该方案n个参与者共享一个组秘钥, 需要其中k个参与者联合参与方可破解密文。在该方案中, 参与者通过分发者生成对应的子秘密份额进行累加后可重构秘密。

1994年, 文献[29]提出了无需分发者的门限秘密共享技术, 并将该技术应用于群组签名方案中。此方案的特点是攻击者经过一次签名后就可以获取群组以及成员的私钥。实施秘密共享计划的一个重要问题是分配给参与者的股份的大小, 可以想象, 一部分参与者可能会试图欺骗, 也就是说, 通过谎报他们所拥有的股份来欺骗任何其他参与者。2003年, 为了解决签名后份额持有者的私钥泄露, 文献[30]提出了基于联合秘密共享技术的(t, n)门限签名方案。因为系统的安全性随着必须保密的信息数量的增加而降低, 如果成功作弊的概率被限制在指定的概率范围内, 即使假定作弊者拥有无限的计算资源, 阈值秘密共享方案也被认为是无条件安全的, 所以可以防止作弊。2008年, 文献[31]提出了无需分发者且可验证份额的秘密共享方案, 是第一个基于CRT的联合随机秘密共享方案。在该方案中, 参与者们联合生成和共享一个秘密并且在秘密分发阶段不使用可信的分发器。2011年, 文献[32]在文献[2]的线性投影几何的基础上, 首次提出了基于线性投影无需分发者的秘密共享方案。该方案利用安全标量积协议和其他安全多方计算的基本协议, 达到了通信低和计算简便的目的, 同时避免了参与者的欺诈行为。2015年, 文献[33]提出了基于CRT的无需分发者且可验证份额的门限秘密共享方案。该方案中, 参与者通过分享秘密份额影子得到属于自己的秘密份额, 并且通过验证秘密份额影子避免了参与者间的欺诈, 在秘密分享阶段不需要可信中心。之后, 为了解决密钥泄露的情况, 文献[34]运用同态秘密共享技术提出了无需分发者的群组密钥生成方案, 既可以协同生成秘密份额, 又可以保护密钥不被泄露。

无分发者的秘密共享方案比较如表 3所示。

表 3 无分发者秘密共享方案比较

下载CSV
方案 优点 缺点
无需分发者的门限秘密共享方案[28] 秘密分发过程无需可信中心 秘密重构阶段有可信中心参与, 会泄露参与者信息
门限秘密共享技术的群组签名方案[29] 防止恶意分发者泄露秘密 一次签名后, 恶意攻击者将会获取群组和成员的私钥
无可信中心的(t, n)门限签名方案[30] 防止签名后参与者的私钥泄露 份额易被恶意份额持有者欺骗
无需分发者且可验证份额的秘密共享方案[31] 可验证秘密份额的合法性 需要可信中心参与验证, 但可信中心存在安全性问题
基于线性投影无需分发者的秘密共享方案[32] 通信低、计算简便, 防止参与者欺诈, 新参与者可加入 尚未开展签名算法的应用研究
无需分发者且可验证份额的门限秘密共享方案[33] 避免了交互过程中欺骗行为, 计算效率高 在验证过程中每个参与者公开了验证信息
基于同态秘密共享无需分发者的群组密钥生成方案[34] 无需分发者, 可生成对应秘密份额, 不泄露密钥, 实用性高 多个秘密做乘法运算, 计算量大, 效率低

1.4 可安全重构秘密共享

门限秘密共享的重点在于秘密重构阶段, 即设置阈值K, 当参与者拥有的秘密份额满足阈值K或者远大于阈值K时, 参与者就可以重构秘密。然而在此过程中, 参与重构秘密的人都可以得知其余参与者的秘密份额。当参与者中有攻击者时, 攻击者可以通过获取其他持有者的份额, 进而恢复秘密, 造成秘密泄露。当K个参与者参与恢复秘密时, 攻击者会提供非法的秘密份额使得其他(K-1)个参与者无法重构秘密, 但是攻击者可以通过私有份额和(K-1)个参与者成功地重构秘密。

当大于K个参与者参与秘密恢复时, 攻击者会伪装成合法的K个参与者参与秘密重构。可验证秘密共享方案可以验证秘密份额的有效性, 当秘密份额出现问题时, 可找出恶意攻击者。但是攻击者已经骗取的合法秘密份额会帮助攻击者重构秘密。因此, 为了优化可验证秘密共享方案, 2014年, 文献[35]提出了可安全重构秘密的共享方案。该方案基于拉格朗日元件, 通过秘密份额和其他持有者的多项式代入值, 即(x, y)中x的值, 以及一些其他信息生成拉格朗日元件; 然后验证每个参与者的拉格朗日元件的有效性, 当都有效时, 即可恢复秘密。此方案在提高方案安全性的同时, 解决了可验证秘密共享方案存在的问题。

1.5 主动式秘密共享

秘密共享技术可以有效地提高秘密的安全性, 但在保存私钥的过程中, 会因为保存私钥时间过长, 导致秘密泄露。1991年, 文献[36]提出了主动式秘密共享(Proactive Secret Sharing)。在该方案中, 将保护秘密时间分成不同阶段, 每个阶段所分配给参与者的秘密份额不同, 这样就可以解决因为保存秘密时间过长而给恶意攻击者时间, 导致秘密泄露这一缺点。1995年, 文献[37]提出了主动秘密分享方案。该方案实现了定时更新份额, 但份额持有者的互相欺骗会导致秘密泄露。2002年, 文献[38]提出了额定更新防欺诈方案, 使用的是离散对数难解性算法, 避免了由于参与者相互欺骗致使秘密泄露的问题。该方案的缺点是在秘密分享的过程中分发者需要全程参与, 而恶意攻击者会根据这一特点攻击该方案。为了改善上述方案, 2004年, 文献[39]提出了一种主动式秘密共享的方案, 具有异步模式的特点, 拓宽了主动式秘密共享的可应用场景, 表明实际环境中份额持有者会加入或离开系统。为了解决这一问题, 近期又有研究者提出了份额持有者可变的主动式秘密共享方案[40]。

2 秘密共享实际应用

2.1 在电子投票中应用

电子投票是指将计算机的网络技术和密码学进行融合, 能智能地完成投票和统计票数等环节的工作。电子投票可以大量减少人为因素, 弥补传统人工投票的不足。现代安全的电子投票方式需要满足以下特征: 电子选票的隐私性, 系统的稳固性、方便性、高效性和普遍验证性, 选民的身份合法性和投票不重复性, 计票的公平性和完整性。目前网络攻击者的数量和手段日益增多, 因此电子投票的安全性需要不断加强, 需要设计出更安全的电子投票方案。

电子投票采用的信息安全技术方案主要有混合网络(Mix - net)、盲签名(Blind Signature)、同态加密(Homomorphic Encryption)和秘密共享弥补4种。上述各项方案的优缺点可以概括为: 混合网络方案可以基本保证选票加密的错误率大大降低[41], 但不能实现对算法的简化、对计算量的减少, 因此只局限于小规模的投票; 盲签名方案主要包括FOO[42]和REVS[43]等, 但在实践中很少使用, 原因是该方案不能对投票结果相同的选票进行计票, 并且投票者操作该方案较为复杂。相比于前两种方案, 同态加密方案可以提高选票的安全性, 但其加解密选票过程复杂, 影响选票的数据处理, 耗费了大量时间, 十分低效。相较于前3种方案, 秘密共享方案整个系统的安全性更强, 选票的数据处理更高效, 且避免了前3种方案的局限性, 可行性更高, 因此秘密共享方案是电子投票领域研究的热点。

在电子投票中应用秘密共享技术方案, 就是将一个储存全部选票信息的机构分配给不同的储存设备, 每个设备分配到不同份额的投票信息, 不同设备中的选票份额可以用于恢复全部选票信息。这种策略具有较高的安全性, 同时避免了人为修改选票结果的恶意影响, 减少了信息的储存空间。现有的秘密共享方案都是以文献[1]的秘密共享研究为主。其秘密共享的核心就是把选票分成许多个不同的份额, 要想恢复原先分解前的选票原信息仅仅靠某几个碎片份额即可。

文献[44]证明了文献[1]秘密共享方案将选票拆分出的不同份额的无误性, 杜绝了人为因素修改选票信息而带来的作弊现象, 提高了电子投票的安全性; 同时, 基于文献[1]秘密共享拥有动态加密性的优势, 提出了秘密计票的方式, 更加确保了保密性。文献[45]证明了文献[1]秘密共享的公开可验证性, 同样确保了选票分享出的碎片份额的无误。文献[46]在文献[1]秘密共享方案的基础上, 对选票在进行拆分份额的步骤前, 先应用El - Gamal加密体制对其进行加密, 再将不同的份额分发出去, 这样, 储存选票碎片的机构就可以直接跳到解密过程, 得到选票的完整信息。该方案省去了中间大量的计算过程和时间。文献[47]以秘密承诺及文献[1]秘密共享为基础, 设计了一个电子投票的方案, 核心是将选票的数据表述为多项式的形式, 同时选民也要做出承诺, 再运用文献[1]秘密共享将选票拆分储存到不同的设备中, 设备计算出选民承诺的总和, 再运用文献[1]秘密共享的解密步骤得到原选票的数据, 并同时完成计票工作。文献[48]结合同态运算, 并采用竞选中候选人的票数代替文献[1]秘密共享门限方案中的拉格朗日插值公式中的系数, 证明了投票结果的无误。

但是, 由于网络上黑客数量和手段的日益增多, 产生了诸多大规模电子投票的恶意攻击事件, 造成了大量选票信息修改和丢失的现象, 进而人为地改变了计票的结果。由此可见, 文献[1]秘密共享方案已无法确保电子投票的安全性和公平性; 而且, 文献[1]秘密共享方案存在诸多缺点: 一是该方案中储存选票碎片的设备越多, 拉格朗日插值多项式的次数就越高, 即大规模电子投票存储设备数量众多, 导致其加解密过程极其复杂且耗时太久; 二是大规模电子投票的选票碎片数据存储量巨大, 容易造成数据容灾的后果; 三是该方案在验证计票结果阶段的计算相当繁琐和复杂, 效率较低。

除了上述基于文献[1]秘密共享方案的电子投票外, 还有基于CRT的秘密共享方案[49]。文献[50]在CRT的基础上, 提出了可以检测秘密共享阈值方案, 与拉格朗日插值多项式相比, 该方案计算便捷, 更加高效。文献[51]在CRT的基础上, 提出了通用的权重阈值方案。文献[52]基于CRT, 提出了Mignotte数列的可验证秘密共享。CRT方案的选票加解密过程是累乘计算存储设备中的选票份额, 类似于拉格朗日插值多项式, 但在大规模电子投票中存在计算复杂、效率低下和数据容灾的缺点。

文献[53]构造了GF(2)上的校验矩阵的方案, 利用了随机线性分组码(Random Linear Block Code, RLBC)的秘密共享方法。其优点在于加解密过程中的方程组系数矩阵的列大概率满秩, 大大减少了计算过程的复杂度和验证阶段的困难度, 同时减少了碎片数据的冗余数量, 解决了大量占用网络带宽和存储空间的问题, 提高了大规模电子投票的效率。文献[54]基于新型的安全多方计算(Secure Multiparty Computation, SMC)协议, 设计了一种新型密码技术, 构造了一种新型的多选多选票结构方案。该方案使用线性迭代计算方法, 适用于大规模、多层次的选举情况, 能有效地解决电子选举中的作弊问题, 实现了电子选举的公平性和安全性。

此外, 文献[55]构造了一种新型多选多选票结构, 基于新型的安全多方计算[56], 采用无通信协议[57], 可以应用于大规模多候选人电子投票实践中, 同时该方案可以满足无收据性和无争议性, 可以实现电子选举的公平性和安全性。

2.2 在数字图像中应用

目前用于数字图像处理的软件有Photoshop和Microsoft Paint等。由于产品软件的不断更新和发展, 人们对于获取图像信息的要求越来越高[58], 图像信息的获取及传输达到了前所未有的深度和广度, 随之带来的信息泄密、网络犯罪以及网络入侵等事件时有发生[59], 也就是说, 数字图像在传输和储存过程中是不安全、不可信的, 加解密数字图像的成功与否不仅对个人信息安全有影响, 而且还涉及到国家网络安全[60], 因此深入研究加解密数字图像意义重大。秘密共享方案已拓展应用到图像领域, 利用该技术分享图像时, 可以保证图像的安全性和完整性[55]。

目前对于数字图像的渐进式可视秘密共享算法存在以下问题: 一是它不支持文献[1]的门限秘密共享方案; 二是其恢复数字图像的能力有限; 三是像素扩展太大。文献[61]提出了一种渐进式可视秘密分享算法, 并在此基础上实现了影子图像可理解的具有多解密能力的渐进式秘密分享算法。通过实验和分析表明: 相比传统可视秘密分享方案, 优点在于加解密数字图像过程计算量小并且能够保护数字图像的细节, 即做到了无损恢复。

文献[62]采用随机数产生像素的技巧进行了图像编码, 针对彩色图像提出了(n, n)图像秘密共享和通用型存取结构及扩充型的算法。在不需要建置基本加密矩阵的前提条件下, 建立视觉秘密共享机制产生随机数的像素技巧进行图像编码, 以产生不需扩展的秘密共享图像的投影片。该算法保持了每个像素点的色彩发生的特定概率, 使得在此概率下所建置成的秘密共享图像在迭合过程中仍可识别出秘密图像, 为秘密共享在数字图像的处理上开拓了新的尝试。

文献[63]详细研究了数字图像秘密共享方案, 并对文献[1]的(r, n)门限秘密共享的基本原理进行了简要概述, 发现使用该方案分享影子图像与原图像的大小一样, 在分享过程中所占用的存储空间较大。为了更好地解决这一缺点, 提出了新的数字图像秘密共享方案, 并证明了该方案的正确性。在该方案中, 影子图像拥有一个属于自己的像素, 影子图像在传输时占用空间减小, 解决了数字图像在分享时内存占用率大的问题。因此, 文献[63]提出的新数字图像秘密共享方案相比于传统的方案更加便于存储和分享。

对于现有的一些应用于图像分享的算法, 文献[58]发现, 当认证码的二进制比特数超过2位时, 这些方案在数字图像恢复后会产生失真。为了提高算法处理后所生成图像的品质, 其利用隐写技术(Exploiting Modification Direction, EMD), 并应用于绝对矩分块截断编码中, 提出了一个适用于绝对矩分块截断编码压缩图像的图像认证方案。经过实验验证后发现, 生成的图像品质得到了很大程度的提升。同时, 利用(n, k)汉明码矩阵嵌入的方法改进了文献[1]的多项式秘密共享方案, 这是一种具有认证能力的自适应的(k, n)门限的秘密共享方案。应用该方案, 碎片图像的品质有了明显改善。同时考虑到该方案的可靠性, 生成认证码仍然使用哈希运算消息认证码(Hash - based Message Authentication Code, HMAC) 的方法, 但由于认证码的长度会影响认证时间, 所以充分增加认证码的长度能够明显缩短认证时间。

对于图像分享的可视多秘密分享方案, 文献[64]提出了具有伪装图像的双秘密图像可视分享方案。在图像分享过程中, 该方案采用图像翻转以实现图像分享, 通过分享后的图像叠加来重构秘密图像。

2.3 在生物特征中应用

将生物特征模板存储于特征数据库中, 当需要进行特征认证时, 可以提供有效帮助。但是特征模板未加密直接储存在数据库中, 容易泄露信息, 安全性不高, 因此对于生物特征的保护变得越来越重要。在保护生物特征上, 秘密共享技术可以保证其安全性和可靠性, 具有非常良好的应用前景。

为了使生物特征模板得到安全储存和可靠保护, 文献[65]利用文献[1]的(t, a)门限秘密共享方案, 提出了一种新的基于秘密分享的生物特征模板保护及存储方案。针对生物特征引入哈希函数[66], 进行单向压缩, 经过处理和实验分析后, 得出该方案可使系统更加安全可靠, 且拥有可靠的数据容灾与恢复能力。该方案可使秘密共享技术在生物特征存储和保护的应用上更加可靠和安全。

秘密共享技术应用于生物特征的秘密存储保护方面具有很大的优势[66]。文献[67]提出了基于秘密共享技术的模板参数管理方案(Secret Sharing Scheme - based Parameter Management, SPM), 将秘密共享技术添加于原有的管理方案上, 主要表现在注册和认证阶段中, 结合(c, n)门限方案提出了SPM方案; 并通过实验验证了SPM在生物特征的存储上有很好的保护作用, 避免了黑客的恶意攻击, 同时也为生物特征模板的保护提供了新的思路。

3 结语

本文从多秘密共享、可验证秘密共享、无分发者秘密共享、可安全重构秘密共享、主动式秘密共享5个方面归纳总结了秘密共享技术的发展。在每个方面, 秘密共享方案得到了不断的优化, 以提高秘密共享效率及其安全性。需要注意的是, 对于不同的秘密共享场景, 所构造的秘密方案也是不同的, 因为不同的应用场景所需要的秘密保护的侧重点不同。此外, 本文列举了秘密共享技术在电子投票、数字图像、生物特征3个方面的应用。未来, 应将秘密共享技术多多应用于实例场景中进行研究, 通过解决新问题, 进一步优化秘密共享方案, 拓宽其应用范围。

参考文献

  • [1]
    SHAMIR A. How to share a secret[J]. Communication of the ACM, 1979, 22(11): 612-613. DOI:10.1145/359168.359176
  • [2]
    BLAKLEY G R. Safeguarding cryptographic keys[C]//Afips IEEE Computer Society, 1979: 242-268.
  • [3]
    SIMMONS G J. An introduction to shared secret and/or shared control schemes and their application[M]//Contemporary Cryptology: The Science of Information Integrity. Wiley-IEEE Press, 1992: 441-497.
  • [4]
    HE J, DAWSON E. Multistage secret sharing based on one-way function[J]. Electronics Letters, 1994, 30(19): 1591-1592. DOI:10.1049/el:19941076
  • [5]
    HE J, DAWSON E. Multi-secret sharing scheme based on one-way function[J]. Electronics Letters, 1995, 31(2): 93-95. DOI:10.1049/el:19950073
  • [6]
    HARN L. Efficient sharing (broadcasting) of multiple secrets[J]. IEEE Proceedings-Computers and Digital Techniques, 1995(3): 237-240.
  • [7]
    CHIEN H Y, JINN-KE J, TSENG Y M. A practical (t, n) multi-secret sharing scheme[J]. Ieice Transactions on Fundamentals of Electronics Communications and Computer Sciences, 2000, 83(12): 2762-2765.
  • [8]
    PIEPRZYK J, ZHANG X M. Multisecret sharing immune against cheating[J]. Informatica, 2002, 26(3): 271-278.
  • [9]
    YANG C C, CHANG T Y, HWANG M S. A (t, n) multi-secret sharing scheme[J]. Applied Mathematics and Computation, 2004(2): 483-490.
  • [10]
    SHAO J, CAO Z. A new efficient (t, n) verifiable multi-secret sharing (VMSS) based on YCH scheme[J]. Applied Mathematics and Computation, 2005(1): 135-140.
  • [11]
    庞辽军, 姜正涛, 王育民. 基于一般访问结构的多重秘密共享方案[J]. 计算机研究与发展, 2006, 43(1): 33-37.
  • [12]
    ZHAO J, ZHANG J, ZHAO R. A practical verifiable multi-secret sharing scheme[J]. Computer Standards & Interfaces, 2007, 29(1): 138-141.
  • [13]
    IBRAHIM M H. Efficient incoercible and universally verifiable multi-authority Yes/No-voting scheme[C]//The 6th International Conference on Informatics and Systems. Cairo, Egypt: INFOS, 2008.
  • [14]
    LIU D, HUANG D P, LUO P, et al. New schemes for sharing points on an elliptic curve[J]. Computers & Mathematics with Applications, 2008, 56(6): 1556-1561.
  • [15]
    DEHKORDI M H, MASHHADI S. An efficient threshold verifiable multi-secret sharing[J]. Computer Standards & Interfaces, 2008, 30(3): 187-190.
  • [16]
    DEHKORDI M H, MASHHADI S. New efficient and practical verifiable multi-secret sharing schemes[J]. Information Sciences, 2008, 178(9): 2262-2274. DOI:10.1016/j.ins.2007.11.031
  • [17]
    LIN C L, HARN L. Unconditionally secure multi-secret sharing scheme[C]//2012 IEEE International Conference on Computer Science and Automation Engineering. Zhangjiajie, China, 2012: 169-172.
  • [18]
    邹惠, 王建东, 宋超. 加权门限多秘密共享方案[J]. 计算机工程, 2012, 38(3): 148-149.
  • [19]
    张艳丽, 张建中. 椭圆曲线上的可验证多秘密共享方案[J]. 计算机工程, 2011, 37(3): 124-125.
  • [20]
    CHOR B, GOLDWASSER S, MICALI S, et al. Verifiable secret sharing and achieving simultaneity in the presence of faults[C]//26th Annual Symposium on Foundations of Computer Science. Portland, OR, USA, 1985: 383-395.
  • [21]
    王永. 可验证多秘密共享的研究及应用[D]. 苏州: 苏州大学, 2010.
  • [22]
    FELDMAN P. A practical scheme for non-interactive verifiable secret sharing[C]//28th Annual Symposium on Foundations of Computer Science. Los Angeles, CA, USA, 1987: 427-438.
  • [23]
    PEDERSEN T P. Non-interactive and information-theoretic secure verifiable secret sharing[C]//11th Annual International Cryptology Conference. Santa Barbara, California, USA, 1991: 129-140.
  • [24]
    STADLER M. Publicly verifiable secret sharing[C]//Proceeding of the 15th Annual International Conference on Theory and Application of Cryptographic Techniques. Zaragoza, Spain, 1996: 190-199.
  • [25]
    肖艳萍. 可验证可更新的秘密共享方案[D]. 长沙: 长沙理工大学, 2012.
  • [26]
    MEADOWS C. Some threshold schemes without central key distributors[J]. Congressus Numerantium, 1985, 46: 187-199.
  • [27]
    INGEMARSSON I, SIMMONS G J. A protocol to set up shared secret schemes without the assistance of a mutually trusted party[C]//Proceedng of the Workshop on the Theory and Application of Cryptographic Techniques. Aarhus, Denmark, 2006: 266-282.
  • [28]
    PEDERSEN T P. A threshold cryptosystem without a trusted party[C]//Proceedings of the 10th Annual International Conference on Theory and Application of Cryptographic Techniques. Brighton, UK, 1991: 522-526.
  • [29]
    HARN L. Group-oriented (t, n) threshold digital signature scheme and digital multisignature[J]. IEE Proceedings-Computers and Digital Techniques, 1994, 141(5): 307-313. DOI:10.1049/ip-cdt:19941293
  • [30]
    王斌, 李建华. 无可信中心的(t, n)门限签名方案[J]. 计算机学报, 2003, 26(11): 1581-1584.
  • [31]
    KAYA K, SELCUK A A. A verifiable secret sharing scheme based on the chinese remainder theorem[C]//9th Annual International Conference on Cryptology. Kharagpur, India, 2008: 414-425.
  • [32]
    XUE Y, WU S, CHEN H. A blakley secret sharing scheme without trusted share distributed, center[C]//2011 Seventh International Conference on Computational Intelligence and Security. Hainan, China, 2011: 612-614.
  • [33]
    杨阳, 朱晓玲, 丁凉. 基于中国剩余定理的无可信中心可验证秘密共享研究[J]. 计算机工程, 2015, 41(2): 122-128.
  • [34]
    HAM L, HSU C F, LI B H. Centralized group key establishment protocol without a mutually trusted third party[J]. Mobile Networks and Applications, 2016, 23(6): 1-9.
  • [35]
    HARN L. Secure secret reconstruction and multi-secret sharing schemes with unconditional security[J]. Security and Communication Networks, 2014, 7(3): 567-573. DOI:10.1002/sec.758
  • [36]
    OSTROVSKY R, YUNG M. How to withstand mobile virus attacks[C]//Tenth Annual ACM Symposium on Principles of Distributed Computing. Montreal, Que, Canada, 1991: 51-59.
  • [37]
    HERZBERG A, JARECKI S, KRAWCZYK H, et al. Proactive secret sharing or: how to cope with perpetual leakage[C]//Proceeding of the 15th Annual International Cryptology Conference on Advances in Cryptology. Santa Barbara, California, USA, 1995: 339-352.
  • [38]
    许春香, 魏仕民, 肖国镇. 定期更新防欺诈的秘密共享方案[J]. 计算机学报, 2002, 25(6): 657-660.
  • [39]
    郭渊博, 马建峰. 异步及不可靠链路环境下的先应式秘密共享[J]. 电子学报, 2004, 32(3): 399-403.
  • [40]
    SCHULTZ D, LISKOV B, LISKOV M. Mobile proactive secret sharing[J]. Acm Transactions on Information and System Security, 2010, 13(4): 458-458.
  • [41]
    JAKOBSSON M, JUELS A, RIVEST R L. Making mix nets robust for electronic voting by randomized partial checking[C]//Proceedings of the 11th USENIX Security Symposium. San Francisco: USENIX, 2002: 339-353.
  • [42]
    FUJIOKA A, OKAMOTO T, OHTA K. A practical secret voting scheme for large scale elections[C]//Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques. Berlin: Springer, 1992: 244-251.
  • [43]
    JOAQUIM R, ZUQUETE A, FERREIRA P. REVS—a robust electronic voting system[J]. IADIS International Journal on WWW/Internet, 2003, 1(2): 47-63.
  • [44]
    BENALOH J C. Secret sharing homomorphisms: keeping shares of a secret (extended abstract)[C]//Conference on the Theory and Application of Cryptolographic Thehniques. Berlin: Springer, 1986: 251-260.
  • [45]
    SCHOENMAKERS B. A simple publicly verifiable secret sharing scheme and its application to electronic voting[C]//Annual International Cryptology Conference. Berlin: Springer, 1999: 148-164.
  • [46]
    李彦江, 马传贵, 黄刘生. 一种电子投票方案[J]. 软件学报, 2005, 16(10): 1805-1810.
  • [47]
    CRAMER R, GENNARO R, SCHOENMAKERS B. A secure and optimally efferent multi-authority election scheme[J]. European Transactions on Telecommunications, 1997, 8(5): 481-490. DOI:10.1002/ett.4460080506
  • [48]
    LIU Y N, ZHAO Q Y. E-voting scheme using secret sharing and K-anonymity[J]. World Wide Web, 2019, 22(4): 1657-1667. DOI:10.1007/s11280-018-0575-0
  • [49]
    刘文杰. 图像秘密共享的研究与应用[D]. 太原: 太原科技大学, 2014.
  • [50]
    ASMUTH C, BLOOM J. A modular approach to key safeguarding[J]. IEEE Transactions on Information Theory, 1983, 29(2): 208-210. DOI:10.1109/TIT.1983.1056651
  • [51]
    IFTENE S. General secret sharing based on the Chinese remainder theorem with applications in e-voting[J]. Electronis Notes in Theoretical Computer Science, 2007, 186: 67-84.
  • [52]
    YUAN L F, LI M C, GUO C, et al. A verifiable E-voting scheme with secret sharing[J]. International Journal of Network Security, 2017, 19(2): 260-271.
  • [53]
    刘霆, 崔喆, 蒲泓全, 等. 基于随机线性分组码的秘密分享在电子投票中的应用[J]. 工程科学与技术, 2019, 51(6): 175-181.
  • [54]
    段德伟. 安全电子选举系统的设计与实现[D]. 成都: 电子科技大学, 2014.
  • [55]
    赵瑞. 基于安全多方计算的电子选举系统设计与实现[D]. 武汉: 华中科技大学, 2008.
  • [56]
    许春香. 安全秘密共享及其应用研究[D]. 西安: 西安电子科技大学, 2003.
  • [57]
    祁明, 肖国镇. 一个适合大规模电子选举的秘密投票方案[J]. 电子科学学刊, 1997, 19(5): 717-720.
  • [58]
    刘海泉. 图像认证技术的研究与应用[D]. 合肥: 安徽大学, 2016.
  • [59]
    李鹏. 图像秘密共享方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2012: 1-12.
  • [60]
    王永. 可验证多秘密共享的研究及应用[D]. 苏州: 苏州大学, 2010.
  • [61]
    闫雪虎. 渐进式图像秘密分享关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
  • [62]
    陈亚丽. 基于随机数的图像信息秘密分享技术[J]. 现代电子技术, 2007(11): 88-91.
  • [63]
    赵真非. 数字图像秘密分享技术的研究[J]. 中小企业管理与科技(下旬刊), 2016(12): 196-197.
  • [64]
    王洪君, 刘毅, 苑卫鑫. 具有伪装图像的可视双秘密分享[J]. 吉林大学学报(理学版), 2015, 53(6): 1251-1256.
  • [65]
    袁德砦. 基于秘密分享的生物特征模板保护及存储方案[J]. 计算机应用研究, 2018, 35(5): 1545-1549.
  • [66]
    张宁, 藏亚丽, 田捷. 生物特征与密码技术的融合——一种新的安全身份认证方案[J]. 密码学报, 2015, 2(2): 159-176.
  • [67]
    王金海, 李雪妍, 崔军, 等. 基于秘密共享的生物特征模板参数管理[J]. 天津工业大学学报, 2016, 35(6): 73-77.