|
|
|
发布时间: 2022-04-25 |
综合能源管理 |
|
|
|
收稿日期: 2021-08-30
基金项目: 国家自然科学基金青年科学基金(51906133);上海市2019年度"科技创新行动计划"高新技术领域项目(19511103700)
中图法分类号: TM621
文献标识码: A
文章编号: 2096-8299(2022)02-0112-07
|
摘要
为解决供热抽汽改造导致的发电机组热电耦合及非线性问题, 提高系统自动发电控制(AGC)跟随能力, 提出了用于解耦控制的前馈补偿解耦算法, 并对解耦后的电功率控制回路设计了基于模糊算法的模糊比例-积分-微分(PID)控制器。仿真结果表明, 利用前馈解耦算法与模糊算法相结合的方案有较好的解耦效果, 并能有效优化AGC跟踪能力, 提高系统控制性能。
关键词
供热改造; 自动发电控制; 解耦控制
Abstract
In order to solve the thermoelectric coupling and non-linear problems of the generator set caused by the reform of heating extraction steam, and improve the automatic generation control (AGC) following ability of the system, a feedforward compensation decoupling algorithm for decoupling control is proposed.After decoupling the electric power control loop, a fuzzy proportion integration differentiation(PID) controller based on fuzzy algorithm is designed.The simulation shows that the combination of the feedforward decoupling algorithm and the fuzzy algorithm has a better decoupling effect and can effectively optimize the AGC tracking ability and improve the system control performance.
Key words
heat supply renovation; automatic generation control; decoupling control
随着能源利用环境的变化, 通过技术改造提高能源利用效率的方案得到广泛应用, 传统发电站通过对发电机组进行供热抽汽改造可以有效提高能源的利用率[1]。但是抽汽供热改造后, 汽轮机中、低压缸进汽量发生变化, 存在强热电耦合特性[2], 对机组的自动发电控制(Automatic Generation Control, AGC)跟踪能力造成了影响。针对这种现象, 文献[3]提出为热电联产机组设计配套蓄热罐及升压设备, 在电网高峰时段充分蓄热, 在电力负荷较低时释放热量进行对外供热。文献[4]通过配置蓄热罐、电蓄热锅炉的方式, 在东北地区供热机组运行方式中计算风电消纳能力和煤耗水平, 起到了热电解耦的作用。但储热设备的建设和维护加大了经济投入和人力维护成本, 收回成本所需的时间难以估计。从节约成本及缩短建设周期的角度出发, 直接从控制系统优化的方向解决供热改造后AGC跟踪问题是非常必要的。为了消除热负荷变动对发电侧的影响, 可采用解耦控制系统。目前, 常用的解耦方法有完全对角矩阵解耦、智能解耦、前馈补偿解耦等[5]。其中, 完全对角矩阵解耦由于自身的原理特性, 在面对复杂耦合关系时, 计算较为困难, 且得到的解耦控制器维数较高, 在实际运用时需要进行简化处理[6-8]。智能解耦算法过于复杂, 导致计算时间较长, 失去了实时性, 在工程上难以应用[9]。前馈补偿解耦的理论和结构相对简单, 其结构只与控制对象相关, 对其他环节影响较小, 适用于工程实际[10]。
由于抽汽供热会造成机组发电侧被控对象特性非线性, 导致常规控制方法控制效果不佳, 因此需要设计一种针对外界干扰和对象不确定性的控制器。针对非线性问题, 不断发展的智能控制成为解决问题的理想方式, 现在主流的智能控制方式有神经网络控制、专家系统控制、模糊控制等。但是, 神经网络控制存在实时性问题[11]。专家系统中专家经验获取较难且需要根据特性变化扩充知识库[12], 均不适用于机组控制需求。模糊算法不要求被控对象的精确数学模型, 适用于解决常规控制难以解决的非线性时变问题[13]。采用模糊控制算法在线实时修正比例-积分-微分(Proportion Integration Differentiation, PID)控制器的参数, 可适应被控对象参数的变化: 文献[14]使用模糊控制器与PI控制器并行对核电站冷却剂平均温度进行控制, 起到了优化控制效果的作用; 文献[15]采用模糊控制器使核电站稳压器压力控制系统性能得到了明显改善; 文献[16]利用模糊自整定控制器, 对火电厂主汽温控制系统进行控制, 提高了响应速度, 减小了超调量。以上研究结果说明, 模糊控制能广泛应用于核电站、火电厂等工业控制。本文设计了一种用于解除热电间耦合作用的前馈补偿解耦控制器, 为解耦后的电功率控制回路设计了一种能够自动修正PID参数的模糊PID控制器, 以提高抽汽后机组AGC跟随能力。仿真结果表明, 在这2种控制器的共同作用下, 能够保证实现较好的解耦效果, 提高系统的控制性能, 优化对AGC指令的跟随效果。
1 热电耦合特性及解耦控制器设计
1.1 热电耦合特性分析
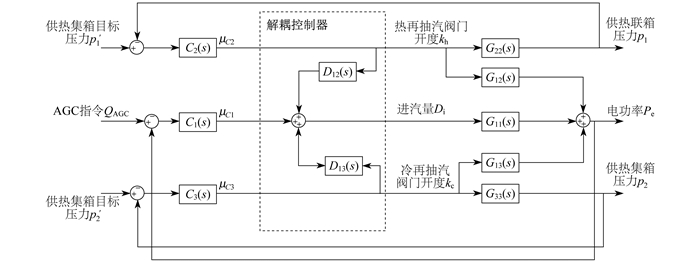
某电厂发电机组进行了供热抽汽改造。改造方案为: 从高压缸和中压缸间、再热器前后分别接出供热抽汽管道, 通过冷再热抽汽(以下简称“冷再”)和热再热抽汽(以下简称“热再”)2种方式对热网用户供热。本文采用抽汽式汽轮机的简化模型, 机组供热供电流程结构如图 1所示。
由锅炉产生的高压蒸汽首先进入高压缸; 完成做功后, 经锅炉再热器, 送入中压缸; 在中压缸完成做功后, 进入低压缸。
由于抽汽供热会影响进入中、低压缸的蒸汽量, 所以会导致供热与电功率之间存在耦合关系。当热负荷增大时, 抽汽蝶阀开度增大, 抽汽量增加, 导致进入中低压缸的蒸汽量减少, 发电功率降低。其中, 冷再和热再分别供给不同用热对象, 2种抽汽模式之间互不影响。
通过调节冷再和热再的抽汽阀门分别对供热联箱和供热集箱供热, 通过集箱对外供热压力指令控制阀门开度, 并影响供热联箱和供热集箱的实际压力。因此, 可将该系统看作是一个三输入三输出耦合系统。输入为进汽量、热再抽汽阀门开度、冷再抽汽阀门开度; 输出为电功率、供热联箱压力、供热集箱压力。
供热抽汽量由供热抽汽阀门开度决定, 受高压缸进汽量的影响较小, 可将该系统的耦合视为热负荷变动导致电功率变化的单向耦合。
此时, 系统的耦合模型表示为
| $ \left[ {\begin{array}{*{20}{c}} {{P_{\rm{e}}}}\\ {{p_1}}\\ {{p_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{G_{11}}(s)}&{{G_{12}}(s)}&{{G_{13}}(s)}\\ 0&{{G_{22}}(s)}&0\\ 0&0&{{G_{33}}(s)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{D_{\rm{i}}}}\\ {{k_{\rm{h}}}}\\ {{k_{\rm{c}}}} \end{array}} \right] $ | (1) |
式中: Pe——机组电功率;
p1, p2——供热联箱压力和供热集箱压力;
G11(s), G22(s), G33(s)——主控通道;
s——拉普拉斯算子;
G12(s), G13(s)——耦合通道;
Di——汽轮机进汽量;
kh, kc——热再阀门开度和冷再阀门开度。
1.2 前馈补偿解耦控制
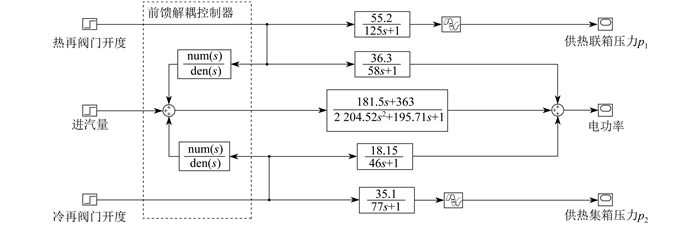
以该机组热电耦合关系建立前馈补偿控制模型, 如图 2所示。
图 2中, AGC指令QAGC和供热目标压力信号(p′1和p′2)为输入信号; 电功率Pe和供热压力(p1和p2)为输出信号; C1(s), C2(s), C3(s)为系统的控制器; μC1, μC2, μC3为控制器输出信号; D12(s), D13(s)为前馈解耦控制器。
此时, 控制器输出信号μC1, μC2, μC3与系统输出量(Pe, p1, p2)的关系式为
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{l}} {{P_{\rm{e}}}}\\ {{p_1}}\\ {{p_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{G_{11}}(s)}&{{G_{12}}(s)}&{{G_{13}}(s)}\\ 0&{{G_{22}}(s)}&0\\ 0&0&{{G_{33}}(s)} \end{array}} \right] \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} 1&{{D_{12}}(s)}&{{D_{13}}(s)}\\ 0&1&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mu _{{\rm{C}}1}}(s)}\\ {{\mu _{{\rm{C}}2}}(s)}\\ {{\mu _{{\rm{C}}3}}(s)} \end{array}} \right] \end{array} $ | (2) |
为了实现解耦, 耦合通道传递函数应为零。此时, 控制器输出与系统输出的关系式为
| $ \left[ {\begin{array}{*{20}{c}} {{p_{\rm{e}}}}\\ {{p_1}}\\ {{p_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{W_{11}}(s)}&0&0\\ 0&{{W_{22}}(s)}&0\\ 0&0&{{W_{33}}(s)} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mu _{{\rm{C}}1}}(s)}\\ {{\mu _{{\rm{C}}2}}(s)}\\ {{\mu _{{\rm{C}}3}}(s)} \end{array}} \right] $ | (3) |
式中: W11(s), W22(s), W33(s)——解耦后的等效传递函数。
D12(s)和D13(s)需要满足以下条件
| $ \left\{ \begin{array}{l} {D_{12}}\left( s \right){G_{11}}\left( s \right) + {G_{12}}\left( s \right) = 0\\ {D_{13}}\left( s \right){G_{22}}\left( s \right) + {G_{13}}\left( s \right) = 0 \end{array} \right. $ | (4) |
可得前馈补偿解耦控制器D12(s)和D13(s), 以及系统的等效传递函数分别为
| $ \left\{ \begin{array}{l} {D_{12}}\left( s \right) = {\rm{ - }}\frac{{{G_{12}}\left( s \right)}}{{{G_{11}}\left( s \right)}}\\ {D_{13}}\left( s \right) = {\rm{ - }}\frac{{{G_{13}}\left( s \right)}}{{{G_{11}}\left( s \right)}} \end{array} \right. $ | (5) |
| $ \left\{ \begin{array}{l} {W_{11}}\left( s \right) = {G_{11}}\left( s \right)\\ {W_{22}}\left( s \right) = {G_{22}}\left( s \right)\\ {W_{33}}\left( s \right) = {G_{33}}\left( s \right) \end{array} \right. $ | (6) |
加入前馈补偿解耦控制器后, 系统等效传递函数与系统主控通道传递函数相同, 消除了耦合通道, 实现了对电功率控制的解耦。
根据某330 MW汽轮机组运行特性[17]和仿真结果, 得到此机组进行供电供热时被控对象的动态特性, 此时系统输入输出的传递函数G(s)表示为
| $ G(s) = \left[ {\begin{array}{*{20}{c}} {\frac{{181.5s + 363}}{{2\;204.52{s^2} + 195.71s + 1}}}&{\frac{{ - 36.3}}{{58s + 1}}}&{\frac{{ - 18.15}}{{46s + 1}}}\\ 0&{\frac{{55.2}}{{125s + 1}}{{\rm{e}}^{ - 121s}}}&0\\ 0&0&{\frac{{35.1}}{{77s + 1}}{{\rm{e}}^{ - 78s}}} \end{array}} \right] $ | (7) |
将式(7)代入式(5)并离散化(取样时间为0.1 s), 可得前馈补偿解耦控制器为
| $ \left\{ \begin{array}{l} {D_{12}}\left( z \right) = {\rm{ }}\frac{{6.935{z^2}{\rm{ - }}13.81z + 6.874}}{{{z^2}{\rm{ - }}1.816z + 0.816\;8}}{\rm{ }}\\ {D_{13}}\left( z \right) = {\rm{ }}\frac{{4.371{z^2}{\rm{ - }}8.704z + 4.333}}{{{z^2}{\rm{ - }}1.816z + 0.816\;4}}{\rm{ }} \end{array} \right. $ | (8) |
式中: z——z变换后的函数自变量。
2 模糊控制器原理及设计
通过前馈补偿解耦控制器对系统进行解耦后, 采用一种能够实施修正PID参数的模糊PID控制器对系统进行控制。
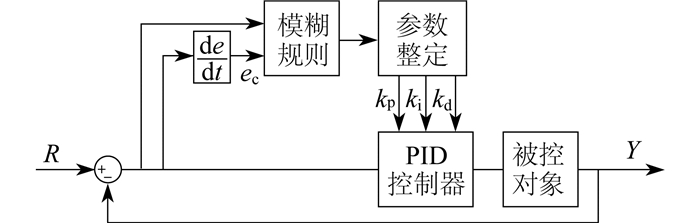
模糊PID控制器的结构框图如图 3所示。图 3中, R和Y分别为控制器的输入量和输出量。
对系统输入与反馈之间的偏差e和偏差变化率ec进行模糊化处理, 并作为模糊规则的输入。通过设置合理的模糊规则表, 输出kp′, ki′, kd′3个输出量作为增益修正常规PID参数, 继而作为模糊PID控制器的实时参数, 对系统进行控制[18]。
控制器的最终参数如下
| $ \left\{ \begin{array}{l} {k_{\rm{p}}} = {G_{\rm{p}}} \times {k_{\rm{p}}}^{\prime} \\ {k_{\rm{i}}} = {G_{\rm{i}}} \times {k_{\rm{i}}}^{\prime} \\ {k_{\rm{d}}} = {G_{\rm{d}}} \times {k_{\rm{d}}}^{\prime} \end{array} \right. $ | (9) |
式中: kp, ki, kd——模糊PID控制器的实时参数;
Gp, Gi, Gd——待修正的常规PID整定参数;
kp′, ki′, kd′——模糊系统输出量。
通过为解耦系统后的电功率控制回路设计模糊PID控制器, 选择合适的模糊规则表、隶属度函数, 实现AGC信号对电功率控制效果的优化。
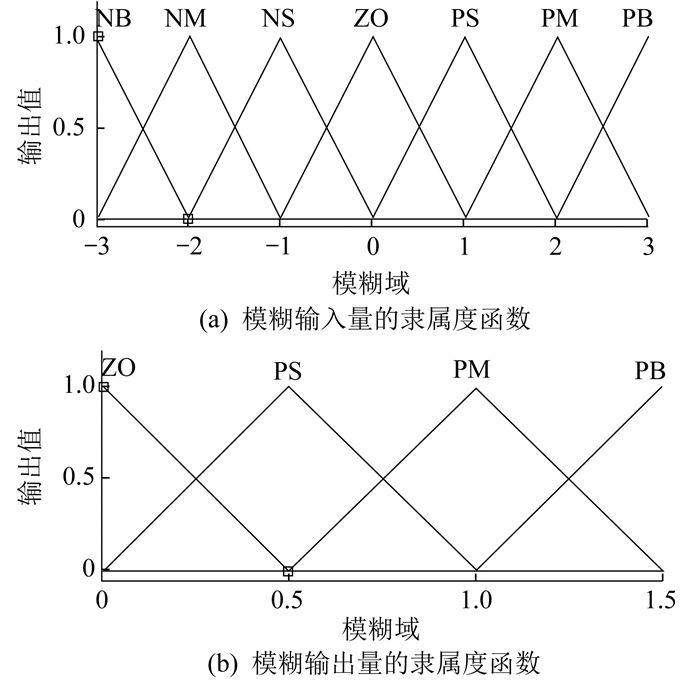
三角形隶属度函数的形状仅与其直线斜率有关, 运算过程较为简单, 所占内存空间也较小。因此, 设置模糊输入量(e, ec)和模糊输出量(k′p, k′i, k′d)的隶属度函数均为三角形函数, 如图 4所示。
此时, 形成了一个两输入三输出的模糊规则系统, 建立3张模糊规则表, 通过PID控制原理指定响应模糊规则。模糊规则表如表 1~表 3所示, 其中“ - ”为空规则。
表 1
kp模糊规则表
| ec | e | ||||||
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PB | — | — | — | — | — | PB |
| NM | PB | PM | — | — | — | PB | PB |
| NS | PB | — | PB | — | PB | — | PB |
| ZO | PB | — | — | — | — | — | PB |
| PS | PB | — | PB | — | PB | — | PB |
| PM | PB | PB | — | — | — | PM | PB |
| PB | PB | — | — | — | — | — | PB |
表 2
ki模糊规则表
| ec | e | ||||||
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PB | — | — | — | — | — | PB |
| NM | PB | PM | — | — | — | PB | PB |
| NS | PB | — | PB | — | PB | — | PB |
| ZO | PB | — | — | — | — | — | PB |
| PS | PB | — | PB | — | PB | — | PB |
| PM | PB | PB | — | — | — | PM | PB |
| PB | PB | — | — | — | — | — | PB |
表 3
kd模糊规则表
| ec | e | ||||||
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PB | — | — | — | — | — | PB |
| NM | PB | PM | — | — | — | PB | PB |
| NS | PB | — | PB | — | PB | — | PB |
| ZO | PB | — | — | — | — | — | PB |
| PS | PB | — | PB | — | PB | — | PB |
| PM | PB | PB | — | — | — | PM | PB |
| PB | PB | — | — | — | — | — | PB |
3 对解耦系统模糊PID控制的仿真实现
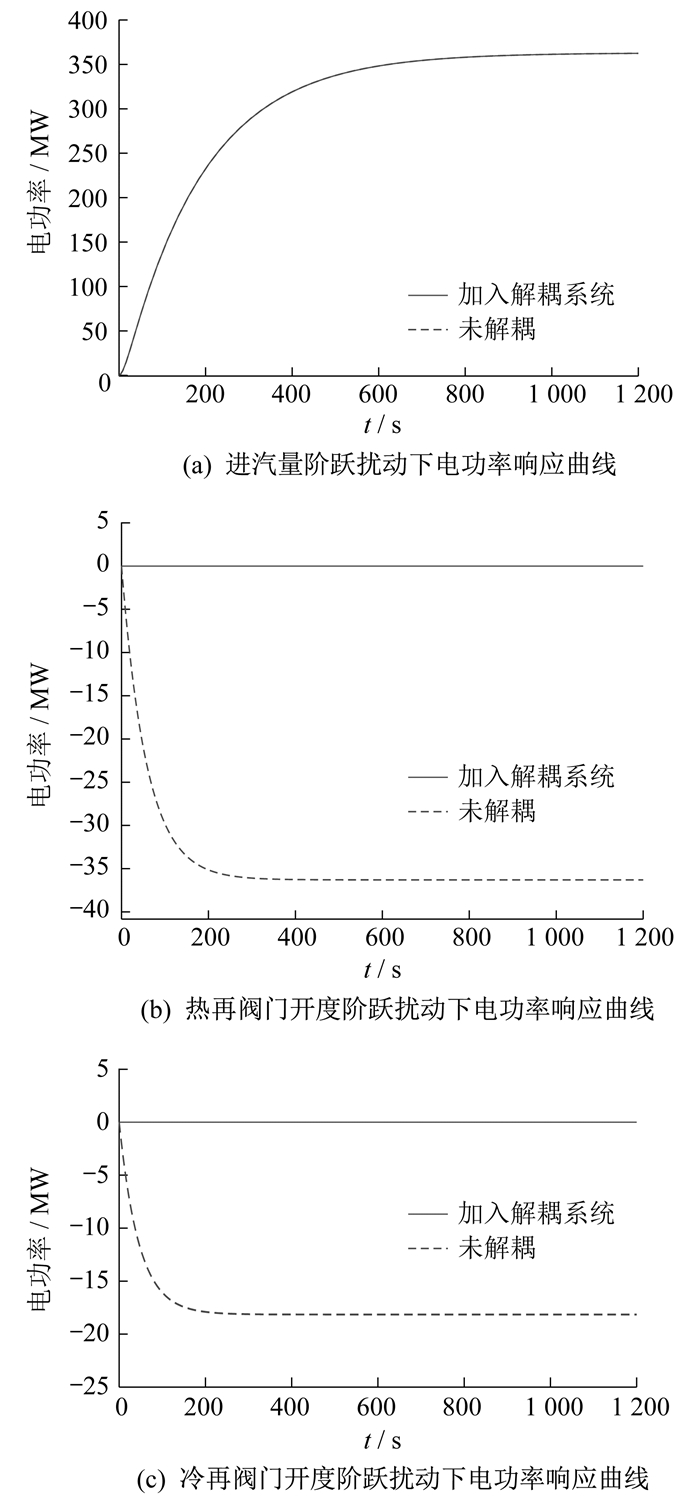
在Simulink仿真平台中建立开环解耦模型, 通过仿真验证系统的解耦性能。分别施加电功率和开度控制阶跃信号, 并与未解耦模型进行对比, 得到仿真结果如图 5所示。
当t<1 200 s时, 通过控制进汽量、热再和冷再抽汽阀门开度阶跃扰动信号得到电功率变化量如下: 解耦前为363.0 MW, -36.4 MW, -18.7 MW; 解耦后为363.0 MW, 0 MW, 0 MW。
由以上仿真结果可知, 只对进汽量施加阶跃扰动时, 解耦前后电功率响应曲线近似一致; 只对抽汽阀门开度施加阶跃扰动时, 解耦前电功率发生扰动, 解耦后电功率基本不受扰动。由此可以得出结论, 前馈补偿解耦控制器在系统中具有较好的解耦效果。
为验证模糊控制器在AGC控制中的优化效果, 在MATLAB/Simulink仿真平台中搭建AGC指令跟踪系统仿真模型, 如图 6所示。其中, fuzzypid模块为模糊PID模块, 其结构以图 3为基础搭建。同时, 搭建未解耦的常规PID控制系统(方案1)和加入前馈补偿解耦控制器的常规PID控制系统(方案2)模型进行仿真, 并与加入前馈补偿解耦控制器的模糊PID控制系统(方案3)进行对比。
根据系统特性, 设置合适的量化因子, 同时使用试凑法整定出常规PID控制器的各参数, 作为对比验证对象及模糊PID控制器中待修正的参数。
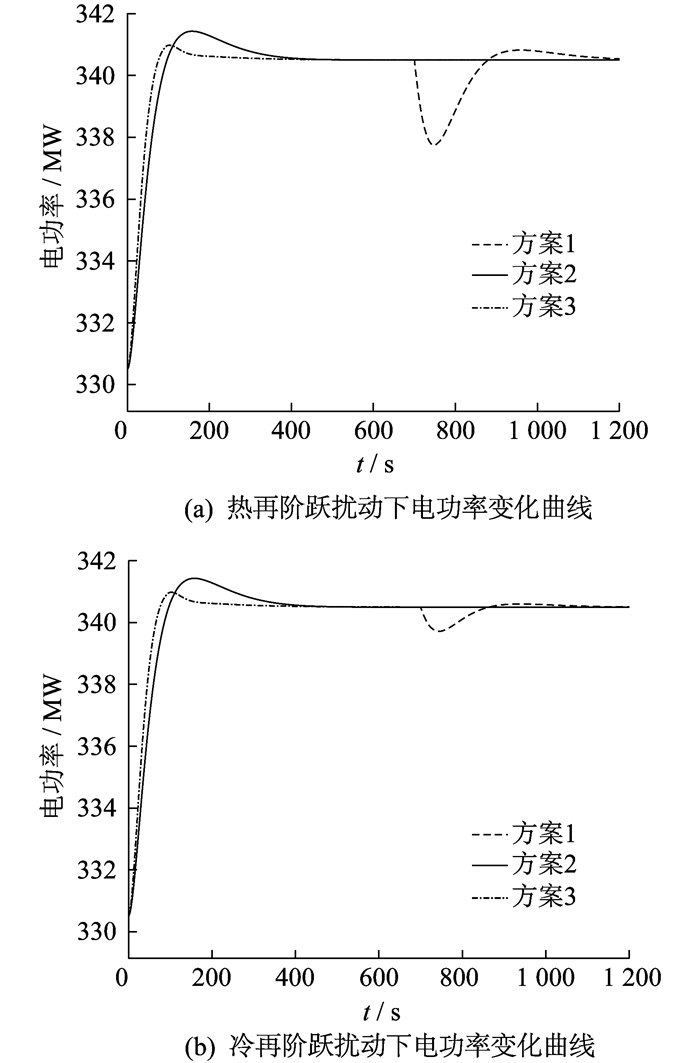
首先, 将AGC指令设定为330.5 MW。在电功率稳定后, 施加一个+10 MW的AGC控制指令, 仿真得到施加指令后各控制器的电功率变化曲线; 并在系统再次达到平衡后, 即系统运行700 s时, 分别加入热再阶跃扰动和冷再阶跃扰动, 得到各控制器的AGC指令跟随控制效果, 如图 7和表 2所示。
表 2
3种控制方案的性能数据指标对比
| 控制方案 | 上升时间/ s | 超调量/ % | 调节时间/ s | 抽汽扰动再稳定时间/s | |
| 热再 | 冷再 | ||||
| 方案1 | 65.2 | 9.0 | 249.4 | 485 | 246 |
| 方案2 | 65.2 | 9.3 | 249.4 | 0 | 0 |
| 方案3 | 39.1 | 4.0 | 76.6 | 0 | 0 |
由图 7和表 2可以看出, 3种控制方案下的系统都能达到收敛的稳定状态。加入解耦常规PID控制器前, 在受到耦合信号扰动时, 系统会发生较大变化, 且较难回到稳定状态; 而加入前馈补偿解耦控制器后, 系统在受到耦合信号扰动时, 被控目标不会受到干扰。
方案3的输出曲线响应速度更快, 超调量更小, 系统上升时间由249.4 s缩短到76.6 s; 超调量由9.3%减少至4.0%, 因此方案3具有更好的控制效果。
为了判断模糊控制器在系统变化时的抗干扰能力, 在800 s时, 对方案2和方案3加入一个内部扰动信号, 得到的输出变化曲线和性能数据指标如图 8和表 3所示。
表 3
2种控制方案的性能数据指标对比
| 控制方案 | 上升时间/ s | 超调量/ % | 调节时间/ s | 内部扰动再稳定时间/s |
| 方案2 | 65.2 | 9.3 | 249.4 | 251.9 |
| 方案3 | 39.1 | 4.0 | 76.6 | 106.8 |
由图 8和表 3可以看出, 在加入扰动信号后, 方案2和方案3都能够回到稳定状态, 具有一定的抗干扰能力。其中, 方案3回到稳定状态的速度更快, 再稳定时间由251.9 s缩短到106.8 s, 说明方案3的控制效果更好, 更能够适应复杂情况。
4 结语
本文针对供热改造后供热供电机组的AGC跟踪效果不理想问题, 利用前馈补偿解耦控制器对系统进行解耦, 通过建立开环解耦仿真模型进行模拟, 验证了该控制器的解耦能力能够有效抵消耦合通道的影响。同时, 设计了一种能够动态调节PID参数的模糊PID控制器, 在Simulink仿真平台中搭建了仿真模型, 并与常规PID控制器进行了动态性能对比。仿真结果表明, 解耦模糊PID控制器相较于解耦常规PID控制器具有更好的动态性能和抗干扰能力, 可实现抽汽改造后供热发电机组的AGC指令跟踪效果优化, 在工程实际中, 具有较好的应对复杂情况的实践价值。
参考文献
-
[1]吴斌, 邵志跃, 胡欣, 等. 215 MW机组工业抽汽供热改造[J]. 热力发电, 2015, 44(5): 87-90.
-
[2]邓拓宇, 田亮, 刘吉臻. 供热机组热电耦合特性分析与解耦协调控制[J]. 系统仿真学报, 2017, 29(10): 2593-2599.
-
[3]刘刚. 火电机组灵活性改造技术路线研究[J]. 电站系统工程, 2018, 34(1): 12-15.
-
[4]裴哲义, 王新雷, 董存, 等. 东北供热机组对新能源消纳的影响分析及热电解耦措施[J]. 电网技术, 2017, 41(6): 1786-1792.
-
[5]桑保华, 薛晓中. 多变量解耦控制方法[J]. 火力与指挥控制, 2007(11): 13-16.
-
[6]张会, 付东翔, 王亚刚. 变风量空调系统恒温解耦控制优化[J]. 计算机仿真, 2014, 31(10): 255-258. DOI:10.3969/j.issn.1006-9348.2014.10.055
-
[7]钱虹, 房振鲁, 杨祖魁, 等. 基于最优Hankel范数近似的核电站电功率与冷却剂平均温度解耦控制方法[J]. 动力工程学报, 2016, 36(5): 383-388. DOI:10.3969/j.issn.1674-7607.2016.05.008
-
[8]钱虹, 周蕾, 房振鲁. 压水堆核电站稳压器压力和水位的解耦控制研究[J]. 核科学与工程, 2017, 37(1): 5-11.
-
[9]白辰, 樊垚, 任章, 等. 基于模糊神经网络的MIMO系统自适应解耦控制[J]. 北京航空航天大学学报, 2015, 41(11): 2131-2136.
-
[10]付焕森, 李元贵. 基于前馈补偿算法温室解耦及PLC控制器设计[J]. 农机化研究, 2016, 38(2): 205-208.
-
[11]李存贺, 王国峰, 李岩, 等. 开关磁阻电机直接自适应神经网络控制[J]. 电机与控制学报, 2018, 22(1): 29-36.
-
[12]隋涛, 孔苓青, 刘秋贺, 等. 专家PID控制在矿井提升机直流调速系统中的应用[J]. 中国科技论文, 2017, 12(2): 226-231.
-
[13]YANG G, DU J M, FU X Y, et al. Asymmetric fuzzy control of a positive and negative pneumatic pressure servo system[J]. Chinese Journal of Mechanical Enginee-ring, 2017, 30(6): 1438-1446.
-
[14]王科, 潘瑾宜. 核电站冷却剂平均温度系统的模糊PI并行控制研究[J]. 上海电力大学学报, 2020, 36(6): 562-566.
-
[15]钱虹, 宋亮, 周蕾, 等. 压水堆核电厂稳压器压力模糊控制器研究及仿真[J]. 核动力工程, 2016, 37(4): 63-67.
-
[16]武彬, 张栾英. 模糊自整定PID控制在主汽温控制中的应用[J]. 计算机仿真, 2015, 32(2): 387-390.
-
[17]卫丹靖, 田亮, 边防, 等. "机跟炉"协调控制系统参数整定规律研究[J]. 华北电力大学学报(自然科学版), 2016, 43(6): 91-96.
-
[18]钱虹, 陈丹, 张鲲鹏, 等. 分布式能源站热负荷侧模糊自适应压力控制器设计[J]. 热能动力工程, 2017, 32(2): 17-24.