|
|
|
发布时间: 2022-04-25 |
计算机与信息科学 |
|
|
|
杜海舟, 冯晓杰 |
收稿日期: 2020-03-18
中图法分类号: TP183
文献标识码: A
文章编号: 2096-8299(2022)02-0183-06
|
摘要
分布式深度学习已经成为深度学习领域最热门的研究之一, 越来越庞大的数据模型和算法都依赖分而治之思想来处理。分布式深度学习系统在快速发展中遇到了许多挑战, 其中最重要的是如何在分布式环境有限的网络带宽中有效地传输大量数据, 以充分利用计算资源高效训练高精度的深度神经网络。针对这个问题, 从参数同步、模型聚合和梯度压缩3个角度讨论不同的数据传输压缩技术, 分别将其用于交错数据传输、减少数据交换频率以及减小单次传输数据量。最后对分布式深度学习的数据传输压缩机制的未来发展趋势进行了讨论和展望。
关键词
分布式深度学习; 模型聚合; 并行计算; 数据传输压缩
DU Haizhou, FENG Xiaojie Abstract
Distributed deep learning has become one of the most popular research fields in the entire deep learning.Increasingly large amounts of data, models and algorithms will rely on the highly intelligent idea of divide and conquer to process.However, the distributed deep learning system has encountered many new challenges in the rapid development, the most important of which is the effective transmission of large amounts of data in the limited network bandwidth of the distributed environment, in order to make full use of computing resources to efficiently train high precision deep neural networks.In response to this problem, this article discusses different techniques of data transmission compression from three perspectives, including parameter synchronization, model aggregation, and gradient compression, which are respectively used for interleaving data transmission, reducing the frequency of data exchange, and the amount of data transmitted each time.The future development trend of distributed deep learning data transmission compression mechanism is discussed and prospected.
Key words
distributed deep learning; model aggregation; parallel computing; data transmission compression
随着大数据、云计算和物联网需求的日益增长, 机器学习尤其是深度学习在图像分类、语音识别、机器翻译以及围棋程序等领域都有了上千万的训练数据以支撑复杂模型的训练, 建立了各种数据分析和决策系统。大数据的兴起也伴随着包含数百万甚至数十亿参数的更高维、更复杂的机器学习模型和深度神经网络的出现。如此大规模的计算, 离不开硬件的支撑。图形处理器GPU有着比中央处理器CPU更强的并行计算能力, 能使复杂的训练更加高效。为了获得更高的预测精度、支持更智能的任务, 需要训练更复杂的神经网络。然而训练大型模型所需的输入数据随模型参数呈指数增长, 对这样大规模的数据训练所涉及的深度神经网络已经超过了单一机器的计算和存储能力, 因此需要在多台计算机之间分配训练工作量, 并从集中式系统转向分布式系统。在这种情况下, 利用计算机集群, 从大数据中训练性能优良的大模型成为分布式深度学习的目标之一。
1 分布式深度学习简介
分布式深度学习能够充分利用集群资源更快地完成训练。当训练数据或模型太大, 无法由单机完成存储和计算时, 就需要将数据或模型进行划分, 并将其分配到各个计算节点上。这分别对应分布式深度学习中2种重要的并行化方式: 数据并行和模型并行。
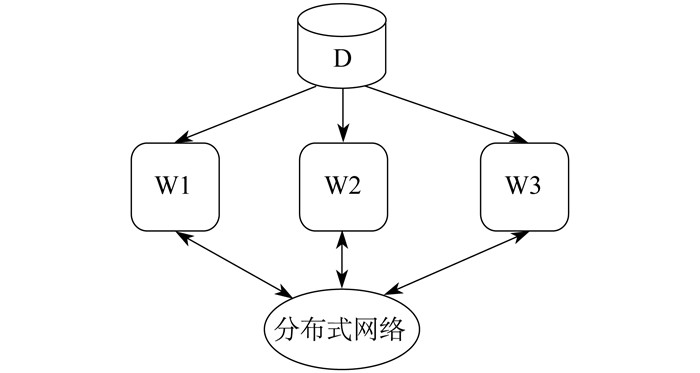
数据并行是先将数据划分到各个计算节点上, 然后各节点利用自身的局部数据对模型进行训练, 具体如图 1所示, 其中D代表数据, W1, W2, W3代表工作节点。
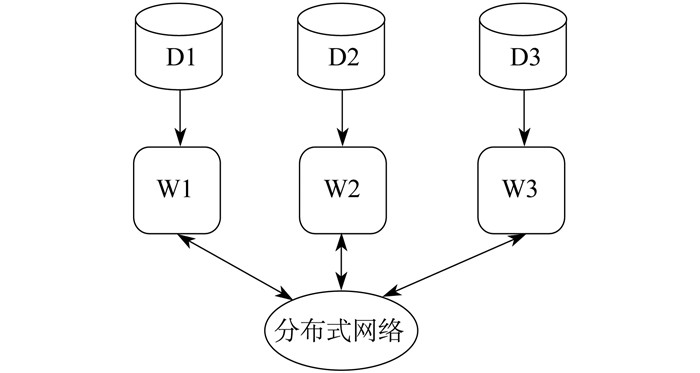
模型并行是先把一个大模型划分成许多小块, 然后把每小块对应的参数分配在不同的计算节点上执行, 具体如图 2所示, 其中D1, D2, D3表示划分到各个节点的数据。数据并行通过分布式网络传输梯度同步模型, 且通过模型并行传输中间计算结果。数据并行和模型并行并不冲突, 两者可以混合使用[1-2]。
并行方式需要与具体的通信架构相结合, 选择中心化还是去中心的架构取决于诸多因素。中心化架构通常利用特别设计的参数服务器(Param-eter Server, PS)[3]将工作节点(客户端)和模型存储节点(服务器)从逻辑上进行区分。各工作节点负责处理本地的数据训练, 并通过参数服务器提供的PUSH与PULL接口与之进行通信。去中心架构依靠集体通信All-Reduce在节点之间传递数据。
将数据和模型划分到多个工作节点后, 再利用单机的并行优化能力进行本地计算, 通过分布式通信将局部模型聚合成全局模型。这就是整个分布式深度学习的基本流程。
与一般的分布式计算相比, 分布式深度学习在数据传输方面更具挑战。这主要是因为分布式深度学习面临着通信需求与受限带宽的考验, 因而其性能和可扩展性受到了极大限制。
(1) 通信的频率高、单次通信量大首先, 深度学习采用迭代式的优化算法进行训练, 迭代频繁且次数多, 使得通信频率很高。其次, 分布式深度学习需要在各个工作节点之间传递神经网络参数或梯度(数据并行), 或者在每个数据样本的中间计算结果(模型并行), 由于需要处理大数据、训练大模型, 从而导致每次的通信量很大。
(2) 网络带宽低、延迟高与大数据、大模型对比, 分布式系统中的网络传输速度往往受限, 导致通信常常成为分布式系统的瓶颈。根据阿姆达尔定律(Amdahl’s Law)[4], 如果某个任务中计算与通信的时间占比为1∶1, 那么无论使用多少台机器, 其加速比都不会超过2倍。
因此, 分布式深度学习的关键是降低通信与计算的时间比, 从而更加高效地训练高精度的模型。
2 分布式深度学习的数据传输压缩
2.1 参数同步
分布式深度学习中的各个计算节点既要独立地进行本地计算, 又可以通过数据交互来确保模型最终能够收敛且收敛到理想的最优点。为了高效地训练高精度模型, 需要在更好的模型性能(列表上方)和更快的训练速度(列表下方)之间进行权衡。这种权衡导致了3种主要的同步模式, 具体如下: 一是整体同步并行(Bulk Synchronous Parallel, BSP)[5], 在每个工作节点处理完局部数据后同步所有更新, 在所有工作节点获取最新的模型后才进行下一次迭代; 二是异步并行(Asynchronous Parallel, AP) [6], 完全去掉工作节点间的同步, 所有的工作节点都尽最大努力地进行通信; 三是延时同步并行(Stale Synchronous Parallel, SSP) [7], 允许最快的工作节点比最慢的工作节点多迭代一定次数, 但是不能超过阈值。
2.1.1 BSP
BSP要求工作节点完成本轮迭代后, 等待集群中的其他未完成节点, 当所有节点都完成各自的任务后, 才共同进入下一轮迭代。BSP使得每个工作节点都能获得最新且一致的全局模型, 保证了分布式算法与单机算法的等价性, 从而利于算法的分析和调试, 并且能够获得最好的模型性能。但是, 由于各个工作节点之间彼此等待, 造成计算资源闲置, 所以阻碍了训练规模的扩展。在带宽受限的情况下, 还会导致各个工作节点集中闲置或争用有限的带宽。
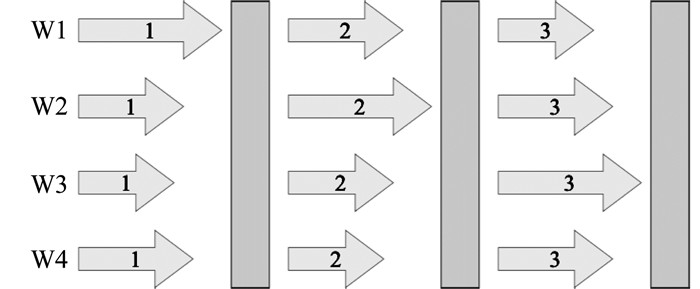
在BSP引入一个全局的同步屏障, 构成整体同步并行模式歧化, 具体如图 3所示。
即所有的工作节点会在这个位置被强制停下, 直到所有的工作节点都完成了同步屏障之前的操作, 整个系统才会进入下一步的计算任务。当使用BSP来实现基于数据并行的分布式优化算法时, 需要与具体的聚合方法相结合[8-10]。
2.1.2 AP
AP是指当集群中的一个工作节点完成本轮迭代后, 无需等待其他节点就可以继续进行后续训练, 具体如图 4所示。异步通信不保证模型的一致性, 各个工作节点无需互相等待, 从而最大化计算和通信资源的利用率。但由于节点之间的模型彼此不一致, 因此会因延迟问题, 给模型聚合带来挑战。
AP最初在共享内存的单机多线程并行中实现, 分为有锁和无锁2种, 各有利弊。文献[11]用Dogwild!将各个工作线程直接无锁地读取和写入最新的模型中进行更新, 发现在优化目标为凸函数且模型更新比较稀疏的情况下, 异步无锁地写入不会对收敛性造成本质影响。此后Dogwild!被扩展到分布式内存系统中, 并在深度学习问题上仍能保持收敛性。为了缓和每一步中覆盖参数的影响, 在这些实现中传递梯度而不是参数。
2.1.3 SSP
为了结合同步与异步各自的优点, 文献[7]提出了在一致和不一致模型之间折中的方案SSP。SSP控制最快和最慢节点之间相差的迭代次数, 使其不超过预设的阈值。延时同步并行模式如图 5所示。只要各个工作节点的迭代次数的差不超过阈值, 各个节点的计算就可以保持独立进行; 但当迭代次数差异太大, 就会触发等待机制, 避免产生过大的延迟。这种方法在异构环境中特别有效, 因为掉队者(stragglers)会受到控制。
Adam项目不要求最快的工作节点等待, 而是维持一个全局时钟, 当发现某些工作节点的更新太陈旧时, 就将其丢弃并将此工作节点的当前模型刷新成参数服务器上的最新模型, 从而既保证有限的延迟, 同时也可以让快的工作节点全速前进。
2.2 模型聚合
模型一致性频谱如图 6所示。
由图 6可知, 从一致性的角度看, 可以进一步增加模型不一致性, 从而推广BSP, SSP, AP。在极端不一致的情况下, 数据交换非常少或不存在, 虽然减少了通信量, 但也意味着必须对接收到的数据采取有效的聚合措施。具体来讲, 可以让许多机器分别进行训练, 然后在训练结束聚合一次或者在训练期间间隔地聚合。从聚合内容的角度来看, 既可以是聚合模型参数或梯度, 又可以是聚合模型的输出。其中: 集成学习(Ensemble Learning)是在训练结束之后聚合模型输出; 模型平均(Model Averaging)是在训练期间间隔地聚合模型参数或梯度。
2.2.1 集成学习
2.2.2 模型平均
模型平均[14]是在不同的机器上并行执行随机梯度下降(Stochastic Grradient Descent, SGD), 仅在训练后聚合一次或每隔几次迭代聚合一次[15]。研究证明, 使用SSP的SGD准确性更高。
为了克服由于不频繁平均而导致的精度下降问题, 文献[16]在弹性平均SGD中引入了所谓的弹性机制, 在当前的全局模型和工作节点的最新更新之间进行权衡, 一方面探索新模型, 另一方面保留一定的历史状态。结果表明, 弹性平均SGD在准确性方面优于DistBelief SGD, 在更新延迟方面表现出一定的容忍度。
在分布式环境下, 算法还应进行检查以确保容错性。Krum[17]是一种拜占庭容错[18] SGD算法, 最多允许f个拜占庭训练代理。通过组合特定的m-f个梯度, Krum能够克服来自网络的对抗性梯度输入。同时, 任何基于线性组合的梯度聚集规则都无法容忍单个拜占庭代理。
2.3 梯度压缩
深度学习的优化算法具有容错性, 可以减少不必要的数据传输开销。一方面, 可以通过不一致视图减少传递信息的频率, 另一方面, 也可以减小每次传输数据的大小。分布式深度学习中有2种节省带宽的通用方法: 一是量化(Quantization), 用有效的数据表示压缩参数或梯度, 减少每个值的占用位数; 二是稀疏(Sparsification), 避免发送不必要的信息, 从而导致稀疏数据的通信。
2.3.1 量化
基于量化的方法减少了表示浮点数所需的位数。极端的偏差量化1位SGD[19], 将每个梯度分量量化为1或-1。该方法在量化过程中首次引入了误差反馈策略, 以补偿上次迭代产生的量化误差。具有多数表决的signSGD[20]在工作节点和服务器之间传输1位的梯度符号, 并使用多数表决进行聚合。其动量变体称为具有多数表决的Signum[21]。通过多数表决, signSGD实现了拜占庭容错。然而, signSGD在某些简单情况下依然可能不收敛。通过使用误差修正技术可以解决这个问题, 从而导致带有错误反馈的SGD(EF-SGD)[22]。通过将梯度划分为块, Dist-EF-SGD及其动量变体[23]传输1位符号和每个块的缩放因子, 以获得更好的模型性能。
无偏量化[24]和QSGD[25]通过随机量化将梯度分别压缩为3级和多级, 并确保压缩后的随机梯度是真实梯度的无偏近似。QSGD使用均匀分布的量化点对梯度进行随机量化。ZipML[26]通过梯度分布动态地选择量化点从而引入了一种最佳量化策略。实践中, 与不使用该技术的无偏量化相比, 使用误差补偿技术的偏差量化能够获得更好的模型性能。
2.3.2 稀疏化
基于稀疏化的方法减少了随机梯度中非零项的数量。与量化策略相比, 稀疏化能够取得更高的通信压缩率。一种极端有效的Top-k稀疏化方法仅传输绝对值最大的梯度分量。其中, 阈值量化[27]和梯度丟弃[28]基于绝对值的两个或单个阈值稀疏梯度。由于在实践中很难选择该阈值, Adacomp[29]根据局部梯度活动自动选择梯度残差。为了解决由于稀疏而导致的精度损失, 深度梯度压缩[30]利用动量校正、局部梯度裁剪、动量因子掩蔽和热身训练实现更高的稀疏度而不降低精度。此类方法只能通过使用某种误差累积才能工作, 否则某些坐标将永远无法更新。
与上述Top-k方案不同, 文献[31]提出了一种随机稀疏化方法, 该方法通过求解约束线性规划来平衡稀疏性和方差, 无偏且不采用误差补偿。
2.3.3 低秩分解和草图方法
低秩分解(Low-rank Factorization)和草图方法(Sketch)也可以视为基于稀疏化的方案。Atomo[32]对梯度的奇异矢量(非坐标)进行重要性采样, 是一种无偏压缩方案。但是, 它的每次迭代都需要完整的奇异值分解, 因而计算代价太大。PowerSGD[33]基于空间迭代和误差反馈提出了一种计算效率更高的偏差低秩梯度压缩方法。
SketchML[34]将梯度值量化到诸多桶中, 然后通过相应的桶索引对每个值进行编码, 同时提出了一种MinMaxSketch算法来近似压缩桶索引。SketchSGD[35]将所有梯度压缩到草图中, 传输各个节点的草图, 然后在合并的草图中恢复最重要的梯度坐标。SketchSGD在模型很大或者工作节点较多时, 会有极高的压缩率和额外计算开销。
3 结语
利用分布式深度学习, 高效地训练高精度的深度神经网络面临着有限网络带宽和大量传输数据的挑战。针对这个问题, 本文从参数同步的角度, 阐述同步、异步和延迟同步3类并行方式; 从模型聚合的角度, 总结集成学习和模型平均2类聚合策略; 从梯度压缩的角度, 讨论量化和稀疏2类压缩方法。可以预见, 分布式深度学习未来将会在这3个方面得到更多的应用和发展。
参考文献
-
[1]DEAN J, CORRADO G, MONGA R, et al. Large scale distributed deep networks[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2012: 1223-1231.
-
[2]CHILIMBI T, SUZUE Y, APACIBLE J, et al. Projectadam: Building an efficient and scalable deep learning training system[C]//11th USENIX Symposium on Operating Systems Design and Implementation. Berkeley: USENIX Association, 2014: 571-582.
-
[3]LI M, ANDERSEN D G, PARK J W, et al. Scaling distributed machine learning with the parameter server[C]//11th USENIX Symposium on Operating Systems Design and Implementation. Berkeley: USENIX Association, 2014: 583-598.
-
[4]AMDAHL G M. Validity of the single processor approach to achieving large scale computing capabilities[C]//Proceedings of the April 18-20, 1967, Spring Joint Computer Conference. New York: ACM, 1967: 483-485.
-
[5]VALIANT L G. A bridging model for parallel computation[J]. Communications of the ACM, 1990, 33(8): 103-111. DOI:10.1145/79173.79181
-
[6]HO Q, CIPAR J, CUI H, et al. More effective distributed ml via a stale synchronous parallel parameter server[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2013: 1223-1231.
-
[7]RECHT B, RE C, WRIGHT S, et al. Hogwild: a lock-free approach to parallelizing stochastic gradient descent[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2011: 693-701.
-
[8]MCDONALD R, HALL K, MANN G. Distributed training strategies for the structured perceptron[C]//Human Language Technologies: The 2010 Annual Conference of the North American Chapter of the Association for Computational Linguistics. Stroudsburg: ACL, 2010: 456-464.
-
[9]ZINKEVICH M, WEIMER M, LI L, et al. Parallelized stochastic gradient descent[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2010: 2595- 2603.
-
[10]CHEN K, HUO Q. Scalable training of deep learning machines by incremental block training with intra-block parallel optimization andblockwise model-update filtering[C]//2016 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE, 2016: 5880-5884.
-
[11]NOEL C, OSINDERO S. Dogwild!-distributed hogwild for cpu & gpu[C]//NIPS Workshop on Distributed Machine Learning and Matrix Computations. Cambridge: MIT Press, 2014: 693-701.
-
[12]FERNÁNDEZ-DELGADO M, CERNADAS E, BARRO S, et al. Do we need hundreds of classifiers to solve real world classification problems?[J]. The Journal of Machine Learning Research, 2014, 15(1): 3133-3181.
-
[13]BA J, CARUANA R. Do deep nets really need to be deep?[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2014: 2654-2662.
-
[14]POLYAK B T, JUDITSKY A B. Acceleration of stochastic approximation byaveraging[J]. SIAM Journal on Control and Optimization, 1992, 30(4): 838-855.
-
[15]MIAO Y, ZHANG H, METZE F. Distributed learning of multilingualdnn feature extractors using gpus[C]//Fifteenth Annual Conference of the International Speech Communication Association. Singapore, 2014: 830-834.
-
[16]ZHANG S, CHOROMANSKA A E, LECUN Y. Deep learning with elastic averagingsgd[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2015: 685-693.
-
[17]BLANCHARD P, GUERRAOUI R, STAINER J, et al. Machine learning with adversaries: byzantine tolerant gradient descent[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2017: 119-129.
-
[18]LAMPORT L, SHOSTAK R E, PEASE M C. The byzantine generalsproblem[J]. ACM Trans Program Lang Syst, 1982(4): 203-226.
-
[19]SEIDE F, FU H, DROPPO J, et al. 1-bit stochastic gradient descent and its application to data-parallel distributed training of speechdnns[C]//Fifteenth Annual Conference of the International Speech Communication Association. Singapore, 2014: 1058-1062.
-
[20]BERNSTEIN J, WANG Y X, AZIZZADENESHELI K, et al. Signsgd: compressed optimisation for non-convex problems[C]//International Conference on Machine Learning. New York: ACM, 2018: 559-568.
-
[21]BERNSTEIN J, ZHAO J, AZIZZADENESHELI K, et al. Signsgd with majority vote is communication efficient and fault tolerant[C]//International Conference on Learning Representations. New Orlean, USA, 2019: 1-20.
-
[22]KARIMIREDDY S P, REBJOCK Q, STICH S U, et al. Error feedback fixessignsgd and other gradient compression schemes[C]//International Conference on Machine Learning. New York: ACM, 2019: 3252-3261.
-
[23]ZHENG S, HUANG Z, KWOK J. Communication-efficient distributed blockwise momentum SGD with error-feedback[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2019: 11450-11460.
-
[24]WEN W, XU C, YAN F, et al. Terngrad: ternary gradients to reduce communication in distributed deep learning[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2017: 1509-1519.
-
[25]ALISTARH D, GRUBIC D, LI J, et al. Qsgd: communication-efficient sgd via gradient quantization and encoding[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2017: 1709-1720.
-
[26]ZHANG H, LI J, KARA K, et al. Zipml: training linear models with end-to-end low precision, and a little bit of deep learning[C]//International Conference on Machine Learning. New York: ACM, 2017: 4035-4043.
-
[27]STROM N. Scalable distributeddnn training using commodity gpu cloud computing[C]//Sixteenth Annual Conference of the International Speech Communication Association. Dresden, Germany, 2015: 1488-1492.
-
[28]AJI A F, HEAFIELD K. Sparse communication for distributed gradient descent[C]//Conference on Empirical Methods in Natural Language Processing. Stroudsburg: ACL, 2017: 440-445.
-
[29]CHEN C Y, CHOI J, BRAND D, et al. Adacomp: adaptive residual gradient compression for data-parallel distributed training[C]//Thirty-Second AAAI Conference on Artificial Intelligence. Menlo Park: AAAI, 2018: 2527-2835.
-
[30]LIN Y, HAN S, MAO H, et al. Deep gradient compression: reducing the communication bandwidth for distributed training[C]//International Conference on Learning Representations. Vancouver, Canada, 2018: 1-14.
-
[31]WANGNI J, WANG J, LIU J, et al. Gradientsparsification for communication-efficient distributed optimization[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2018: 1299-1309.
-
[32]WANG H, SIEVERT S, LIU S, et al. Atomo: communication-efficient learning via atomic sparsification[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2018: 9850-9861.
-
[33]VOGELS T, KARIMIREDDY S P, JAGGI M. Powersgd: practical low-rank gradient compression for distributed optimization[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2019: 14236-14245.
-
[34]JIANG J, FU F, YANG T, et al. Sketchml: accelerating distributed machine learning with data sketches[C]//Proceedings of the 2018 International Conference on Management of Data. New York: ACM, 2018: 1269-1284.
-
[35]IVKIN N, ROTHCHILD D, ULLAH E, et al. Communication-efficient distributed sgd with sketching[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2019: 13144-13154.
