|
|
|
发布时间: 2022-06-25 |
智能电网技术 |
|
|
|
收稿日期: 2021-10-28
基金项目: 甘肃省高等学校产业支撑引导项目(2020C-34);甘肃省高等学校创新基金(2021B-430)
中图法分类号: TM76
文献标识码: A
文章编号: 2096-8299(2022)03-0257-07
|
摘要
根据分布式光伏发电特性,通过对中压配电网中无功优化的分析,找到潮流、电压波动和无功容量与光伏发电无功功率间的定量关系。利用粒子群优化(PSO)算法,基于逆变器的分布式光伏发电中压配电网的无功优化,明确了控制无功功率以支持配电网和电压调节的方法。实例仿真结果说明,该方法能够有效减少光伏发电系统中压配电网的电压升高和逆潮流问题。
关键词
无功优化; 分布式光伏发电; 中压配电网; 电压调节; PSO算法
Abstract
According to the characteristics of distributed PV generation, and reactive power optimization in medium voltage distribution network is analyzed, and the quantitative relationship between the PV reactive power of the tidal current, voltage fluctuation and reactive power capacity is established.PSO algorithm is introduced based on distributed PV inverter of medium voltage distribution network reactive power optimization method, to make clear about the control of reactive power in support of the distribution network and the method of voltage regulation.The simulation results show that the proposed method can effectively reduce the voltage rise and tide reversal problems of the voltage distribution network in the PV generation system.
Key words
reactive power optimization; PV distributed generation; medium voltage distribution grid; voltage regulation; particle swarm potimization
近年来, 光伏(Photovoltaic, PV)发电在可再生能源发电中所占的比重越来越大, 但分布式光伏并网的高渗透率也对电能质量带来了挑战。由于光伏发电造成的电能与需求不匹配, 导致电网中出现了节点电压升高、逆潮流和无功功率不足等情况[1], 因此引入无功优化方法来解决配电网系统操作与控制的难题。配电网中无功功率控制有3种策略: 集中控制、分散控制和局部控制[2]。基于逆变器的分布式光伏发电的集中无功优化适合中压(Medium Voltage, MV)配电网的策略是依托配电网中光伏发电系统提供的无功功率。因此, 集中式无功优化策略有助于减少光伏系统的有功功率输出和优化电网运行。
目前, 通过无功功率对电压调节的方法可采取以下方式: 恒功率因数、有功功率相关的功率因数、有功功率依赖无功功率及电压依赖无功功率调节等。集中无功优化策略是通过由配电网运行人员改变高压和中压值来控制无功功率, 有助于实现系统的稳定性和可靠性。在通信脱机过程中, 由电压相关无功调节方法控制的局部配电网具有优势。文献[3-4]提出了一种改进性的电压依赖无功功率特性和电压敏感性的分析方法。文献[5-6]提出了多目标无功优化问题的2个冲突目标, 该算法的性能可使有功损耗最小化, 并改善电压分布。
1 分布式光伏发电中压配电网中无功功率优化分析
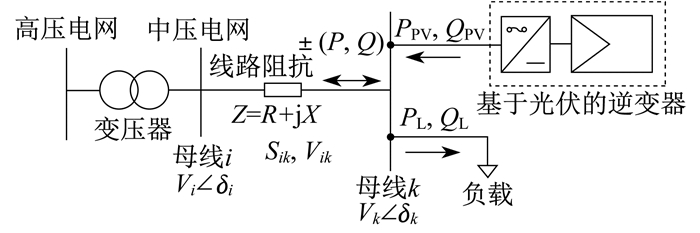
本文提出的基于逆变器的分布式光伏发电(PV)中压配电网(MV)无功优化简化网络如图 1所示。其目的是控制中压配电网中的无功功率转换。其中, PPV和QPV为光伏发电的有功和无功功率; PL和QL为负载的有功损耗和无功损耗; Z为配电线路阻抗; δi和δk为母线i和k的电压角; Vi和Vk为母线i和k的电压。
1.1 分布式光伏发电中压配电网潮流分析
结合电网电压变化分析有功功率和无功功率。图 1所示为带负荷分布式光伏发电系统中典型的一对中压配电网母线, 同时是考虑从系统侧接入的母线i和k之间的等效电路。其视在功率Sik为
| $ {S_{ik}} = {V_{ik}}I_{ik}^* = {P_{ik}} + {\rm{j}}{Q_{ik}} $ | (1) |
式中: Vik——母线i和k之间的电压;
Iik*——2个母线网络的电流;
Pik, Qik——Sik组成的无功功率和有功功率。
以电压灵敏度来确定基于分布式光伏发电的无功功率, 母线i潮流的有功功率和无功功率为
| $ \left\{ {\begin{array}{*{20}{c}} {{P_i}{\rm{ = }}{V_i}\sum\limits_{k = 1}^N {{V_k}\left( {{C_{ik}}\cos {\delta _{ik}} + {B_{ik}}\sin {\delta _{ik}}} \right)} }\\ {{Q_i}{\rm{ = }}{V_i}\sum\limits_{k = 1}^N {{V_k}\left( {{C_{ik}}\sin {\delta _{ik}} - {B_{ik}}\cos {\delta _{ik}}} \right)} } \end{array}} \right. $ | (2) |
式中: Pi, Qi——母线i的有功功率和无功功率;
Vi, Vk——母线i和k的电压;
N——总线网络的数量;
Gik, Bik——母线i和k之间配电线的电导和电纳;
δik——母线i和k之间的母线电压角。
通过求解式(2)中的潮流方程, 得到的电压灵敏度矩阵为
| $ \left[ {\begin{array}{*{20}{c}} {\Delta \delta }\\ {\Delta V} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_{{\rm{ \mathsf{ δ} P}}}}}&{{F_{{\rm{ \mathsf{ δ} Q}}}}}\\ {{F_{{\rm{VP}}}}}&{{F_{{\rm{VQ}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta P}\\ {\Delta Q} \end{array}} \right] $ | (3) |
式中: Δδ——配电网母线电压角的变化;
ΔV——配电网母线电压的变化;
FδP, FδQ——母线电压对有功功率和无功功率的灵敏度;
FVP, FVQ——母线电压大小对有功功率和无功功率的灵敏度;
ΔP, ΔQ——有功功率和无功功率的变化。
通过分析等值电抗的变化特性以及潮流状态在等值前后的一致性, 根据等值前后电压无功特性保持一致的原则, 利用本地数据求取等值参数, 然后在优化计算中, 根据优化前后电压偏差的不变性对优化电压进行修正。
1.2 分布式光伏发电中压配电网的电压降
图 1所示的配电网采用分布式电源连接, 通过分析网络图可计算出通过配电线的电压降估值为
| $ \Delta V \approx \frac{{R\left( {{P_{{\rm{PV}}}} - {P_{\rm{L}}}} \right) + X\left( { \pm {Q_{{\rm{PV}}}} - {Q_{\rm{L}}}} \right)}}{{{V_{\rm{N}}}}} $ | (4) |
式中: R, X——配电线路的电阻和电抗;
VN——标称总线电压。
由式(4)可知, 由于电抗较高, 中压配电网的X/R值较为规律, 因此配电线路的电压变化依赖配电线路的阻抗和所接负载的功率因数。此外, 分布式发电系统还会造成电压升高与逆潮流, 但配电网注入光伏发电的无功功率可以降低电压与减少逆潮流, 有助于电压控制。
1.3 分布式光伏发电无功功率容量
基于逆变器的分布式光伏发电在优化配置逆变器时考虑了光伏系统的发电概率, 通过逆变器的光伏发电有功功率和无功功率受到逆变器自身容量的限制[7-9], 具体为
| $ \sqrt {P_{{\rm{PV}}i}^2 + Q_{{\rm{PV}}i}^2} \le S_{PVi}^{\max } $ | (5) |
式中: PPVi, QPVi——光伏系统母线i的有功功率和无功功率;
SPVimax——光伏系统母线i的最大视在功率。
配电网中所有的光伏发电单元的功率因数(Power Factor, PF)必须在0.9和滞后的PF之间。如果光伏发电单元产生最大的视在功率, 其有功功率[10]为
| $ {P_{{\rm{PV}}i}} = {S_{{\rm{PV}}i}}\cos \left( {{\theta _{{\rm{PV}}}}} \right) = {S_{{\rm{PV}}i}}{\rm{PF}} $ | (6) |
式中: SPVi——光伏系统母线i的视在功率;
θPV——光伏系统有功功率角。
因此, 光伏逆变器必须能够处理视在功率比光伏发电最大有功功率高10%左右的电流。光伏发电的最大无功功率[11]为
| $ {Q_{{\rm{PV}}i}} = S_{{\rm{PV}}i}^{\max }\sin \left( {{\theta _{{\rm{PV}}}}} \right) = S_{{\rm{PV}}i}^{\max } \times {\rm{PF}} $ | (7) |
由式(7)可知, 光伏发电的无功功率依赖于分布式光伏发电的视在功率和功率因数[12]。图 2为基于逆变器的分布式光伏发电的有功-无功图, 包括一个光伏发电的无功总量。其中, SPV, N为光伏系统额定视在功率; PPV(t)为光伏发电的有功功率函数; QPV(t)为光伏发电的无功功率与时间的函数; SPV(t)为光伏发电的视在功率与时间的函数。由图 2可知, 无功功率的供应有助于降低有功功率的注入。
2 利用PSO算法的无功优化
以基于逆变器的分布式光伏发电无功优化为目标, 通过标称电压来调节电压, 优化母线网络的无功功率。研究的目标函数与约束条件可设置如下。
2.1 目标函数
光伏发电的无功输出可以计算为配电网中不同母线网络中出现的总无功功率[12], 因此, 无功优化可以定义为有约束目标优化的问题, 为
| $ {\rm{Min}}\;F = \sum\limits_{i = 1}^N {\left\{ {{Q_{{\rm{L}}i}} + {V_i}\sum\limits_{k = 1}^n {{V_k}\left[ {{G_{ik}}\sin \left( {{\delta _{ik}}} \right) - {B_{ik}}\cos \left( {{\delta _{ik}}} \right)} \right]} } \right\}} $ | (8) |
式中: QLi——与光伏连接的母线i负荷所要求的无功功率;
n——由第i条母线连接的母线数量。
2.2 约束函数
优化算法中约束服从于目标函数, 包括网络电压VG和光伏发电的无功功率QPV输出范围, 其调节的上下限为
| $ \left\{ {\begin{array}{*{20}{c}} {{P_i} = {P_{{\rm{G}}i}} + {P_{{\rm{PV}}i}} - {P_{{\rm{L}}i}}}\\ {{Q_i} = {Q_{{\rm{G}}i}} + {Q_{{\rm{PV}}i}} - {Q_{{\rm{L}}i}}} \end{array}} \right. $ | (9) |
| $ V_{{\rm{PV}}i}^{\min } \le {V_{{\rm{PV}}i}} \le V_{{\rm{PV}}i}^{\max } $ | (10) |
| $ Q_{{\rm{PV}}i}^{\min } \le {Q_{{\rm{PV}}i}} \le Q_{{\rm{PV}}i}^{\max } $ | (11) |
式中: PGi, QGi——由电网反馈给母线i的有功功率和无功功率;
PLi, QLi——母线i负荷所要求的有功功率和无功功率;
VPVimin, VPVimax——与光伏连接的母线i可能的最小电压和最大电压;
QPVimin, QPVimax——与光伏连接的母线i的最小功率和最大无功功率。
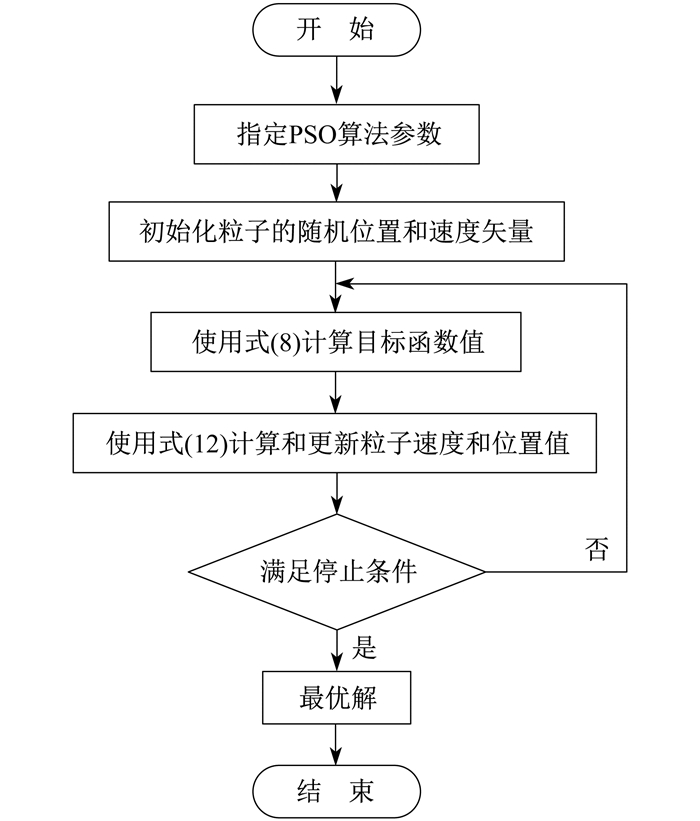
2.3 PSO算法
根据前述所提供的优化算法中目标函数和约束条件要求, 采用PSO算法解决优化问题。PSO算法的数值解释[13]为
| $ \begin{array}{l} \\ \left\{ {\begin{array}{*{20}{l}} {v_j^{k + 1} = {w_j}v_j^k + {c_1}{n_{{\rm{rand}}}} \times \left( {{p_{{\rm{best}}, j}} - s_j^k} \right) + {c_2}{n_{{\rm{rand}}}} \times \left( {{g_{{\rm{best}}, j}} - s_j^k} \right)}\\ {Q_{{\rm{PV}}i}^{k + 1} = Q_{{\rm{PV}}i}^k + \left( {v_j^{k + 1} \times C} \right)} \end{array}} \right. \end{array} $ | (12) |
式中: vjk——迭代第k次时粒子j的速度;
vjk+1——粒子j的修正速度;
wj——粒子j的速度权函数;
c1, c2——权重系数;
nrand——[0, 1]的随机数;
pbest, j——粒子j的个体极值;
sjk——迭代第k次时粒子j的当前位置;
gbest, j——粒子j的全局极值;
QPVik——迭代第k次时母线i上光伏的无功功率;
C——压缩因子。
为了提高PSO算法的收敛性, 引入压缩因子, C=0.352, 为
| $ C = \frac{2}{{\left| {2 - \varphi - \sqrt {{\varphi ^2} - 4} } \right|}}\;\;\;\;\left( {4.1 \le \varphi \le 4.2} \right) $ | (13) |
随着功率因数角φ值的增大, 由于粒子群体种类增加, 所以压缩因子C减小并收敛变慢。
2.4 解决过程
3 结果与分析
以单一径向22 kV配电系统为例, 配电网以115 kV/22 kV电网为主, 采用10 MW配电变压器[17]。单馈线路系统如图 4所示。
馈线由包括变压器母线在内的5条母线组成。利用光伏发电的无功优化, 在电网规范下馈线中的电压保持在正常值的±5%[18]。利用一个15 min的负载数据样本建模配电网中的负载变化, 对一天15 min额定值2 MW的光伏发电功率数据进行采样, 并将其缩放为系统中发电功率变化的模型[19], 随后采取集中控制策略探究光伏系统和变压器有载分接开关的运行情况。径向配电网参数如表 1所示。
表 1
径向配电网参数
| 参数 | 变量值 |
| 额定变压器 | 10 MW, 115 kV/22 kV |
| 各额定光伏系统/MW | 2 |
| 各线路阻抗/(Ω·km-1) | 0.210 67+j0.298 6 |
| 各线路长度/km | 10 |
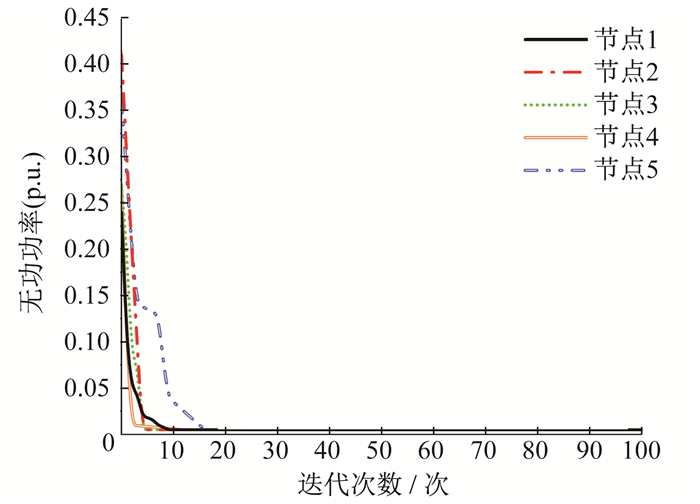
图 5为在配电网中采用PSO算法无功优化的适应性曲线。由图 5可知, 在第15次迭代时, 所有配电网的无功功率收敛至零, 提供了遵循目标函数和约束条件的最佳解。
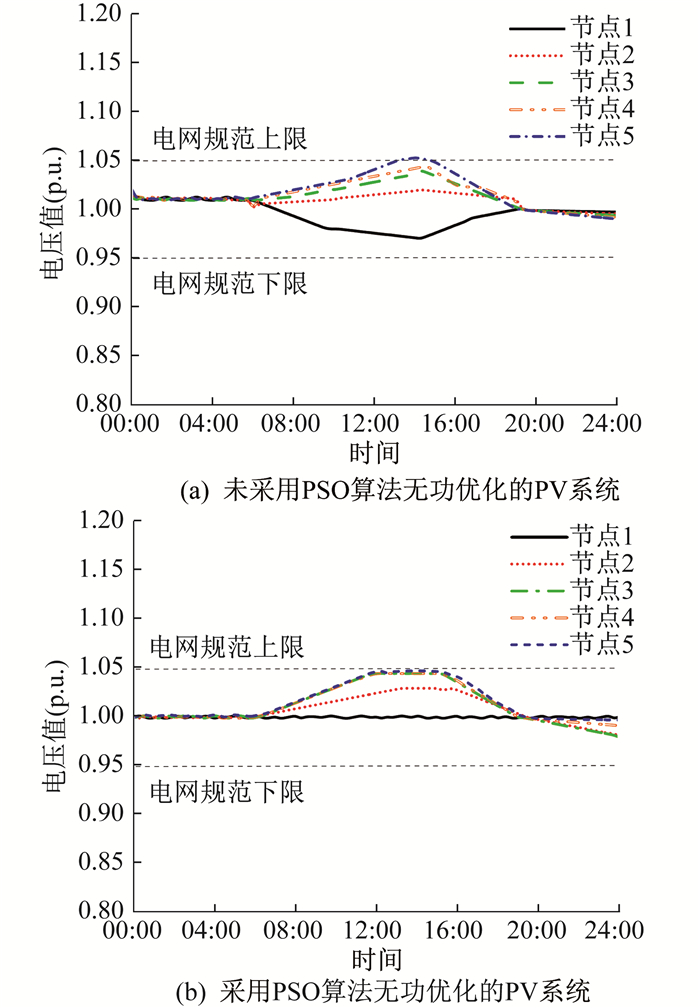
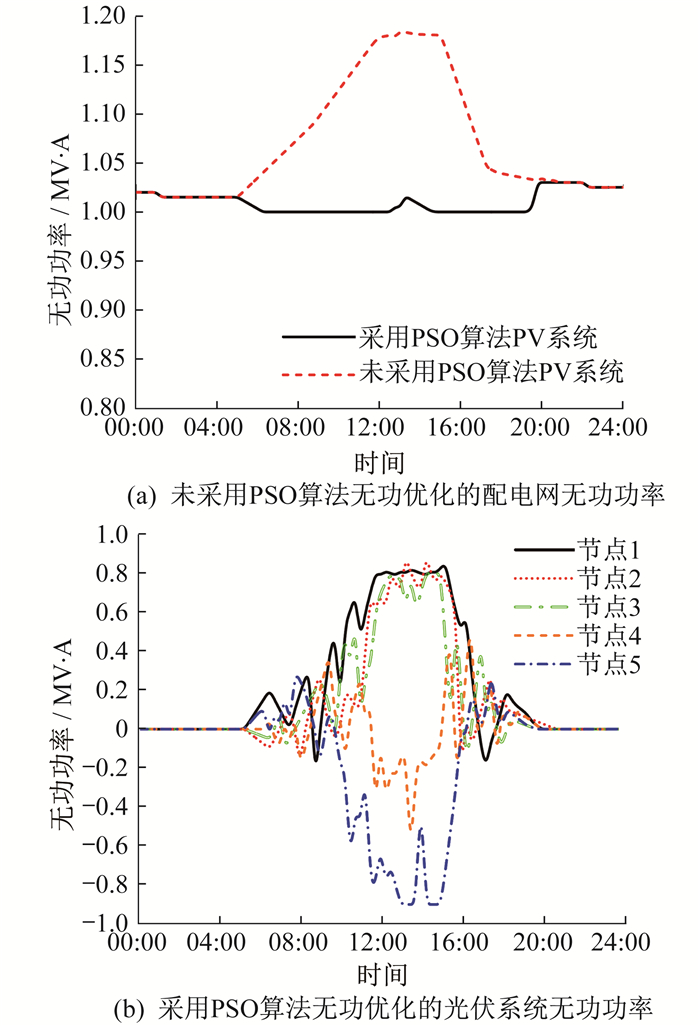
图 6为光伏系统日总线电压仿真结果。由图 6(a)可以看出, 除第5条光伏总线的电压大小超过电网规范限值外, 其余均在规定范围内。究其原因, 是由于第5条光伏总线是一条40 km的长线路, 11:00到15:30时, 产生的高有功功率注入配电网, 导致了逆潮流和电压升高的问题。由图 6(b)可知, 提出的无功算法将所有总线电压值控制在规定的范围内。
图 7为配电网和光伏系统日无功功率变化。由图 7(a)可知, 对照组会从电网中吸收更多的无功, 这是因为配电网中逆潮流造成了有功损耗和无功损耗, 导致配电网无功功率增加[20]。基于PSO算法的无功优化能将配电网的无功值降低到接近零, 光伏发电中对配电网的无功功率消耗少。由图 7(b)可知, 该算法可得约束条件下各段光伏系统的无功优化。
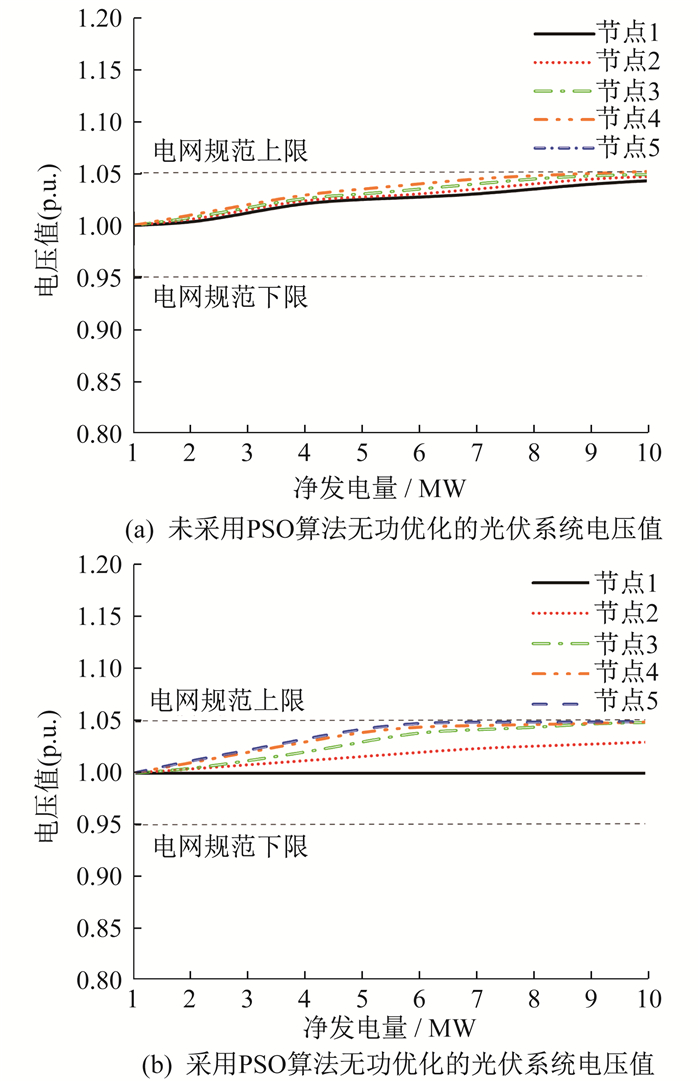
图 8为在净发电量为1~10 MW时, 采用与未采用PSO算法无功优化的光伏系统电压仿真结果。由图 8(a)可知, 当增加净发电量时, 节点1母线电压增加, 节点5母线电压超过1.05(p.u.), 母线电压超出电网规范要求的范围。由图 8(b)可知, 采用PSO算法的无功优化的光伏系统可将光伏系统所有母线电压控制在电网规范要求的范围内。
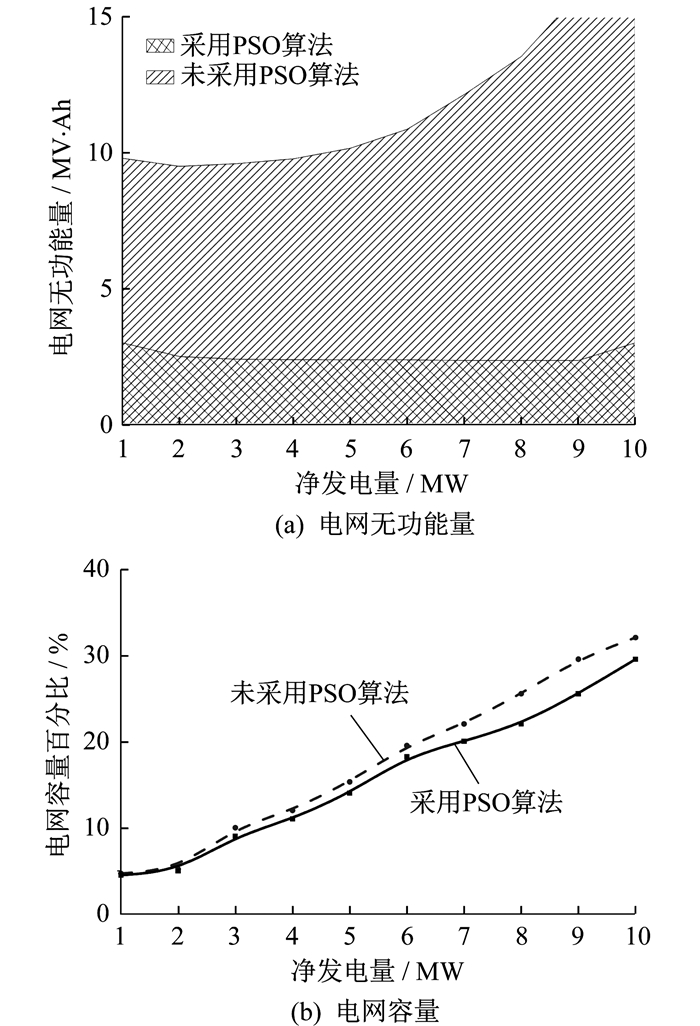
图 9为无功优化的光伏系统仿真结果。由图 9(a)可知, 采用PSO算法时从配电网中消耗的无功能量少, 其值小于3 MV·Ah。由图 9(b)可知, 采用PSO算法时, 每个净发电量处的电网容量更少。
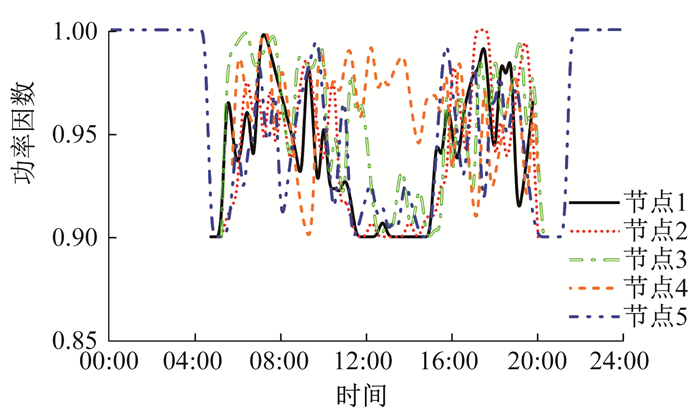
图 10为采用PSO算法日无功优化调节光伏系统功率因数的仿真结果。由图 10可知, 基于PSO算法的无功优化可通过光伏系统功率因数作为仿真约束进行调节, 由于系统设置功率因数受到超前值0.9和滞后值0.9的限制, 在04:00和22:00附近时, 系统进入PSO调节前后有一定的波动性, 但总体范围符合要求。
4 结语
针对分布式光伏发电中存在的节点电压升高、逆潮流和无功功率不足等问题, 对分布式光伏发电中压配电网中无功优化进行了分析, 提出了利用PSO算法对中压配电网进行无功优化的策略, 以实现基于逆变器的分布式光伏电源的电压调节和无功优化。验证了基于PSO算法的5条母线的中压配电网系统的有效性, 实现了母线无功优化与电压偏差最小的目标函数。通过对比未采用和采用PSO算法无功优化的光伏系统的仿真结果发现, 该方法能解决高光伏发电中无功优化的问题, 能够将所有母线电压控制在电网规范规定的范围内, 能够以最小配电网无功功率提供光伏系统最优无功功率。
参考文献
-
[1]李谆. 电网调度运行中无功功率和电压问题的探讨[J]. 低碳世界, 2016(33): 37-38.
-
[2]王亚光. 交流-直流型电子电力变压器的控制与应用[D]. 武汉: 华中科技大学, 2015.
-
[3]SAMADI A, ERIKSSON R, SODER L, et al. Coordinated active power dependent voltage regulation in distribution grids with PV Systems[J]. Trans Power, 2014, 29(3): 1454-1464.
-
[4]林志超, 罗步升, 宋志坚. 基于非参数估计的电压暂降下敏感设备故障率评估[J/OL]. 电测与仪表. (2016-07-08)[2021-03-26]. http://kns.cnki.net/kcms/detail/23.1202.TH.20210107.1650.020.html.
-
[5]YANG H T, LIAO J T. MF-APSO-Based multiobjective optimization for PV system reactive power regulation[J]. IEEE Transactions on Sustainable Energy, 2015, 6(4): 1346-1355. DOI:10.1109/TSTE.2015.2433957
-
[6]周成, 芮涛, 王群京. 基于模型预测控制的微电网多目标协调优化[J]. 电测与仪表, 2019, 56(22): 44-50.
-
[7]金明雨, 艾芊, 高烨, 等. 光伏并网对继电保护及电能质量的影响分析[J]. 供用电, 2015, 32(12): 71-74. DOI:10.3969/j.issn.1006-6357.2015.12.015
-
[8]肖朝霞, 樊世军, 杨庆新. 基于分层控制策略的光伏-蓄电池系统动态提高并网点功率因数[J]. 电工技术学报, 2016, 31(7): 107-117. DOI:10.3969/j.issn.1000-6753.2016.07.013
-
[9]樊世军. 光伏-蓄电池系统为电网提供有功无功支持研究[D]. 天津: 天津工业大学, 2016.
-
[10]范钧慧, 徐楠, 刘皓明. 含分布式风光电源的配电系统故障恢复策略[J]. 江苏电机工程, 2014, 33(1): 1-4.
-
[11]张贵涛, 龚芬, 王丽晔, 等. 光伏并网逆变器电能质量控制策略[J]. 电力科学与技术学报, 2017, 32(4): 50-56. DOI:10.3969/j.issn.1673-9140.2017.04.008
-
[12]付天宇. 电网友好型分布式光伏发电系统[J]. 通信电源技术, 2018, 35(2): 52-53.
-
[13]谭丹, 杨洪耕. 基于故障识别法的电压暂降监测点的优化配置[J]. 电力系统保护与控制, 2013, 41(20): 7-12. DOI:10.7667/j.issn.1674-3415.2013.20.002
-
[14]沈晓东, 刘俊勇, 刘彦. 基于节点不平衡功率的粒子群潮流转移控制算法[J]. 电力系统自动化, 2012, 36(7): 1-5.
-
[15]孔维珍. 基于微粒群算法的城市轨道交通列车运行调整研究[D]. 兰州: 兰州交通大学, 2013.
-
[16]陈思佳, 赵诗琰, 王广君. 高渗透率下兼顾光伏出力和网损的配电网运行优化方法[J/OL]. 电测与仪表. (2013-01-07)[2021-03-26]. http://kns.cnki.net/kcms/detail/23.1202.TH.20201010.1442.002.html.
-
[17]石江浩, 李锴, 张师. 基于PSO的风电并网系统多时段无功优化控制[J]. 电气开关, 2020, 58(4): 44-46. DOI:10.3969/j.issn.1004-289X.2020.04.011
-
[18]赵金焕, 马平. 计及DG功率不确定性的配电网多目标无功优化[J]. 电气工程学报, 2020, 15(3): 65-71.
-
[19]李昌华, 毕成功, 李智杰. 基于改进PSO算法的人群疏散模型[J]. 系统仿真学报, 2020, 32(6): 1000-1008.
-
[20]刘梦依, 邱晓燕, 张志荣, 等. 计及风光出力相关性的配电网多目标无功优化[J]. 电网技术, 2020, 44(5): 1892-1899.