|
|
|
发布时间: 2022-06-25 |
计算机与信息科学 |
|
|
|
收稿日期: 2021-10-22
基金项目: 上海市青年科技英才扬帆计划(19YF1416800)
中图法分类号: TL333
文献标识码: A
文章编号: 2096-8299(2022)03-269-05
|
摘要
为了将代理模型应用于核工程反应堆热工水力现象中,以再淹没现象为研究对象,构建代理模型,并通过控制实验参数的数量,来化解精度与效率之间的矛盾。首先使用拉丁超立方方法抽取输入样本,并通过RELAP5建模获取输出样本,由MATLAB分别构建RBF神经网络代理模型和Kriging代理模型,对包壳峰值温度(PCT)进行拟合。然后分析比较了2种代理模型的拟合结果,发现2种代理模型的相对误差值均小于0.15%,均适用于再淹没现象;Kriging代理模型的拟合精度高于RBF神经网络代理模型。
关键词
RBF神经网络; Kriging; 代理模型; 再淹没现象
Abstract
In order to apply the surrogate model to the thermal hydraulic phenomena of nuclear engineering reactors, this paper takes the reflood phenomenon as the research object, constructs the surrogate model, and solves the contradiction between accuracy and efficiency by controlling the number of experimental parameters.Firstly, the input samples are extracted by Latin hypercube method, and the output samples are obtained by RELAP5 modeling and calculation.The RBF neural network and Kriging surrogate model are constructed by MATLAB to fit the peak temperature of cladding.The fitting results of RBF and Kriging surrogate models are analyzed and compared.It is found that the relative errors of the two surrogate models are less than 0.15%, which can be applied to the reflood phenomenon.The fitting accuracy of Kriging surrogate model is higher than that of RBF neural network surrogate model.
Key words
radial basis function neural network; Kriging; surrogate model; reflood phenomenon
最佳估算加不确定性分析方法是近年来核电厂安全评审的主要方法。在利用反应堆最佳估算热工水力程序进行事故计算时, 需要进行不确定度评估以保证计算结果的保守性, 而不确定性评估需要通过大量的样本点抽样计算从而得到输出结果(如包壳峰值温度等关键参数)的不确定性。为了节省计算时间, 同时又能保证拟合计算的精度, 最为有效的方法是建立代理模型。
近年来, 代理模型技术及基于代理模型的优化算法在航空、汽车等行业得到了广泛应用和深入发展。2001年, SIMPSON T W等人[1]全面而系统地论述了代理模型技术、试验设计技术的理论进展, 并为代理模型在工程实践中的应用提出了指导性建议; 2006年, 刘克龙等人[2]将Kriging代理模型[3]应用于结构形状优化方法研究; 2011年, 孙美建和詹洁[4]将Kriging代理模型应用于机翼气动外形优化; 2014年, 白俊强等人[5]将改进的径向基函数(Radial Basis Function, RBF)神经网络[3]应用在翼梢小翼优化设计; 2020年, 夏志等人[6]将常用的4种代理模型应用于水下结构物基座阻抗性研究, 发现Kriging代理模型对拟合基座参数有较好的适用性; 2021年, 肖乾等人[7]将RBF神经网络代理模型应用于车辆/轨道参数多目标优化。然而针对核工程热工水力现象方面的代理模型应用很少, 相关的文献也不多见。因此, 将各种常用代理模型应用于核工程的热工水力现象中, 从而解决不确定性评估中精度与效率的矛盾是本文的研究重点。
常用的代理模型包括Kriging代理模型、RBF代理模型、支持向量机、多项式响应面模型和人工神经网络模型等, 然而不同的代理模型对于同一问题的适用性是不同的。为了探究代理模型在热工水力现象中的适用性, 本文选择大破口事故中的第3阶段——再淹没现象作为案例, 建立以RBF神经网络和Kriging为基础的代理模型, 并比较代理模型的计算结果与RELAP5程序计算结果之间的误差。
1 数学模型
由于RBF神经网络和Kriging模型对非线性函数均有良好的拟合能力, 且能适应复杂的非线性函数, 所以本文选择了这2种数学形式的代理模型来替代反应堆热工水力计算中复杂的再淹没现象模拟计算。
1.1 RBF神经网络代理模型
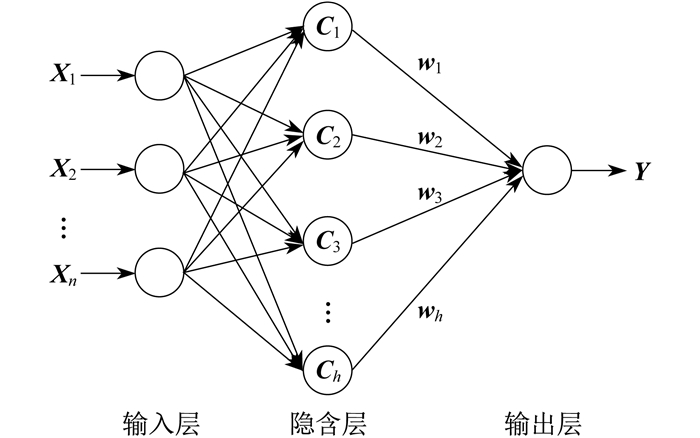
RBF神经网络是一种使用径向基函数作为激活函数的人工神经网络, 其输出是输入的径向基函数和权重系数的线性组合。RBF神经网络的原理如图 1所示。图 1中: 输入层Xj(j=1, 2, 3, …, n, n为样本点个数)为第j个样本点的设计变量向量; 隐含层Cj(j=1, 2, 3, …, h, h为隐含层结点数)为第j个样本点对应的径向基函数向量; wj(j=1, 2, 3, …, h)为第j个样本点对应的权值向量; 输出层Y为目标函数向量, 由隐含层中带有权值的径向基函数相加而得出。
RBF神经网络的激活函数可表示为
| $ R\left( {{x_j} - {c_i}} \right) = {{\rm{e}}^{\frac{{{{\left\| {{x_j} - {c_i}} \right\|}^2}}}{{2{\sigma ^2}}}}} $ | (1) |
式中: xj——第j个输入样本;
ci——第i个节点的中心;
σ——宽度参数, 控制节点的径向范围。
由RBF神经网络结构可得到网络的输出为
| $ {y_i} = \sum\limits_{i = 1}^h {{w_{ij}}} {{\rm{e}}^{\frac{{{{\left\| {{x_j} - {c_i}} \right\|}^2}}}{{2{\sigma ^2}}}}} $ | (2) |
式中: wij——基函数权重。
采用最小二乘法的损失函数可表示为
| $ L = \frac{1}{j}\sum\limits_{j = 1}^h {{{\left\| {{d_j} - {y_j}{c_i}} \right\|}^2}} $ | (3) |
式中: j——样本个数;
dj——样本点与中心点ci对应的宽度。
1.2 Kriging代理模型
Kriging代理模型作为一种改进的线性回归分析技术, 包含了一个线性回归部分和一个随机过程。通常Kriging代理模型可以表示为
| $ f\left( x \right) = g\left( x \right) + z\left( x \right) $ | (4) |
式中: g(x)——确定性部分, 称为确定性漂移;
z(x)——随机过程, 称为涨落。
z(x)具有以下的统计性质
| $ \left\{ {\begin{array}{*{20}{l}} {E\left( {z\left( x \right)} \right) = 0}\\ {{\rm{Var}}\left( {z\left( x \right)} \right) = {\sigma ^2}}\\ {E\left( {z\left( {{x^i}} \right), z\left( x \right)} \right) = {\sigma ^2}R\left( {\theta , x, {x^i}} \right)} \end{array}} \right. $ | (5) |
式中: E——期望;
Var——方差;
R(θ, x, xi)——点x和点xi之间的相关函数, 表示样本点之间的空间相关性;
θ——相关函数中的参数, 通过优化θ可以调节样本点之间的相关性。
相关函数直接影响到Kriging代理模型的精度, 而高斯相关函数模型相对平滑且无限可微, 在大多数工程问题中可以得到较好的计算结果, 因此应用范围最广。
高斯模型函数为
| $ R\left( {\theta , {d_i}} \right) = {{\rm{e}}^{\left( { - \frac{{{d^2}}}{{{\theta ^2}}}} \right)}} $ | (6) |
式中: di——第i个输入样本与待测点x之间的距离。
用样本点xi的响应值yi的线性加权叠加插值来计算待测点x响应值, 可得
| $ \hat f\left( x \right) = \mathit{\boldsymbol{w}}{\left( x \right)^{\rm{T}}}\mathit{\boldsymbol{Y}}\left( x \right) $ | (7) |
式中: w(x)——待求权系数向量, w(x)=[w1, w2, w3, …, wn]T;
Y(x)=[y1, y2, y3, …, yn]T。
根据无偏条件和方差最小条件, 并结合拉格朗日乘子法, 可以求得权系数向量w(x)。
2 代理模型在再淹没现象中的应用
再淹没现象发生在大破口失水事故的第3个阶段。安注系统的冷却水注入堆芯, 当水到达燃料棒底端时开始进入再淹没。由于燃料棒表面温度过高, 冷却水不会立刻润湿包壳, 而是先蒸发成蒸汽膜, 润湿前沿推进的速度会低于冷却剂注入的速度, 直到淹没整个堆芯。再淹没过程会经历从单相液、核态沸腾、过渡沸腾、膜态沸腾到单相汽的流型, 计算复杂且程序运行时间过长。因此, 在进行不确定性评估之前建立代理模型可以显著提高评估效率。
FEBA[8-9]是由德国卡尔斯鲁厄核研究中心设计的, 用来模拟再淹没现象的实验。本文针对再淹没现象建立实验台架, 利用最佳估算系统程序RELAP5模拟实验工况, 通过拉丁超立方抽样并运行程序得到训练样本; 再利用训练样本建立RBF神经网络代理模型和Kriging代理模型, 并与验证样本比较代理模型计算结果和RELAP5程序计算结果的误差, 分析两类代理模型的适用性。
2.1 实验建模及重要参数选择
实验环路流程是, 冷却水由下部水箱(相当于堆芯底部)以恒定流速注入测试段(模拟堆芯再淹没阶段), 在测试段中发生再淹没现象, 加热棒(模拟堆芯)由初始的过热状态到被冷却水淹没后逐渐冷却, 台架的顶部装有汽水分离器及压力控制系统来维持恒定的系统压力。
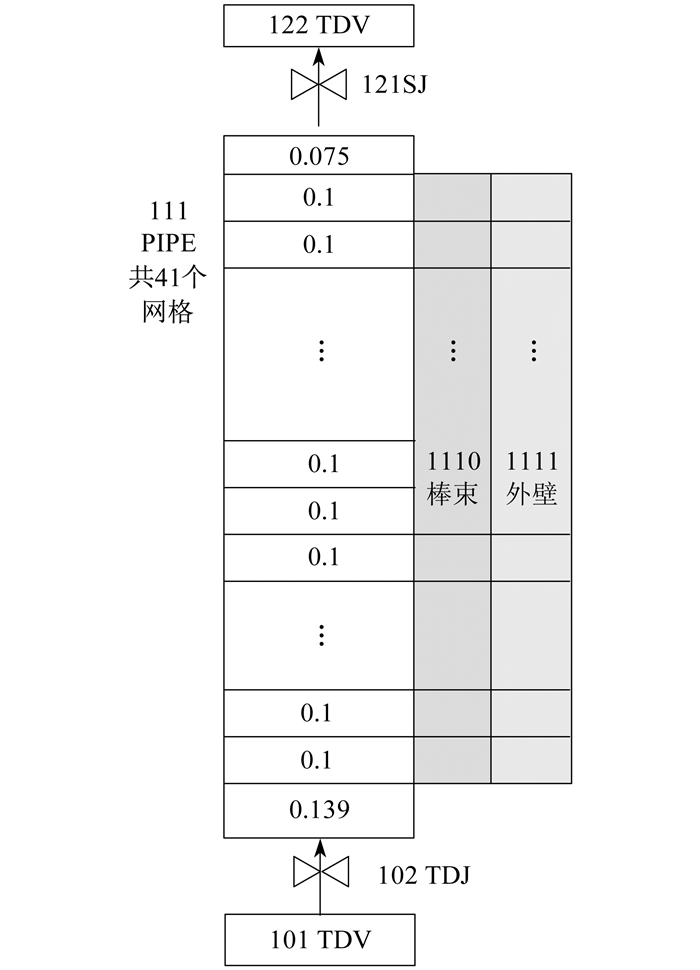
RELAP5对FEBA台架的建模节点图[10]如图 2所示。
图 2中, 101 TDV模拟实验台架的进口水箱, 用来确定冷却水的温度边界; 102 TDJ模拟入口的阀门, 用以限定冷却剂流入测试段进口流速的边界条件; 111 PIPE模拟测试段, 在轴向上划分出41个子控制体, 上下腔室分别由第一个和最后一个不加热子控制体模拟, 长度分别为0.139 m和0.075 m; 由中间长度均为0.1 m的39个子控制体模拟加热段, 且一一对应热构件的轴向节点; 热构件1110模拟电加热棒束, 1111模拟无热源的金属外壁。根据材料结构, 在1110棒束上径向划分9个节点, 在1111外壁上划分3个节点。模拟过程中, 在热构件1110和1111上都应用了再淹没模型, 最大加密节点数设置为64。
由FEBA台架的评估情况认为RELAP5程序可以正确地模拟再淹没这一物理现象, 但对包壳峰值温度(Peak Cladding Temperature, PCT)的预测仍存在一定的不确定性, 且在安全评审和概率安全评价分析中的重要关注点是再淹没过程包壳的峰值温度, 因此本文选择PCT作为模型输出结果。
为了选择对PCT造成影响的输入参数, 这里可以参考以下几类参数[12]:
(1) 基本参数, 包括边界条件, 如流速、功率等, 以及材料物性、几何尺寸、网格划分等;
(2) 全局模型参数, 包括不同流型的本构关系模型, 如过渡沸腾壁面传热系数、泡状流相间摩擦力等;
(3) 模型中的局部重要参数, 包括涉及模型选择的重要阈值, 模型公式中的系数, 如临界韦伯数、气泡直径、最小膜态沸腾温度等。
为了节省程序的计算时间, 本文选择了216工况[11]下的进口流速、系统压力和进口冷却水温度3个基本参数作为模型输入参数, 参数的不确定性范围如表 1所示。
表 1
基本参数及其不确定性范围
| 参数名称 | 不确定性范围 |
| 进口流速/(m·s-1) | 0.038±10% |
| 系统压力/MPa | 0.41±10% |
| 冷却水温度/K | 310±5 |
2.2 代理模型的建立及误差分析比较
代理模型的建立流程为: 使用拉丁超立方方法对3个输入参数在各自取值范围内分层抽样100组; 将100组输入样本代入RELAP5程序, 得到输出结果, 这里选择PCT作为关键的输出样本; 将输入和输出组成的样本分为训练样本和测试样本, 利用训练样本分别建立RBF神经网络代理模型和Kriging代理模型; 将测试样本的输入点代入代理模型得到输出, 并比较结果误差, 分析其适用性。
在上述流程中只取了100组数据的原因是因为运行出一组数据所花的时间成本较高, 而且本文的研究目的是初步尝试将各种代理模型应用于热工水力工程, 所以选取的数据样本没有太大。上述3个基本参数取值范围内由RELAP5程序计算得出100组的PCT相对取值范围是1 121.4~1 131.4 K。这里将100组样本分为不同比例的5组, 对比RBF神经网络代理模型和Kriging代理模型在不同训练样本数目下训练出的模型精度误差, 用以分析2种代理模型对于拟合再淹没现象的适用性和稳定性。
通过不同比例的样本数目构建RBF神经网络代理模型和Kriging代理模型的精度检验结果如表 2所示。
表 2
RBF神经网络和Kriging代理模型的精度检验
| 样本/个 | 相对误差/% | 均方误差 | |||||
| 训练 | 测试 | RBF | Kriging | RBF | Kriging | ||
| 50 | 50 | 0.112 9 | 0.022 6 | 12.917 8 | 0.854 2 | ||
| 60 | 40 | 0.025 6 | 0.004 3 | 15.795 8 | 0.557 5 | ||
| 70 | 30 | 0.099 9 | 0.042 0 | 8.734 5 | 2.018 3 | ||
| 80 | 20 | 0.068 5 | 0.014 6 | 17.113 8 | 2.145 1 | ||
| 90 | 10 | 0.081 9 | 0.014 5 | 8.875 5 | 1.304 2 | ||
表 2中: 训练样本为构建代理模型时所需的训练点; 测试样本为对构建好的代理模型进行测试的点; 均方误差是指代理模型的拟合值与RELAP5程序获得的测试真值之间差值的平方和的平均数; 相对误差是指对应的拟合值与测试真值之间差值的平均数与测试真值平均数的比值。
由表 2可以看出: 在各比例下, Kriging代理模型和RBF代理模型最小相对误差的比例均为6∶ 4, 但2种模型的相对误差值均不随训练样本数目的增加而出现确定性规律; 在5组样本中, Kriging代理模型的相对误差不超过0.05%, 而RBF代理模型的相对误差不超过0.15%, 即2种模型均适用于再淹没现象。
从均方误差值来看, Kriging代理模型的最小值比例为6∶ 4, 与最小相对误差比例相同, 而RBF代理模型的最小值比例为7∶ 3, 与最小相对误差比例不同; 从数值上看, Kriging代理模型的值在0~2.5之间, 而RBF代理模型的值都较大, 在8~18之间。这表明2种代理模型拟合的误差值与RELAP5程序计算所得的PCT误差值相差不大, 即100组数据能够满足再淹没现象的拟合需求且并未造成过拟合[12]。由Kriging代理模型的值比RBF代理模型小, 可以判断出Kriging代理模型的拟合精度比RBF代理模型更高。
3 结语
针对热工水力程序中的不确定性评估需要用大量样本进行计算且耗时长等特点, 本文提出了通过建立代理模型的方法来解决热工水力程序不确定性评估中计算精度与效率的矛盾。以再淹没现象为案例, 通过数据分析表明, RBF神经网络代理模型和Kriging代理模型的拟合结果与RELAP5输出参数的相对误差值都不超过0.15%, 且在均方误差值上2种代理模型拟合的误差值与RELAP5程序计算所得的PCT误差值相差不大, 并未造成过拟合, 即两者均适用于再淹没现象; 但是相比于RBF神经网络代理模型, Kriging代理模型拟合结果的均方误差值更小, 表明在本案例中Kriging代理模型的拟合精度高于RBF神经网络代理模型。
基于代理模型在反应堆热工水力现象中的应用现状, 在之后的研究中可以将支持向量机、人工神经网络等更多类型的代理模型用于反应堆热工水力现象中, 并通过对比分析模型耗时、拟合精度等参数, 可以选出最适用于反应堆热工水力现象的代理模型。
参考文献
-
[1]SIMPSON T W, PEPLINSKI J D, KOCHET P N, et al. Metamodels for computer—based engineering design: survey and recommendations[J]. Engineering with Computers, 2001, 17(2): 129-150. DOI:10.1007/PL00007198
-
[2]刘克龙, 姚卫星, 穆雪峰. 基于Kriging代理模型的结构形状优化方法研究[J]. 计算力学学报, 2006(3): 90-93.
-
[3]ALEXANDER I J F, ANDRAS S, ANDY J K. 基于代理模型的工程设计: 实用指南[M]. 韩忠华, 张科旋, 译. 北京: 航空工业出版社, 2018: 43-53.
-
[4]孙美建, 詹浩. Kriging模型在机翼气动外形优化中的应用[J]. 空气动力学学报, 2011, 29(6): 759-764. DOI:10.3969/j.issn.0258-1825.2011.06.012
-
[5]白俊强, 王丹, 何小龙, 等. 改进的RBF神经网络在翼梢小翼优化设计中的应用[J]. 航空学报, 2014, 35(7): 1865-1873.
-
[6]夏志, 刘均, 程远胜. 基于代理模型的水下结构物基座阻抗特性快速预报[J]. 中国舰船研究, 2020, 15(3): 81-87.
-
[7]肖乾, 罗超, 欧阳志许, 等. 基于RBF神经网络代理模型的车辆/轨道参数多目标优化[J]. 机械强度, 2021, 43(2): 319-326.
-
[8]IHLE P, RUST K. FEBA-flooding experiments with blocked arrays evaluation report[R]. Karlsruhe: Kernforschuntgszentrum Karlsruhe GMBH, 1984.
-
[9]IHLE P, RUST K. FEBA-flooding experiments with blocked arrays data report 1, test series Ⅰ through Ⅳ[R]. Karlsruhe: Kernforschuntgszentrum Karlsruhe GMBH, 1984.
-
[10]HOCHREITER L E, LEE N, MASSIE H W, et al. PWR FLECHT SEASET 161-rod bundle flow blockage task, task plan report[R]. [S. l. ]: Westinghouse Electric Corporation, 1980.
-
[11]李冬. 最佳估算模型的不确定性量化方法研究及再淹没模型评估的应用[D]. 上海: 上海交通大学, 2017.
-
[12]高震宇. 基于深度卷积神经网络的图像分类方法研究及应用[D]. 合肥: 中国科学技术大学, 2018.