|
|
|
发布时间: 2022-08-25 |
综合能源管理 |
|
|
|
收稿日期: 2022-03-13
中图法分类号: TM615
文献标识码: A
文章编号: 2096-8299(2022)04-0379-07
|
摘要
并网逆变器死区会降低输出电压波形质量, 同时也会对负载和电网造成不同程度的影响。为减小死区效应及外部干扰对逆变器输出性能的影响, 提出了一种具有死区效应的光伏逆变系统积分滑模控制策略。对死区机理进行分析, 并建立逆变器数学模型; 构造带有比例积分项的抗扰动状态观测器, 对干扰状态进行有效估计; 结合矢量控制构建一类非奇异终端滑模控制器, 采用Lyapunov函数证明系统的渐进稳定性。最后, 通过仿真验证了所提控制方法的有效性。
关键词
逆变器; 死区效应; 参数不确定; 积分滑模控制
Abstract
Dead zone of grid-connected inverter will reduce the quality of output voltage waveform and affect load and power grid in different degrees. In order to reduce the influence of dead zone effect and external disturbance on the output performance of photovoltaic inverter, an integral sliding mode control with dead zone effect was proposed. Dead zone mechanism was analyzed, considering the dead zone to establish the inverter mathematical model. An anti-disturbance state observer with proportional integral term was constructed to estimate the disturbance state effectively. A class of non-singular terminal sliding mode controller was constructed with vector control, and the asymptotic stability of the system was proved by Lyapunov function. Finally, the effectiveness of the proposed control method was verified by simulation.
Key words
inverter; dead zone effect; parameter uncertainty; integral sliding mode control
光伏发电在新能源发电领域的占比越来越大, 因此光伏发电系统的核心设备——并网逆变器及其对电网质量的影响得到了广泛研究。三相光伏并网逆变器的控制目标是快速动态响应、零稳态误差、强鲁棒性和低谐波失真。为实现上述控制目标, 国内外学者提出了很多逆变器控制策略, 如比例积分控制、重复控制等, 有效提高了逆变器的输出效果[1-2]。
文献[3]通过分析三相逆变器输出电压的谐波失真, 建立了逆变器数学模型, 提出了一种离散积分滑模控制, 以补偿系统的非线性。为了减小参数不确定和负载扰动的影响, 文献[4]设计了降阶扩张状态观测器以实时估计系统的总扰动, 同时设计改进型重复控制器实现了系统的零稳态误差。文献[5-6]对逆变器死区效应进行了研究, 尤其文献[6]通过对死区的机理研究, 总结了死区对光伏并网逆变系统的不良影响。文献[7-11]主要针对逆变系统的外界干扰和参数不确定问题, 改进了传统控制方法, 引入神经网络或深度学习算法以实现自适应控制, 从而实现输出跟踪期望。现有技术均在一定程度上提高了逆变器的输出能力, 改善了电能质量。但是目前的研究工作中鲜有文献在建立逆变器数学模型时将死区效应考虑在内, 且逆变器控制效果较差。
基于上述分析, 本文提出了一种具有死区效应的光伏逆变系统积分滑模控制策略, 在建立逆变器数学模型和设计控制器时考虑了死区效应。所设计的控制器不仅能够充分利用状态观测器对外界干扰、参数不确定性以及死区引起的干扰进行有效估计, 而且通过非奇异终端滑模控制方法有效避免了传统方法的奇异缺陷, 从而改善了逆变系统的性能, 提高了并网电能质量。最后, 通过动力系统仪器使用与测量(Power System Instrumentation and Measurement, PSIM)仿真验证了所提控制方法的有效性。
1 逆变器死区分析及建模
1.1 死区效应分析
在实际控制系统中, 为防止逆变器上下桥臂同时导通, 必须在开关器件的控制信号中注入一定的死区时间。此外, 开关器件动作本身有一定的延迟, 从而导致实际开关信号与理想信号之间存在一定的时间差。这一时间差称为逆变器死区。
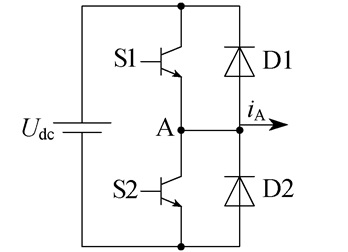
A相桥臂电路示意如图 1所示, 其中指定电流的流出方向为正方向。图 1中, Udc为逆变器直流侧电压, S1和S2为开关信号, D1和D2为反向二极管。在死区持续期间, S1和S2处于关闭状态。因此, A相电流iA的方向决定了D1和D2的开关状态。当iA < 0时, 电流流过D1, 死区期间A相端电压为Udc。当iA>0时, 电流流过D2, 死区期间A相的端电压为零。很明显, 在死区A相的端电压不受开关装置的影响, 而是取决于相电流的方向。
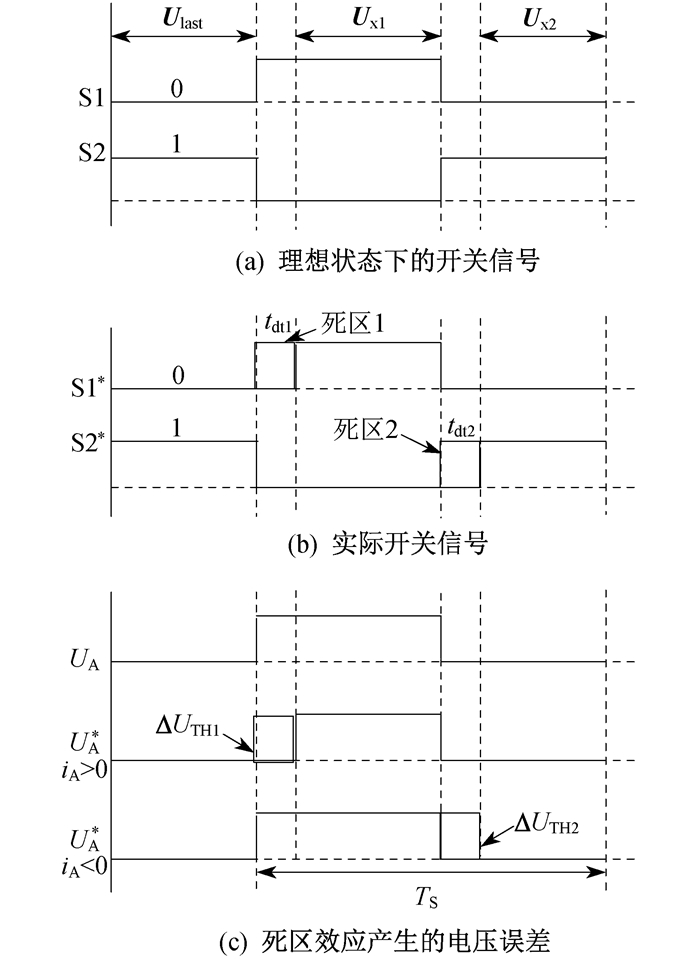
逆变器开关器件在理想状态下和实际运行中的开关信号, 以及开关器件产生的死区效应所引起的电压误差如图 2所示。图 2中, Ulast为上一周期电压矢量, Ux1为第1电压矢量, Ux2为第2电压矢量; tdt1为第1死区时间; tdt2为第2死区时间, S1*和S2*表示实际运行中的开关信号; UA和UA*分别表示A相理想输出端电压和实际输出端电压; TS表示1个完整的开关周期。
由图 2(c)可以明显看出, 逆变器理想输出端电压与考虑死区后输出端电压存在的电压误差为ΔUTH1和ΔUTH2, 其将直接影响并网逆变器的转换效率。因此, 有必要对逆变器开关器件在工作时产生的死区进行建模, 并在考虑死区效应的基础上进行逆变器控制策略的研究。
1.2 死区建模
本文以A相为例, 在考虑到死区会影响逆变器输出电压的情况下进行推导[6]。由于开关状态不连续, 因此在逆变器建模过程中采用了状态空间平均法。为了便于分析, 将逆变器直流侧电容等效成2个电压均为Udc/2的电容串联。假设所引入的逆变器死区时间为td, 开关器件导通时间为ton, 关断时间为toff。
以A相为例, 可得逆变器理想输出电压为
| $U_{\mathrm{AN}^{\prime}}=\frac{U_{\mathrm{dc}}}{2}(2 S-1)$ | (1) |
式中: S——开关函数, 当上桥臂导通时S=1, 当下桥臂导通时S=0。
存在开关函数S的系统是离散的, 且系统开关频率远大于基波频率。为了消除逆变器的时变特性, 用开关周期平均算子对式(1)进行变形, 算子公式为
| $\langle U(t)\rangle_{T_{\mathrm{S}}}=\frac{1}{T_{\mathrm{S}}} \int_t^{t+T_{\mathrm{S}}} U({\tau}) \mathrm{d} \tau$ | (2) |
式中: U(·)——电路中的电量, 本文中指逆变器输出相电压;
| $\left\langle U_{\mathrm{AN}^{\prime}}\right\rangle_{T_{\mathrm{S}}}=\frac{U_{\mathrm{dc}}}{2}\left(2\langle S\rangle_{T_{\mathrm{S}}}-1\right)$ | (3) |
考虑死区时间和开关器件延迟时间, 得到的开关函数S′在1个周期内的平均值为
| $\left\langle S^{\prime}\right\rangle_{T_{\mathrm{S}}}=\frac{T_{\text {on }} \pm\left(t_{\mathrm{d}}+t_{\text {on }}-t_{\text {off }}\right)}{T_{\mathrm{S}}}=D \pm D^{\prime}$ | (4) |
式中: Ton——理想状态下开关管的导通时间;
D——理想状态下的占空比;
D′——考虑死区延迟后的占空比。
D和D′的代数和为实际占空比。其符号取决于A相电流的符号, 当iA < 0时取“+”, 否则取“-”。
由于系统中开关频率远大于基波频率, 且采用了正弦脉宽调制, 因此调制波在1个周期内可近似成常数, 占空比D可表示为
| $D=\frac{1}{2}\left(1+\frac{U_{\mathrm{m}}}{U_{\mathrm{tri}}}\right)$ | (5) |
式中: Um——调制波幅值;
Utri——三角载波幅值。
将式(4)和式(5)代入式(3)中, 得到逆变器A相输出电压在1个周期内的平均值为
| $\left\langle U_{\mathrm{AN}^{\prime}}\right\rangle_{T_{\mathrm{S}}}=U_{\mathrm{dc}}\left(\frac{U_{\mathrm{m}}}{2 U_{\mathrm{tri}}} \pm D^{\prime}\right)$ | (6) |
同理可得三相电压型逆变器的输出电压表达式。为了便于书写以及后续建模, 引入符号函数sgn(), 表达式可改写为
| $ \left\{\begin{array}{l} \left\langle U_{\mathrm{AN}}\right\rangle_{T_{\mathrm{S}}}=\frac{U_{\mathrm{dc}}}{2 U_{\mathrm{tri}}} U_{\mathrm{m}}-\operatorname{sgn}\left(i_{\mathrm{A}}\right) U_{\mathrm{dc}} D^{\prime} \\ \left\langle U_{\mathrm{BN}}\right\rangle_{T_{\mathrm{S}}}=\frac{U_{\mathrm{dc}}}{2 U_{\mathrm{tri}}} U_{\mathrm{m}}-\operatorname{sgn}\left(i_{\mathrm{B}}\right) U_{\mathrm{dc}} D^{\prime} \\ \left\langle U_{\mathrm{CN}}\right\rangle_{T_{\mathrm{S}}}=\frac{U_{\mathrm{dc}}}{2 U_{\mathrm{tri}}} U_{\mathrm{m}}-\operatorname{sgn}\left(i_{\mathrm{C}}\right) U_{\mathrm{dc}} D^{\prime} \end{array}\right. $ | (7) |
| $ \operatorname{sgn}\left(i_{\mathrm{A}}\right)=\left\{\begin{array}{l} 1, i_{\mathrm{A}} \geqslant 0 \\ -1, i_{\mathrm{A}}<0 \end{array}\right. $ | (8) |
式中: UAN, UBN, UCN——逆变器A相、B相、C相的输出电压;
iA, iB, iC——逆变器A相、B相、C相的输出电流。
与逆变器理想输出电压表达式相比, 式(7)多出了-sgn(iK)UdcD′(K=A, B, C)。该部分是在考虑死区和开关延时后所产生的电压损耗, 称为死区畸变电压ΔUDT。
2 考虑死区效应的系统建模
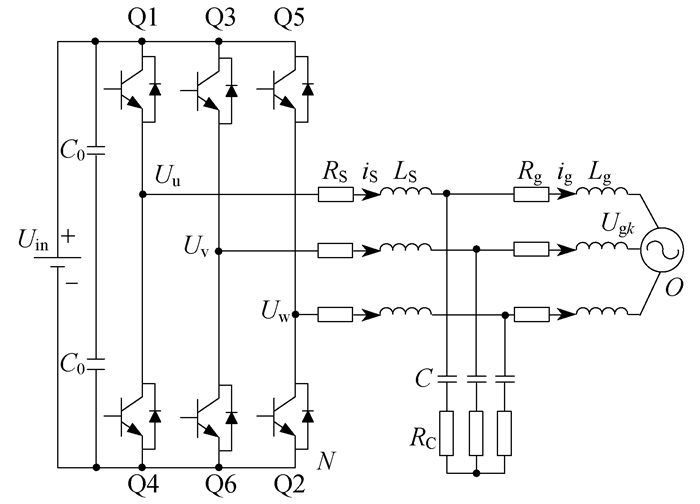
三相电压型逆变器电路拓扑如图 3所示。本文将以此为研究对象进行建模分析。图 3中, Uin为逆变器直流侧输入电压; C0为直流电容; Q1~Q6为逆变器开关器件; Uu, Uv, Uw分别为A相, B相, C相线电压; RS, iS, LS分别为开关器件等效串联电阻、逆变器输出侧电流、逆变器侧电感; Rg, ig, Lg分别为网侧电感的等效串联电阻、网侧电流、网侧电感; C为滤波电容; RC为电容C的等效串联电阻; UgK为网侧电压, K=A, B, C。
在考虑死区效应的情况下, 根据基尔霍夫电压定律可得:
| $ \begin{aligned} &L_{\mathrm{s}} \frac{\mathrm{d} i_K}{\mathrm{~d} t}+\left(R_{\mathrm{L}}+R_{\mathrm{S}}\right) i_K+U_{\mathrm{g} K}= \\ &U_{\mathrm{dc}} S_K+\Delta U_{\mathrm{DT}}+U_{\mathrm{NO}}, K=\mathrm{A}, \mathrm{B}, \mathrm{C} \end{aligned} $ | (9) |
式中: RL——逆变器侧电感的等效串联电阻;
SK——门极信号;
UNO——N点与O点之间的电压。
由于逆变器是对称的三相系统, 所以有
| $ \begin{aligned} U_{\mathrm{NO}}=&-\frac{U_{\mathrm{dc}}}{3} \sum\limits_{K=\mathrm{A}, \mathrm{B}, \mathrm{C}} S_K+\\ & \frac{t_{\mathrm{d}}+t_{\mathrm{on}}-t_{\mathrm{off}}}{3 T_{\mathrm{S}}} U_{\mathrm{dc}} \sum\limits_{K=\mathrm{A}, \mathrm{B}, \mathrm{C}} \operatorname{sgn}\left(i_K\right) \end{aligned} $ | (10) |
在考虑死区效应后, 结合基尔霍夫电流定律, 可得三相电压型逆变器的数学模型为
| $ \left\{\begin{array}{l} L_{\mathrm{S}} \frac{\mathrm{d} i_K}{\mathrm{~d} t}= U_{\mathrm{dc}}\left(S_K-\frac{1}{3} \sum\limits_{K=\mathrm{A}, \mathrm{B}, \mathrm{C}} S_K\right)+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; \Delta U_K-\left(R_{\mathrm{L}}+R_{\mathrm{S}}\right) i_K-U_{\mathrm{g} K} \\ L_{\mathrm{g}} \frac{\mathrm{d} i_{\mathrm{g} K}}{\mathrm{~d} t}=-R_{\mathrm{g}} i_{\mathrm{g} K}-U_{\mathrm{g} K}+U_{\mathrm{C}} \\ C \frac{\mathrm{d} U_{\mathrm{C}}}{\mathrm{d} t}=i_K-i_{\mathrm{g} K}+R_{\mathrm{C}} C\left(\frac{\mathrm{d} i_K}{\mathrm{~d} t}-\frac{\mathrm{d} i_{\mathrm{g} K}}{\mathrm{~d} t}\right) \end{array}\right. $ | (11) |
| $ \Delta U_K=\frac{t_{\mathrm{d}}+t_{\mathrm{on}}-t_{\text {off }}}{3 T_{\mathrm{S}}} \sum\limits_{K=\mathrm{A}, \mathrm{B}, \mathrm{C}} \operatorname{sgn}\left(i_K\right)+\Delta U_{\mathrm{DT}} $ | (12) |
式中: igK——网侧电流, K=A, B, C;
UC——电容C的端电压。
定义状态变量x(t)=[x1, x2, x3]T=[iK, ig, UC]T, 将逆变器运行中出现的故障问题、开关器件的老化和损耗, 以及外界干扰问题作为一项复合干扰d, 从而得到系统的状态空间表达式和输出方程为
| $ \left\{\begin{array}{l} \mathit{\boldsymbol{\dot{x}}}=\mathit{\boldsymbol{A x}}+\mathit{\boldsymbol{B u}}+\mathit{\boldsymbol{G}} \\ \mathit{\boldsymbol{y}}=\mathit{\boldsymbol{F x}} \end{array}\right. $ | (13) |
式中:
A, B——系统矩阵和控制矩阵;
u——系统输入;
G——系统干扰;
y——系统标量输出;
F——观测矩阵。
其中,
3 状态观测器设计
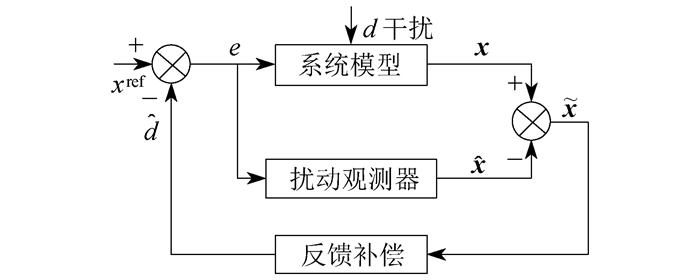
根据状态观测器抗扰动的基本思想[12-14]设计控制系统, 如图 4所示。图 4中, xref为参考输入;
本文设计的扰动状态观测器模型为
| $ \left\{\begin{array}{l} \mathit{\boldsymbol{\dot{\hat{x}}}}=\mathit{\boldsymbol{A}} \hat{\boldsymbol{x}}+\mathit{\boldsymbol{B u}}+\hat{\boldsymbol{G}}+\mathit{\boldsymbol{M}} \tilde{\boldsymbol{x}} \\ \hat{\boldsymbol{y}}=\boldsymbol{F} \hat{\boldsymbol{x}} \end{array}\right. $ | (14) |
式中:
M——观测误差的反馈矩阵, M∈R3×3;
从而得到观测误差动态方程为
| $ \dot{\tilde{\boldsymbol{x}}}=\dot{\boldsymbol{x}}-\dot{\hat{\boldsymbol{x}}}=(\boldsymbol{A}-\boldsymbol{M}) \tilde{\boldsymbol{x}}+(d-\hat{d}) $ | (15) |
定理 考虑系统表达式(13)和式(14), 应用Lyapunov理论, 如果满足G(s)=E[sI-(A-M)]-1为严格正实矩阵, 同时ζ(0, t)=∫0tHT(d-
证明 通过系统重构, 总能找到矩阵E和M使得G(s)为严格正实矩阵。
假设ζ1(0, t)≥-γ12, ζ2(0, t)≥-γ22, γ1和γ2是与γ具有相同性质的有限正常数, 且不依赖时间t(t>0)。
由假设知ζ(0, t)可以表示为
| $ \zeta(0, t)=\zeta_1(0, t)+\zeta_2(0, t) \geqslant-\gamma^2 $ | (16) |
本文选择带有积分项的状态观测干扰, 设定干扰估计值
| $ \hat{d}=\boldsymbol{L}_1 \boldsymbol{H}+\int_0^t \boldsymbol{L}_2 \boldsymbol{H} \mathrm{d} \tau+\hat{d}({0}) $ | (17) |
式中: L1, L2——与广义误差信号H同阶的对角矩阵, L1=diag{l11, l12, l13}, L2=diag{l21, l22, l23};
由此可得:
| $ \left\{\begin{array}{l} \zeta_1(0, t)=\int_0^t \boldsymbol{H}^{\mathrm{T}}\left[d-\int_0^t \boldsymbol{L}_2 \boldsymbol{H} \mathrm{d} \tau-\hat{d}({0})\right] \mathrm{d} \tau \\ \zeta_2(0, t)=-\int_0^t \boldsymbol{H}^{\mathrm{T}} \boldsymbol{L}_1 \boldsymbol{H} \mathrm{d} \tau \end{array}\right. $ | (18) |
令
| $ \begin{aligned} &\int \zeta_1(0, t)=\int_0^t \dot{\boldsymbol{\rho}}^{\mathrm{T}} \boldsymbol{\varrho} \boldsymbol{\rho} \mathrm{d} \tau \geqslant\\ &\frac{1}{2} \min _{i=1, 2, 3}\left\{\omega_i\right\}\left[\boldsymbol{\rho}^{\mathrm{T}} \varepsilon(t)-\boldsymbol{\rho}^{\mathrm{T}} \varepsilon({0})\right] \geqslant\\ &-\frac{1}{2} \min _{i=1, 2, 3}\left\{\omega_i\right\} \boldsymbol{\rho}^{\mathrm{T}} \boldsymbol{\varepsilon}({0}) \geqslant-\gamma_1^2\\ &\zeta_2(0, t)=-\int_0^t \dot{\boldsymbol{\rho}}^{\mathrm{T}} \boldsymbol{L}_{\mathrm{1}} \dot{\boldsymbol{\rho}} \mathrm{d} \boldsymbol{\tau} \geqslant\\ &-\max _{i=1, 2}\left\{\boldsymbol{L}_i\right\} \int_0^t \dot{\boldsymbol{\rho}}^{\mathrm{T}} \dot{\boldsymbol{\rho}} \mathrm{d} \boldsymbol{\tau} \geqslant-\gamma_2^2 \end{aligned} $ | (19) |
式中: ε——关于t的时间函数;
ζi>0, i=1, 2, 3。
综上, 式(14)设计的状态观测器符合Lyapunov稳定性理论, 定理得到证明。
4 控制器设计及稳定性分析
针对系统模型式(11)采用非奇异终端滑模控制进行控制器设计。假设逆变器输出电流、网侧电流、电容C端电压的给定参考值分别为iKref, igref, UCref, 得x1, x2, x3的误差分别为
| $ \dot{\boldsymbol{\sigma}}=\boldsymbol{A} \boldsymbol{\sigma}-\boldsymbol{A} \boldsymbol{k}^{\mathrm{ref}}+\boldsymbol{B u}-d $ | (20) |
式中: σ=[σ1, σ2, σ3]T; kref=[x1ref, x2ref, x3ref]T。
采用非奇异终端滑模控制方法设计控制器, 构造参数矩阵J1和J2分别为
| $ \left\{\begin{array}{l} \boldsymbol{J}_1=\theta_1 \boldsymbol{\sigma}+\theta_2 \int_0^t \boldsymbol{\sigma} \mathrm{d} \tau \\ \boldsymbol{J}_2=\dot{\boldsymbol{J}}_1=\theta_1 \dot{\boldsymbol{\sigma}}+\theta_2 \boldsymbol{\sigma} \end{array}\right. $ | (21) |
式中: θ1, θ2——系统设计参数, 均大于零。
系统控制律设计如下
| $ \left\{\begin{aligned} e=& \frac{1}{b}\left(e_1-e_2+\hat{d}\right) \\ e_1=& \boldsymbol{A} x-\frac{\theta_2}{\theta_1} \times \boldsymbol{\sigma} \\ e_2=& \int_0^t k_1 \operatorname{sgn}(s) \mathrm{d} \tau+\\ & \int_0^t \frac{q}{\theta_1 p} \boldsymbol{\delta}^{-1} \boldsymbol{J}_2^{2-\frac{p}{q}} \mathrm{~d} \tau+\int_0^t k_2 s \mathrm{~d} \tau \end{aligned}\right. $ | (22) |
式(22)中, b, p, q, k1, k2, δ均为系统设计参数。其中, p和q均为奇数, 且满足1 < (p/q) < 2;k1和k2均大于零; δ=diag{δ1, δ2}, δ1和δ2均大于零。
由此可得:
| $ \begin{aligned} \boldsymbol{J}_2=& \theta_1\left[\boldsymbol{A} \boldsymbol{\sigma}-\boldsymbol{A} \boldsymbol{k}^{\mathrm{ref}}+\boldsymbol{B} \boldsymbol{u}-d\right]+\theta_2 \boldsymbol{\sigma}=\\ & \theta_1\left[\boldsymbol{A} \boldsymbol{\sigma}-\boldsymbol{A} \boldsymbol{k}^{\mathrm{ref}}+\left(e_1-e_2+\hat{d}\right)-d\right]+\theta_2 \boldsymbol{\sigma}=\\ & \theta_1\left[\boldsymbol{A} \boldsymbol{\sigma}-\boldsymbol{A} \boldsymbol{k}^{\mathrm{ref}}+\left(\boldsymbol{A} \boldsymbol{x}-\frac{\theta_2}{\theta_1} \times \boldsymbol{\sigma}-e_2+\hat{d}\right)-d\right]+\\ & \theta_2 \boldsymbol{\sigma}=\theta_1(\hat{d}-d)-\theta_1 e_2 \end{aligned} $ | (23) |
| $ \begin{aligned} \dot{\boldsymbol{J}}_2=& \theta_1(\dot{\hat{d}}-\dot{d})-\theta_1\left[k_1 \operatorname{sgn}(s)+\frac{q}{\theta_1 p} \boldsymbol{\delta}^{-1} \boldsymbol{J}_2^{2-\frac{p}{q}}+k_2 z\right]=\\ & \theta_1(\dot{\hat{d}}-\dot{d})-\theta_1 k_1 \operatorname{sgn}(s)-\\ & \frac{q}{p} \boldsymbol{\delta}^{-1} \boldsymbol{J}_2^{2-\frac{p}{q}}-\theta_1 k_2 z \end{aligned} $ | (24) |
定义滑模z面为
| $ \boldsymbol{z}=\boldsymbol{J}_1+\boldsymbol{\delta} \boldsymbol{J}_2^{\frac{p}{q}} $ | (25) |
式中: z=[z1, z2]T;
| $ \boldsymbol{J}_2^{\frac{p}{q}}=\left[\mathit{\boldsymbol{J}}_{21}^{\frac{p}{q}}, \mathit{\boldsymbol{J}}_{22}^{\frac{p}{q}}\right]^{\mathrm{T}} \text { 。} $ |
设定Lyapunov函数为
| $ \begin{aligned} \dot{V}=& z^{\mathrm{T}} \dot{z}=z^{\mathrm{T}}\left[\boldsymbol{J}_2+\frac{p}{q} \boldsymbol{\delta} \boldsymbol{J}_2^{\frac{p}{q}-1} \mathit{\boldsymbol{\dot{J}}}_2\right]=\\ & \frac{p}{q} z^{\mathrm{T}} \boldsymbol{\delta} \boldsymbol{J}_2^{\frac{p}{q}-1}\left[\dot{\boldsymbol{J}}_2+\frac{q}{p} \boldsymbol{\delta}^{-1} \boldsymbol{J}_2^{2-\frac{p}{q}}\right]=\\ & \frac{\theta_1 p}{q} z^{\mathrm{T}} \boldsymbol{\delta} \boldsymbol{J}_{2}^{\frac{p}{q}}\left[(\dot{\hat{d}}-\dot{d})-k_1 \operatorname{sgn}(s)-k_2 z\right] \leqslant \\ &-\frac{\theta_1 p}{q} \min _{i=1, 2}\left\{\boldsymbol{\delta}_i \boldsymbol{J}_{2 i}{\frac{p}{q}}\right\}\left[k_1\|z\|+k_2\|z\|^2+\right.\\ &\left.z^{\mathrm{T}}(\dot{\hat{d}}-\dot{d})\right] \end{aligned} $ | (26) |
由于
| $ \begin{aligned} \dot{V} \leqslant &-\frac{\theta_1 p}{q} \min _{i=1, 2}\left\{\boldsymbol{\delta}_i \boldsymbol{J}_{2 i}^p-1\right.\\ & {\left[k_1\|z\|+k_2\|z\|^2\right] \leqslant 0 } \end{aligned} $ | (27) |
因此, 系统将在有限时间内到达并保持在非奇异终端滑模面z=0内。继而, J1和J2也将在有限时间内收敛到零并保持在原点, 即J1=J2=0, 从而保证了系统稳定。当J1和J2处于滑动模态时, 误差实现了
为了消除滑模控制中的“抖振”现象, 用饱和函数sat(s/α)代替符号函数sgn(s), 公式为
| $ \operatorname{sat}\left(\frac{s}{\alpha}\right)=\left\{\begin{array}{l} \operatorname{sgn}\left(\frac{s}{\alpha}\right), \left|\frac{s}{\alpha}\right| \geqslant 1 \\ \frac{s}{\alpha}, \left|\frac{s}{\alpha}\right|<1 \end{array}\right. $ | (28) |
式中: α——边界层宽度。
5 仿真分析
为了验证本文控制策略的合理性, 利用PSIM对系统进行仿真验证。逆变系统各参数设置如下: 输入直流电压为360 V; 输出交流电压为220 V; 开关频率为10 kHz; 额定负载为44 Ω; 输出滤波电感为(4±2)mH; 输出滤波电容为(28.2±13)μF。所设计控制器中的各个参数具体取值: p=13;q=11;δ1=δ2=0.001;k1=100;k2=8×103; θ1=θ2=12。
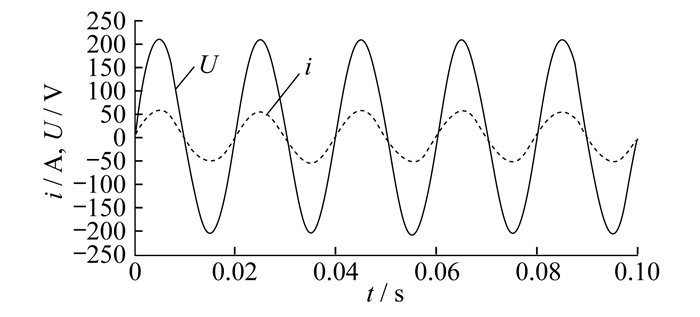
5.1 额定负载启动
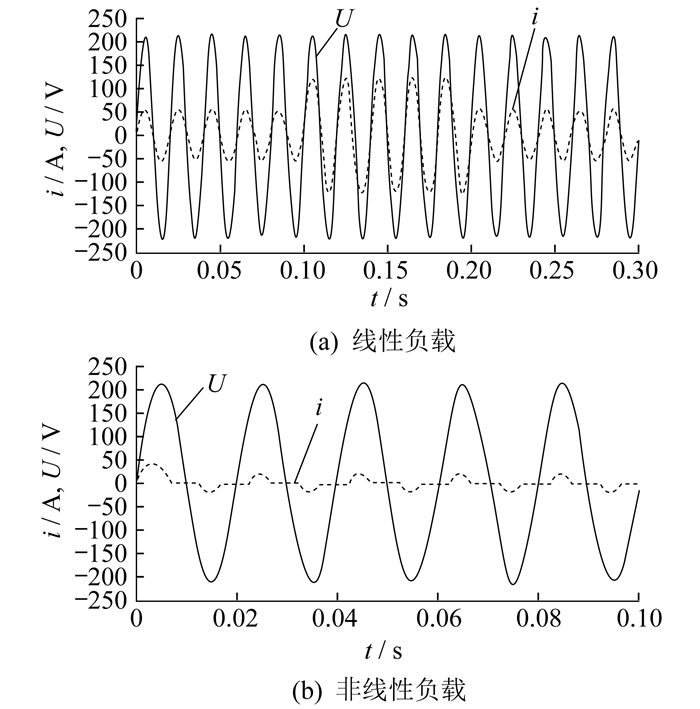
5.2 负载扰动情况
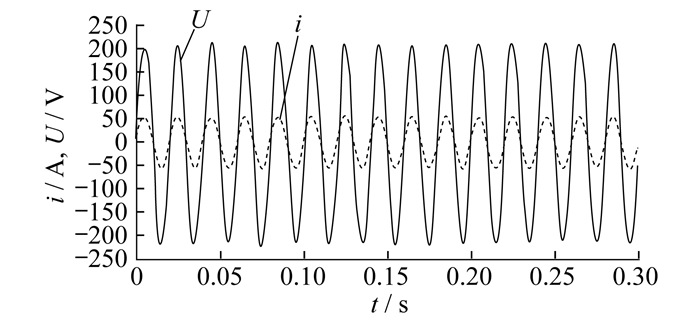
5.3 死区和切换延时
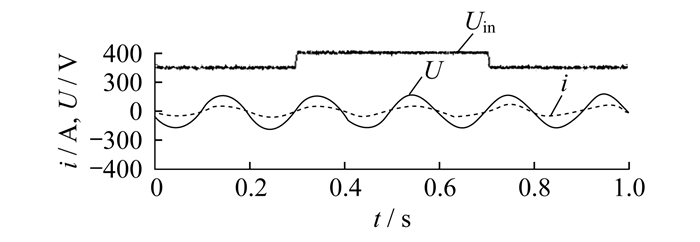
5.4 直流侧电压扰动
6 结语
本文分析了逆变器死区效应, 最终得出了死区会降低逆变器输出电压的结论。同时, 以三相逆变器中的A相为例, 采用状态空间平均法建立了包含死区效应、参数不确定以及外界干扰情况下的非精确数学模型。通过比例积分状态观测器对逆变系统中存在的外界干扰和参数不确定性等多种干扰因素进行有效估计, 并结合非奇异终端滑模控制推导出了逆变器反馈控制律, 设计了合理的控制器。通过PSIM平台进行了仿真验证, 所设计的控制器能够保证系统在存在死区效应、外界干扰和参数不确定的情况下, 仍能精确跟踪到期望输出信号, 具有良好的追踪性能和较强的鲁棒性。
参考文献
-
[1]吴斌, 杨旭红. 基于改进遗传PI和重复控制的三相逆变器并网研究[J]. 电力科学与技术学报, 2021, 36(6): 151-156.
-
[2]汪洋, 陈权, 胡存刚. 基于PI+重复控制的三电平逆变器研究[J]. 电力电子技术, 2021, 55(7): 113-116. DOI:10.3969/j.issn.1000-100X.2021.07.027
-
[3]黄庆义, 段启迪, 郝翔, 等. 具有精确非线性补偿的三相光伏并网逆变器滑模变结构控制策略[J]. 电源学报, 2013(4): 81-87.
-
[4]钟傲男, 周兰, 姜福喜. 基于降阶扩张状态观测器的逆变系统重复控制设计[J]. 信息与控制, 2022, 51(1): 88-97.
-
[5]曹雷, 张建成. 光伏并网逆变器死区效应研究[J]. 电网与清洁能源, 2010, 26(9): 48-53. DOI:10.3969/j.issn.1674-3814.2010.09.012
-
[6]张前进, 周林, 毛明轩, 等. 逆变器死区建模及其对大型光伏并网系统的影响[J]. 太阳能学报, 2020, 41(9): 161-168.
-
[7]LEI M Y, ZHANG Y, MENG L X, et al. A novel adaptive model predictive control based three-phase inverter current control method[J]. Applied Sciences, 2019, 9(24): 5413. DOI:10.3390/app9245413
-
[8]MOHAMMED S A Q, RAFAQ M S, CHOI H H, et al. A robust adaptive PI voltage controller to eliminate impact of disturbances and distorted model parameters for 3-phase CVCF inverters[J]. IEEE Transactions on Industrial Informatics, 2020, 16(4): 2168-2176. DOI:10.1109/TII.2019.2891243
-
[9]YANG T G, CAI Z H, XUN Q. Adaptive backstepping-based H∞ robust controller for photovoltaic grid-connected inverter[J]. IEEE Access, 2020, 8: 17263-17272.
-
[10]WEI R J, CHENG M W, LIU Y K. Design of adaptive control and fuzzy neural network control for single-stage boost inverter[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5434-5445.
-
[11]YANG G L, YIN J Z, HUANG Z Y, et al. A method to improve the reliability of three-level inverter based on equivalent input disturbance and repetitive control combinations[J]. Microelectronics Reliability, 2020, 114: 113837.
-
[12]刘洪臣, 苏振霞. 双降压式全桥逆变器非线性现象的研究[J]. 物理学报, 2014, 63(1): 1-9.
-
[13]BARAMBONESV O, ALKORTA P, DE DURANA J M G. A real-time estimation and control scheme for induction motors based on sliding mode theory[J]. Journal of the Franklin Institute, 2014(8): 4251-4270.
-
[14]KAMAL E, AITOUCHE A, ABBES D. Robust fuzzy scheduler fault tolerant control of wind energy systems subject to sensor and actuator faults[J]. International Journal of Electrical Power & Energy Systems, 2014, 55: 402-419.