光伏发电(Photovoltaic, PV) 是最可靠的发电技术之一, 已被广大学者研究证实光伏电池在寿命周期内所生产的电能可及时补偿制造过程中所消耗的能量, 是值得大力推广的清洁绿色能源技术^[1]。但光伏组件的光电效率通常只有15%~18%, 其余大部分太阳辐照转化为热能导致电池温度升高, 从而降低了光电效率^[2]。

KEN JR E C和RUSSELL M C提出了光伏发电与废热回收为一体的新型集热器概念, 称为光伏/光热(Photovoltaic/Thermal, PV/T)技术^[3]。为验证PV/T系统的应用潜力和节能性, 不少学者将该系统与已商业化的PV系统进行了对比。FU H D等人^[4]比较了PV系统、太阳能热水器和PV/T系统在香港、拉萨、北京和上海4个城市不同气象条件下的运行情况, 研究表明: 在有限的房屋面积内, 采用PV/T系统获得的光电光热收益比采用PV系统和太阳能热水器组合的总收益多。PANG W等人^[5]对比了不同结构的PV和PV/T模块, 研究得出PV/T系统的成本低于传统的PV系统, 并可在3年内回收成本。姚博伟等人^[6]以上海市的年气象数据为计算依据, 对太阳能热水系统及PV/T系统的年运行性能进行了分析, 结果表明, 太阳能热水系统具有较高的年平均综合效率, 同时具有较短的静态回收周期, 而PV/T系统一年中仅在7月和9月具有较高的综合效率。

以上研究表明PV/T系统具有较好的光电光热综合收益, 但均未考虑PV/T系统生产能耗远高于PV系统这一环境性因素, 而且对PV/T系统与PV系统在能量偿还时间和二氧化碳减排量两个方面的对比研究较少。本文以北京、上海、广州、昆明和哈尔滨5个城市的气象数据为依据, 对比分析了PV/T系统和PV系统的年收益, 并从能量偿还时间和生命周期内减少的碳排放量两个方面, 分析得出两套系统在不同气象条件下的节能特性。

PV组件和PV/T集热器通常采取倾斜放置, 需要将所在地区水平面上的直射辐照、散射辐照和地面反射转换为倾斜面上的总辐照, 计算公式为^[7]

$G_{\mathrm{T}}=\left(G-G_{\mathrm{d}}\right) R_{\mathrm{b}}+G_{\mathrm{d}}\left(\frac{1+\cos \beta}{2}\right)+G\left(\frac{1-\cos \beta}{2}\right) \sigma$

(1)

式中: G_T——倾斜面上的太阳总辐照量, W/m²;

G——水平面上的太阳总辐照量, W/m²;

G_d——水平面上太阳散射辐照量, W/m²;

R_b——倾斜面与水平面上太阳直射辐照量的比值;

β——倾斜面与水平面之间的夹角, (°);

σ——地面反射率, 取σ=0.2。

$\begin{array}{l} \ \ \ \ \ R_{\mathrm{b}}= \\ \frac{\frac{\pi}{180} \omega_{\mathrm{s}}^{\prime} \sin (\varphi-\beta) \sin \delta+\cos (\varphi-\beta) \cos \delta \sin \omega_{\mathrm{s}}^{\prime}}{\frac{\pi}{180} \omega_{\mathrm{s}} \sin \varphi \sin \delta+\cos \varphi \cos \delta \sin \omega_{\mathrm{s}}} \end{array}$

(2)

式中: ω_s^′——倾斜面太阳日出日落的时角, (°);

φ——当地纬度, (°);

δ——太阳赤纬角, (°);

ω_s——水平面太阳日出日落的时角, (°)。

本文借鉴文献[4]中PV系统的数学模型, 主要由玻璃封装层和光伏电池层的热平衡方程组成。方程分别为

$\begin{array}{l} d_{\mathrm{g}} \rho_{\mathrm{g}} c_{\mathrm{g}} \frac{\partial T_{\mathrm{g}}}{\partial t}=h_{\mathrm{e}, \mathrm{g}}\left(T_{\mathrm{e}}-T_{\mathrm{g}}\right)+\\ \ \ \ \ \ \ h_{\mathrm{a}}\left(T_{\mathrm{a}}-T_{\mathrm{g}}\right)+\frac{T_{\mathrm{pv}}-T_{\mathrm{g}}}{R_{\mathrm{g}, \mathrm{pv}}}+G \alpha_{\mathrm{g}} \end{array}$

(3)

$\begin{aligned} &\left(\gamma d_{\mathrm{pv}} \rho_{\mathrm{pv}} c_{\mathrm{pv}}+d_{\mathrm{b}} \rho_{\mathrm{b}} c_{\mathrm{b}}\right) \frac{\partial T_{\mathrm{pv}}}{\partial t}= \\ &\quad \frac{T_{\mathrm{g}}-T_{\mathrm{pv}}}{R_{\mathrm{g}, \mathrm{pv}}}+h_{\mathrm{a}}\left(T_{\mathrm{a}}-T_{\mathrm{g}}\right)+Q_{\mathrm{pv}}-P_{\mathrm{pv}} \end{aligned}$

(4)

式中: d, ρ, c——材料厚度、密度和比热容, 单位分别为m, kg/m³, J/kg·K;

下标g, pv, b——光伏电池封装玻璃、光伏电池和基板;

T——温度, K;

h, R——不同介质间的换热系数和热阻, 单位分别为W/(m²·K), K·m²/W;

下标e，a——等效环境和周围环境;

α_g——光伏电池封装玻璃对太阳辐照的有效吸收率;

γ——光伏电池的覆盖率;

Q_pv——光伏电池对太阳辐照的吸收量W/m²;

P_pv——光伏组件的实时发电功率, W/m²。

其中: 光伏电池对太阳辐照的吸收量公式为

$Q_{\mathrm{pv}}=\frac{G\left(1-\xi_{\mathrm{g}}\right) \tau_{\mathrm{g}} \alpha_{\mathrm{pv}}}{1-\left(1-\alpha_{\mathrm{pv}}\right) \xi_{\mathrm{g}} \tau_{\mathrm{g}}{ }^2}$

(5)

式中: ξ_g——玻璃盖板反射率;

τ_g——玻璃盖板透光率;

α_pv——光伏电池对太阳辐照的有效吸收率。

本文借助五参数法建立了光伏组件及PV/T集热器的光电输出模型, 具体如下:

$P_{\mathrm{pv}}=U \cdot I$

(6)

$I=I_{\mathrm{ph}}-I_{\mathrm{o}}\left[\exp \left(\frac{U+I R_{\mathrm{s}}}{\alpha}\right)-1\right]-\frac{U+I R_{\mathrm{s}}}{R_{\mathrm{sh}}}$

(7)

式中: U, I——电压和电流;

I_ph——光生电流;

I_o——反向饱和电流;

R_s, R_sh——串联电阻和并联电阻;

α——理想因子修正系数。

式(7)中的各变量均随光伏电池温度的变化而变化。另外, 可根据牛顿法求得标准工况下的其他参数, 方程如下:

$\begin{aligned} &I_{\mathrm{sc}, \mathrm{ref}}=I_{\mathrm{ph}, \mathrm{ref}}- \\ &\quad I_{\mathrm{o}, \mathrm{ref}}\left[\exp \left(\frac{I_{\mathrm{sc}, \mathrm{ref}} R_{\mathrm{s}, \mathrm{ref}}}{\alpha_{\mathrm{ref}}}\right)-1\right]-\frac{I_{\mathrm{sc}, \mathrm{ref}} R_{\mathrm{s}, \mathrm{ref}}}{R_{\mathrm{sh}, \mathrm{ref}}} \end{aligned}$

(8)

$I_{\mathrm{ph}, \mathrm{ref}}=I_{\mathrm{o}, \mathrm{ref}}\left[\exp \left(\frac{U_{\mathrm{oc}, \mathrm{ref}}}{\alpha_{\mathrm{ref}}}\right)-1\right]-\frac{U_{\mathrm{oc}}}{R_{\mathrm{sh}, \mathrm{ref}}}$

(9)

$\begin{gathered} I_{\mathrm{m}, \mathrm{ref}}=I_{\mathrm{ph}, \mathrm{ref}}-I_{\mathrm{o}, \mathrm{ref}}\left[\exp \left(\frac{U_{\mathrm{m}, \mathrm{ref}}+I_{\mathrm{m}, \mathrm{ref}} R_{\mathrm{s}, \mathrm{ref}}}{\alpha_{\mathrm{ref}}}\right)-1\right]- \\ \frac{U_{\mathrm{m}, \mathrm{ref}}+I_{\mathrm{m}, \mathrm{ref}} R_{\mathrm{s}, \mathrm{ref}}}{R_{\mathrm{sh}, \mathrm{ref}}} \end{gathered}$

(10)

$\begin{aligned} &\frac{I_{\mathrm{m}, \text { ref }}}{U_{\mathrm{m} \text {, ref }}}=\\ &\frac{I_{\mathrm{o}, \text { ref }}}{\alpha_{\text {ref }}} \exp \left(\frac{U_{\mathrm{m}, \text { ref }}+I_{\mathrm{m}, \text { ref }} R_{\mathrm{s}, \mathrm{ref}}}{\alpha_{\mathrm{ref}}}\right)+\frac{1}{R_{\mathrm{sh}, \mathrm{ref}}}\\ &1+\left(\frac{I_{\mathrm{o}, \text { ref }} R_{\mathrm{s}, \text { ref }}}{\alpha_{\mathrm{ref}}}\right) \exp \left(\frac{U_{\mathrm{m}, \text { ref }}+I_{\mathrm{m}, \text { ref }} R_{\mathrm{s}, \text { ref }}}{\alpha_{\mathrm{ref}}}\right)+\frac{R_{\mathrm{s} \text {, ref }}}{R_{\mathrm{sh}, \text { ref }}} \end{aligned}$

(11)

$\frac{I_{\mathrm{o}}}{I_{\mathrm{o}, \text { ref }}}=\left(\frac{T_{\mathrm{pv}}}{T_{\mathrm{pv}, \text { ref }}}\right)^3 \exp \left(\frac{V_{\mathrm{si}, \mathrm{ref}}}{k T_{\mathrm{pv}, \text { ref }}}-\frac{V_{\mathrm{si}}}{k T_{\mathrm{pv}}}\right)$

(12)

式中: 下标ref——标准测试条件下的参数;

I_sc——短路电流;

α_ref——标准测试条件下的理想因子修正系数;

U_oc——开路电压;

I_m, U_m——最大功率点电流和电压;

V_si——硅材料能隙值, J;

k——波尔兹曼常数。

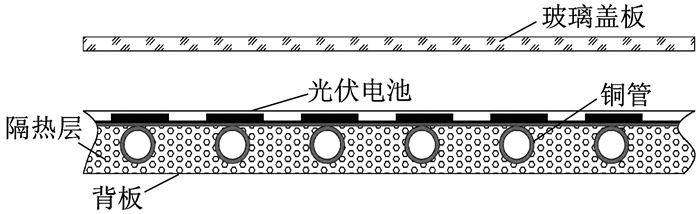
典型水冷型PV/T集热器(以下简称“PV/T集热器”)的结构示意图如图 1所示。PV/T的控制方程参考文献[8]。该模型由玻璃盖板、层压光伏电池、铜管、铜管内冷却水和保温水箱的能量方程组成。

由于存在空气夹层, 故相对常规光伏组件, PV/T集热器的玻璃盖板的能量平衡方程为

$\begin{gathered} d_{\mathrm{g}} \rho_{\mathrm{g}} c_{\mathrm{g}} \frac{\partial T_{\mathrm{g}}}{\partial t}=h_{\mathrm{a}}\left(T_{\mathrm{a}}-T_{\mathrm{g}}\right)+h_{\mathrm{e}, \mathrm{g}}\left(T_{\mathrm{e}}-\right. \\ \left.T_{\mathrm{g}}\right)+h_{\mathrm{g}, \mathrm{pv}}\left(T_{\mathrm{pv}}-T_{\mathrm{g}}\right)+G \alpha_{\mathrm{g}} \end{gathered}$

(13)

光伏电池层由PV单元、胶膜(Ethylene Vinyl Acetate, EVA)和吸热层3部分组成。其热传导公式为

$\begin{array}{r} \left(\gamma d_{\mathrm{pv}} \rho_{\mathrm{pv}} c_{\mathrm{pv}}+d_{\mathrm{ab}} \rho_{\mathrm{ab}} c_{\mathrm{ab}}\right) \frac{\partial T_{\mathrm{pv}}}{\partial t}= \\ \frac{T_{\mathrm{g}}-T_{\mathrm{pv}}}{R_{\mathrm{g}, \mathrm{pv}}}+\frac{T_{\mathrm{a}}-T_{\mathrm{pv}}}{R_{\mathrm{a}, \mathrm{pv}}}+Q \end{array}$

(14)

式中: 下标ab——PV/T集热器的吸收层;

Q——光伏电池层与铜管接触部分热传导。

光伏电池层与铜管接触部分的热传导为

$Q=\frac{T_{\mathrm{t}}-T_{\mathrm{pv}}}{A_{\mathrm{t}} \cdot R_{\mathrm{pv}, \mathrm{t}}}+Q_{\mathrm{pv}}-P_{\mathrm{pv}}$

(15)

式中: 下标t——铜管;

A——材质面积, m²。

铜管的热平衡方程式为

$A_{\mathrm{t}} \rho_{\mathrm{t}} c_{\mathrm{t}} \frac{\partial T_{\mathrm{t}}}{\partial t}=\pi D_{\mathrm{t}, \mathrm{in}} h_{\mathrm{w}, \mathrm{t}}\left(T_{\mathrm{w}}-T_{\mathrm{t}}\right)+\frac{T_{\mathrm{pv}}-T_{\mathrm{t}}}{R_{\mathrm{pv}, \mathrm{t}}}$

(16)

式中: D——直径, m;

下标in, w——铜管内径和铜管内冷却水。

铜管内冷却水的热平衡公式为

$A_{\mathrm{t}, \text { in }} \rho_{\mathrm{w}} c_{\mathrm{w}} \frac{\partial T_{\mathrm{t}}}{\partial t}+\dot{m} c_{\mathrm{w}} \frac{\partial T_{\mathrm{w}}}{\partial y}=\pi D_{\mathrm{t}, \mathrm{in}} h_{\mathrm{w}, \mathrm{t}}\left(T_{\mathrm{w}}-T_{\mathrm{t}}\right)$

(17)

式中: $ \dot m$——铜管内冷却水流量, kg/s;

y——水流方向的计算步长。

保温水箱内的能量方程为

$M_{\mathrm{wt}} c_{\mathrm{w}} \frac{\partial T_{\mathrm{wt}}}{\partial t}=\frac{T_{\mathrm{a}}-T_{\mathrm{wt}}}{R_{\mathrm{a}, \mathrm{wt}}}+\sum\limits_j \dot{m} c_{\mathrm{w}}\left(T_{\mathrm{wout}}^j-T_{\mathrm{win}}\right)$

(18)

式中: M_wt——水箱内冷却水质量, kg;

下标wt, wout, win——水箱内冷却水, 集热器的出口和进口;

j——铜管数目。

能量偿还时间(Energy Pay Back Time, EPBT)是评判能源系统是否有效的指标之一, 能量偿还时间越短则越有效。其公式为

$Y_{\text {EвPT }}=\frac{E_{\text {in }}}{E_{\text {out }}}$

(19)

式中: Y_EBPT——能量偿还时间, a;

E_in——能源系统寿命周期内输入的总能量, kWh;

E_out——能源系统运行时每年输出的能量, kWh/a。

光伏系统减排CO₂潜力是衡量光伏系统建筑节能的另一个重要指标。考虑PV系统和PV/T系统在生产过程中的耗能, 其减排CO₂潜力的计算公式如下。

PV系统和PV/T系统的减排公式分别为

$M_{\mathrm{pv}, \mathrm{PM}}=\left(E_{\text {total }}-E_{\text {in }}\right) \psi$

(20)

$M_{\text {pvt }, \mathrm{PM}}=\left(E_{\text {total }}+H_{\text {total }}-E_{\text {in }}\right) \psi$

(21)

式中: M_{pv, PM}, M_{pvt, PM}——PV系统和PV/T系统在产品寿命周期内的减碳排量, kg;

E_total——PV系统在产品寿命周期内产生的总电量, kWh;

H_total——PV/T系统在产品寿命周期内产生的总热量, kWh;

ψ——CO₂排放因子, 取0.6 kg/kWh^[9]。

因为PV/T系统同时输出光电和光热两种能源, 为了便于计算, 将PV/T系统在寿命周期内产生的热量折算成提供相同热量时需要的耗电量。

本文选取北京、上海、广州、昆明和哈尔滨5个城市, 分别代表了寒冷地区、夏热冬冷地区、

夏热冬暖地区、温和地区和严寒地区的气象特征^[10]。基于典型年气象数据, 利用C++程序对PV系统和PV/T系统的年收益情况进行数值分析。两套系统的光伏组件均采用250 W多晶硅组件, 总面积为1.64 m², 光伏电池面积为1.46 m², 标准测试条件下光电效率为17.2%。根据我国建筑给水排水设计标准, PV/T系统中的水箱容积设为100 L。两套系统每天运行时间为7∶00~17∶00。若日终水箱温度大于或等于40 ℃, 则认为其满足了热水的使用条件^[11], 第2天系统将重新注入冷却水。冷却水水温假设与当日7∶00的环境温度一致。若第2天7∶00的环境温度小于5 ℃, 则水温默认设为5 ℃。这是因为当水温低于4 ℃时, 水的异常膨胀特性使水的结构更接近冰, 容易发生结冰现象^[12]。

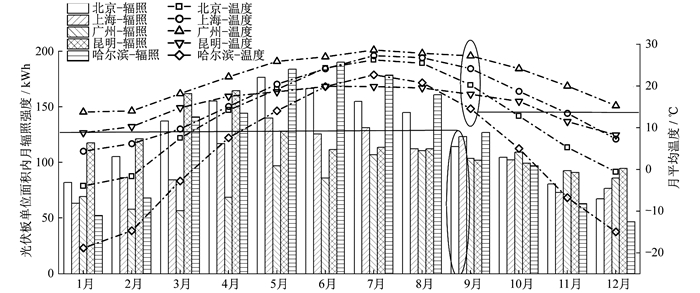
两套系统均按5个城市的最佳倾角, 正南方向安装。北京、上海、广州、昆明和哈尔滨的最佳安装倾角分别为33°, 22°, 18°, 25°, 38°。5个城市最佳倾角表面上获得的光伏板单位面积内月辐照强度和月平均温度如图 2所示。

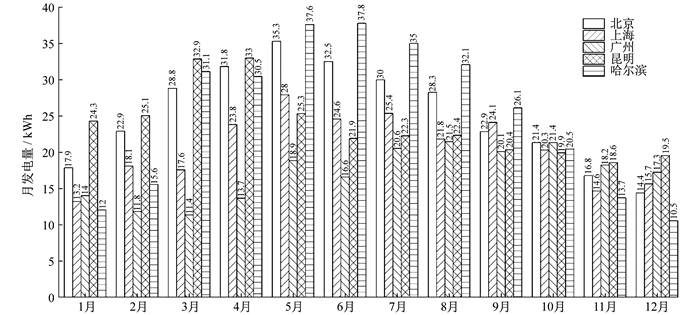
两套系统在5个城市的月发电量如图 3和图 4所示。由图 3和图 4可以看出, 两套系统的发电量主要取决于所在城市的辐照强度; 光伏板在北方城市获取的年辐照量均高于南方城市, 因此两套系统在北京和哈尔滨的年发电量均高于其他3个南方城市。两套系统在9月~12月时各个城市的发电量相近, 而5月~8月时各城市的月发电量差距较大, 其中北京和哈尔滨的月发电量较高。

计算对比两套系统的年发电量可知, PV/T系统在5个城市的月发电量均小于PV系统。其原因是, 为了增大光热输出, PV/T系统的玻璃盖板与光伏电池之间通常设有空气夹层, 使得入射光在光疏与光密介质之间多次折射和反射, 大幅降低了太阳辐照的有效吸收率^[13]。实际运行时, PV/T系统中光伏组件的工作温度沿流动方向逐渐升高, 并随着水温的升高而升高, 光伏组件的工作温度远高于PV系统中光伏组件的工作温度^[14]。因此, PV/T系统的光电收益低于常规PV系统。

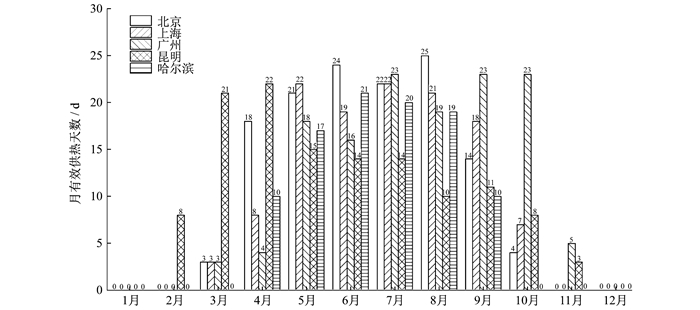
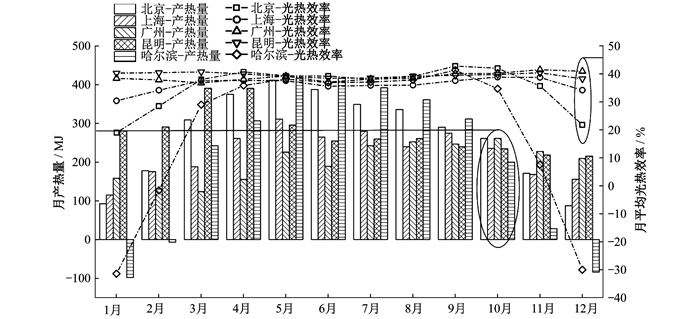
PV/T系统在5个城市的月有效供热天数如图 5所示。PV/T系统在5个城市的月产热量和月平均光热效率如图 6所示。由图 5中数据分析可知, 广州和昆明分别地处夏热冬暖地区和温和地区, 可满足用户需求的年有效供热天数较多, 分别为134 d和126 d; 北京在4月~8月内, 每月均可获得较多的有效供热天数, 年有效供热天数为131 d; 上海和哈尔滨分别为120 d和97 d。

由图 2可知, 广州和昆明的太阳辐照强度分别集中在7月~10月和2月~5月, 其他3个城市则集中在5月~8月, 上述时段满足用户供热需求的天数较多。在太阳辐照强度集中的时段内, 室外环境温度高, 集热器热损小, 发电量大, PV/T系统更容易获得热能和电能, 因此能极大地满足用户供热和用电需求。根据图 4和图 6中的数据计算可得, 在上述时段内, 太阳辐照强度最低的是广州, 其平均月产热量为250.5 MJ, 平均月发电量为19.6 kWh; 辐照量较高的北京和哈尔滨, 上述时段的平均月产热量分别为370.6 MJ和399.0 MJ, 而月发电量分别介于25.8 ~31.5 kWh, 28.6~33.2 kWh。

随着各地太阳辐照强度的下降, 系统发电量也随之减少, 环境温度对PV/T系统光热效率的影响逐渐显现。室外环境温度与初始水温的温差越大, 则光热效率越高, 产热量越大。反之, 当初始水温远高于环境温度, 在热传导过程中导致热量损失, 光热效率下降, 导致产热量不足。以冬季为例, 北京和哈尔滨两地的PV/T系统设定初始水温为5 ℃, 远高于环境温度, 导致系统在循环时热损较高, 两地在冬季的产热量远低于南方城市。尤其是哈尔滨地处严寒地区, 冬季寒冷且时间跨度长, 其中有5个月的时间不能向用户提供有效供热, 年产热量和有效供热天数最少, 年平均光热效率只有28.79%, 远低于其他城市。与之相反的是昆明地区, 由于地理环境和气候的优势, 日照长、年平均气温适中, 冬季月平均产热量均在200 MJ以上, 因此, 昆明集热持续时间段较长, 年平均光热效率最高, 达到了39.54%。

考虑到PV/T系统输出电和热两种能量的品位不均等, 本文利用文献[15]提出的评价方法对PV/T系统的综合效率进行评价, 其公式为

$\eta_0=\eta_{\mathrm{t}}+\gamma \frac{\eta_{\mathrm{pv}}}{\eta_{\text {power }}}$

(22)

式中: η₀——PV/T系统的综合效率;

η_t——PV/T系统的光热效率;

η_pv——PV/T系统光电效率;

η_power——当地火电厂的发电效率, 取0.38。

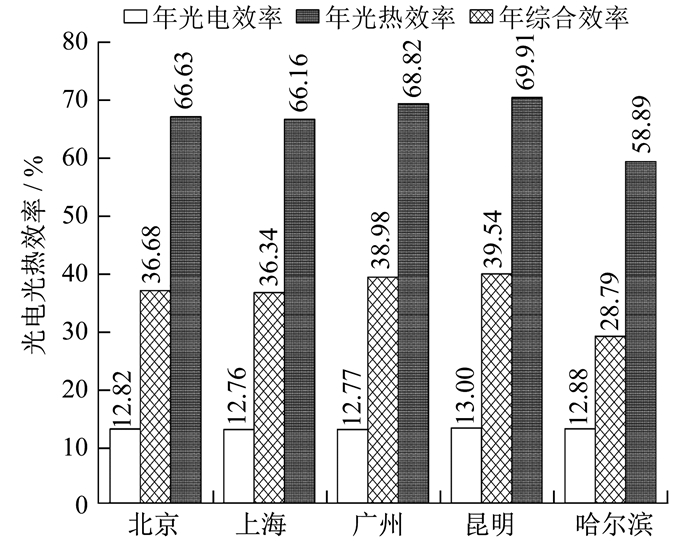
PV系统的综合效率也可以根据式(22)计算得到, 其中光热效率为零。PV/T系统在5个城市的年综合效率如图 7所示。

由图 7可以看出, 北京和上海的年综合效率相近, 分别为66.63%和66.16%。昆明的年综合效率最高, 达到了69.91%, 其次为广州, 年综合效率为68.82%。而哈尔滨的年综合效率则为58.89%。计算PV系统的年综合效率后比较得知, PV/T系统的年综合效率远高于传统的PV系统。

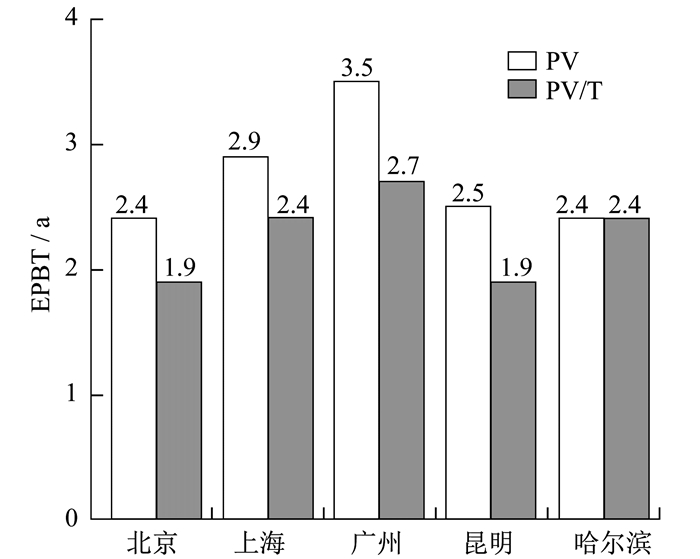
中国光伏行业协会发布的《关于光伏行业所谓的“高耗能”问题分析》一文中指出, 光伏组件能耗为1.52 kWh/W。文献[16]分析了PV/T系统和光伏建筑一体式PV/T系统的生产能耗, 指出PV/T系统的生产能耗主要由玻璃、隔热层、热吸收层、框架、光伏电板和配件系统构成, 并给出了具体数值。由上述研究计算可知, 常规PV系统的生产能耗约为722.9 kWh, PV/T系统的生产能耗约为2 295.7 kWh。结合两套系统的年收益, 得到系统的能量偿还时间如图 8所示。

对于PV系统, 发电量最多的北京和哈尔滨, 两地的能量偿还时间最短, 约为2.4 a, 而发电量最低的广州的能量偿还时间最长, 约为3.5 a。对于PV/T系统, 综合收益较高的昆明和北京具有较短的能量偿还时间, 均为1.9 a; 上海和哈尔滨的时间长于昆明和北京, 约为2.4 a; 综合收益最差的广州则需要2.7 a。综合对比两套系统, 除哈尔滨以外, PV/T系统的能量偿还时间均比PV系统短。

系统的CO₂减排量取决于在产品寿命周期内所得获得的能量。考虑系统组件衰减因素和时间价值问题, 两套系统在产品寿命周期内的收益公式需分别计算。

PV系统在产品寿命周期内产生的总电量为

$E_{\mathrm{total}}=E_{\mathrm{pv}, \mathrm{E}} \sum\limits_{t=0}^T \frac{\left(1-f_{\mathrm{E}}\right)^t}{(1+r)^t}$

(23)

式中: E_{pv, E}——PV系统的年发电量, kWh/a;

f_E——光伏组件的电衰减率, 取0.8%;

r——贴现率, 取2%。

PV/T系统的光电成本和常规光伏发电成本一致。增加的热能效益为系统产生的总热量H_total, 可将PV/T系统每年产生的总热量折算成提供相同热量时需要的耗电量, 具体公式为

$\begin{gathered} E_{\mathrm{pvt}, \text { total }}=E_{\text {total }}+H_{\text {total }}= \\ E_{\mathrm{pvt}, \mathrm{E}} \sum\limits_{t=0}^T \frac{\left(1-f_{\mathrm{E}}\right)^t}{(1+r)^t}+E_{\mathrm{pvt}, \mathrm{H}} \sum\limits_{t=0}^T \frac{\left(1-f_{\mathrm{H}}\right)^t}{(1+r)^t} \end{gathered}$

(24)

式中: E_{pvt, E}——PV/T系统的年发电量, kWh/a;

E_{pvt, H}——PV/T系统每年产生的总热量折算成相同的电能, kWh/a;

f_H——光伏组件的热衰减率, 取0.3%。

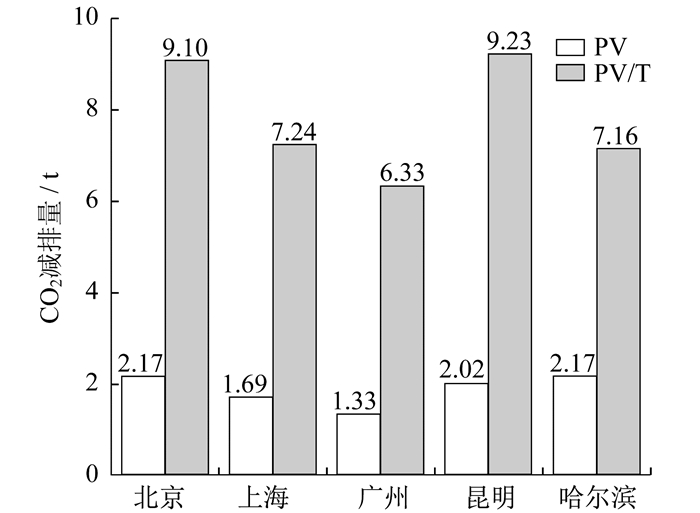
两套系统在产品寿命周期内的CO₂减排量如图 9所示。

由图 9可知, PV/T系统的CO₂减排量介于6.33~9.23 t, 其中综合效益最好的两个城市北京和昆明减排量最多; PV系统的CO₂减排量介于1.33~2.17 t; PV/T系统的CO₂减排量约为PV系统的3~5倍, 具有更好的建筑减排能力。

本文以北京、上海、广州、昆明、哈尔滨5个典型城市的气象数据为基础, 从能量偿还时间和CO₂减排量两个方面, 对比分析了PV系统与PV/T系统的节能特性和环保性。主要结论如下。

(1) PV/T系统的月发电量均小于PV系统。

(2) PV/T系统具有可观的光热收益, 其光电光热综合效率远高于常规PV系统, 介于58.89%~69.91%。

(3) PV/T系统的生产能耗高于PV系统, 但其能量偿还时间短于PV系统。PV/T系统的CO₂减排量约为PV系统的3~5倍。年有效收益和经济性计算结果均表明, PV/T系统相比传统的PV系统具有更好的应用潜力。