|
|
|
发布时间: 2022-12-25 |
智能电网技术 |
|
|
|
收稿日期: 2022-05-15
中图法分类号: TM41
文献标识码: A
文章编号: 2096-8299(2022)06-0569-06
|
摘要
变压器故障概率计算复杂、应用性强, 是工程实践和研究领域中最为关切的问题之一。分析了变压器故障概率计算方法研究现状, 并重点提出了融合故障树分析和设备状态量评价的变压器故障概率综合计算方法。基于故障树分析方法获取变压器故障因素及故障树底事件, 与对应状态量建立关联后进行评价, 并采用模糊综合评判法求取变压器故障状态量表征权重, 最终构建出变压器故障概率综合计算公式模型。以实际计算案例验证了所提方法的应用效果。
关键词
电力变压器; 故障概率; 故障树分析; 设备状态量; 模糊综合评判
Abstract
As one of the most concerned problems in the engineering practice and the research field, the fault probability calculation of transformer is complex and practical.The paper analyzes the general research status of fault probability calculation.A comprehensive new calculation approach is put forward, by connecting the method fault tree analysis (FTA) and the equipment criteria evaluation.The transformer fault tree and the bottom events are analyzed based on FTA, and then evaluated after correlated with the equipment criteria, and the fuzzy comprehensive evaluation (FCE) method is used to calculate the weights of the criteria indexes before the fault probability formula model is finally established.In terms of an actual case, the application effect of the proposed method is verified.
Key words
power transformer; fault probability; fault tree analysis; equipment criteria; fuzzy comprehensive evaluation
电力变压器设备的故障概率, 既是工程实践中非常关切的实际问题, 也是研究领域重点关注的问题之一。我国电力行业中, 可采用强迫停运率、非计划停运时间等频率或时间指标来衡量变压器设备的故障概率[1], 但多用于统计; 国家电网公司输变电设备风险评估相关导则[2]指出, “设备发生故障的概率由设备状态决定”, 这一内涵使其特别适用于基于状态评估的个体电力设备概率风险评价研究, 其在本质上是由一定时间内发生故障的条件概率密度所决定的[3]。这种基于设备状态形式的个体故障概率, 是大部分设备管理人员更希望获取的, 但在目前的计算研究中普遍存在诸多难点。本文在综述主要研究方法现状的基础上, 提出了一种综合故障树分析(Fault Tree Analysis, FTA)与设备状态量评价的新方法模型, 以期达到合理、快捷估算变压器故障概率风险的目的。
1 变压器设备故障概率计算方法研究现状
电力变压器故障概率的分析和计算, 目前主要有基于设备状态评价指标的方法[4-7]、基于FTA的方法[8-10]和基于马尔可夫理论的方法[11-13]3类常用方法。其中, 设备状态指标方法多以具体设备状态评价为基础, 充分考虑了设备的个体信息, 针对性强, 但样本统计数据获取周期长且具有滞后性, 状态指标评价方法不统一, 关系函数需要复杂的拟合选优或对经验公式的修正过程[14]; FTA方法对变压器故障原因分析比较全面、直观, 且定性定量相结合、逻辑性强, 但该方法比较复杂,基本事件多,建树工作量大, 尤以不同底事件的概率估算和影响权重赋值分配的难度特别大; 马尔可夫理论方法充分利用变压器故障的可修复性、状态无记忆性的随机特点, 对各种状态考虑比较充分, 但主要缺点在于各种状态持续时间、故障率和修复率等是基于大量历史样本数据统计所得, 获取困难, 且对个体设备的针对性不强。
此外, 文献[15]将模糊层次分析理论和人工神经网络理论引入变压器平均故障率的评估计算中, 形成了二者相结合的评估优化方法, 但存在很多问题。如误差反传网络的构建、学习样本的训练、输出值的可靠性等问题。文献[16]提出可采用因果分析网络图(链条或领结模型)进行故障原因与结果的双向分析, 思路清晰、优势明显, 但缺点是缺乏完整模型和必要的演算案例分析, 主要原因在于网络结构复杂, 大量中间事件概率难以确定。文献[17]创新性地提出了一种基于振动特性及其监测变压器故障率预测模型, 思路简捷, 但由于振动参量样本数量有限且关注因素比较单一, 故可信度受到一定影响。
变压器故障概率的分析和计算, 本身具有较高的复杂性, 再加上其定量计算的属性, 客观上也增加了研究难度。因此, 找到科学准确同时又简单易行的方法非常必要。
2 综合FTA与状态量评价的变压器故障概率计算方法
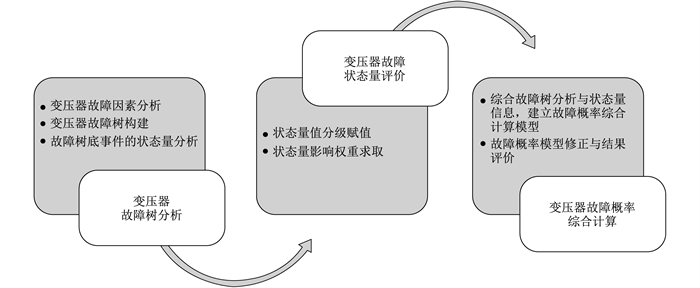
本文所研究的变压器故障取广义上的概念, 包含变压器典型内外部故障及可以继续引发严重故障的不正常状态, 以使研究对象的内涵得到扩展。在以变压器状态技术性评估为中心的基础上, 将FTA和设备状态量评价进行融合, 可以形成一种既能保留FTA全面、直观、逻辑性强的优点, 又能充分考虑个体设备状态信息的综合性方法。变压器故障概率综合计算方法流程, 如图 1所示。
2.1 变压器故障树分析
2.1.1 变压器故障因素分析
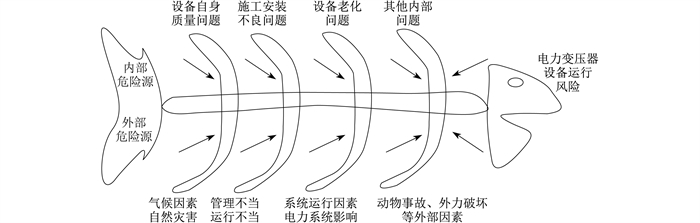
其中: 在故障概率分析计算过程中, 内部因素是主要因素和最重要的风险来源, 是关注的重点和核心; 外部因素大多与大环境(自然环境、电力系统、企业管理等)有很大关联, 通常仅作为次要因素, 但也应该给予一定的关注。在变压器风险因素识别和分类方面, 可分为内部因素和外部因素两大类, 如图 2所示。
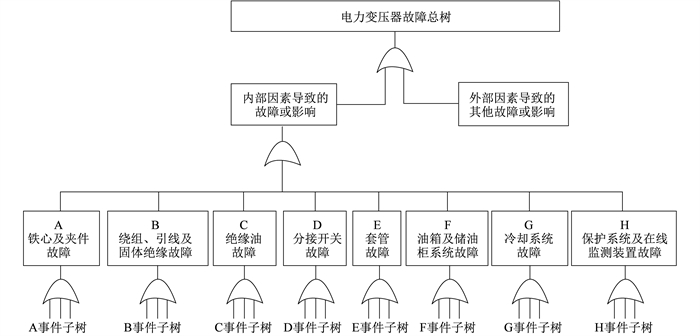
2.1.2 变压器故障树构建
2.1.3 故障树底事件状态量分析
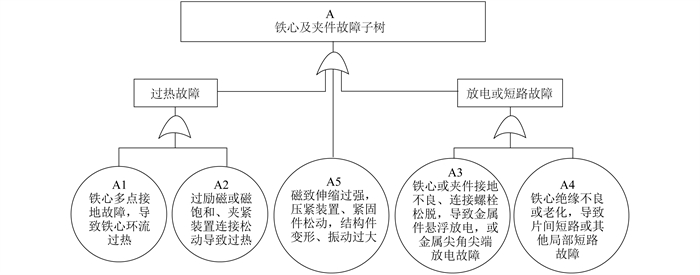
对变压器故障底事件进行分析, 关键是对其状态表征信息量进行技术分析和综合评判。以A事件的底事件A1~A5为例, 具体分析如表 1所示。其表征量的选取, 是下一步状态量赋值及对表征权重评价的基础。其他各子树底事件分析方法相同, 最终可完成整个故障树对应状态表征量的分配。
表 1
A子树的底事件对应的状态表征量分析
| 底事件分析 | 状态量编号Zi | 具体对应的状态表征量 |
| A1 | Z1 | 铁心接地电流; 铁心绝缘电阻; 油中溶解气体分析(Dissolved Gas Annlysis, DGA); 油温; 瓦斯继电器信号; 空载损耗 |
| A2 | Z2 | 声音及振动; 运行电压检查; 油温; 瓦斯继电器信号 |
| A3 | Z3 | 油中微量金属(铁); DGA; 铁心绝缘电阻; 高频等局部放电信号 |
| A4 | Z4 | 铁心绝缘电阻; DGA; 励磁试验; 空载电流和空载损耗 |
| A5 | Z5 | 声音及振动; 过励磁及谐波电流; 中性点电流; 扫描频谱响应或短路阻抗分析 |
2.2 变压器故障状态量评价
上述故障树的建立、底事件状态量的分配, 均为定性分析阶段, 后续将在此基础上, 进行量化评价计算。量化评价计算, 是对能够表征故障的各种信息参量进行劣化程度分级赋值, 并对各表征程度进行评价以获取状态量对顶事件的表征权重; 二者的乘积, 即为各状态量对变压器故障概率的影响度。
2.2.1 变压器故障状态量值分级赋值
对故障树各底事件对应状态量的量值进行分级赋值, 需要结合状态评价方法、分级依据或经验值等[18], 以底事件为单位进行。它是表征故障可能性及状态量劣化程度的重要指标。
以A1底事件为例, 其分级赋值方法考虑状态因素如下: 运行中铁心接地电流大于0.1 A为异常, 大于0.3 A为严重异常; 铁心对夹件或对外壳的绝缘电阻小于100 MΩ或接近零为严重异常, 绝缘电阻较低可结合变化趋势分析; 通常热点温度较高, C2H6和C2H4增长较快; 若存在不稳定的铁心多点接地, 属低能量火花放电, 并有局部过热特征, 这时伴随少量H2和C2H2产生; 油温升高, 并可能与铁心接地电流存在一定关联性; 轻瓦斯可能连续动作; 空载损耗是否异常等。评价中, 状态量劣化程度评价值Ri范围可分为4级, 即0~2(非常低)、2~5(比较低)、5~8(比较高)、8~10(非常高)。其中: 劣化程度赋值0表示状态量均正常, 底事件无任何劣化现象; 劣化程度赋值为10, 表示状态量劣化非常严重, 强烈反映底事件劣化故障可能性。
2.2.2 基于模糊综合评判方法的故障权重求取
变压器故障各底事件及其状态量评价指标对故障概率的表征程度, 是FTA定量计算的另一项重要内容, 可采用模糊综合评判(Fuzzy Comprehensive Evaluation, FCE)方法进行求取。FCE利用模糊集理论和最大隶属度原则, 可对具有模糊性的各种因素进行考量, 能较好地克服评价指标属性的模糊性, 使得描述更加客观[19-20]。
应用中, 表征权重Wi的范围区间为0~1, 代表该底事件状态量对变压器发生故障的影响程度大小; 而考量时关注的重点是, 通过底事件状态量对变压器故障可能性分析判断的可行性、有效性、准确可靠性等。仍以A事件及A1底事件权重Wi的评价为例, 其FCE赋权过程如表 2所示。由表 2可知, 该事件故障表征权重W1=0.84。同样, 可得到A事件的其他各底事件权重分别为W2=0.62, W3=0.40, W4=0.52, W5=0.37。更多各底事件获取与此相同, 不再逐一列出。
表 2
A1底事件评价项目及表征权重求取和综合隶属度
| 评价项目及综合隶属度 | 分级赋值 | |||
| 很强[0.8~1.0] | 较强[0.5~0.8) | 较弱[0.2~0.5) | 很弱[0~0.2) | |
| 状态量数据可获取性及全面性(20%) | 0.8 | |||
| 故障机理逻辑性及对故障传递直接程度(50%) | 1.0 | |||
| 排除干扰、诊断故障原因的可操作性(10%) | 0.8 | |||
| 该事件引发故障实例充分性(20%) | 0.5 | |||
| 综合隶属度 | 0.74 | 0.1 | 0 | 0 |
2.3 变压器设备故障概率综合计算
2.3.1 故障概率计算模型建立
在完成上述故障树的建立及底事件对应状态量分析、状态量量化分级赋值和表征权重定量计算后, 可建立出综合的变压器故障概率计算公式模型, 即
| $ P = K\left( {{P_0} + {P_0}\sum\limits_{i = 1}^n {{R_i}} {W_i}} \right) $ | (1) |
式中: P——所要求的变压器综合故障概率;
K——修正系数;
P0——基本故障概率;
n——存在故障可能性的底事件总数量;
Ri——变压器故障各底事件状态量值的分级评价值, i=1, 2, 3, …;
Wi——各底事件状态量对变压器故障的表征权重, i=1, 2, 3, …。
本综合计算方法中: 求取的故障概率P, 表示该台目标变压器在一年时间内的故障概率, 可以用“%”形式表达; 求取P时采用累加求和的形式, 本身符合非相关性故障概率之间可以累加的逻辑规律, 如果所关注和纳入实际计算的底事件总数量n较多, 则最终所得综合故障率必然较高。此外对于P0, 其基础值可以根据统计结果合理选定。国际上, CIGRE WG A2.37工作组曾统计了世界上21个国家中56个电力企业变压器故障率, 折算成平均成年故障率约为0.57次/百台年, 即0.57%;我国国家能源局对全国范围内220 kV及以上变压器进行的综合统计数据表明, 2011~2020年强迫停运率为0.122~0.354次/百台年, 可知我国过去10年平均单台变压器年故障率约为0.2%。本文选定此历史平均值作为计算中P0的取值, 即P0=0.2%, 相对更适用一些。
2.3.2 变压器故障概率模型修正
上述变压器故障树的建立和故障概率计算中, 主要以变压器自身影响因素及其对应特征量为中心, 当考虑各类外部影响因素时, 其计算和评价将变得极其复杂。为简化外部次要影响因素的计算, 可综合外部大环境影响程度的高低给出影响因子进行调节修正。该修正系数K非本文研究重点, 其参考取值可选1.0~1.3。
2.3.3 变压器故障概率计算结果分级
根据本文概率公式内涵及状态量值、权重值的取值范围, 并综合修正系数, 可对变压器故障概率计算结果作一定分级, 如故障概率非常低(P < 0.5%)、较低(0.5%≤P < 2.0%)、较高(2.0%≤P < 10.0%)、非常高(P≥10.0%)等。
该故障概率的分级并非统一, 不同应用场景和重要等级的变压器, 以及不同用户的承受能力, 使得对应可接受概率具有一定的灵活性和多样性。另外, 不同故障概率等级结果结合运维管理策略, 可进一步采取不同的处理措施。
3 变压器故障概率算例分析
3.1 变压器案例简述
某供电公司对其所辖电站某2#主变于2007年12月28日投运, 容量为180 MW, 预试时发现油中总烃为550 μL/L, 其中乙炔为0.12 μL/L。对变压器停运进行电气试验, 发现铁心对地绝缘电阻为零, 其他检查测试未见明显异常[21]。
3.2 算例故障概率分析计算
(1) 该变压器铁心对地绝缘电阻为零, 同时总烃超标, 还发现了乙炔气体, 但其他检查测试未见异常, 故可以将故障事件锁定在与铁心及夹件相关的故障范围之内, 其他底事件均不予考虑。因此, 本案例中需要纳入实际计算的底事件总数量n为5。
(2) 通过对A1~A5各项底事件对应的状态量逐一分析[10, 18, 22], 可以得出劣化程度评价值Ri, 其中A1和A3对应评价值较高, A4对应评价值较低, A2和A5极低, 具体如表 3所示。
表 3
案例中状态量劣化值分析及Ri评价
| 相关底事件 | 对应状态量劣化值分析 | Ri |
| A1 | 运行中铁心接地电流无异常, 或未进行测量; 铁心对地绝缘电阻为零, 严重异常; 总烃较高, 并产生少量C2H2, 具有低能放电特征, 表明存在放电; 油温未见明显升高; 未见瓦斯继电器动作信号。综合判断其铁心接地或绝缘存在较明显问题 | 8 |
| A2 | 未见高频率尖锐声; 运行电压值无异常, 无过励磁; 未见油温升高; 未见轻瓦斯继电器动作信号。综合判断其不存铁心磁饱和致热问题 | 0 |
| A3 | DGA正常, 未发现微量金属超标; 少量C2H2产生; 铁心对地绝缘电阻为零, 严重异常; 无局放测试数据。综合判断其铁心或夹件金属存在一定放电问题 | 6 |
| A4 | 铁心绝缘电阻异常; 少量C2H2产生; 过励磁试验时分析DGA, 励磁试验、空载电流和空载损耗均未见异常。综合判断其铁心或夹件绝缘可能存在老化导致对地绝缘不良, 但并无明显短路故障 | 2 |
| A5 | 未见变压器本体声音异常增大, 无明显杂音、异常振动; 铁心结构及绕组变形测试未见异常; 未见瓦斯继电器动作信号。综合判断其铁心夹件不存在明显变形问题 | 0 |
(3) 变压器故障外部影响因素信息不足, 可按照中等影响程度取值, 故修正系数K取1.15。
(4) 最后, 依据R1~R5评价值、W1~W5权重系数、K值和式(1), 计算可得该变压器综合故障率为: P=1.15×[0.2%+0.2%×(8×0.84+0×0.62+6×0.40+2×0.52+0×0.37)]=2.57%。
3.3 验证分析
该案例事件经后续检修人员排油进入变压器内部检查发现, 有一个温度计座偏斜与铁心的尖角接触, 并有放电烧伤痕迹。分析认为, 温度计座与铁心的距离太近, 在交接试验时用2 500 V兆欧表无法发现该缺陷, 而当变压器运行后温度上升, 铁心硅钢片和温度计座都受热膨胀, 二者发生了相互碰触[21]。可见, 该变压器故障的根本原因为铁心异常接地问题及放电性问题。这与计算分析中事件A1(铁心多点接地导致故障)和事件A3(金属件松动导致放电故障)的状态量劣化程度评价值高度相符。同时, 本案例计算结果中P大于2.0%, 说明该变压器存在较高的故障率。这也与其实际存在的故障隐患类型相符。由此体现了本方法的有效性和准确性。
此外, 实例计算中的主要工作集中在对应状态量劣化值的分析赋值上, 相当于常规的状态评价打分, 与主流的基于状态评价加关系函数拟合的常规算法相比, 本方法节省了样本库采集、不同函数建模比选等大量时间[23], 使得计算效率更高, 体现出新算法良好的简捷性。
4 结语
本文通过对故障概率分析和计算的研究, 提出了一种将故障树分析与设备状态量评价相结合的综合计算方法, 融合了二者的优点。该方法基于FTA进行故障因素全面分析、基于FCE进行表征权重科学赋值, 使得故障概率整体比较准确可靠; 同时, 应用故障诊断专业技术成果, 快速评估状态量信息价值, 使故障概率计算在难度和复杂度方面均大大降低。通过问题变压器的实际算例, 验证了新方法的准确性和简捷性。但变压器检测方法和故障诊断技术是在不断发展进步的, 所以在变压器故障树底事件的分解重组、权重赋值精准度提升等方面, 后续还需要进一步的深入研究。
参考文献
-
[1]中国电力企业联合会. 中国电力行业可靠性年度发展报告[M]. 北京: 中国建材工业出版社, 2020.
-
[2]国网浙江省电力公司. 输变电设备风险评估导则: Q/GDW 1903-2013[S]. 北京: 国家电网公司, 2014.
-
[3]吴星. 输变电设备故障率预测及状态检修[D]. 西安: 西安科技大学, 2018.
-
[4]刘家郡. 水电厂主变压器的风险评估方法研究[D]. 长沙: 长沙理工大学, 2015.
-
[5]张忠会, 王卉, 何乐彰, 等. 基于风险评估旳电力变压器检修策略研究[J]. 中国农村水利水电, 2014(4): 159-162.
-
[6]孟珂. 基于改进层次分析法的变压器状态评价归一化模型研究[D]. 武汉: 武汉大学, 2018.
-
[7]李潮. 基于风险评估的配电网状态检修策略研究[D]. 成都: 西华大学, 2018.
-
[8]孙鹏, 陈绍辉. 基于故障率及设备重要程度的变压器风险矩阵模型[C]//2011年云南电力技术论坛论文集. 昆明, 2011: 277-281.
-
[9]韩超. 大型电力变压器的故障诊断与风险评估[D]. 北京: 华北电力大学, 2017.
-
[10]田姗. 基于故障案例的变压器风险评估体系研究[D]. 北京: 华北电力大学, 2017.
-
[11]刘宾. 电力变压器的故障诊断与风险评估[D]. 济南: 山东大学, 2013.
-
[12]张桦, 魏本刚, 李可军, 等. 基于变压器马尔可夫状态评估模型和熵权模糊评价方法的风险评估技术研究[J]. 电力系统保护与控制, 2016, 44(5): 134-140.
-
[13]吕汤. 基于配电网运行风险的设备状态检修策略研究[D]. 广州: 华南理工大学, 2018.
-
[14]柳杨, 杜预, 王志武, 等. 基于状态的核电厂大型电力变压器故障概率分析[J]. 电力设备管理, 2020(1): 75-77.
-
[15]吴莹. 大型变压器定量风险评估方法研究[D]. 长沙: 长沙理工大学, 2012.
-
[16]程建伟, 白翠粉, 刘通, 等. 基于故障模式的输变电设备故障风险分析[J]. 高电压技术, 2015, 41(12): 77-79.
-
[17]邓军, 孟杰, 潘志城, 等. 基于振动检测技术的电力变压器故障概率预测模型[J]. 变压器, 2020, 57(11): 37-40.
-
[18]中国电力科学研究院. DL/T 1685-2017油浸式变压器(电抗器)状态评价导则[S]. 北京: 国家能源局, 2017.
-
[19]张婷. 配电变压器的风险评估与状态检修策略研究[D]. 兰州: 兰州交通大学, 2020.
-
[20]汪洋, 陶悦玥, 魏天一, 等. 电力变压器状态评价方法研究[J]. 湖北电力, 2017, 41(3): 25-31.
-
[21]刘勇, 侯向红, 杨城, 等. 新型电力变压器结构原理及常见故障处理[M]. 北京: 中国电力出版社, 2014: 10-12.
-
[22]刘念. 电气设备状态监测与故障诊断[M]. 北京: 中国电力出版社, 2016: 89-99.
-
[23]杨擎柱, 程养春, 李斐然, 等. 基于现场数据的变压器首次故障率研究[J]. 高电压技术, 2022, 48(5): 1855-1864.