随着“碳达峰”“碳中和”目标的提出, 在我国能源转型过程中, 新能源的重要程度再次得到提升。在众多的新能源中, 风力发电和光伏发电无疑是当前发展最为迅速, 也是未来最有前途的。据国家能源局统计, 2020年全国新增发电设备容量中, 风力发电为7 167万kW, 同比增长178.7%, 光伏发电为4 820万kW, 同比增长81.7%^[1]。但我国的风能和太阳能资源主要集中在偏远地区, 受到送出线路的制约以及风力、光伏发电的电能质量因素的影响, 产生了弃风弃光现象。据统计, 我国每年仅风力、光伏等可再生能源弃电约1 000亿kWh。

为了更好地消纳新能源, 提高风能和太阳能的利用率, 减少弃风弃光率, 有必要搭建风光储发电系统。风光储发电系统就是利用风力发电和光伏发电的互补性来抵消其随机性和波动性而产生的发电系统。对于系统来说, 最为关键的指标是供电的经济性和可靠性, 而对这两个指标起决定性作用的步骤就是设计初期的容量配置。

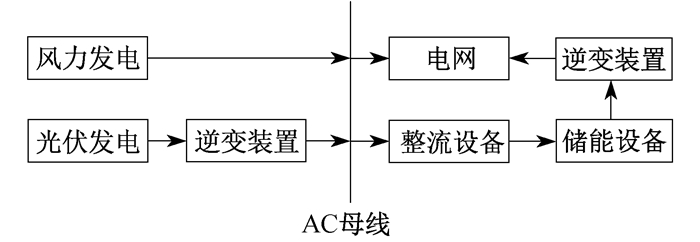
系统的结构示意如图 1所示。其主要工作原理为: 光伏发电经逆变装置后与风力发电共同汇入AC母线向电网供电, 若电网该时刻无法消纳全部电量, 且二者差值电量能够使储能设备正常工作, 则将多余电量经整流设备转化为直流电, 供储能设备工作。这部分存储能量可在风力、光伏发电出力不足时向电网补足部分功率缺额。

图 1 风光储发电系统结构

目前, 风光储发电系统的研究热点和重点主要是系统容量的优化配置和系统能量管理策略两个方面。其中, 系统容量的优化配置是能量管理策略的基础。容量配置过剩会导致资金投入过多和弃风弃光量增加, 容量配置过低则无法充分利用当地的风光资源, 造成电网缺电率升高, 进而破坏电力系统的稳定性。因此, 在设计风光储发电系统时, 解决容量配置问题至关重要。

系统容量配置优化过程如下: 一是收集分析数据, 主要包括当地的风速、太阳辐照度、温度, 以及电力负荷数据、电网送出线路的容量等; 二是根据收集到的数据选择合适的设备型号, 并对各单元建立相应的模型; 三是确定目标函数(如可靠性最高、能源成本最优、收益最大化等)和约束条件(如场地规模约束、负荷缺电率约束、成本约束等); 四是采用适当的算法进行求解, 在得出最优解或非劣最优解后进行系统联合仿真调试, 验证所得解的有效性, 若验证成功即可得出结论。

配置优化实际上是一个多目标优化问题(Multi-objective Optimization Problem, MOP), 求解这类问题最初主要采用传统的优化算法如线性规划和迭代技术^[2], 目前使用较为广泛的是启发式算法, 主要有遗传算法(Genetic Algorithm, GA)、粒子群优化算法(Particle Swarm Optimization, PSO)及其改进算法。

GA是基于达尔文的生物进化理论和孟德尔的遗传定律通过模拟自然选择和自然遗传过程中发生的繁殖、杂交和突变现象而提出的。生物可以通过遗传和变异来适应外界环境, 优胜劣汰, 因此基因优良的种群生存的几率更大, 能够更好地将自己的优良基因遗传给下一代。

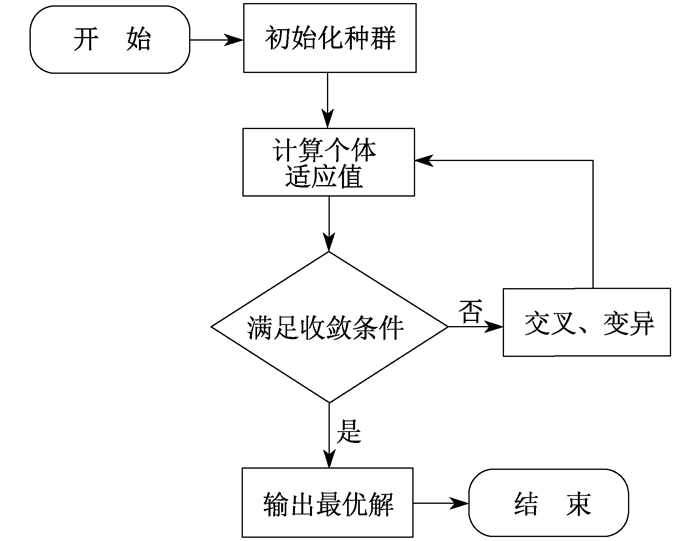
使用GA求解问题时的流程如图 2所示。

图 2 遗传算法流程

首先, 问题的每个可能的解都被编码成种群里不同的个体, 随机产生一些个体(即初始解), 并根据预定的目标函数对每个个体进行评价, 进而给出一个适应度值。基于此适应度值, 选择个体用于复制下一代。“好”的个体被选择复制, 而“坏”的个体则被淘汰, 这也就是所谓的适者生存。然后, 将选择出来的个体经过交叉和变异算子进行再组合, 生成新的一代。这一群新个体由于继承了上一代的一些优良性状, 因而在整体性能上要优于上一代, 并逐步朝着更优解的方向进化。最后, 重复上述步骤, 评判适应度值, 在达到收敛条件后得出所求问题的最优解^[3]。

从上述基本原理分析可以发现, GA的优点如下: 一是适合求解离散数值问题; 二是由于其结果就是目标函数的最优解, 不需要再对目标函数进行求导等复杂计算, 故使用过程较为简便; 三是适用范围广, 不局限于求解某类特定的问题。其缺点如下: 一是计算时间冗长, 在处理个体数目较大的问题时尤为明显; 二是其参数的设置对解的影响很大, 且参数的设置往往需要一定的使用经验; 三是易出现早熟现象, 这是由于其后期的搜索能力有所下降所致。

文献[4-6]均采用了传统的GA对风光储系统进行容量配置。文献[4]开发了一种优化的综合可再生能源模型, 采用GA确定光伏板的倾斜角度, 以及风力涡轮机和蓄电池储能系统的最佳容量, 成功设计了一套风光蓄电池储能系统为印度卡纳塔克邦一个偏远地区的4个负载部门供电。文献[5]提出了一种考虑实际系统和组件生命周期的系统最佳容量配置方法。以生命周期成本最小化、可再生能源渗透率最大化和污染物排放最小化为目标, 采用GA确定了风机、光伏板和储能设备的容量, 并且已应用于浙江省东福山岛的一个风光储发电系统的设计和开发。文献[6]利用GA优化了叙利亚的一个由光伏、风机、储能电池、柴油发电机组成的混合风光储发电系统容量配置, 提升了系统的可靠性和整体经济效益。

虽然传统GA有较大的应用价值, 但存在上述缺点, 使用范围并不广泛。但其改进算法, 由于在一定程度上克服了这些缺点, 得到了广泛应用, 如第二代非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm, NSGA)及其改进算法。

贾成真等人^[7]提出以系统收益和全生命周期年均值成本为经济性指标, 在考虑系统售氢效益的前提下, 建立满足系统的弃风弃光率、功率缺额率约束的多目标容量优化配置模型, 采用NSGA-Ⅱ算法进行求解, 得到了适合风光氢多能源系统内部的日前协调优化调度的容量配置方案。

NSGA-Ⅱ算法的优势在于: 该算法将父代种群与子代种群进行合并, 使得下一代的种群可以从双倍的空间中进行选取, 从而保留了最为优秀的所有个体; 引进精英策略, 确保优良基因得以保存下去, 提高了结果的精度; 使用拥挤度和拥挤度比较算子, 克服了NSGA中需要人为设定共享参数的缺陷, 且将其作为种群中个体间的比较标准, 使得准Pareto域中的个体能均匀地扩展到整个Pareto域, 保证了种群的多样性。但是在使用过程中, NSGA-Ⅱ算法仍然难以兼顾寻优深度和寻优速度。针对这一问题, SHENG W X等人^[8]提出了一种基于层次凝聚聚类^[9]截断策略的改进NSGA-Ⅱ算法, 考虑最小投资成本、最小能量期望和最小线路损失的目标, 得到了一个综合解, 最后利用该方法对内蒙古IEEE33总线系统进行了设计。仿真结果表明, 该方案可以在投资成本和供电可靠性之间获得合理的结果。

除改进算法本身外, 还可以引入其他算法, 通过算法的组合或提前对潜在可行解进行处理来扬长避短。孙海霞等人^[10]将入侵杂草算法引入到GA中, 利用入侵杂草算法中的变异因子选取优秀个体, 减小传统GA陷入局部最优的概率, 提高了算法的寻优能力和收敛速度, 其性能明显优于传统GA。

总而言之, 研究人员分别从如何提升优良基因遗传的概率和扩大搜索域的角度来解决收敛于局部最优解的问题, 通过改变适应度值的计算方式和排序方式在一定程度上缩短了计算时间。这些方法都取得了不错的效果, 使得GA算法更加适用于解决系统容量配置问题。

PSO算法是以同种动物群体(如鸟群、鱼群等)之间的社会信息共享提供了一个进化优势(如食物、栖息地等影响生存、繁殖的重要信息)。这一算法, 最早由EBERHART R博士和KENNEDY J博士于1995年总结提出。某些生物群体在觅食过程中, 有时需要分散寻找, 有时需要集体搜寻。对于整个群体来说, 总有一些个体对食物所在地较为敏感, 拥有较为准确的位置信息。例如, 在鸟群觅食过程中, 它们会不断分享各自所掌握的信息, 准确的信息则会被更多地分享和接收。随着精准食源信息被传播, 鸟群最终会聚集在食物所在地, 达到觅食的目的^[11]。通俗地说, 在使用PSO算法时, “寻找食物”的过程就是求解问题的过程, 每只“鸟”就相当于一个解, 当“鸟”飞行时, 也就是以某一速度在解空间中移动。这时它们的位置会被记录, 这些位置就是潜在的解。

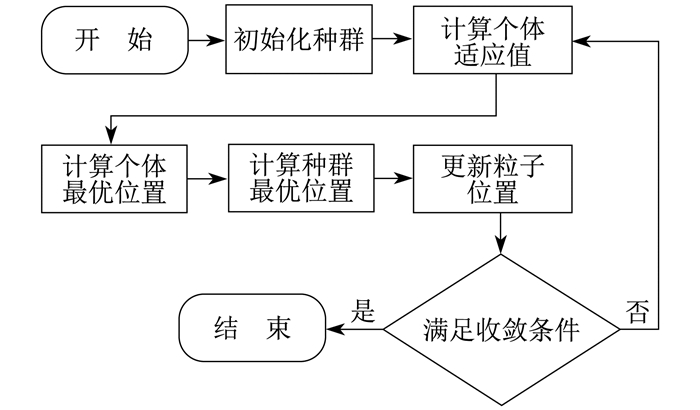
PSO算法的步骤^[12]如下: 一是初始化种群, 即初始化各类参数, 包括搜索空间、学习因子、收敛条件, 以及每个粒子允许的速度范围和最初的位置等; 二是根据适应度函数计算各粒子的适应值, 并计算各粒子的最优位置; 三是利用速度和位置更新公式来更新粒子的速度和位置; 四是计算更新后各粒子的最优位置, 并更新种群的最优位置; 五是判断是否满足收敛条件, 若不满足则转到第3步, 若满足则输出结果。上述算法步骤如图 3所示。

图 3 粒子群优化算法流程

PSO算法在优化容量配置方面的应用更为广泛。其优点主要有: 一是在三维坐标中定义各粒子, 使得搜索过程更加灵活、直观; 二是在解决复杂问题时计算速度明显快于GA; 三是可操作性高, 能够衍生出多种改进算法。同时, PSO算法存在以下缺点: 一是计算非坐标问题的性能较差, 甚至无法得到最优解; 二是存在粒子早熟问题, 导致收敛于局部最优解。

PSO算法及其改进算法是解决风光储发电系统容量配置优化问题的最优选择之一。由于其具有上述优点, 因此成为应用最为广泛的优化算法。

文献[13]针对阿拉伯偏远地区提出了一种基于智能电网负荷管理应用的混合可再生能源系统的最优容量配置方案。该方案将成本最小和可靠性最高作为优化目标, 采用PSO算法求解, 在MATLAB平台上进行仿真, 确定了系统各部分的最优容量配置, 最大限度地提高了系统的产能。文献[14]采用基本的PSO算法对所研究的系统进行了容量配置优化, 并取得了较好的结果。文献[15]采用了ε约束方法来求解系统的3个目标函数(即负荷缺电率、二氧化碳排放量和系统总成本最小化), 在对目标函数进行预处理后, 采用PSO算法进行了求解。

在面对复杂的优化问题时, 研究人员对基本的PSO算法做出了一些改进。胡仕灿^[16]提出了一种自适应权重的PSO算法, 可根据目标函数的变化随时对权重系数进行调整。戴航等人^[17]提出了一种双适应度混沌PSO算法, 将混沌算法融入PSO算法, 并对基本的PSO算法的适应度函数进行了改进。改进后的PSO算法在解决储能优化运行问题时性能更佳, 其全局寻优能力比基本的PSO算法更强, 储能系统收益更高, 经济性更好, 储能出力曲线更加合理。

另外, 为了克服PSO算法易陷入局部最优解的缺陷, 有学者提出了量子粒子群(Quantum Particle Swarm Optimization, QPSO)算法。其基本思想是利用粒子的波粒二象性, 模拟粒子的量子行为, 增加粒子运动轨迹的不确定性。刘鹏飞^[18]在QPSO算法的基础上又引入了混沌算法和精英粒子学习的策略, 解决了粒子容易早熟的问题。针对同一算例分别采用PSO算法、QPSO算法、基于混沌的QPSO算法来配置系统容量, 在各自都能满足负荷缺电率等指标的前提下进行仿真实验。结果显示, 与PSO算法和QPSO算法相比, 基于混沌的QPSO算法的总投资成本分别低13.9%和18.7%。林敏怡等人^[19]在QPSO算法的基础上加入了自适应中心权重思想, 引入权重系数, 扩大了粒子搜寻的范围, 使每个粒子更具创造力, 提升了全局搜索能力, 防止了局部收敛。

除PSO算法及其改进算法具有较好的使用效果外, 将两种不同的启发式算法相结合, 也能取得令人满意的结果。MALEKI A等人^[20]以年总成本最小化为目标函数, 采用多种改进的PSO算法优化了风光储发电系统的容量配置, 最终结果显示具有收缩因子的PSO算法求解结果最优。

综上, 对于PSO算法的改进方式主要有3种: 一是改进动态惯性的权重系数提高算法的全局搜索能力和解的精确度; 二是引入波粒二象性, 增强粒子运动范围的不确定性, 提升全局搜索能力; 三是与其他算法相结合。

本文主要综述了两种算法及其改进算法在风光储发电系统容量配置方面的应用, 对这两种算法的基本原理、优缺点、基本算法和改进算法的应用以及算法的改进方式都进行了深入的分析和总结。在接下来的工作中, 风光储发电系统容量配置优化方面的研究重点如下: 在不断改进基础算法的同时, 引进新的启发式算法, 拓宽容量配置优化的策略和选择; 加强容量配置与能量管理策略的联系, 二者的共同目标都是造就成本更低、效率更高的风光储混合发电系统, 因此将能量管理策略融入容量配置优化过程当中, 采取并行优化的方式, 也能取得更加理想的效果; 引入人工智能, 如机器学习等, 有助于提升负荷预测的精度, 使得容量配置优化结果更加精确。