|
|
|
发布时间: 2023-04-28 |
综合能源管理 |
|
|
|
收稿日期: 2022-04-02
中图法分类号: TK01;TM744;TM711
文献标识码: A
文章编号: 2096-8299(2023)02-0167-08
|
摘要
多能微网系统结构及设备耦合关系复杂,接入新能源的不确定性为系统运行带来巨大挑战。基于Beta拟合的光伏发电模型和两参数威布尔分布的风力发电模型,采用分解求解法进行了多能耦合潮流计算。然后对33节点电网和33节点热网耦合的多能源系统进行了算例分析,利用蒙特卡洛法提取不确定性样本,进一步提出了考虑光伏、风电和电、热负荷不确定性的概率潮流计算方法。最后运用该方法完成了概率潮流的算例分析,从概率潮流计算方法和各子网络的潮流计算结果两方面验证了方法的有效性。
关键词
不确定性; 多能微网; 概率潮流
Abstract
The complex structure and equipment coupling relationship of multi-energy microgrid system and the uncertainty of the connected new energy sources bring great challenges to the system operation.Based on the Beta-fitted photovoltaic power generation model and the wind power generation model with two-parameter Weibull distribution, the decomposition solution method is used for multi-energy coupled tide calculation.Subsequently, this paper analyzes the arithmetic case of the multi-energy system coupled with 33-node grid and 33-node thermal network, extracts uncertainty samples by Monte Carlo method, further proposes a probabilistic tide calculation method considering the uncertainty of PV, wind power, electric and thermal loads.Finally, the method is used to analyze the probabilistic power flow, and the effectiveness of the method is verified from two aspects: the probabilistic power flow calculation method and the power flow calculation results of each subnetwork.
Key words
uncertainty; multi-energy micronetworks; probabilistic power flow
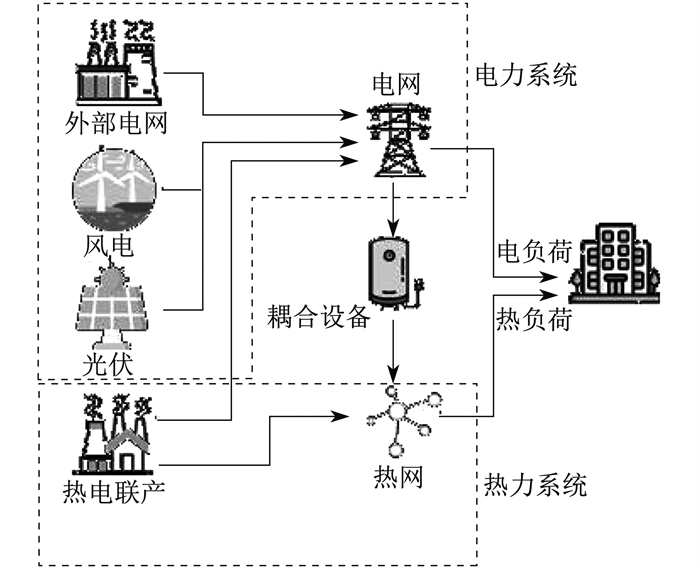
随着经济社会的发展和新型城镇化水平的提高, 能源负荷需求总量不断增加, 能源供需匹配矛盾凸显, 与此同时, 传统化石燃料开发应用造成的生态环境问题和能源供应保障问题, 也引起了更多的重视[1]。世界各国正积极推动新能源与多能互补融合技术的发展, 促进以可再生能源为主导的低碳、清洁、高效的能源体系建设[2]。综合能源系统优化整合本地可再生资源, 综合考虑了多种能源类型相互转换以及不同物理空间能源相互融通。基于多能互补技术和能源梯级利用等理论, 综合能源系统充分利用系统内各种能源自身特点, 通过多能源协同的规划设计、优化调度等手段, 综合提升系统的能源利用效率[3]。
区域级综合能源系统主要面向工业园区和社区等特定区域用能场景。该系统不仅可以同时考虑配电网、配气网和区域热网的逐时耦合, 还可以考虑能源梯级利用技术和可再生能源接入[4]。作为综合能源在区域中的应用, 多能微网系统是能源供应网络的终端环节, 可充分考虑终端用户多种能源形式的负荷特性, 兼顾用户分布式可再生能源接入[5]。通过多种能源系统间的深度协同优化与耦合运行, 以满足较小空间区域中不同用户的多元化能源负荷需求。随着光伏、风电等清洁能源的大规模接入电网, 可再生能源具有波动性、随机性等特点, 增加了电力系统运行风险。
多能源系统概率潮流计算通过在系统中引入随机变量的统计特征, 在此基础上由潮流计算得到系统状态量的统计特征, 从而定量评估不确定性因素对综合能源系统的影响。电力系统的不确定性因素包括风力发电的风速不确定性、光伏发电的光照辐射不确定性、电力负荷需求不确定性、系统故障不确定性等[6]。多能源耦合系统不确定因素还包括热力负荷波动性、温度、能源设备出力波动等。文献[7]通过研究验证了光伏出力Beta分布概率模型, 并利用极大似然估计求出了形状参数值。文献[8-9]提出了风速的概率分布模型: Webull分布或正态分布。文献[10]提出了用于风速分布估计的混合密度模型, 成功避免了最佳带宽的选择过程, 提高了拟合精度。文献[11]将综合能源系统中的电、热、气负荷建模为正态分布, 该方法在概率潮流计算中被广泛应用。文献[12]利用Copula理论构建了计及光伏出力和负荷相关性的联合概率分布模型, 探究了其对电力系统运行状态的影响。文献[13]提出了一种内点法结合随机因子更新的方法, 通过原始对偶内点法的参数结果更新调节因子来调节机会约束满足的概率, 并验证了该方法在含风电厂电力系统随机最优调度的正确性和有效性。文献[14]利用粒子群算法对分布式光伏发电中压配电网进行无功优化, 通过控制无功功率以支持配电网和电压调节, 解决了分布式光伏中压配电网的逆潮流问题。然而, 目前在多能微网系统中同时考虑可再生能源发电出力和负荷不确定性的概率潮流计算研究较少。
本文首先构建了含多种电热耦合设备的多能微网系统模型, 建立不确定因素的概率模型, 包括光伏出力、风机出力、电力负荷、热力负荷的概率模型; 然后根据选用的蒙特卡洛概率潮流分析方法, 提出概率潮流计算流程; 最后通过算例分析不确定因素对电热耦合潮流运行的影响。
1 电热耦合多能微网系统模型
1.1 电力系统模型
电力系统由供电设备、变压器、输配电网以及用电负荷组成。电热耦合的多能微网系统中电力系统通常为配电网级。本文采用的经典直角坐标系下交流潮流数学模型可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{P_i} - \sum\limits_{j = 1}^n {\left[ {{e_i}\left( {{G_{ij}}{e_j} - {B_{ij}}{f_j}} \right) + {f_i}\left( {{G_{ij}}{f_j} + {B_{ij}}{e_j}} \right)} \right]} = 0}\\ {{Q_i} - \sum\limits_{j = 1}^n {\left[ {{f_i}\left( {{G_{ij}}{e_j} - {B_{ij}}{f_j}} \right) - {e_i}\left( {{G_{ij}}{f_j} + {B_{ij}}{e_j}} \right)} \right]} = 0} \end{array}} \right. $ | (1) |
式中: P、Q——有功、无功功率;
Gij、Bij——节点导纳矩阵中电导、电纳;
ei、ej——节点i和节点j电压的实部;
fi、fj——节点i和节点j电压的虚部。
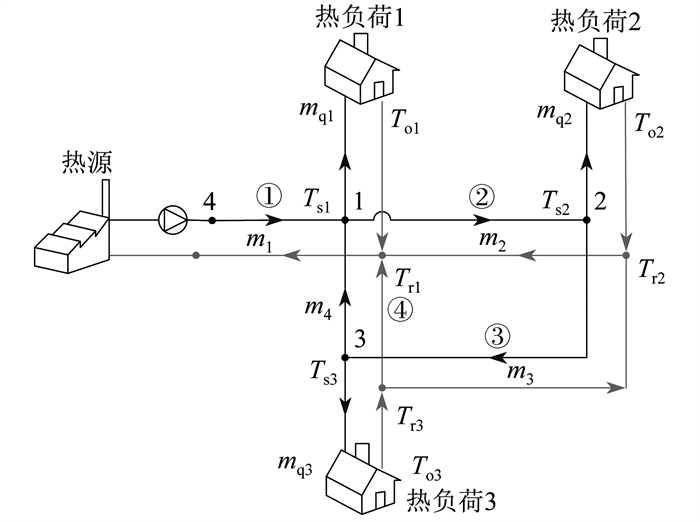
1.2 热力系统模型
1.2.1 水力模型
水力模型用来求解热力系统中管段流量和各管段压力的关系, 包括流量连续性方程和压头损失方程, 可以仅考虑流量连续性方程, 压头损失沿管路计算。具体表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{Am}} = {\mathit{\boldsymbol{m}}_{\rm{q}}}}\\ {\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{h}}_{\rm{f}}} = \mathit{\boldsymbol{O}}}\\ {\mathit{\boldsymbol{K}}|\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{m}} = \mathit{\boldsymbol{O}}} \end{array}} \right. $ | (2) |
式中: A——供热网络的节点-支路关联矩阵;
m——管段流量列向量;
mq——节点注入流量列向量;
B——供热网络的基本回路矩阵;
hf——压头损失列向量;
O——零矩阵;
K——管段阻力系数矩阵[16]。
1.2.2 热力模型
热力模型描述热网中热量传递过程, 用于计算节点供、回热温度, 包括节点功率方程、管段温降方程以及混合节点温度方程。具体表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = {C_{\rm{p}}}{\mathit{\boldsymbol{m}}_{\rm{q}}}\left( {{\mathit{\boldsymbol{T}}_{\rm{s}}} - {\mathit{\boldsymbol{T}}_{\rm{o}}}} \right)}\\ {{\mathit{\boldsymbol{T}}_{{\rm{end }}}} = \left( {{\mathit{\boldsymbol{T}}_{{\rm{start }}}} - {\mathit{\boldsymbol{T}}_{\rm{a}}}} \right){{\rm{e}}^{ - \frac{{\lambda {\mathit{\boldsymbol{L}}}}}{{{C_{{\rm{p}}\mathit{\boldsymbol{m}}}}}}}} + {\mathit{\boldsymbol{T}}_{\rm{a}}}}\\ {\left( {\sum {{{\mathit{\boldsymbol{m}}}_{{\rm{out }}}}} } \right){\mathit{\boldsymbol{T}}_{{\rm{out }}}} = \sum {{\mathit{\boldsymbol{m}}_{{\rm{in }}}}} {\mathit{\boldsymbol{T}}_{{\rm{in }}}}} \end{array}} \right. $ | (3) |
式中: Ф——节点热功率列向量;
Cp——水的比热容, J/(kg·K);
Ts——节点供热温度列向量;
To——负荷节点返回温度列向量;
Tstart、Tend——管段中沿水流方向的首、末端温度列向量;
Ta——外部环境温度列向量;
λ——每单位长度管段的传热系数;
L——管段长度列向量;
min、mout——流入、流出节点管段质量流量列向量;
Tin、Tout——流入、流出节点回热温度列向量。
1.3 耦合设备模型
耦合设备模型包括热电联产机组(CHP)、热泵(HP)和电锅炉(EB)等。
1.3.1 热电联产机组
CHP通过消耗天然气产生电能和热能。根据热电比可调与否分为定热电比机组和变热电比机组两种。定热电比和变热电比机组模型可分别表达为
| $ {C_{\rm{m}}} = \frac{{{\mathit{\Phi }_{{\rm{CHP}}}}}}{{{P_{{\rm{CHP}}}}}} $ | (4) |
| $ {C_{\rm{z}}} = \frac{{{\mathit{\Phi }_{{\rm{CHP}}}}}}{{\eta {F_{{\rm{in }}}} - {P_{{\rm{CHP}}}}}} $ | (5) |
式中: Cm、Cz——热电比固定值、可变值;
ΦCHP、PCHP——CHP机组产生的热功率、电功率;
η——CHP机组的冷凝效率;
Fin——燃料输入速率。
1.3.2 热泵
热泵是将低品位热能转化为高品位热能的装置。在此过程中仅需消耗少量电能就能满足负荷的供热需求。热泵一般模型如下
| $ {k_{{\rm{COP}}, {\rm{HP}}}} = \frac{{{\mathit{\Phi }_{{\rm{HP}}}}}}{{{P_{{\rm{HP}}}}}} $ | (6) |
式中: kCOP, HP——热泵性能系数;
ΦHP——热泵产生的热功率;
PHP——热泵消耗的电功率。
在实际运行中, 热泵与CHP设备可以联合运行来改善设备出力。考虑电转热设备和CHP设备联合运行, 其组成能源站的模型, 热电效率可表示为
| $ \gamma = \frac{{{\mathit{\Phi }_{{\rm{CHP}}}} + w{P_{{\rm{CHP}}}}{k_{{\rm{COP}}, {\rm{HP}}}}}}{{{P_{{\rm{CHP}}}}(1 - w)}} $ | (7) |
式中: γ——等效热电比;
w——热泵消耗的电功率占CHP发出电功率的比例。
1.3.3 电锅炉
电锅炉能将电能直接转化为热能, 在供热网中主要作为调峰热源。电锅炉模型表示为
| $ {\eta _{{\rm{EB}}}} = \frac{{{\mathit{\Phi }_{{\rm{EB}}}}}}{{{P_{{\rm{EB}}}}}} $ | (8) |
式中: ηEB——电锅炉电热转化效率;
ΦEB——电锅炉产生的热功率;
PEB——电锅炉消耗的电功率。
2 概率潮流模型及算法求解流程
概率潮流计算考察多重不确定性因素, 例如负荷功率和发电机出力随时变化, 网络结构由于故障或检修而改变、测量和估计误差等。本文主要考虑的不确定性因素包括光伏发电量不确定性、风力发电量不确定性和电热负荷不确定性。
2.1 随机变量概率模型
2.1.1 光伏出力概率模型
光伏概率模型的Beta分布概率密度函数表示为
| $ \begin{array}{c} f\left( {{P_{\rm{V}}}} \right) = \frac{{\Gamma (\alpha + \beta )}}{{\Gamma (\alpha ) + \Gamma (\beta )}}{\left( {\frac{{{P_{\rm{V}}}}}{{{P_{{\rm{V}}, \max }}}}} \right)^{(\alpha - 1)}}.\\ {\left( {1 - \frac{{{P_{\rm{V}}}}}{{{P_{{\rm{V}}, \max }}}}} \right)^{(\beta - 1)}} \end{array} $ | (9) |
式中: PV——光伏电源出力;
Γ——Gamma函数;
PV, max——光伏功率的最大值;
α、β——Beta分布的尺度参数和形状参数。
2.1.2 风机出力概率模型
风电机组出力具有很强的波动性、随机性和间歇性。本文采用两参数威布尔分布描述风速的随机特性。其概率密度函数表示为
| $ f\left( {{v_{{\rm{WT}}}}} \right) = \frac{{{K_{{\rm{WT}}}}}}{{{D_{{\rm{WT}}}}}}{\left( {\frac{{{v_{{\rm{WT}}}}}}{{{D_{{\rm{WT}}}}}}} \right)^{{K_{{\rm{WT}} - 1}}}}\exp \left[ { - {{\left( {\frac{{{v_{{\rm{WT}}}}}}{{{D_{{\rm{WT}}}}}}} \right)}^{{K_{{\rm{WT}}}}}}} \right] $ | (10) |
式中: vWT——风速;
KWT——形状参数;
DWT——尺度参数。
通常, 观测到的风速是10 m高度处的风速(用v1表示)。该风速值与风机轮毂高度h处的风速vh两者之间关系式如下
| $ {v_h} = {v_1}{\left( {\frac{h}{{10}}} \right)^{\frac{1}{7}}} $ | (11) |
风力发电机的出力与风速之间的关系可以表示为一次函数型, 其表达式为
| $ {P_{\rm{W}}} = \left\{ {\begin{array}{*{20}{c}} 0&{0 \le {v_h} \le {v_{{\rm{ci}}}}, {v_{{\rm{co}}}} \le {v_h}}\\ {P_{\rm{W}}^{\rm{r}}\frac{{{v_h} - {v_{{\rm{ci}}}}}}{{{v_{\rm{r}}} - {v_{{\rm{ci}}}}}}}&{{v_{{\rm{ci}}}} \le {v_h} \le {v_{\rm{r}}}}\\ {P_{\rm{W}}^{\rm{r}}}&{{v_{\rm{r}}} \le {v_h} \le {v_{{\rm{co}}}}} \end{array}} \right. $ | (12) |
式中: PW——风电场有功出力;
PWr——风电场额定出力;
vci、vr、vco——风力发电机的切入风速、额定风速及切出风速。
在并网型风力发电机中, 风机并网有不同的控制模式, 在进行概率潮流分析计算中, 往往需要根据实际情况选择不同的风电控制方法, 确定潮流计算中节点类型。当采用恒电压时, 可以在电力系统潮流计算中等效为PV节点(有功功率和电压幅值给定); 当采用恒功率因数时, 通常等效为PQ节点(有功功率和无功功率给定)。此时, 风电场输出的无功功率QW表示为
| $ {Q_{\rm{W}}} = {P_{\rm{W}}}\tan \left( {{\theta _{\rm{W}}}} \right) $ | (13) |
式中: θW——风电场对应的功率因数角, 根据风机在电网中的不同节点类型, 功率因数可以假设为正值和负值。
2.1.3 电力负荷和热力负荷概率模型
现有负荷概率模型中, 一般假设电力负荷和热力负荷均服从正态分布ε~N(μ, σ2), 并且负荷需求的标准差为均值的5 % ~20 %。在电力负荷概率模型中, 还假设负荷的功率因数保持恒定。
电力负荷有功功率的概率密度函数表示为
| $ f\left( {{E_{\rm{L}}}} \right) = \frac{1}{{\sqrt {2\pi {\sigma _{{E_{\rm{L}}}}}} }}\exp \left[ { - \frac{{{{\left( {{E_{\rm{L}}} - {\mu _{{E_{\rm{L}}}}}} \right)}^2}}}{{2\sigma _{{E_{\rm{L}}}}^2}}} \right] $ | (14) |
式中: EL——电负荷的有功功率;
σEL——有功功率的标准差;
μEL——有功功率的数学期望。
热力负荷的概率密度函数可以表示为
| $ f\left( {{H_{\rm{L}}}} \right) = \frac{1}{{\sqrt {2\pi {\sigma _{{H_{\rm{L}}}}}} }}\exp \left[ { - \frac{{{{\left( {{H_{\rm{L}}} - {\mu _{{H_{\rm{L}}}}}} \right)}^2}}}{{2\sigma _{{H_{\rm{L}}}}^2}}} \right] $ | (15) |
式中: HL——热力负荷功率;
σHL——热力负荷的标准差;
μHL——热力负荷功率的数学期望。
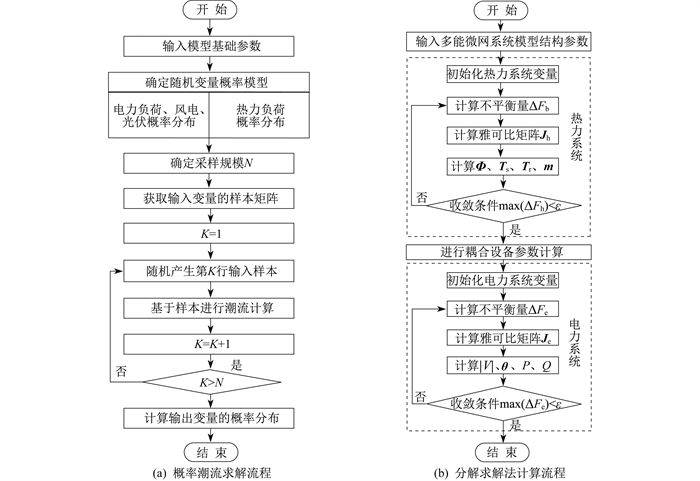
2.2 概率潮流算法流程
考虑电热耦合多能流稳态模型具有非线性特性, 本文采用的潮流计算求解方法为牛顿-拉夫逊法[17]。多能耦合潮流计算采用分解求解法, 在电力系统中应用牛顿法求解时, 找出电力系统相应的模型变量并以矩阵形式列写相应的求解方程, 通过牛顿法迭代进行求解。热力系统中应用牛顿法求解时, 需对模型公式进行相应的整理, 列写矩阵形式的求解方程, 然后通过迭代方法进行求解。
当CHP运行在以热定电模式下时, 电力系统中具有电源功能的节点有功功率表示为
| $ {P_{{\rm{CHP}}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{\mathit{\Phi }_{{\rm{CHP}}}}}}{{{C_{\rm{m}}}}}, }&{{\rm{CHP}}}\\ {\frac{{{\mathit{\Phi }_{{\rm{CHP}}}}}}{\beta }, }&{{\rm{CHP}} + {\rm{HP}}} \end{array}} \right. $ | (16) |
其中, “CHP”表示仅考虑热电联产情况, “CHP+HP”表示考虑热电联产和热泵情况。本文选用分解求解法进行多能耦合潮流计算, 采用蒙特卡洛法抽样进行模拟[18]。首先确定采样规模N, 通过抽样生成大量随机样本, 构成样本矩阵, 使输入模型的随机变量完全随机。在此基础上, 将随机变量输入到所建立模型中进行求解, 每次潮流计算模型求解收敛后, 将输出参数保存, 然后将新一组输入随机变量输入模型进行求解, 直到全部采样数据计算完成。
概率潮流算法流程如图 3所示。其中, Tr为节点回热温度, |V|为节点电压幅值绝对值, θ为节点电压相角, P为节点有功功率, Q为节点无功功率。
3 算例分析
3.1 算例说明
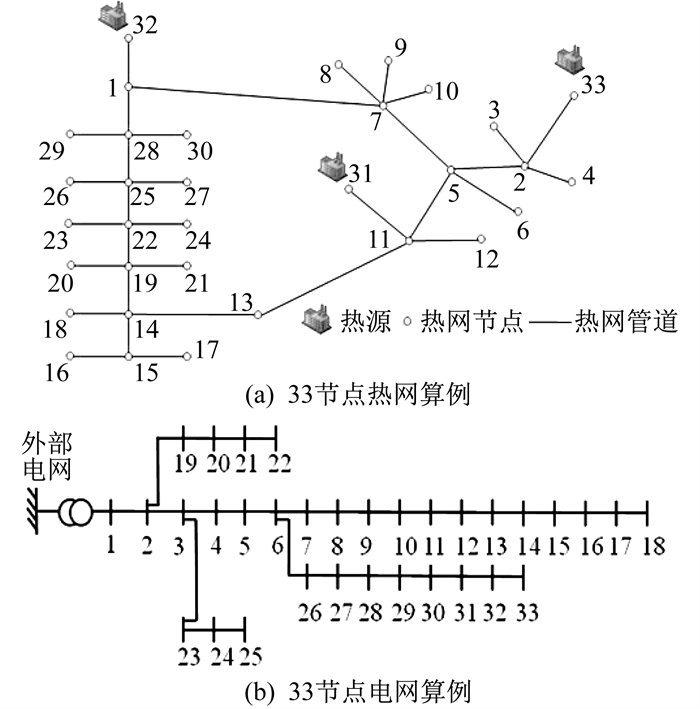
本文中算例采用33节点电网与33节点热网耦合形成的多能源系统。该节点电网系统是从实际等值出的经典配电网模型, 常用于基于MATLAB的电力系统分析中[19]。热网和电网节点算例如图 4所示。
电网处于并网运行状态, 节点1作为平衡节点并入外部电网, 节点22和25光伏并网, 节点10和30风机并网。热网节点31与电网节点18通过能源站1耦合, 耦合设备为CHP运行在以热定电模式下。热网节点32处为能源站2, 供能设备为燃气锅炉。能源站3为热网节点33与电网中节点33耦合, 耦合设备为CHP, 热网节点33为热平衡节点, 热网仅考虑稳态运行模式。能源站1、3中的CHP机组COP为1.3, 其热功率分别为3 MW和2.5 MW。热源供热温度为100 ℃, 负荷出水温度为30 ℃, 环境温度为10 ℃。
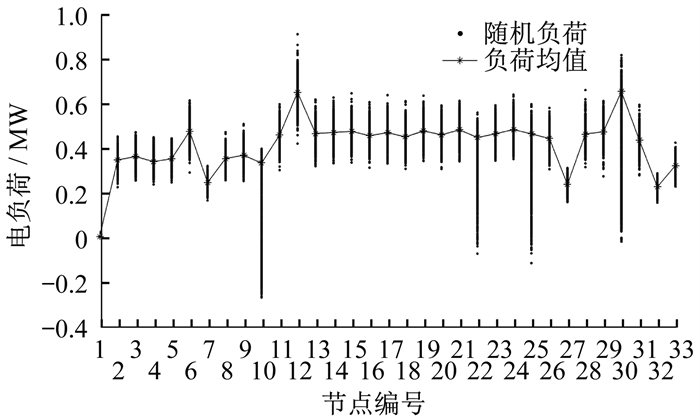
系统中输入的不确定性因素中, 风力发电机组的参数设置如下: vci =3 m/s, vco=17 m/s, vr=11 m/s, θW=0.95。风机概率模型中分布参数KWT=2.18, DWT=7.92[20], 风力发电机组额定容量为0.5 MW。光伏的额定光照强度为500 W/m2, 光伏分布参数α和β分别为0.42和1.39。光伏额定容量为0.5 MW。电力负荷、热力负荷的概率模型服从正态分布, 负荷数据标准差均为期望的10 %。本文中概率潮流计算程序通过MATLAB编程实现。
3.2 不确定性因素对潮流计算过程的影响
3.3 结果分析
3.3.1 热网概率潮流计算结果分析
在热网潮流计算结果中, 重点分析热网中各节点、管段未知量计算是否准确, 以及热网中各节点在概率潮流下的计算分布规律。热网的未知量包括: 各负荷节点的供、回热温度, 热网管段中的质量流量和各热网源节点发出的热功率。在概率潮流计算中, 主要分析各节点状态量的概率分布, 在统计数据基础上分析系统运行状态。
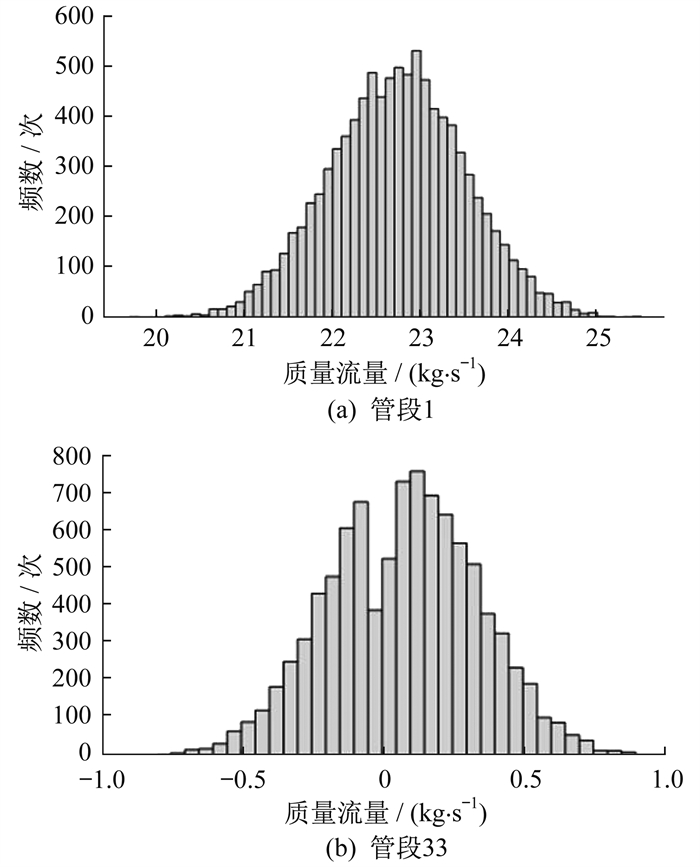
将热网计算结果未收敛数据剔除后, 分析热网中各节点的管段流量分布情况, 以管段1和管段33为例, 其质量流量频数分布直方图如图 6所示。由图 6可知: 管段1质量流量频数分布大体呈现正态分布; 管段33中, 节点33为平衡节点。该节点的供热功率由热网整体计算得到。此节点的质量流量大小同时关系到热源节点供给网络的热量。该管段的质量流量出现负值, 表示质量流量的流向相反。坐标轴两侧出现对称, 与管段1相似, 也基本呈现正态分布。
热网中各节点供热温度如图 7所示。由图 7可知, 节点供热温度在98~100 ℃之间变化, 总体网络供热情况较好。在环状热网中, 由于多个供热节点共同向网络供热, 网络中的热量传递出现不确定的方向, 因而节点供热温度变化情况复杂。
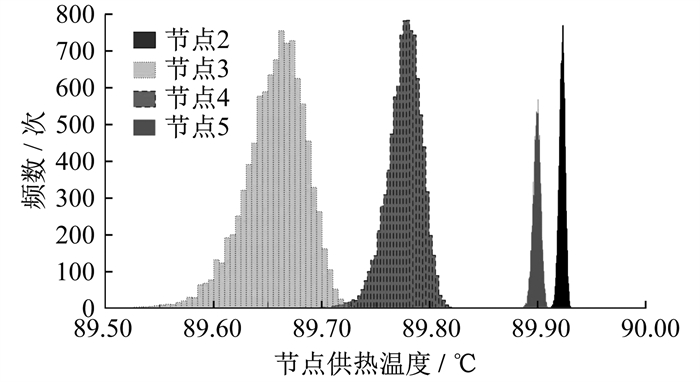
节点2~5的供热温度频数分布直方图如图 8所示。由图 8可知: 节点3~5是节点2的下游节点, 按照热量传递的方向, 节点2的温度均值高于其他3个节点, 且从各节点温度的变化范围来看, 节点2的温度变化范围也小于其下游的节点; 值得注意的是节点5与节点2的距离在节点4和节点2之间, 但是其温度均值高于节点4, 是由于节点5处于该热网的环网上, 其他热源节点的供热同样会对该节点的温度分布产生影响。这种环状网络中复杂的热源间供热影响与辐射状网络略有不同。
3.3.2 电网概率潮流计算结果分析
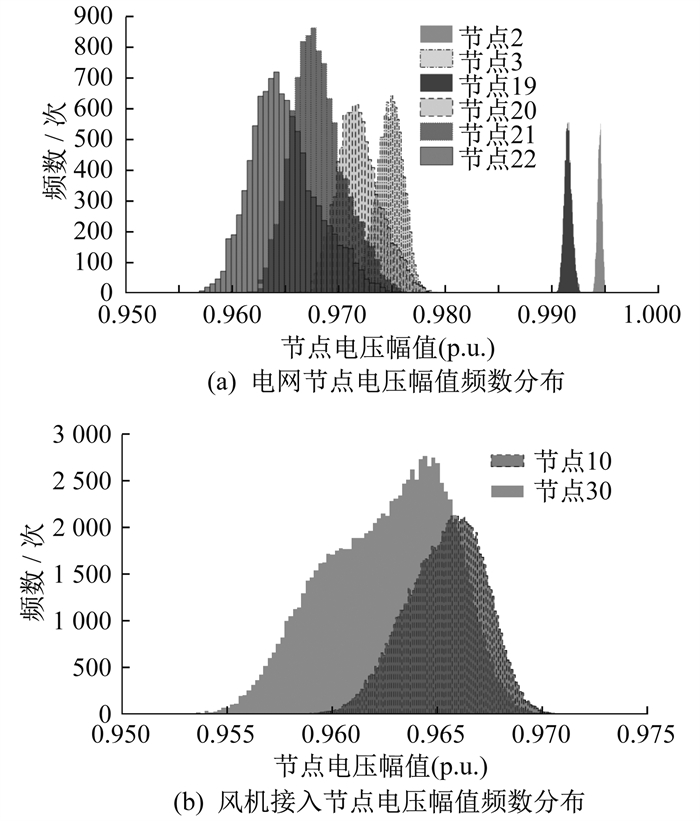
蒙特卡洛抽样中抽样次数越多, 其结果与实际值的误差越小, 概率潮流计算所需要的时间就越长, 从兼顾计算时间和计算精度考虑, 取1 000次蒙特卡洛抽样计算以表示概率潮流计算结果。此时节点2、3、19、20、21、22的电压幅值频数和风机接入节点的电压幅值频数分布直方图如图 9所示。
由图 9可知, 节点2和节点3的电压高于其他节点, 且变化范围小于其他节点。在电网中如果同一线路上有2个PV节点, 那么这条线路上的电压将沿2个PV节点依次降低。由电压幅值频数分布可知其概率分布, 在节点20、21、22的概率分布中, 逐渐表现出正偏态分布。这是由于节点22接入了光伏, 该节点与其同线路相邻的节点20、21的电压幅值呈现正偏态分布。电网中风机接入节点中, 受到风机接入的影响, 节点电压幅值与负偏态分布相似。
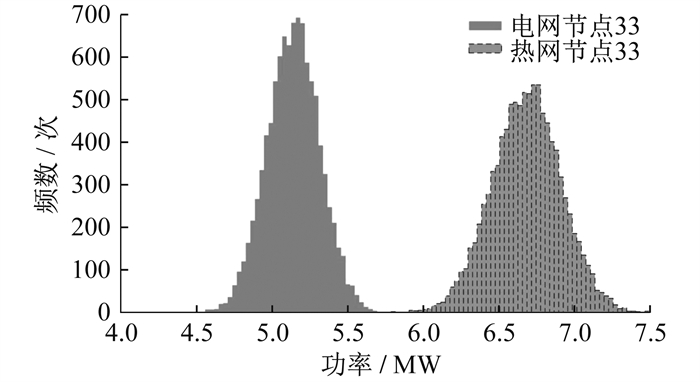
3.3.3 耦合设备的概率潮流计算结果分析
4 结论
(1) 在环状热网中, 多个热源同时供能时, 环网中管段流量方向不定, 同时在组成环网的节点中供热温度受到各热源节点的温度影响, 都增加了热网分析的复杂性。在热网运行状态中应格外关注。
(2) 受到可再生能源接入的影响, 光伏接入的节点电网电压幅值频数分布呈现正偏态分布, 而风机接入的节点电网电压幅值频数分布呈现负偏态分布。
参考文献
-
[1]邵成成, 王锡凡, 王秀丽, 等. 多能源系统分析规划初探[J]. 中国电机工程学报, 2016, 36(14): 3817-3829.
-
[2]ZHANG X X, LOVATI M, VIGNA I, et al. A review of urban energy systems at building cluster level incorporating renewable-energy-source (RES)envelope solutions[J]. Applied Energy, 2018, 230: 1034-1056. DOI:10.1016/j.apenergy.2018.09.041
-
[3]HUAGN W J, ZHANG N, CHENG Y H, et al. Multienergy networks analytics: standardized modeling, optimization, and low carbon analysis[J]. Proceedings of the IEEE, 2020, 108(9): 1411-1436. DOI:10.1109/JPROC.2020.2993787
-
[4]余晓丹, 徐宪东, 陈硕翼, 等. 综合能源系统与能源互联网简述[J]. 电工技术学报, 2016, 31(1): 1-13.
-
[5]MANCARELLA P. MES (multi-energy systems): an overview of concepts and evaluation models[J]. Energy, 2014, 65: 1-17. DOI:10.1016/j.energy.2013.10.041
-
[6]林济铿, 刘阳升, 徐振华, 等. 基于改进稀疏概率分配法的计及参数不确定性的电力系统时域仿真[J]. 中国电机工程学报, 2019, 39(8): 2297-2306.
-
[7]王敏, 丁明. 含大型太阳能发电系统的极限传输容量概率计算[J]. 电力系统自动化, 2010, 34(7): 31-35.
-
[8]丁明, 吴伟, 吴红斌, 等. 风速概率分布参数预测及应用[J]. 电网技术, 2008, 32(14): 10-14.
-
[9]隋冰彦, 侯恺, 贾宏杰, 等. 基于最大熵原理的含风电和电动汽车电力系统概率潮流[J]. 电网技术, 2016, 40(12): 3696-3705.
-
[10]MIAO S W, XIE K G, YANG H J, et al. A mixture kernel density model for wind speed probability distribution estimation[J]. Energy Conversion and Management, 2016, 126: 1066-1083.
-
[11]CHAUDRY M, WU J Z, JENKINS N. A sequential monte carlo model of the combined GB gas and electricity network[J]. Energy Policy, 2013, 62: 473-483.
-
[12]陆为华, 李国庆, 董存, 等. 计及光伏出力与负荷相关性的电力系统概率潮流计算方法[J]. 分布式能源, 2019, 4(5): 1-9.
-
[13]龚锦霞, 郑元黎. 基于内点法的含风电厂电力系统随机最优潮流[J]. 上海电力学院学报, 2019, 35(6): 518-524.
-
[14]李旭炯, 孙林花, 杨郭明. 基于逆变器的分布式光伏发电中压配电网无功优化[J]. 上海电力大学学报, 2022, 38(3): 257-263.
-
[15]舒印彪, 张智刚, 郭剑波, 等. 新能源消纳关键因素分析及解决措施研究[J]. 中国电机工程学报, 2017, 37(1): 1-8.
-
[16]LIU X, WU J, JENKINS N, et al. Combined analysis of electricity and heat networks[J]. Applied Energy, 2016, 162: 1238-1250.
-
[17]罗杰. 基于MATLAB的牛顿拉夫逊法电力潮流计算与实现[J]. 科技广场, 2010(3): 183-184.
-
[18]张建华, 王昕伟, 蒋程. 基于蒙特卡罗方法的风电场有功出力的概率性评估[J]. 电力系统保护与控制, 2014, 42(3): 82-87.
-
[19]KASHEM M A, GANAPATHY V, JASMON G B, et al. A novel method for loss minimzation in distribution networks[C]//DRPT2000. International Conference on Electric Utility Deregulation and Restructuring and Power Technologies. Proceedings(Cat. No. 00EX382). London, UK: IEEE, 2000, 251-256.
-
[20]ZHANG S X, CHENG H Z, LI K, et al. Multi-objective distributed generation planning in distribution network considering correlations among uncertainties[J]. Applied Energy, 2018, 226: 743-755.