|
|
|
发布时间: 2023-08-28 |
控制与检测技术 |
|
|
|
收稿日期: 2023-04-13
基金项目: 上海市自然基金项目(20ZR1421300)
中图法分类号: TP273
文献标识码: A
文章编号: 2096-8299(2023)04-0387-06
|
摘要
为适应低温多效蒸馏(LT-MED)海水淡化末效浓盐水温度控制系统存在的非线性时变和迟滞严重的特点, 针对基于经验人为设定的PID控制器效果不佳的问题, 提出了一种改进鲸鱼优化算法(WOA), 以实现PID控制器参数的自动整定。首先, 确定浓盐水温度控制系统的传递函数模型; 然后, 对基本WOA求解精度低、易陷入局部最优的缺陷对算法进行改进, 实现PID控制器的参数优化。MATLAB R2019a平台的仿真实验结果表明, 改进WOA算法具有更快的迭代速度和更强的全局寻优能力。改进WOA-PID控制器响应速度快且超调小, 能够有效控制浓盐水温度以保障海水淡化系统正常稳定运行。
关键词
浓盐水温度; 改进鲸鱼优化算法; PID控制器参数优化; 仿真分析
Abstract
In order to adapt to the characteristics of nonlinear time variation and severe hysteresis in the temperature control system of low-temperature multi-effect distillation (LT-MED) seawater desalination, an improved whale optimization algorithm (IWOA) is proposed for the problem of poor effect of PID controller artificially set based on experience to achieve autotuning of PID controller parameters.Firstly, the transfer function model of the brine temperature control system is determined, and then the algorithm is improved for the defects of low accuracy and easy to fall into local optimization of the basic WOA algorithm, so as to realize the parameter optimization of the PID controller.The simulation results in MATLAB R2019a platform show that the improved WOA algorithm has faster iteration speed and stronger global optimization ability.
Key words
brine temperature; improved WOA algorithm; PID parameter optimization; simulation analysis
作为提出最早、发展最为成熟的一种海水淡化技术, 低温多效蒸馏(Low Temporature Multi-Effect Distillation, LT-MED)海水淡化技术凭借操作温度低、结垢和腐蚀风险低、造水比和产水效率较高等优势, 已成为海水淡化技术的主流并得以广泛应用[1]。将该海水淡化技术用于生产中时, 需严格控制系统内温度、压力、液位等参数, 以将海水淡化蒸发器的换热效果维持在最佳水平, 保障产品水量正常和水质优良。当系统正常运行时, 要求末效浓盐水温度保持在50 ℃以下, 维持在45.6 ℃为最佳[2]。过高的浓盐水温度易造成蒸发器中换热管结垢现象, 从而破坏蒸发器的主体设备; 过低的浓盐水温度则代表进入蒸发器的蒸汽总量不足, 将影响产品水量甚至直接造成产品水质不合格。因此, 将浓盐水温度控制在一定范围内十分必要。
作为目前控制领域中最为成熟的控制方式, 比例积分微分(Proportion Integration Diffe, PID)控制能够解决绝大多数线性时不变系统的控制问题[3], 但对于复杂对象的控制主要基于经验通过反复调试来整定PID控制器参数, 仍难以达到最优的控制精度。近年来新型智能算法层出不穷, 如粒子群算法[4]、鲸鱼算法[5]、布谷鸟算法[6]、灰狼算法[7]、蝴蝶算法[8]等, 凭借独特优势广泛运用于优化问题。现有研究将智能算法与传统PID控制算法相结合以实现PID控制器参数的自动整定[9]。文献[10]提出了一种遗传模糊免疫算法, 用于在线整定PID参数; 文献[11]提出了一种改进果蝇优化的PI控制器参数在线整定算法, 实现系统更快的响应速度和更为稳定的功率输出; 文献[12]将鲸鱼算法用于PID独立变桨控制参数整定并验证了该算法的有效性和实用性。目前已有部分学者对海水淡化系统温度控制进行了研究。鲍克勤等人[13]设计了基于线性自抗扰算法的温度控制器, 相较于传统PID控制, 能有效控制海水淡化系统首效出口凝结水温度; 曲径幽[14]将模糊控制理论与PID控制理论相结合, 提高了浓盐水温度控制系统的控制精度及动态响应速度。
本文对基本鲸鱼优化算法(Whale Optimization Algorithm, WOA)进行改进, 设计了一种改进WOA-PID控制器以优化LT-MED海水淡化系统末效浓盐水温度控制系统的PID控制器参数, 在实现最佳适应度的同时, 自动整定最优参数。仿真结果表明, 相较于传统PID控制, 将改进WOA算法与传统PID控制相结合的改进WOA-PID控制, 在超调量、调节时间等方面具有优越性, 明显提升浓盐水温度的控制性能。
1 浓盐水温度控制系统模型
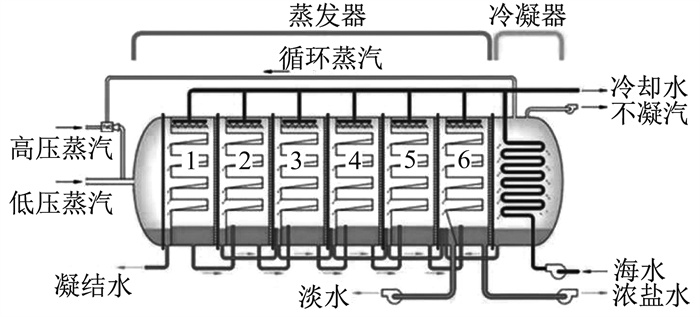
LT-MED海水淡化系统工艺流程如图 1所示。
由图 1可知, 从冷凝器进入的海水经预热和脱气后, 一部分海水作为入料海水流入各效蒸发器, 喷淋在蒸发器内部的换热管束顶端再沿着管壁外流下。热源蒸汽在换热管束内部被入料海水经冷凝蒸发后放出大量的热。管壁外海水吸热经蒸馏后分为两部分, 一部分作为浓盐水通过压力差的作用流向下一效, 直至末效由浓盐水泵排出; 一部分形成蒸汽, 作为下一效蒸发器的热源蒸汽流至下一效的换热管束中, 经冷凝形成淡水, 多余海水则经过效间泵继续流至下一效继续进行海水淡化。如此反复至末效蒸发器, 淡水(产品水)由产品水泵排出[15]。
可见, 在LT-MED海水淡化系统运行过程中, 产品水的生成主要依靠各效蒸发器的换热实现。可以将蒸发器看一个换热器, 其内部为一个热平衡系统, 而将各效温度控制在稳定范围是维持该热平衡的关键。第6效浓盐水温度与众多因素有关, 如进入本效的海水流量和海水温度、末效蒸发器的温度及蒸发器内的蒸汽与海水的换热空间分布等[16]。由于海水经过受热蒸发为浓盐水的过程非常短, 温度的变化具有滞后性, 因此该被控对象具有非线性、时变性和纯滞后等特点。
第6效蒸发器的蒸汽通过蒸发器内的换热管道将热量传递给进入第6效海水, 主要经历2次换热过程: 一是蒸汽将热量传递给换热管道; 二是换热管道经过热传导将热量传递至海水。因此, 可将浓盐水温度控制模型看作成一个二阶惯性环节, 考虑到温度变化具有一定的滞后性, 可将该被控对象的动态模型传递函数近似为
| $ G(s)=\frac{K \mathrm{e}^{-T_3 s}}{\left(T_1 s+1\right)\left(T_2 s+1\right)} $ | (1) |
式中:K——放大系数;
T1、T2——惯性时间常数;
T3——纯滞后时间;
s——拉普拉斯算子。
本文利用在某个时间段内现场测得的大量浓盐水温度数据, 采用系统辨识[17]有关算法得到所辨识的末效浓盐水温度控制系统传递函数的参数为: T1=8、T2=6、T3=1、K=3。该控制系统的传递函数为
| $ G(s)=\frac{3 \mathrm{e}^{-s}}{(8 s+1)(6 s+1)} $ | (2) |
2 改进WOA整定的PID控制器设计
2.1 鲸鱼优化算法
WOA采用随机或最佳搜索代理的独特机制以模拟鲸鱼的狩猎行为, 并使用螺旋方式以模拟座头鲸的泡泡网攻击机制: 假设当前最优个体为猎物, 群体中的其他个体均向最优个体逼近, 这是WOA与其他群优化算法的主要区别[18]。WOA主要分为3个阶段: 包围猎物、搜索猎物(觅食)和狩猎行为(泡泡网攻击)。
包围猎物阶段对应算法的全局搜索阶段。由于在搜索空间中, 最优猎物位置是未知的, 因此WOA假设当前的最佳候选解是目标猎物或接近最优解, 其他候选位置将向最佳猎物位置移动并更新位置。该阶段行为的数学模型表示为
| $ D=\left|\boldsymbol{C} \boldsymbol{X}^*(t)-\boldsymbol{X}(t)\right| $ | (3) |
| $ \boldsymbol{X}(t+1)=\boldsymbol{X}^*(t)-\boldsymbol{A D} $ | (4) |
式中:t——迭代次数;
A、C——系数向量;
X*(t)——最好的鲸鱼个体位置;
X(t)——当前鲸鱼个体位置。
系数向量A和C的定义为
| $ \boldsymbol{A}=2 a \boldsymbol{r}_1-a $ | (5) |
| $ \boldsymbol{C}=2 \boldsymbol{r}_2 $ | (6) |
式中:r1、r2——[0, 1]中的随机向量;
a——收敛因子。
随迭代次数增加, a值从2线性减小至0。a定义为
| $ a=2-\frac{2 t}{t_{\max }} $ | (7) |
式中:tmax——最大迭代次数。
鲸鱼采用收缩包围方式进行猎物搜索。算法设定: 当
| $ D=\left|\boldsymbol{C} \boldsymbol{X}_{\text {rand }}(t)-\boldsymbol{X}(t)\right| $ | (8) |
| $ \boldsymbol{X}(t+1)=\boldsymbol{X}_{\text {rand }}(t)-\boldsymbol{A D} $ | (9) |
式中:Xrand——随机选择的鲸鱼个体位置向量。
座头鲸以螺旋运动游向猎物完成狩猎行为, 对应算法中的局部开发(螺旋更新位置)阶段。鲸鱼在靠近最佳鲸鱼个体时, 会采取螺旋方式进行游走觅食, 以搜索鲸鱼个体至最佳鲸鱼个体之间可能存在的最优解。整个螺旋更新过程即鲸鱼个体从当前位置游向最佳鲸鱼个体位置的过程。鲸鱼个体的泡泡网捕食行为除了与
| $ D_p=\left|\boldsymbol{X}_{\text {rand }}(t)-\boldsymbol{X}(t)\right| $ | (10) |
| $ \boldsymbol{X}(t+1)=D_p \mathrm{e}^{b l} \cos (2 \pi \boldsymbol{l})+\boldsymbol{X}_{\text {rand }}(t) $ | (11) |
| $ \boldsymbol{X}(t+1)=\left\{\begin{array}{l} \boldsymbol{X}^*(t)-\boldsymbol{X}(t) \quad p<0.5 \\ D_p \mathrm{e}^{b l} \cos (2 \pi \boldsymbol{l})+\boldsymbol{X}_{\mathrm{rand}}(t) \quad p \geqslant 0.5 \end{array}\right. $ | (12) |
式中:b=1;
l——[-1, 1]中的随机向量。
本文选择时间乘以误差绝对值积分(Integrated Time Absolute Erron, ITAE)作为适应度函数, 为
| $ J_{\mathrm{ITAE}}=\int_0^{+\infty} t|e(t)| \mathrm{d} t $ | (13) |
式中:e(t)——末效浓盐水温度设定值与实际值的差值。
2.2 改进WOA
针对WOA收敛速度慢、易陷入局部最优等缺点, 本文对该算法的3个阶段分别进行改进: 引入非线性收敛因子和非线性时变的自适应权重策略, 并改进螺旋更新方式进行优化。
2.2.1 非线性收敛因子
由式(7)可知, a为从[2,0]中随着迭代次数增加而线性递减的收敛因子。a的线性变化可能会导致迭代前期搜索和后期寻优失去平衡, 不利于全局搜索和局部开发过程。因此, 本文引入一种在迭代前期衰减程度低、后期衰减程度提高的非线性收敛因子a′, 使得鲸鱼在前期能够较大步长游走以更好寻找全局最优解、后期减小游走步长以提升寻找最优解的精度, 从而有效平衡全局搜索时的开发能力和局部搜索时的挖掘能力。该非线性收敛因子a′具体表示为
| $ a^{\prime}=1-\left(\frac{t}{t_{\max }}\right)^h(e+\mu)+n k $ | (14) |
式中:h、μ、k——常数;
e——欧拉常数;
n——区间[0, 1]的随机常数。
2.2.2 非线性时变的自适应权重
由式(5)和式(9)可知, 收敛因子a的大小将直接决定A值, 而A值代表鲸鱼的游走步长。当
| $ w=1-\frac{\left(\mathrm{e}^{\frac{t}{t_{\max }}}-1\right)}{\mathrm{e}-1} $ | (15) |
引入w后, 式(4)和式(11)分别更新为
| $ \boldsymbol{X}(t+1)=\boldsymbol{X}^*(t)-w \boldsymbol{A} D $ | (16) |
| $ \boldsymbol{X}(t+1)=w D_p \mathrm{e}^{b l} \cos (2 \pi \boldsymbol{l})+\boldsymbol{X}_{\text {rand }}(t) $ | (17) |
2.2.3 改进螺旋更新方式
WOA中鲸鱼在靠近最佳鲸鱼个体时采取的螺旋方式为对数螺旋更新方式。该位置更新方法通过正态变异算子进行干扰, 易陷入局部最优, 降低算法寻优的各态历经性。文献[20]提出阿基米德螺旋更新方式克服对数螺旋更新方式的缺点, 能够扩大搜索范围, 提升算法对于未知领域的探索能力。因此, 本文将阿基米德螺旋方式代替鲸鱼优化算法中的对数螺旋更新方式, 式(17)更新为
| $ \boldsymbol{X}(t+1)=w D b \boldsymbol{l} \cos (2 \pi \boldsymbol{l})+\boldsymbol{X}_{\mathrm{rand}}(t) $ | (18) |
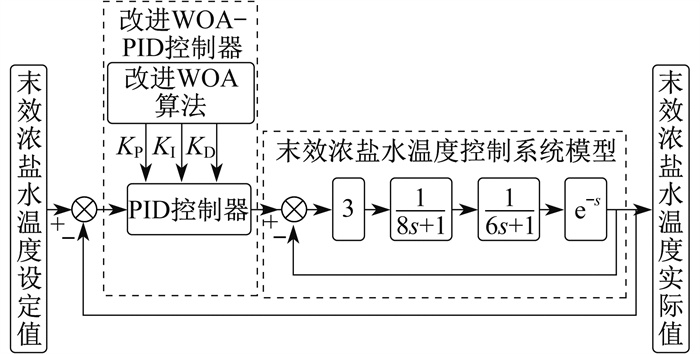
2.3 改进WOA优化PID控制系统原理
本文设计的基于改进WOA的LT-MED海水淡化系统的末效浓盐水温度控制系统, 主要由改进WOA控制器和末效浓盐水温度控制系统模型组成。改进WOA-PID控制器采用本文改进的WOA实现对PID控制器参数的优化, 末效浓盐水温度控制系统模型则采用式(2)所示的传递函数模型。该控制系统原理如图 2所示。其中, KP、KI、KD分别为比例系数、积分系数、微分系数。
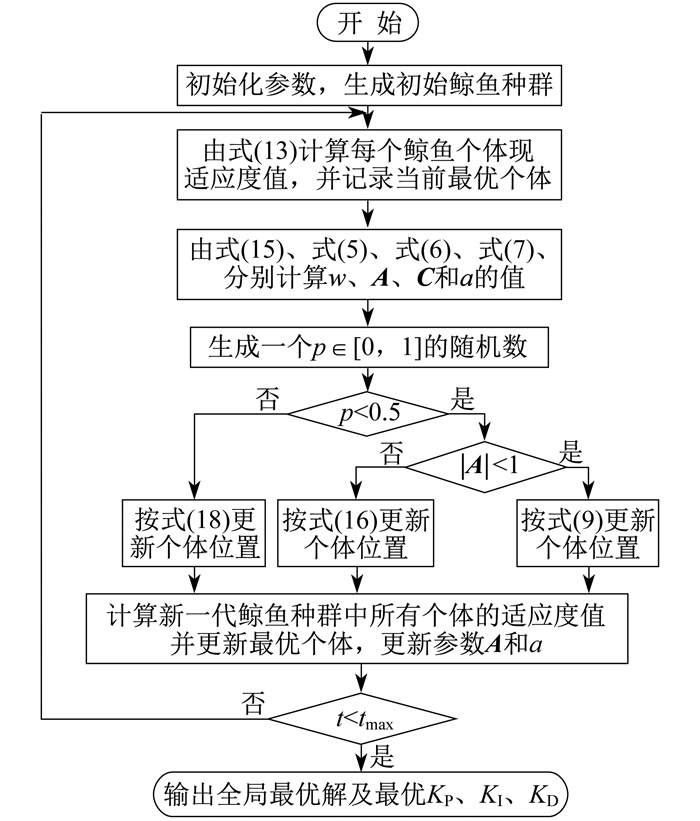
2.4 改进WOA优化PID控制参数流程
改进WOA优化PID参数的算法流程如图 3所示。
算法的具体步骤如下。
(1) 根据寻优参数特性确定搜索目标空间的维数, 设置一组种群规模为n的鲸鱼种群模拟KP、KI、KD的优化过程, 初始化鲸鱼的初始位置和迭代次数tmax=100。
(2) 根据定义的ITAE计算每条鲸鱼个体的适应度值, 并通过比较每条鲸鱼个体的适应度值更新鲸鱼个体的最佳位置并记录最优值。
(3) 根据算法相关公式计算影响鲸鱼位置的相关参数值, 判断是否满足算法规则p<0.5和
(4) 比较新一代所有鲸鱼个体的适应度值, 更新位置最优的鲸鱼个体和算法的有关参数。
(5) 判断迭代次数是否达到最大迭代次数100。若是, 则输出全局最优解和最优KP、KI、KD值; 若不满足终止条件则返回继续迭代寻优。
3 仿真实验与结果分析
3.1 传统PID控制器
使用MATLAB R2019a平台完成模型搭建和仿真分析。选择阶跃信号作为输入以模拟LT-MED海水淡化系统末效浓盐水温度变化。仿真模型搭建完毕后, 根据PID控制原理经过多次调试进行PID控制器的参数整定, 得到基于经验整定的PID控制器参数为: KP=0.886 5;KI=0.074 2;KD=1.714 3。
3.2 改进WOA-PID控制器
设置种群规模n=30, 最大迭代次数tmax=100, 维数dim=3;根据整定PID控制器参数的经验, 首先将参数KP、KI、KD的范围分别设置为[0, 0.1]、[0, 0.1]和[0, 10]。通过反复调试并对比实验运行得到的适应度结果, 最终确定参数KP、KI、KD的范围分别为[0, 0.1]、[0, 0.1]和[0, 7]。
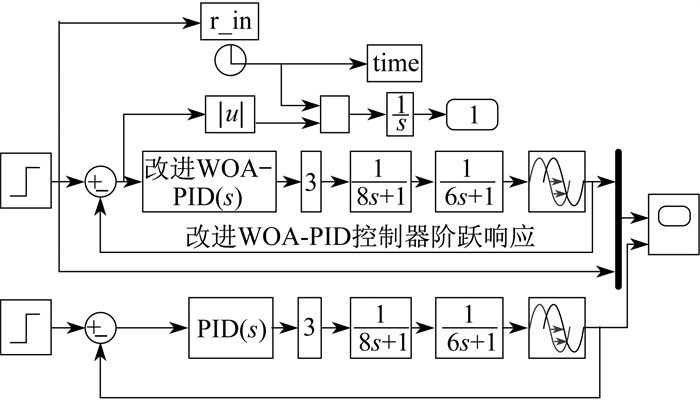
搭建的Simulink仿真模型由传统PID控制和改进WOA-PID控制两部分组成, 仿真模型如图 4所示。其中, r_in为变量名,
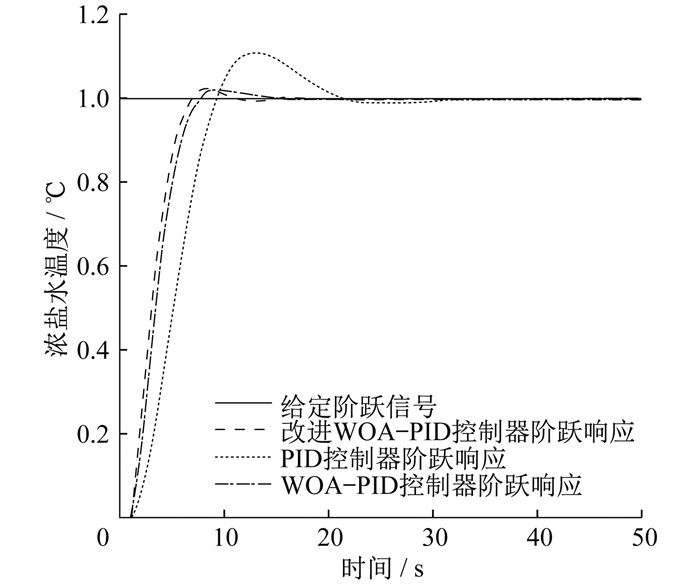
运行后得到传统PID与改进WOA-PID控制的阶跃响应, 再与WOA-PID控制进行对比。3种控制方式的阶跃响应对比如图 5所示。
由图 5可知, 相较于传统PID控制, 改进WOA-PID控制系统响应速度和超调得到明显改善。3种控制方式的阶跃响应性能指标和控制器参数值如表 1所示。
表 1
3种控制方式的阶跃响应性能指标和控制器参数值
| 控制器 | 超调量/% | 调节时间/s | 上升时间/s | KP | KI | KD |
| 传统PID | 11.1 | 35.158 | 12.940 | 0.886 5 | 0.074 2 | 1.7143 |
| WOA-PID | 2.2 | 25.742 | 8.892 | 0.989 8 | 0.0901 | 4.444 9 |
| 改进 WOA-PID |
2.5 | 14.630 | 8.116 | 0.038 6 | 0.095 3 | 6.604 8 |
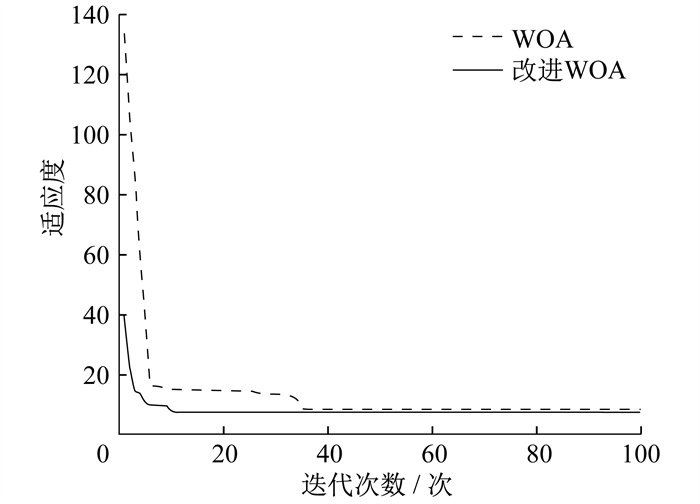
WOA与改进WOA的适应度寻优对比曲线如图 6所示。由图 6可知, 在环境相同的情况下, 改进WOA在迭代11次时达到最优适应度, 相较于WOA迭代53次达到最优适应度, 具有更快的收敛速度和更优的适应度值。
4 结论
为将LT-MED海水淡化系统末效浓盐水温度控制在合理范围内以保障系统正常运行, 从而实现最优产水和最佳经济效益, 本文提出了一种基于改进WOA的PID控制, 通过引入非线性收敛因子和非线性时变的自适应权重策略, 并改进螺旋更新方式以优化PID控制器参数。经过传统PID控制器、WOA-PID控制器和改进WOA-PID控制器的对比仿真实验, 得到以下结论。
(1) 相较于基于经验人工经过多次调试整定参数的传统方法, 通过改进WOA能够实现PID控制器参数的自动整定, 节省大量人力的同时获取最优参数值。
(2) 相较于WOA, 改进WOA具有更快的收敛速度和更高的寻优精度, 搜索全局能力更强, 能有效避免陷入局部最优, 保证末效浓盐水温度控制系统的输出稳定。
(3) 改进WOA优化的PID控制系统具有良好的动态响应性能, 实现响应速度快、超调量较小和抗干扰能力强的理想控制效果。
参考文献
-
[1]刘承芳, 李梅, 王永强, 等. 海水淡化技术的进展及应用[J]. 城镇供水, 2019(2): 54-58. DOI:10.3969/j.issn.1002-8420.2019.02.015
-
[2]鲍克勤, 孙蕊, 黄伟. 基于变论域模糊理论的海水淡化温控系统[J]. 计算机仿真, 2020, 37(8): 148-152. DOI:10.3969/j.issn.1006-9348.2020.08.032
-
[3]魏上云, 马靖, 胡晓兵, 等. 基于改进SA-WOA算法优化热封刀温度控制系统PID参数的研究[J]. 四川大学学报(自然科学版), 2022, 59(4): 70-76.
-
[4]赵乃刚, 邓景顺. 粒子群优化算法综述[J]. 科技创新导报, 2015, 12(26): 216-217. DOI:10.3969/j.issn.1674-098X.2015.26.104
-
[5]许德刚, 王再庆, 郭奕欣, 等. 鲸鱼优化算法研究综述[J]. 计算机应用研究, 2023, 40(2): 328-336. DOI:10.19734/j.issn.1001-3695.2022.06.0347
-
[6]张晓凤, 王秀英. 布谷鸟搜索算法综述[J]. 计算机工程与应用, 2018, 54(18): 8-16.
-
[7]张晓凤, 王秀英. 灰狼优化算法研究综述[J]. 计算机科学, 2019, 46(3): 30-38.
-
[8]丁元明, 夏清雨, 张然, 等. 蝴蝶优化算法研究综述[J]. 科学技术与工程, 2023, 23(7): 2705-2716.
-
[9]谷洋洋, 李来春, 张绍娟. 基于智能PID控制的燃气锅炉燃烧控制系统研究[J]. 热能动力工程, 2015, 30(3): 413-417.
-
[10]汤伟, 王帅, 王玲利. 基于遗传模糊免疫算法的比例-积分-微分参数整定优化[J]. 科学技术与工程, 2018, 18(31): 152-159.
-
[11]王福忠, 陶新坤, 田广强. 基于改进果蝇算法优化的微电网逆变器恒功率控制算法[J]. 电力系统保护与控制, 2021, 49(21): 71-79.
-
[12]曾冰, 黄凌翔, 彭郎军, 等. 基于鲸鱼群算法的PID独立变桨控制参数整定方法[J]. 船舶工程, 2020, 42(增刊1): 550-553.
-
[13]鲍克勤, 刘擘, 汤豪. 基于LADRC的低温多效海水淡化温度控制[J]. 昆明理工大学学报(自然科学版), 2022, 47(1): 38-45.
-
[14]曲径幽. 海水淡化温度模糊-PID控制的设计与实现[J]. 自动化应用, 2014(7): 11-13.
-
[15]刘世佳. 低温多效蒸馏海水淡化监控系统的设计与实现[D]. 天津: 天津理工大学, 2018.
-
[16]黄金. 低温多效蒸馏海水淡化系统建模与控制研究[D]. 济南: 山东大学, 2022.
-
[17]鄢文刚. 面向工业控制与软测量建模的系统辨识方法研究[D]. 杭州: 浙江大学, 2019.
-
[18]刘昊东, 邹必昌. 基于鲸鱼算法优化长短期记忆网络的短期负荷预测[J]. 电子世界, 2021(3): 41-42.
-
[19]安国庆, 史哲文, 马世峰, 等. 基于RF特征优选的WOA-SVM变压器故障诊断[J]. 高压电器, 2022, 58(2): 171-178.
-
[20]CHEN Y D, WEI T H, GONG T X. Research on optimal layout of cutter-head system of rock tunnel-boring machine based on Archimedes spiral theory[J]. Advances in Mechanical Engineering, 2018, 10(2): 151-160.