|
|
|
发布时间: 2023-10-28 |
清洁安全发电 |
|
|
|
收稿日期: 2023-02-24
中图法分类号: TK37
文献标识码: A
文章编号: 2096-8299(2023)03-0472-07
|
摘要
针对燃煤电厂中煤粉细度难以测量的问题, 提出了一种基于遗传算法优化最小二乘支持向量机(LSSVM)超参数的煤粉细度软测量方法。通过制粉系统特性试验, 综合分析出影响磨煤机煤粉细度参数的主要因素。采用遗传算法优化支持向量机超参数方法构建煤粉细度软测量模型。将该方法用于特性试验, 发现检验样本的均方根误差为1.7%, 证明煤粉细度软测量方法有效, 满足煤粉细度模型精确预测的需求。
关键词
煤粉细度; 参数优化; 最小二乘支持向量机; 软测量
Abstract
Aiming at the problem that it is difficult to measure pulverized coal fineness in coal-fired power plants, a soft measurement method of pulverized coal fineness based on genetic algorithm optimization of least square support vector machine super parameters is proosed in this paper.The main factors affecting pulverized coal fineness parameters of pulverized coal mill are analyzed comprehensively through the characteristic experiment of pulverized coal system.The soft sensor model of pulverized coal fineness is constructed by the superparameter method of support vector machine optimized by genetic algorithm.The method is applied to a practical case, and the root-mean-square error of the test sample is 1.7%, which proves the validity of the soft measurement method of pulverized coal fineness, and meets the demand of accurate prediction of pulverized coal fineness model.
Key words
coal fineness; parameters optimization; least squares support vector machine; soft measurement
我国火力发电厂以燃煤为主, 主要燃烧方式为煤粉燃烧。原煤经给煤机进入磨煤机, 并被磨成煤粉, 一次风携带煤粉通过喷燃器进入锅炉燃烧。煤粉粒径直接影响锅炉内燃烧状态, 煤粉粒径过大, 会增加锅炉机械未完全燃烧热损失; 煤粉粒径过小, 又会增加磨煤机电耗和磨煤设备磨损[1]。因此, 需要寻求一种有效、可靠的方法测量煤粉细度。
由于直吹式制粉系统取样比较困难, 一般只能通过制粉系统调整试验来获取磨煤机出口各煤粉管的煤粉细度。近年来, 有些电厂安装了煤粉在线采样或风粉速度、煤粉浓度在线监测装置。如廖宏楷等人[2]开发的直吹式制粉系统风煤在线测量系统, 冯磊华等人[3-6]开发的改进LS - SVM的直吹式制粉出力软测量建模, 孔令君等人[7]研发的直吹式制粉系统风粉在线监测装置, 苏志刚等人[8-9]开发的中储式制粉系统出力在线监测软测量建模, 綦守荣[10]对中储式钢球磨制粉系统的建模与优化控制开展的研究, 唐耀华等人[11]提出了基于软测量技术的双进双出磨煤机入炉煤量计算方法。这些监测装置都致力于一次风管风速和煤粉浓度的监测, 缺乏对锅炉燃烧有较大影响的煤粉细度指标的实时测量和现场验证等研究。本文通过对某电厂磨煤机运行情况进行分析, 提出了一种基于遗传算法参数优化的最小二乘支持向量机(LSSVM)的煤粉细度软测量方法。
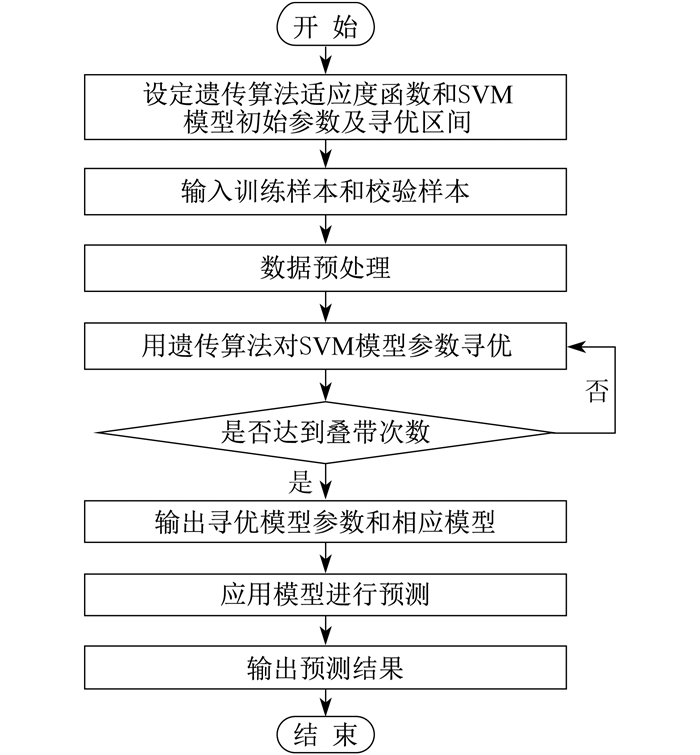
1 基于参数优化的最小二乘支持向量机
1.1 最小二乘支持向量机
支持向量机(Support Vector Machine, SVM), 是一种二类分类的模型, 其特点是通过选用合适的核函数和核参数对样本空间进行映射处理。最小二乘支持向量机(Least Squares Support Vector Machine, LSSVM)是对支持向量机的改进, 将凸二次规划问题转换为线性规划问题, 使参数搜索范围从三维转换为二维, 大大降低了计算复杂度, 提高了求解速度, 同时又保证了计算精度。
LSSVM算法流程[12-15]如下: 设样本为n维向量的k个样本集{(x1, y1), (x2, y2), (x3, y3), …, (xk, yk)}, 其问题目标函数为
| $f({\mathit{\boldsymbol{x}}})=\boldsymbol{w} {\mathit{\boldsymbol{x}}}+b$ | (1) |
式中: w——可调的权重向量;
x——输入向量;
b——偏置权重。
为了将输入空间映射到特征空间, LSSVM采用非线性函数将非线性估计问题转化为高维特征空间的线性函数估计问题。假设所有训练数据都能够在精度ε下采用线性函数拟合, 并考虑到允许存在拟合误差, 引入松弛因子ξi*、ξi修正拟合函数, 拟合函数和修正拟合函数分别为
| $ \left\{\begin{array}{l} y_{i}-\boldsymbol{w} x_{i}-b \leqslant \varepsilon \\ \boldsymbol{w} x_{i}+b-y_{i} \leqslant \varepsilon \end{array} \quad i=1, 2, 3, \cdots, k\right. $ | (2) |
| $\begin{cases}y_i-\boldsymbol{w} x_i-b \leqslant \varepsilon+\xi_i & \xi_i \geqslant 0 \\ \boldsymbol{w} x_i+b-y_i \leqslant \varepsilon+\xi_i^* & \xi_i^* \geqslant 0\end{cases}$ | (3) |
式中: yi——对应的期望响应;
xi——输入模式的第i个例子。
基于结构化风险最小化原则, 将上述修正拟合函数的回归估计问题转化为最小化函数问题, 为
| $ R\left(\boldsymbol{w}, \xi_{i}, \xi_{i}^{*}\right)=\frac{1}{2} \boldsymbol{w} \boldsymbol{w}+C \sum\limits_{i=1}^{k} \xi_{i}+\xi_{i}^{*}$ | (4) |
式中: C——惩罚因子;
k——样本数量。
同时, 为求解上述优化问题, 引入拉格朗日函数, 如式(5)所示。
| $ \begin{aligned} & L\left(\boldsymbol{w}, b, \xi, \xi^{*}, \alpha, \alpha^{*}, \gamma, \gamma^{*}\right)= \\ & \frac{1}{2} \boldsymbol{w} \boldsymbol{w}+C \sum\limits_{i=1}^{k}\left(\xi+\xi^{*}\right)-\sum\limits_{i=1}^{k} \alpha_{i}\left[y_{i}-\left(\xi_{i}+\varepsilon+f\left(x_{i}\right)\right)\right] \\ & -\sum\limits_{i=1}^{k} \alpha_{i}^{*}\left[\xi_{i}^{*}+\varepsilon+f\left(x_{i}\right)-y_{i}\right]-\sum\limits_{i=1}^{k}\left(\gamma_{i} \xi_{i}+\gamma_{i}^{*} \xi_{i}^{*}\right) \end{aligned}$ | (5) |
其中: αi、αi*≥0, γi、γi*≥0, i=1, 2, 3, …, k。式(4)的最优解为拉格朗日函数L的鞍点。在鞍点处, 函数L是关于w、b、ξi、ξi*的极小点, 是关于参数αi、αi*、γi、γi*的极大点。
由于函数L在鞍点处是关于w、b、ξi、ξi*极小点, 将w、b、ξi、ξi*导数设为零, 可得到问题最优解条件, 为
| $ \left\{\begin{array}{l} \frac{\partial}{\partial \boldsymbol{w}} L=0 \rightarrow \boldsymbol{w}=\sum\limits_{i=1}^{k}\left(\alpha_{i}-\alpha_{i}^{*}\right) x_{i} \\ \frac{\partial}{\partial b} L=0 \rightarrow \sum\limits_{i=1}^{k}\left(\alpha_{i}-\alpha_{i}^{*}\right)=0 \\ \frac{\partial}{\partial \xi_{i}} L=0 \rightarrow C-\alpha_{i}-\gamma_{i}=0 \\ \frac{\partial}{\partial \xi_{i}^{*}} L=0 \rightarrow C-\alpha_{i}^{*}-\gamma_{i}^{*}=0 \end{array}\right.$ | (6) |
为方便求解, 将式(6)代入式(5), 获得拉格朗日函数的对偶函数, 为
| $ \begin{aligned} & L\left(\boldsymbol{w}, b, \xi, \xi^{*}, \alpha, \alpha^{*}, \gamma, \gamma^{*}\right)= \\ & \frac{1}{2} \sum\limits_{i, j=1}^{k}\left(\alpha_{i}+\alpha_{i}^{*}\right)\left(\alpha_{j}+\alpha_{j}^{*}\right)\left(x_{i} x_{j}\right) \\ & -\sum\limits_{i=1}^{k}\left(\alpha_{i}+\alpha_{i}^{*}\right) \varepsilon+\sum\limits_{i=1}^{k}\left(\alpha_{i}+\alpha_{i}^{*}\right) y_{i} \end{aligned}$ | (7) |
若令K(xi, xj)=φ(xi)·φ(xj), φ为映射函数, 则式(7)转换为
| $ \begin{aligned} & \tilde{\omega}\left(\alpha, \alpha^{*}\right)_{w, b, \xi, \xi^{*}}= \\ & -\frac{1}{2} \sum\limits_{i, j=1}^{k}\left(\alpha_{i}-\alpha_{i}^{*}\right)\left(\alpha_{j}-\alpha_{j}^{*}\right) K\left(x_{i}, x_{j}\right) \\ & -\sum\limits_{i=1}^{k}\left(\alpha_{i}+\alpha_{i}^{*}\right) \varepsilon+\sum\limits_{i=1}^{k}\left(\alpha_{i}+\alpha_{i}^{*}\right) y_{i} \end{aligned}$ | (8) |
式中:
K(xi, xj)——多项式核函数。
此时, w表达式为
| $ \boldsymbol{w}=\sum\limits_{i=1}^{k}\left(\alpha_{i}-\alpha_{i}^{*}\right) \varphi\left(x_{i}\right)$ | (9) |
若记wx=w0, 函数f(x)可表示为
| $ f(x)=\sum\limits_{i=1}^{k}\left(\alpha_{i}-\alpha_{i}^{*}\right) K\left(x, x_{i}\right)+b=\omega_{0}+b$ | (10) |
核函数具有降低高维空间计算复杂度的能力, 在构造高性能LSSAM中起着重要作用。本文采用径向基核函数评估非线性模型。径向基核函数表达式为
| $ K\left(x_{i}, x_{j}\right)=\exp \left|\frac{\left\|x_{i}-x_{j}\right\|^{2}}{2 \sigma^{2}}\right|$ | (11) |
式中: σ——尺度参数。
按照库恩-塔克条件定理, 在鞍点处为
| $ \left\{\begin{array}{l} \alpha_{i}\left[\varepsilon+\xi_{i}-y_{i}+f\left(x_{i}\right)\right]=0 \\ \alpha_{i}^{*}\left[\varepsilon+\xi_{i}+y_{i}-f\left(x_{i}\right)\right]=0 \end{array} \quad i=1, 2, 3, \cdots, k\right.$ | (12) |
由式(12)可知, αiαi*=0, αi和αi*都不会同时为非零。由式(5)和式(8)可得
| $ \left\{\begin{array}{l} \xi_{i} \gamma_{i}=0 \\ \xi_{i}^{*} \gamma_{i}^{*}=0 \end{array} \quad i=1, 2, 3, \cdots, k\right.$ | (13) |
由式(13)可知, 对应于αi=C, 或αi*=C的f(xi)与yi的误差可能大于ε, 对应于αi∈(0, C)或αi*∈(0, C)的f(xi)与yi的误差必然等于ε, 也即ξi=0或ξi*=0。根据该结果, 即可求出b, 进而获得最优解。
1.2 遗传算法
1.3 性能指标
RMSE常用于衡量预测值与真实值之间的偏差。本文采用RMSE评价煤粉细度预测模型的有效性为
| $ E_{\mathrm{RMS}}=\sqrt{\frac{\sum\limits_{i=1}^{n}\left(y_{\text {pre }}-y_{\text {real }}\right)^{2}}{n}}$ | (14) |
式中: ypre——预测的煤粉细度, %;
yreal——实测煤粉细度, %;
n——检验样本个数。
2 制粉系统特性试验
在不同煤种情况下, 通过试验了解磨煤机煤粉细度性能参数与动态分离器转速、磨煤机加载力、磨煤机一次风量、磨煤机出力等因素的关系, 为制粉系统性能参数软测量提供依据。磨煤机采用上海重型机器厂生产的HP型弹簧变加载磨煤机。煤粉细度通过煤粉等速取样装置等速采样获取。本文基于MATLAB仿真平台非线性拟合函数, 建立磨煤机煤粉细度与动态分离器转速、磨煤机加载力、磨煤机一次风量、磨煤机出力等因素之间函数关系, 确定系数(R - square)和RMSE为拟合函数评价指标以评价拟合函数可靠性。其中, R - square值越接近1, 表明在构建的函数关系中, 各个变量对磨煤机煤粉细度解释能力越好, 即模型对数据拟合能力越好。
整理试验原始数据, 可获得制粉系统运行参数如动态分离器转速(或静态分离器挡板开度)、一次风量、给煤量、煤质成分、锅炉负荷对煤粉细度的影响特性, 同时可分析煤粉细度变化对锅炉灰渣含碳量的影响。
2.1 动态分离器转速对煤粉细度的影响规律
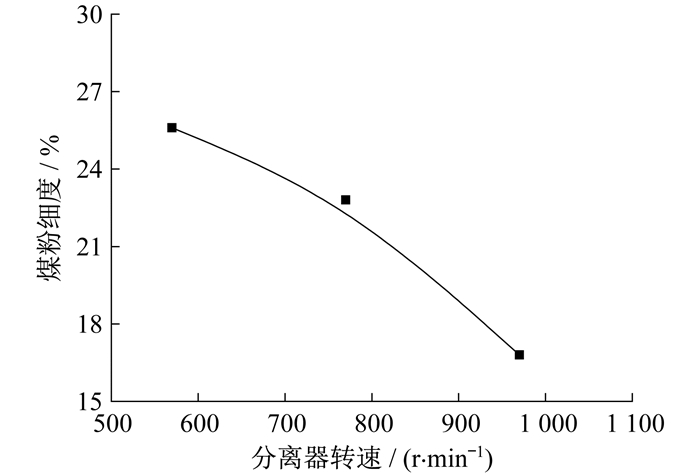
针对某电厂HP型磨煤机, 研究了动态分离器转速对煤粉细度的影响。控制B磨煤机给煤量为50 t/h, 一次风量为107 t/h, 在560~1 020 r/min范围内改变动态分离器转速。具体如图 2所示。
由图 2可知, 随动态分离器转速上升, 煤粉细度值下降。动态分离器转速从560 r/min提至1 020 r/min, 煤粉细度相应从21.2%降至7.4%。煤粉颗粒在磨煤机中受气流曳力和离心力的共同作用, 离心力与曳力的比值为分离强度, 其与动态分离器转速的平方成正比。动态分离器的转速越高, 其分离强度就越强, 分离效果就越好, 煤粉细度越小。同样, 在低负荷(278 MW)条件下, B磨煤机动态分离器转速从560 r/min提至960 r/min, 煤粉细度相应从20.4%降至13.2%。具体如图 3所示。
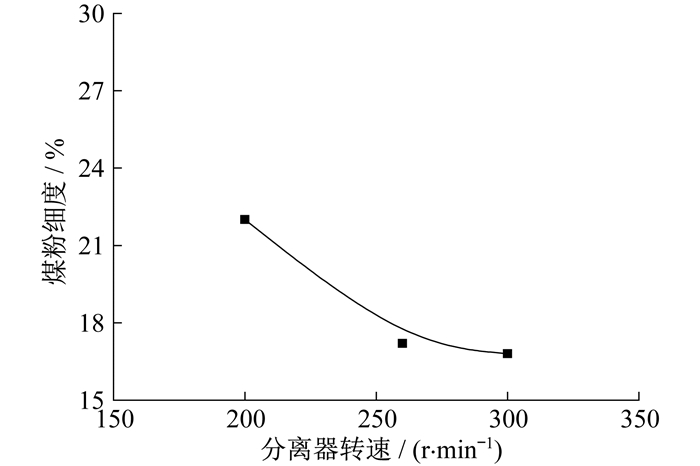
控制C磨煤机给煤量为38 t/h, 一次风量为88 t/h, 在200~300 r/min范围内改变动态分离器转速, 规律同样类似。具体如图 4所示。
随动态分离器转速由200 r/min升高到300 r/min, 煤粉细度由22%降为17.2%。磨煤机动态分离器转速与煤粉细度拟合结果如表 1所示。
表 1
磨煤机动态分离器转速与煤粉细度拟合结果
| 运行条件 | 函数类型 | R-square | RMSE |
| B磨煤机+高负荷 | Sum of Sine | 0.974 9 | 1.151 0 |
| B磨煤机+低负荷 | Rational | 0.950 0 | 1.238 0 |
| C磨煤机+高负荷 | Power | 0.968 4 | 0.732 1 |
2.2 磨煤机出力对煤粉细度的影响规律
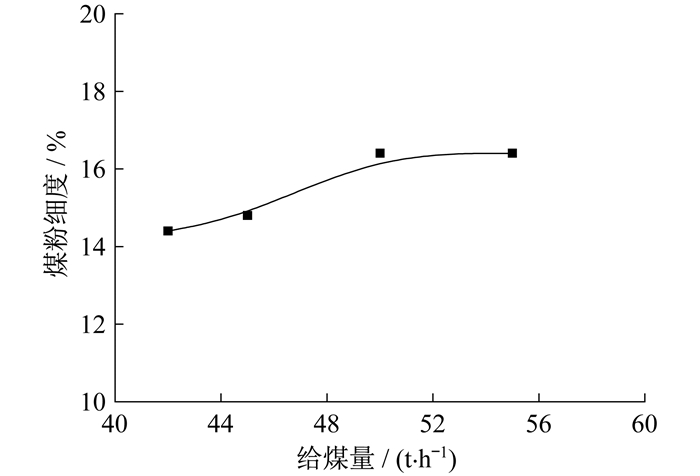
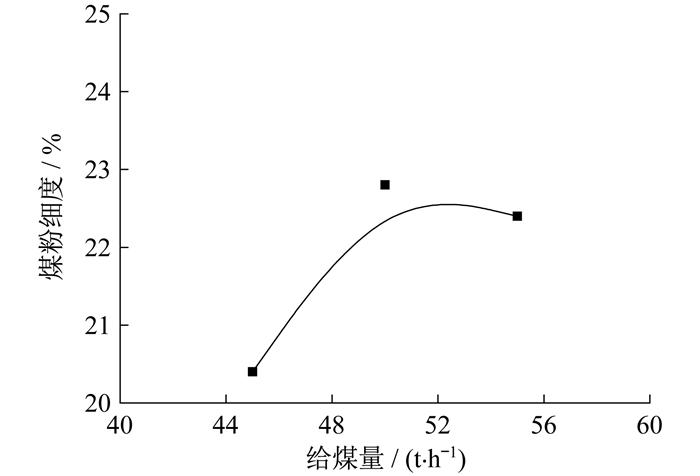
针对B磨煤机研究给煤量对煤粉细度的影响规律。控制B磨煤机动态分离器转速为770 r/min, 一次风量为105 t/h, 在42~55 t/h范围内改变磨煤机出力。具体如图 5所示。
由图 5可知, 随给煤量增加, 煤粉细度值随之增大, 由出力为42 t/h时的14.4%增加到出力为55 t/h时的17.2%。由于给煤量增加, 磨中研磨不充分的煤粉比例增加, 煤粉细度增大; 给煤量增加, 而一次风量没有变化, 导致一次风对煤粉的干燥作用下降, 磨煤机内温度低, 煤的可磨指数降低, 也会导致煤粉细度增大。对比图 2和图 5发现, 与动态分离器转速相比, 给煤量对煤粉细度影响相对较小。磨煤机给煤量与煤粉细度拟合结果如表 2所示。
表 2
磨煤机给煤量与煤粉细度拟合结果
| 运行条件 | 函数类型 | R-square | RMSE |
| B磨煤机+全工况 | Polynomial | 0.943 2 | 0.380 5 |
2.3 一次风量对煤粉细度的影响规律
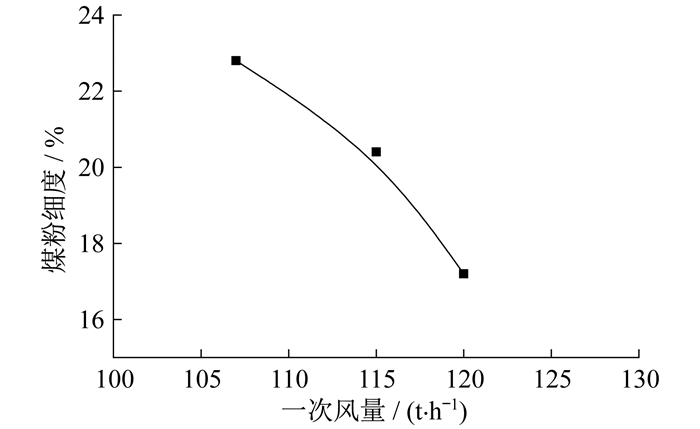
针对B磨煤机研究一次风量变化对煤粉细度的影响规律。控制B磨煤机动态分离器转速为770 r/min, 磨煤机给煤量为50 t/h, 在95~107 t/h范围内改变一次风量。磨煤机一次风量对煤粉细度的影响规律如图 6所示。
随着一次风量的增加, 煤粉细度值逐渐升高, 说明煤粉越来越粗, 并且随一次风量增加, 改变一次风量对煤粉细度的影响越来越明显, 煤粉细度由一次风量95 t/h的16.4%增加到107 t/h的18.4%。对比图 2和图 6可以发现, 一次风量对煤粉细度的影响没有动态分离器转速明显。动态分离器转速、一次风量和磨煤机给煤量3个因素中, 动态分离器转速对煤粉细度的影响最为显著, 磨煤机一次风量与煤粉细度拟合结果如表 3所示。
表 3
磨煤机一次风量与煤粉细度拟合结果
| 运行条件 | 函数类型 | R-square | RMSE |
| B磨煤机+全工况 | Linear Fitting | 0.827 3 | 0.784 9 |
2.4 煤质2时动态分离器转速、给煤量与一次风量对煤粉细度的影响规律
针对B磨煤机, 采用2种锅炉燃用煤质(煤质1和煤质2), 研究动态分离器转速、给煤量和一次风量对煤粉细度的影响规律。具体如图 7至图 9所示。
由图 7至图 9可知, 燃用煤质2时磨煤机给煤量、动态分离器转速和一次风量对煤粉细度影响趋势类似。煤质1哈氏可磨性系数为98, 高于煤质2的91, 说明煤质2较煤质1可磨性差, 因此相同条件下煤质2的煤粉细度值更大, 煤粉更粗。磨煤机在煤质2时动态分离器转速、给煤量、一次风量与煤粉细度拟合结果如表 4所示。
表 4
磨煤机在煤质2时动态分离器转速、给煤量、一次风量与煤粉细度拟合结果
| 影响因素 | 函数类型 | R-square | RMSE |
| 煤质2+动态分离器转速 | Polynomial | 0.925 9 | 1.681 0 |
| 煤质2+给煤量 | Smoothing Spline | 0.899 7 | 0.864 0 |
| 煤质2+一次风量 | Polynomial | 0.934 2 | 1.093 0 |
2.5 静态分离器挡板开度对煤粉细度的影响规律
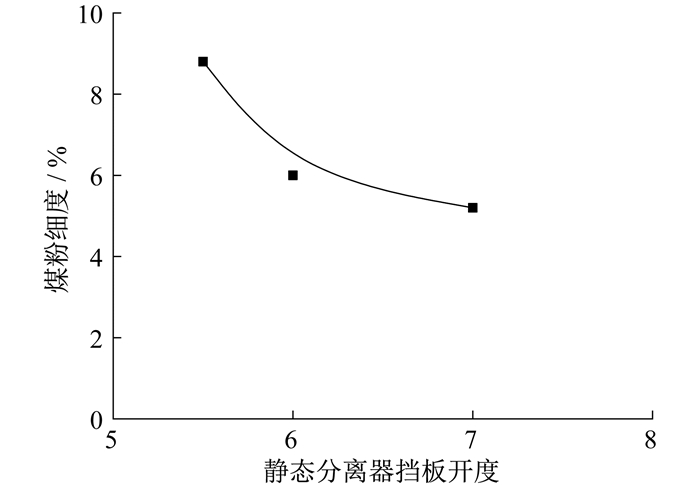
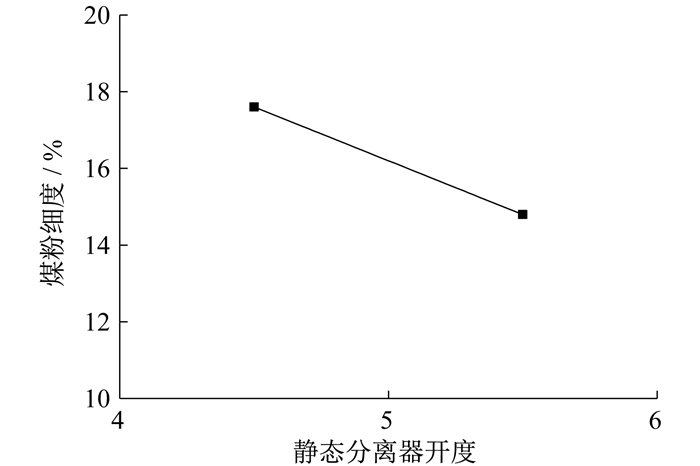
针对D、E磨煤机研究静态分离器挡板开度对煤粉细度的影响规律, 具体如图 10和图 11所示。
随着静态分离器挡板开度变大, 分离器开度变小, 对煤粉分离作用更强, 因此煤粉细度值减小, 煤粉更细。D磨煤机静态分离器挡板开度由5.5增大到7.0, 煤粉细度由8.8%降低为5.2%。E磨煤机静态分离器挡板开度由4.5增大为5.5, 煤粉细度由17.6%降低为14.8%。磨煤机静态分离器挡板开度与煤粉细度拟合结果如表 5所示。
表 5
磨煤机静态分离器挡板开度与煤粉细度拟合结果
| 运行状态 | 函数类型 | R-square | RMSE |
| D磨煤机+低负荷 | Rational | 0.855 8 | 1.118 0 |
2.6 煤粉细度与灰渣含碳量关系分析
3 煤粉细度特性试验
磨煤机煤粉细度特性模型的输入参数拟选取如下: 选取磨煤机入口风量和磨煤机入口风温表征进入磨煤机的一次风的状态对磨煤机特性的影响; 给煤量表征给煤对磨煤特性的影响; 分离器挡板转速表征分离器对磨煤机运行特性的影响; 煤质特性取Aar, 挥发分Vdaf和全水分Mt共3个参数表征煤质对磨煤机运行特性的影响; 将煤粉细度作为输出参数, 用SVM建立模型。SVM模型的ε精度为0.01, 当训练误差小于0.001时停止, 利用遗传算法对模型参数g寻优区间(0, 200)和C寻优区间(0, 500)进行寻优, 核函数选为径向基函数。当模型预测的结构误差达到最小值时获得模型参数, 确定模型。
选取16个试验工况及50个在线获取的工况数据作为训练样本, 建立煤粉细度特性模型, 最终对参与训练的试验工况和未参与训练的试验工况的煤粉细度进行预测, 结果如图 12所示。
由图 12可知, 大部分样本的煤粉细度预测值与煤粉细度真实值一致, 经计算得到预测的煤粉细度与真实的煤粉细度间RMSE为1.7%。结果表明, 基于遗传算法优化LSSVM超参数的煤粉细度软测量方法能够准确地预测煤粉细度。
4 结语
本文基于遗传算法优化SVM超参数方法, 成功构建了煤粉细度的软测量模型, 以实现煤粉细度的在线软测量, 解决了燃煤电厂中煤粉细度难以测量的问题。将该方法应用于实际燃煤电厂, 以RMSE为性能评价指标, 证明了该方法的可靠性。结果表明: 试验样本的RMSE为1.7%, 满足煤粉细度软测量模型的预测精度。煤粉细度软测量模型的成功构建, 为进一步优化煤粉细度和磨机出力的控制奠定坚实的基础。同时, 对提高锅炉的燃烧效率具有积极的意义。
参考文献
-
[1]周强泰, 周克毅, 冷伟, 等. 锅炉原理[M]. 北京: 中国电力出版社, 2013: 8.
-
[2]廖宏楷, 周昊, 杨华, 等. 风煤在线测量的锅炉燃烧优化系统[J]. 动力工程, 2005, 25(4): 559-562.
-
[3]冯磊华, 桂卫华, 杨锋. 基于改进LS-SVM的制粉出力软测量建模[J]. 控制工程, 2012, 19(6): 944-946.
-
[4]冯磊华. 双进双出钢球磨煤机直吹式制粉系统建模及控制[D]. 长沙: 中南大学, 2011.
-
[5]冯磊华, 桂卫华, 杨锋. 改进LS-SVM的直吹式制粉出力软测量建模[J]. 电机与控制学报, 2011, 15(11): 79-82. DOI:10.3969/j.issn.1007-449X.2011.11.014
-
[6]冯磊华, 桂卫华, 杨锋. 基于一种改进灰关联分析的双进双出钢球磨制粉出力软测量建模[J]. 仪器仪表学报, 2010, 31(9): 2062-2067.
-
[7]孔令君, 郭秀峰. 风粉在线监测在直吹式制粉系统上的应用研究[J]. 通用机械, 2008(7): 55-59.
-
[8]苏志刚, 王培红, 于向军, 等. 中储式制粉系统出力在线监测软测量建模[J]. 中国电机工程学报, 2007, 27(29): 90-95.
-
[9]苏志刚. 球磨机制粉出力的软测量研究[D]. 南京: 东南大学, 2007.
-
[10]綦守荣. 中储式钢球磨制粉系统的建模与优化控制研究[D]. 保定: 华北电力大学, 2008.
-
[11]唐耀华, 刘海宝, 朱峰, 等. 基于软测量技术的双进双出磨煤机入炉煤量计算[J]. 仪表技术与传感器, 2012(5): 27-28.
-
[12]蒋淳, 魏雪丽, 陆远忠, 等. 支持向量机在地震综合预测中的初步应用[J]. 中国地震, 2006, 22(3): 303-310.
-
[13]李建中, 周昊, 王春林, 等. 支持向量机技术在动力配煤中灰熔点预测的应用[J]. 煤炭学报, 2007, 32(1): 81-84.
-
[14]梁绍华. 基于在线优化技术的分层燃烧试验研究及应用[D]. 杭州: 浙江大学, 2008.
-
[15]王春林. 大型电站锅炉配煤及燃烧优化的支持向量机建模与实验研究[D]. 杭州: 浙江大学, 2007.
-
[16]李建中. 煤粉分配器的试验及基于支持向量机的灰熔点预测[D]. 杭州: 浙江大学, 2006.
-
[17]李昆仑, 张炘, 廖频. 基于遗传算法的支持向量机参数优化研究[J]. 电脑知识与技术, 2018, 14(9): 185-186.
-
[18]于青, 赵辉. 基于GA的ε-支持向量机参数优化研究[J]. 计算机工程与应用, 2008, 44(15): 139-141.
-
[19]马静, 李星野, 徐荣. 基于高斯核支持向量机和遗传算法的优化组合研究[J]. 经济数学, 2017, 34(1): 11-17.
-
[20]曹路, 欧阳效源. 基于遗传算法的支持向量机的参数优化[J]. 计算机与数字工程, 2016, 44(4): 575-577.
-
[21]万源, 童恒庆, 朱映映. 基于遗传算法的多核支持向量机的参数优化[J]. 武汉大学学报(理学版), 2012, 58(3): 255-259.