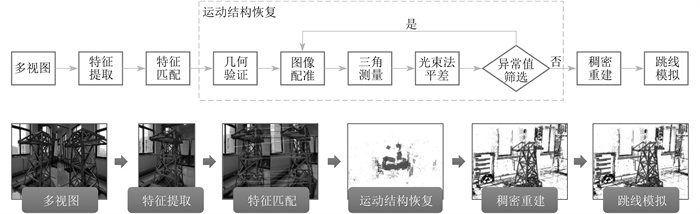
|
|
|
发布时间: 2024-12-28 |
智能设备 |
|
|
|
收稿日期: 2024-08-21
中图法分类号: TM751
文献标识码: A
文章编号: 2096-8299(2024)06-0520-07
|
摘要
输电线路铁塔跳线长度测量的准确性是影响电力系统稳定运行的关键问题之一。传统测量方法存在精度不足、操作复杂和误差较大等问题。为提高跳线长度测量的精度和效率,提出了一种基于可见光图像三维建模技术的跳线计算方法。该方法借助特征提取、运动结构恢复和稠密重建技术,实现了对铁塔的精确三维建模,并通过悬链线模型模拟跳线长度,在跳线安装前进行精确模拟。实验结果表明,该方法在跳线长度测量中具有较高的可行性和精确性。与其他三维建模方法相比,该方法在精度与效率之间取得了良好的平衡,能够较好地满足实际工程需求。
关键词
输电线路; 铁塔; 跳线长度测量; 三维建模; 特征提取
Abstract
The accuracy of measuring the jumper length of transmission line towers has been a critical factor affecting the stable operation of power systems. Traditional measurement methods often suffer from insufficient precision, complexity, and susceptibility to human error. To enhance the accuracy and efficiency of jumper length measurement, a 3D modeling technique based on visible light imagery is proposed. This method leverages feature extraction, structure from motion, and dense reconstruction techniques to achieve precise 3D modeling of the jumper, and simulates the jumper length using the catenary model, providing an accurate pre-installation simulation. Experimental results demonstrate that this method performs in capturing the spatial position and dimensions of both the tower and the jumper, significantly improving measurement accuracy and efficiency. Compared to existing techniques, this approach achieves a favorable balance between accuracy and efficiency, meeting the practical demands of engineering applications effectively.
Key words
transmission line; tower; jumper length measurement; 3D modeling; feature extraction
跳线装置作为输电线路工程附件安装的重要组成部分,由软跳线和硬跳线构成[1]。软跳线通常采用多股柔性铜线或铝线制造,能够适应输电线路的弯曲变化,常用于转角、分支和终端等位置。硬跳线则采用实心铜杆或铝杆,结构坚硬,适用于直线段,可维持跳线的稳定性。随着国家“十四五”规划的推进,工业和信息化部明确指出,到2025年,将基本建成智能化、绿色化的新型电力基础设施体系。因此,许多现有电力走廊的线路需要改建或新建[2]。随着电压等级的提高和导线分裂数的增加,耐张塔上的跳线装置愈发大型化、复杂化,合理的长度设计成为输电线路设计的重要部分[3]。然而,相关行业标准中对跳线设计值仅限定了误差范围,传统的本线模拟法、高空比量法、图解法或Excel计算不仅过程复杂,成本也较高,难以确保放样的精确性,致使跳线安装质量参差不齐。此外,跳线验收规范仅规定了跳线与横杆单塔之间的最小间距,施工人员为满足要求,往往将跳线设计得过长[4],使其过于松弛,易在风偏时因空气间隙不足而发生放电[5],进而造成较大经济损失,影响电力系统的稳定运行。
近年来,随着装配式施工技术的不断发展,跳线装配式施工技术在各大电网建设重点工程中也逐步应用[6-7]。在输电塔线体系方面,文献[8]通过建立有限元模型,分析了单塔与两基三跨塔线体系的动力特性;文献[9]利用蒙特卡洛模拟法计算了不同工况下输电塔架结构的可靠度。但在计算耐张塔跳线长度时,需考虑多个参数,如导线与横担的夹角、横担的尺寸、耐张串的长度和倾斜角等,且设计的构架需依据相位进行独特调整。目前,已有众多学者对跳线展开了广泛研究。文献[10]对特高压直流耐张塔软/硬跳线方案进行了风偏计算,探讨了各种跳线方案的优缺点和适用条件。文献[11]利用三维激光扫描建立了耐张塔及跳线的三维模型,但计算量大,且现场安装精度不足。文献[12]提出了一种基于线性拟合和差值补偿的跳线安装设计方法,简化了1 000 kV单回路特高压交流输电线路跳线设计,解决了因输电线路边界条件变化导致的“逐塔逐相”反复计算跳线线长的问题,但引入补偿值增大了现场技术人员复核参数的难度,研究结果不具普适性。文献[13]通过理论计算得出了跳线的电场强度、子导线型号及系统参数等,但该研究仅对部分参数进行了优化,未提出系统解决方案。文献[14]提出了基于无人机单目视觉的测量方法,根据相机的线性成像原理识别跳线弧垂最低点与其上方横担的垂直距离,以测量跳线弧垂,但由于焦距固定,需保持无人机与跳线的相对距离不变,操作较为复杂。文献[15]结合CAD软件,通过斜抛物线曲线计算跳线长度。文献[16]建立了具有普适性的通用坐标系,优化了耐张串下倾角的计算方法,提升了跳线计算精度,但该方法计算复杂度高,需要建立规范坐标系,输入耐张串连板长度和线束调整值等参数。
跳线系统复杂,其设计过程涉及多个因素,如跳线长度、弧垂以及平视弧垂计算等。目前的研究成果通常需要对每个塔位和相位逐一进行计算,设计方法和计算过程复杂,施工过程中操作性也较差。为此,本文提出了一种跳线长度的计算流程,包括获取可见光图片、基于可见光图片建立装配式跳线的三维模型,以及跳线安装前的模型可视化。这一流程不仅提升了测量的精度和效率,减少了人工操作的误差和风险,还通过动态模拟优化了电力系统的稳定性和可靠性。在方法验证部分,针对本文提出的三维建模技术,通过多组仿真和实验,对该方法在实际应用中的效率和准确性进行了全面评估。
1 三维模型的建立
1.1 模拟流程
1.2 特征提取
为了从尚未安装装配式跳线的铁塔图像中提取出具有稳定性的关键点,使其能够在不同视角的图像中被匹配和识别,本文采用尺度不变特征变换(Scale Invariant Feature Transform,SIFT)算法进行特征提取。为确保特征提取的效果,将图像的最大尺寸限制为3 200像素,以提升处理效率,并将最大特征点数量设定为8 192,以保证每幅图像能够捕捉到足够的细节。在特征提取时,使用多个尺度空间,参数设置为4个尺度层,确保在不同尺度下均能提取到稳定的特征。为加快处理过程,特征提取环节还启用了图像处理器加速。
在不同尺度上对无人机拍摄的铁塔图像I(x,y) 进行高斯模糊处理,构建高斯差分(Difference of Gaussians,DoG),可用公式表示为
| $ L(x, y, \sigma)=G(x, y, \sigma) I(x, y) $ | (1) |
式中:L(x,y,σ)——模糊处理后的图像;
x,y——图像中像素点的横、纵坐标;
σ——尺度参数;
G(x,y,σ)——高斯核函数。
计算高斯差分以检测尺度空间中的极值点,计算公式为
| $ D(x, y, \sigma)=L\left(x, y, k_0 \sigma\right)-L(x, y, \sigma) $ | (2) |
式中:D(x,y,σ)——高斯差分;
k0——控制高斯模糊尺度变化的常数,取
| $ k_0=\sqrt{2} \text { 。} $ |
通过计算不同尺度上的D(x,y,σ),找到尺度空间中的极值点,即潜在的特征点。为实现特征点的精确定位,对检测到的极值点进行细化。采用二阶泰勒展开对极值点附近进行近似,并通过Hessian矩阵和梯度向量来调整特征点位置,可用公式表示为
| $ \boldsymbol{H}=\left[\begin{array}{ll} \frac{\partial^2 D}{\partial x^2} & \frac{\partial^2 D}{\partial x \partial y} \\ \frac{\partial^2 D}{\partial y \partial x} & \frac{\partial^2 D}{\partial y^2} \end{array}\right] $ | (3) |
| $ \boldsymbol{G}=\left[\begin{array}{l} \frac{\partial D}{\partial x} \\ \frac{\partial D}{\partial y} \end{array}\right] $ | (4) |
| $ \hat{\boldsymbol{x}}=-\boldsymbol{H}^{-1} \boldsymbol{G} $ | (5) |
式中:H——极值点的Hessian矩阵;
G——梯度向量;
在每个特征点邻域内,计算梯度方向并分配主方向,以确保特征点在旋转和尺度变化下保持不变。在此基础上,生成SIFT描述子,用于图像之间的特征匹配。
1.3 特征匹配
在不同视角的杆塔图像中找到相同的特征点,以便于后续的三维重建。特征匹配通常利用最近邻搜索算法来实现,对于每个图像中的特征点,在其他图像中找到最近的特征点,即具有最小欧氏距离的特征点。为提高匹配的可靠性,SIFT算法使用比值测试,筛选出更为可靠的匹配对。这一方法可用公式表示为
| $ d\left(\boldsymbol{f}_i, \boldsymbol{f}_j\right)=\sqrt{\sum\limits_{k=1}^{128}\left[\boldsymbol{f}_i(k)-\boldsymbol{f}_j(k)\right]^2} $ | (6) |
| $ \frac{d_1}{d_2}<t_{\mathrm{h}} $ | (7) |
式中:
d1,d2——某特征点描述子在另一图像中找到的最近、次近特征点描述子的欧氏距离;
th——经验参数,取0.75。
为进一步提高匹配的准确性,需对特征匹配结果进行几何验证。通过计算基础矩阵或本质矩阵,剔除不符合几何约束的错误匹配。本文将比率测试设为0.8,最大距离约束设为0.7,并使用交叉检查。通过特征匹配,可以得到同一场景下不同图像中相同的特征点对。这些匹配结果可用于估计相机的位姿,并进行三维点云重建。
1.4 运动结构恢复
运动结构恢复的目标是从特征匹配结果中推算出相机的位姿(位置和方向),并重建稀疏三维点云。通过基础矩阵或本质矩阵来估计两幅图像之间的相对位姿。本质矩阵的计算公式为
| $ \boldsymbol{E}=\boldsymbol{K}^{\mathrm{T}} \boldsymbol{F} \boldsymbol{K} $ | (8) |
式中:E——本质矩阵;
K——相机内参矩阵;
F——基础矩阵。
基础矩阵描述的是两幅图像间的几何关系,本质矩阵则进一步考虑了相机的内参信息。通过相机的位姿和匹配的特征点进行三角化,并计算该电力场景中各个三维点的坐标。三角化的基本公式如下:
| $ \boldsymbol{X}=\mathit{\pmb{λ}}_1 \boldsymbol{P}_1 \boldsymbol{x}_1=\mathit{\pmb{λ}}_2 \boldsymbol{P}_2 \boldsymbol{x}_2 $ | (9) |
式中:X——三维点坐标向量;
λ1,λ2——图像坐标扩展到三维空间的尺度因子;
P1,P2——相机投影矩阵;
x1,x2——图像点坐标向量。
通过不断加入新的电力杆塔图像,逐步优化相机位姿和稀疏点云。随后,采用光束平差(Bundle Adjustment,BA)算法最小化重投影误差,调整优化相机的位姿和三维点的坐标,以提高重建精度。BA算法的优化目标函数为
| $ E_0=\min\limits _{R_i, t_i, X_j} \sum\limits_{i, j}\left\|\boldsymbol{x}_{i \boldsymbol{j}}-\boldsymbol{P}_t\left(\boldsymbol{R}_i, \boldsymbol{t}_{i}, \boldsymbol{X}_{j}\right)\right\|^2 $ | (10) |
式中:E0——捆绑调整中的重投影误差;
Ri —第i台相机的旋转矩阵;
ti —第i台相机的平移向量;
Xj —第j个三维点的坐标向量;
xij——第i台相机看到的第j个点的图像坐标向量;
1.5 稠密重建
若相机参数已知,在寻找空间中具有光度一致性的点,并对场景进行立体匹配时,可采用多视图立体法(Multi-View Stereo,MVS)进行稠密重建。本次实验将图像的最大尺寸限制在2 000像素,设置几何一致性检查以确保不同视角下匹配点的一致性,将最大几何一致性成本设为3.0以控制几何一致性的误差范围。在进行匹配时,将窗口半径设为5,计算图像相似性。MVS通过整合多个视角的图像信息,为每幅图像计算深度图,进而通过视差计算图像中每个像素点的深度。深度计算公式如下:
| $ D_{\mathrm{p}}(x, y)=\frac{b f}{\delta} $ | (11) |
式中:
b——基线距离;
f——焦距;
δ——视差。
将所有深度图进行融合,生成稠密点云。在融合过程中考虑视角和重叠区域,以确保点云的连续性和完整性。至此,输电线路铁塔三维模型构建完成。
1.6 输电线路的悬链线理论
在输电线路中,电线以杆塔为支持物悬挂。首先,假设跳线是由两个固定点悬挂起来的柔性且不可伸长的绳索或电缆,且跳线的线长远远大于其直径。同时,由于跳线大多采用多股细金属线构成的绞合线(常为钢芯铝绞线),其刚性对悬挂空间曲线形状的影响很小,只适合承受张力而不适合承受显著的弯矩。其次,假设作用在跳线上的荷载沿其线长均匀分布。基于以上两个假设,悬挂的跳线呈悬链线形状,且悬链线模型在无风、恒温等稳定工况下适用性较强,故本文采用悬链线模型对跳线长度进行模拟。然而,随着外部环境如风荷载和温度变化,跳线的实际受力状态会发生改变,悬链线模型的适用性也会受到限制。例如,极端风速、冰荷载可能导致跳线形态偏离悬链线模型的预测结果。此时需考虑将该模型与其他模型(如Catenary-Parabolic混合模型)结合使用,以提高复杂工况下的预测精度。此外,温度变化引起的热胀冷缩效应也可能导致跳线长度变化,在这种情况下,需要引入温度补偿机制。文献 [18]基于悬链线理论和抛物线理论分别对架空输电线路导线的静力特性进行了分析,并研究了均匀覆冰条件下,风、气温等气象条件对导线静力特性的影响,效果较好。
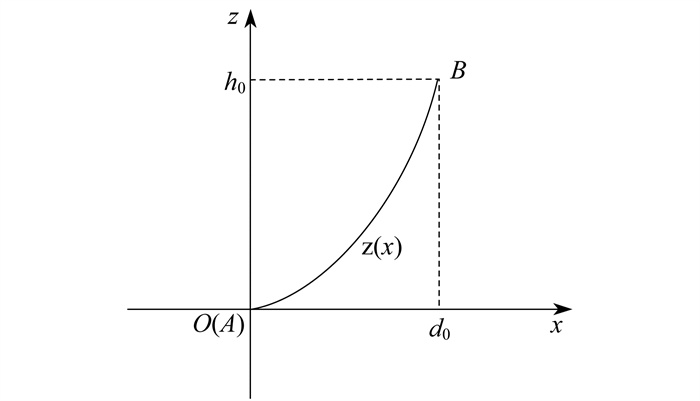
由三维建模可得到需安装跳线的
悬链线在平面上的函数z(x)公式为
| $ z(x)=a \cdot \cosh \left(\frac{x}{a}\right)-a $ | (12) |
式中:a——悬链线参数。
两端点的水平距离d0的计算公式为
| $ d_0=\sqrt{\left(x_{\mathrm{A}}-x_{\mathrm{B}}\right)^2+\left(y_{\mathrm{A}}-y_{\mathrm{B}}\right)^2} $ | (13) |
两端点高度差h0的计算公式为
| $ h_0=\left|z_{\mathrm{A}}-z_{\mathrm{B}}\right| $ | (14) |
悬链线参数a的求解方程为
| $ h_0=a \cdot\left[\cosh \left(d_0 / a\right)-1\right] $ | (15) |
该方程是非线性的,需使用数值方法求解参数a。在悬链线模型中,参数a会直接影响跳线的弧垂形状。a值越大,跳线的弧度越小,代表了跳线在受力较小、距离较短情况下的形态。由于跳线的实际物理特性会影响弧垂形状,所以参数a会根据跳线的端点距离和高度差进行动态调整,以确保生成的跳线形状符合实际工况。
从而,得到悬链线长度l为
| $ l=\int_0^{d_0} \sqrt{1+\left[\frac{\mathrm{d} z(x)}{\mathrm{d} x}\right]^2} \mathrm{~d} x $ | (16) |
2 实验设置及结果分析
2.1 实验设置
本实验使用的无人机型号为大疆无人机avata,相机为对角线尺寸14.94 mm的影像传感器,运行Colmap的PC操作系统为Windows,显卡配置为NVIDIA GeForce RTX 4060 Laptop GPU GDDR 6 @ 8 GB,处理器配置为13th Gen Intel(R)Core(TM)i7-13700 H,2 400 MHz。图像分辨率为4 096×3 072,三维建模Max_image_slze为3 200,Max_num_features为8 192,Max_num_ matches为32 768。
为保证实验结果准确,6位志愿者分别站在不同位置,使用无人机从不同高度和角度对铁塔进行拍摄,以捕捉到铁塔的全貌和细节。志愿者记录了每个拍摄点的坐标、高度、与铁塔的距离等参数,共计6组样本。
基于以上6组样本进行建模,重建后的铁塔点云模型示意如图 3所示。
针对点云模型中短杆、长杆以及模拟生成的跳线,采用选中对应点云的方式测量距离。
2.2 实验结果及分析
三维模型中长杆和短杆长度的测量结果分别如表 1和表 2所示。其中,6位志愿者分别测量3次,测量出的A、B点坐标分别为Auv、Buv(u=1,2,3,4,5,6;v=1,2,3)。
表 1
长杆长度测量结果
| 两点坐标/m | 长杆长度/m | 平均值/m | 误差百分比/% | 两点坐标/m | 长杆长度/m | 平均值/m | 误差百分比/% | |
| A11(−1.446 07,0.921 77,−0.059 24) | 0.934 04 | A41(0.533 12,0.726 75,−0.271 41) | 0.938 22 | |||||
| B11(−2.561 85,0.328 98,1.710 25) | B41(−1.409 36,0.734 60,−0.093 66) | |||||||
| A12(−1.459 85,0.905 07,−0.074 74) | 0.935 46 | 0.933 20 | 0.19 | A42(0.534 11,0.721 83,−0.249 08) | 0.937 79 | 0.939 55 | 0.49 | |
| B12(−2.573 25,0.330 67,1.706 34) | B42(−1.409 36,0.734 60,−0.093 66) | |||||||
| A13(−1.445 81,0.915 84,−0.063 60) | 0.930 10 | A43(−1.409 13,0.701 43,−0.074 71) | 0.942 63 | |||||
| B13(−2.548 23,0.335 94,1.704 46) | B43(0.542 50,0.720 26,−0.252 08) | |||||||
| A21(0.728 10,−0.119 48,3.840 65) | 0.944 24 | A51(−0.397 43,1.125 37,1.726 09) | 0.940 74 | |||||
| B21(2.813 87,0.135 13,3.897 71) | B51(1.960 25,1.386 37,2.017 04) | |||||||
| A22(0.717 75,−0.119 12,3.840 70) | 0.942 63 | 0.936 87 | 0.20 | A52(−0.414 97,1.127 54,1.710 84) | 0.948 26 | 0.939 19 | 0.45 | |
| B22(2.799 50,0.140 03,3.892 34) | B52(1.959 87,1.391 68,2.016 60) | |||||||
| A23(0.720 68,−0.115 84,3.842 08) | 0.923 75 | A53(−0.414 97,1.127 54,1.710 84) | 0.928 57 | |||||
| B23(2.759 20,0.151 76,3.883 37) | B53(1.910 93,1.377 99,2.014 34) | |||||||
| A31(−0.688 49,0.778 40,−0.299 53) | 0.938 66 | A61(0.153 40,0.927 21,−0.741 15) | 0.915 34 | |||||
| B31(−1.153 38,0.272 56,1.586 09) | B61(−1.689 91,0.948 56,−0.776 86) | |||||||
| A32(−0.711 82,0.759 20,−0.308 57) | 0.938 18 | 0.937 69 | 0.29 | A62(0.153 40,0.927 21,−0.741 15) | 0.913 77 | 0.914 67 | 2.17 | |
| B32(0.153 40,0.927 21,−0.741 15) | B62(−1.686 63,0.942 71,−0.784 89) | |||||||
| A33(−0.709 50,0.754 35,−0.309 57) | 0.936 22 | A63(0.153 86,0.933 32,−0.739 28) | 0.914 90 | |||||
| B33(−1.150 65,0.257 62,1.578 63) | B63(−1.688 35,0.925 99,−0.788 21) |
表 2
短杆长度测量结果
| 两点坐标/m | 短杆长度/m | 平均值/m | 误差百分比/% | 两点坐标/m | 短杆长度/m | 平均值/m | 误差百分比/% | |
| A11(−2.039 91, 1.426 09, 0.974 43) | 0.342 36 | A41(−0.399 43, 0.752 79, −0.162, 92) | 0.336 06 | |||||
| B11(−1.996 98,0.646 04,0.816 89) | B41(−0.380 66, 1.451 17, −0.154 26) | |||||||
| A12(−2.061 75, 1.421 01, 0.995 75) | 0.346 79 | 0.343 03 | 1.15 | A42(−0.388 36, 1.456 33, −0.102 51) | 0.340 95 | 0.340 70 | 1.82 | |
| B12(−2.000 76, 0.648 49, 0.790 46) | B42(−0.414 11, 0.750 78, −0.165 91) | |||||||
| A13(−2.046 36, 1.416 23, 0.983 19) | 0.339 86 | A43(−0.412 21, 0.740 09, −0.152 38) | 0.345 08 | |||||
| B13(−2.013 93, 0.644 06, 0.814 14) | B43(−0.382 41, 1.456 89, −0.155 49) | |||||||
| A21(1.726 43, 0.019 38, 3.860 54) | 0.348 11 | A51(0.600 47, 2.149 20, 1.968 85) | 0.350 38 | |||||
| B11(1.604 47, 0.727 92, 4.149 77) | B51(0.705 89, 1.270 55, 1.873 21) | |||||||
| A22(1.617 95, 0.731 91, 4.149 90) | 0.350 41 | 0.348 37 | 0.39 | A52(0.577 49, 2.133 01, 1.943 18) | 0.348 04 | 0.350 40 | 0.98 | |
| B22(1.722 42, 0.015 46, 3.859 59) | B52(0.769 03, 1.275 70, 1.842 75) | |||||||
| A23(1.717 81, 0.019 98, 3.860 59) | 0.346 59 | A53(0.560 08, 2.142 04, 1.937 64) | 0.352 79 | |||||
| B13(1.605 84, 0.709 43, 4.188 35) | B53(0.769 03, 1.275 70, 1.842 75) | |||||||
| A31(−0.892 23, 0.571 47, 0.607 89) | 0.329 46 | A61(−0.634 30, 0.916 90, −0.766 96) | 0.353 60 | |||||
| B31(−0.931 73, 1.242 30, 0.798 15) | B61(−0.654 61, 1.598 66, −0.561 77) | |||||||
| A32(−0.932 12, 1.248 88, 0.803 06) | 0.329 75 | 0.334 72 | 3.54 | A62(−0.742 47, 0.922 38, −0.759 34) | 0.346 04 | 0.347 05 | 0.02 | |
| B32(−0.892 50, 0.570 51, 0.617 29) | B62(−0.658 19, 1.591 97, −0.582 12) | |||||||
| A33(−0.921 91, 1.245 03, 0.809 40) | 0.344 95 | A63(−0.686 22, 0.928 66, −0.755 34) | 0.341 16 | |||||
| B33(−0.886 11, 0.538 27, 0.601 70) | B63(−0.712 14, 1.587 64, −0.562 20) |
由表 1和表 2可以看出,三维模型在长杆和短杆的长度测量中表现出了较高的精度,误差均未超过4%。无论是点的坐标还是长度测量,样本间的差异均较小,进一步说明了基于Colmap的三维建模技术的稳定性和准确性。
对模拟生成的跳线长度进行测量,结果如 表 3所示。
表 3
模拟生成跳线长度的测量结果
| 两点坐标/m | 跳线长度/m | 平均值/m | 误差百分比/% | 两点坐标/m | 跳线长度/m | 平均值/m | 误差百分比/% | |
| A11(−1.449 11, 0.917 32, −0.061 97) | 0.620 32 | A41(0.500 46, 0.731 62, −0.246 25) | 0.629 10 | |||||
| B11(−2.023 61, 1.413 27, 0.974 21) | B41(−0.314 21, 1.458 55, −0.149 38) | |||||||
| A12(−1.439 12, 0.896 26, −0.056 66) | 0.626 41 | 0.622 65 | 0.43 | A42(0.546 54, 0.730 70, −0.256 15) | 0.624 60 | 0.618 52 | 0.24 | |
| B12(−2.035 84, 1.427 21, 0.977 44) | B42(−0.388 36, 1.456 33, −0.102 51) | |||||||
| A13(−1.461 41, 0.942 43, −0.063 20) | 0.621 23 | A43(−0.328 54, 1.443 12, −0.140 48) | 0.601 88 | |||||
| B13(−2.018 59, 1.424 22, 0.974 10) | B43(0.529 60, 0.747 87, −0.259 63) | |||||||
| A21(0.717 30, −0.139 40, 3.839 53) | 0.629 22 | A51(−0.414 97, 1.127 54, 1.710 84) | 0.650 56 | |||||
| B21(1.592 82, 0.717 09, 4.183 04) | B51(0.603 97, 2.146 70, 1.917 69) | |||||||
| A22(0.717 33, −0.109 28, 3.866 73) | 0.614 35 | 0.625 01 | 0.81 | A52(−0.323 56, 1.158 75, 1.703 91) | 0.619 13 | 0.630 06 | 1.62 | |
| B22(1.600 74, 0.710 65, 4.181 34) | B52(0.600 47, 2.149 20, 1.968 85) | |||||||
| A23(0.716 68, −0.132 58, 3.834 58) | 0.631 47 | A53(−0.384 60, 1.891 26, 1.765 31) | 0.620 50 | |||||
| B23(1.592 82, 0.717 09, 4.183 04) | B53(0.602 96, 2.176 32, 1.998 80) | |||||||
| A31(−0.895 25, 1.257 11, 0.804 99) | 0.640 29 | A61(−0.718 59, 1.602 80, −0.594 51) | 0.647 18 | |||||
| B31(−0.700 16, 0.787 68, −0.306 48) | B61(0.113 76, 0.911 63, −0.693 34) | |||||||
| A32(−0.685 10, 0.759 39, −0.310 35) | 0.626 16 | 0.631 90 | 1.92 | A62(0.157 91, 0.951 50, −0.730 51) | 0.614 56 | 0.630 72 | 1.73 | |
| B32(−0.906 08, 1.263 40, 0.768 64) | B62(−0.654 40, 1.597 77, −0.582 58) | |||||||
| A33(−0.685 88, 0.766 69, −0.294 92) | 0.629 27 | A63(−0.745 84, 1.602 35, −0.590 30) | 0.630 42 | |||||
| B33(−0.905 56, 1.267 22, 0.759 25) | B63(0.113 76, 0.911 63, −0.693 34) |
由表 3可以看出,基于Colmap方法的三维建模技术在跳线长度测量中表现出了较高的精度,误差均在可接受范围内,各样本的测量误差百分比均低于2%。
为了验证本文所采用Colmap方法的效率和准确性,通过实验对本文方法与Alicevision meshroom[19]、Gaussian-splatting(30 k)[20]方法进行对比。3种方法的实验数据如表 4所示。
表 4
3种三维建模方法的实验数据
| 三维建模方法 | 测量时间/min | 长杆平均直线距离/m | 直线距离平均误差/% | 模拟跳线平均距离/m | 跳线平均误差/% |
| Colmap | 45 | 0.938 60 | 0.39 | 0.626 5 | 1.05 |
| Alicevision meshroom | 17 | 0.643 40 | 31.19 | 0.597 9 | 3.56 |
| Gaussian-splatting(30ak) | 210 | 0.932 13 | 0.31 | 0.625 3 | 0.86 |
由 表 4可以看出,虽然Gaussian-splatting(30 k)方法在测量精度上稍占优势,但其测量时间过长,适用于机械零部件的精密建模或风电设备叶片结构的精细测量等精度要求极高的场景。Alicevision meshroom方法虽然测量时间较短,但测量结果的准确性和完整性不理想,适用于建筑物快速三维扫描、灾后救援中的建筑物或道路状况评估等精度要求不高的场景。相比之下,Colmap方法不仅具有较高的测量精度,而且测量时间相对较短,适用于输电线路跳线测量等精度要求较高且时间相对宽裕的电力系统巡检与维护场景。与表 1、表 3中的数据对比后发现,本文所采用的Colmap方法在测量精度上接近Gaussian-splatting(30 k)方法,且测量误差显著低于Alicevision meshroom方法。
3 结语
本文针对输电线路铁塔装配式跳线的测量问题,提出了一种基于三维建模技术的跳线模拟方法,并通过实验验证了该方法的效率和准确性。实验结果表明,本方法在不同条件下均呈现出较高的测量精度。与现有三维建模方法对比,本方法在测量精度上接近Gaussian-splatting(30 k)方法,且测量误差显著低于Alicevision meshroom方法。综合而言,本方法在测量时间与测量精度之间达到了良好平衡,并有效降低了传统测量方法中可能出现的人工误差和安全风险。其应用为输电线路的设计、施工和维护提供了有力支撑,具有广泛的工程应用前景和推广价值。未来可从三维重建的精度、跳线的模拟计算等方面进一步优化,以应对更为复杂的电力系统环境,并拓展其在其他工程领域中的应用。
参考文献
-
[1]胡选, 张要强, 潘少成, 等. 1000 kV交流特高压有关联双柱组合耐张塔软跳线设计[J]. 电力建设, 2009, 30(11): 13-16.
-
[2]叶俊松, 鲁飞. 利用牵张设备张力拆除500 kV杭乔架空导线的技术运用[J]. 上海电力学院学报, 2015, 31(4): 381-383.
-
[3]陈建忠, 李勇伟, 张小力. 750 kV输电线路耐张塔刚性跳线的研究开发[J]. 电力建设, 2006, 27(10): 19-22.
-
[4]刘兴亚, 郭世广. 输电线路跳线工艺过长的风险与措施分析[J]. 集成电路应用, 2022, 39(1): 148-149.
-
[5]陶铃宏, 李涛, 甘宏军, 等. 跳线绝缘子在台风中的风偏特征分析[J]. 电瓷避雷器, 2017(4): 157-159.
-
[6]刘兴亚, 周洋. 特高压交流输电线路跳线安装施工技术[J]. 集成电路应用, 2021, 38(12): 94-95.
-
[7]陆国智, 李从刚. 四分裂跳线装配式安装施工技术[J]. 电力建设, 2013, 34(4): 102-106.
-
[8]纪冬梅, 赵大乐, 姚秀平, 等. 大跨越高压输电塔线体系的动力特性分析[J]. 上海电力学院学报, 2012, 28(6): 501-504.
-
[9]牛群凯, 朱瑞, 朱全军, 等. 基于蒙特卡洛模拟法的输电塔架结构可靠度分析[J]. 上海电力学院学报, 2018, 34(3): 291-296.
-
[10]赵远涛, 李京凯, 刘文勋, 等. ±800 kV特高压直流耐张塔跳线的优化方案[J]. 电力建设, 2012, 33(2): 27-31.
-
[11]罗望春, 李庭坚, 姜诚, 等. 基于三维空间模型的特高压耐张塔跳线间隙检测方法[J]. 计算机测量与控制, 2019, 27(9): 37-41.
-
[12]李铁鼎, 雷雨泽, 程述一, 等. 基于线性拟合和差值补偿的跳线计算方法研究[J]. 四川电力技术, 2020, 43(1): 6-11.
-
[13]郝阳, 王恩久, 陈建忠, 等. 750 kV输电线路四分裂刚性跳线系统[J]. 电力建设, 2013, 34(12): 102-105.
-
[14]杨少倩, 蔡鑫. 基于单目测量方法的输电线路跳线弧垂测量研究[J]. 设备管理与维修, 2024(10): 28-30.
-
[15]张锴, 徐劲松. ±500 kV直流耐张塔跳线长度计算的一种新方法[J]. 中国新技术新产品, 2022(18): 72-74.
-
[16]朱冠旻, 郭思亮, 许克克, 等. 装配式跳线线长通用精确计算方法[J]. 广东电力, 2023, 36(7): 40-49.
-
[17]SCHÖNBERGER J L, FRAHM J M. Structure-from-motion revisited[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA: IEEE, 2016: 4104-4113.
-
[18]周兴扬, 沈泓, 胡天硕, 等. 基于悬链线公式的输电线路弧垂三维模拟及安全距离校验[J]. 电气工程学报, 2015, 10(12): 44-49.
-
[19]GRIWODZ C, GASPARINI S, CALVET L, et al. Alicevision meshroom: an open-source 3D reconstruction pipeline[C]//Proceedings of the 12th ACM Multimedia Systems Conference (MMSys 2021). Istanbul, Turkey: ACM, 2021: 241-247.
-
[20]KERBL B, KOPANAS G, LEIMKUEHLER T, et al. 3D Gaussian splatting for real-time radiance field rendering[J]. ACM Transactions on Graphics, 2023, 42(4): 139.