|
|
|
发布时间: 2024-12-28 |
控制与检测技术 |
|
|
|
收稿日期: 2024-04-02
中图法分类号: TM73
文献标识码: A
文章编号: 2096-8299(2024)06-0547-08
|
摘要
在直流侧源荷大量接入的多端口交直流配电网中,由于不同交流配电台区存在变压器负载差异和线路阻抗差异,导致传统下垂控制策略无法实现多个不同AC/DC变流器对直流功率的合理分配。针对这一问题,提出了一种基于虚拟压降的自适应下垂控制策略。该策略在保证功率合理分配的同时,无需获取阻抗信息即可消除线路阻抗对功率分配的影响。首先,针对不同AC/DC变流器所在交流配电变压器的负载差异,设计自适应功率控制器对下垂系数进行动态调整,实现直流侧功率的自适应分配;然后,针对多个变流器之间直流线路阻抗不一致问题,设计了基于虚拟压降的阻抗补偿器,消除因线路阻抗不一致而带来的影响,并通过电压补偿器减少直流电压偏差;最后,通过仿真验证了所提策略可以自适应分配直流侧功率,消除线路阻抗对功率分配的影响,减少直流母线电压偏差。
关键词
交直流配电网; AC/DC变流器; 自适应下垂控制; 虚拟压降
Abstract
In the multi-port AC/DC distribution network with a large number of DC side source loads, due to the differences in transformer loads and line impedences in different AC distribution stations, the traditional droop control cannot realize the reasonable allocation of DC power to multiple different AC/DC converters. To solve this problem, an adaptive droop control strategy based on virtual voltage drop is proposed, which can eliminate the influence of line impedance on power allocation without obtaining impedance information while ensuring reasonable power allocation. Firstly, an adaptive power controller is designed to dynamically adjust the droop coefficient to realize the adaptive DC side power allocation according to the load difference of the AC/DC converter in the AC distribution transformer. Then, for the inconsistency of DC line impedance between multiple converters, an impedance compensator based on the virtual voltage drop is designed to eliminate the influence of line impedance inconsistency, and the DC voltage deviation is reduced by the voltage compensator. Then, the stability analysis provides theoretical support for the proposed control strategy. Finally, simulation results show that the proposed strategy can adaptively allocate DC side power, eliminate the influence of line impedance on power allocation, and reduce the DC bus voltage deviation.
Key words
AC/DC distribution network; AC/DC converter; adaptive droop control; virtual voltage drop
随着电动汽车(Electric Vehicle,EV)充电负荷和分布式光伏(Photovoltaic,PV)大量接入低压交流配电网,无序、冲击性的功率潮流波动会引起线路网损增加、电能质量降低等问题[1-2]。交直流配电技术因具有线路损耗小、电能质量优、就地消纳效率高等优势,逐渐成为承载新型直流电源和负荷规模化接入电网的有效途径[3-5]。在多端口交直流配电网中,因直流负荷和电源可以通过多个AC/DC变流器与多个交流台区进行能量交互,从而具有更灵活的功率调节能力[6]。
AC/DC变流器常采用下垂控制策略稳定直流电压,其功率分担率主要由下垂增益决定。下垂增益可分为固定下垂增益或可变下垂增益[7]。固定下垂增益控制虽然可根据变流器的额定容量采用恒定的下垂常数值分配功率[8-9],但容易使额定功率小的变流器在直流侧负荷突增的情况下出现过载问题。针对这一问题,文献[10]提出了一种自适应下垂增益控制策略,实现了在多个变流器间根据变流器剩余容量分配EV充电站充电功率。但这种方法存在当变流器工作在满载时直流电压偏差较大,且当变流器线路阻抗差异较大时功率分配出现偏差等问题。文献[11]根据不同变流器下垂系数间的比值关系,对下垂曲线进行平移优化,在避免变流器过载的同时,减少了直流电压偏差。文献[12]提出了自适应下垂增益控制并使直流电压偏差最小化的方法,但仍存在线路阻抗不匹配,影响AC/DC变流器功率分配的问题。文献[13-14]以自适应虚拟阻抗的方式,实现了功率的合理分配,但只考虑了线路阻抗对功率均分的影响。
上述研究通过调整下垂系数实现了功率的自适应分配,并消除了线路阻抗对功率均分的影响,但由于交流侧负载大小不同,导致AC/DC变流器功率分配存在差异,因此需要考虑在功率分配不一致时消除线路阻抗的影响。本文以多端口交直流混合配电网为研究对象,提出了一种基于虚拟压降的变流器自适应下垂控制策略,通过实时调整下垂系数,实现了AC/DC变流器的功率自适应分配,消除了线路阻抗对功率分配精确性的影响,减少了直流母线电压偏差。
1 传统下垂控制策略的局限性
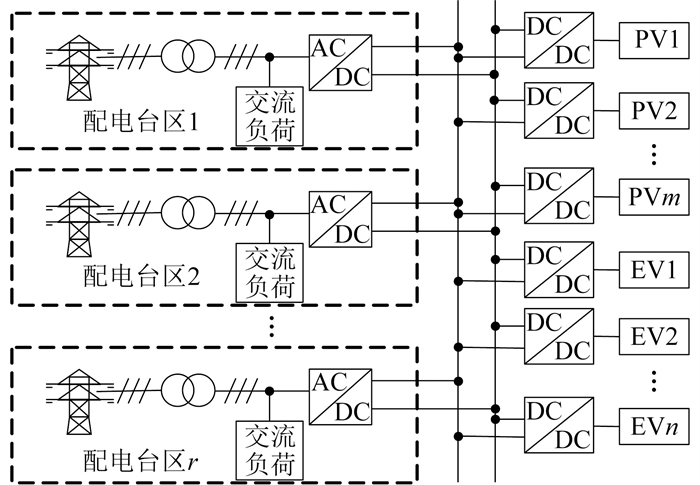
多端口交直流配电网的拓扑结构如图 1所示。其中,r代表配电台区数量,m代表PV数量,n代表EV数量。每个配电台区包含变压器和交流负荷,并通过1个AC/DC变流器连接在直流配电网的公共直流母线上。直流配电网中的PV单元和EV充电单元通过DC/DC变流器连接在直流母线上。PV单元工作在最大功率跟踪模式下,EV充电单元是具有一定随机性的直流负荷。PV单元发电功率优先通过EV充电单元在直流侧进行消纳,多余或不足部分再与交流电网进行功率交换。由于两者的功率波动都会影响直流母线电压,因此通过具有双向功率变换能力的AC/DC变流器维持直流电压母线稳定。
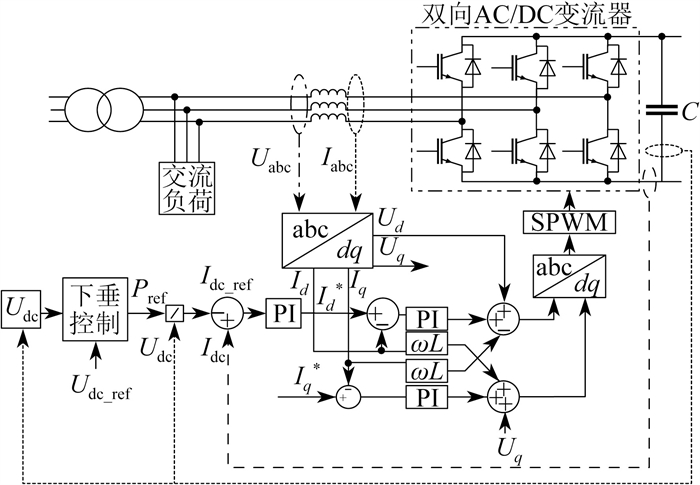
双向AC/DC变流器控制框图如图 2所示[15]。其中:Uabc和Iabc分别为交流侧的三相电压和电流;Ud、Uq、Id、Iq分别为两相旋转坐标系下实际电压和电流的dq轴分量;Id*、Iq*分别为两相旋转坐标系下参考电流的dq轴分量;Udc、Udc_ref分别为变流器实际输出电压和直流侧额定电压;Pref为考虑线路阻抗后的变流器参考功率;Idc、Idc_ref分别为变流器直流侧电流的实际值和参考值;PI表示PI控制器;ω表示角速度;L表示电感;SPWM(Sinusoidal Pulse Width Modulation)表示正弦脉宽调制技术。
当采用传统固定下垂增益的AC/DC变流器控制策略时,双向AC/DC变流器表达式为
| $ \left(P_0-P\right) k=U_{\mathrm{dc} \text {_}\text { ref }}-U_{\mathrm{dc}, i} $ | (1) |
式中:P0——额定电压下的输出功率;
P——实际电压下的输出功率;
k——固定下垂系数;
Udc,i——第i号配电台区的变流器实际输出电压。
k的表达式为
| $ k=\frac{U_{\mathrm{dc} \_ \text {ref }}-U_{\mathrm{dc} \_\min }}{P_0-P_{\max }} $ | (2) |
式中:Udc_ min——变流器直流侧电压最小值;
Pmax——额定功率。
由式(1)和式(2)可知,采用传统固定下垂系数时存在如下问题:一是输出电压偏差会随着功率的增加而增大,当变流器输出功率达到额定功率时,会造成实际输出电压与额定电压偏差较大;二是当多个配电台区通过不同AC/DC变流器并联运行时,由于每个台区变压器的剩余容量不同,故采用相同的固定下垂系数可能导致变压器出现过载;三是多个AC/DC变流器直流线路阻抗的存在及其差异,会导致AC/DC变流器的输出功率与理论值不符。
2 改进下垂控制策略
2.1 基于虚拟压降的自适应下垂控制策略
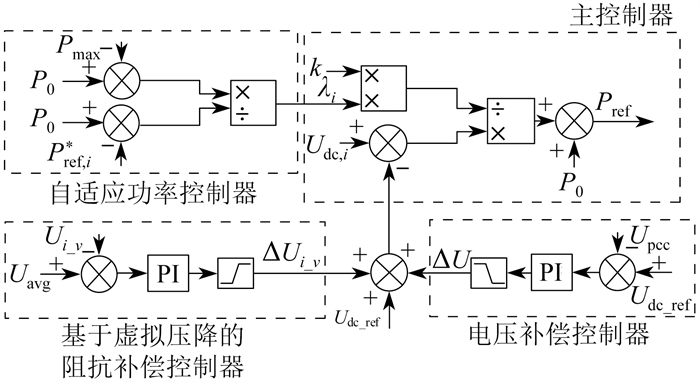
针对以上问题,本文提出了一种基于虚拟压降的自适应下垂控制策略,以实现功率自适应分配,消除线路阻抗影响,减少直流母线电压偏差。基于虚拟压降的自适应下垂控制策略如图 3所示。其中:Pref*,i为第i号配电台区未考虑线路阻抗时的变流器参考功率;λi为第i号配电台区的变流器功率补偿系数;Uavg为各个变流器产生的虚拟压降平均值;Ui_v为第i号配电台区的AC/DC变流器引入新的下垂系数后产生的虚拟压降;
由图 3可知,首先,通过自适应功率控制器实时调整下垂曲线,在防止变流器所在台区变压器过载的情况下,变压器剩余容量通过自适应功率控制器输出λi,与固定下垂系数k相乘得到新的下垂系数,改变变流器承担直流侧功率的比例;然后,通过基于虚拟压降的阻抗补偿控制器,输出补偿变量
2.2 自适应功率控制器
本文的自适应功率控制器以保证所在配电台区变压器不过载为目标,根据对应变压器剩余容量实时调整变流器承担的直流侧功率比例。变压器剩余容量计算公式为
| $ P_{\mathrm{T}, i}=S_{\mathrm{N}, i}-S_{\text {load }, i} $ | (3) |
式中:PT,i——第i号配电台区变压器剩余容量;
SN,i——第i号配电台区变压器额定容量;
Sload,i——第i号配电台区交流负荷。
通过自适应功率控制器得到AC/DC变流器在逆变或整流时的参考输出功率为
| $ P_{\text {ref }, i}^*=\left\{\begin{array}{l} -P_{\mathrm{L}} \frac{S_{\text {load }, i} / S_{\mathrm{N}, i}}{\sum\limits_{i=1}^r S_{\text {load }, i} / S_{\mathrm{N}, i}}, U_{\mathrm{dc} \_ \text {ref }}<U_{\mathrm{dc}, i}<U_{\mathrm{H}} \\ 0, U_{\mathrm{dc}, i}=U_{\mathrm{dc} \_ \text {ref }} \\ P_{\mathrm{L}} \frac{P_{\mathrm{T}, i}}{\sum\limits_{i=1}^r P_{\mathrm{T}, i}}, U_{\mathrm{L}}<U_{\mathrm{dc}, i}<U_{\mathrm{dc} \_ \text {ref }} \end{array}\right. $ | (4) |
式中:PL——直流母线与各个配电台区之间的总交换功率;
UH——变流器输出最大电压;
UL——变流器输出最小电压。
PL表达式为
| $ P_{\mathrm{L}}=\sum\limits_{p=1}^m P_{\mathrm{PV}, p}-\sum\limits_{q=1}^n P_{\mathrm{EV}, q} $ | (5) |
式中:PPV,p——第p个PV的输出功率;
PEV,q——第q个EV的充电功率。
自适应功率控制器的输出λi表达式为
| $ \lambda_i=\frac{P_0-P_{\max }}{P_0-P_{\mathrm{ref}, i}^*} $ | (6) |
将得到的功率补偿系数送入主控制器,与固定下垂控制系数k相乘,得到新的下垂系数。
2.3 基于虚拟压降的阻抗补偿控制器
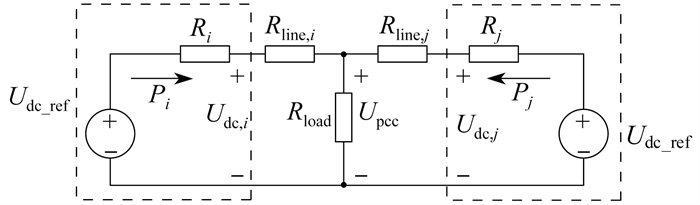
由于各个AC/DC变流器与直流负载之间的直流电缆距离可能存在差异,从而导致线路阻抗不匹配,进而影响AC/DC变流器功率的精确分配。因此,本文提出基于虚拟压降的阻抗补偿控制器,以消除线路阻抗对AC/DC变流器输出功率的影响。为了便于分析,以第i号和第j号两个配电台区AC/DC变流器为例进行分析,其直流互联的等效简化模型如图 4所示[16]。其中,Pi和Pj分别为第i号和第j号配电台区的变流器输出功率;Ri和Rj分别为第i号和第j号配电台区的变流器下垂控制的等效阻抗;Rline,i和Rline,j分别为第i号和第j号配电台区的线路阻抗;Udc,i和Udc,j分别为第i号和第j号配电台区的变流器输出电压;Rload为直流负载等效阻抗。
由图 4可知,在传统固定下垂系数的下垂控制策略中,两个配电台区AC/DC变流器的功率和电压表达式为
| $ \left\{\begin{array}{l} P_i=\frac{\left(U_{\mathrm{dc} \text { _ref }}-U_{\mathrm{pcc}}\right) U_{\mathrm{dc}{ \text {_ref }}}}{R_i+R_{\text {line }, i}} \\ P_j=\frac{\left(U_{\text {dc_ref }}-U_{\mathrm{pcc}}\right) U_{\mathrm{dc} \text { _ref }}}{R_j+R_{\text {line }, j}} \end{array}\right. $ | (7) |
由式(7)推导可得:
| $ \frac{P_i}{P_j}=\frac{R_j+R_{\operatorname{line}, j}}{R_i+R_{\operatorname{line}, i}} $ | (8) |
在消除线路阻抗影响的理想情况下,变流器的输出功率应与下垂增益呈反比,为
| $ P_i R_i=P_j R_j $ | (9) |
由式(8)可知,各变流器输出功率之比不等于其下垂增益的反比;而由式(9)可知,当控制各个变流器的输出功率与其下垂阻抗之积相等时,线路阻抗影响被消除。因此,本文定义Pi、Ri为各个变流器的虚拟压降,当各个变流器产生的虚拟压降相等时,不同变流器之间的功率分配仅由其下垂阻抗决定。
结合本文提出的基于虚拟压降的阻抗补偿控制器,定义第i号配电台区AC/DC变流器引入新的下垂系数后产生的虚拟压降为
| $ U_{i_{-} v}=\left(P_0-P_i\right) k \lambda_i $ | (10) |
得到各个变流器产生的虚拟压降及虚拟压降的平均值Uavg,计算各虚拟压降与其平均值的误差,然后,通过PI控制器得到
| $ U_{\mathrm{avg}}=\frac{U_{i_{-} v}+U_{j_{-} v}}{2} $ | (11) |
| $ \Delta U_{i_{-} \mathrm{v}}=\left(k_{\mathrm{p} 1}+\frac{k_{\mathrm{i} 1}}{s}\right)\left(U_{\mathrm{avg}}-U_{i_{-} \mathrm{v}}\right) $ | (12) |
式中:Uj_v——第j号配电台区的AC/DC变流器引入新的下垂系数后产生的虚拟压降;
kp1,ki1——阻抗补偿控制器的比例系数和积分系数;
s——复变量。
2.4 电压补偿控制器
采用上述改进下垂控制策略时,随着变压器负载率变化,变流器的下垂系数及直流母线电压会在一定范围内变化,从而与额定直流电压产生电压偏差。为了减少电压偏差,通过电压补偿控制器得到一个电压补偿量
| $ \Delta U=\left(k_{\mathrm{p} 2}+\frac{k_{\mathrm{i2}}}{s}\right)\left(U_{\mathrm{dc} \_ \text {ref }}-U_{\mathrm{pcc}}\right) $ | (13) |
式中:kp2,ki2——电压补偿控制器的比例系数和积分系数。
将额定直流电压叠加电压补偿量与线路阻抗补偿量作为改进后的直流参考电压。改进后的下垂控制表达式为
| $ \left(P_0-P_i\right) k \lambda_i=U_{\text {dc } \_ \text {ref }}-U_{\mathrm{dc}, i}+\Delta U+\Delta U_{i_{-} \mathrm{v}} $ | (14) |
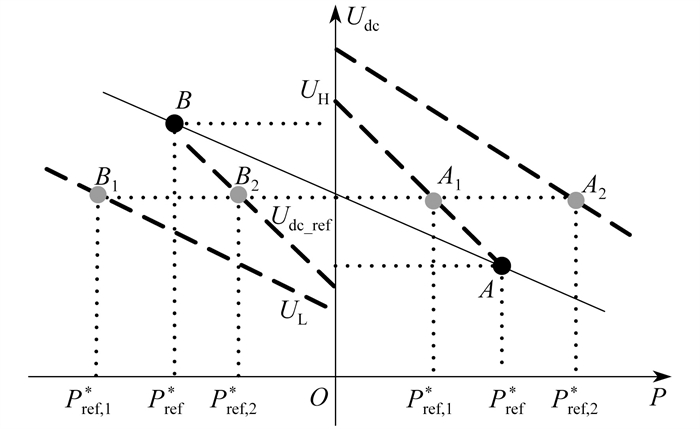
以两台额定容量相等的AC/DC变流器互联的交直流混合配电系统为例,传统下垂控制与改进后的下垂控制曲线对比如图 5所示。其中,实线为传统下垂控制曲线。由于变流器额定容量相同,使得第1台AC/DC变流器和第2台AC/DC变流器的下垂曲线重合在一起。经过A1、B1点的虚线和经过A2、B2点的虚线分别为改进后的第1台AC/DC变流器和第2台AC/DC变流器的下垂曲线。设第1台AC/DC变流器对应配电变压器的剩余容量小于第2台AC/DC变流器对应配电变压器的剩余容量。
由图 5可知,传统下垂控制在变压器剩余容量状态变化时保持固定的功率分配特性。随着AC/DC变流器整流功率增大,其平衡点移动到A点,随着变流器逆变功率增大,其平衡点移动到B点。当AC/DC变流器处于整流状态时,剩余容量小的变压器承受相同的整流功率,容易造成变压器过载;当AC/DC变流器处于逆变状态时,负载率小的变压器分配相同的功率,不利于实现最优潮流。应用改进下垂控制策略后,当变流器处于整流状态时,两台AC/DC变流器的平衡点分别移动到了A1和A2点。此时剩余容量小的第1台AC/DC变流器的输出功率低于第2台AC/DC变流器的输出功率,实现了功率的合理分配,且此时工作电压接近额定电压。当变流器处于逆变状态时,变流器的平衡点分别移动到了B1和B2点,此时剩余容量小的第1台AC/DC变流器得到更多的逆变功率,工作电压仍接近额定电压。
2.5 改进下垂控制策略后系统稳定性分析
为了研究改进下垂控制策略对系统稳定性的影响,本文对图 3中改进下垂控制进行小信号建模[17]。通过联立式(1)至式(7)、式(10)至式(14),得到系统的特征方程为
| $ A s^2+B s+C=0 $ | (15) |
式中:A,B,C——特征方程的二次项系数、一次项系数和常数项。
其中,
| $ \left\{\begin{aligned} A= & 2 R_{\text {line }}-2 k_{\mathrm{p} 2} R_{\text {line }}+U_{\mathrm{dc} \_ \text {ref }} k_{\mathrm{p} 1} k \lambda_i \\ B= & 2 \omega R_{\text {line }}^2+2 U_{\text {dc_ref }} R_{\text {line }} k \lambda_i-2 k_{\mathrm{p} 2} \omega R_{\text {line }}^2- \\ & 2 k_{\text {i2 }} R_{\text {line }}+U_{\text {dc__ref }} \omega R_{\text {line }} k_{\mathrm{p} 1} k \lambda_i+U_{\mathrm{dc} \_ \text {ref }} k_{\mathrm{i} 1} k \lambda_i \\ C= & U_{\text {dc_ref }} k_{\mathrm{i} 1} \omega R_{\text {line }} k \lambda_i-2 k_{\mathrm{i} 2} \omega R_{\text {line }}^2 \end{aligned}\right. $ | (16) |
式中:Rline——线路阻抗。
稳定性分析参数如表 1所示。
表 1
稳定性分析参数
| 参数 | 数值 | 参数 | 数值 | |
| Rline/Ω | 0.1 | kp1 | 0.4 | |
| kp2 | 3 | ki1 | 10 | |
| ki2 | 40 | Udc_ref/V | 750 | |
| kλi | 0.000 1~0.001 | ω/(rad/s) | 20~100 |
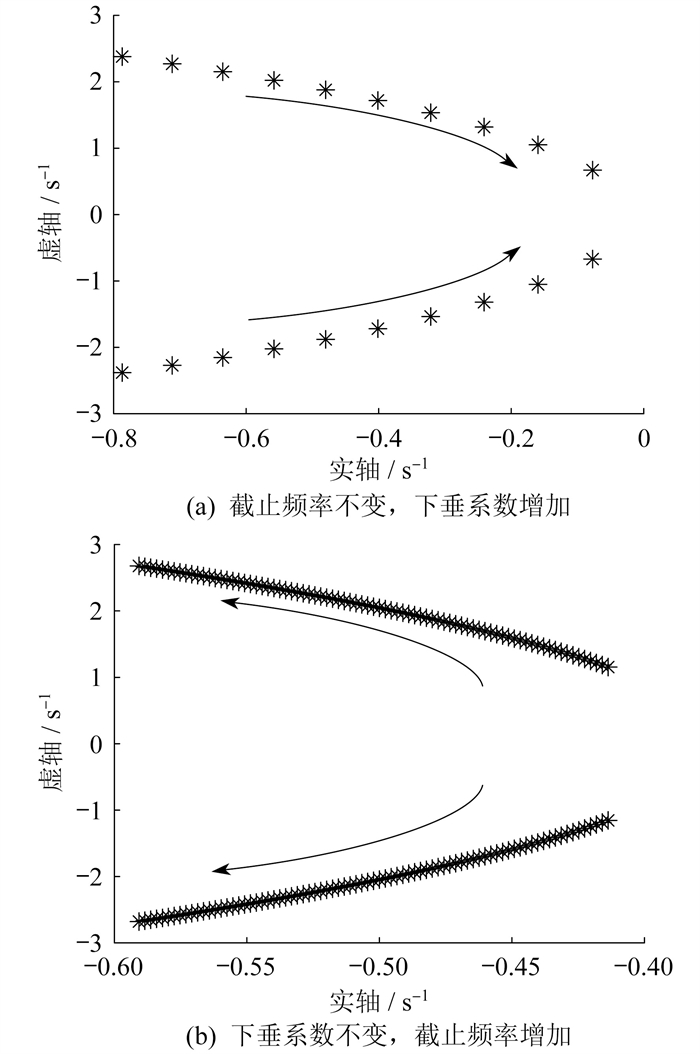
将表 1参数代入式(15)中,绘制不同参数变化的根轨迹,具体如图 6所示。
由图 6(a)可知,随着下垂系数的增大,全部根均位于左半平面,证明系统一直处于稳定状态。由图 6(b)可知,频率变化范围内的全部根仍全部位于左半平面,系统仍然保持稳定。
3 算例分析
3.1 仿真模型及方案分析
在MATLAB/Simulink平台搭建如图 1所示的多端口交直流配电网,验证本文所提策略的有效性。设置交流配电台区数量为2,仿真模型参数如 表 2所示。其中,SN,1和Rline,1分别为第1号配电台区的变压器额定容量和线路阻抗,SN,2和Rline,2分别为第2号配电台区的变压器额定容量和线路阻抗。
表 2
仿真模型参数
| 参数 | 数值 | 参数 | 数值 | |
| SN, 1/kVA | 250 | Rline,1/Ω | 0.10 | |
| SN, 2/kVA | 250 | Rline,2/Ω | 0.12 | |
| P0 | 0 | UH/V | 760 | |
| Udc_ref/V | 750 | UL/V | 740 |
采用以下3种方案对AC/DC变流器在不同工况下的性能进行对比。方案1:采用式(1)和式(2)所述的传统下垂控制策略,此时下垂增益为固定值。方案2:采用文献[10]所述的自适应控制策略,此时下垂增益根据变压器和负载情况变化。方案3:采用本文提出的基于虚拟压降的自适应下垂控制策略。
3.2 AC/DC变流器处于逆变状态的性能对比
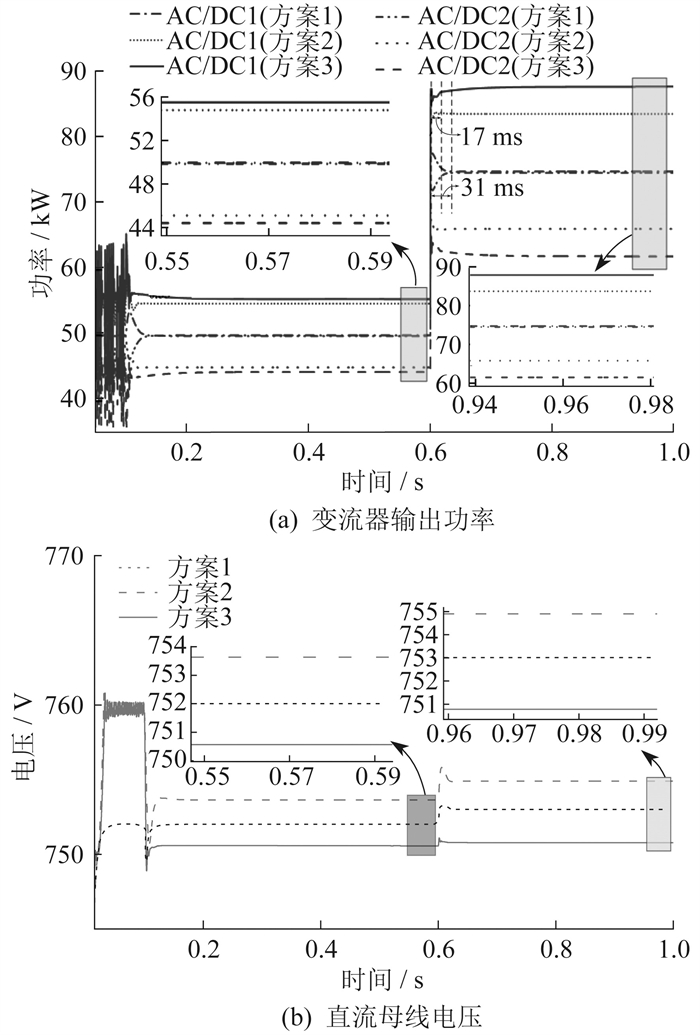
为了验证AC/DC变流器处于逆变状态时本文所提策略在负载突变时的有效性:在t=0 s时,设置第1号配电台区的变流负荷Sload,1=150 kW,第2号配电台区的交流负荷Sload,2=120 kW,EV总充电功率PEV=50 kW,PV总发电功率PPV=150 kW;在t= 0.6 s时,Sload,1增大为170 kW,PPV增大为200 kW,Sload,2和PEV保持不变。此时变流器均处于逆变状态。逆变状态时不同方案下的变流器输出功率与直流母线电压对比如图 7所示。
由图 7(a)可知:2台变流器若采用方案1中的固定下垂控制策略,会导致不同负载率的变压器接受相同的直流侧功率,不能实现功率的最大化利用;当采用方案2时,AC/DC变流器会根据变压器负载率分配直流侧功率,但是由于线路阻抗的存在,导致方案2的下垂控制策略不能实现有功功率的精确分配;当采用方案3时,本文所提策略可以对线路阻抗造成的分配偏差进行自适应调整,使最终的分配结果与理论值一致。在t=0.6 s发生负载突变时,传统下垂控制策略经过31 ms达到稳态,而本文所提策略经过17 ms即可重新达到稳态。由图 7(b)可知,方案1和方案2的下垂控制策略随着分配功率的增大产生较大的电压偏差,而本文所提策略可以减小直流母线的电压偏差,在t=0.6 s负载突变时,电压的波动范围最小,具有良好的电压恢复性能。
3.3 AC/DC变流器处于整流状态的性能对比
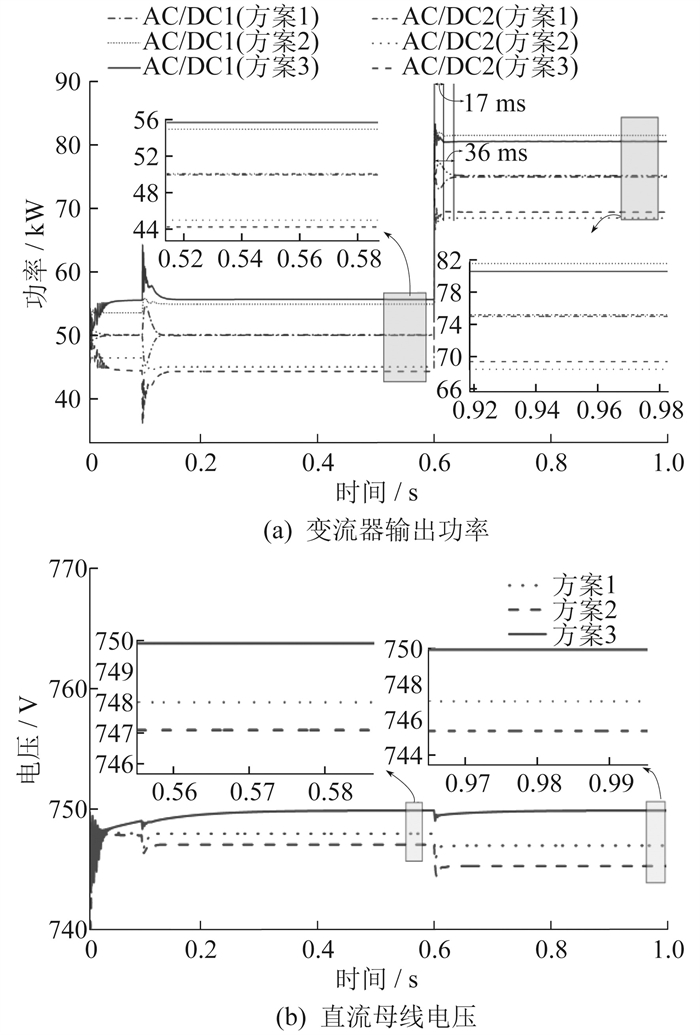
为了验证AC/DC变流器处于整流状态时,本文所提策略在负载突变时的有效性:在t=0 s时设置Sload,1=60 kW,Sload,2=100 kW,PEV=150 kW,PPV= 50 kW;在t=0.6 s时Sload,1增大为75 kW,PEV增大为200 kW,Sload,2和PPV保持不变。此时变流器均处于整流状态。整流状态时不同方案下的输出功率和母线电压如图 8所示。
由图 8(a)可知:两台变流器若采用方案1的下垂控制策略,会导致不同剩余容量的变压器承担相同的直流侧负荷,造成高负载的变压器过载;当采用方案2的下垂控制策略时,两台变流器可根据变压器的剩余容量分配EV的充电功率,但由于方案2没有考虑线路阻抗对功率分配的影响,因而无法精确分配有功功率。相比之下,本文所提策略使功率分配结果与理论值一致,可以对因线路阻抗造成的分配偏差进行自适应调整。在t=0.6 s发生负载突变时,本文所提策略在整流状态下更快达到稳态,具有更优异的动态响应性能。由图 8(b)可知,在t=0.6 s负载突变时,本文所提策略具有更好的直流电压恢复性能。
3.4 线路阻抗变化时不同方案性能对比
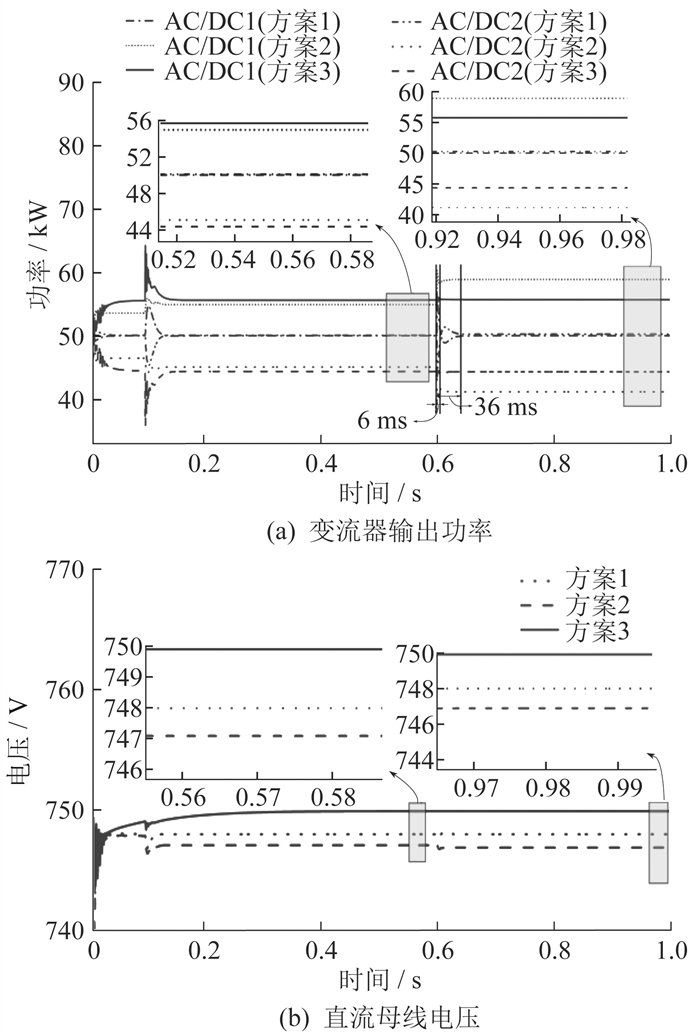
在实际交直流配电网运行过程中,由于线路老化和环境温度的变化,会使线路阻抗发生变化。为了验证本文所提策略在线路阻抗变化时的有效性:在t=0 s时设置Sload,1=60 kW,Sload,2=100 kW,PEV=150 kW,PPV=50 kW;在t=0.6 s时保持功率不变,线路阻抗Rline,2增大为0.15 Ω。此时,变流器均处于整流状态。线路阻抗变化时不同方案下的输出功率和母线电压如图 9所示。
由图 9(a)可知:当t=0.6 s线路阻抗发生变化时,方案1和方案2的下垂控制策略并没有考虑到线路阻抗的影响,导致功率分配结果的偏差增大;而方案3采用本文所提策略,在线路阻抗发生变化时,系统稳定后的分配结果与式(4)的计算结果基本一致,能够消除线路阻抗对功率分配的影响。在t=0.6 s线路阻抗发生变化后,方案1经过约36 ms才能达到稳态,而方案3只经过6 ms便重新达到稳态,具有更优异的动态响应性能。此外,由 图 9(b)可知,本文所提策略即使在线路阻抗突变的情况下也可以有效减少电压偏差,保持系统稳定运行。
4 结语
本文提出了一种基于虚拟压降的自适应下垂控制策略。该策略通过调节每个变流器的局部下垂增益,使得AC/DC变流器的输出功率能够根据对应变压器负载情况进行自适应分配,并通过基于虚拟压降的阻抗补偿策略和电压补偿策略,消除了线路阻抗的影响,减少了直流母线电压偏差,有效提高了系统运行的稳定性。
参考文献
-
[1]LI B, CHEN M Y, KAMMEN D M, et al. Electric vehicle's impacts on China's electricity load profiles based on driving patterns and demographics[J]. Energy Reports, 2022(8): 26-35.
-
[2]CLEMENT-NYNS K, HAESEN E, DRIESEN J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J]. IEEE Transactions on Power Systems, 2010, 25(1): 371-380. DOI:10.1109/TPWRS.2009.2036481
-
[3]CHAUDHARY S K, GUERRERO J M, TEODORESCU R. Enhancing the capacity of the AC distribution system using DC interlinks—a step toward future DC grid[J]. IEEE Transactions on Smart Grid, 2015, 6(4): 1722-1729. DOI:10.1109/TSG.2015.2404313
-
[4]ZHANG L, CHEN Y, SHEN C, et al. Releasing more capacity for EV integration by DC medium voltage distribution lines[J]. IET Power Electronics, 2017, 10(15): 2116-2123. DOI:10.1049/iet-pel.2017.0172
-
[5]张明珂, 邱晓燕, 孙旭, 等. 多端柔性交直流配电网接纳电动汽车能力评估方法[J]. 电气传动, 2022, 52(18): 53-59.
-
[6]张学, 裴玮, 邓卫, 等. 交直流混合配电网的运行模式和协调控制方法[J]. 供用电, 2016, 33(8): 27-31.
-
[7]吴在军, 谢兴峰, 杨景刚, 等. 直流配电网电压控制技术综述[J]. 电力工程技术, 2021, 40(2): 59-67.
-
[8]刘佳易, 秦文萍, 韩肖清, 等. 交直流双向功率变换器的改进下垂控制策略[J]. 电网技术, 2014, 38(2): 304-310.
-
[9]张学, 裴玮, 范士雄, 等. 含多端柔性互联装置的交直流混合配电网协调控制方法[J]. 电力系统自动化, 2018, 42(7): 185-191.
-
[10]PEI W, DENG W, ZHANG X, et al. Potential of using multiterminal LVDC to improve plug-in electric vehicle integration in an existing distribution network[J]. IEEE Transactions on Industrial Electronics, 2015, 65(2): 3101-3111.
-
[11]LI B, LI Q, WANG Y, et al. A novel method to determine droop coefficients of DC voltage control for VSC-MTDC system[J]. IEEE Transactions on Power Delivery, 2020, 35(5): 2196-2211.
-
[12]RAZA A, HUANG Q, LI J, et al. Adaptive drooping control scheme for VSC-MTDC system with multiple renewable energy sites based on variable droop constant[J]. International Journal of Electrical Power and Energy Systems, 2023, 144: 1-15.
-
[13]PENG Z S, WANG J, BI D Q, et al. Droop control strategy incorporating coupling compensation and virtual impedance for microgrid application[J]. IEEE Transactions on Energy Conversion, 2019, 34(1): 277-291.
-
[14]LIU S, MIAO H, LI J, et al. Voltage control and power sharing in DC microgrids based on voltage-shifting and droop slope-adjusting strategy[J]. Electric Power Systems Research, 2023, 214: 108814.
-
[15]米根锁, 谌杰, 高磊, 等. VSC-MTDC系统下垂控制优化策略[J]. 电力系统及其自动化学报, 2020, 32(1): 101-107.
-
[16]李圣清, 颜石, 郑剑, 等. 基于改进下垂法的光伏微网有功均分控制策略[J]. 电力电子技术, 2022, 56(5): 88-92.
-
[17]尚淑婷. 微电网逆变器PV/QF下垂控制技术的研究[D]. 秦皇岛: 燕山大学, 2014.