|
|
|
发布时间: 2019-02-10 |
|
|
|
|
收稿日期: 2018-04-13
基金项目: 国家自然科学基金(51266013);航空科学基金(2013ZB56002, 2013ZB56004)
中图法分类号: V211.3
文献标识码: A
文章编号: 1006-4729(2019)01-0016-05
|
摘要
为了分析入流速度攻角的连续变化对螺旋桨非定常特性的影响, 应用滑移网格技术对螺旋桨运动进行了数值分析。结果表明:螺旋桨的时均拉力会随攻角的增大而增加; 对于各单独叶片而言, 向下运动时, 随着攻角的增大, 拉力会逐渐增加, 向上运动时, 拉力则会减小; 在特定方位角时, 随着攻角的增大, 桨叶前端的轴向速度会略微增大, 桨叶后端的轴向速度在小攻角时也会发生略微的变化, 但在攻角较大时变化较明显; 随着攻角的增大, 桨叶所受到的周期性非定常载荷的波动会逐渐加剧。
关键词
攻角; 螺旋桨; 滑移网格技术; 非定常数值分析
Abstract
In order to analyze propeller unsteady characteristics induced by attack angle, sliding mesh method is utilized to simulate propeller moving.The results show that time-averaged thrust of propeller grows with the increase of attack angle.For isolated blades, when blade moves down, thrust is increased gradually with the increase of attack angle, and when blade moves up, it is reduced gradually.At a special angle, axial velocity of the front of propeller increases slightly, and axial velocity of the propeller back also increases slightly when attack angle is small, but it changes obviously when attack angle is large.The periodic unsteady load of blade is exacerbated at attack angle.
Key words
attack angle; propeller; sliding mesh; unsteady numerical analysis
近年来, 通用航空产业快速发展, 而飞机的发展始终伴随着螺旋桨的深入应用, 因此研究螺旋桨的气动特性具有重要意义。从螺旋桨分析方法的发展历程来看, 螺旋桨的气动特性分析方法主要有动量理论、叶素理论、涡流理论、实验技术及数值模拟方法等。数值模拟方法的发展又可以分为以工程应用为主的激励盘理论和以理论研究为主的非定常方法。激励盘理论是采用无厚度的圆盘来代替螺旋桨。文献[1-3]对该方法做了较深入的研究应用, 但无法真实模拟出桨叶上的流场变化和非定常问题, 如单片桨叶气动力的周期性变化。非定常方法则能够解决这一问题, ROOSEENBOOM E W M等人[4]和STRUERMER A W[5]分别应用该方法分析了滑流对机翼的干扰作用和螺旋桨气动力的非定常变化; 高飞飞[6]分析了螺旋桨转速的变化对其非定常特性的影响规律; 梁伟等人[7]研究了自由入流速度的变化对螺旋桨非定常特性的影响规律。本文基于螺旋桨所受气流攻角的连续变化, 详细分析了螺旋桨的非定常变化规律, 以期为螺旋桨飞机的设计提供参考。
1 计算模型和网格生成
1.1 计算模型
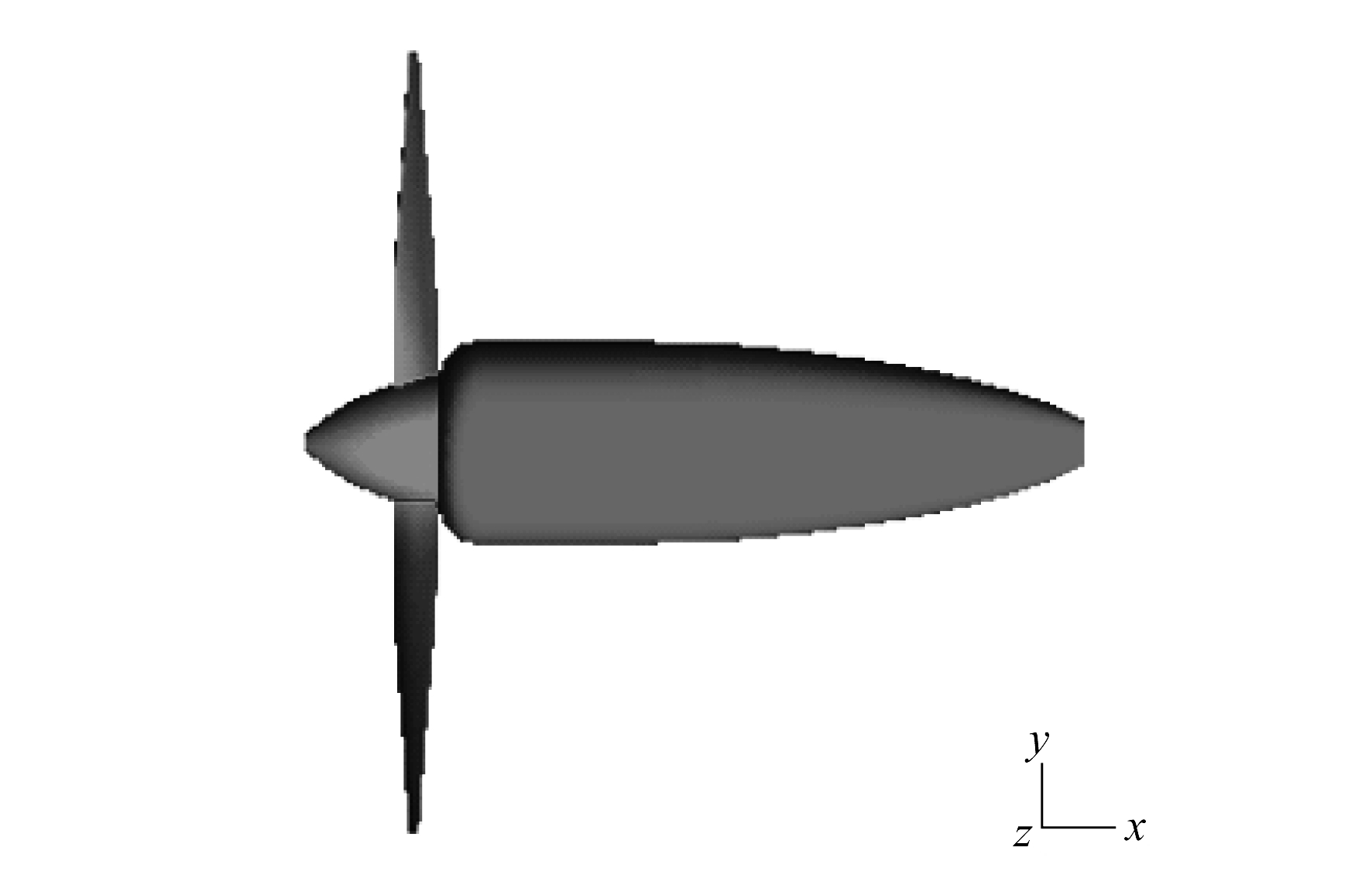
本文所用的计算模型是一个“螺旋桨+短舱”构型, 桨平面直径D=0.5 m, 如图 1所示。
1.2 网格划分
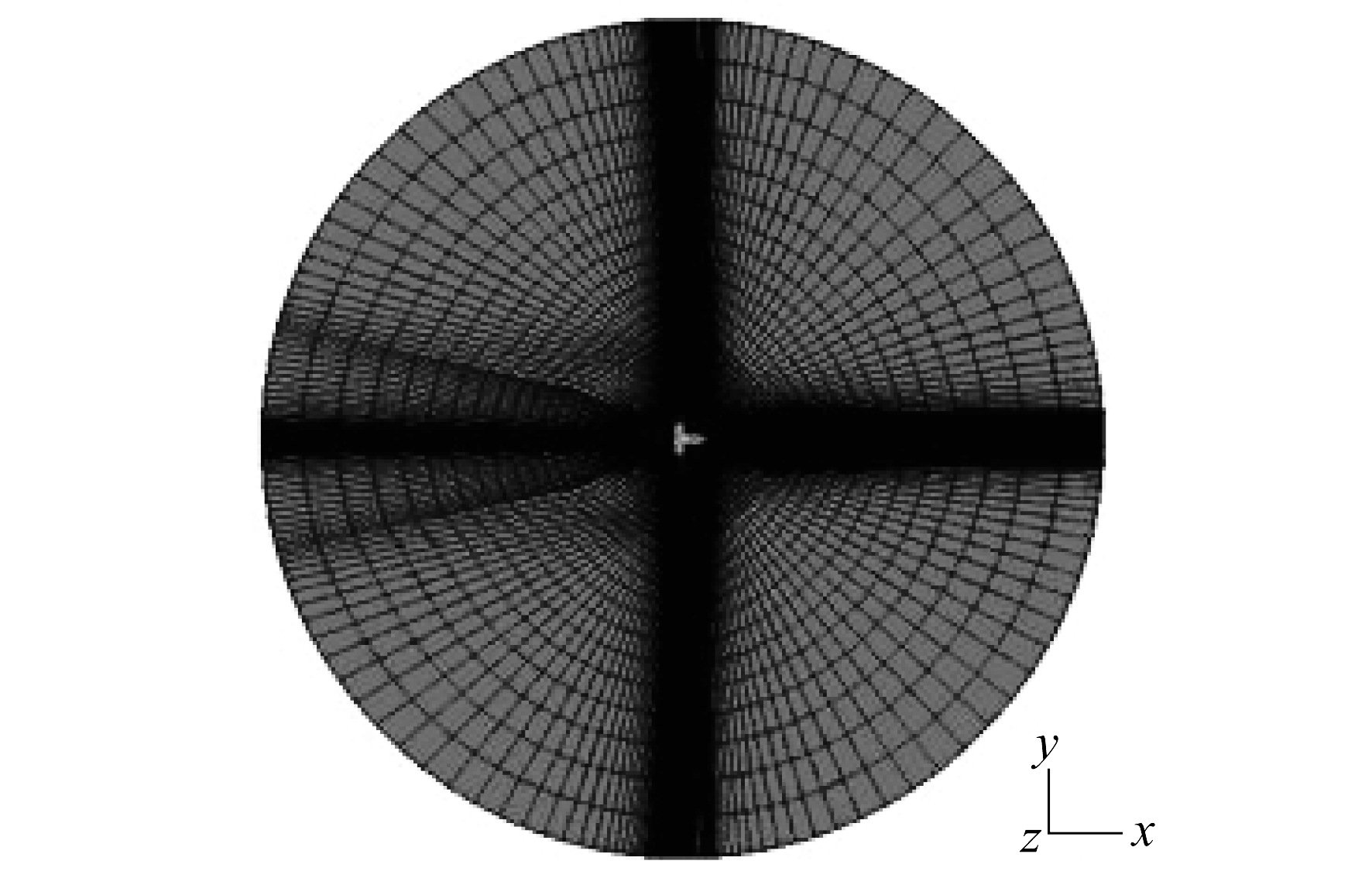
图 2为短舱对称平面上的网格分布。
将整个计算域划分为静止域和旋转域, 两个区域之间的数据交换采用滑移网格技术来实现。对计算域进行结构化网格划分时, 为保持两片桨叶周围网格的一致性, 应先对其中一片桨叶区域进行划分, 然后通过旋转得到整个旋转域内的网格。
2 数值模拟方法
通过求解非定常三维可压缩的雷诺平均纳维-斯托克斯方程组来获取计算的数值解, 引入Spalart-Allmaras湍流模型[8]以封闭方程组。远场边界为压力远场, 计算构型边界为壁面; 空间离散是基于有限体积法, 时间离散是基于时间推进法, 离散格式均为二阶; 求解方法为基于压力耦合方程组的半隐式方法。
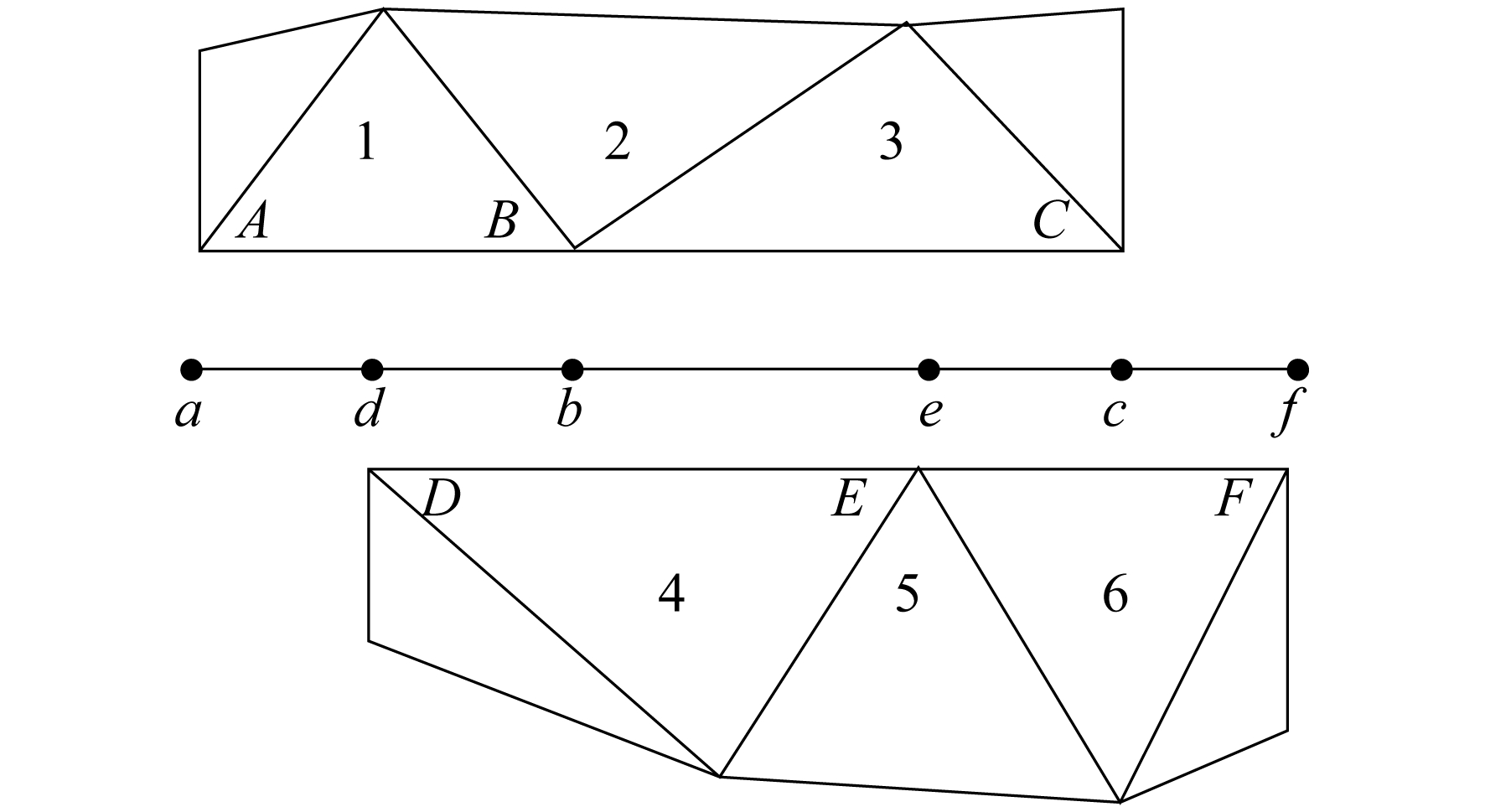
螺旋桨运动非定常模拟的关键点是滑移网格技术的应用。滑移网格技术是在旋转参考坐标系和混合平面法的基础上发展而来的[9]。滑移网格模型允许相邻网格之间相对滑动, 因此网格面不需要在分界面上排列, 滑移网格技术的关键是计算流进每个网格分界面的两个非一致的分界面区域。二维网格分界面如图 3所示[9]。分界面区域由A-B面、B-C面、D-E面、E-F面组成, 交叉处产生a-d面、d-b面、b-e面等。在两个单元区域重叠处产生d-b面、b-e面、e-c面而组成内部区域, 剩余的a-d面和c-f面成对形成周期性区域。例如, 计算分界面流入4单元的流量时, 用d-b面和b-e面代替D-E面, 并从1单元和3单元各自传递信息到4单元。
在进行信息传递时应满足守恒型积分方程
| $\frac{\mathrm{d}}{\mathrm{d} t} \int_{V} \rho \phi \mathrm{d} V+\int_{\partial V} \rho \phi\left(\boldsymbol{u}-\boldsymbol{u}_{\mathrm{g}}\right) \cdot \mathrm{d} \boldsymbol{S}=$ $\quad \int_{\partial V} \Gamma \nabla \phi \mathrm{d} \boldsymbol{S}+\int_{V} S_{\phi} \mathrm{d} V$ |
式中:t——时间;
V——任意控制体;
ρ——空气密度;
φ——通用标量;
u——速度矢量;
ug——网格运动速度;
S——控制体的面积;
Γ——扩散系数;
Sφ——φ的源项。
3 计算结果与分析
3.1 计算验证
3.2 螺旋桨及各单独叶片的拉力随攻角的变化
桨的时均拉力随攻角的变化曲线如图 6所示。
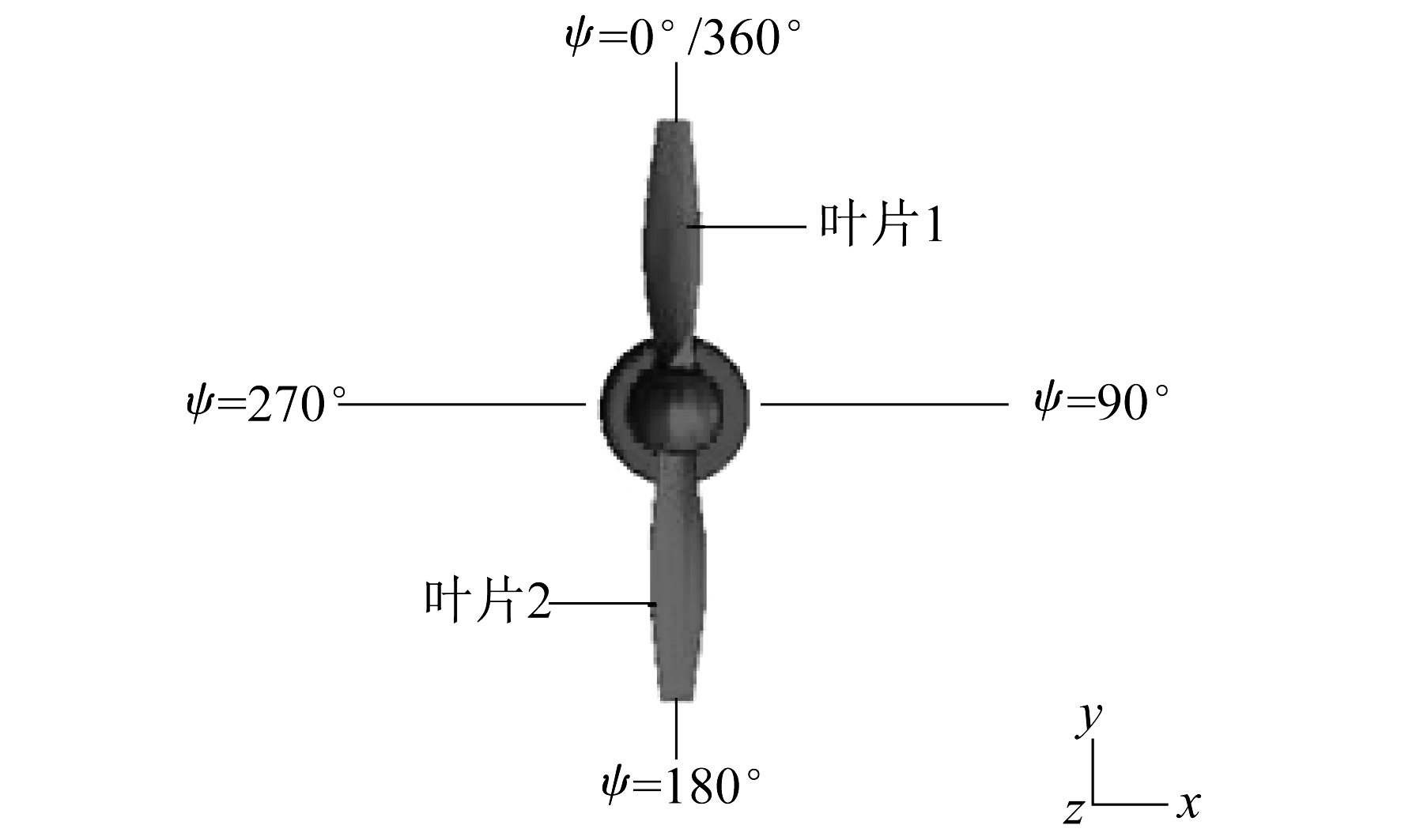
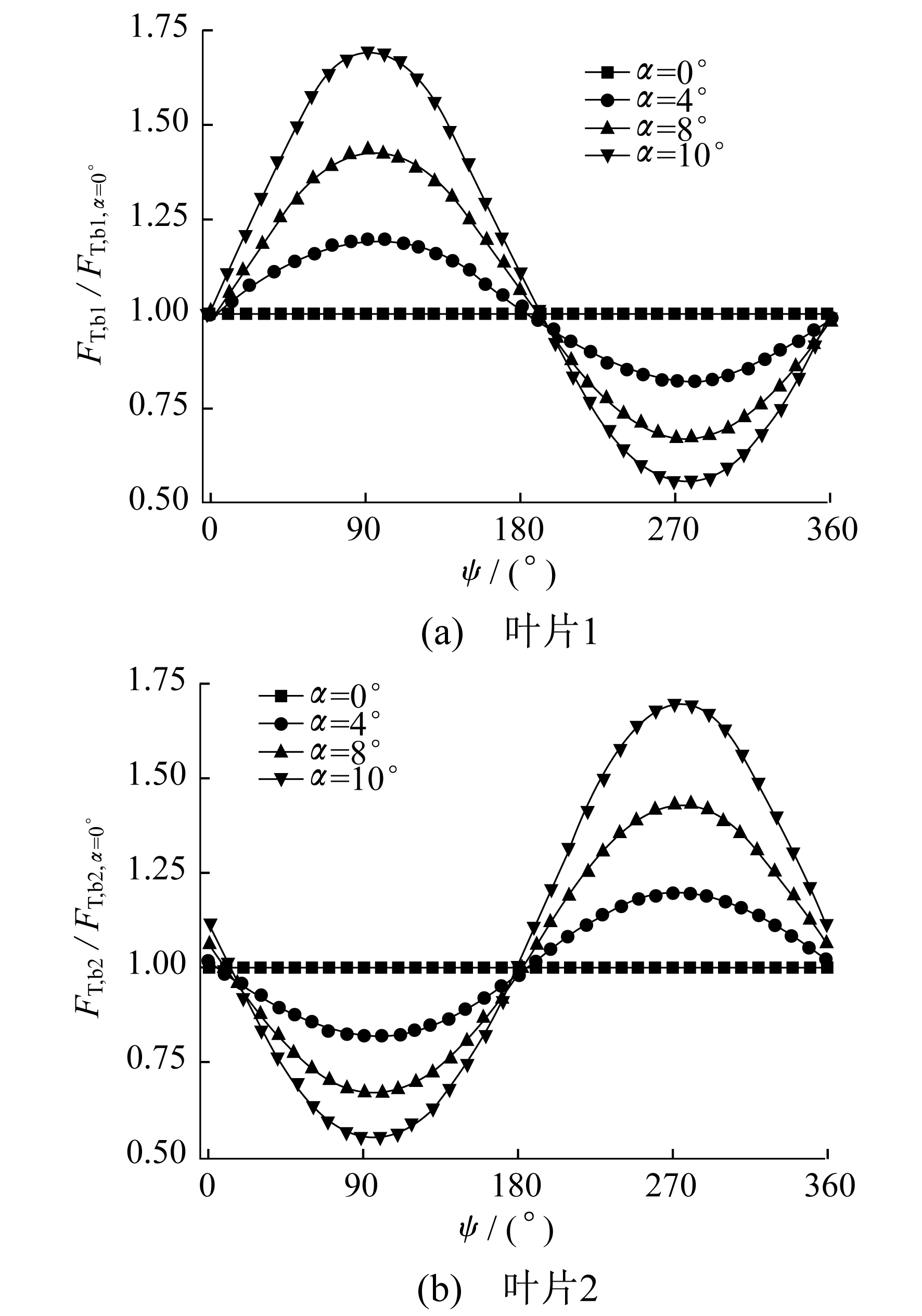
由图 6可以看出, 当自由流速和转速不变时, 流向桨叶的攻角的逐渐增加会使得桨的时均拉力FT, ave随之增大。例如, 攻角为12°与攻角为0°时相比, 拉力增加了1.37 N, 占攻角为0°时拉力的9.28%。另外, 由于两叶片相距180°, 可忽略叶片之间的相互干扰, 因此叶片1的拉力FT, b1和叶片2的拉力FT, b2的曲线完全重合, 且其总和正好等于整个螺旋桨的拉力FT。
与攻角为12°时的拉力增量相比, 不同攻角时拉力的相对增量及其占12°时增量的百分比如表 2所示。
由表 2可知, 随着攻角的增大, 拉力的相对增量占12°时增量的比重也在增大, 也就是说, 攻角的增加会使得拉力增量的增幅变大。
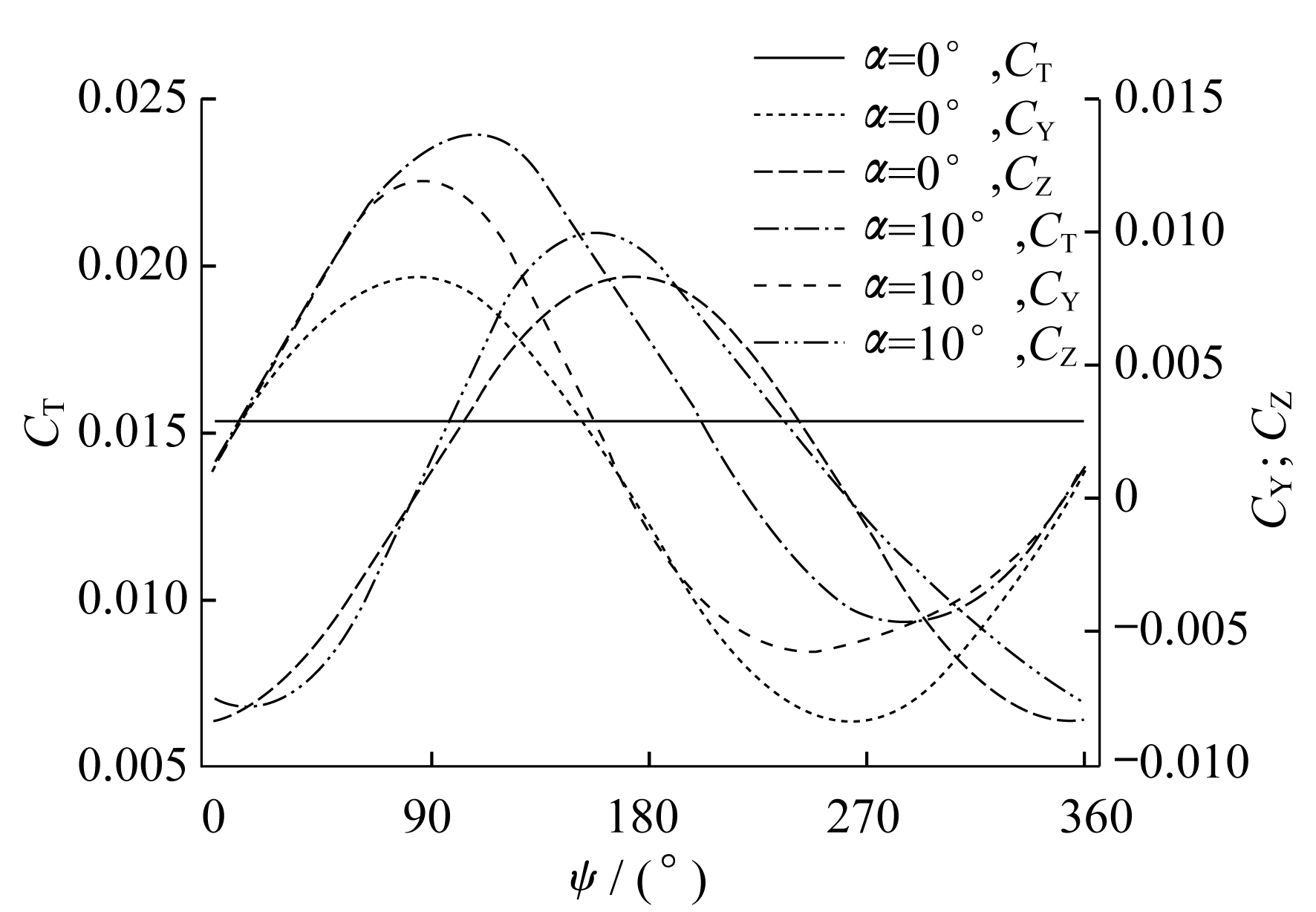
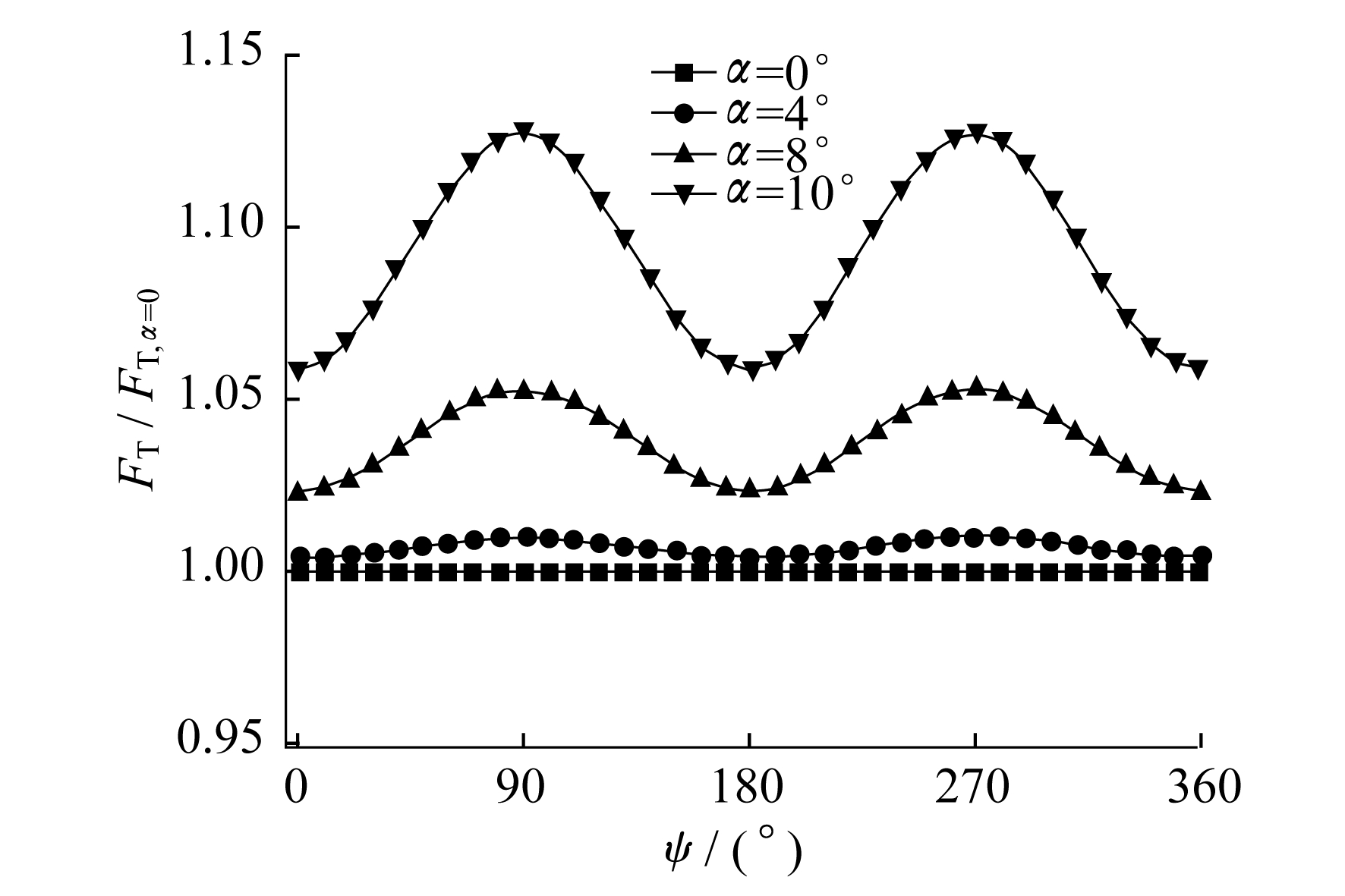
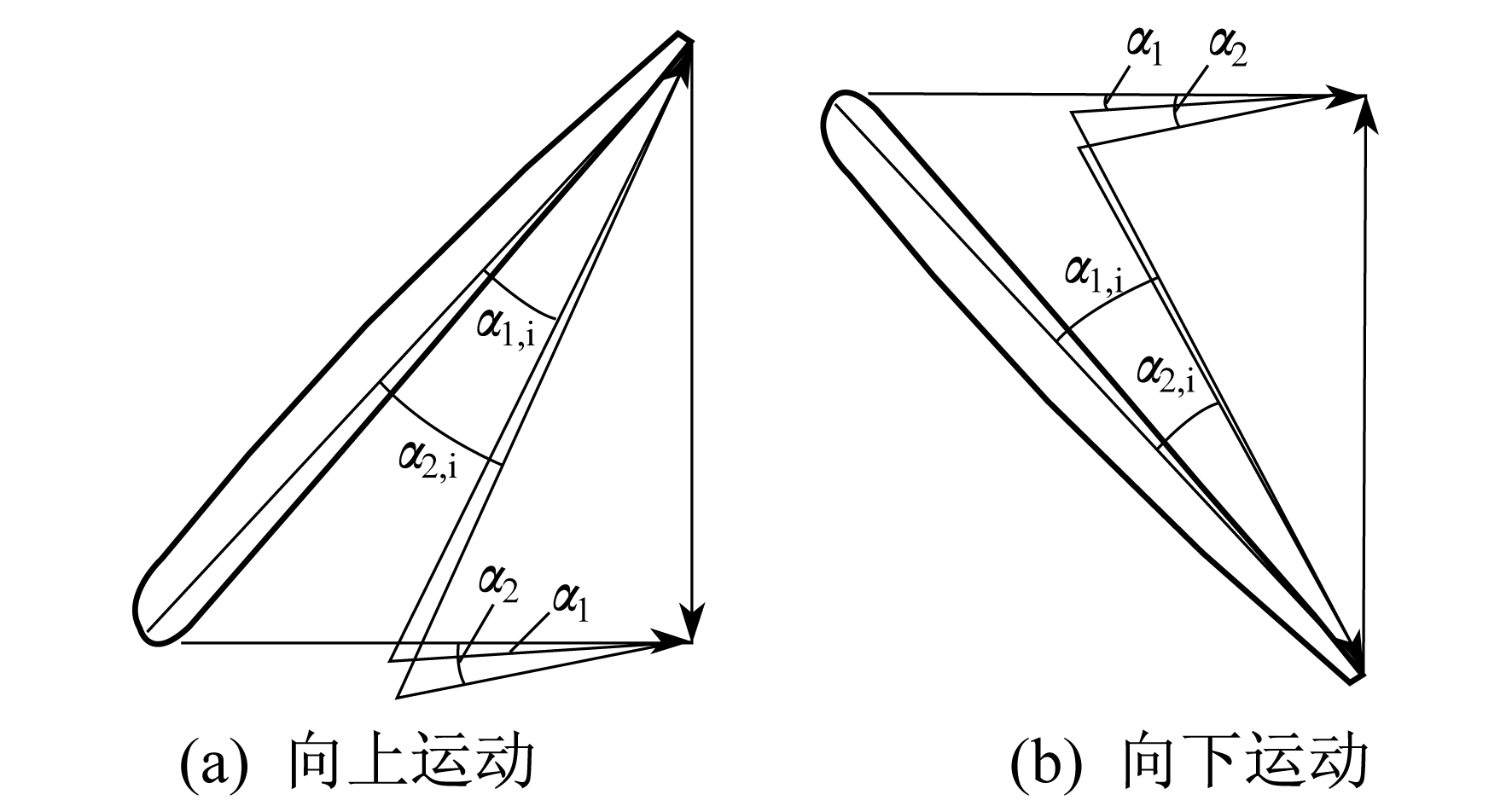
不同攻角时, 叶片和螺旋桨的拉力分别如图 7和图 8所示。叶素当地攻角随自由入流攻角的变化如图 9所示。α1和α2为自由入流攻角, α1, i和α2, i为叶素当地攻角。由图 7和图 8可知, 当攻角α=0°时, 在方位角0°~360°内, FT, b1, FT, b2, FT几乎不发生变化, 呈一条平直线。这是因为当来流作用于每片桨叶时, 对于叶片的叶素而言, 绕过桨叶的流动具有轴对称性, 入流的速度方向和大小始终是相同的, 因此不会引起气动力的变化。而当攻角非零时, 入流的变化会使拉力呈现正弦曲线变化。
表 2
不同攻角时拉力的相对增量及其占比
| 攻角/($^{\circ}$) | 拉力相对增量/N | 拉力相对增量百分比/% |
| $0 \rightarrow 2$ | 0.0169 | 1.23 |
| $2 \rightarrow 4$ | 0.0888 | 6.48 |
| $4 \rightarrow 6$ | 0.1724 | 12.58 |
| $6 \rightarrow $8 | 0.2862 | 20.88 |
| $8 \rightarrow 10$ | 0.3610 | 26.35 |
| $10 \rightarrow 12$ | 0.4451 | 32.48 |
图 7中, 随着攻角的增大, 桨叶在向下运动时, 拉力会逐渐增大; 向上运动时, 拉力会逐渐减小。这是因为向下运动时, 攻角逐渐增大, 使得叶片叶素的当地入流攻角增大了, 如图 9(a)所示。α2 > α1使得α2, i > α1, i; 向上运动时, 叶片叶素的当地入流攻角则减小了, 如图 9(b)所示, α2 > α1使得α2, i < α1, i。
值得注意的是, 利用叶素理论对桨叶向上运动时的叶片叶素进行分析时, 在当前计算条件下, 攻角为12.5°是当地入流攻角变化的分界点。当攻角从0°→12.5°变化时, 其当地入流攻角是逐渐减小的, 当攻角大于12.5°时, 当地入流攻角则会逐渐增大, 因此这也是在研究中攻角选择为0°~12°的原因。
3.3 螺旋桨轴向速度场随攻角的变化
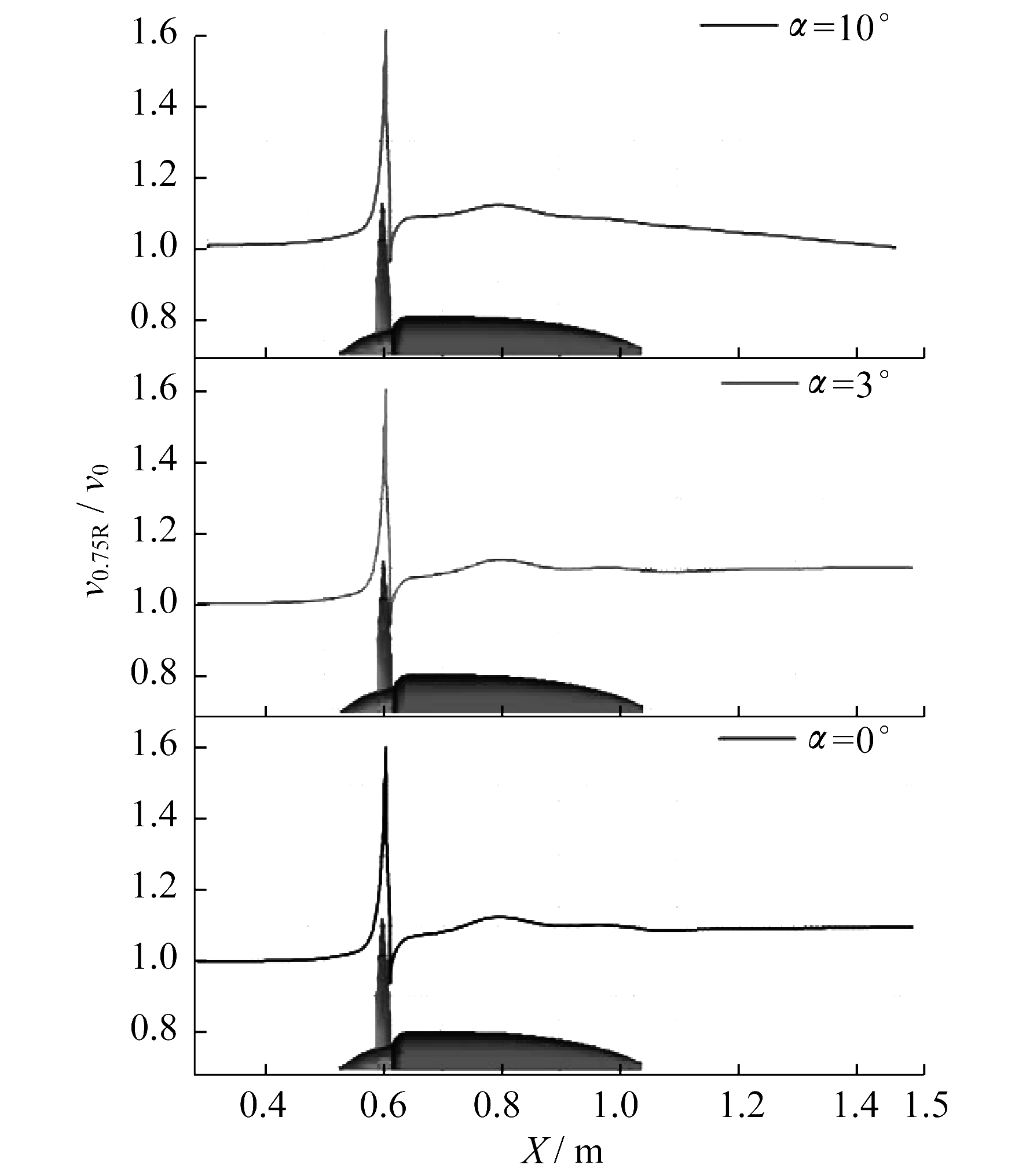
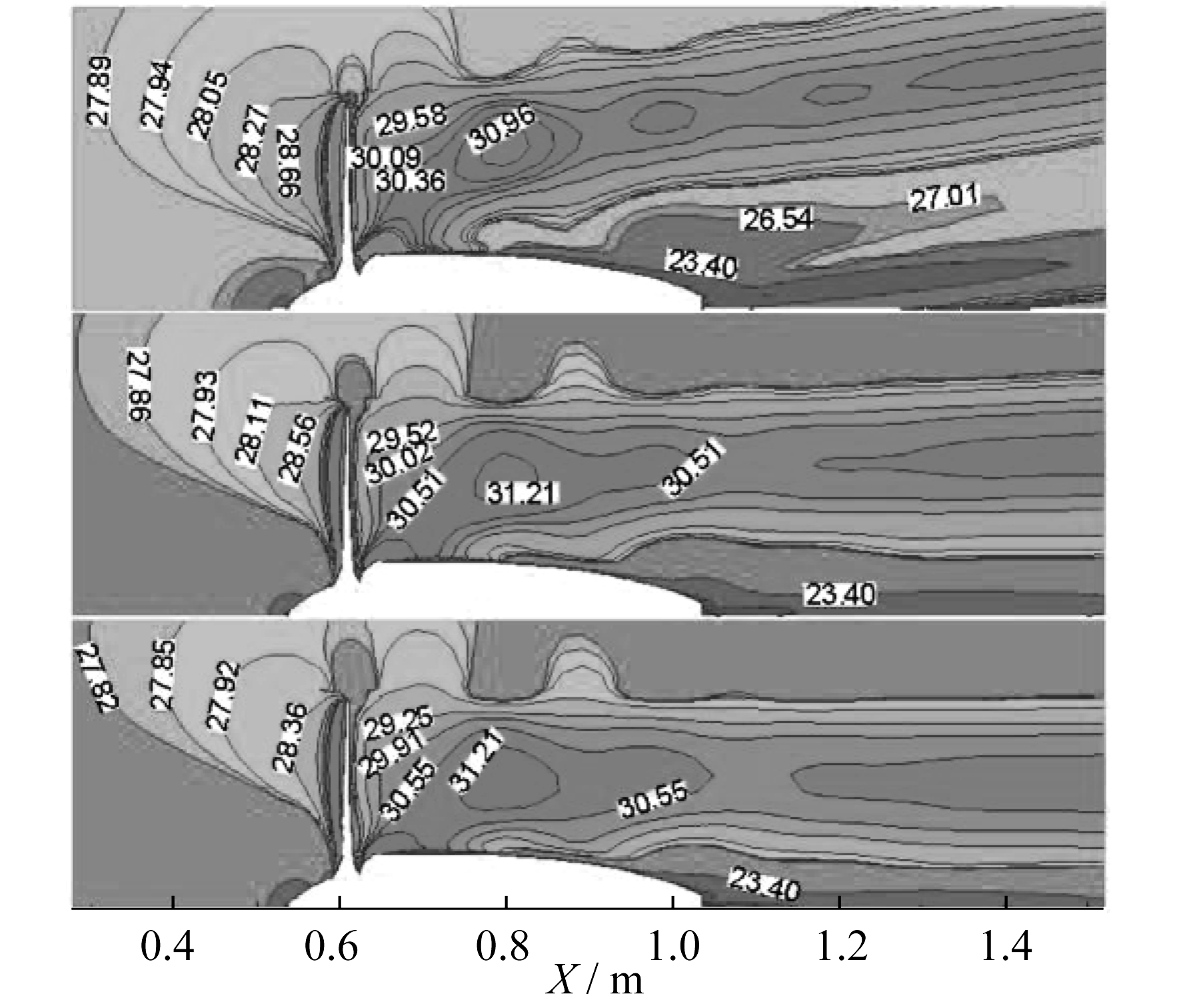
为了分析螺旋桨的轴向速度场随攻角的变化, 此处选取时刻t=0.063 s, 桨叶0.75R处前后一段距离(X为0.3~1.5 m)内的轴向速度, 结果如图 10所示。由图 10可以看出, 随着攻角的增大, 桨叶前端轴向速度会略微增大, 增量最大值不超过自由入流速度的1.5%;而在攻角较小时(如攻角为3°), 桨叶后端轴向速度的变化量仍然是微量的, 增量最大值不超过自由入流速度的2%。但在攻角较大时(如攻角为10°), 从短舱后端开始, 轴向速度会逐渐减小而趋于自由入流速度, 变化量可以达到自由入流速度的10.4%。在其他时刻下, 攻角的变化对螺旋桨轴向速度场存在类似的规律。图 11为该时刻不同攻角时螺旋桨前后流场的速度分布。
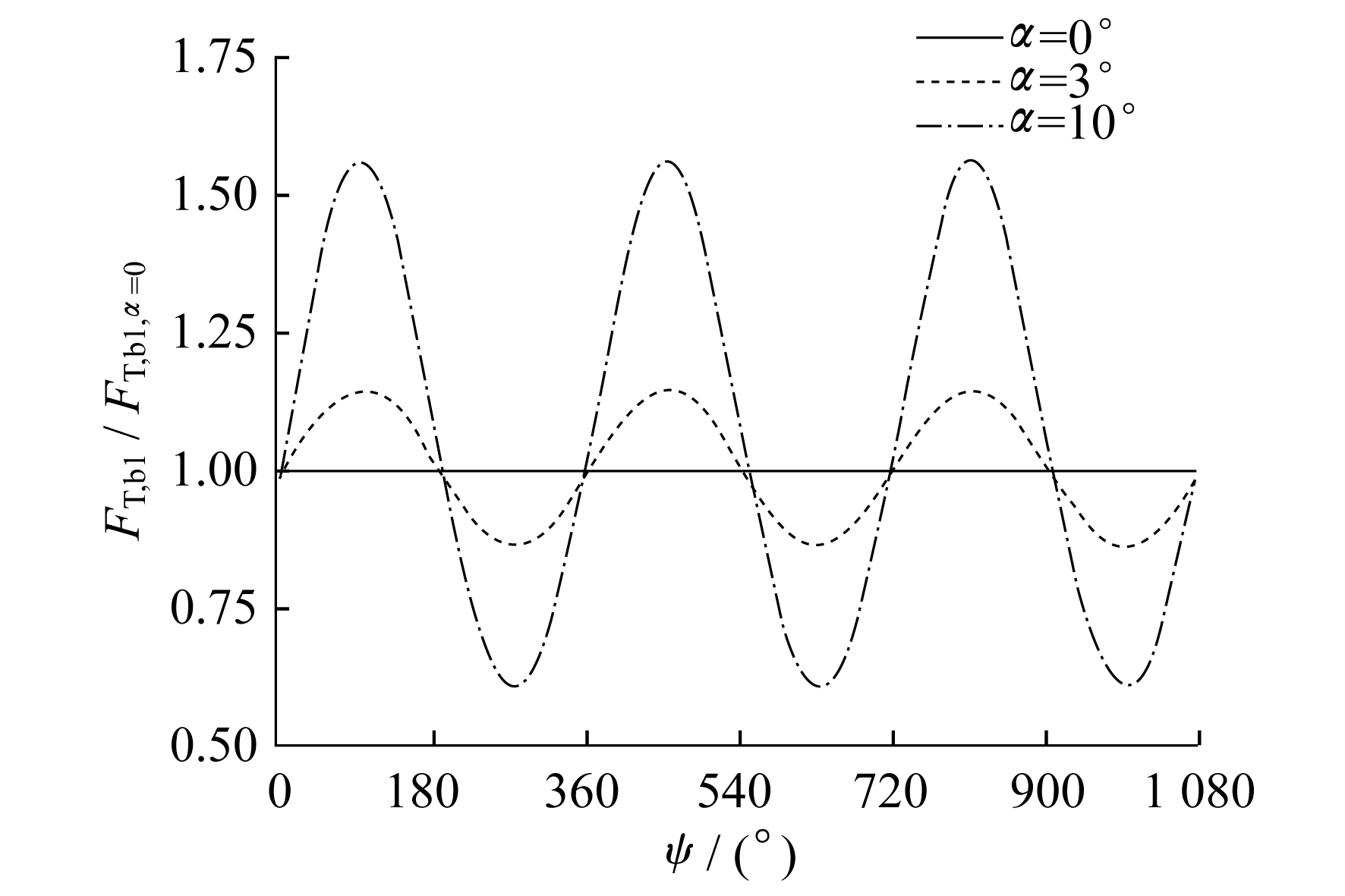
3.4 桨叶载荷随攻角的变化
在运动过程中, 螺旋桨各叶片始终承受着周期性的变化载荷, 载荷会随着攻角的变化而发生变化, 如图 12所示。当攻角较小时(如攻角为3°), 周期性载荷的波动会显得平缓, 而当攻角较大时(如攻角为10°), 载荷的波动则显得比较剧烈。因此, 对于螺旋桨飞机而言, 在较小的攻角下飞行可以延长螺旋桨的疲劳破坏寿命。
4 结论
本文对螺旋桨的非定常特性进行了分析, 获得如下结论。
(1) 随着入流速度攻角的增加, 螺旋桨及各叶片的时均拉力也会增加, 而且增加的幅度逐渐加大。
(2) 当攻角为0°时, 各叶片和螺旋桨在0°~360°方位角内的拉力均呈现平直线; 攻角大于0°时, 叶片的拉力在0°~360°方位角内呈现的是正弦曲线变化, 整个螺旋桨的拉力曲线呈驼峰状。对于各单独叶片而言, 向下运动时, 随着攻角的增大, 拉力会逐渐增加; 向上运动时, 拉力则会减小。
(3) 在特定方位角时, 随着攻角的增大, 桨叶前端的轴向速度会略微增加, 桨叶后端的轴向速度在小攻角时也会发生略微的变化, 但在攻角较大时变化较明显。
(4) 随着攻角的增大, 桨叶所受到的周期性非定常载荷的波动会逐渐加剧。
参考文献
-
[1]基于激励盘理论的螺旋桨滑流数值模拟研究[J]. 空气动力学报, 2012, 30(2): 219-222.
-
[2]基于等效盘模型的滑流对涡桨飞机气动性能的影响[J]. 航空学报, 2008, 29(4): 845-852. DOI:10.3321/j.issn:1000-6893.2008.04.013
-
[3]HEISE R, MEYER C J, BACKSTROM T W. CFD simulation of helicopter flow fields using an actuator disk main rotor model[J]. R & D Journal, 2007, 23(3): 26-32.
-
[4]ROOSENBOOM E W M, STUERMER A W, SCHRODER A. Advanced experimental and numerical validation and analysis of propeller slipstream flows[J]. Journal of Aircraft, 2010, 47(1): 284-291. DOI:10.2514/1.45961
-
[5]STUERMER A W. Unsteady CFD simulation of propeller installation effects[R]. AIAA 2006-4969, 2006.
-
[6]基于CFD技术的螺旋桨非定常流场数值模拟[J]. 科学技术与工程, 2011, 11(30): 7564-7569. DOI:10.3969/j.issn.1671-1815.2011.30.054
-
[7]基于滑动网格的螺旋桨复杂绕流数值模拟研究[J]. 航空计算技术, 2011, 45(3): 45-49. DOI:10.3969/j.issn.1671-654X.2011.03.012
-
[8]SPALART P, ALLMARAS S. A one-equation turbulence model for aerodynamic flows[R]. AIAA-92-0439, 1992.
-
[9]江帆, 黄鹏. Fluent高级应用与实例分析[M].北京: 清华大学出版社, 2008: 206-207.
-
[10]螺旋桨滑流对水平尾翼气动特性的影响[J]. 应用数学和力学, 2016, 37(5): 492-499. DOI:10.3879/j.issn.1000-0887.2016.05.005