|
|
|
发布时间: 2019-02-10 |
|
|
|
|
收稿日期: 2018-09-12
基金项目: 上海市地方能力建设项目(14110500900)
中图法分类号: TM743
文献标识码: A
文章编号: 1006-4729(2019)01-0043-10
|
摘要
当分布式电网结构复杂时, 如果在所有节点安装谐波检测装置, 会使得测量准确性和经济性降低。首先综合考虑谐波监测系统中相量量测单元的可观性、系统测量冗余度、通信通道要求、设备退出等多种情况, 实现谐波状态估计监测点的优化。然后, 利用误差分析检出优化监测点所采集数据中可能存在的不良数据, 并利用概率密度曲线判断状态估计结果是否满足精度要求, 以评估谐波监测点优化方案的可行性与精确度。最后, 通过仿真与算例进行了理论验证。
关键词
分布式电网; 谐波监测; 相量量测单元; 状态估计
Abstract
When the distributed grid structure is complex, if the harmonic detection device is installed in all nodes, the accuracy and economy will be reduced.The observable of PMU system, the redundancy of system measurement, communication channel requirement and equipment exit conditions are considered synthetically, and the optimization of the monitoring point of harmonic state estimation is realized.Then, the unqualified collected data of the monitoring points are checked.Next, the probability density curve is used to determine whether a state estimation results meet the accuracy requirement, and based on the results, to assess the feasibility and accuracy of the optimization scheme of harmonic monitoring.Finally, through the simulation and numerical examples, theoretical advancement is verified.
Key words
distributed grid; harmonic monitor; phasor measurement unit; state estimation
虽然在分布式电网的每条母线和支线安装谐波监测装置能够有效地测量出网络的谐波分布或谐波状态, 但目前应用在谐波监测系统中的相量量测单元(Phasor Measurement Unit, PMU)装置造价较高, 当分布式电网结构复杂时, 如果在所有节点安装PMU装置, 成本较高, 经济性变差。此外, 现有的通信线路受到限制, 对每个节点的数据进行同步传送和处理难度较大。因此, 电力系统谐波的完全测量是不经济也是不现实的。
针对工程的实际需求, 国内外学者提出了各种谐波状态估计法。文献[1]针对大型区域电网有相对独立调度的特点, 提出了基于PMU应用并行式算法的动态状态估计方法。该方法利用Kalman滤波算法结合塔接式并行算法, 应用PMU测量数据进行系统状态估计, 对大型电力系统网络有较好的适应性和效果。文献[2]采用二进制编码方式的遗传算法求解PMU投资经济性和估计误差加权的数学模型, 得到不同位置不同PMU数量情况下谐波状态估计误差, 进而选择最优解。但该方法计算速度慢, 需要的迭代次数多, 可能出现不收敛的现象。文献[3]提出了一种基于数字规划的算法, 通过计算状态增广关联矩阵并使用最小二乘算法, 实现了PMU数量最少情况下整个系统仍保持可观测。文献[4]将对半搜索和模拟退火法算法相结合来求解PMU配置模型, 进而获得了PMU最少的配置方案。由此可知, 电力系统PMU配置方法较多, 不同的方法具有不同的优缺点。
随着电网规模的进一步扩大、数据收集的延迟性增强、边界点量测不足、元件的参数不精确、边界条件等值化简等使得谐波状态估计精度和实时性受到很大的影响, 所以在进行谐波监测点优化的同时要关注优化布点后对估计结果精度的影响。为此, 本文将在谐波监测点优化的基础上, 使用重复检测法检出优化监测点所采集数据中残差较大、突变明显的数据, 并利用概率密度曲线判断状态估计结果是否满足精度要求, 从而评估谐波监测点优化方案的可行性与精确度。最后, 通过仿真软件进行验证。
1 分布式电网谐波监测点优化配置数学模型的建立
在实际应用中, PMU优化策略的研究主要分为两部分:一是注重在使系统全局可观测(进行谐波状态估计必不可少的条件)的情况下尽可能减少PMU的分布; 二是在谐波状态估计之外满足一些特定的监测任务, 所需的模型条件也不尽相同[5]。
本文在建立谐波监测点优化配置模型时, 希望得到的监测点分布模型能够满足系统的可观性要求, 即由优化模型下的监测数据得到系统谐波状态估计的同时, 尽可能提高系统的冗余度, 以保证估计结果的精确度, 减小误差。
在分布式电网线路上, 将线路中与每个节点相关联的支路数目定义为节点出线度d, 节点i的出线度为di。
当前监测点数目下, 节点被重复量测数(直接量测与间接量测都计入)与总状态量比值定义为状态估计的节点冗余度r, 节点i的冗余度记为ri。在计算节点冗余度时, 规定系统公共耦合点的节点一定要安装监测装置, 故计算公式为
| $ r_{i}=\frac{d_{i}+1}{n} x_{i} $ | (1) |
式中:n——系统结构中总的节点数目, 即测量方程总的状态量;
xi——标志节点是否作为监测点。
| $ x_{i}=\left\{\begin{array}{ll} 0 & \text { 节点 } i \text { 未安装有 PMU } \\ 1 & \text { 节点 } i \text { 安装有 PMU } \end{array}\right. $ | (2) |
在当前测量配置下, 将系统所有节点的重复测量数量相加, 即节点冗余度加和, 称为系统冗余度R
| $ R=\sum_{i=1}^{n} r_{i}=\sum_{i=1}^{n} \frac{d_{i}+1}{n} x_{i} $ | (3) |
在分析计算结束后, 将得到的PMU监测点分布结果组成一个集合, 定义为监测点分布总集合P。
2 多目标优化配置模型的优化
2.1 多目标优化函数
为了进一步提高模型的准确性和可观测性, 再加入冗余度最大目标, 可使模型更完善。通过相关文献及研究发现[6-12], 冗余度的提高有利于提升测量结果的精确度, 但不会对方程的解造成影响。至此, 定义以下面3个函数作为多目标模型的优化目标。
(1) 谐波监测点数目最少。根据xi的定义, 如果设置节点监测点则置1, 否则置0, 可以列写目标函数J1(x)为
| $ \min J_{1}(x)=\sum_{j=1}^{n} x_{j} $ | (4) |
式中谐波监测点数目最少的目标函数也可以乘以PMU设备的单价, 将数目最少变为费用最少。
(2) 系统冗余度最大。为了满足一般性多目标规划的定义, 需以系统冗余度的相反数最小为原则。其目标函数J2(x)为
| $ \min J_{2}(x)=-\sum_{i=1}^{n} \frac{d_{i}+1}{n} x_{i} $ | (5) |
(3) 若每个节点都设为谐波监测点, 则系统冗余度最大, 因此需在谐波监测点最少的配置结果中选取系统冗余度最大的解。其具体目标函数J3(x)为
| $ \min J_{3}(x)=\sum_{i=1}^{n} x_{i}-\sum_{i=1}^{n} \frac{d_{i}+1}{n} x_{i} $ | (6) |
2.2 优化模型的可观性约束
谐波监测点优化的前提条件是能够获取全部的系统谐波状态, 即建立的优化模型的约束条件为保持系统可观性。如果系统中的所有节点均是可观测的, 那么系统一定可观。
工程中, 直接安装有监测装置的节点或者安装有监测装置的相邻节点都是可观的, 具体约束函数fi为
| $ f_{i}=\sum_{j=1}^{n} a_{i j} x_{j} $ | (7) |
式中, 表示关联性的aij的具体定义为
| $ a_{i j}=\left\{\begin{array}{ll} 1 & i=j \\ 1 & i \text { 与 } j \text { 相联 } \\ 0 & i \text { 与 } j \text { 不相联 } \end{array}\right. $ | (8) |
电力系统中的一些节点没有直接接入电源, 也没有直接负载出线, 可以认为这样的节点不可能有谐波源注入, 或者注入的谐波含量非常少。这样的节点定义为零注入量节点, 可以不加测量而作为伪测量值出现。在监测点优化时若将零注入节点的情况考虑进去, 则需要对约束函数进行修改, 具体公式为
| $ f_{i}=\sum_{j=1}^{n} a_{i j} x_{j}+\sum_{j=0}^{n} a_{i j} y_{i j} \geqslant 1 $ | (9) |
| $ \sum_{i=1}^{n} a_{i j} y_{i j}=z_{j} $ | (10) |
式中:yij为二进制变量, 具体定义为
| $ \mathrm{y}_{\mathrm{ij}}=\left\{\begin{array}{ll} 0 & \text { 节点 } \mathrm{i} \text { 不能由相联的零注人 } \\ 1 & \text { 节点 } \mathrm{i} \text { 可由相联的零注人 } \end{array}\right. $ | (11) |
由此, 可以得到:如果节点j是零注入节点, 则有zj=1, 而对所有与该节点相联的节点, 则有∑yij=zj=1;如果节点j不是零注入节点, 则有zj=0, yij=0。
模型的整体优化变量集合用X表示
| $X=\left[x_{1} \cdots x_{n}, y_{11} \cdots y_{n 1}, y_{12} \cdots y_{n 2}, y_{1 n} \cdots y_{n n}\right]^{\mathrm{T}}$ | (12) |
其中, 与零注入节点相关联的元素为1, 其他元素为零。
整合全部不等式和等式约束, 写为矩阵形式
| $A_{\text {ineq }} X=\left[\begin{array}{lllll}A & B_{1} & B_{2} & \cdots & B_{n}\end{array}\right] X \geqslant b_{\text {ineq }}$ | (13) |
| $A_{\mathrm{eq}} X=\left[\begin{array}{lllll}0 & _{n \times n} & C_{1} & C_{2} & \cdots & C_{N}\end{array}\right] X=b_{\mathrm{eq}}$ | (14) |
式中的矩阵A表示节点的关联矩阵, 元素Bi, Ci, bineq, beq分别为
| $ B_{i}=\left[\begin{array}{ccc} a_{11} z_{1} & \cdots & 0 \\ \vdots & \vdots & \vdots \\ 0 & \cdots & a_{n i} z_{i} \end{array}\right] $ | (15) |
| $ C_{i}=\left[\begin{array}{cccc} 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ a_{1 i} & a_{2 i} & \cdots & a_{n i} \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & 0 \end{array}\right] $ | (16) |
| $b_{\text {ineq }}=\left[\begin{array}{llll}1 & 1 & \cdots & 1\end{array}\right]^{\mathrm{T}}$ | (17) |
| $b_{\mathrm{eq}}=\left[\begin{array}{llll}z_{1} & z_{2} & \cdots & z_{n}\end{array}\right]^{\mathrm{T}}$ | (18) |
3 应用0-1线性规划的监测点优化算法
本文优化模型的目标是在谐波监测点最少的配置结果中选取系统冗余度最大的解, 且使优化模型满足系统可观性要求。但当分布式电网结构复杂时, 必须考虑在各种工况条件下, 在多目标模型的基础上更加精确地布置谐波监测点。在分布式电网中, 一个节点是否安装PMU可以认为是一个0-1决策问题; 如果一个系统中有n个节点, 那么谐波监测点优化就变为2n个组合的NP问题, 安装PMU的节点值设为1, 反之设为0。因此, 在电力系统谐波监测点优化中应用0-1整数规划方法可以很好地解决此问题。
3.1 考虑单台PMU设备退出情况下的优化
系统中安装多台PMU设备, 当某一谐波监测点发生故障时也能使其余设备正常监测, 谐波监测点的布点依然能够实现全系统的谐波状态估计可观性, 即电力系统的N-1原则——一台设备的退出不影响剩余设备及整个系统的正常工作。这样的设想考虑到实际电力系统的应用情况, 能够提高谐波监测系统的可靠性与稳定性。在N-1原则下, 谐波监测点的优化分布模型应有所变化, 但基本与原模型保持一致。
在优化模型中, 系统中每个节点本身或者与之相关联的节点必须安装有PMU谐波监测装置来保证系统全部节点的可观性, 以仿真模型IEEE 14节点系统的节点1为例, 节点1与节点2和节点5相关联, 为了保证节点1的可观性, 有以下约束式
| $x_{1}+x_{2}+x_{5} \geqslant 1$ | (19) |
但在N-1原则下的布点优化方案中, 每个节点都必须得到两次观测, 才能在其中一个监测设备故障退出时依然保证节点的可观性, 进而使整个系统可观。在考虑这一情况时, 就不能再进行零注入节点的合并了, 因为此时零注入节点的合并会影响电力系统的网络拓扑, 不能体现任意PMU退出的情况。
仍以仿真模型IEEE 14节点的节点1为例, 此时约束条件变为:x1+x2+x5≥2。修改原有的约束条件, 得到单台PMU退出情况下的优化, 即
| $ f_{i}+\sum_{j=1}^{n} a_{i j} y_{i j} \geqslant 2 $ | (20) |
| $ f_{i}=\sum_{j=1}^{n} a_{i j} u_{i j}+\sum_{j=1}^{n} a_{i j} z_{j} y_{i j} $ | (21) |
加入新的约束条件后, 可以保证任意一个PMU设备退出时系统依旧可观。
3.2 考虑单条线路退出情况下的优化
在分布式电网中有多种分布式能源。分布式能源对于环境条件的依赖性使得系统的运行方式发生调整, 也有可能因为故障等原因使线路停运, 因此要考虑在系统某条线路退出时监测点的优化分布方案。
单条线路退出时, 对模型的影响可以用以下约束来体现
| $ f_{i}^{k} \geqslant 1 $ | (22) |
| $ f_{i}^{k}=\sum_{j=1}^{n} a_{i j}^{k} u_{i j}+\sum_{j=1}^{n} a_{i j}^{k} y_{i j}^{k} $ | (23) |
| $\sum a_{i j}^{k} y_{i j}^{k}=z_{j}$ | (24) |
其中,
| $ a_{i j}^{k}=\left\{\begin{array}{lr} 0 & \text { 线路 } k \text { 在 } i \text { 和 } j \text { 之间 } \\ a_{i j} & \text { 线路 } k \text { 不在 } i \text { 和 } j \text { 之间 } \end{array}\right. $ | (25) |
式(23)与式(9)的形式基本相同, 只是所有的变量都由与中断线路有关的变量替换, 用来表示考虑线路如果中断的情况。
3.3 考虑通信通道数目限制情况下的优化
如果系统中可利用的通信通道有限, 在这种条件下进行监测点优化, 需要考虑新的约束条件。使用较少的通信通道完成监测信息的传递也是满足经济性要求的一部分。
首先对新的二进制变量wij进行定义, 即
| $w_{i j}=$ $\left\{\begin{array}{ll}0 & \text { 母线 } i \text { 安装监测装置不可使母线 } j \text { 可观测 } \\ 1 & \text { 母线 } i \text { 安装监测装置可以使母线 } j \text { 可观测 }\end{array}\right.$ | (26) |
设受到限制的最大通信通道数目为m。
在此约束条件下, 优化模型变为
| $ f_{i}=a_{i j} x_{i}+\sum_{j=1, j \neq i}^{n} a_{i j} w_{j i} \geqslant 1 $ | (27) |
| $ \mathrm{g}_{\mathrm{i}}=\mathrm{mx}_{\mathrm{i}}-\sum_{\mathrm{j}=0, \mathrm{j} \neq \mathrm{i}}^{\mathrm{n}} \mathrm{a}_{\mathrm{ij}} \mathrm{w}_{\mathrm{ij}} \geqslant 0 $ | (28) |
式中:fi——保持系统可观测的约束条件;
gi——通信通道的约束条件。
如果加入系统零注入节点后, 约束条件需作进一步的改进。具体公式为
| $ f_{i}=a_{i j} x_{i}+\sum_{j=1, j \neq i}^{n} a_{j i} w_{j i}+\sum_{j=1}^{n} a_{j i} y_{i j} \geqslant 1 $ | (29) |
| $ \mathrm{g}_{\mathrm{i}}=\mathrm{mx}_{\mathrm{i}}-\sum_{\mathrm{j}=0, \mathrm{j} \neq \mathrm{i}}^{\mathrm{n}} \mathrm{a}_{\mathrm{ij}} \mathrm{w}_{\mathrm{ij}} \geqslant 0 $ | (30) |
| $ \sum_{i=1}^{n} a_{i j} y_{i j}=z_{j} $ | (31) |
4 不良数据检出与谐波监测点优化质量的评估
在进行谐波监测点优化后, 监测点数目减少, 费用降低, 测量冗余度降低, 但有可能引起状态估计误差的增大, 因此有必要对优化布点后的谐波状态估计结果进行评估, 以判断布点优化后的结果是否会使估计误差过大。
影响估计结果精度的因素有不良数据、布点方式、系统结构准确度等。设备故障、通信线路传输错误等将引起很大的误差, 但这在监测点优化分布中已经考虑进去了, 下面主要针对不良检测数据带来的误差进行分析。
本文的不良数据检测在考虑了合理的测量误差的基础上, 将影响结果精度的不良数据筛除。为了提高精度, 在谐波状态估计数据中选择1 000组数据, 取数据的平均值作为最终的估计结果。其计算式为
| $Y_{(h)} \boldsymbol{U}_{(h)}=\boldsymbol{I}_{(h)}$ | (32) |
式中:Y——导纳矩阵;
U(h), I(h)——节点h次谐波电压和谐波电流。
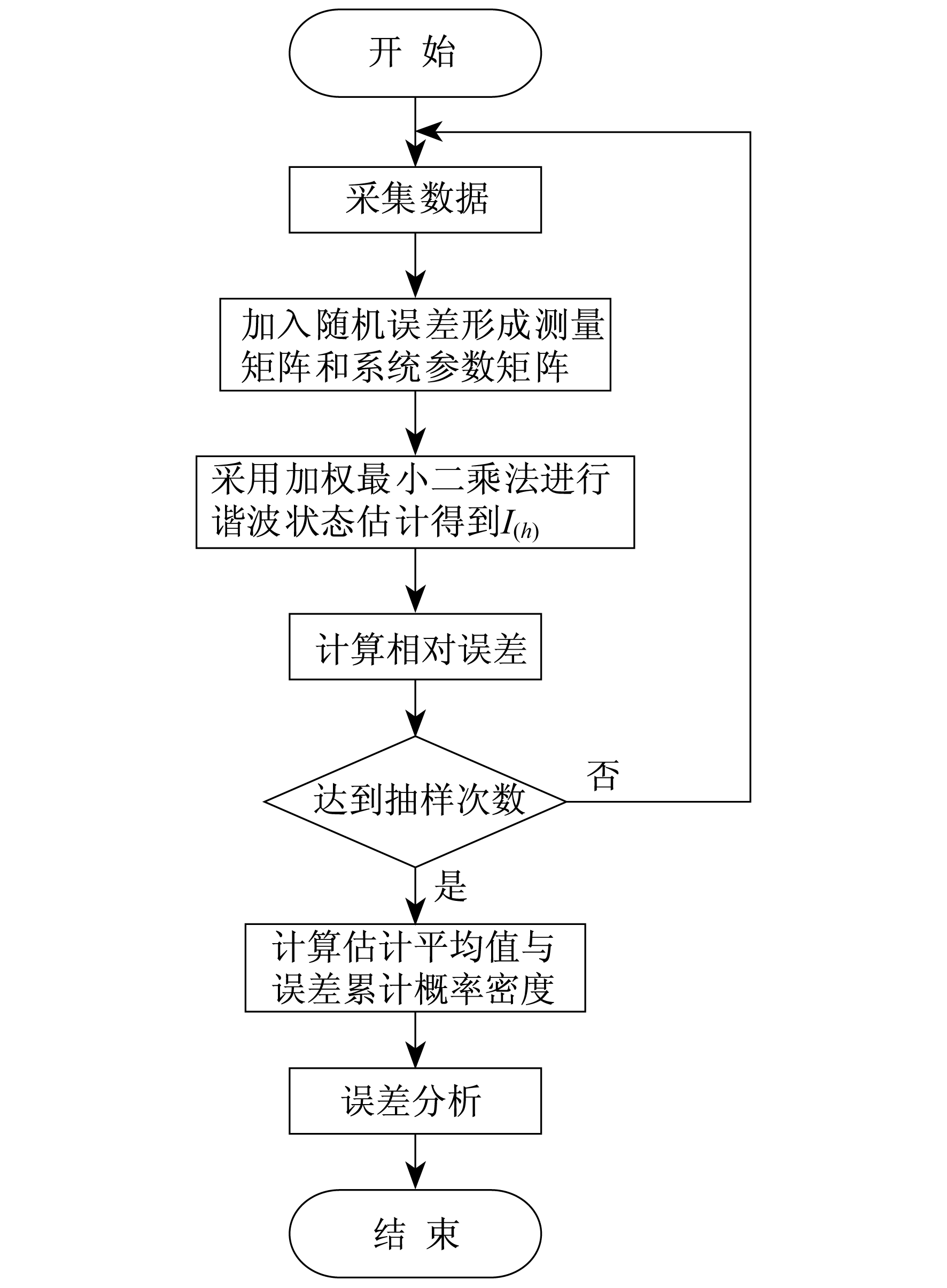
计算结果作为真值, 与谐波状态的估计结果进行对比, 具体的流程如图 1所示。
(1) 在MATLAB中生成随机数, 作为测量误差加入测量数据真值中, 参数矩阵中也需要加入随机误差作为参数误差。
(2) 利用加权最小二乘算法得到估计结果$\hat{I}_{(h)}$。
(3) 计算估计结果的相对误差$\dot{I}_{i(h)}$。
| $ \dot{I}_{i(h)}=\left|\frac{\hat{I}_{i(h)}-\dot{I}_{i(h)}}{\dot{I}_{i(h)}}\right| \times 100 \% $ | (33) |
(4) 对估计结果进行重复抽样, 获得1 000组数据。
(5) 取估计结果的均值, 然后计算状态估计的概率密度曲线以及状态估计结果的累计概率密度曲线$P_{i_{i(h)}}$反映了状态估计的相对误差低于某一定值的概率, 我们可以利用该概率确定状态估计相对误差的波动范围。
| $\begin{array}{l} P_{i_{i(h)}}= \\ \text { 状态估计结果的相对误差小于 } \dot{I}_{i(h)} \text { 的次数 } \\ \hline \text { 仿真次数 } \end{array}$ | (34) |
文献[13-14]讨论了测量误差与概率误差的分布形式。本文选取高斯分布与均匀分布两种误差分布形式来确定加入的量测误差与参数误差。在进行谐波状态估计精度评估时, 认为测量误差服从均值为零的均匀分布, 参数误差服从均值为零的高斯分布。
在数据的采集过程中, 误差被认为是有害的, 会使数据的可信度下降。量测数据中的误差可以看作信号中的噪声, 我们期望采集到的有用信号中, 噪声越少越好。测量数据的误差被认为是随机的, 可以采用信号处理中的信噪比(Signal-Noise Ration, SNR)来描述。尽管学术界在不同应用场合对于信噪比有着不同的解释, 但其核心定义是不变的:信号与噪声的比值就是信噪比。本文使用信噪比的概念来确定服从均匀分布U[a, b]的误差的a值与b值。
| $ S_{\mathrm{NR}}=10 \lg \frac{P_{\mathrm{s}}}{P_{\mathrm{u}}} $ | (35) |
式中:Ps——测量数据真值中的幅值最大值;
Pu——测量数据误差的方差, 也即均匀分布的方差。
本文将信噪比的取值设定为20, 因为误差分布服从均值为零的均匀分布, 所以有a=-b, 利用式(36)可以获得均匀分布的上限a和下限b。
| $ P_{\mathrm{u}}=\frac{P_{\mathrm{s}}}{10^{\frac{s_{\mathrm{NR}}}{10}}}=\frac{(b-a)^{2}}{12} $ | (36) |
由此可以得到完整的测量数据误差分布, 在MATLAB中生成随机数, 与真值相叠加得到含有均匀分布误差的测量值; 并认为系统参数误差服从均值为零, 方差为0.01的高斯分布 也就是
也就是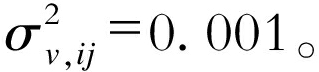 其中的Htrue, i为系统参数矩阵内各节点真值, 由已知谐波量进行谐波潮流计算得到。
其中的Htrue, i为系统参数矩阵内各节点真值, 由已知谐波量进行谐波潮流计算得到。
5 IEEE 14节点系统仿真及算例分析
5.1 谐波状态估计仿真
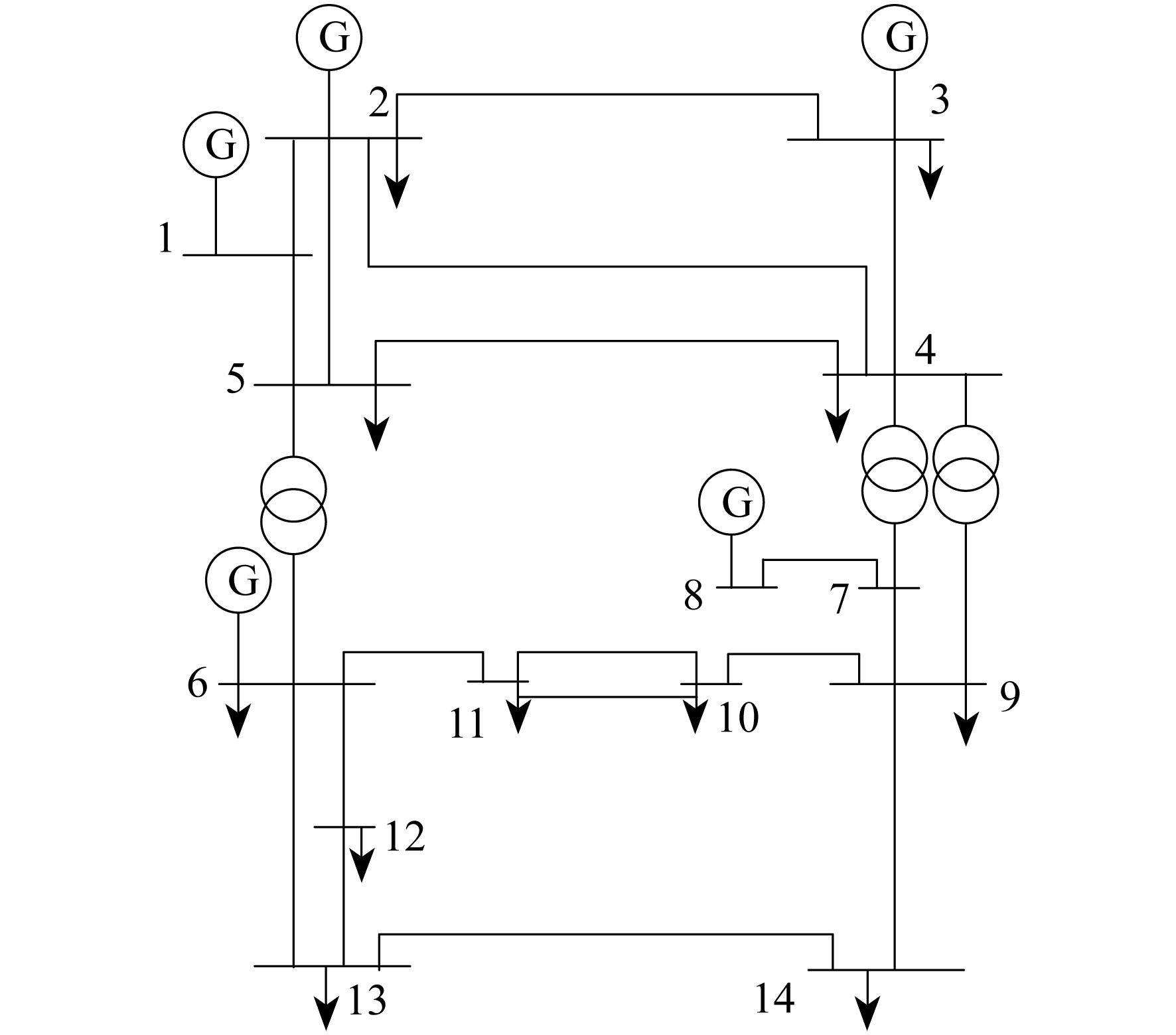
本文使用IEEE 14节点系统进行算例分析, 在MATLAB中进行仿真实验。IEEE 14节点系统结构如图 2所示。
仿真中, 电力传输线路使用π型等效线路模型, 节点间的变压器用短路阻抗模型进行仿真。原因是变压器绕组的不同连接会对谐波电流相位产生影响, 而且变压器还可以真实地模拟出变压器的饱和特性。仿真模型中的负荷由给定的有功功率、无功功率和电压来表示, 负荷所产生的谐波阻抗由文献[15]中的定义来确定。系统中加入了两个谐波源, 用以代表分布式电网中会产生谐波的分布式电源。仿真时间均为0.15 s。
使用MATLAB中的POWERSYSTEM工具箱来搭建IEEE 14节点系统的仿真模型, 模拟实际系统在运行中的情况。IEEE 14节点系统具体参数如表 1所示。其中, 数值用标幺值表示, SB=100 MW。
表 1
IEEE 14节点支路数据(p.u.)
| A支路号 | 首末端母线号 | 支路电阻 | 支路电抗 | 1/2充电电容电纳 |
| 1 | 1-2 | 0.01938 | 0.05917 | 0.0264 |
| 2 | 2-3 | 0.04699 | 0.01979 | 0.0219 |
| 3 | 2-4 | 0.05811 | 0.17632 | 0.0187 |
| 4 | 1-5 | 0.05403 | 0.22304 | 0.0246 |
| 5 | 2-5 | 0.05695 | 0.17388 | 0.0170 |
| 6 | 3-4 | 0.06701 | 0.17103 | 0.0173 |
| 7 | 4-5 | 0.01335 | 0.04211 | 0.0064 |
| 8 | 7-8 | 0 | 0.17615 | 0 |
| 9 | 7-9 | 0 | 0.11001 | 0 |
| 10 | 9-10 | 0.03181 | 0.08450 | 0 |
| 11 | 6-11 | 0.09498 | 0.19890 | 0 |
| 12 | 6-12 | 0.12291 | 0.15581 | 0 |
| 13 | 6-13 | 0.06615 | 0.13027 | 0 |
| 14 | 9-14 | 0.12711 | 0.27038 | 0 |
| 15 | 10-11 | 0.08205 | 0.19207 | 0 |
| 16 | 12-13 | 0.22092 | 0.19988 | 0 |
| 17 | 13-14 | 0.17093 | 0.34802 | 0 |
| 18 | 5-6 | 0 | 0.25202 | 0 |
| 19 | 4-7 | 0 | 0.20912 | 0 |
| 20 | 4-9 | 0 | 0.55618 | 0 |
在节点3和节点9加入谐波注入源。节点3模拟风力发电装置中的变频器, 对系统进行谐波注入; 节点9模拟光伏发电装置, 让系统模拟分布式电网。具体谐波注入参数如表 2所示。
表 2
注入谐波源参数
| 谐波次数 | 节点3谐波源 | 节点9谐波源 | ||
| 幅值 | 相角/(°) | 幅值 | 相角/(°) | |
| 1 | 1.0000 | -49.56 | 1.0000 | 46.92 |
| 5 | 0.1941 | -67.77 | 0.0702 | -124.40 |
| 7 | 0.1309 | 11.90 | 0.0250 | -29.87 |
| 11 | 0.0758 | -7.13 | 0.0136 | 23.75 |
| 13 | 0.0586 | 69.57 | 0.0075 | 71.50 |
| 17 | 0.0379 | 46.53 | 0.0062 | 77.12 |
| 19 | 0.0329 | 116.46 | 0.0032 | 173.43 |
| 23 | 0.0226 | 87.47 | 0.0043 | 178.02 |
| 25 | 0.0241 | 159.32 | 0.0013 | -83.45 |
| 29 | 0.0193 | 126.79 | 0.0004 | -80.45 |
对系统的节点2、节点6、节点8、节点9进行数据量测。在获得的量测数据中叠加0.03的高斯分布误差, 对线路参数加入均值为零、方差为0.01的高斯分布误差, 作为谐波状态估计的测量值。然后采用加权最小二乘法对30次以内的谐波状态进行估计。以电压相角为例, 具体的测量值与估计值如表 3和表 4所示。
表 3
节点谐波电压相角测量值(°)
| 节点 编号 | 基波 | 5次 谐波 | 7次 谐波 | 11次 谐波 | 13次 谐波 | 17次 谐波 | 19次 谐波 | 23次 谐波 | 25次 谐波 | 29次 谐波 |
| 1 | -0.000 27 | -91.627 | -108.600 | -174.070 | -34.113 | -177.660 | -177.960 | -106.960 | 95.571 | 79.615 |
| 2 | -5.680 20 | -72.204 | -72.106 | -149.230 | -23.901 | -128.340 | -104.260 | -37.524 | 68.383 | 42.044 |
| 3 | -14.233 00 | -20.063 | 47.413 | 10.991 | 81.598 | 46.983 | 109.870 | 68.428 | 135.100 | 93.929 |
| 4 | -10.442 00 | -39.706 | 16.649 | -56.394 | -8.993 | -77.060 | -23.137 | -70.870 | -1.219 | -3.385 |
| 5 | -8.834 80 | -42.532 | 12.548 | -63.232 | -17.405 | -89.514 | -38.453 | -96.669 | -38.387 | -104.600 |
| 6 | -8.851 60 | -42.583 | 12.474 | -63.344 | -17.531 | -89.665 | -38.612 | -96.835 | -38.556 | -104.700 |
| 7 | -10.431 00 | -39.781 | 16.555 | -56.537 | -9.162 | -77.287 | -23.399 | -71.226 | -1.645 | -3.904 |
| 8 | -10.431 00 | -39.790 | 16.552 | -56.537 | -9.161 | -77.287 | -23.401 | -71.238 | -1.651 | -3.927 |
| 9 | -10.437 00 | -39.814 | 16.508 | -56.612 | -9.251 | -77.405 | -23.533 | -71.406 | -1.864 | -4.160 |
| 10 | -10.474 00 | -42.299 | 13.000 | -62.256 | -16.049 | -86.895 | -34.725 | -88.375 | -25.072 | -58.860 |
| 11 | -9.816 20 | -43.442 | 11.387 | -64.905 | -19.283 | -91.614 | -40.515 | -98.011 | -38.899 | -101.800 |
| 12 | -9.869 00 | -48.586 | 5.505 | -74.040 | -29.958 | -105.280 | -55.644 | -116.350 | -58.167 | -127.300 |
| 13 | -10.045 00 | -48.113 | 4.479 | -77.874 | -30.880 | -106.310 | -56.691 | -117.290 | -59.974 | -127.700 |
| 14 | -11.548 00 | -49.594 | 3.023 | -77.642 | -34.150 | -110.660 | -62.593 | -123.050 | -65.874 | -132.500 |
表 4
冗余量测谐波电压相角估计值(°)
| 节点 编号 | 基波 | 5次 谐波 | 7次 谐波 | 11次 谐波 | 13次 谐波 | 17次 谐波 | 19次 谐波 | 23次 谐波 | 25次 谐波 | 29次 谐波 |
| 1 | -0.000 2 | -91.368 | -108.750 | -174.540 | -35.102 | -179.360 | -179.870 | -109.960 | 97.630 | 81.513 |
| 2 | -5.080 2 | -71.204 | -73.650 | -149.790 | -24.302 | -129.380 | -105.290 | -38.600 | 70.187 | 44.412 |
| 3 | -13.336 0 | -20.765 | 48.615 | 11.797 | 83.687 | 47.781 | 112.650 | 70.427 | 137.100 | 95.025 |
| 4 | -10.421 0 | -39.706 | 16.649 | -56.394 | -8.993 | -77.060 | -23.137 | -70.870 | -1.219 | -3.385 |
| 5 | -9.934 0 | -41.433 | 14.570 | -65.137 | -19.405 | -90.011 | -42.345 | -99.161 | -40.774 | -108.430 |
| 6 | -9.951 0 | -44.481 | 14.970 | -65.445 | -19.431 | -90.178 | -42.315 | -99.838 | -40.664 | -108.820 |
| 7 | -11.634 0 | -41.480 | 17.655 | -57.131 | -10.661 | -78.015 | -27.124 | -76.245 | -2.588 | -5.742 |
| 8 | -11.534 0 | -41.715 | 17.692 | -57.934 | -10.568 | -78.145 | -27.567 | -76.457 | -2.542 | -5.326 |
| 9 | -11.737 0 | -43.397 | 17.509 | -58.513 | -10.254 | -78.586 | -27.445 | -76.558 | -2.864 | -6.452 |
| 10 | -11.775 0 | -43.397 | 14.000 | -64.153 | -17.041 | -87.778 | -38.879 | -90.256 | -27.077 | -60.770 |
| 11 | -10.254 0 | -45.428 | 13.183 | -65.707 | -21.287 | -92.536 | -44.678 | -101.240 | -40.998 | -5.742 |
| 12 | -10.565 0 | -45.587 | 7.041 | -71.108 | -28.259 | -107.760 | -57.981 | -121.470 | -63.568 | -130.330 |
| 13 | -11.547 0 | -45.716 | 5.279 | -75.779 | -32.282 | -107.220 | -59.684 | -121.360 | -63.173 | -130.540 |
| 14 | -11.749 0 | -50.691 | 3.023 | -78.541 | -35.170 | -110.990 | -62.978 | -123.270 | -67.775 | -137.780 |
将得到的估计值与真值做对比, 得到估计值的相对误差如表 5所示。经过计算对比, 除极个别点外, 节点电压相角的估计结果的相对误差大多控制在20%以内。
表 5
节点电压估计相对误差
| 节点 编号 | 基波 | 5次 谐波 | 7次 谐波 | 11次 谐波 | 13次 谐波 | 17次 谐波 | 19次 谐波 | 23次 谐波 | 25次 谐波 | 29次 谐波 |
| 1 | 0.259 250 | 0.002 827 | 0.001 381 | 0.002 700 | 0.028 992 | 0.009 569 | 0.010 733 | 0.028 048 | 0.021 544 | 0.023 840 |
| 2 | 0.105 630 | 0.013 850 | 0.021 413 | 0.003 753 | 0.016 778 | 0.008 103 | 0.009 879 | 0.028 675 | 0.026 381 | 0.056 322 |
| 3 | 0.063 020 | 0.034 990 | 0.025 352 | 0.073 333 | 0.025 601 | 0.016 985 | 0.025 303 | 0.029 213 | 0.014 804 | 0.011 668 |
| 4 | 0.002 020 | 0.002 121 | 0.003 233 | 0.003 244 | 0.003 232 | 0.002 323 | 0.021 333 | 0.002 121 | 0.002 111 | 0.002 122 |
| 5 | 0.124 410 | 0.025 839 | 0.061 141 | 0.030 127 | 0.114 910 | 0.005 552 | 0.101 214 | 0.025 779 | 0.043 100 | 0.036 616 |
| 6 | 0.124 200 | 0.044 572 | 0.200 096 | 0.033 168 | 0.108 379 | 0.005 721 | 0.095 903 | 0.031 012 | 0.054 701 | 0.039 351 |
| 7 | 0.115 320 | 0.042 709 | 0.066 445 | 0.010 506 | 0.163 649 | 0.009 419 | 0.159 195 | 0.070 466 | 0.021 300 | 0.022 020 |
| 8 | 0.105 742 | 0.048 379 | 0.068 874 | 0.024 709 | 0.153 586 | 0.011 101 | 0.178 027 | 0.073 261 | 0.032 310 | 0.356 201 |
| 9 | 0.124 550 | 0.089 993 | 0.060 637 | 0.033 579 | 0.108 457 | 0.015 257 | 0.166 235 | 0.072 151 | 0.536 596 | 0.021 310 |
| 10 | 0.124 210 | 0.025 958 | 0.076 923 | 0.030 471 | 0.061 811 | 0.010 162 | 0.119 626 | 0.021 284 | 0.079 970 | 0.032 450 |
| 11 | 0.044 600 | 0.045 716 | 0.157 724 | 0.012 357 | 0.103 926 | 0.010 064 | 0.102 752 | 0.032 996 | 0.053 960 | 0.010 210 |
| 12 | 0.070 520 | 0.161 726 | 0.279 042 | 0.039 600 | 0.056 713 | 0.023 556 | 0.041 999 | 0.044 005 | 0.092 853 | 0.023 802 |
| 13 | 0.149 520 | 0.049 820 | 0.178 650 | 0.026 902 | 0.045 402 | 0.008 560 | 0.052 795 | 0.034 700 | 0.053 340 | 0.022 240 |
| 14 | 0.017 400 | 0.022 120 | 0 | 0.011 579 | 0.029 868 | 0.002 982 | 0.006 151 | 0.001 788 | 0.028 858 | 0.039 849 |
5.2 监测点优化算例分析
与上述仿真一样, 算例中使用IEEE 14节点的改进网络进行分析。系统中线路编号共20个, 在考虑零输入节点的优化中, 将节点7配置为零输入节点。具体模型信息如表 6所示。
各节点与相邻节点间的可观测性的关系如表 7所示。
以节点1为例, 如果将节点1配置为谐波监测点, 那么与之相关联的节点1、节点2和节点5都成为可观测节点, 用符号标出来, 各个节点均如此分析, 建立如表 8所示的PMU布点策略。
表 6
IEEE 14节点系统的节点信息
| 系统 | 支路数量/条 | 零注人节点编号 | 单节点最大出线度/条 |
| IEEE 14 | 20 | 7 | 5 |
表 7
IEEE 14系统各节点的可观测性关系
| 节点 | 节点 | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| 1 | √ | √ | √ | |||||||||||
| 2 | √ | √ | √ | √ | √ | |||||||||
| 3 | √ | √ | √ | |||||||||||
| 4 | √ | √ | √ | √ | √ | √ | ||||||||
| 5 | √ | √ | √ | √ | √ | |||||||||
| 6 | √ | √ | √ | √ | √ | |||||||||
| 7 | √ | √ | √ | |||||||||||
| 8 | √ | √ | ||||||||||||
| 9 | √ | √ | √ | √ | √ | |||||||||
| 10 | √ | √ | √ | √ | ||||||||||
| 11 | √ | √ | √ | |||||||||||
| 12 | √ | √ | √ | |||||||||||
| 13 | √ | √ | √ | √ | ||||||||||
| 14 | √ | √ | √ | |||||||||||
利用节点分析表格可以得到相应的节点观测约束, 以节点1为例, 节点可观性由式(18)约束, 其他节点以此类推。在获得节点可观性约束之后, 代入优化模型中, 再根据不同考虑因素进行监测点优化, 经MATLAB程序运算得到的优化布点结果见表 9与表 10所示。
表 8
多种情况下的PMU布点策略
| 系统 | 不考虑零注人节点 | 考虑零注入节点 | 单台PMU退出节点 | 单条线路退出节点 |
| IEEE 14 | 2, 6, 7, 9 | 2, 6, 9 | 1, 2, 4, 6, 9, 10, 13 | 1, 3, 6, 9, 10, 13 |
表 9
考虑通信通道数量限制情况下的PMU优化个
| 受约束的通信通道 | 考虑零注人节点 | 不考虑零注入节点 |
| 1 | 7 | 7 |
| 2 | 5 | 5 |
| 3 | 4 | 4 |
| 4 | 4 | 3 |
| 5 | 4 | 3 |
| 6 | 4 | 3 |
| 7 | 4 | 3 |
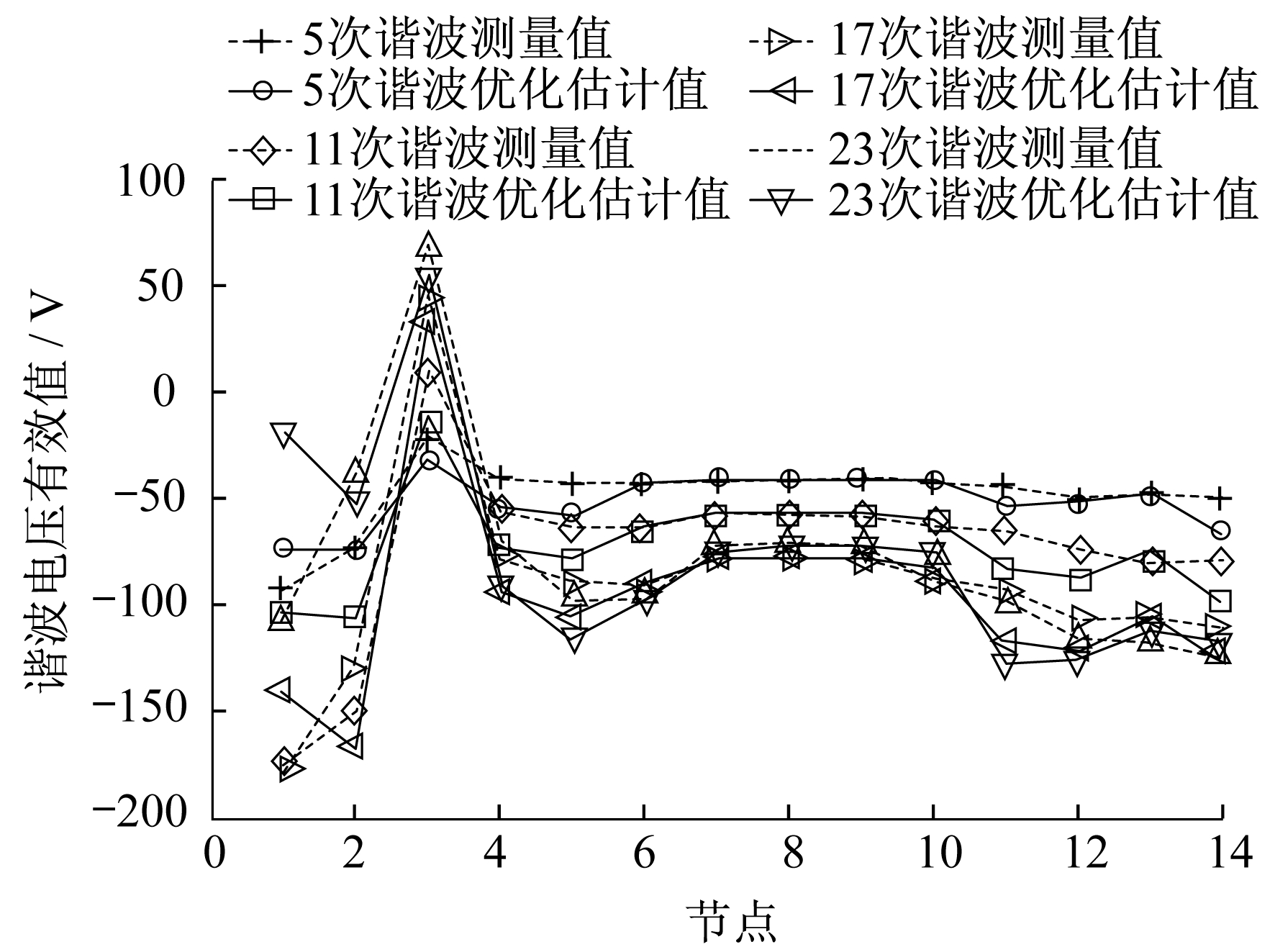
表 10中的数据为采用单一考虑冗余度最优情况下的布点(2, 6, 7, 9)时的谐波状态估计结果。以5次、11次、17次、23次谐波为例, 其谐波电压的测量值与优化布点后的估计值的对比曲线如图 3所示。
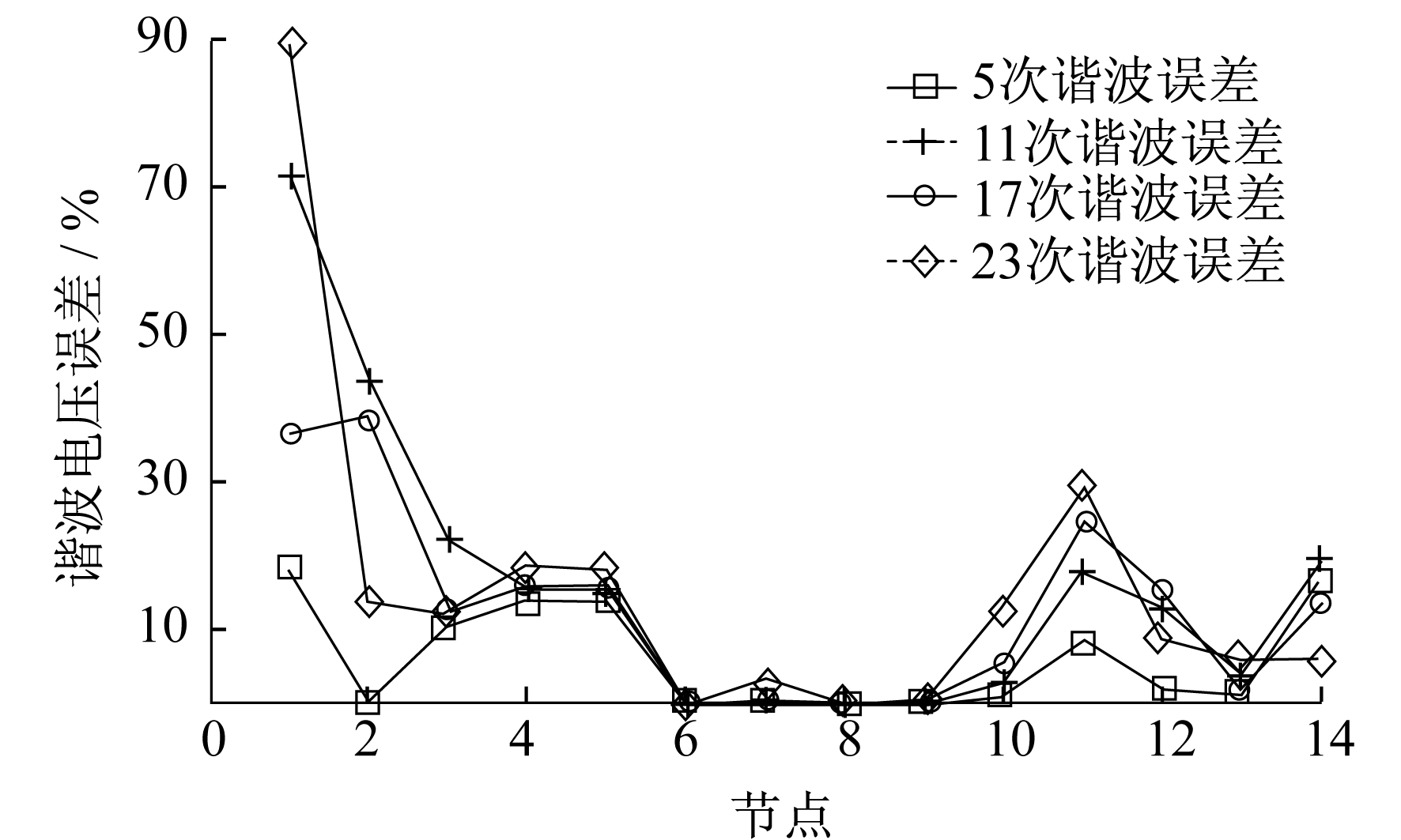
通过与表 3和表 4的对比可知, 布点优化使系统测量冗余度降低, 带来的副作用是使谐波状态估计结果误差增大, 其所对应的误差大小如图 4所示。为了控制布点优化结果的误差, 需要对结果进行多次寻优, 最终选择在误差容忍情况下的优化值。
5.3 不良数据检出与评估效果仿真
如上所述, 谐波监测点优化使系统测量冗余度降低, 但却使谐波状态估计结果误差增大。利用所建的仿真算例及本文优化布点方案, 参照上述的精度计算步骤进行1 000次数据抽样, 得到累计概率密度曲线, 以节点3为例, 节点3的5次谐波状态估计值的相对误差小于40%的概率为76%。以此类推, 可以读出不同次数谐波出现的不同相对误差的概率, 如表 11所示。
表 10
PMU优化布点后的电压相角谐波状态估计值(°)
| 节点编号 | 基波 | 5次谐波 | 7次谐波 | 11次谐波 | 13次谐波 | 17次谐波 | 19次谐波 | 23次谐波 | 25次谐波 | 29次谐波 |
| 1 | -0.7123 | -73.092 | -76.512 | -102.50 | -27.160 | -140.700 | -165.000 | -17.833 | 84.130 | 71.820 |
| 2 | -5.6801 | -72.664 | -75.961 | -105.60 | -0.736 | -167.000 | 128.020 | -51.334 | -82.920 | 44.106 |
| 3 | -15.1420 | -30.652 | -36.108 | -10.92 | 69.400 | 34.455 | 97.311 | 55.985 | 122.610 | 81.892 |
| 4 | -11.9060 | -53.765 | 1.700 | -72.01 | -24.970 | -93.400 | -40.150 | -89.570 | -19.700 | -2.275 |
| 5 | -10.6420 | -56.503 | -2.303 | -78.74 | -33.290 | -105.800 | -55.360 | -115.130 | -56.340 | -124.830 |
| 6 | -8.8459 | -42.522 | 12.556 | -63.32 | -17.540 | -89.820 | -38.600 | -96.859 | -38.990 | -104.720 |
| 7 | -9.8817 | -39.516 | 17.111 | -55.67 | -8.235 | -76.730 | -23.160 | -74.767 | -11.280 | -49.440 |
| 8 | -10.4280 | -39.759 | 16.585 | -56.58 | -9.247 | -77.540 | -23.470 | -71.527 | -2.698 | -2.750 |
| 9 | -10.4280 | -39.757 | 16.584 | -56.59 | -9.253 | -77.550 | -23.470 | -71.533 | -2.708 | -2.754 |
| 10 | -10.7890 | -41.074 | 14.816 | -59.23 | -12.300 | -81.400 | -27.650 | -75.166 | -3.425 | -56.835 |
| 11 | -10.7200 | -52.584 | -0.688 | -82.73 | -39.710 | -116.800 | -67.720 | -127.580 | -72.700 | -139.100 |
| 12 | -9.1376 | -50.796 | -1.436 | -87.18 | -44.660 | -120.500 | -69.180 | -125.220 | -65.730 | -127.360 |
| 13 | -9.2855 | -46.721 | 6.026 | -74.03 | -29.830 | -104.400 | -53.250 | -111.010 | -53.200 | -118.080 |
| 14 | -14.6580 | -66.082 | -15.888 | -97.51 | -53.100 | -124.300 | -69.870 | -116.960 | -51.550 | -163.332 |
通过观察所得估计结果的误差概率密度曲线, 结合不同的测量要求, 可以判断谐波估计结果的误差是否符合要求。
根据抽样数据计算的估计值概率密度曲线可知, 当设定的量测误差和参数误差分别服从均匀分布和高斯分布时, 谐波估值的概率密度曲线近似高斯分布, 估计值的期望值即为抽样后的均值; 而且谐波次数越高, 概率密度分布的置信区间越窄, 估计值更接近真实值。根据各节点数据得到的近似高斯分布曲线可判断得到的谐波估计是否准确。
表 11
节点3谐波状态估计值误差≤40%的概率统计
| 谐波次数/次 | 相对估计误差≤40% | 谐波次数/次 | 相对估计误差≤40% |
| 5 | 76 | 17 | 69 |
| 7 | 73 | 23 | 62 |
| 11 | 72 | 25 | 65 |
| 13 | 70 | 29 | 60 |
6 结论
(1) 谐波监测点优化使系统测量冗余度降低, 将得到的估计值与真实值经过计算对比, 除极个别点外, 节点电压相角的估计结果的相对误差大多都控制在20%以内, 但使谐波状态估计结果误差增大。为了减少估计误差, 需要对寻优结果进行多次筛选, 直至满足电力系统电能质量数据测量的容忍度要求。
(2) 利用概率密度曲线能够有效辨识数据的误差概率, 从而将不良数据检出。本文使用IEEE 14节点电力系统的结构数据, 得到近似高斯分布的估值概率密度曲线。通过观察可知, 谐波次数越高, 概率密度分布的置信区间越窄, 且估计值更接近真实值。
(3) 对优化后的监测点数据进行对比分析, 证明本文所提方法可以为提高谐波监测优化的评估精度提供参考。
参考文献
-
[1]基于PMU的分布式电力系统动态状态估计新算法[J]. 电力系统自动化, 2005, 29(4): 34-39. DOI:10.3321/j.issn:1000-1026.2005.04.007
-
[2]基于遗传算法的PMU配置对谐波状态估计质量影响的研究[J]. 电力系统保护与控制, 2010, 38(21): 233-236. DOI:10.7667/j.issn.1674-3415.2010.21.045
-
[3]电力系统PMU最优配置数字规划算法[J]. 电力系统自动化, 2006, 30(9): 1-5. DOI:10.3321/j.issn:1000-1026.2006.09.001
-
[4]于尔铿, 刘广一, 周京阳, 等.能量管理系统[M].北京: 科学出版社, 1998: 274-282.
-
[5]分布式电源对配电网电能质量的影响及改善[J]. 电力电子技术, 2013, 47(11): 58-60. DOI:10.3969/j.issn.1000-100X.2013.11.022
-
[6]王建, 李兴源, 邱晓燕.含有分布式发电装置的电力系统研究综述.电力系统自动化, 2005, 29(24): 90-97.
-
[7]ACKERMANN T, AANDWESSON G, SODER L. Distributed generation: a definition[J]. Electric Power Systems Research, 2001, 57(3): 195-204. DOI:10.1016/S0378-7796(01)00101-8
-
[8]分布式电源对配电网谐波分布影响的研究[J]. 电气应用, 2011, 31(12): 61-65.
-
[9]分布式光伏发电对配电网电压的影响及电压越限的解决方案[J]. 电网技术, 2010, 34(10): 140-146.
-
[10]DUFOUR C, BELANGER J. On the use of real-time simulation technology in smart grid research and development[J]. IEEE Trans on Industry Applications, 2014, 50(6): 3963-3970. DOI:10.1109/TIA.2014.2315507
-
[11]WU M, XIE L, CHENG L, et al. A study on the impact of wind farm spatial distribution on power system sub-synchronous oscillations[J]. IEEE Trans on Power Systems, 2016, 31(3): 2154-2162. DOI:10.1109/TPWRS.2015.2455873
-
[12]基于状态估计法的配网谐波源定位技术[J]. 智能电网, 2016, 4(7): 962-967.
-
[13]电力系统最小信息损失状态估计的信息学原理[J]. 中国电机工程学报, 2015, 25(6): 11-16.
-
[14]REN J, KEZUNOVIC M. An adaptive phasor estimator for power system waveforms containing transients[J]. IEEE Trans on Power Delivery, 2012, 27(2): 735-745. DOI:10.1109/TPWRD.2012.2183896
-
[15]BI T, LIU H, FENG Q, et al. Dynamic phasor model-based synchrophasor estimation algorithm for m-class PMU[J]. IEEE Trans on Power Delivery, 2015, 30(3): 1162-1171. DOI:10.1109/TPWRD.2014.2353816