|
|
|
发布时间: 2019-02-10 |
|
|
|
|
收稿日期: 2018-05-15
基金项目: 上海市自然科学基金(15ZR1418400)
中图法分类号: TP391.4
文献标识码: A
文章编号: 1006-4729(2019)01-0083-07
|
摘要
针对存在更复杂运动模式的无序运动人群密集场景, 提出了一种有监督的密集场景人群分群检测算法, 不仅能够实现运动前景的自动定位和跟踪, 而且还能够在有先验信息的条件下准确定位分群区域。结合个体之间运动轨迹时空距离特征、运动方向特征、格兰杰因果性特征、热能图特征以及运动相关性特征, 采用结构化支持向量机在训练集上进行训练, 对测试集人群进行了分组测试。选用了大量真实室内外密集人群无序运动场景视频进行测试, 试验结果表明, 该方法对密集人群分组有较好的处理效果。
关键词
人群分组; 结构化支持向量机; 相关性聚类
Abstract
A supervised automatic group detection algorithm is proposed for complex movement pattern in crowds of disordered movement, which can locate and track movement automatically in foreground, and position the group area accurately with prior information.The spatiotemporal characteristics, movement direction characteristics, Granger causality characteristics, hot map characteristics and movement correlation characteristics of individual trajectories are combined, and the structured support vector machine(SVM) framework is used to train the characteristics to achieve the goal of crowd grouping.The algorithm combines various physical features and social characteristics, and makes the best use of the effective information in the group, making grouping more accurate.
Key words
crowd group; strutural support vector machine; correlation clustering
随着世界范围内城市化进程的不断推进, 人群聚集现象变得越来越突出, 如体育比赛、游行示威、恐怖活动等, 密集人群中小群体检测技术在智能监控、虚拟现实、公共安全等方面的应用也越来越普遍。通常情况下, 在一个群体中有50%~70%的人是以小群体的形式行动[1], 故人群中个体之间的相互作用对于群体现象的研究十分重要[2]。然而, 由于人类的社会性, 人群中的相互作用不仅发生在个体与个体之间, 而且也发生在各个小群体之间, 所以密集人群中小群体检测也受到越来越多的关注。
密集人群的运动场景从宏观上可以分为两种类型——结构化的运动场景和非结构化的运动场景[3]。在结构化的运动场景中, 人群运动发生在共同的路径上, 运动路径不会频繁发生变化, 并且场景中的每个空间位置都有一个关键的群体行为, 例如公路自行车赛、马拉松比赛等。在非结构化拥挤的场景中, 行人在不同的方向上自由移动, 每个空间位置往往有几个群体行为。此外, 人群之间由于存在遮挡等复杂的相互作用, 进一步增加了在非结构化运动场景中对人群分割的难度, 而本文将在非结构化的密集运动场景中进行群体检测。
在基于群组的方法中[4], 拥挤人群具有高噪声或高复杂度的特点, 小群体被认为是组成人群的基本要素, 就导致有一部分个体难以区分。识别群体是掌握人群中复杂的社会动态和规范集体行为的重要步骤[5], 就给计算机视觉带来了新的挑战, 因为群体比单个个体或整个人群来说更难以表征。
目前, 有些算法是通过物理模型(例如流体力学[6])来分析人群特性的。此类算法在极其密集的人群中有效, 但由于其忽视了单个个体的主观目的和目标, 因而具有一定的局限性。文献[7]提出了行人动力学的社会力量模型, 认为任何朝向目标移动的行人都会受到周围行人的影响。文献[8]认为社会关系会影响人们在人群中的行为方式, 强调大多数人倾向于团体活动。这些算法都是通过由空间邻近性和速度特征的组合来定义社会学群体间的亲密度, 从而逐次合并小群体。本文结合了轨迹时空特征[9]、个体运动方向特征[9]、格兰杰因果性特征[10]、热能图特征[11-12]以及个体之间运动相关性特征[12], 将对群体的检测视为有监督的相关性聚类[13], 采用结构支持向量机(Support Vector Machine, SVM)对提取的特征进行训练分类[14-15]。为了保证算法的鲁棒性, 试验采用的数据集均为现实场景中的视频图像。
1 相关性聚类
一个群体, 可以被定义为两个或两个以上的人员, 根据物理身份(空间邻近性)和社会身份(小群体内规则)达成共同目标并共享成员。
首先, 将群体检测作为一个聚类问题进行处理, 以获得各特征的权值。将一组行人编号为P={a, b, …}, 设函数Y(P)作为解决这个聚类问题的所有可能出现的方案。那么当a∈P, ∃y∈Y(P)且∪y∈Y(P)y=P, y={y1, y2, y3, …}为一系列有效解。
相关性聚类算法将权值矩阵Wab作为输入。对于一个确定的|Wab|, 当Wab > 0时, 行人a和行人b属于同一个小群体; 当Wab < 0时, 行人a和行人b不属于同一小群体。因此, 需要将同一聚类y中元素对的总和最大化
| $ M=\arg \max _{y \in Y(P)} \sum_{y \in Y} \sum_{a \neq b \in y} W_{d}^{a b} $ | (1) |
式中:
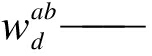 行人a和行人b的亲和度。
行人a和行人b的亲和度。
将W中的成对元素亲和度参数化为有界不相似度量权重的线性组合及其补充
| $ W_{d}^{a b}=\alpha^{\mathrm{T}}(1-d(a, b))-\beta^{\mathrm{T}} d(a, b) $ | (2) |
式中:α, β——参数;
d(a, b)——组合特征。
根据不同场景的不同聚类规则, 式(2)中的参数W=[α, β]保证了每个特征在识别群组时所占的比重有所不同。对于最佳参数W的选择受到文化、社会环境以及场景天气等诸多因素的影响, 故采用学习框架来得到最合适的聚类规则。
2 特征提取
本文算法设计了5个特征, 分别为轨迹时空距离特征d1, 运动方向特征d2, 格兰杰因果性特征d3, 热能图特征d4, 运动相关性特征d5, 用来捕捉运动行人的物理和社会身份, 以及识别他们之间存在的共同目标。因此, 两个成对的行人特征向量定义为
| $d(a, b)=\left[d_{1}, d_{2}, d_{3}, d_{4}, d_{5}\right]$ | (3) |
2.1 轨迹时空距离特征
在现实场景中, 行人在不同的位置形成不同的小群体, 小群体内个体之间的距离通常小于群体成员与其他群体成员之间的距离。在时间窗T中, 设行人a的轨迹为la, 行人b的轨迹为lb。由于受到障碍物的遮挡或行人之间的互相遮挡, 行人a和行人b不一定在每一帧图像中都同时出现, 因此设行人a和行人b同时出现在一帧图像中形成的轨迹分别为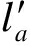 和
和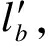 共同出现的时间为{t1, t2, t3, …, tn}。那么两轨迹之间的距离可表示
共同出现的时间为{t1, t2, t3, …, tn}。那么两轨迹之间的距离可表示
| $D = \sum\limits_{t = {t_1}}^{{t_n}} {\exp } \left( { - \sqrt {{{\left( {x_a^t - x_b^t} \right)}^2} + {{\left( {y_a^t - y_b^t} \right)}^2}} } \right)$ | (4) |
式中:
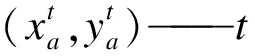 时刻行人a的坐标;
时刻行人a的坐标;
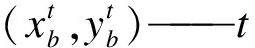 时刻行人b的坐标。
时刻行人b的坐标。
然后定义
| $ d_{1}(a, b)=\frac{D}{\max \left(N_{a}, N_{b}\right)} $ | (5) |
式中:Na, Nb——行人a和行人b在时间窗T内的图像中出现的次数。
2.2 运动方向特征
在无序运动的人群中, 一个小群体内的行人往往会有一个共同的目的地, 因此他们的运动方向在通向目的地的过程中会基本保持一致。
对于行人a在第τ帧时在i∈la的运动方向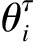 近似计算为(i为行人a在τ帧时的位置)
近似计算为(i为行人a在τ帧时的位置)
| $ \theta_{i}^{\tau}=\left\{\begin{array}{cc} \frac{\pi}{2} & x_{i}^{\tau+1}-x_{i}^{\tau}, y_{i}^{\tau+1}-y_{i}^{\tau} \gt 0 \\ \frac{3 \pi}{2} & x_{i}^{\tau+1}-x_{i}^{\tau}, y_{i}^{\tau+1}-y_{i}^{\tau} \lt 0 \\ \arctan \left(\frac{y_{i}^{\tau+1}-y_{i}^{\tau}}{x_{i}^{\tau+1}-x_{i}^{\tau}}\right) & \text { 其 } \text { 他 } \end{array}\right. $ | (6) |
对于行人b在第τ帧时在j∈lb以相同的方法可以得到 (j为行人b在τ帧时的位置)。定义两人运动方向的夹角为运动方向特征d2, 当d2接近于零时, 表明此时两者运动方向基本一致, 否则两者的运动方向存在偏差。d2可定义为
(j为行人b在τ帧时的位置)。定义两人运动方向的夹角为运动方向特征d2, 当d2接近于零时, 表明此时两者运动方向基本一致, 否则两者的运动方向存在偏差。d2可定义为
| $ d_{2}(a, b)=\mid \theta_{i}^{\tau}-\theta_{j}^{\tau} $ | (7) |
2.3 格兰杰因果性特征
在运动轨迹足够平稳的情况下, 采用格兰杰因果性关系来衡量行人a对行人b运动路径影响的程度。设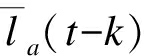 为轨迹la在时间窗t-k到t-1的轨迹信息(k为因果分析的迟延值), 利用
为轨迹la在时间窗t-k到t-1的轨迹信息(k为因果分析的迟延值), 利用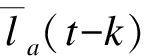 通过最小二乘法对轨迹la在t时刻预测为
通过最小二乘法对轨迹la在t时刻预测为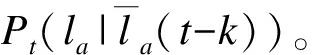 预测的误差定义为
预测的误差定义为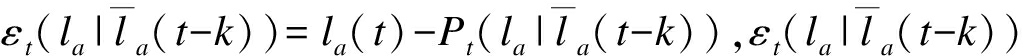 的方差定义为
的方差定义为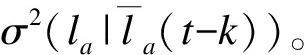
| $ \begin{array}{l} \sigma^{2}\left(l_{a} \mid \bar{l}_{a}(t-k)\right) \gt \\ \sigma^{2}\left(l_{a} \mid \bar{l}_{a}(t-k), \bar{l}_{b}(t-k)\right) \end{array} $ | (8) |
如果式(8)成立, 则说明行人b对行人a的运动轨迹产生了影响。
引入约束和非约束模型的残差平方和分别为
| $ R_{\mathrm{e} 1}=\sum_{t=1}^{n} \varepsilon_{t}\left(l_{a} \mid \bar{l}_{a}(t-k)\right)^{2} $ | (9) |
| $ \mathrm{R}_{e 2}=\sum_{i=1}^{n} \varepsilon_{\mathrm{t}}\left(1_{\mathrm{a}} \mid \overline{\mathrm{l}}_{\mathrm{a}}(\mathrm{t}-\mathrm{k}), \overline{\mathrm{I}}_{\mathrm{b}}(\mathrm{t}-\mathrm{k})\right)^{2} $ | (10) |
式中:n——分析图像的总帧数。
定义测试统计为
| $ S_{b \rightarrow a}=\frac{\frac{R_{\mathrm{e} 1}-R_{\mathrm{e} 2}}{k}}{\frac{R_{\mathrm{e} 2}}{n-2 k-1}} $ | (11) |
本文采用Fisher-Snedecor分布来计算格兰杰因果性特征, 故
| $\begin{array}{l} {d_3}(a,b) = \\ \mathop {\max }\limits_{S\left\{ {{S_{b \to a,S}}_{a \leftarrow b}} \right\}} \int_0^S F (x\mid k,n - 2k - 1){\rm{d}}x \end{array}$ | (12) |
2.4 热能图特征
在不同的位置, 小群体的形成和散开对于群体检测来说也是一个非常有效的信息, 因此采用热能图来描述群体活动成为一个十分有用的特征。当轨迹穿过一个区域, 这个区域将被定义为一个区域热源。通过这种方式, 轨迹可以被转换成一系列热源。此外, 为了进一步捕捉轨迹的时间信息, 在不同的热源上引入衰减因子, 使得“较早的”热源(即离轨迹起点较近的小块)的热能较小, 而“较新的”热源将具有较大的热能。
假设在当前的分组中, 轨迹la的热源区域Ru1×v1的能量衰减为
| $ E_{\mathrm{a}}=\overline{E_{a\left(u_{1} \times v_{1}\right)}} \cdot e^{-k_{\mathrm{t}} \cdot t_{\mathrm{int}}} $ | (13) |
式中:u1, v1——区域的长和宽;
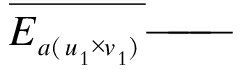 累积的热能;
累积的热能;
e-kt·tint——衰减周期;
kt——衰减因数;
tint——行人a在热源区域的时间。
当轨迹la由路径(p, q)进入热源区域Ru1×v1在相关网格(u, v)处热源开始激发, 其热源衰减过程Ha(u, v)为
| ${H_{a(u,v)}} = \sum\limits_{p = 1}^{{u_1}} {\sum\limits_{q = 1}^{{v_1}} {{E_a}} } \cdot {e^{ - {k_{\rm{s}}}\left\| {(p - u,q - v)} \right\|}}$ | (14) |
式中:ks——在不同路径、不同距离下的重要性参数;
(p-u), (q-v)——轨迹la由路径(p, q)进入热源与网络(u, v)的距离。
把每一个轨迹都构建热能图, 其热能图特征可表示为
| ${d_4}(a,b) = \sum\limits_{u = 1}^{{u_1}} {\sum\limits_{v = 1}^{{v_1}} {{H_a}} } (u,v){H_b}(u,v)$ | (15) |
2.5 运动相关性
如果行人a和行人b属于同一小群体, 则其运动轨迹一致, 表明两人的运动相关性比较高, 从t→t+1时刻, 行人a和行人b的运动相关性可表示为
| ${d_5}(a,b) = \frac{1}{2}\sum\limits_{\tau = t}^{t + 1} {\frac{{v_\tau ^a \cdot v_\tau ^b}}{{\left\| {v_\tau ^a} \right\| \cdot \left\| {v_\tau ^b} \right\|}}} $ | (16) |
式中:
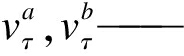 行人a和行人b在τ时刻的速度。
行人a和行人b在τ时刻的速度。
3 结构化SVM
本文采用结构化SVM来模拟和学习预测解决方案。SVM是一种监督式机器学习方法, 用于分类和模式识别等。在该方法中, 支持向量被用来表示决策边界, 并将低维输入空间的线性不可分数据映射到高维特征空间, 使其线性可分离。该算法将在第i个时间窗口所有可能两两成对的行人轨迹所提取的特征作为输入xi, xi={[1-di(a, b); di(a, b)]}, yi为人群分类结果。构建一个由输入到输出的分类映射, 输入输出对为{(x1, y1), (x2, y2), (x3, y3), …, (xn, yn)}。根据相关性聚类算法获得Wd, 然后经过Frank-Wolfe算法迭代300次得到最优权值W[15]。由判别函数F测量(x, y)对之间的兼容性, 并为那些良好的匹配给出高分。判别函数为
| ${\rm{F}}({\rm{x}},{\rm{y}};{\rm{W}}) = {{\rm{W}}^T}\sum\limits_{{\rm{y}} \in {\rm{Y}}} {\sum\limits_{{\rm{a}} \ne {\rm{b}} \in {\rm{y}}} {{{\rm{x}}^{{\rm{ab}}}}} } $ | (16) |
通过最小化一个凸目标函数, 参数可以通过一组实例{(x1, y1), (x2, y2), (x3, y3), …, (xn, yn)}在大范围框架中学习。凸目标函数为
| ${\min _W}\frac{1}{2}{\left\| W \right\|^2} + C\sum\limits_{i = 1}^n \varepsilon i$ | (17) |
其中:∀i:εi≥0; ∀i, ∀y≠yi:WTδφi(y)≥Δ(y, yi)-εi; δ(φi(y))=φ(xi, yi)-φ(xi, y); Δ(y, yi)为损失函数。
4 损失函数
本文参考了文献[16]的损失函数。与其他损失函数相比, 该损失函数对处理大量人群和单独个人有较好的效果。该算法假设每一个单独存在的行人轨迹Ti会与自身的影子αTi相连接。y和yi两种聚类方法各自对应的生成森林为Q和R。Q和R各自连接的元素分别为树集Q1, Q2, Q3, …, 以及R1, R2, R3, …。Qj中元素的个数为|Qj|, 创建生成树需要的链接为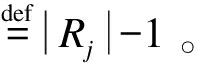 定义子树πQ(Rj)为仅考虑Rj中存在的Q部分之间的成员关系, 树Rj对应森林Q的部分。如果R中Qj部分在子树|πR(Qj)|中, 则
定义子树πQ(Rj)为仅考虑Rj中存在的Q部分之间的成员关系, 树Rj对应森林Q的部分。如果R中Qj部分在子树|πR(Qj)|中, 则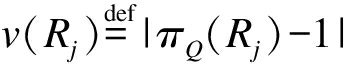 为恢复原始树的链接数。Rj的精确度可以由缺失链路的数量除以创建该生成树所需的最小链路数量计算得出, 故精确度可表示为
为恢复原始树的链接数。Rj的精确度可以由缺失链路的数量除以创建该生成树所需的最小链路数量计算得出, 故精确度可表示为
| $ \begin{aligned} P_{R}=& 1-\frac{\sum_{j} v\left(R_{j}\right)}{\sum_{j} c\left(R_{j}\right)}=\\ & \frac{\sum_{j}\left|R_{j}\right|-\left|\pi_{Q}\left(R_{j}\right)\right|}{\sum_{j}\left|R_{j}\right|-1} \end{aligned} $ | (18) |
yi和y两种聚类方法各自对应的生成森林为Q和R。Q和R各自连接的元素分别为树集Q1, Q2, Q3, …和R1, R2, R3, …。Qj中元素的个数为|Qj|, 创建生成树需要的链接为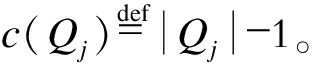 定义子树πR(Qj)为仅考虑R中存在的Qj部分之间的成员关系, 树Qj对应森林R的部分。如果R中Qj部分在子树|πR(Qj)|中, 则
定义子树πR(Qj)为仅考虑R中存在的Qj部分之间的成员关系, 树Qj对应森林R的部分。如果R中Qj部分在子树|πR(Qj)|中, 则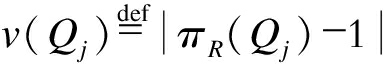 为恢复原始树的链接数。Qj的召回误差可以由缺失链路的数量除以创建该生成树所需的最小链路数量计算得出。故Q的召回率可表示为
为恢复原始树的链接数。Qj的召回误差可以由缺失链路的数量除以创建该生成树所需的最小链路数量计算得出。故Q的召回率可表示为
| $ \begin{array}{r} R_{Q}=1-\frac{\sum_{j} v\left(Q_{j}\right)}{\sum_{j} c\left(Q_{j}\right)}= \\ \frac{\sum_{j}\left|Q_{j}\right|-\left|\pi_{R}\left(Q_{j}\right)\right|}{\sum_{j}\left|Q_{j}\right|-1} \end{array} $ | (19) |
由给定精确度P, 召回率R和F1-score将损失函数定义为
| $\Delta\left(y, y_{i}\right)=1-F_{1}$ | (20) |
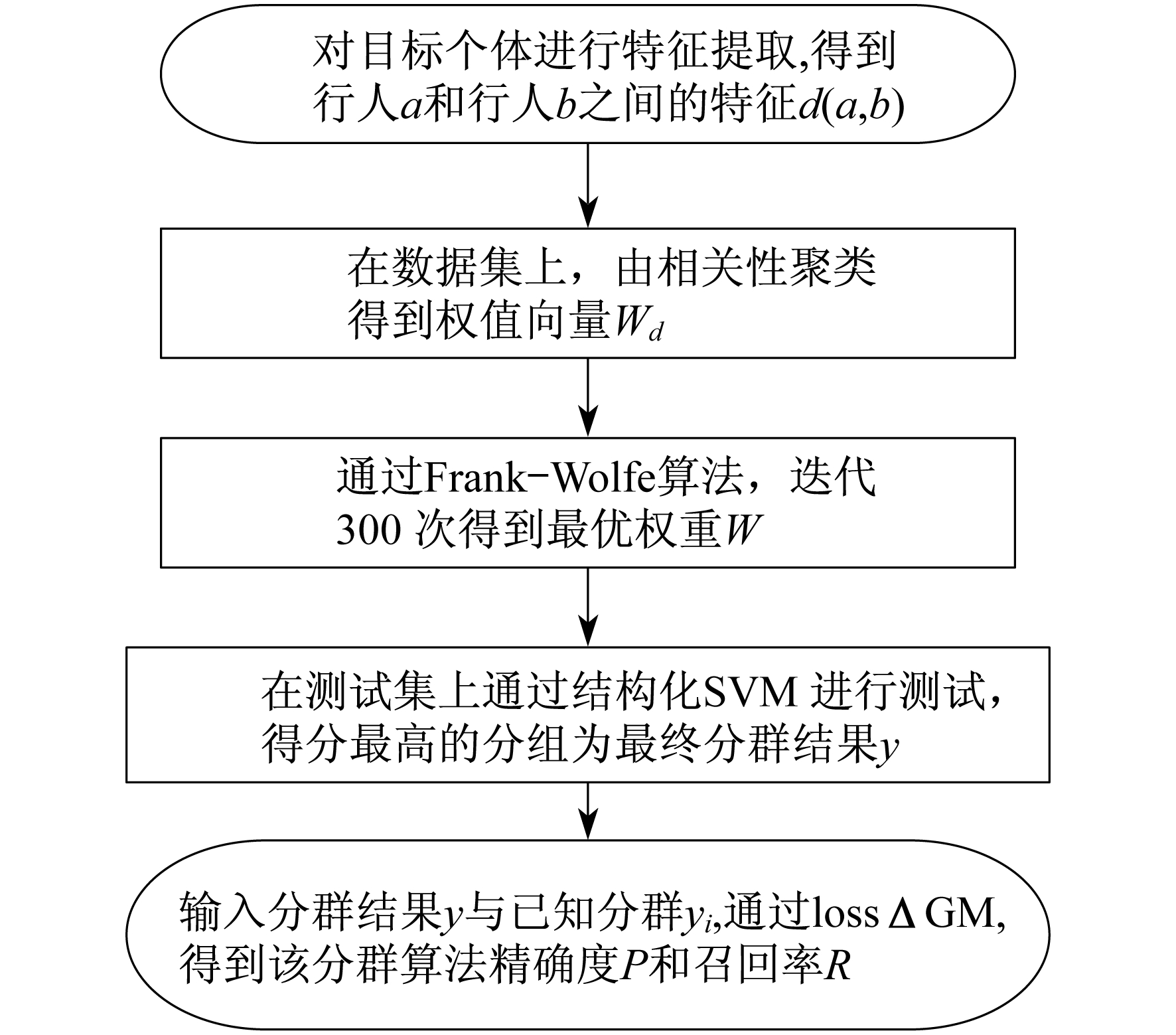
试验算法流程如图 1所示。
5 试验结果
本文在MPT和GVEII数据集上进行测试, 数据集MPT和GVEII主要包括来自公共场所摄像机拍摄的不同场景条件下大量行人活动的视频(取4个群体典型视频)。算法使用MATLAB软件实现, 试验均在Intel i5 CPU, 4 G RAM下进行。将本文算法与文献[16]算法进行对比, 结果如表 1所示。
表 1中, 场景1为数据集GVEII中的一个室内场景, 场景2为MPT中街道交叉口场景, 场景3为MPT中机场内的场景, 场景4为MPT中马路上的场景。
表 1
两种算法的测试精确度对比%
| 数据集 | 本文算法 | 文献[16] | ||
| 精确度 | 召回率 | 精确度 | 召回率 | |
| 场景1 | 88.76 | 88.16 | 84.12 | 84.71 |
| 场景2 | 91.54 | 88.81 | 88.46 | 87.12 |
| 场景3 | 85.48 | 81.54 | 83.87 | 80.00 |
| 场景4 | 98.08 | 96.23 | 96.15 | 92.59 |
由表 1可知, 本文算法的精确度和召回率均高于文献[16], 故在分割个体和小群体方面, 本文算法要优于文献[16]的算法。
将参数W=[α, β]=[w1, w2, w3, …, w10]代入式(2), 得
| $ \begin{aligned} W_{d}^{a b}=& \alpha^{\mathrm{T}}(1-d(a, b))-\beta^{\mathrm{T}} d(a, b)=\\ & w_{1}+w_{2}+w_{3}+w_{4}+w_{5}-\left(w_{6}+w_{1}\right) d_{1}-\\ & \left(w_{7}+w_{2}\right) d_{2}-\left(w_{8}+w_{3}\right) d_{3}-\\ & \left(w_{9}+w_{4}\right) d_{4}-\left(w_{10}+w_{5}\right) d_{5} \end{aligned} $ | (21) |
每个特征占分群得分的比例由式(21)中的常数项决定, 其编码为特征本身系数的绝对值。
图 2为式(21)中特征归一化的系数。
由图 2可知, 在任何一个数据集中, 轨迹时空距离特征都占有最高比重, 其他特征的重要性随着视频序列的改变而有所变化。例如, 在场景1和场景3中, 运动方向特征在测量分群算法得分时起重要作用, 而场景2中, 运动方向特征所占比例极小。运动相关性特征在场景2和场景3中十分重要, 但在场景1和场景4中热能图特征的关键性更高。
图 3为不同场景分组检测结果对比。图 3中, 第一列为本文算法试验结果, 第二列为文献[16]试验结果。根据已知分组情况, 在场景1中, 本文算法正确分组6个, 错误分组零个; 文献[16]算法正确分组5个, 错误分组1个。在场景2中, 本文算法正确分组10个, 错误分组2个; 文献[16]算法正确分组9个, 错误分组5个。在场景3中, 本文算法正确分组5个, 错误分组3个; 文献[16]算法正确分组5个, 错误分组3个。在场景4中, 本文算法正确分组3个, 错误分组零个; 文献[16]算法正确分组2个, 错误分组零个。由此表明, 本文算法的分组情况在整体上优于文献[16]算法。
在密集度较小的场景中, 行人运动轨迹受同一组行人运动影响较大, 文献[16]中的轨迹相似性特征对行人分组十分有利。但在密集度较大的场景中, 一个人的运动轨迹不仅受到同一组行人的影响, 而且也受到周围多个行人的影响。因此, 文献[16]中的轨迹相似性特征在密集度大的拥挤场景中会使错误分组的情况增多。
本文算法通过连续能量最小化的方法提取了行人的坐标和轨迹信息[17]。在现实场景中, 经常有不精确的地平面投影或跟踪误差, 会造成定位行人坐标误差。由于自动人体检测器的定位误差会产生许多轨迹碎片, 当计算轨迹时空距离特征和格兰杰因果性特征时, 大量的轨迹碎片会影响群体检测的效果。因此, 通过减小窗口的大小, 可以最小化每个例子中的分割轨迹的数量, 并恢复大部分轨迹的原始效果。
6 结语
在无序运动的场景中, 人群不仅有空间性特征, 而且还保留有社会特征, 因此本文提取了个体之间运动轨迹时空特征、运动方向特征、格兰杰因果性、热能图特征以及运动相关性特征来捕捉和表征不同群体的特性。为了得到有效的聚类规则, 采用了结构化支持向量机。该算法综合了各个物理特征和社会特征, 最大程度地利用了群体中的有效信息, 使得分组更为精确。经过试验结果比较可知, 本文的检测效果要高于文献[16]的算法。
参考文献
-
[1]SOCHMAN J, HOGG D C. Who knows who—inverting the social force model for finding groups[C]//IEEE International Conference on Computer Vision Workshops. IEEE, Barcelona, Spain, 2011: 830-837.
-
[2]GE W, COLLINS R T, RUBACK R B. Vision-based analysis of small groups in pedestrian crowds[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2012, 34(5): 1003.
-
[3]基于多层自适应聚类模型的密集人群分群检测算法[J]. 上海电力学院学报, 2017, 33(1): 91-96.
-
[4]SHAO J, CHEN C L, WANG X. Scene-independent group profiling in crowd[C]//Computer Vision and Pattern Recognition. IEEE, Columbus, OH, USA, 2014: 2227-2234.
-
[5]DURLAUF S N. A framework for the study of individual behavior and social interactions[J]. Sociological Methodology, 2010, 31(1): 47-87.
-
[6]MOORE B E, ALI S, MEHRAN R, et al. Visual crowd surveillance through a hydrodynamics lens[J]. Communications of the Acm, 2011, 54(12): 64-73. DOI:10.1145/2043174.2043192
-
[7]HELBING D, MOLNR P. Social force model for pedestrian dynamics[J]. Physical Review E Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics, 1995, 51(5): 4282.
-
[8]BANDINI S, GORRINI A, MANENTI L, et al. Crowd and pedestrian dynamics: empirical investigation and simulation[C]//Proceedings of Measuring Behavior, Utrecht, The Netherlands, 2012: 308-311.
-
[9]ZHAO Q, SHAO J, ZHAO Y. A multistage filtering for detecting group in the crowd[C]//International Conference on Audio, Language and Image Processing. IEEE, Shanghai, China, 2017: 771-774.
-
[10]GRANGER C W J, GHYSELS E, SWANSON N R, et al. Essays in econometrics: investigating causal relations by econometric models and cross-spectral methods[J]. Journal of Econometrics, 2001, 2(2): 111-120.
-
[11]LIN W, CHU H, WU J, et al. A heat-map-based algorithm for recognizing group activities in videos[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2015, 23(11): 1980-1992.
-
[12]ZHOU B, TANG X, WANG X. Coherent filtering: detecting coherent motions from crowd clutters[C]//Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 2012: 857-871.
-
[13]BANSAL N, BLUM A, CHAWLA S. Correlation clustering[J]. Machine Learning, 2004, 56(1/3): 89-113.
-
[14]SHAH N, KOLMOGOROV V, LAMPERT C H. A multi-plane block-coordinate Frank-wolfe algorithm for training structural SVMs with a costly max-oracle[C]//Computer Vision and Pattern Recognition. IEEE, Boston, MA, USA, 2015: 2737-2745.
-
[15]LI J W, ZHOU X L, CHAN S X, et al. Object tracking using a convolutional network and a structure doutput SVM[J]. Computational Visual Media, 2017(4): 1-11.
-
[16]SOLERA F, CALDERARA S, CUCCHIARA R. Socially constrained structural learning for groups detection in crowd[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2016, 38(5): 995-1008.
-
[17]MILAN A, ROTH S, SCHINDLER K. Continuous energy minimization for multitarget tracking[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2014, 36(1): 58-72.