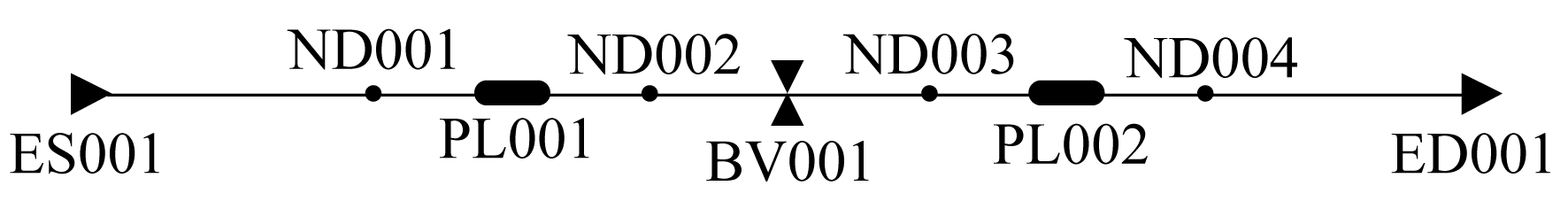|
|
|
发布时间: 2019-04-10 |
|
|
|
|
收稿日期: 2019-01-24
中图法分类号: TE832;TE88
文献标识码: A
文章编号: 1006-4729(2019)02-0101-06
|
摘要
针对高压管输天然气在阀门启闭瞬间产生的水力波动、不稳定流动等现象, 以湖北某天然气门站为例, 在已知天然气管网等相关设备参数的基础上, 探究考证此现象对天然气管网安全的影响。一方面, 通过力学方程对产生水力波动的天然气控制体进行受力分析, 推导求解出最大的水力扰动压强约为0.093 MPa; 另一方面, 利用模拟软件RealPipe-Gas对水力波动过程进行仿真模拟, 确定扰动压强大致为0.06~0.09 MPa。采用控制变量法, 模拟不同变量工况下流量、管网压力、管径对波动大小的影响, 分析水力波动对系统造成的影响, 并给出了减轻波动的相应措施。
关键词
管输天然气; 输配波动; 扰动压强; 影响变量
Abstract
In view of the phenomenon of"hydraulic"fluctuation and unstable flow generated by high-pressure pipe natural gas in the moment of valve opening and closing, a natural gas gate station in Hubei is taken as an example.Based on the known natural gas pipeline network and other related equipment parameters, the impact of this phenomenon on the safety of natural gas pipeline network is explored and verified.On the one hand, the mechanical equation is used to analyze the natural gas control body which produces the"hydraulic"fluctuation, and the maximum "hydraulic" disturbance pressure is derived to be about 0.093 MPa.On the other hand, the simulation software RealPipe-Gas is used to simulate the "hydraulic" fluctuation process.By comparing and analyzing the two results, it is determined that the disturbance pressure is between 0.06 MPa and 0.09 MPa.The method of variable control is used to simulate the influence of flow rate, pipe network pressure and pipe diameter on the fluctuation under different variable conditions, to analyze the influence of"hydraulic" fluctuation on the system, and to give corresponding measures to mitigate fluctuations.
Key words
pipeline natural gas; transmission and distribution fluctuation; disturbance pressure; influence factor
天然气资源的分布与需求存在地域上的不平衡, 且天然气需求愈来愈大, 使得天然气管网不断向着高压力、大口径的方向快速发展[1-2]。天然气供应用户前, 需要进行调压, 由于焦耳-汤姆逊效应[3], 天然气温度会骤降, 并释放巨大的冷量。国内外专家将管输天然气余压回收系统与需要电力、旋转机械能或冷能的系统相结合, 设计出新的复合系统, 以达到回收天然气压力能的目的[4-5]。
天然气是高压流体, 具有一定的惯性, 当压力能利用系统遇到事故工况或定期停机维护时, 管道中的阀门突然关闭, 天然气受阻而流速突然变小, 其惯性会使管道内局部压强突然升高。这一过程中形成的水力波动对管道的影响不可小觑[6-7]。
20世纪60年代, TAYLOR T D等人[8-9]以质量方程和动量方程为基础, 编制了针对管网瞬态输气的计算机程序, 采用特征线法、有限差分法及同步差分法进行求解; VOSTRY Z等人[10]分析了环境等因素对天然气管网稳态与瞬态运行的影响, 并且给出了处理这些不确定因素的合理工程指导; 王寿喜[11]提出了能够同时应用于稳态环境下的气体管网与液体管网的线性分析法的原理和模型; 唐建峰等人[12]基于连续性方程、动量方程、能量守恒方程和SHB-WR气体方程建立了天然气管网不稳定流动模型, 采用隐式中心差分法对方程进行求解。目前, 很多国内外学者对管网天然气运行工况进行了仿真模拟, 但针对天然气管路切换和阀门启停瞬间所产生的水力波动, 以及水力波动扰动的压强大小和危害程度、管路切换过程能否实现无扰切换等问题仍有待进一步研究和论证。
本文通过中国石油管道科技研究中心研发的RealPipe-Gas模拟软件进行建模仿真, 并与理论计算值相比较, 得到了天然气管道阀门开启、关闭时的扰动压强数值范围。通过控制变量法, 找出了影响扰动压强数值范围的因素, 并提出了相应的解决措施。
1 管输天然气水力波动的研究与计算
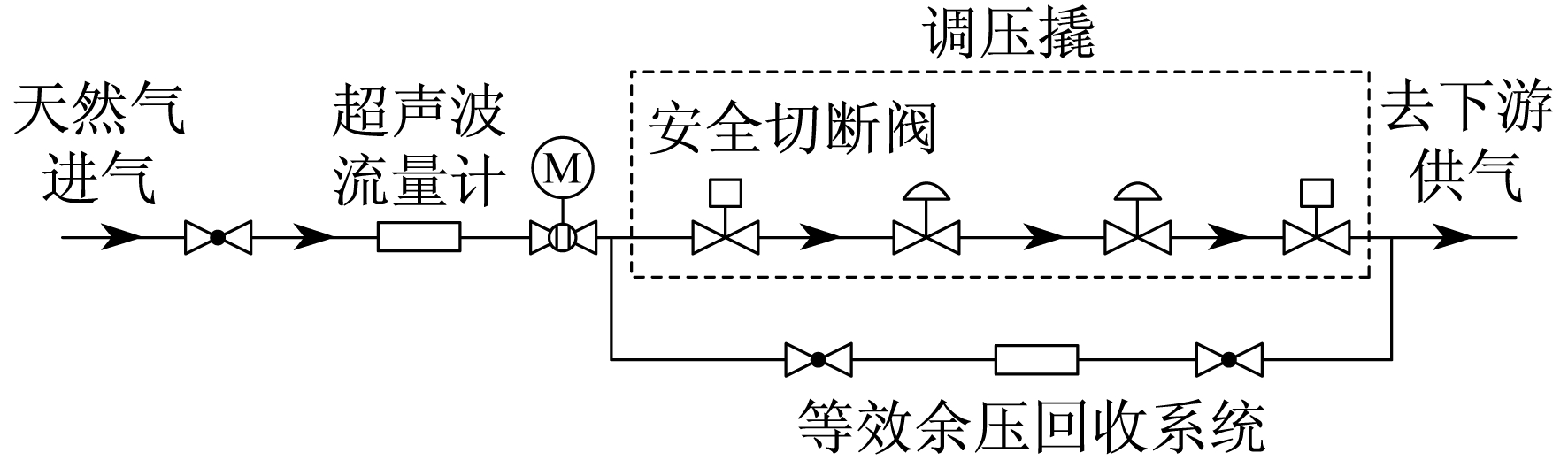
由于分输站调压管路系统较为复杂, 因此对其进行简化。图 1为简化后的物理模型图, 管道外径取273 mm, 管壁厚取10 mm, 该简化图也基本适用于所有分输站建设的天然气余压回收系统分析。
1.1 水力波动压强的计算
假设管道内天然气流速为v, 压强为p, 考虑高压天然气的可压缩性, 忽略管道的变形和天然气与管道的摩擦阻力影响。当t=0时, 管道阀门突然关闭, 紧贴阀门的流体由于受到阀门的阻挡, 流速突变为零, 这层流体受到后面来流的未变流速的流体的压缩, 其压强突增了Δp。这种压缩必然会一层一层地往上游传播, 形成一种压缩波, 其传播速度为c。
阀门附近受压缩的流体压强为p+Δp, 而上游未受影响的流体压强仍然为p, 此时流体整体有Δp的压差, 压力的不平衡会使流体发生倒流, 原本受压缩的流体会因倒流而逐渐发生膨胀, 压强也会减小。这种压强的降低也会一层一层地向下游传播, 形成所谓的膨胀波, 其传播速度也为c。
现实情况中, 由于流体或者天然气是有黏性的, 且流体和管材也不具有完全弹性, 流体的动能会被消耗, 最终流体静止, 波动停止。工程上, 一方面希望水击现象对管道造成的伤害越小越好, 另一方面希望水击现象持续的时间越短越好, 因此在管道天然气压力扰动现象中, 对压强的大小和压强波传播速度的快慢进行估算十分必要[13-14]。
当t=Δt时, 压缩波向上游传播了Δs的距离, 作用在该管段内流体上的所有沿管轴方向的合力为F, 如图 2所示。
依据动量定理对受压缩部分流体进行分析, 可以得到:物体动量的增量等于该物体所受合力的冲量。用公式表示为
| $F t=m \cdot \Delta v$ | (1) |
由图 2可得:
| $[p-(p+\Delta p)] A \cdot \Delta t=\rho \cdot \Delta s \cdot A(0-v)$ | (2) |
式中:Δp——天然气压力波, Pa;
A——管道横截面的面积, m2;
ρ——正常流动时的天然气密度, kg/m3。
式(2)化简后可得:
| $\Delta p=\rho v c$ | (3) |
1.2 压强波传播速度的计算
根据质量守恒定律, 经过δt后的管段里的质量应该等于原有的质量加上补流进的质量, 即:
| $(\rho+\delta \rho)(A+\delta A) c \delta t=\rho A c \delta t+\rho A v \delta t$ | (4) |
略去高阶微量, 可以得到:
| $ v=c\left(\frac{\delta \rho}{\rho}+\frac{\delta A}{A}\right) $ | (5) |
根据流体体积模量的计算公式, 以及材料力学中对正应力和线应变的计算可以得到:
| $ v=c\left(\frac{1}{K}+\frac{d}{E s}\right) \Delta p $ | (6) |
式中:K——天然气的体积模量;
d——管道的直径;
E——管壁的弹性模量;
s——管壁的厚度。
将水击压强的计算结果代入方程, 消去Δp可以得到:
| $ c=\left[\frac{\frac{K}{\rho}}{1+\frac{K d}{E s}}\right]^{\frac{1}{2}}=\frac{c_{0}}{\left[1+\frac{K d}{E s}\right]^{\frac{1}{2}}} $ | (7) |
式中:c0——所求c前一时段的波速值。
根据实际工程数据, 在5 MPa, 20 ℃时, 管道中的波速大约是400 m/s[15]。
1.3 管道天然气流速与水力波动最大压强的计算
标准工况下, 天然气密度ρ为0.717 4 kg/m3, 流量为68 000 m3/h, 管径为273 mm; 5 MPa压力下, 天然气密度为38.19 kg/m3, 计算可得流速v=6.06 m/s。
根据式(3), 分别代入密度、流速、波速的值, 可得出在管道天然气阀门启闭瞬间产生的类似水击现象的压强扰动下, 最大的扰动压强约为0.093 MPa。
2 仿真模拟
天然气工业中, 在计算各种气体状态参数时, 状态方程采用较多是RKS方程、P-R方程、BWRS方程、AGA8方程[16-17]。BWRS方程因其在常温范围内较广的适应性和较为理想的计算精确度, 是最适合5 MPa下管网天然气工况的气体状态方程, 在对天然气压力扰动过程进行模拟时可以选用。
流体系统内介质的运动规律都遵循质量守恒、动量守恒和能量守恒三大定律, 分别由连续性方程、运动方程和能量方程来描述, 在采用RealPipe-Gas软件进行仿真模拟时, 将管道内的流动近似看成一维, 管网中天然气控制方程联合天然气实际气体的物性方程, 就构成了封闭的方程组, 再综合运用“蛙跳”“迎风”等策略对方程进行求解。
2.1 管输天然气水力波动过程仿真模拟
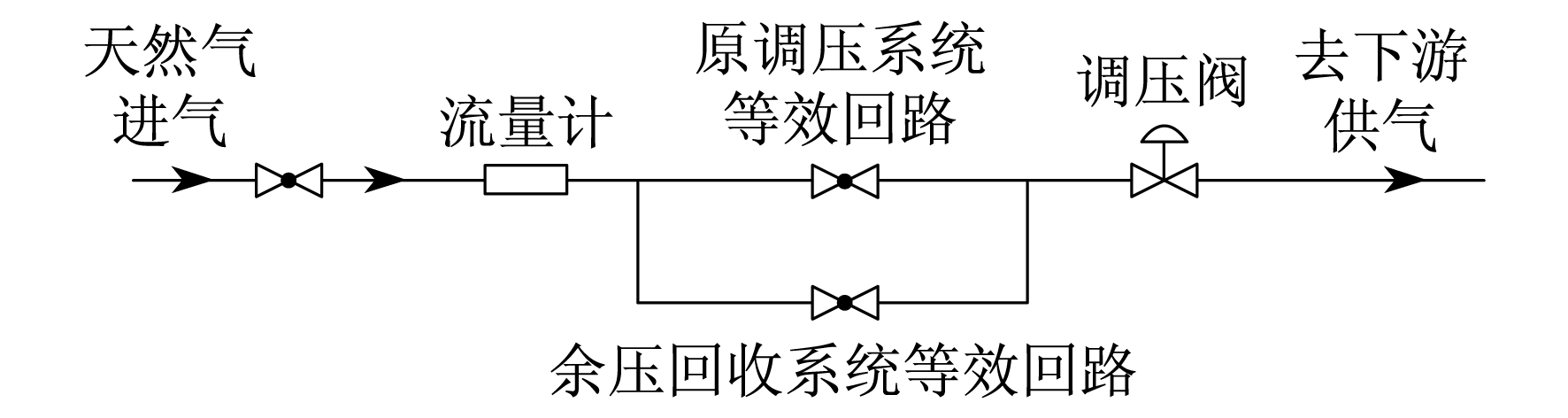
采用RealPipe-Gas软件对管网天然气输配过程进行仿真模拟, 但对于天然气管路切换瞬间管道中天然气流体的变化过程, 该软件并不能完全模拟出所有设备, 且天然气水力波动属于瞬态响应, 软件中的调压阀无法适应此过程, 因此需要对原简化的物理模型再次进行简化改造。图 3为简化改造后的仿真物理模型。
2.2 RealPipe  Gas软件仿真模拟
Gas软件仿真模拟
2.2.1 仿真模型的建立
用RealPipe-Gas软件建立原调压管线和压力能回收系统管线, 由于软件无法模拟实际的分输站调压原件和压力能回收组件, 所以对两管线进行简化。用两个截止阀代替两个管路的调压部件, 两个管路汇合后用理想调节阀将压力调节到合适的大小。具体建立的系统模型如图 4所示。
2.2.2 工况运行
点击瞬态运行后, 将截断阀BV001, BV002, BV003全部打开, 设置分输站进口流量, 调节理想调节阀, 然后监视管段PL006的出口压力和标况下的进口流量。当压力稳定在2 MPa左右时, 开始进行管路切换操作。在实际管路切换过程中, 为确保系统的正常安全运行, 往往会先打开待切换管路阀门, 等调压稳定后再关闭原管路阀门。工况以最不利情况考虑, 结合模拟软件的特性, 开阀行程时间=关阀行程时间=0.01 s。下面分别对开阀和关阀两个过程中管路中产生的天然气水力波动过程进行模拟。
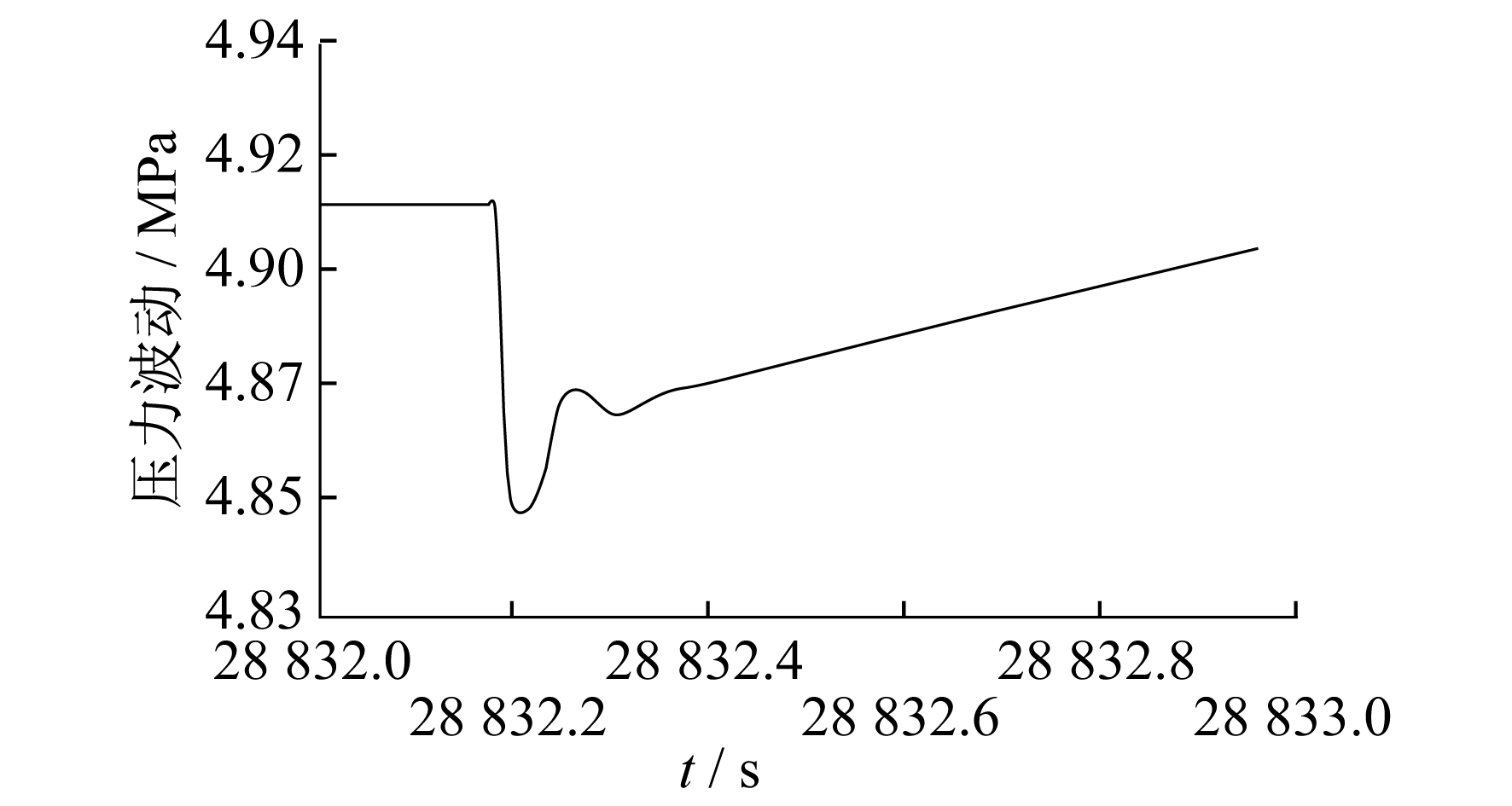
(1) 开阀过程中管道压力变化模拟。先打开截断阀BV004, 观察截断阀打开之后对原管路的影响, 监测管段PL004的出口压力趋势曲线, 如图 5所示。
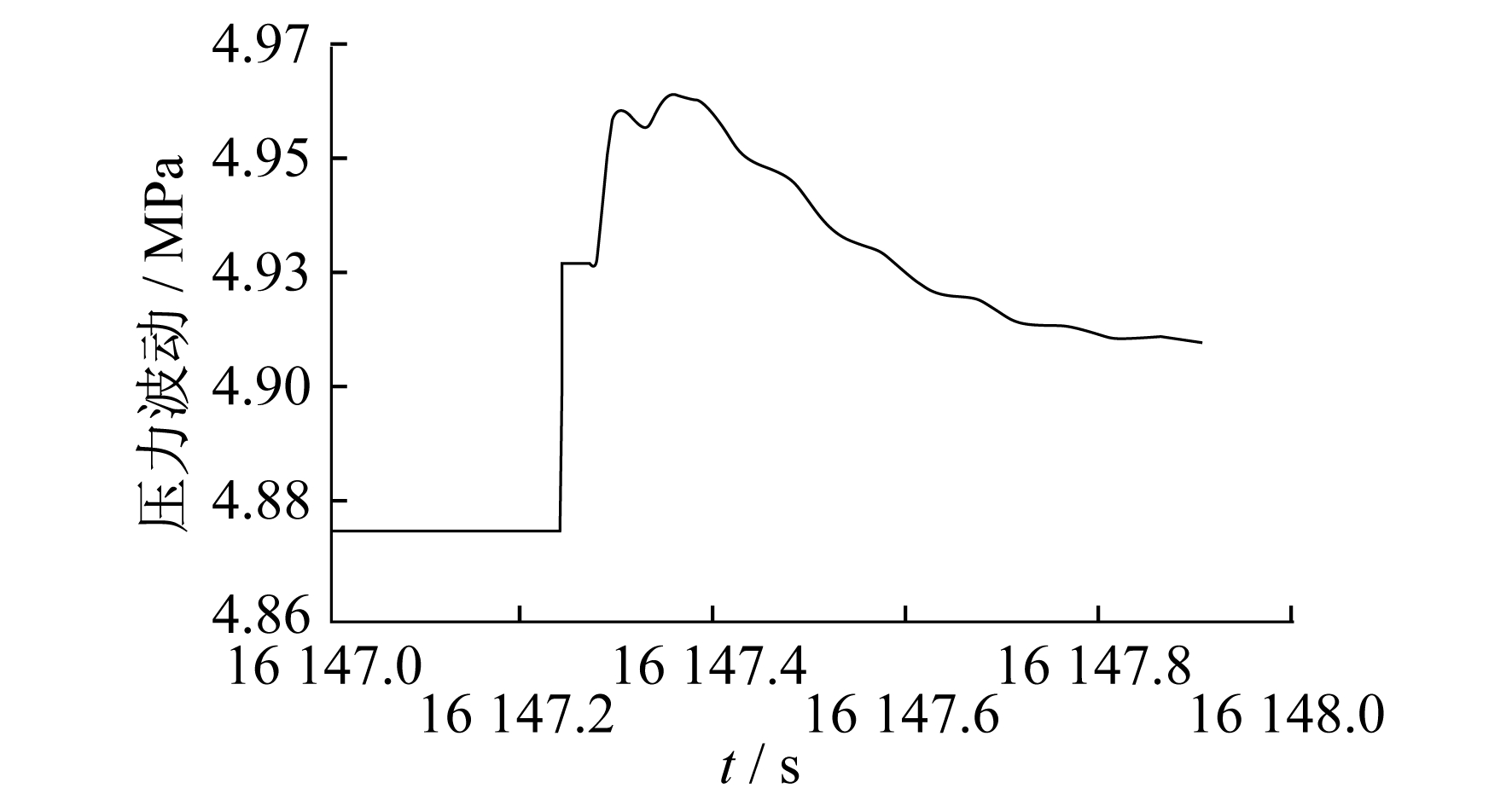
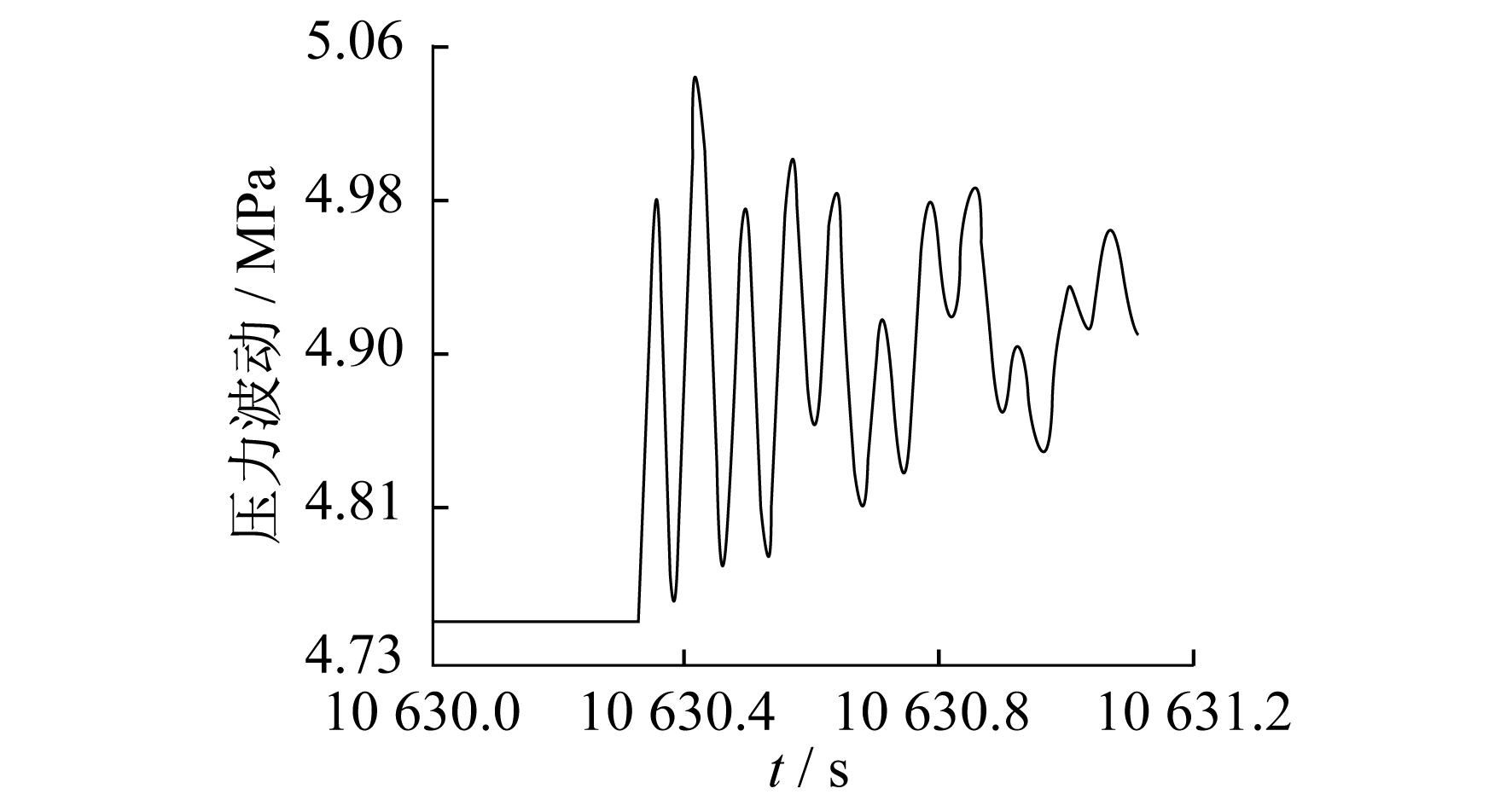
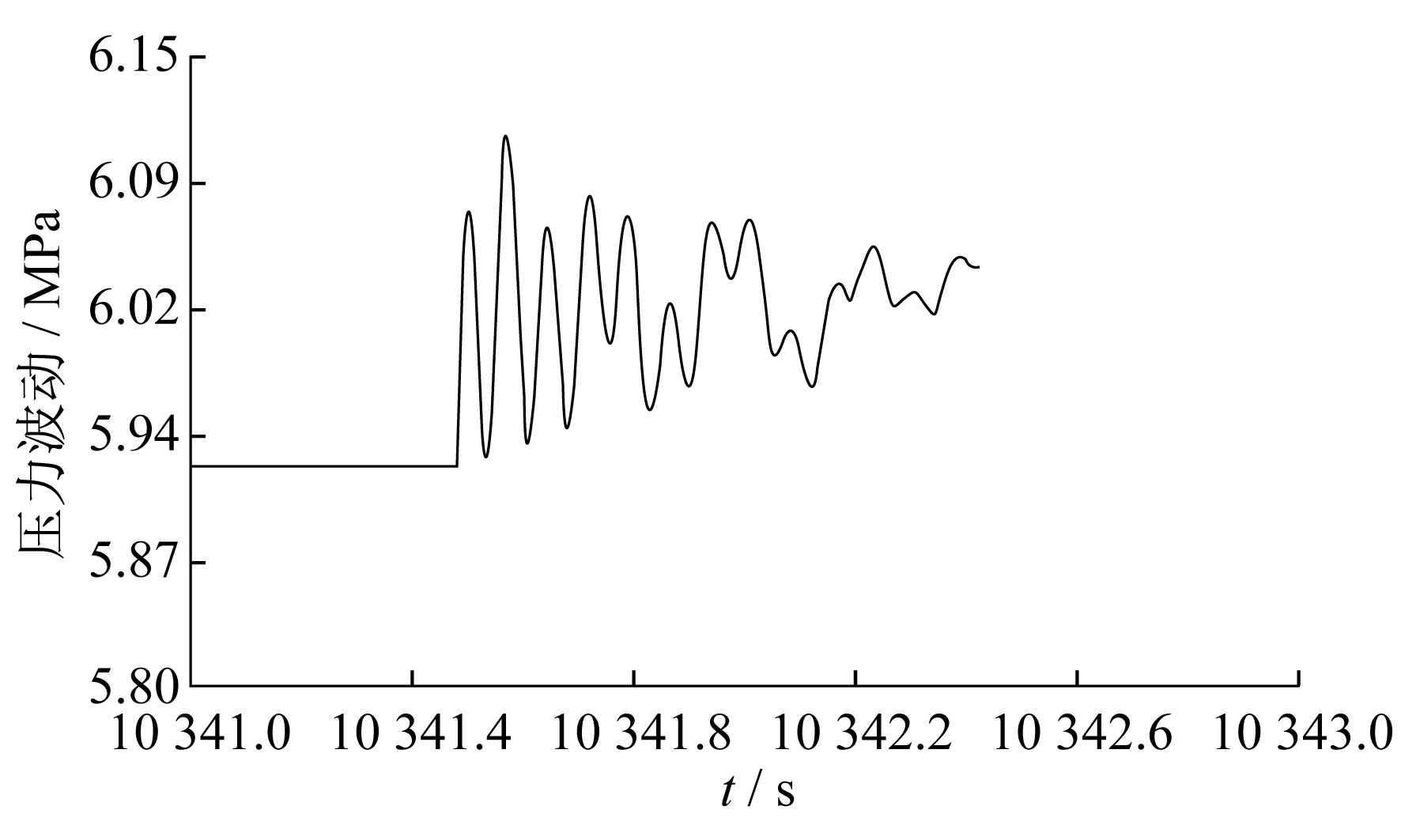
(2) 关阀过程中管道压力变化模拟。当压力稳定在2 MPa附近时, 关闭截断阀BV003(截断阀BV004为开启状态), 监测管段PL003的出口压力趋势曲线, 如图 6所示。
图 5和图 6中, 横坐标为压力稳定时截断阀BV004开启后的时间变化, 步长为0.1 s, 因操作切入点的时间不一致, 数值大小的起点会有差距, 但对模拟无影响, 本文只选取10段作分析。下文模拟图的处理相同。
2.2.3 结果读取
2.3 仿真模拟结果分析
在开阀的过程中, 产生的水力扰动使管网压强往减小趋势变化, 最大开阀扰动压强约为0.067 0 MPa。在关阀的过程中, 产生的水力扰动使管网压强往增大趋势变化, 最大关阀扰动压强约0.080 9 MPa。通过比较水力扰动压强的两个最大值可知, 关阀产生的最大水力扰动要比开阀产生的扰动剧烈。
与天然气控制体的计算结果对比后可知, 两者在同一数量级, 且较为相近, 因此可判断在5 MPa及20 ℃条件下由于阀门启闭造成的水力扰动压强在0.06~0.09 MPa之间, 且随着时间的推移, 扰动压强的强度会逐渐减弱。
3 天然气水力波动的影响因素和结果分析
3.1 影响因素研究
为研究管输天然气水力波动大小的影响因素, 对仿真模拟进行简化, 如图 7所示。
根据公式Δp=ρvc, 由于ρ和c都与气体压力大小有关, 流速v与管道内气体流量和管径大小有关, 因此下文将根据上述简化流程进行模拟仿真, 探讨管道内天然气压力、流量及管径对水力波动的具体影响。
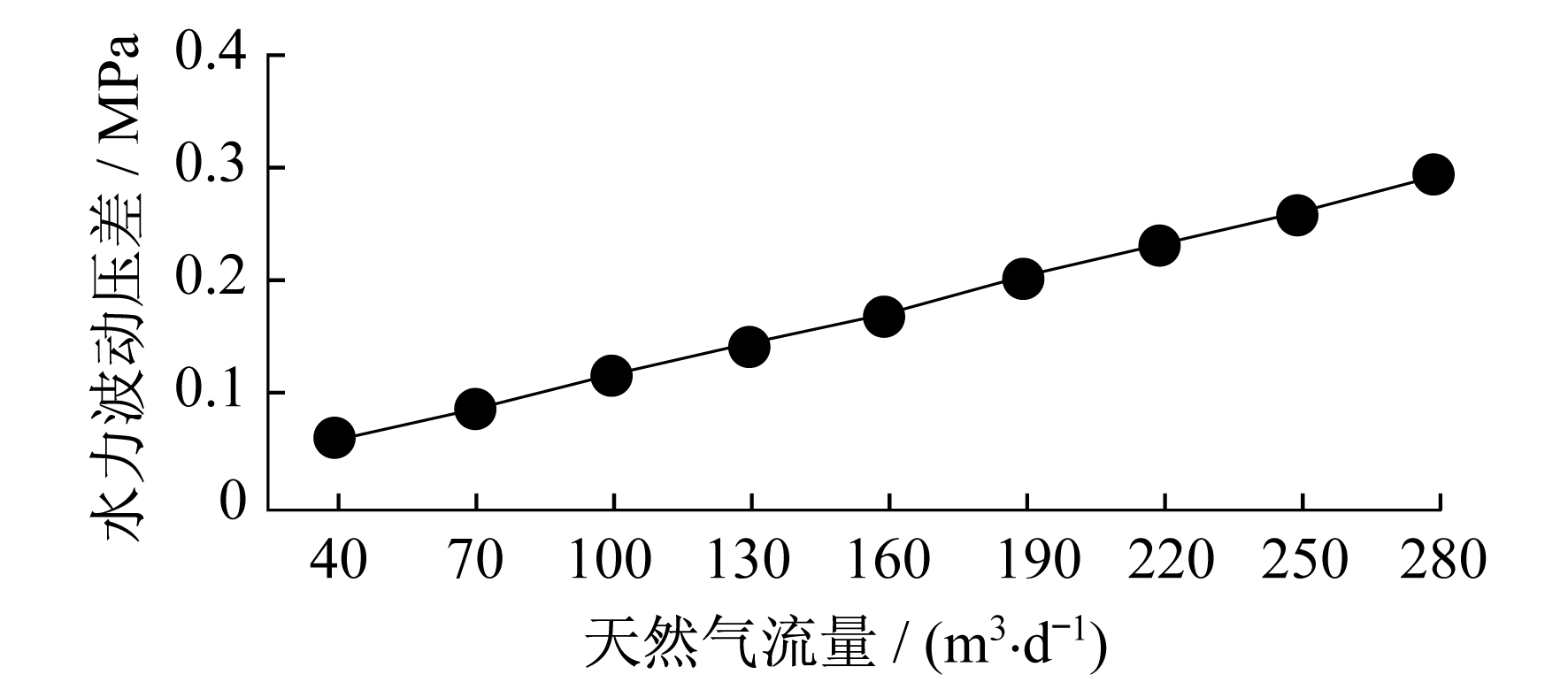
3.1.1 流量
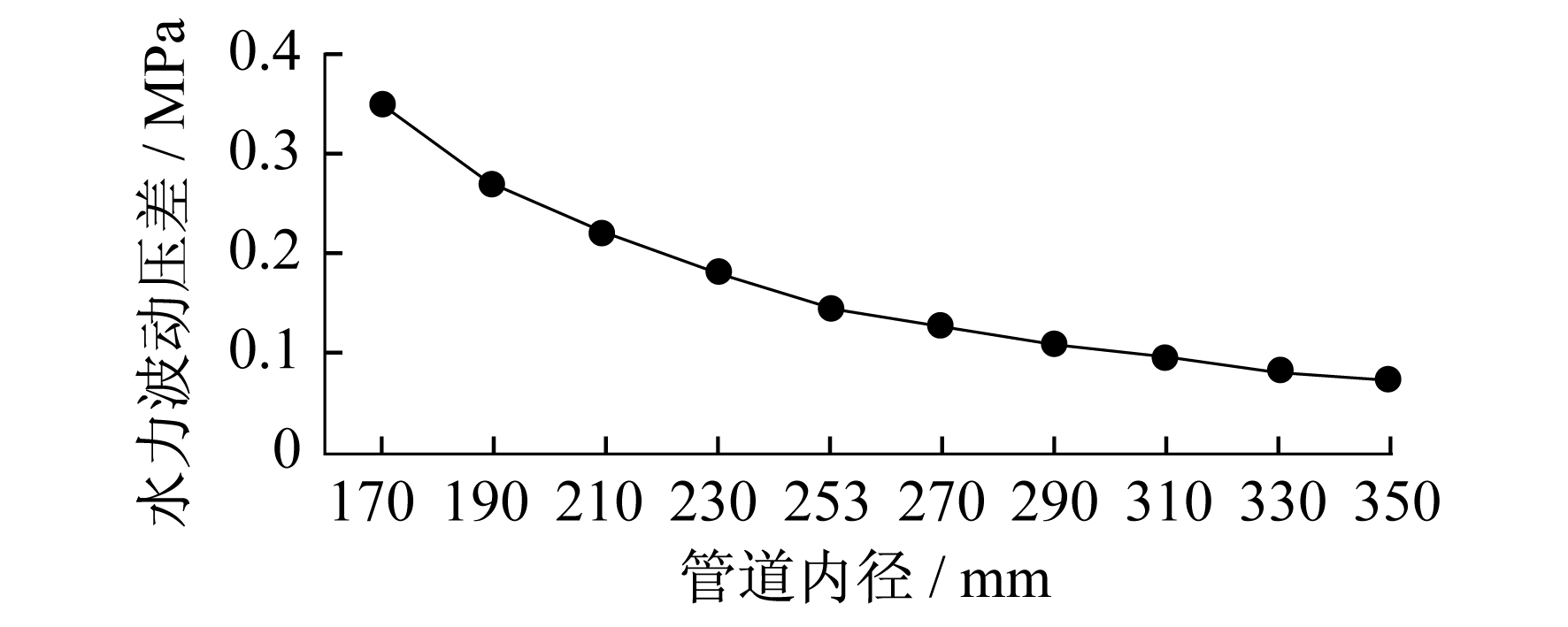
3.1.2 管径
3.1.3 管网压力
3.2 管网水力波动的结果分析
3.2.1 对阀门的影响
在调压管路的切换过程中, 阀门的启闭瞬间会使管网中的天然气产生水力波动, 致使管网发生协同振动, 同时还伴随噪声污染的产生。若管网中的压力振荡幅度较大, 可能会对调压阀主膜片及其指挥器中膜片造成冲击, 损坏膜片, 使整个调压系统丧失调压功能。
以EZR调压阀为例, 主膜片需要直接承接来流天然气的压力, 其主要制作材料为17E97丁腈橡胶, 最大允许工作压力为7.24 MPa, 最大允许工作差压值为5.52 MPa。如当管网中的水力波动差压超过了最大允许工作差压值, 那么调压系统就会失去调压功能。另外, 不同阀门膜片有各自不同的疲劳限度, 当膜片接收到高频率高压差的气流冲击后, 也会对其工作寿命产生影响。
由于在5 MPa及20 ℃条件下阀门启闭造成的水力扰动压强在0.06~0.09 MPa之间, 远小于原管道压力的数量级, 因此只要分输站调压阀配置正确, 在正常规范的操作下, 压力波对管道产生的冲击仍在管网能够承受的范围之内, 就不会对管网造成严重危害。但会对阀门膜片造成一定的疲劳, 将在一定程度上减少其使用寿命。
3.2.2 对天然气计量的影响
天然气的贸易过程中主要有两种计量方式, 一种是按热值量的多少进行计量交易, 另一种是按体积的大小进行计量交易。两种计量方式各有利弊, 热值计量方式可以准确衡量出天然气中所蕴含的经济价值, 具有很高的科学性, 但由于不同来源不同品质的天然气资源的热值大小不一, 造成了实际计量过程的困难, 且计量设备较为昂贵。体积计量方式虽然原理不够科学, 但由于天然气中的主要成分大致相同, 忽略了其他因素的干扰后, 贸易过程简单方便, 易于实现, 且计量设备较为便宜, 因此我国一直采用按体积计量的方式进行天然气贸易。
气体的体积大小与天然气压力相关。在5 MPa及20 ℃条件下, 天然气密度为38.193 5 kg/m3。在最大水力扰动压强的影响下, 天然气压强变为5.09 MPa, 此时天然气密度为38.950 1 kg/m3, 两者密度相差0.756 6 g/m3。由此可知, 管网中水力波动情况也会对天然气的精确计量造成一定的影响。
4 结论
经过研究, 管路中的天然气水力波动瞬时或短时间内不会对输气管道造成严重的危害, 但仍需要一些方法和措施减小水力波动大小。根据探究结果和实际工程经验提出以下几条建议, 以减轻压力波对管道造成的影响。
(1) 在现实工况下, 天然气水力波动压强与天然气流量成正比, 与管道直径成反比, 所以在条件允许的情况下, 适当增加管径或减小管道中天然气流量, 可以达到减小管道中天然气流速的目的, 从而减小水力波动。
(2) 在容易发生水力波动的部位设置蓄能器或稳压罐, 用以吸收冲击压力, 缓解管网水力波动, 或者安装安全阀, 限制压力的突然升高。
(3) 在常规管路切换时, 尽量延长开关阀门的时间, 保证先开阀, 再关阀。当出现故障时, 需要紧急切换管路, 在开关阀门时, 也要尽量保证先开后关。
(4) 在条件允许的情况下, 减小发生水力波动的管道长度, 减小压力波传播的时间, 并且使用弹性较好的管道, 以吸收管道内的振动。
参考文献
-
[1]天然气管网压力能利用与水合物联合调峰研究[J]. 煤气与热力, 2010, 30(8): 27-30. DOI:10.3969/j.issn.1000-4416.2010.08.009
-
[2]LAM P L. The growth of Japan's LNG industry: lessons for China and Hong Kong[J]. Energy Policy, 2000, 28(5): 327-333. DOI:10.1016/S0301-4215(00)00035-5
-
[3]门站调压节流引起管道低温的分析[J]. 煤气与热力, 2009, 29(1): 1-4. DOI:10.3969/j.issn.1000-4416.2009.01.001
-
[4]中国天然气工业发展前景与挑战[J]. 天然气工业, 2014, 34(2): 1-11. DOI:10.3787/j.issn.10000976.2014.02.001
-
[5]城市门站压力能回收设备研究应用进展[J]. 煤气与热力, 2010, 30(7): 18-20. DOI:10.3969/j.issn.1000-4416.2010.07.006
-
[6]黄李冰.水击计算方法和水击理论研究[D].郑州: 郑州大学, 2012.
-
[7]水击基本方程的改进[J]. 水利学报, 2007(8): 948-952. DOI:10.3321/j.issn:0559-9350.2007.08.010
-
[8]TAYLOR T D, WOOD N E, POWERS J E. A computer simulation of gas flow in long pipelines[J]. Society of Petroleum Engineers Journal, 1962, 2(4): 297-302. DOI:10.2118/107-PA
-
[9]HALLO P J. Application of digital simulation techniques to a natural gas transmission system[J]. Journal of Petroleum Technology, 1969, 21: 1091.
-
[10]VOSTRY Z, STYBLO M. Gas network simulation and uncertainty of pipe leg surroundings parameters[M]. Galveston: Pipeline Simulation Interest Group, 2009.
-
[11]管网稳态分析线性化法[J]. 天然气工业, 1987(4): 62-67.
-
[12]川气东送管道模拟仿真软件研发[J]. 天然气工业, 2008, 28(3): 114. DOI:10.3787/j.issn.1000-0976.2008.03.037
-
[13]任东芮.水击理论及水击波速研究[D].郑州: 郑州大学, 2016.
-
[14]董晨钟.水击基本理论研究[D].郑州: 郑州大学, 2014.
-
[15]水头压力及管道特性对水击波速变化的影响[J]. 水利水电技术, 2004(11): 84-86. DOI:10.3969/j.issn.1000-0860.2004.11.026
-
[16]STARLING K E, HAN M S. Thermo data refined for LPG-14 mixtures[J]. Hydrocarb Process, 1972, 51(5): 129-132.
-
[17]求解BWRS方程中压缩因子的数值方法[J]. 管道技术与设备, 2009(3): 14-16. DOI:10.3969/j.issn.1004-9614.2009.03.005