|
|
|
发布时间: 2019-04-10 |
|
|
|
|
收稿日期: 2019-01-05
基金项目: 国家自然科学基金(51507098);上海市电站自动化技术重点实验室项目(13DZ2273800)
中图法分类号: TM614
文献标识码: A
文章编号: 1006-4729(2019)02-0181-06
|
摘要
提出了运用马尔科夫法和序贯蒙特卡洛抽样的风电场可靠性模型并进行了并网可靠性评估。通过对风电场历史运行数据的统计, 利用马尔科夫法得到风电机组有功输出状态之间的转移率, 采用便于工程实现的正常、降额及故障3个状态作为风机故障模型并通过马尔科夫法计算得到状态概率及持续时间。利用序贯蒙特卡洛法对风机状态及其持续时间进行多重抽样, 所提出的模型经过IEEE-RTS79可靠性测试系统进行综合模拟, 并分析了不同风电渗透率下系统可靠性水平。实验结果表明所构建的模型能反映任意时间段的风机出力及可靠性水平。
关键词
风电场; 马尔科夫; 序贯蒙特卡洛; 多重抽样
Abstract
A wind farm reliability model using Markov chain and sequential Monte Carlo multistage is proposed and a grid-connected reliability evaluation is carried out.Through the statistics of the historical operation data of the wind farm, the transfer rate between the active output states of the wind turbines is obtained with the Markov method.Then, the three states of normal, derating and fault that are easy to implement are proposed as the wind turbine fault model and the state probability and duration are obtained with the Markov method.The Sequential Monte Carlo method is used to multiply the wind turbine state and its duration.The proposed model is comprehensively simulated by the IEEE-RTS79 reliability test system, and the system reliability level under different wind power penetration rates is analyzed.The experimental results show that the constructed model can reflect the wind turbine output and reliability level at any time.
Key words
wind farm; Markov; Sequential Monte Carl; multistage sampling
随着各国能源环境问题的日益突出, 发展新能源成为解决能源问题的重要手段, 风力发电相对于常规能源来说具有低排放、低污染等诸多优点。近年来全球风力发电行业正以每年20%的增速迅速扩张, 大规模风电场的建设使得其发电成本大幅下降, 但风力发电的间歇性、高渗透率等特点会增加电力系统的风险等级, 对电力系统调度产生一定影响[1]。风电场可靠性评估可为系统确定合理的充裕度, 指导系统规划运行, 并在电力系统的优化调度中, 运用适当的风险系数预测短期内系统抵御突发状况的能力[2-3]。建立合理的风电场模型对发电系统可靠性研究具有重要意义。
风电场并网在一定程度上缓解了能源问题, 但也给电力系统可靠性以及评估模型带来一定难度。当前针对风电场可靠性评估, 国内外学者进行了一系列研究。文献[4]通过威布尔分布描述的风速特性结合风电机组的功率特性, 建立风电场出力概率模型, 但其未考虑风机的随机故障。文献[5]考虑到风速的边缘概率分布, 利用Copula函数模拟产生风速序列, 在一定程度上解决了风速不确定性的问题, 但其受到风电场规模的限制, 当风电机组规模较大时会带来较大困难。文献[6]综合考虑了风速随机性条件, 采用聚类的方法将风电场建成类似多状态降额的常规机组, 但其未考虑风电机组的故障模型。文献[7]将状态抽样法应用于复杂电力系统的可靠性评估当中, 将系统随机状态出现的概率由其出现的频率近似估计, 模拟的过程和复杂程度与系统规模无关, 解决了大规模电网的可靠性评估问题, 但是其故障模型仅为两状态模型, 未能考虑降额状态的影响。文献[8]通过非序贯蒙特卡洛方法模拟了某风电系统可靠性模型, 但其抽样方法为单一的状态抽样, 不能反映不同持续时间的风机状态。文献[9]对风电场发电容量可信度进行了研究, 比较了不同风电场渗透率下对发电系统可靠性的影响。
针对现有方法的不足, 本文基于历史风速数据, 通过马尔科夫法得到风电机组各个出力状态概率及持续时间。在此基础上将风机故障模型分为正常、降额及故障3个状态, 通过序贯蒙特卡洛法对风机出力及故障模型进行状态和持续时间抽样, 并进行风电场并网可靠性分析。最后, 分析不同风电渗透率对发电系统可靠性的影响。
1 基于马尔科夫法的风机多状态出力模型和故障模型
出力模型和故障模型是风能特性分析、风电场可靠性评估研究的基础。马尔科夫链可根据已知状态通过其转移率得到各个状态出现的概率及持续时间, 故本文选用该方法对多状态的风机出力及故障进行模拟。
1.1 马尔科夫法原理
设Xt表示t时刻的离散型随机变量。该变量随时间变化的条件分布函数仅与它的当前值有关, 如式(1)所示。
| $P\left(X_{t+1}=s_{j} \mid X_{0}, X_{1}=s_{1}, \cdots X_{t}=s_{i}\right)= \\ P\left(X_{t+1}=s_{j} \mid X_{t}=s_{t}\right)$ | (1) |
式中:sj——随机变量可能的状态值, j=0, 1, 2, …。
状态转移概率依赖于前一个值的随机过程称为马尔科夫过程。马尔科夫法是通过转移概率定义的, 随机变量从当前时刻到下一个时刻, 状态si转移到状态sj的概率为
| $P(i \rightarrow j):=P_{i, j}=P\left(X_{t+1}=s_{j} \mid X_{t}=s_{i}\right)$ | (2) |
πk(t)表示离散型随机变量Xt取值为sk的概率, 则随机变量Xt+1取值为si的概率为
| $\pi_{i}^{(t+1)}=P\left(X_{t+1}=s_{i}\right)=$ $P\left(X_{t+1}=s_{i} \mid X_{t}=s_{0}\right) \cdot P\left(X_{t}=s_{0}\right)+$ $P\left(X_{t+1}=s_{i} \mid X_{t}=s_{1}\right) P\left(X_{t}=s_{1}\right)+\cdots=$ $\sum\limits_{k} P\left(X_{t+1}=s_{i} \mid X_{t}=s_{k}\right) \cdot P\left(X_{t}=s_{k}\right)=$ $\sum P_{k, i} \cdot \pi_{k}^{(t)}$ | (3) |
假设状态数目为n, 则
| $ \left(\pi_{1}^{(t+1)}, \cdots, \pi_{n}^{(t+1)}\right)= \\ \left(\pi_{1}^{(t)}, \cdots, \pi_{n}^{(\mathrm{t})}\right)\left[\begin{array}{cccc} P_{1,1} & P_{1,2} & \cdots & P_{1, n} \\ P_{2,1} & P_{2,2} & \cdots & P_{2, n} \\ \vdots & \vdots & & \vdots \\ P_{n, 1} & P_{n, 2} & \cdots & P_{n, n} \end{array}\right] $ | (4) |
1.2 出力模型
1.2.1 风能转换模型
风能的不稳定性和间歇性使得风速及其出力呈现非线性的关系, 其转换关系表示如下
P(v)=
| $P(v)= \\ \left\{\begin{array}{cc}0 & 0 \leqslant v \leqslant v_{\mathrm{ci}}, v>v_{\mathrm{co}} \\ P_{\mathrm{R}}\left(A+B v+C v^{2}\right) & v_{\mathrm{ci}}<v \leqslant v_{\mathrm{r}} \\ P_{\mathrm{R}} & v_{\mathrm{r}}<v \leqslant v_{\mathrm{co}}\end{array}\right.$ | (5) |
式中:v——风机的实际风速;
PR——风机的额定功率;
vci, vr, vco——风机的切入风速、额定风速和切出风速;
A, B, C——模型参数值, 可由vci, vr和vco得到。
1.2.2 基于马尔科夫法的出力模型
对于得到的输出功率必须使用合适的方法量化各个输出状态并与其他状态明确区分开来。马尔科夫矩阵简化了数值计算的过程, 适用于随机性输出功率序列的建模。考虑到风机的惯性作用, 通过风机出力得到的状态转移模型相比根据风速建立的模型惯性较大, 需要的离散状态数目较少。采用马尔科夫法得到的风机出力模型可通过较少的状态得到较高的精度[10-11]。风机的状态转移矩阵表示如下:
| $ P=\left[\begin{array}{cccc} 1-\sum\limits_{j=1 \atop j \neq 1}^{N} p_{1 j} & p_{12} & \cdots & p_{1 N} \\ p_{21} & 1-\sum\limits_{j=1 \atop j \neq 2}^{N} p_{2 j} & \cdots & p_{2 N} \\ \vdots & \vdots & \ddots & \vdots \\ p_{N 1} & p_{N 2} & \cdots & 1-\sum\limits_{j=1 \atop j \neq N}^{N} p_{N_{j}} \end{array}\right] $ | (6) |
| $ \left\{\begin{array}{ll} p_{i j} \geqslant 0 & i, j=1,2,3, \cdots, N \\ \sum\limits_{j=1}^{n} p_{i j}=1 & i, j=1,2,3, \cdots, N \end{array}\right. $ | (7) |
P的统计值受到样本数量的影响。当样本数量足够时, 可获得满足一定误差要求的状态转移矩阵, 其统计值将无限接近于真实值。马尔科夫的逼近过程可表示为
| $G(\infty) P=G(\infty)$ | (8) |
式中:G(∞)——风电系统长期状态概率, 表示系统状态趋于无限大时各个状态趋于某个稳定值。
根据不同出力之间的转移率可得到各个出力状态的持续时间ti, 即
| $ t_{i}=\frac{8760}{\sum\limits_{j=1 \atop j \neq N}^{N} p_{i j}} $ | (9) |
1.3 基于马尔科夫法的风机故障模型
1.3.1 风机系统状态划分
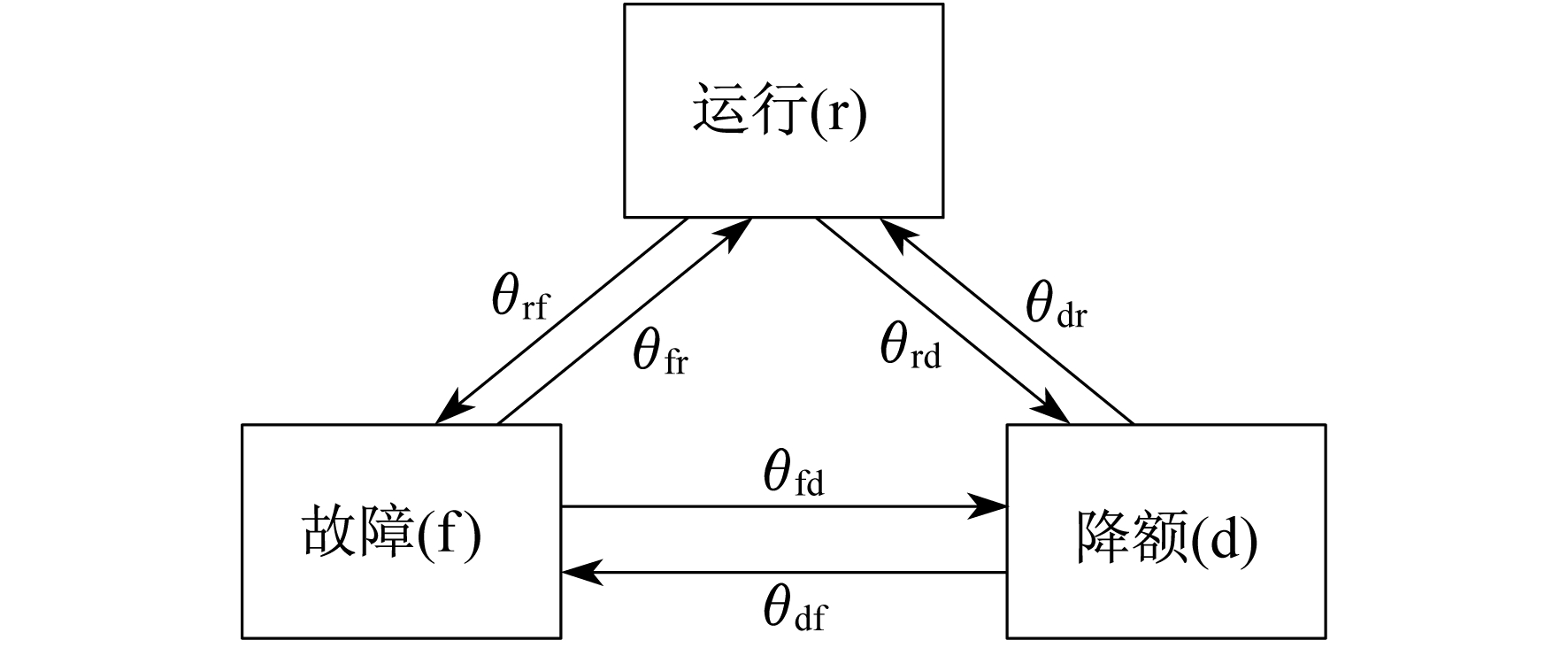
风机系统可靠性评价需要建立不同的运行状态分类。通常情况下, 风机系统运行状态可分为运行和故障两个状态, 不过依据概率原则, 对其状态划分越细致, 对运行可靠性的指导性越高, 导致所需实际数据获取难度增大。为了减少计算负担, 在对风机系统状态评估以适中为宜。本文将风机系统分为3个状态, 具体如图 1所示。运行、降额及故障状态的转移率θ(单位:次/年)可由风电场的历史故障数据统计得到, 其下标代表状态转移的方向。
状态1(运行r):此状态下风机内部无故障部件, 风机系统在计划方式下运行。
状态2(降额d):风机系统中某些约束无法满足条件, 经调整后, 需要切除部分负荷来保证风电机组的稳定运行。此过程恢复等待时间较长, 对风机整体可靠性有一定影响。
状态3(故障f):此状态下由于系统内部元件的故障, 会有暂时性的停机, 考虑到停机时间和维修方式的影响, 会有不同程度的负荷缺失状态。
1.3.2 基于马尔科夫法的风机状态模型
假设风机的初试状态为G(0), 由马尔科夫矩阵的定义可知, 经过单位时间的风机状态可表示为
| $G(1)=G(0) P$ | (10) |
由此可知, 经过m个单位时间后风机的状态转移可表示为
| $G(m)=G(0) P^{m}$ | (11) |
已知风机的初始状态及其状态转移矩阵可得每个时刻其状态分布的稳态值。运行、降额及故障3个状态概率公式可表示为
| $ \left[\begin{array}{ccc} 1 & 1 & 1 \\ \theta_{\mathrm{rd}} & -\theta_{\mathrm{dr}}-\theta_{\mathrm{df}} & \theta_{\mathrm{fd}} \\ \theta_{\mathrm{rf}} & \theta_{\mathrm{df}} & -\theta_{\mathrm{fr}}-\theta_{\mathrm{fd}} \end{array}\right]\left[\begin{array}{c} P_{\mathrm{r}} \\ P_{\mathrm{d}} \\ P_{\mathrm{f}} \end{array}\right]=\left[\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right] $ | (12) |
式中:Pr, Pd, Pf——风机运行、降额和故障的概率。
停留在运行、降额和故障的平均持续时间, 如式(13)所示。
| $t_{\mathrm{r}}=\left(\theta_{\mathrm{rd}}+\theta_{\mathrm{rf}}\right) \\ t_{\mathrm{d}}=\left(\theta_{\mathrm{dr}}+\theta_{\mathrm{df}}\right) \\ t_{\mathrm{f}}=\left(\theta_{\mathrm{fd}}+\theta_{\mathrm{fr}}\right)$ | (13) |
式中:tr, td, tf——正常运行、降额及故障的持续时间, 由各个状态的转移率得到。
2 基于序贯蒙特卡洛多重抽样的风电场并网可靠性评估
对于多状态系统, 非序贯蒙特卡洛法仅对系统的随机状态进行抽样, 不考虑系统各个状态持续时间, 不能反映各个时间点风机出力及故障状态, 而实际上风机的状态持续时间是随机的, 因此非序贯蒙特卡洛法会带来较大误差[12]。序贯蒙特卡洛法从系统状态和该状态实际持续时间出发, 根据已确定的平均持续时间抽取得到任何持续时间的状态, 反映了系统时序运行过程, 并且具有统计概率分布的能力, 因此本文通过序贯蒙特卡洛法对风电场进行并网可靠性评估。
2.1 序贯蒙特卡洛抽样法原理
序贯蒙特卡洛法根据被抽样元件的概率抽取元件的状态, 然后由已确定状态的平均持续时间得到其实际持续时间, 最终组合得到元件各个状态的时序结果。
假设一个两状态的系统, 分别为G1和G2, 其对应的概率分别为PG1和PG2, 随机抽取一个在[0, 1]范围的数UK, 可得到如下关系式
| $ D_{\mathrm{K}}=\left\{\begin{array}{ll} G_{1} & P_{G 2} \leqslant U_{\mathrm{K}} \leqslant P_{G 1}+P_{G 2} \\ G_{2} & 0 \leqslant U_{\mathrm{K}} \lt P_{G 2} \end{array}\right. $ | (14) |
式中:DK——随机变量的状态。
抽取m′个随机数, 根据式(14)得到各个状态集合D={G1, G2, G3, …, Gn}, 重复上述过程m′次即得到该系统总的状态集合。
在可靠性分析中, 指数分布是重要的分布类型, 对于服从指数分布的随机变量, 其状态持续时间及累积概率分布函数如下
| $ R=F\left(t_{\mathrm{D}}\right)=1-\mathrm{e}^{-\frac{1}{t} t_{\mathrm{D}}} $ | (15) |
式中:R——[0, 1]间服从均匀分布的随机数;
F(tD)——状态时间的累计概率分布函数;
tD, t——该状态实际持续时间和平均持续时间。
将式(15)经过反变换得到实际持续时间tD的表达式为
| $t_{\mathrm{D}}=F^{-1}(R)=-t \ln (R)$ | (16) |
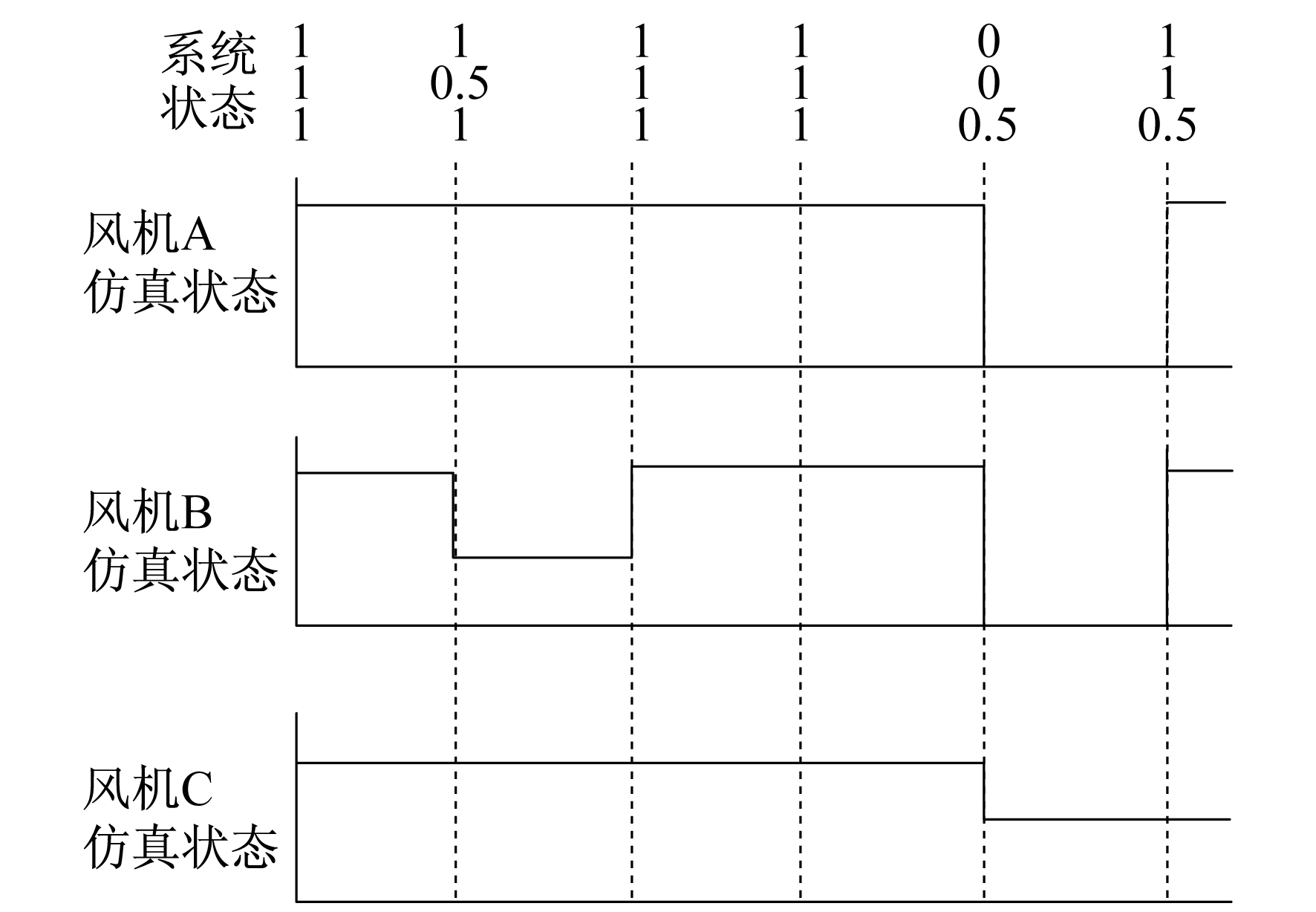
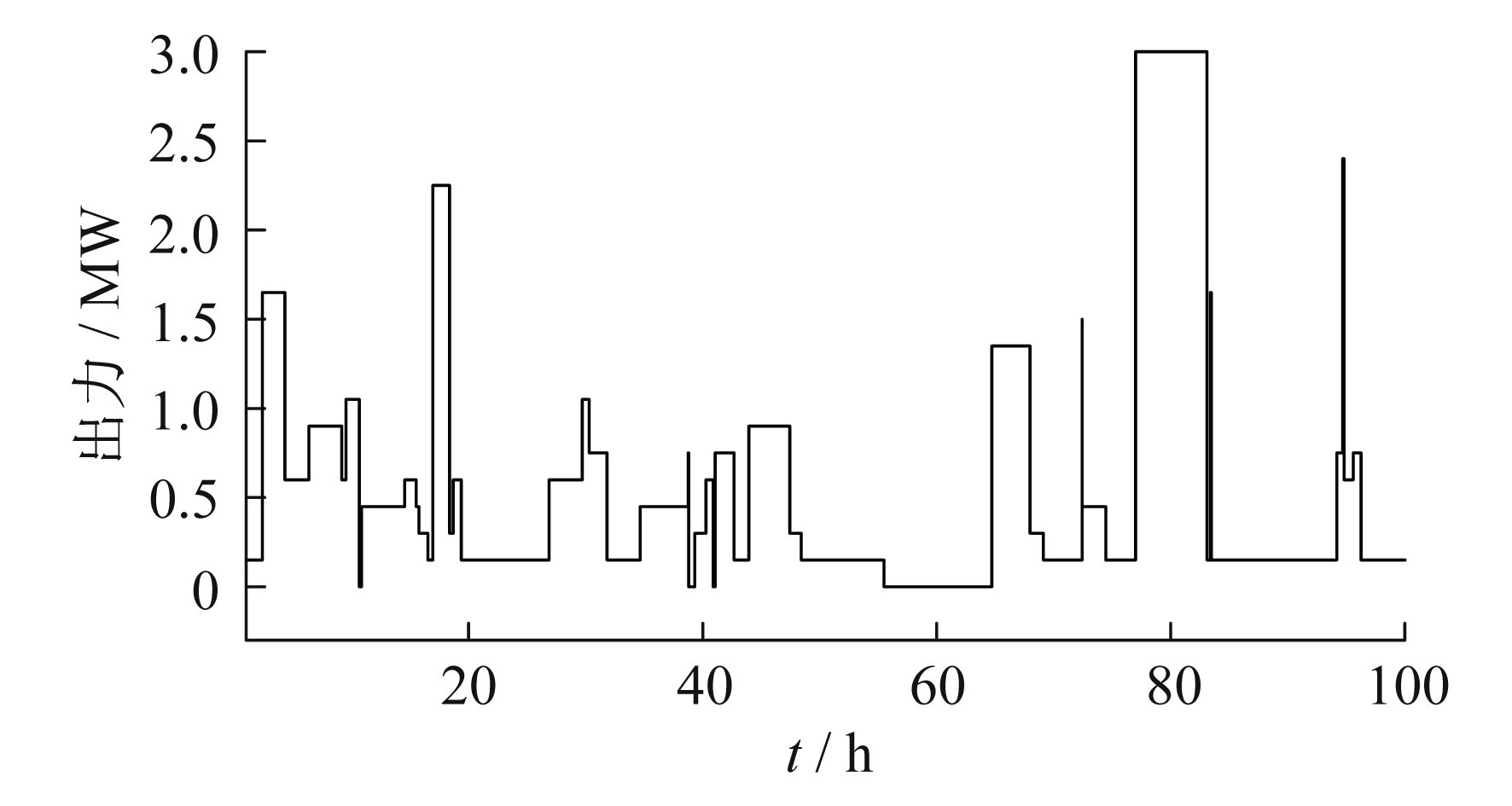
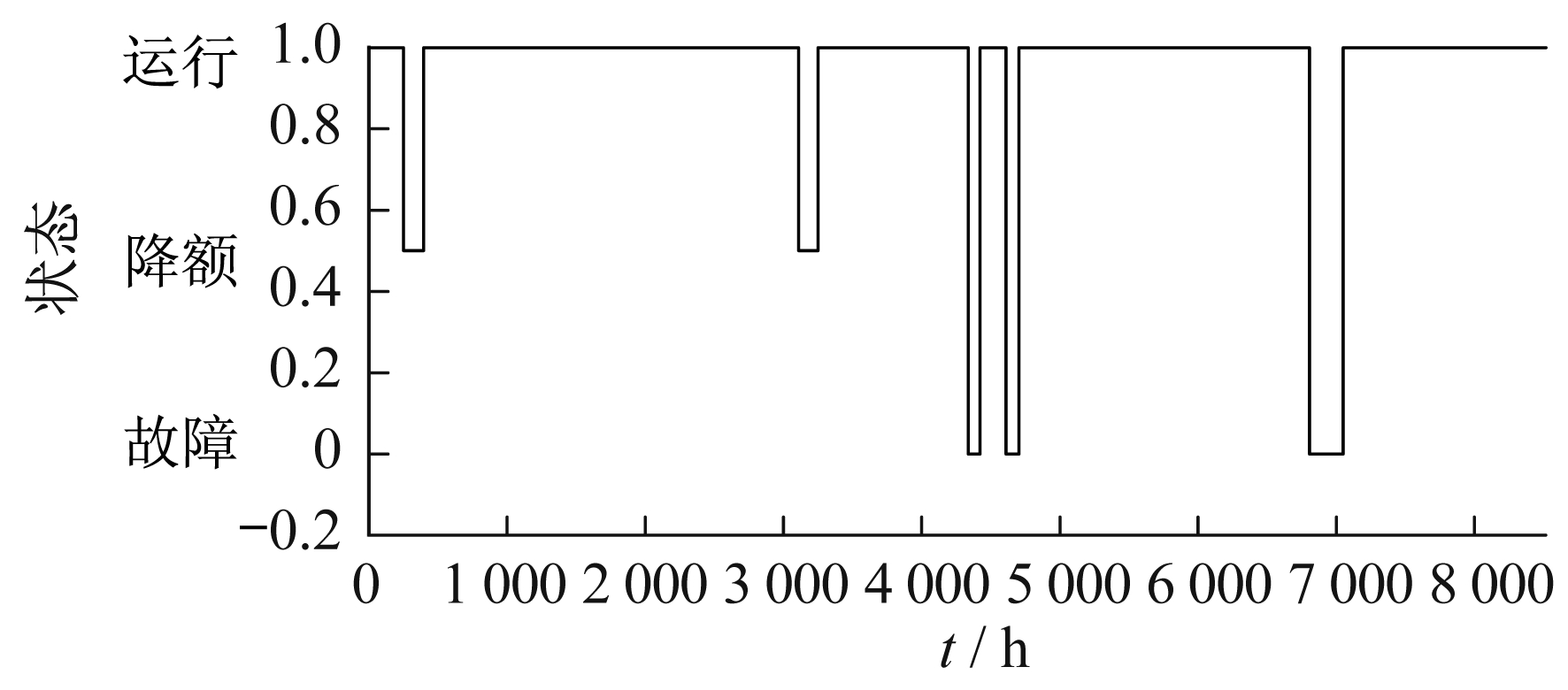
以A, B, C 3台风机为例, 对其状态及实际持续时间进行模拟, 采样结果如图 2所示。
图 2给出了在一定采样时间内通过对风机运行状态序列模拟确定系统的状态转移过程。0, 0.5, 1分别表示风机所处的状态, [1 1 1], [1 0.5 1]表示各个时刻风机构成的系统组合状态, 根据各个状态的变化时刻, 按时间序列组合每台风机的状态便可得到风电场的总体状态。
2.2 序贯蒙特卡洛法评估风电场并网可靠性流程
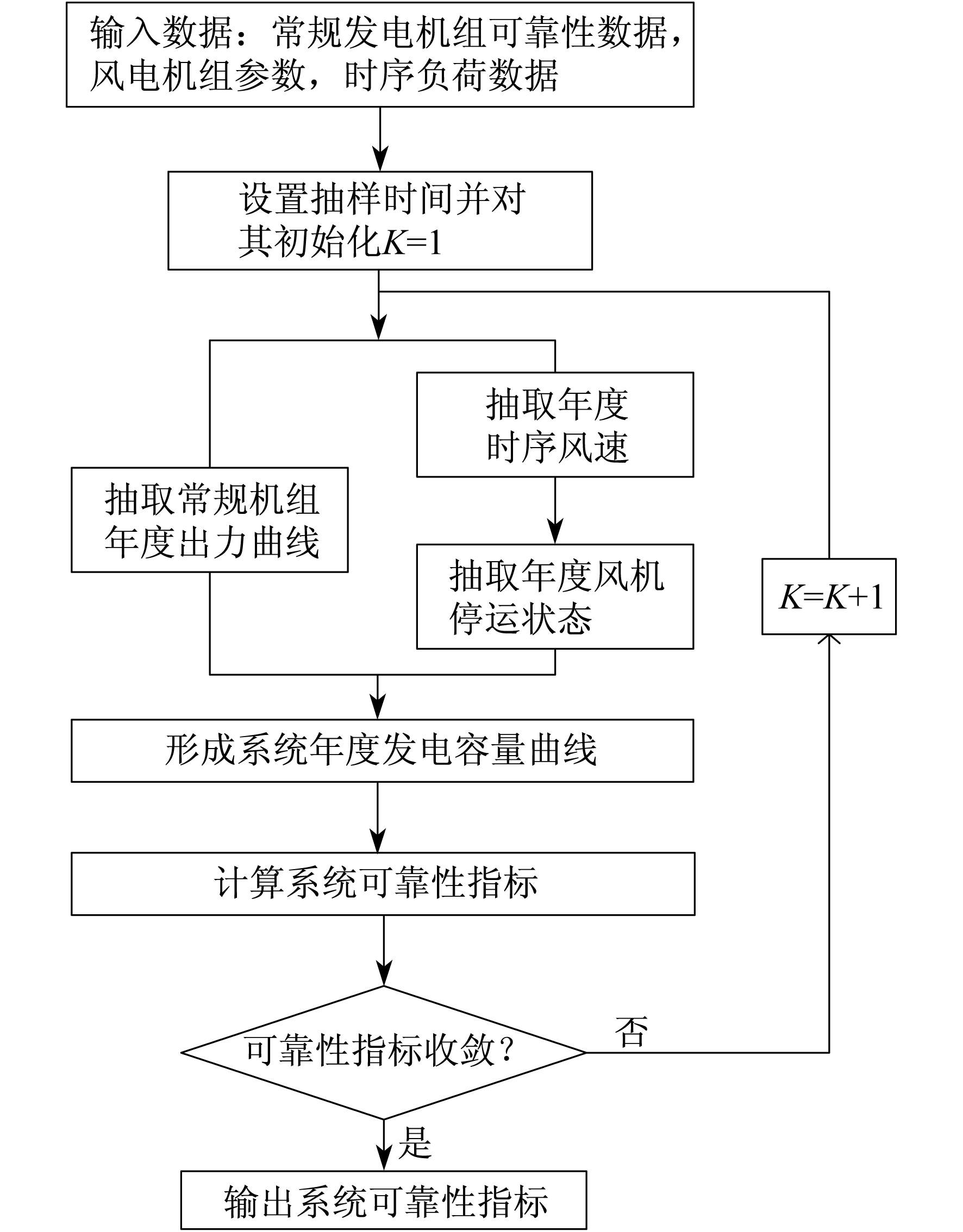
运用序贯蒙特卡洛法进行风电场并网可靠性评估, 首先获取风机出力及故障状态、常规发电机组的出力, 再在风电机组负荷曲线上叠加常规机组的年度出力曲线, 形成系统年度发电容量曲线之后, 计算系统的可靠性指标。算法流程如图 3所示。
3 算例仿真分析
风机占发电系统的比例较低, 使得单一的风电场并不能单独维持可靠性, 必须通过与火电等其他形式的能源组合发电来提升可靠性[13]。本文通过IEEE-RTS79可靠性测试系统进行风电系统可靠性评估[14]。IEEE-RTS79系统主要是通过标准化数据库来测试和比较不同发电系统可靠性结果, 其包括32台常规发电机、10条母线、5个变压器等, 系统的总装机容量为3 045 MW, 负荷峰值为2 850 MW。本文中装机容量、年小时负荷及各发电机模型数据由该系统得到。发电系统的可靠性指标主要有缺电时间期望ELOLE及期望缺供电量EEENS, 其反映了整个发电系统在一定时间内不满足负荷需求的发电时间以及在这段时间内因负荷不足造成需求电量减少的总和, 表达式分别如下
| $ E_{\mathrm{LOLE}}=\frac{1}{N} \sum\limits_{t=1}^{N} X_{t}=\frac{1}{N} \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{8760} X_{i, j} $ | (17) |
| $E_{\mathrm{EENS}}=\frac{1}{N} \sum_{i=1}^{N} e_{i}$ | (18) |
其中:N——仿真年限。
为了降低随机事件的偶然性, 需要进行一定时间跨度的模拟使结果更精确。
3.1 风机多状态出力概率及持续时间
对某风电场3 MW风机进行仿真, 通过对风电场历史风况数据进行统计, 将风机出力均分为21个状态。根据风电场风机历史故障数据统计, 把风机故障状态分为运行、降额及故障3个状态。
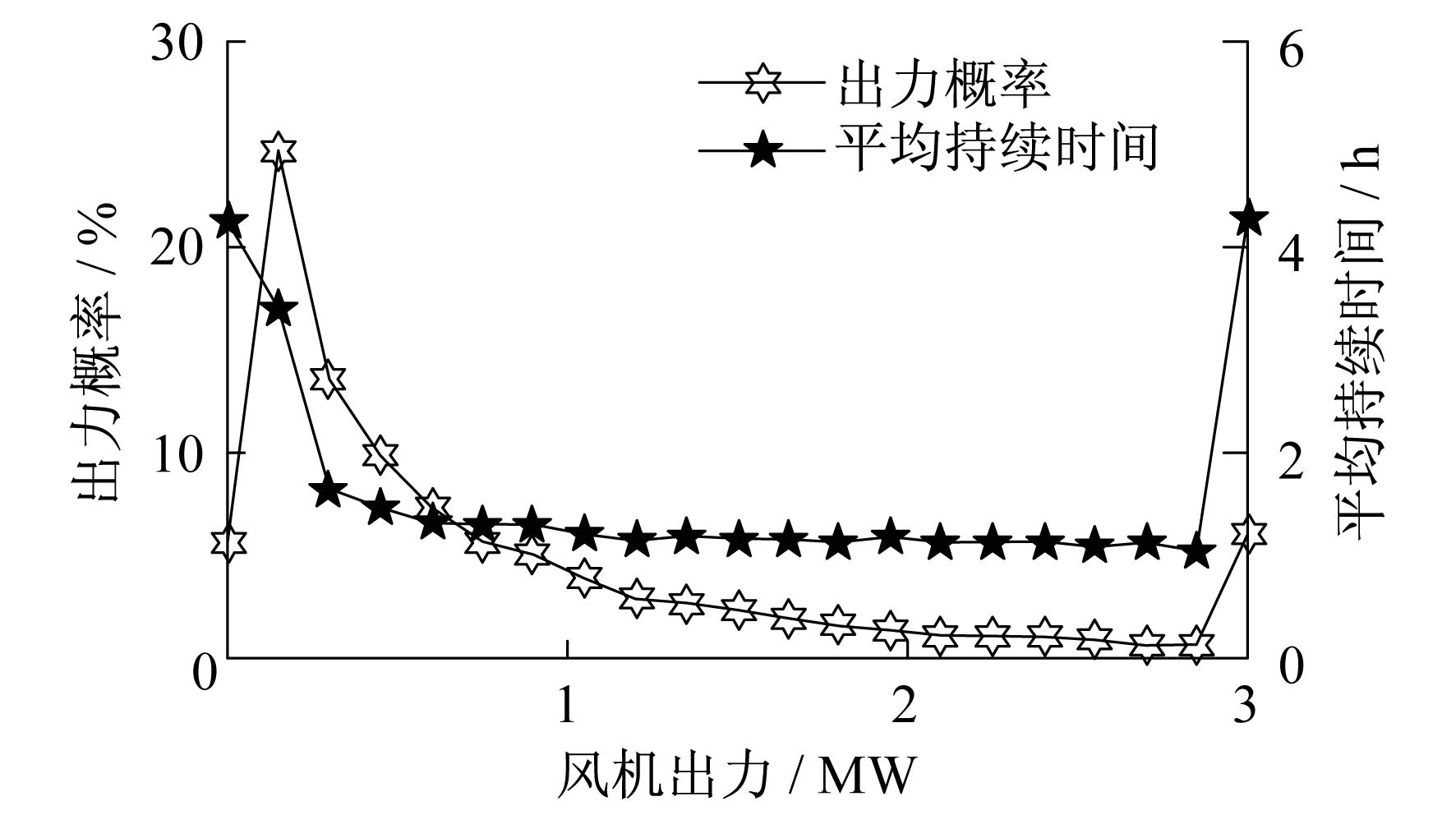
已知该风电场的切入风速、额定风速和切出风速分别为3 m/s, 12 m/s, 和20 m/s。结合出力模型可得到风电机组各个出力状态的概率及平均持续时间的统计结果, 具体如图 4所示。
根据风机历史故障数据统计得到运行(r)、降额(d)及故障(f)3个状态之间的转移率如表 2所示。结合风机故障模型可得3个状态的概率和平均持续时间计算结果, 如表 3所示。
表 2
风机3个状态之间的转移率
| 状态变化 | 转移率/次 |
| r→r | 0 |
| r→d | 12.65 |
| r→f | 6.54 |
| d→r | 45.15 |
| d→d | 0 |
| d→f | 0 |
| f→r | 54.25 |
| f→d | 0 |
| f→f | 0 |
表 3
风机3个状态的概率和平均持续时间统计结果
| 状态 | 現率/% | 平均持续时间/h |
| 运行 | 78.44 | 621.75 |
| 降额 | 9.88 | 157.37 |
| 故障 | 11.68 | 168.00 |
3.2 风机运行仿真结果
3.3 风电场并网可靠性评估
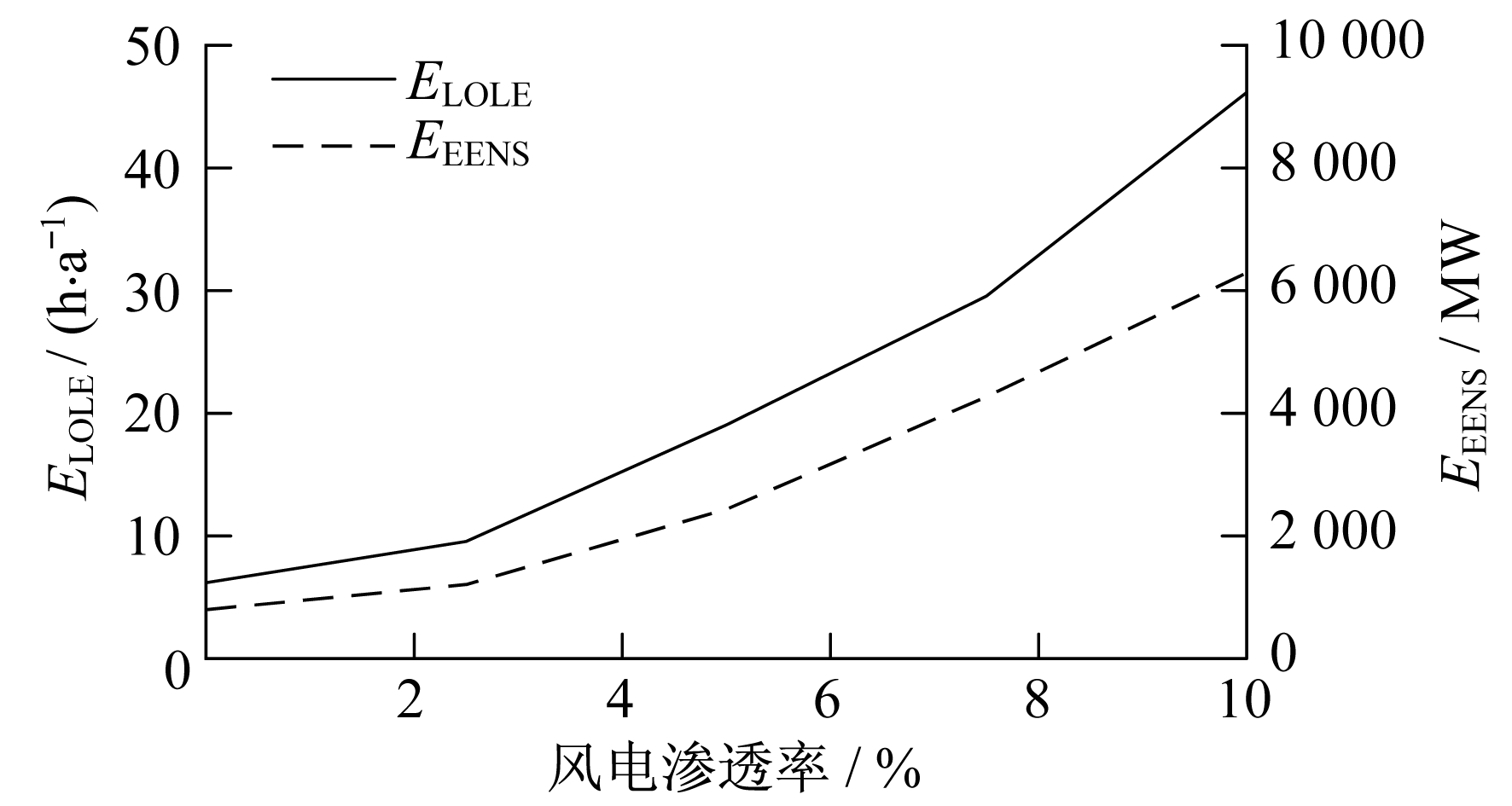
含风电场的发电系统可靠性评估受风电渗透率的影响[15]。风电渗透率由风电功率占系统电网功率的百分比得到。为了研究其对系统可靠性的影响, 可增加一定装机容量的风电机组, 并减小等额的常规发电机组。针对上文中得到的风机模拟结果, 分5次增加风电场并网容量, 每次均增加60 MW的容量, 相应减小等额的常规发电机组容量, 然后分别对其可靠性进行评估, 可靠性指标结果如图 7所示。
图 7反映了风电渗透率对系统可靠性的影响, 最初测试系统中并入60 MW容量时, 风电渗透率为2%, 系统可靠性较高, 随着风电场并网容量的增加, 风电渗透率逐渐增加, 发电系统ELOLE和EEENS逐渐上升, 可靠性水平下降, 这与风电的随机性和间歇性有关。因此, 当整个发电系统的装机容量一定时, 风电占整个发电系统的比例不宜过大, 否则会导致可靠性不能满足期望要求。
4 结语
本文建立了风机出力模型及故障模型, 将有功输出均分成21个状态, 并将风机故障状态分成运行、降额及故障3个状态, 根据状态转移矩阵得到各个状态概率及其平均持续时间指标, 通过序贯蒙特卡洛抽样法直观反映了随机状态下的风机时序运行仿真结果, 最后结合可靠性测试系统模拟得到不同风电渗透率下的风电机组并网可靠性指标。然而在风电机组并网后, 所提出的模型仍认为系统常规发电机组继续可用, 可靠性计算结果比未考虑风电机组时偏乐观, 因此在以后的研究中需要在常规发电机组可靠性模型上做进一步的改进。
参考文献
-
[1]综合能源系统可靠性评估的研究现状及展望[J]. 高电压技术, 2017, 43(1): 114-121.
-
[2]含风电场的发电系统可靠性分析[J]. 电力系统及其自动化学报, 2014, 26(10): 41-45. DOI:10.3969/j.issn.1003-8930.2014.10.008
-
[3]李玉敦.计及相关性的风速模型及其在发电系统可靠性评估中的应用[D].重庆: 重庆大学, 2012.
-
[4]考虑风电出力概率分布的电力系统可靠性评估[J]. 电网技术, 2013, 37(9): 2585-2591.
-
[5]计入风速与风电机组故障相关性的风电场可靠性建模及其应用[J]. 中国电机工程学报, 2016, 36(11): 2900-2908.
-
[6]基于解析法的风电场可靠性模型[J]. 电力自动化设备, 2010, 30(10): 79-83. DOI:10.3969/j.issn.1006-6047.2010.10.018
-
[7]基于非时序状态抽样法的发电系统可靠性评估[J]. 电气应用, 2016(18): 32-36.
-
[8]非序贯蒙特卡洛法在发电系统可靠性评估中的应用[J]. 计算机与数字工程, 2013, 41(6): 1021-1023. DOI:10.3969/j.issn.1672-9722.2013.06.048
-
[9]大规模风电场的发电充裕度与容量可信度评估[J]. 电网技术, 2012, 36(6): 200-206.
-
[10]一种用于序贯蒙特卡洛仿真的风电机组多状态可靠性模型[J]. 电力系统保护与控制, 2013, 41(08): 73-80.
-
[11]基于多目标蒙特卡洛法的全电压序列一体化电网可靠性评估[J]. 电网技术, 2016, 40(9): 2866-2870.
-
[12]考虑维度重要性的电力系统可靠性评估拟蒙特卡洛方法[J]. 电力系统自动化, 2016, 40(16): 31-37.
-
[13]QIN Z, LI W, XIONG X. Generation system reliability evaluation incorporating correlations of wind speeds with different distributions[J]. IEEE Transactions on Power Systems, 2013, 28(1): 551-558. DOI:10.1109/TPWRS.2012.2205410
-
[14]GRIGG C. The IEEE reliability test system 1996[J]. IEEE Transactions on Power Systems, 1999, 14(3): 1019-1020.
-
[15]电网接纳风电能力的评估及应用[J]. 电力系统自动化, 2011, 35(4): 70-76.