|
|
|
发布时间: 2019-04-10 |
|
|
|
|
收稿日期: 2019-01-05
文献标识码: A
文章编号: 1006-4729(2019)02-0175-06
|
摘要
针对焊接图像缺乏纹理的问题, 研究了一种弱纹理检测跨尺度聚合的立体匹配算法。根据张氏标定法, 对双目视觉传感器进行标定, 得到了双目视觉传感器的外部和内部参数。然后, 对双目视觉传感器获取的焊缝图片进行中值滤波、二值化等一系列图片预处理。利用弱纹理检测跨尺度聚合算法对焊缝图像进行立体匹配, 得出焊缝图像视差图, 再从视差中恢复距离, 得到了焊枪的高度信息。对双目视觉传感器采集的焊缝图像进行实验, 实验结果验证了弱纹理检测跨尺度聚合的立体匹配算法的可靠性。
关键词
双目视觉; 弱纹理检测; 标定; 图像处理; 立体匹配
Abstract
In order to solve the problem of lack of texture in welding image, a stereo matching algorithm for weak texture detection by cross-scale polymerization is studied.According to Zhang's calibration method, by calibrating binocular vision sensor, the external and internal parameters of binocular vision sensor is obtained.Then, a series of images, such as median filtering, binary image processing are preprocessed.Because stereo matching is the most critical link of binocular vision technology, the algorithm of cross-scale polymerization of weak texture detection is used to obtain parallax map of weld image by stereo matching of weld image.The distance can be recovered from the parallax to obtain the height information of the welding gun.The welding seam images collected by binocular vision sensor is tested and the results show that the reliability of the proposed algorithm is verified.
Key words
binocular vision; weak texture detection; calibration; image processing; stereo matching
双目视觉传感器从多个不同角度获取丰富的场景信息, 通过三角法等视差原理获得场景内目标物的深度信息, 可有效解决单目传感器无法测得目标深度信息的难点[1]。基于双目视觉传感器的双目立体视觉技术已逐渐应用于各个领域中[2]。双目立体视觉技术包括图像获取, 摄像机标定、图像预处理和立体匹配4个过程。
从二维焊缝图像中提取焊缝特征点的三维信息, 需通过视觉传感器标定获取视觉传感器的外部参数和内部参数。目前, 视觉传感器标定方法主要有射影标定法、自标定法、正交消隐法、相机纯旋转标定法和平面模板两步法等[3]。2016年, 长春理工大学的张超等学者[4]提出了一种基于位姿约束的标定算法, 是将相对位姿作为约束条件解出双目视觉的初始内部参数, 再通过重复迭代剔除误差率较大的标定图像, 当误差率小于指定值时得到较精确的双目视觉内部参数。2018年, 南京航天航空大学的姜涛课题组[5]采用单应性矩阵求解双目视觉内外参数, 有效解决了现有变焦镜头标定方法难度大、精度低的问题。
对焊缝图像的预处理可以避免焊接过程中产生的弧光飞溅, 但会给焊缝图像带来噪声污染, 影响后续立体匹配的效果[6]。2018年, 上海交通大学的王志刚等研究者[7]采用一种焊缝图像预处理算法, 提高了算法的精度和实时性。该方法在消除噪声的同时, 通过保留信号的边缘, 极大程度地提高了焊缝图像处理的细节。
匹配的复杂性是立体匹配的关键。立体匹配是基于若干不同视角拍摄的图像找出匹配点的对应关系, 利用视差得到深度信息[8]。正确的选择和研究匹配算法是一个难点, 这是由于对于一幅图像上的某个像素或特征, 另一幅图像可能有若干特征与之相似。近年来, 基于图切割和置信度传递的优化算法被广泛应用。2018年, 西悉尼大学的MITCHELL D等学者[9]研究了一种立体置信度估计的深度体系结构, 与现有的基于深度卷积神经网络只依赖匹配代价估计视差图不同, 该网络通过同时使用两个异构输入估计立体置信度, 对提高立体匹配算法的精度具有重要意义。这种结构的局限性是对缺乏纹理的图像匹配精度较低, 也会影响视差精度。
获取物体的深度信息可根据来自不同相机的图像求解视差。基于以上分析, 针对焊件表面大多是弱纹理且缺乏独特的特征点导致立体匹配困难的问题, 本文提出了一种弱纹理检测跨尺度聚合的立体匹配算法, 通过检测弱纹理区域利用不同的梯度进行跨尺度聚合, 来提高立体匹配的精度。
1 焊缝图像预处理
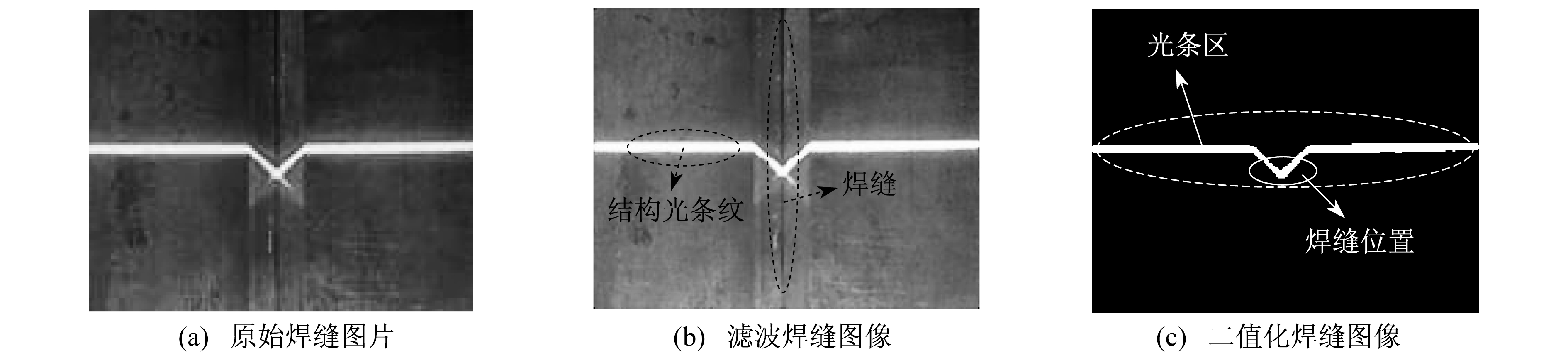
焊缝图像预处理的第一步是图像滤波。中值滤波既可以有效去除图像噪声又可以保留焊缝图像的边缘细节, 为后续准确提取焊缝特征点提供有利条件。滤波后, 为减少背景因素干预, 再对焊缝图像进行二值化处理, 整个过程如图 1所示。图像二值化把焊缝图像中灰度值超过所设灰度阈值的线结构光条纹区域定义为目标区域, g(x, y)表示像素灰度值(其中x, y分别表示二维图像的横坐标值和纵坐标值), T表示设定的灰度阈值。公式如下
| $g(x, y)=\left\{\begin{array}{ll}255 & g(x, y) \gg T \\ 0 & g(x, y)<T\end{array}\right.$ | (1) |
2 双目视觉标定
2.1 张氏标定法
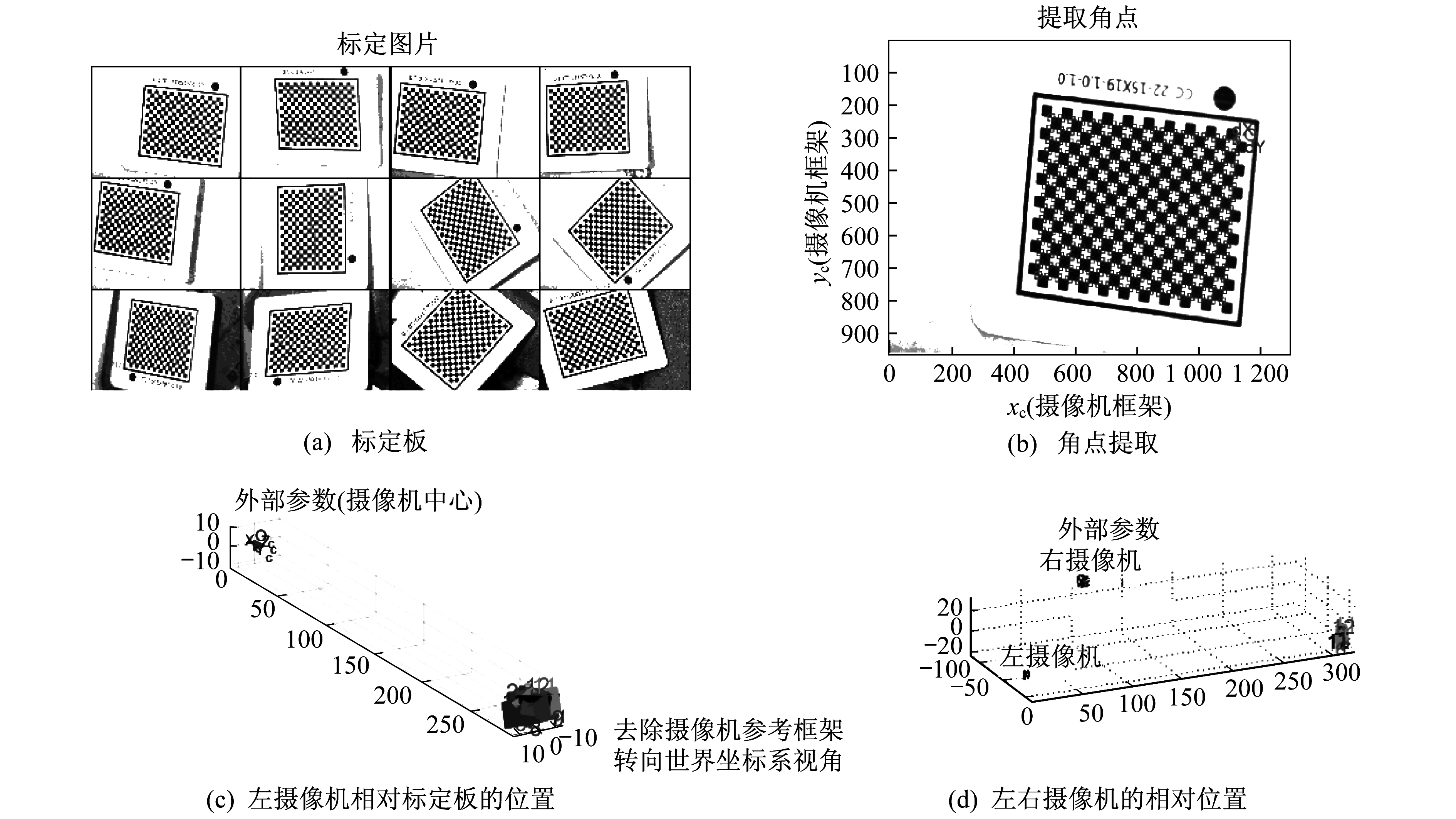
采用张氏标定法标定双目视觉传感器。首先, 通过相机拍摄标定板对不同位置的各个角度的图像进行标定。采用16×20的棋盘格作为相机的标定物, 每个格子边长为1 mm, 共采集12对焊缝标定板图片, 如图 2所示。然后, 通过误差分析、角点剔除和角点再提取得到左摄像机相对标定板的位置和左右摄像机的相对位置, 从而得到双目视觉传感器的参数。
2.2 视差与深度的关系
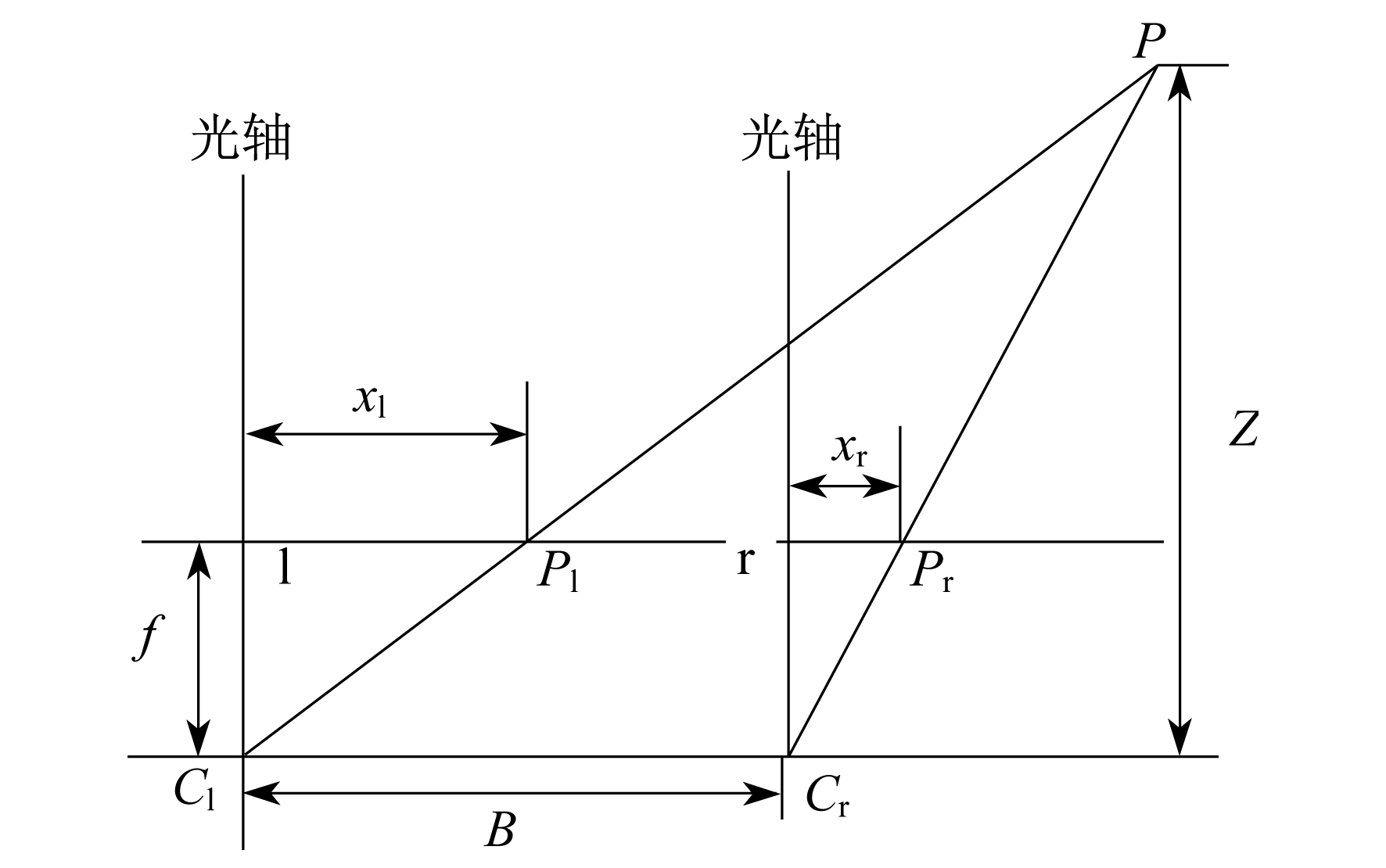
视差和深度的关系如图 3所示。
B为两个传感器之间的距离。Z为目标到传感器的距离, 即深度。P点为目标位置。Pl, Pr为目标在左右两个传感器上的成像点。Cl, Cr为左右摄像机位置。f为传感器镜头焦距。ax为传感器参数。用xl, xr表示目标两个成像的坐标。由中心映射关系得
| $ Z=\frac{B a_{x}}{x_{1}-x_{\mathrm{r}}} $ | (2) |
xl-xr为目标位置P点的视差, 用d表示, 则式(2)可表示为
| $ Z=\frac{B a_{x}}{d} $ | (3) |
可以看出, 物体的深度与视觉传感器参数、基线的长度以及像素点的视差有关, 物体的深度信息与像素点的视差成反比关系。标定得到传感器参数后, 即可通过立体匹配得到视差值[10]。
3 目标图像立体匹配
只要找到焊缝左右图像中的匹配对应点并求出视差, 即可得到深度信息。匹配对应点即匹配代价最小的点。以左焊缝图像为基准图, 检测焊缝图像的纹理情况, 将焊缝图像分割成纹理区域和弱纹理区域, 利用输入左右焊缝图像的色彩信息以及梯度信息计算匹配代价。
3.1 弱纹理区域检测
弱纹理区域的实质是其灰度信息在图像中的变化很小甚至几乎不变化。范海瑞课题组根据两个特征对弱纹理区域进行检测:一是固定区域内的颜色变化; 二是像素的梯度变化[11]。实验发现颜色值的变化对最后的匹配结果影响很小, 因此实验中对焊缝图像进行纹理和弱纹理区域的分割时, 根据焊缝图像像素灰度梯度特性变化就可以提取出焊缝图像弱纹理区域, 设图像I中任意像素(x, y), 如果此像素(x, y)属于弱纹理区域, 则满足以下公式
| $ \left\{\begin{array}{ll} \delta^{2}(x, y) & \lt \delta_{T}^{2} \\ g(x, y) & \lt g_{T} \end{array}\right. $ | (4) |
其中,
| $\delta^{2}(x, y)=\frac{1}{N} \sum\limits_{(u, v) \in W(x, y)}(I(u, v)-\bar{I}(x, y))^{2}$ | (5) |
| $\begin{aligned} g(x, y)=& \frac{1}{N} \sum\limits_{(u, v) \in W(x, y)}|I(u, v)-I(u+1, v)|+\\ &|I(u, v)-I(u, v+1)| \end{aligned}$ | (6) |
式中:gT, δT——灰度阈值;
N——窗口像素的个数;
W(x, y)——以像素(x, y)为中心的窗口;
I(u, v)——像素的灰度值;
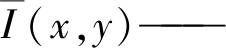 像素灰度的平均值。
像素灰度的平均值。
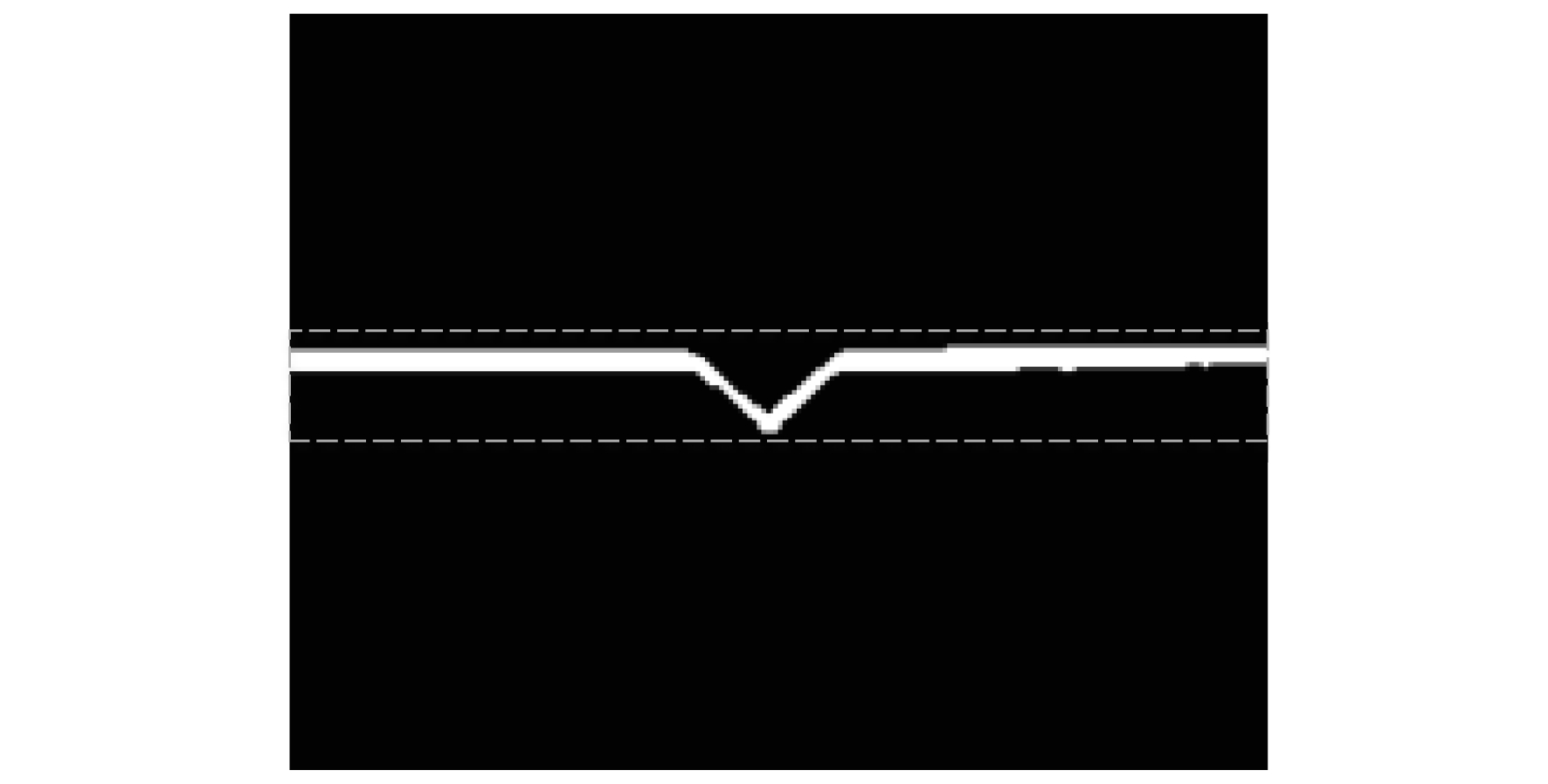
图 4为焊缝图像弱纹理区域检测结果, 其中虚线框中白色部分表示焊缝图像弱纹理区域, 其余黑色部分表示焊缝图像纹理区域。
3.2 代价计算
差的绝对值之和(Sum of Absolute Differences, SAD)算法是一种图像匹配算法, 具有匹配精度高、速度快等优点, 缺点是在边缘区域匹配精度不高[12]。基于图像梯度的代价计算法在图像边缘也能得到较高的匹配精度, 能够弥补SAD算法的缺点。因此, 在计算匹配代价中, 采用截断颜色差和截断梯度差组合, 同时加入x方向和y方向梯度算子进行代价计算。设焊缝图像对左图像IL, 右图像IR, p是左图像中一点, 匹配代价如下
| $ \begin{aligned} C(p, d)=& (1-\alpha) \cdot C_{\mathrm{AD}}(p, d)+\alpha \\ & \left[C_{\mathrm{grad}_{-} \mathrm{x}}(p, d)+C_{\mathrm{grad}_{\mathrm{y}}}(p, d)\right] \end{aligned} $ | (7) |
其中,
| $\begin{aligned} C_{\mathrm{AD}}(p, d)=& \min \left[\frac{1}{3} \sum\limits_{i=\mathrm{R}, \mathrm{G}, \mathrm{B}} \mid I_{\mathrm{L}}^{i}(p)-\right.\\ &\left.I_{\mathrm{R}}^{i}(p, d) \mid, T_{\mathrm{AD}}\right] \end{aligned}$ | (8) |
| $\begin{aligned} C_{\mathrm{grad}_{-}\mathrm{x}}(p, d)=& \min \left(\mid \nabla_{x} I_{\mathrm{L}}(p)-\right.\\ &\left.\nabla_{x} I_{\mathrm{R}}(p, d) \mid, T_{\mathrm{grad}}\right) \end{aligned}$ | (9) |
| $C_{\text {grad_y }}(p, d)=\min \left(\mid \nabla_{y} I_{\mathrm{L}}(p)-\right. \\ \left.\nabla_{y} I_{\mathrm{R}}(p, d) \mid, T_{g r a d}\right)$ | (10) |
其中:C(p, d)——视差为d时点p的匹配代价;
α——颜色差和梯度差之间的平衡因子;
R, G, B——彩色图像的3个通道;
TAD, Tgrad——颜色和梯度的截断阈值;
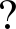 x,
x,
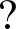 y——图片在x和y方向的梯度算子。
y——图片在x和y方向的梯度算子。
3.3 代价聚合
代价聚合本质是对代价计算的结果进行去噪, 去噪包含特定滤波核实则是加权最小二乘(Weighted Least Square, WLS)优化问题, 因此匹配代价聚合公式如下
| $ \begin{array}{c} \tilde{C}(p, d)=\underset{z}{\operatorname{arg\;min}} \sum\limits_{q \in \tilde{N}} W(p, q) \cdot \\ \|z-C(q, d)\|^{2} \end{array} $ | (11) |
式中:
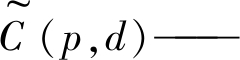 聚合后的匹配代价;
聚合后的匹配代价;
z——期望优化目标值;
q——p的邻域像素点;
 像素p的邻域窗口;
像素p的邻域窗口;
d——视差值;
W(p, d)——高斯滤波核, 衡量像素点之间相似性的相似性核。
式(11)的最小二乘优化解如下
| $\tilde{C}(p, d)=\sum\limits_{q \in \tilde{N}} W(p, q) \cdot C(q, d)$ | (12) |
目前大多数研究都是最细尺度, 即原图像尺度上进行的代价聚合。在原图像尺度下, 代价聚合可以在纹理区取得良好的效果。但是在立体匹配的对应搜索中, 不同尺度上的信息是交互处理的。因此, 代价聚合不能像传统方法只在最细尺度上进行操作, 应该采用由粗到细的跨尺度算法。
为了确保匹配的准确性, 保证多尺度视差的一致性, 对于图像的弱纹理和无纹理区域, 在不同尺度上进行代价聚合[13-14]。式(11)仅包含单一尺度图片, 不涉及其他尺度的图片信息, 根据尺度空间理论, 将式(11)扩展为如下公式
| $\begin{array}{l} \tilde v = \mathop {\arg \;\min }\limits_{\{ {z^s}\} _{s = 0}^S} \sum\limits_{s = 0}^S {\sum\limits_{{q^s} \in {{\tilde N}_s}} {W({p^s},{q^s}) \cdot } } \\ \;\;\;\;\;{\left\| {{z^s} - {C^s}({q^s},{d^s})} \right\|^2} \end{array}$ | (13) |
式中:
 扩展后的匹配代价;
扩展后的匹配代价;
s——尺度参数;
S——尺度个数, 即第几个尺度;
zs——第s个尺度上的期望优化目标值;
ps, qs——第s个尺度上的像素点及其邻域像素点;
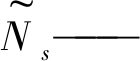 像素ps的领域窗口;
像素ps的领域窗口;
Cs(qs, ds)——像素qs在s尺度上的匹配代价。
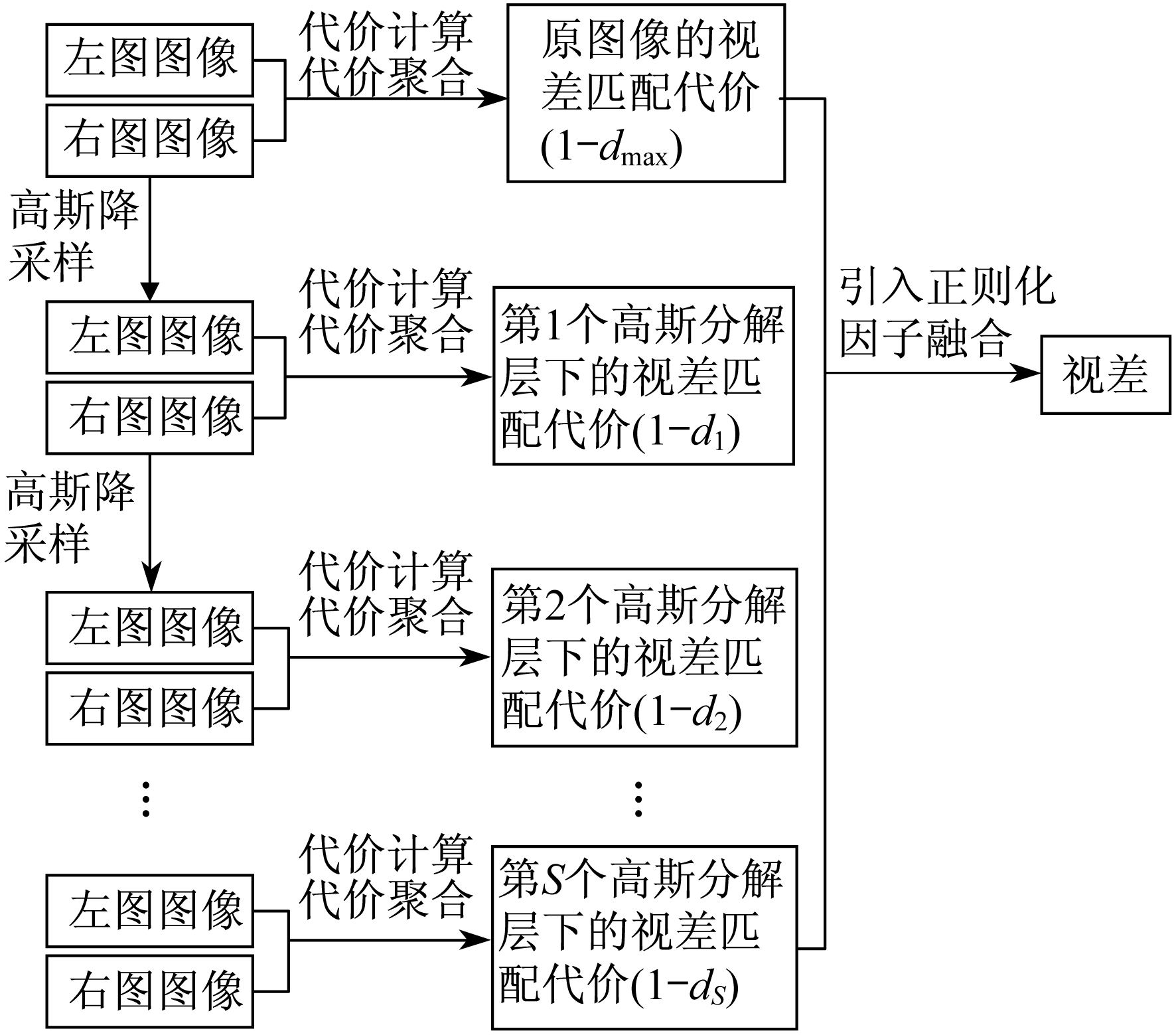
C0为图像原始尺度匹配代价。将原左右图像IL, IR使用高斯金字塔变换分解到0, 1, 2…S高斯分解层, 分别在第0, 1, 2…S高斯分解层下计算匹配代价并独立进行代价聚合, 得到匹配代价卷C0, C1, C2…CS。图 5为跨尺度代价聚合流程图。
| $\tilde{v}=\left[{{\tilde C}^0}\left(p^{0}, d^{0}\right) \tilde{C}^{1}\left(p^{1}, d^{1}\right) \cdots \tilde{C}^{S}\left(p^{S}, d^{S}\right)\right]^{\mathrm{T}}$ | (14) |
式(14)的解为每个尺度上分别进行高斯平滑代价聚合的结果, 对于任意s尺度的高斯平滑代价聚合结果为
| $\tilde{C}^{s}\left(p^{s}, d^{s}\right)=\sum\limits_{q^{s} \in \tilde{N_{s}}} W\left(p^{s}, q^{s}\right) \cdot C^{s}\left(q^{s}, d^{s}\right)$ | (15) |
为了得到最后的视差图, 对每层匹配代价进行融合, 保证相邻尺度相同像素一致性是融合的关键, 式(13)引入正则化约束项, 则
| $ \begin{array}{l} \hat v = \mathop {\arg \;\min }\limits_{\{ {z^s}\} _{s = 0}^S} \sum\limits_{s = 0}^S {\sum\limits_{{q^s} \in {{\tilde N}_s}} {W({p^s},{q^s})\;{{\left\| {{z^s} - {C^s}({q^s},{d^s})} \right\|}^2}} } + \\ \lambda \cdot {\sum\limits_{s = 1}^S {\left\| {{z^s} - {z^{s - 1}}} \right\|} ^2} \end{array} $ | (16) |
式中:λ——正则化因子。
式(16)的求解为凸优化问题, 可以通过求解目标函数的驻点得到最优解。设优化目标函数为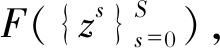 令
令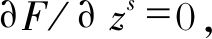 则
则
| $ \left\{\begin{array}{c} (1+\lambda) z^{s}-\lambda z^{s+1}=\tilde{C}^{s}\left(p^{s}, d^{s}\right) \quad s=0 \\ -\lambda z^{s-1}+(1+2 \lambda) z^{s}-\lambda z^{s+1}=\tilde{C}^{s}\left(p^{s}, d^{s}\right), \\ s=1,2,3, \cdots, S-1 \\ -\lambda z^{s-1}+(1+\lambda) z^{s}=\tilde{C}^{s}\left(p^{s}, d^{s}\right) s=S \end{array}\right. $ | (17) |
图像分解为S+1个尺度, 因此有S+1个线性方程, 此方程组可表示为
| $A \hat{v}=\tilde{v}$ | (18) |
A是(S+1)×(S+1)维的对角矩阵, 即
| $A=\left[\begin{array}{cccccc}1+\lambda & -\lambda & & & \\ -\lambda & 1 +2 \lambda & -\lambda & & & \\ & \cdots & \cdots & & \\ & & \cdots & \cdots & \\ & & -\lambda & 1+2 \lambda & -\lambda \\ & & & -\lambda & 1+\lambda\end{array}\right]$ |
A矩阵可逆, 可得
| $ \hat{v}=A^{-1} \tilde{v} $ | (19) |
正则化因子的引入, 使细尺度匹配代价被粗尺度匹配代价修正, 因此只需求出最细尺度的匹配代价, 即选取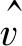 中s=0的匹配代价聚合结果。
中s=0的匹配代价聚合结果。
4 实验验证
感知焊接过程中环境实时变化, 实施调整焊枪位置是研究的重点。用双目视觉传感器能够采集丰富的信息, 适应环境性好, 具有非接触不易干扰的良好特性, 避免了环境的不确定性对焊接成品质量的影响。由于焊缝属于精密检测, 要求传感器获取的焊缝图像质量高, 图像系数畸变小, 所以本文选择摄像效果良好的MER-132-30UM/C, USB接口帧曝光CCD工业数字相机。镜头的选择取决于镜头的焦距f的大小, 根据实际情况, 实验平台选择f=35 mm的镜头。
实验过程中, 双目视觉传感器从不同位置拍摄焊缝全貌。然后, 对焊缝图像进行中值滤波、二值化处理得到焊缝信息。通过视觉传感器标定, 得到传感器参数。根据代价计算和代价聚合得到最小的匹配代价, 即焊缝左右图像匹配对应点, 从而得到焊缝视差图。再从视差中恢复深度信息, 得到焊枪的高度信息, 实时调整焊枪高度。图 6为位置1焊缝左图像, 图 7为处理之后的焊缝视差图。从焊缝视差图中获取最小视差可得到焊缝到传感器距离(焊缝深度信息)。
改变传感器到焊缝距离, 进行多次实验, 用SAD算法和本文提出的算法分别对焊缝图像进行立体匹配, 记录下每次的实验数据。统计结果如表 1和表 2所示。
表 1
本文算法测得焊缝深度信息
| 位置 | 实际距离 | 实验距离 | 偏差 | 误差率/ % |
| mm | ||||
| 1 | 20.8 | 22.05 | 1.25 | 6.0 |
| 2 | 25.6 | 27.04 | 1.44 | 5.6 |
| 3 | 30.5 | 29.68 | -0.82 | 2.7 |
| 4 | 35.0 | 32.98 | -2.02 | 5.8 |
| 5 | 39.7 | 42.31 | 2.61 | 6.6 |
表 2
SAD测得焊缝深度信息
| 位置 | 实际距离 | 实验距离 | 偏差 | 误差率/ % |
| mm | ||||
| 1 | 20.8 | 26.57 | 5.77 | 27.7 |
| 2 | 25.6 | 31.36 | 5.76 | 22.5 |
| 3 | 30.5 | 34.72 | 4.22 | 13.8 |
| 4 | 35.0 | 27.53 | -7.47 | 21.3 |
| 5 | 39.7 | 31.98 | -7.72 | 19.4 |
对比表 1和表 2可知, 跨尺度代价聚合算法得到的焊缝深度信息误差率均小于10%, 相对于SAD算法, 本文提出的算法误差率更低。实验结果表明, 本文提出的跨尺度代价聚合法实现立体匹配精度更高, 提取焊缝深度信息效果更好。
5 结语
针对双目视觉传感器的焊缝深度信息提取研究, 本文采用了弱纹理检测跨尺度聚合的立体匹配算法来获得焊缝图像视差图。首先, 通过双目视觉传感器获取焊缝图像, 对焊缝图像进行中值滤波、二值化处理, 去除图像噪声, 减少图像背景干扰。然后, 通过标定得到视觉传感器参数, 进一步得到视差和深度的关系。最后, 采用弱纹理检测跨尺度聚合算法进行立体匹配, 获取焊缝图像视差图, 得到焊缝视差。与SAD算法比较, 由跨尺度代价聚合算法计算得到的焊缝深度信息误差率均小于10%, 提取焊缝深度信息效果更好。
参考文献
-
[1]基于折光鱼眼全景相机的双目立体视觉标定[J]. 中国科技论文, 2016, 11(8): 913-919. DOI:10.3969/j.issn.2095-2783.2016.08.015
-
[2]基于偏振双目视觉的无纹理高反光目标三维重构[J]. 红外与毫米波学报, 2017, 36(4): 432-438. DOI:10.11972/j.issn.1001-9014.2017.04.009
-
[3]KIM S, MIM D, KIM S, et al. Unified confidence estimation networks for robust stereo matching[J]. IEEE Transactions on Image Processing, 2019, 28(3): 1299-1313. DOI:10.1109/TIP.2018.2878325
-
[4]基于位姿约束的大视场双目视觉标定算法[J]. 光学学报, 2016, 36(1): 205-214.
-
[5]基于单应性矩阵的变焦双目视觉标定方法[J]. 光学学报, 2018, 38(3): 360-368.
-
[6]LYU X Q, GU D X, WANG Y D, et al. Feature extraction of welding seam image based on laser vision[J]. IEEE Sensors Journal, 2018, 18(11): 4715-4724. DOI:10.1109/JSEN.2018.2824660
-
[7]爬壁机器人焊缝跟踪过程中的焊缝检测与识别研究[J]. 热加工工艺, 2018(1): 210-213.
-
[8]YANG J H, JIA Z Y, LIU W, et al. Precision calibration method for binocular vision measurement systems based on arbitrary translations and 3D-connection information[J]. Measurement Science and Technology, 2016, 27(10): 105009. DOI:10.1088/0957-0233/27/10/105009
-
[9]MITCHELL D, GU F. Autonomous weld seam identification and localization using eye-in-hand stereo vision for robotic arc welding[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(5): 288-301. DOI:10.1016/j.rcim.2013.01.004
-
[10]立体匹配中视差图计算方法的研究进展[J]. 遥感信息, 2017, 32(2): 7-14. DOI:10.3969/j.issn.1000-3177.2017.02.002
-
[11]一种改进Census变换与梯度融合的立体匹配算法[J]. 光学学报, 2018, 38(2): 267-277.
-
[12]基于跨尺度引导图像滤波的稠密立体匹配[J]. 光学学报, 2018, 38(1): 232-238.
-
[13]基于金字塔变换跨尺度代价聚合的立体匹配[J]. 系统仿真学报, 2016, 28(9): 2227-2234.
-
[14]WILLIE M, IN KYU P. Deep self-guided cost aggregation for stereo matching[J]. Pattern Recognition Letters, 2018, 112: 168-175. DOI:10.1016/j.patrec.2018.07.010