近年来, 大停电事故频频发生^[1]。其中, 系统脆弱元件的故障有可能使得故障波及范围更广。因此, 如何准确地找到电网的脆弱环节并进行预防是一个非常重要的课题。目前, 基于复杂网络理论的电力系统脆弱性研究受到国内外学者的广泛关注^[2]。文献[3-9]通过边介数法对线路进行了脆弱性评估。但是, 复杂网络理论着重体现电网各电气元件之间的拓扑结构, 不能充分体现各电气元件间的电气属性。同样, 电力网络中的各个元件存在多重联系, 简单的有向图不能真实刻画电力网络的特性^[10]。因此, 本文采用能有效处理元件之间多元关系的超图理论。

超网络理论是近些年提出的仍处于模型构建和描述阶段的理论^[11]。1970年, 贝尔热C提出了超图的最初概念^[12]。2011年, 王众托院士在文献[10]和文献[13]中对基于超图的超网络理论的应用进行了归纳总结。文献[14]将超网络、复杂网络和D谱理论应用于评估网络中的重要节点。文献[15]将超网络理论应用于微博, 以识别影响力较大的关键节点。在电网中, 节点和线路之间除了物理上的连接关系之外, 仍存在其他多种电气联系, 且两者相互影响。超图理论能将具有相同属性的对象以集合的形式归类, 体现出各个对象之间的隐含联系。因此, 通过超图理论能够体现节点和线路之间的隐含联系, 从而更准确有效地判别其脆弱性。

超图的定义如下:设V={v₁, v₂, v₃, …, v_n}是一个有限集, 若满足:

(1) E_i=φ, i=1, 2, 3, …, m;

(2) 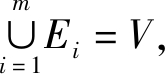记E={E₁, E₂, E₃, …, E_m}

则称H=(V, E)为超图, 记为(V, E)或H。其中, V的元素v₁, v₂, v₃, …, v_n为超图的节点; E为超图中超边的集合, E={E₁, E₂, E₃, …, E_m}。

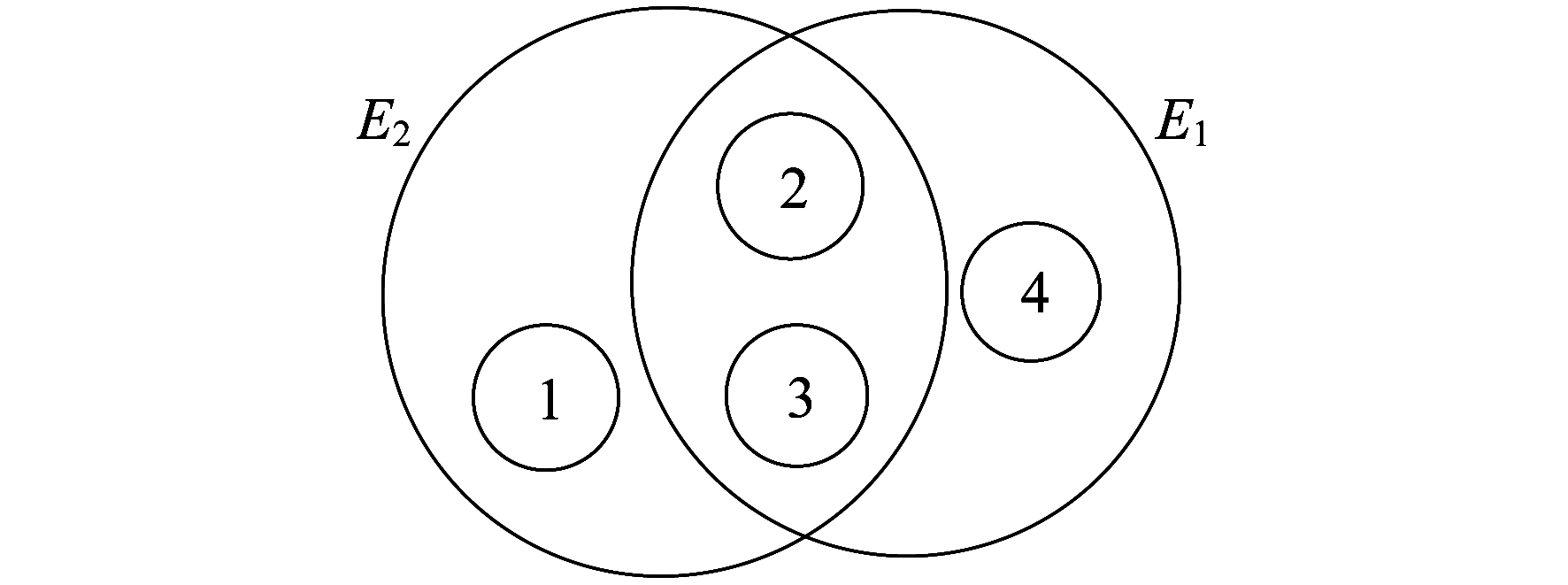
超图可以用图形来表示^[14]。例如, 超边E₁与节点2, 节点3, 节点4存在关联, E₂与节点1, 节点2, 节点3存在关联, 则以超图的形式表达为E₁(2, 3, 4), E₂(1, 2, 3), 其图形如图 1所示。

本文将电力系统中的线路作为超图中的节点, 简称超图节点; 以电力系统中的节点作为超图中的超边, 简称超图超边。根据节点和线路之间的联系, 建立简单的加权超图模型。通过电网中最基本的潮流来判断节点和线路之间的联系。

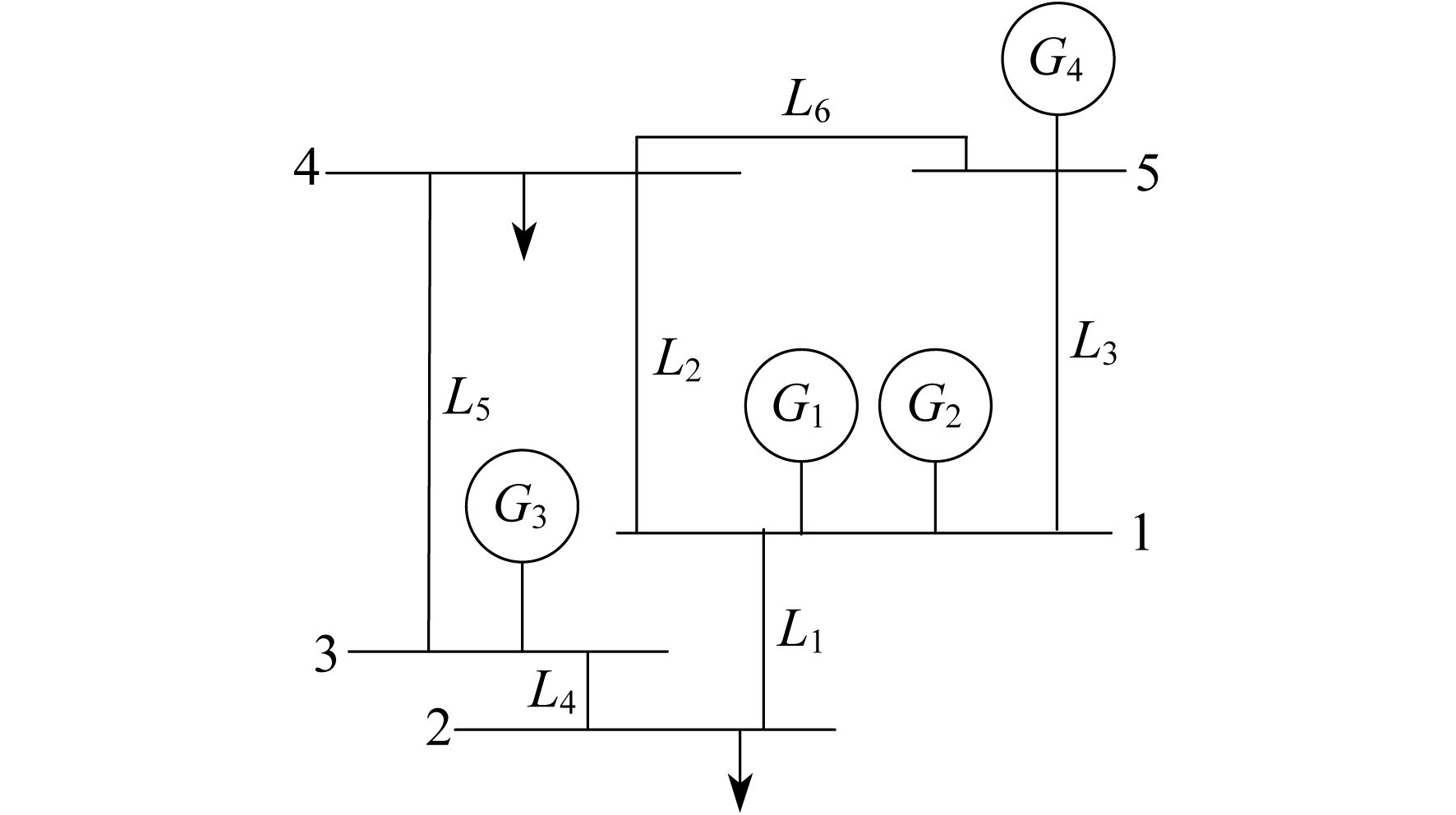
以IEEE-5节点系统为例, 如图 2所示。IEEE-5节点系统中, 节点1, 节点3, 节点5为发电节点, 节点2和节点4为负荷节点。在电力系统中, 潮流从发电节点流向负荷节点。因此, IEEE 5节点系统的所有发电-负荷路径有:1—2; 1—4—3—2; 1—4; 3—2; 5—1—2; 5—1—4—3—2; 5—4—3—2; 5—4; 5—1—4。显然, 在任意一条发电-负荷路径中, 所有的节点和线路都相互联系。根据与各超图超边存在联系的超图节点, 从而建立适用于电力系统的超图模型。

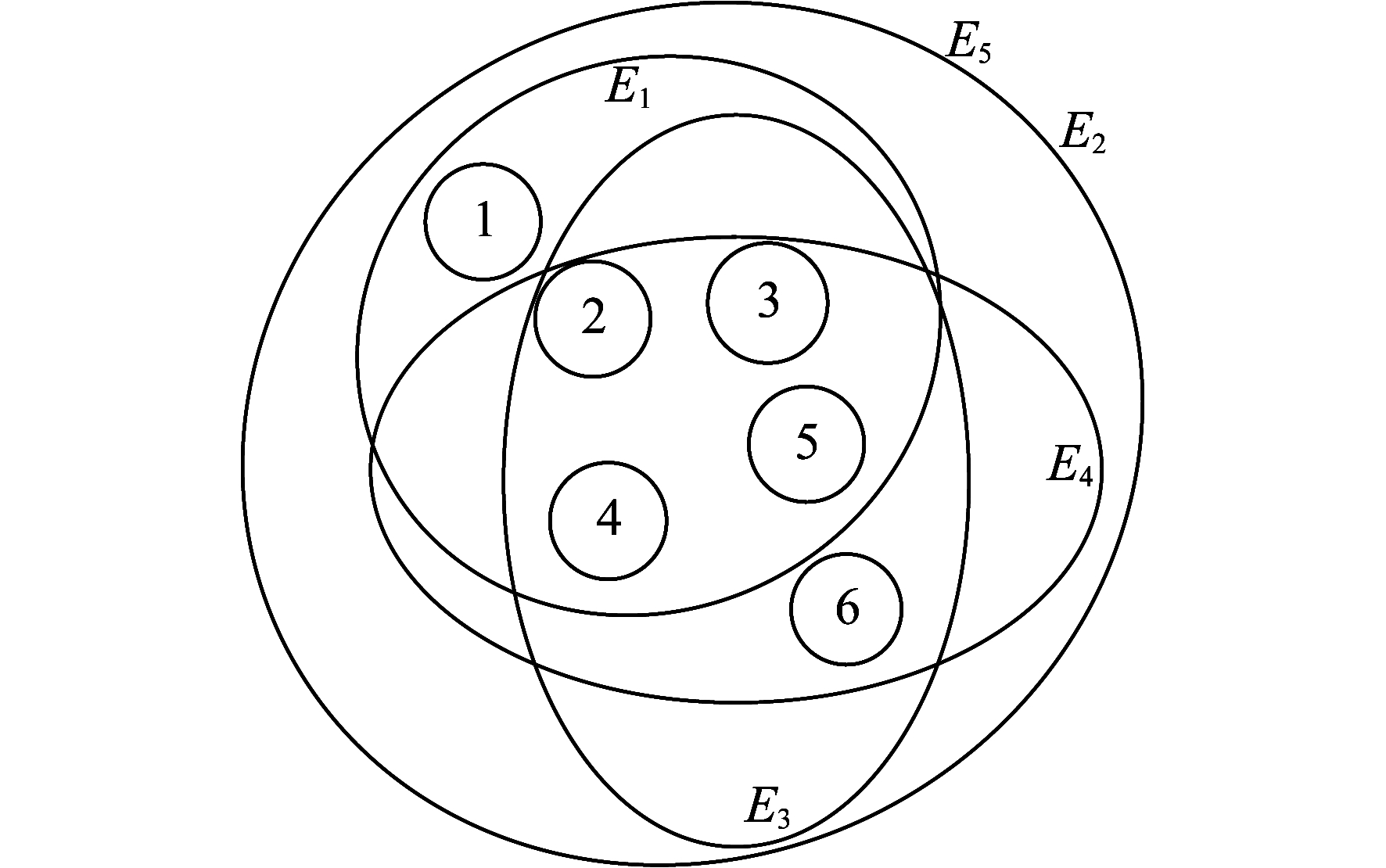
IEEE-5节点系统的超图模型中, 超图节点为V=[1, 2, 3, 4, 5, 6], 超图超边为E=[E₁, E₂, E₃, E₄, E₅].节点与线路之间的联系为:E₁(1, 2, 3, 4, 5), E₂(1, 2, 3, 4, 5, 6), E₃(2, 3, 4, 5, 6), E₄(2, 3, 4, 5, 6), E₅(1, 2, 3, 4, 5, 6)。IEEE-5节点系统的超图示例如图 3所示。

在数域空间中的每一个对象都可以当作一个质点, 并且每一个对象周围都存在一个场域^[16], 在该场域内的任一对象(除本体以外)都会受到它的作用。因此, 在整个空间中可以确定数据场。数据场理论的基本观点为:在同一数据空间中, 数据对象之间相互联系、相互影响; 每一个数据对象既对其他数据对象产生作用, 同时也受到其他所有对象的影响; 所有数据对象的作用力呈现出空间分布的特性, 并且随着对象之间距离的增加而衰弱, 随着该对象本身质量的增加而增强^[17]; 在数值计算上, 数据场的数学表达式具有多种形式, 依据具体问题域的不同而有所不同^[17]。

在给定空间Ω中的数据对象x, ∀y∈Ω, 记对象x在点y处产生的势值为Φ_x(y), 则Φ_x(y)应同时满足:

(1) Φ_x(y)是定义在空间Ω上的连续、光滑、有限函数;

(2) Φ_x(y)各向同性;

(3) Φ_x(y)是距离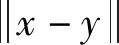的单值递减函数。当时, Φ_x(y)达到最大值, 但不是无穷大; 当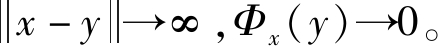

本文选用经典的核力场作为势函数

$\phi_{x}(y)=m_{\mathrm{c}} \mathrm{e}^{-\left(\frac{\left\| {x-y} \right\|}{\sigma}\right)^{k_{\mathrm{c}}}}$

(1)

式中:m_c——场源强度;

σ——影响因子, 用于控制对象之间的作用程度;

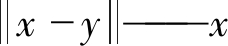与y之间的最短路径距离;

k_c——距离指数。

根据文献[17]所述, 短程场的势函数能更好地描述对象之间的相互作用, 因此选择k=2。

空间中任一点x的势值可以表示为

$\psi(x)=\sum\limits_{i=1}^{n} \phi_{i}(x)=\sum\limits_{i=1}^{n} m_{i} \mathrm{e}^{-\left(\frac{\left\| {x-x_{i}} \right\|}{\sigma}\right)^{2}}$

(2)

若x=x_i, 则

本文将数据场理论应用于电力系统, 并对电网中的线路进行分析。线路可以作为一个物理粒子; 线路的质量M为线路对整个系统的影响能力; 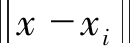为线路x与线路x_i的最短路径距离; σ为线路的影响因子, 具体定义及计算如下。

假设电网中的线路周围同样存在场域, 能够影响周围其他线路。本文将数据场理论应用于超图理论, 作为评价电力系统中线路的脆弱性指标。根据式(2), 计算每一条线路在超图模型中的势值需要线路的质量(m_i)、辐射距离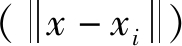以及影响因子(σ)。

线路的质量表示线路辐射周围线路的能力。线路的质量越大, 其辐射能力越大。在一般图模型中, 没有对线路质量的具体描述, 可以将其理解为该线路的固有属性, 比如拓扑结构(度乘积^[18]、边介数)和运行状态(熵等)。

本文定义F_L={f_l1, f_l2, f_l3, …, f_ln}为线路的一组属性。首先, 本文定义G为发电机节点, L为负荷节点, 节点发电度D_G(i)为节点i的邻居节点的发电量之和, 节点负荷度D_L(i)为节点i的邻居节点的负荷量之和, 则有

$ D_{\mathrm{G}}(i)=\sum\limits_{j} P_{\mathrm{G}j} $

(3)

$D_{\mathrm{L}}(i)=\sum\limits_{j} P_{\mathrm{L} j}$

(4)

式中:i, j——节点编号;

P_Gj——节点j的发电量;

P_Lj——节点j的负荷量。

基于节点发电度和节点负荷度, 可以得出线路发电度乘积D_PG(k)和线路负荷度乘积D_PL(k)。

$D_{\mathrm{PG}}(k)=D_{\mathrm{G}}(p) \times D_{\mathrm{G}}(q)$

(5)

$D_{\mathrm{PL}}(k)=D_{\mathrm{L}}(p) \times D_{\mathrm{L}}(q)$

(6)

式中:p, q——线路k两端的节点编号。

线路的度乘积属性f_l1(k)公式为

$ f_{11}(k)=\frac{1}{2}\left[D_{\mathrm{PG}}(k)+D_{\mathrm{PL}}(k)\right. $

(7)

线路的电气介数属性f_l2(k)公式为^[19]

$ \begin{aligned} f_{12}(k)=B_{k}(p, q) =\\ \sum_{i \in G, i \in L} \sqrt{W_{i} W_{j}} \left| {I^{i j}(p, q)} \right| \end{aligned} $

(8)

式中:W_i——发电机节点i的发电量;

W_j——负荷节点j的负荷量;

I^ij(p, q)——发电机节点i至负荷节点j路径上注入单位电流后, 线路k上引起的电流。

线路的潮流转移熵属性f_l3公式为^[20]

$ f_{13}(k)=H_{\mathrm{T}}(k)=-\sum\limits_{m=1}^{S} \beta_{m k} \ln \beta_{m k} $

(9)

$\beta_{m k}=\frac{\Delta \lambda_{m k}}{\sum\limits_{m=1}^{S} \Delta \lambda_{m k}}$

(10)

$\Delta \lambda_{m k}=P_{m k}-P_{m 0}$

(11)

式中:H_T(k)——线路k的潮流转移熵;

S——系统线路总数;

β_mk——潮流转移冲击率;

Δλ_mk——潮流增量;

P_mk——线路k断开后, 线路m上的潮流。

由于线路的各个属性原则上具有不可公性。比如两个属性之间的数值差距较大, 会导致无法反应属性之间的优劣性。因此, 本文将各个属性归一化, 将线路的所有属性值都控制在[0, 1]内。然后将F_L={f_l1, f_l2, f_l3}综合成以α={α₁, α₂, α₃}为投影方向的一维投影值z_k

$ z_{k}=\sum\limits_{i=1}^{3} \alpha_{i} f_{1 i} $

(12)

z_k为线路的多属性综合评估指标, 投影方向α_i实际上反应的是各个属性的权值。为了计算简便, 本文假设α₁=α₂=α₃=1/3。最终通过公式M=f(z_k)求得线路的质量。

本文基于Floyd的推广算法, 对所构建的超图模型中的最短路径进行计算。

定义^[21]  超图h中的长度为Q的路径定义为顶点-超边交错序列(x₁, E₁, x₂, E₂, …, x_Q+1, E_Q+1), 简称为P(x₁-x_Q+1), 且满足:

(1) x₁, x₂, x₃, …, x_Q+1为h中互异的顶点;

(2) E₁, E₂, E₃, …, E_Q+1为h中互异的超边。

假设超边的权值矩阵为w(E_i)_1×n, 称之为超边权。x_i到x_q+j的最小权路径称为x_i到x_q+j的最短路径。

$ P\left(x_{i}-x_{Q+i}\right)=\min \left[\sum\limits_{n=1}^{Q} w\left(E_{n}\right)\right] $

(13)

超边的权值越大, 则线路之间的距离越远, 线路之间的影响则越弱。

本文将电网中的发电节点和负荷节点作为超图中的超边。一个节点的发电量或者负荷量越大, 则该节点周围的线路影响力也越大。因此, 本文定义超边的权值w(i)为

$ w(i)=\frac{1}{\max \left(P_{G i}, P_{L i}\right)} $

(14)

若节点的发电量或者负荷量越大, 则该条线路与邻近线路的距离越近, 对邻近线路的影响就越大。

根据核力场所对应的高斯势中的“3σ规则”可知:每个对象的场域范围为以该对象为中心、半径等于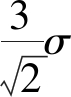的空间, 即对象之间的相互作用力程为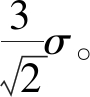对于已给定的势函数形态, 数据场的分布由影响因子σ决定, 而影响因子的选取必须符合该网络中数据的内在分布^[16]。熵是用来度量不确定性大小的指标^[16]。熵值越大, 不确定性越大。因此, 本文采用势熵来衡量势场分布的合理性^[22]。

定义超图势熵E为

$ E=-\sum\limits_{i=1}^{n} \frac{P_{\mathrm{L}}(i)}{Z} \ln \left(\frac{P_{\mathrm{L}}(i)}{Z}\right) $

(15)

$Z=\sum\limits_{i=1}^{n} P_{\mathrm{L}}(i)$

(16)

$P_{\mathrm{L}}(i)=\sum\limits_{j=1}^{n} \phi_{j}\left(v_{i}\right)=\sum\limits_{j=1}^{n} m_{j} \mathrm{e}^{-\left(\frac{\left\| {x_{i}-x_{j}} \right\|}{\sigma}\right)^{2}}$

(17)

式中:P_L(i)——线路i的势值;

Z——整个网络的势值。

根据熵的性质判断, 当超图势熵最小时, 超图的场分布最不均匀, 其不确定性最小。因此, 将求解σ的问题转化为求势熵最小的优化问题。

根据数据场理论的定义, 本文认为线路同样存在场域, 并对其场域内的其他对象产生影响。若该对象本身处于其他对象的场域内, 也将受到其他对象的影响。本文假设线路只对其场域内的其他线路产生影响, 而对超出其场域的线路所造成的影响忽略不计, 则可根据该线路对其场域内的其他线路所造成的影响之和来判断该线路的脆弱性。因此, 本文定义线路影响率(Influence Rate of Line, IRL)为

$ R_{\mathrm{IL}}(j)=\frac{\sum\limits_{i=1}^{h} \phi_{j}\left(v_{i}\right) \times m_{i}}{\sum\limits_{j=1}^{n} \sum\limits_{i=1}^{n} \phi_{j}\left(v_{i}\right) \times m_{i}} \times 100 \% $

(18)

IRL表示线路j对整个电网的影响程度。当IRL越大, 则该条线路对电网的影响程度越大, 也意味着其越脆弱。当IRL越小, 则该条线路对电网的影响程度越小, 也就意味着其不重要。

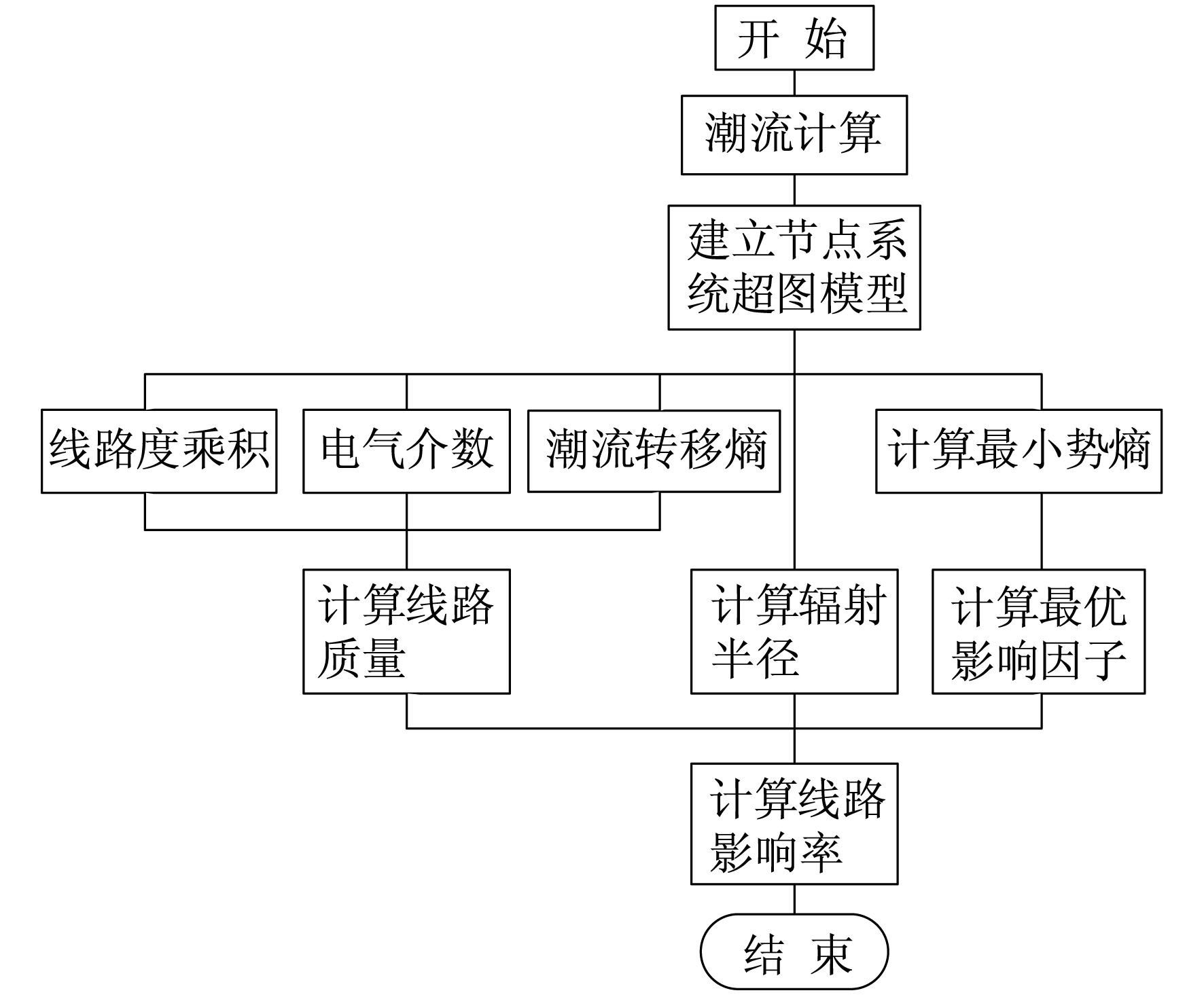
根据上文所述, 线路影响率计算流程如图 4所示。

本文选用IEEE-39标准节点系统来验证有效性。

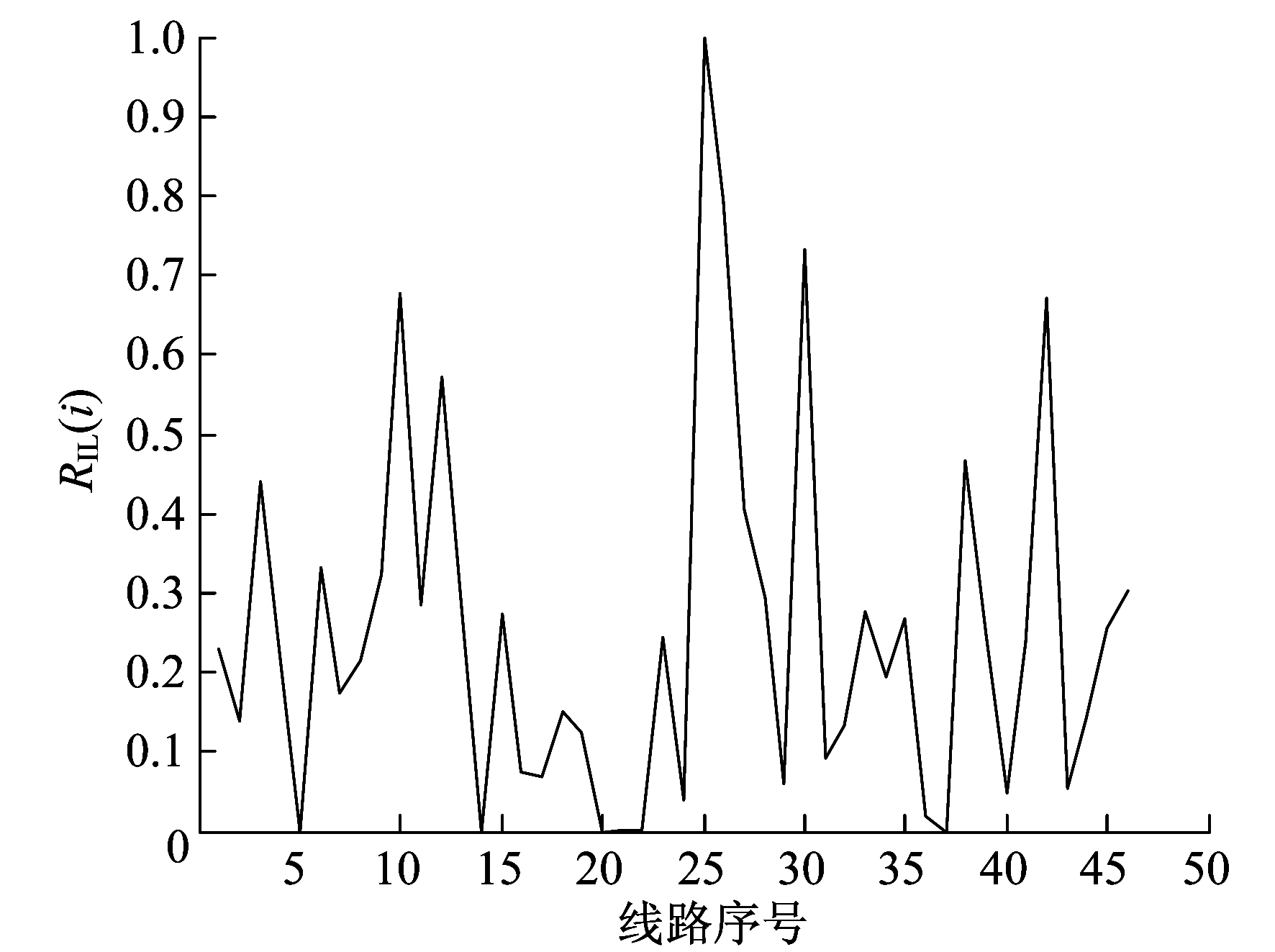
假设质量为投影值的线性函数, 则本文设m=z; 在求得质量和超图最短路径之后, 将最短路径中的最大值作为影响因子的上界, 将最短路径的最小值作为影响因子的下界。采用黄金比例搜索算法缩小搜索范围, 直至满足精度要求。计算得影响因子σ=0.002 6, 然后根据线路之间的作用力程为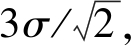求得每条线路的影响范围至少为0.001 9。计算得出的线路影响率指标如图 5所示。

从上述结果中选取指标排名前10的线路, 与文献[6]和文献[8]进行对比分析, 如表 1所示。表 1中影响率指标为归一化后的结果。文献[6]将线路电抗作为权重结合介数, 对线路进行脆弱性分析。文献[8]根据拓扑结构角度的介数指标和运行状态角度的潮流熵, 综合评价线路的脆弱性。本文利用超图理论所建立的超图模型, 将发电机节点和负荷节点与线路之间的联系具现化, 并通过数据场理论对线路进行分析, 求得线路对整个网络的影响。

由表 1可以看出, 线路15—16, 16—17, 17—18在文献[6]和文献[8]的结果中并不靠前, 但是如果这些线路断开, 将会对电网中发电机节点和负荷节点产生较大的影响。线路16—19在文献[6]中排名第3, 线路13—14在文献[8]中排名第1, 这些线路的介数值比较高, 但断开后所产生的影响并不大。因此, 基于复杂网络理论的介数法能够从一定程度上评价线路的脆弱性, 但是不够全面。本文建立的超图模型能清晰地反应出电力系统中发电机、负荷和线路之间的联系, 能更准确地判别线路的脆弱性。

在排名前10的线路中, 文献[6]与本文方法有5条线路相同。两者之间存在差异的原因主要有:超图理论基于节点和线路之间的虚拟联系与复杂网络理论基于节点和线路的物理连接存在差异; 文献[6]采用电抗作为介数权重, 并且只考虑了拓扑结构, 而超图理论综合考虑了线路的自身属性和拓扑特征。同样, 文献[8]得出的关键线路与本文方法有5条线路相同。文献[8]将介数法和熵相结合, 从拓扑结构和运行状态综合考虑线路的脆弱性, 但只是通过加权的形式。相比之下, 本文方法更为合理有效。

正确判断电网中的脆弱线路对防范大停电事故具有重要意义。本文提出了一种基于超图理论的线路脆弱性评估方法, 为大型电网的线路脆弱性评估提供了参考依据。

(1) 基于电力系统中最基本的潮流得到电网中节点和线路之间的联系, 从而建立适用于电力系统的超图模型。该模型能充分体现电力元件之间的多元关系。

(2) 从拓扑结构和运行状态两个角度建立了线路的质量指标, 能够有效衡量线路对电网的影响能力。

(3) 利用数据场理论中的拓扑势定义了线路影响率, 对线路进行脆弱性评估。其体现了线路在整个电网中的影响程度, 影响程度越大, 则线路越脆弱。