|
|
|
发布时间: 2019-08-10 |
|
|
|
|
收稿日期: 2018-04-18
基金项目: 上海高校青年教师培养资助计划(ZZsdl15092);上海电力学院人才引进基金(K2014-044)
中图法分类号: TM773
文献标识码: A
文章编号: 1006-4729(2019)04-0345-04
|
摘要
单相接地故障消除之后, 相控式消弧线圈应退出运行, 不再输出补偿电流, 中性点电压恢复至正常状态。但在某变电站的录波记录中发现, 系统中性点电压呈现出低频振荡的现象。为此, 采用电工学的基本原理, 分析了产生低频振荡的原因, 并通过PSCAD/EMTDC仿真证实了该理论分析的结果。最后, 提出了抑制低频振荡的措施。
关键词
相控式消弧线圈; 单相接地故障; 谐振接地; 中性点电压振荡
Abstract
After a single-phase-to-ground fault is eliminated, the phase-controlled arc suppression coil should exit without any compensation currents.Then, the neutral voltage will return to normal state.However, the phenomenon of low-frequency oscillation of the neutral voltage is found in the recording of a substation.For this reason, the basic circuit principles are adopted, the causes of low frequency oscillation are analyzed, and the suppression methods are put forward.Finally, the theoretical analysis is verified through PSCAD/EMTDC simulation.
Key words
phase-controlled arc suppression coil; single-phase-to-ground fault; resonant grounding; oscillation of the neutral voltage
我国中压配电网普遍采用中性点经消弧线圈接地方式来消除单相接地故障[1-3]。在实际中, 常见的消弧线圈有调匝式消弧线圈、调容式消弧线圈及相控式消弧线圈。与其他两种消弧线圈相比, 相控式消弧线圈具有响应速度快、输出电流可以连续调节等优点, 因此发展迅速[4-5]。相控式消弧线圈的工作原理是利用晶闸管改变输出电流的大小, 以补偿单相接地故障电流。其投入/退出工作的控制方式为[6-7]:中性点位移电压较低时, 跟踪线路对地电容电流的变化, 调节相控式消弧线圈的电感值; 当中性点位移电压高于设定阈值时, 认为发生接地故障, 控制器命令相控式消弧线圈工作; 单相接地故障消除之后, 当中性点位移电压低于设定阈值时, 认为接地故障消失, 控制器命令相控式消弧线圈退出工作。
相控式消弧线圈的本体是一个高短路阻抗变压器, 其实质是通过改变该变压器一、二次侧之间的短路阻抗达到调节补偿电流的目的[8]。这与调匝式消弧线圈不同, 因此相控式消弧线圈的控制策略会带来许多新的问题。本文针对相控式消弧线圈退出时中性点电压的振荡现象开展研究, 理论分析其原因并进行仿真验证, 最后提出了相应的抑制措施。
1 中性点电压振荡现象
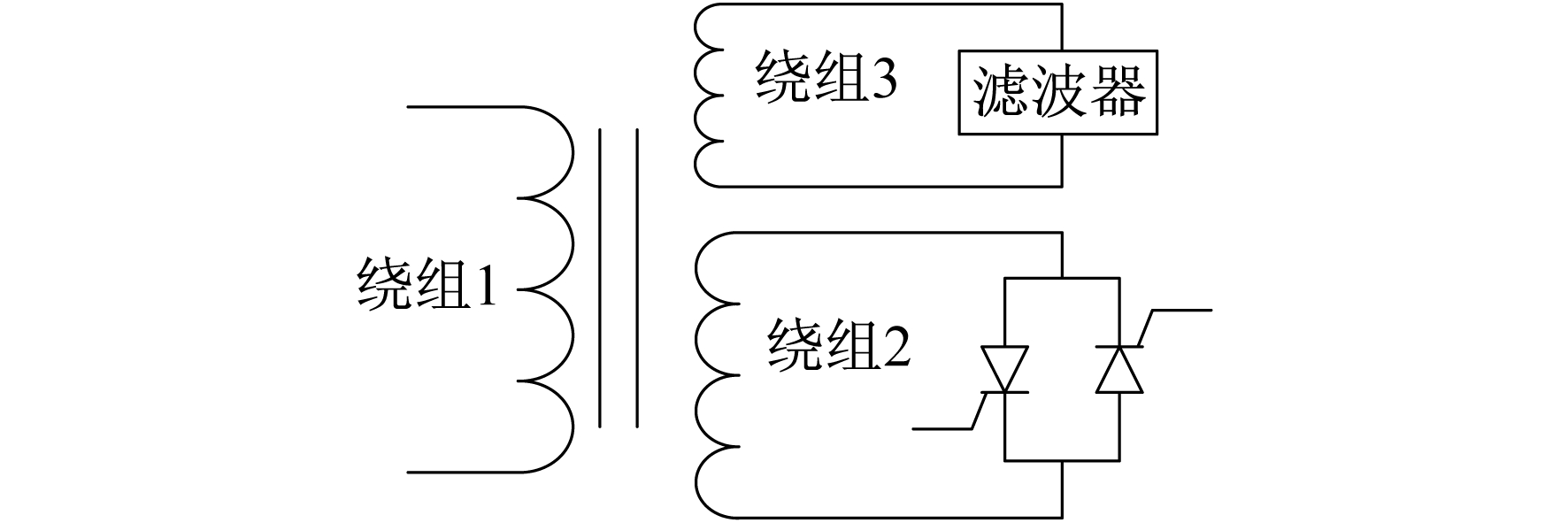
某35 kV变电站中性点装设相控式消弧线圈, 结构如图 1所示[9-10]。其中, 绕组1接系统中性点, 以提供补偿电流; 绕组2是相控式消弧线圈的主要部分, 接入一对反向并联的晶闸管, 以控制补偿电流的大小; 绕组3接滤波器, 以滤除补偿电流中的高次谐波。
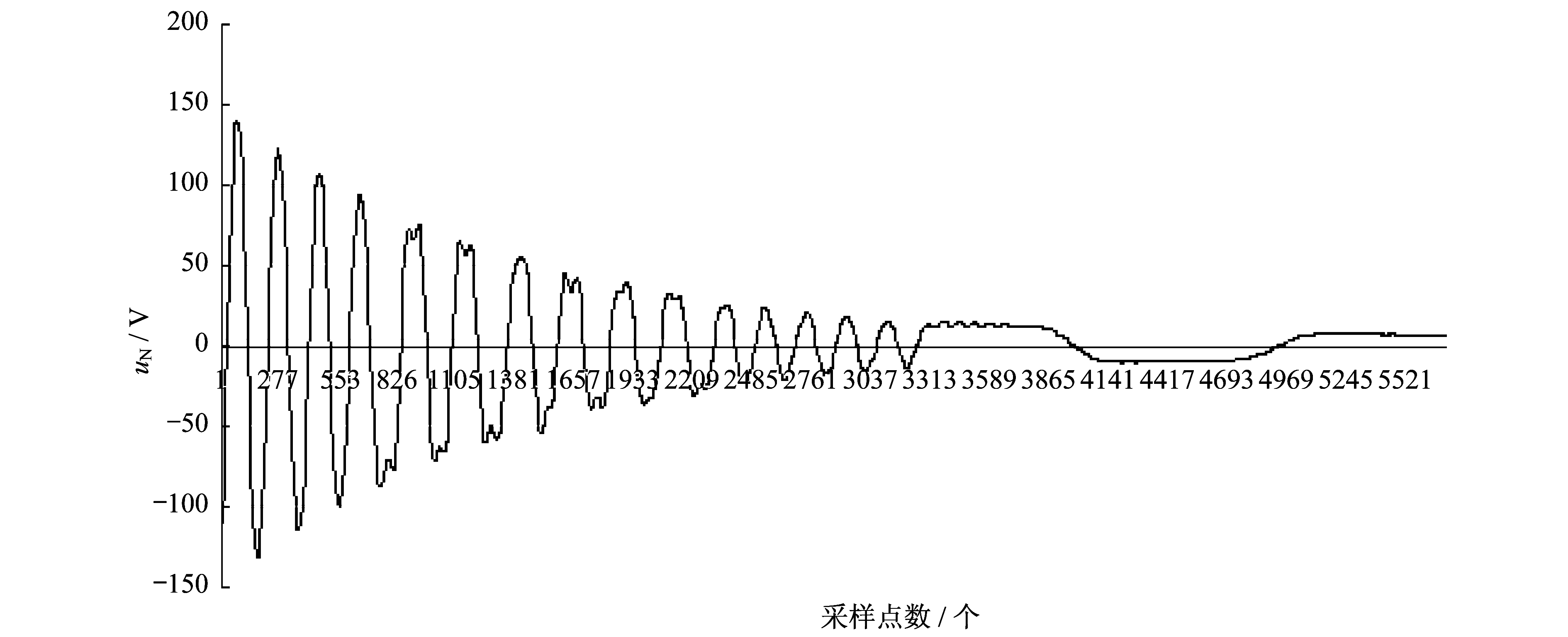
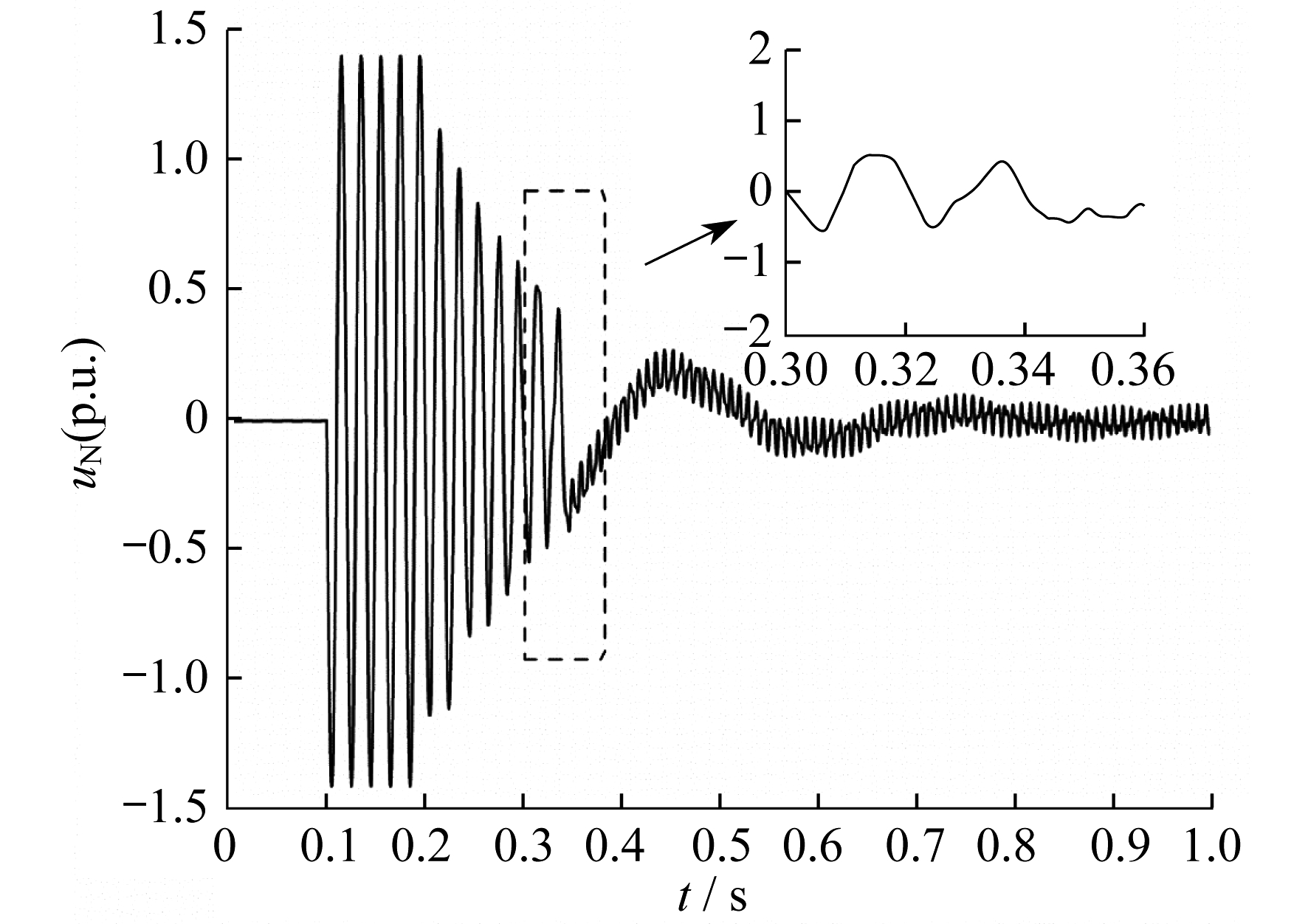
某次单相接地故障消除后, 录波装置获取的中性点电压波形如图 2所示。由图 2可以看出, 故障消除之后中性点电压的幅值逐渐减小, 当中性点电压的幅值减小至设定阈值以下时, 相控式消弧线圈退出运行。在相控式消弧线圈退出之后, 中性点电压幅值继续减小, 但波形呈现低频振荡。
按照理论情况, 中性点电压应该恢复至电网正常状态, 幅值很小[11], 但由图 2发现, 消弧线圈退出工作之后, 中性点却仍存在低频振荡的正弦波电压。
对于相控式消弧线圈来说, 退出工作意味着绕组2回路中的晶闸管关断, 即绕组2开路。而绕组3回路一般装设3次、5次谐波滤波器。有人认为低频振荡的原因是:绕组3中滤波元件(电容和电感)与系统对地电容发生谐振, 从而造成低频振荡。本文将通过理论和仿真分析指出该观点的错误之处, 并从理论和仿真两个方面说明低频振荡的原因。
2 理论分析
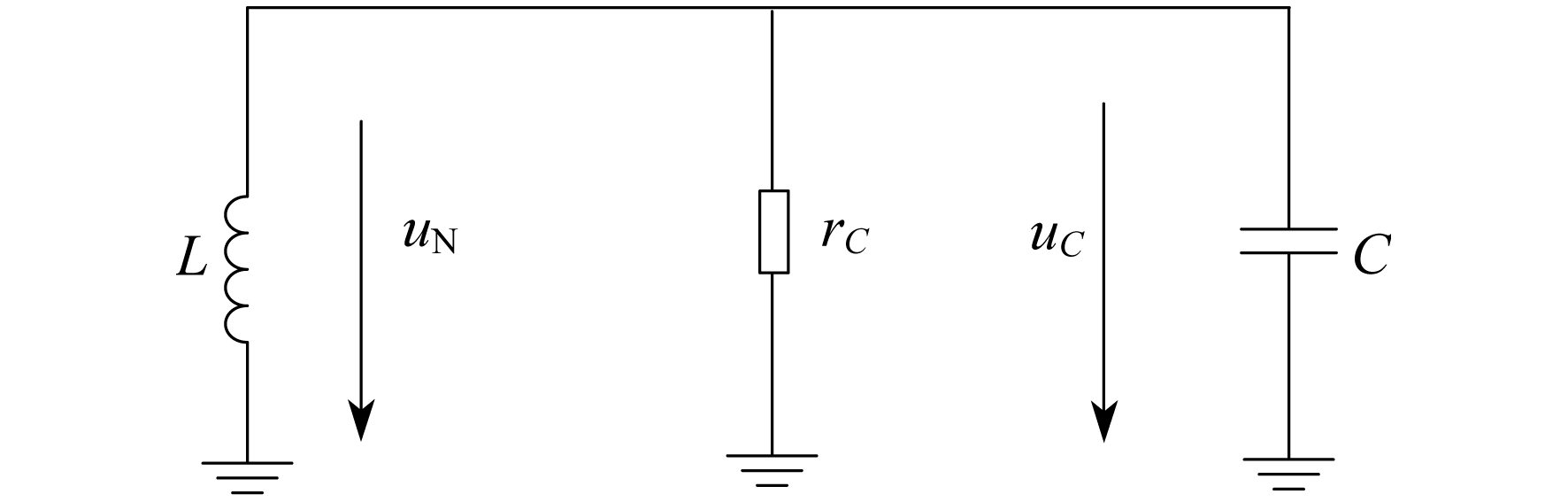
真实的接地故障消失之后, 控制器需要根据中性点电压是否小于阈值(如15%相电压)来决定是否发出接地故障消失的命令, 进而使晶闸管闭锁。因此, 从真实接地故障消失到晶闸管闭锁有一定的时间延迟, 在这段延迟时间里, 相控式消弧线圈依旧工作。此时, 相控式消弧线圈与对地电容串联, 其等效电路如图 3所示[12]。
根据电路原理,列出如下微分方程
| $ \left\{\begin{array}{l} i_{C}=C \frac{\mathrm{d} u_{C}}{\mathrm{d} t} \\ u_{C}=u_{\mathrm{N}}=-L \frac{\mathrm{d} i}{\mathrm{d} t} \\ i=i_{C}+\frac{u_{\mathrm{N}}}{r_{C}} \end{array}\right. $ | (1) |
初值条件为
| $ \left\{\begin{array}{l} \left.u_{C}\right|_{t=0}=u_{C}(0) \\ \left.\frac{\mathrm{d} u_{C}}{\mathrm{d} t}\right|_{t=0}=\frac{i_{C}(0)}{C} \end{array}\right. $ | (2) |
式中:uC(0), iC(0)——起始时刻电容电压及流过电容的电流。
解方程组(2)可得
| $ \begin{aligned} u_{\mathrm{N}}(t)=& e^{-b t}\left[u_{C}(0) \frac{\omega_{0}}{\omega_{1}} \sin \left(\omega_{1} t+\varphi\right)+\right.\\ & \left.\frac{i_{C}(0)}{\omega_{1} C} \sin \omega_{1} t\right] \end{aligned} $ | (3) |
其中,
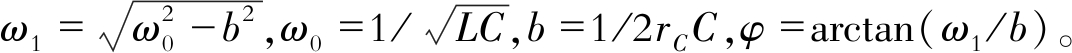
考虑到脱谐度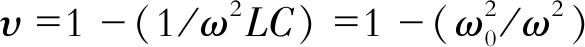 及阻尼率d=1/rCωC, 有
及阻尼率d=1/rCωC, 有
| $ \omega_{0}=\omega \sqrt{1-v} $ | (4) |
| $ \omega_{1}=\omega \sqrt{1-v-\left(\frac{d}{2}\right)^{2}} $ | (5) |
| $ b=\frac{\omega d}{2} $ | (6) |
单相接地故障消失之后, 控制器需要检测中性点电压的大小, 判断是否低于设定的阈值。在这段时间里, 消弧线圈与对地电容发生串联谐振, 中性点电压中含有频率为ω1的分量。
根据式(5)可以发现, 当脱谐度不同时, 存在以下两种振荡情况。
(1) 当脱谐度υ≥0(全补偿和欠补偿)时, 1-υ-(d/2)2<1, ω1<ω, 此时中性点电压的频率稍微低于工频, 周期比工频电压大, 呈现低频振荡波形。
(2) 当脱谐度υ < 0(过补偿)时, 1-υ-(d/2)2 > 1, ω1 > ω, 此时中性点电压的频率稍微高于工频, 周期比工频电压小, 呈现高频振荡波形。
3 仿真分析
3.1 无滤波器相控式消弧线圈退出时情况仿真
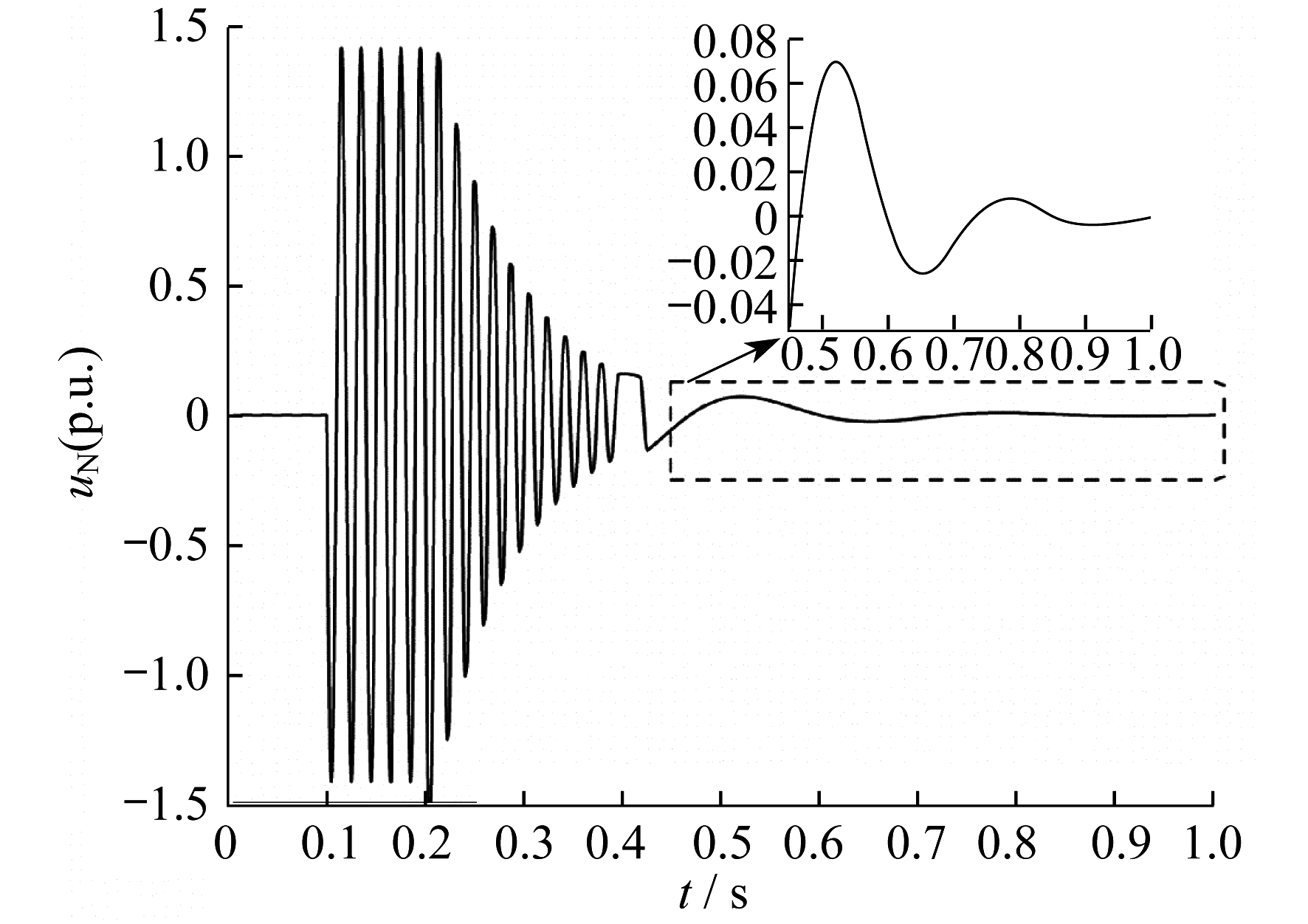
3.2 低频振荡
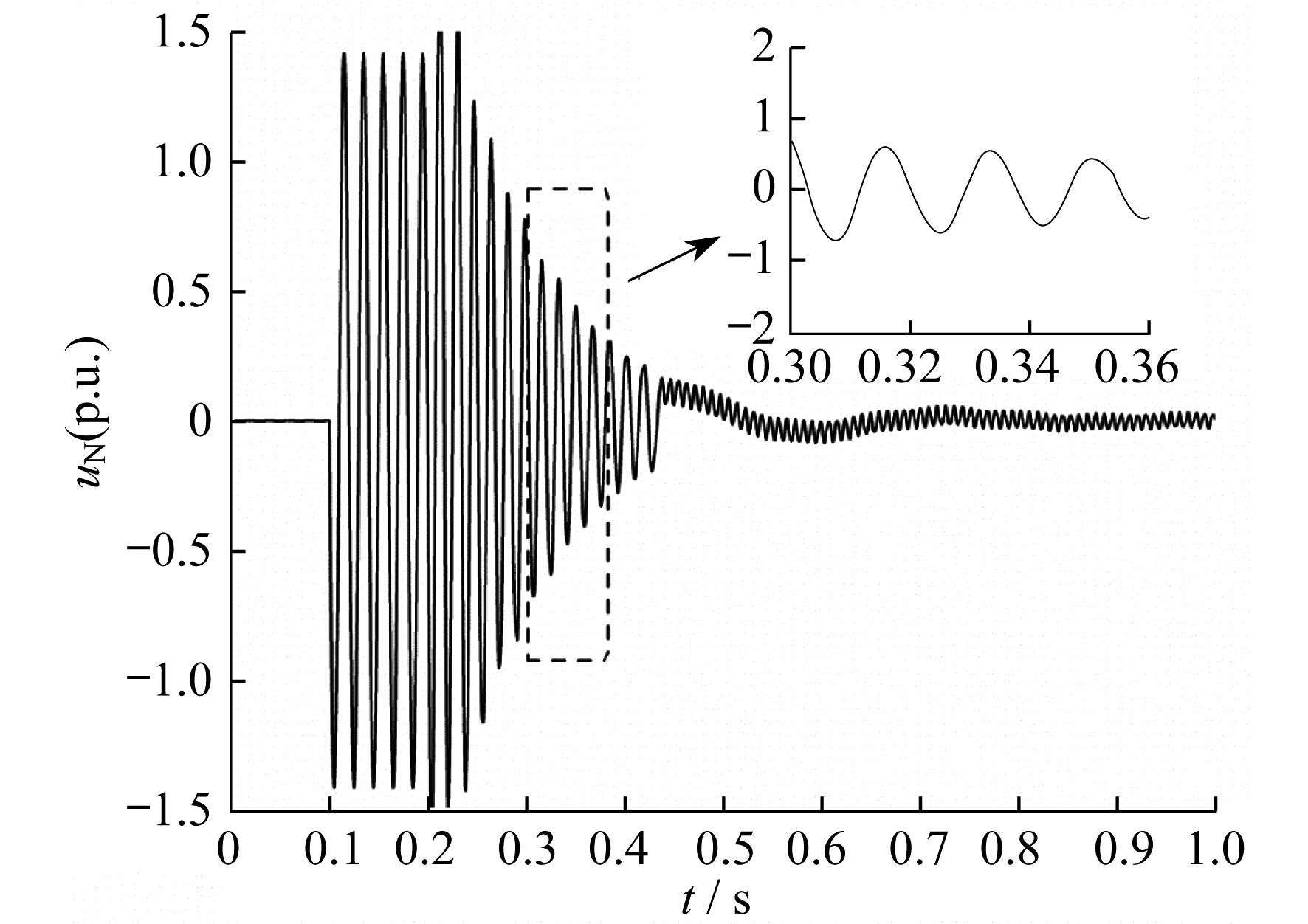
3.3 高频振荡
4 低频振荡的原因及抑制措施
与调匝式消弧线圈不同, 相控式消弧线圈的本质是高短路阻抗变压器式电抗器, 一次侧存在励磁电抗, 其值非常大。在上述仿真中, 相控式消弧线圈的励磁电抗为18 kΩ, 相当于57.295 8 H的电感。当相控式消弧线圈退出工作后, 相当于一个57.295 8 H的电抗器接在中性点与大地之间。这个电抗器会代替相控式消弧线圈的等效电感, 继续与系统对地电容发生谐振。根据式(5), 该谐振的频率为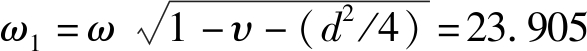 rad/s, 其周期为262.839 3 ms, 与图 5的结果一致。这就解释了图 2中出现低频振荡现象的原因是:励磁电抗与系统对地电容的谐振造成了低频振荡。
rad/s, 其周期为262.839 3 ms, 与图 5的结果一致。这就解释了图 2中出现低频振荡现象的原因是:励磁电抗与系统对地电容的谐振造成了低频振荡。
由此可见, 破坏励磁电抗与系统对地容抗的谐振条件是抑制这种低频振荡的有效措施。因此, 相控式消弧线圈退出时, 反向并联的晶闸管不关断, 而是在某控制角下持续导通。此时, 相当于在绕组2串联一个远远小于励磁电抗的阻抗。根据相控式消弧线圈的结构示意图及变压器的原理可知, 励磁电抗相当于被绕组2的小阻抗“短路”。这样谐振条件就难以成立, 从而抑制了低频振荡。
5 结语
本文通过理论和仿真两方面的分析, 解释了相控式消弧线圈退出后发生低频振荡现象的原因, 认为相控式消弧线圈的励磁电抗与线路对地容抗发生谐振是产生低频振荡的直接原因。因此, 对以相控式消弧线圈为代表的随调式消弧线圈的控制仍有待进一步的研究。
参考文献
-
[1]适合于城市电网中性点接地方式的选择[J]. 上海电力学院学报, 2017, 33(3): 221-228.
-
[2]单相接地故障与串联谐振的辨识[J]. 上海电力学院学报, 2014, 30(6): 563-568.
-
[3]基于小波包的配电网故障选线距离判别方法[J]. 上海电力学院学报, 2014, 30(5): 423-427.
-
[4]WANG W, YAN L, ZENG X, et al. Principle and design of a single-phase inverter-based grounding system for neutral-to-ground voltage compensation in distribution networks[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 1204-1213. DOI:10.1109/TIE.2016.2612180
-
[5]JUSIC A, AGACEVIC J, BAJRAMOVIC Z, et al. Automatic compensation coil-petersen coil in distribution grid[J]. Advanced Technologies, Systems and Applications, 2017(3): 145-154.
-
[6]消弧线圈响应时间的探讨[J]. 高电压技术, 2008, 34(7): 1353-1357.
-
[7]电容电流反馈补偿系统的研究[J]. 高电压技术, 2007, 33(4): 110-113. DOI:10.3969/j.issn.1003-6520.2007.04.028
-
[8]高短路阻抗变压器式消弧线圈滤波参数的计算[J]. 变压器, 2014, 51(8): 16-20.
-
[9]SUN Y, ZHENG W, XU, W. A new method to model the harmonic generation characteristics of the thyristor controlled reactors[C]//Proceedings of the Power Tech, Lausanne, 1-5 July, 2007, New York: IEEE, 2007: 1785-1790.
-
[10]JIA Q, WANG N, LIN D, et al. A thyristor controlled neutral grounding reactor for medium voltage power networks[C]//Proceedings of the Transmission and Distribution Conference and Exhibition: Asia and Pacific, Dalian, China, 18-18 Aug. 2005. New York: IEEE, 2005: 1-4.
-
[11]基于零序电流比值法的小电流接地选线方法及仿真计算[J]. 上海电力学院学报, 2012, 28(5): 427-430.
-
[12]单相接地故障下高阻抗式消弧线圈运行特性的研究[J]. 煤炭工程, 2013, 45(1): 96-98.
-
[13]采用改进有源补偿技术的中性点电压柔性控制方法[J]. 电力系统自动化, 2016(24): 111-117. DOI:10.7500/AEPS20160112001
-
[14]中性点经消弧线圈接地系统小电流接地故障暂态等值电路及暂态分析[J]. 中国电机工程学报, 2015, 35(22): 5703-5714.