|
|
|
发布时间: 2019-08-10 |
|
|
|
|
收稿日期: 2018-04-18
中图法分类号: TM734
文献标识码: A
文章编号: 1006-4729(2019)04-0339-06
|
摘要
为了实现负荷侧的“削峰填谷”, 在用户侧降低充电费用和电池损耗成本, 提出了一种基于虚拟电价理论的电动汽车充放电优化策略。利用虚拟电价建立负荷侧的电价模型; 利用动态分时电价建立用户侧的充电电价模型, 将两个电价模型进行匹配整合, 形成完整的电动汽车充放电的优化调度模型。为优化上述模型, 确保整个调度的可实施性, 在模型中使用BP神经网络和遗传算法进行预测与优化, 同时使用小波分析和模糊聚类方法对充放电负荷进行去噪, 并划分不同的电价时段, 最后使用MATLAB软件对该模型进行了仿真验证。
关键词
电动汽车; 虚拟电价; 削峰填谷; 充放电优化
Abstract
In order to achieve the "peak shaving" on the load side and to reduce the charging and the battery consumption cost on the users' side, virtual time-of-use tariffs are used to establish the electricity price model on the load side, and the dynamic time-of-use tariffs are used to establish the model of charging price on the users' side.Then the two tariff models are matched and integrated to form a complete optimal scheduling model.In order to optimize this model and ensure the enforceability of the whole scheduling, using the BP neural network and the genetic algorithm to predict and optimize.The wavelet analysis and the fuzzy cluster are used to de-noise the charging load and divide the time frame of tariffs.Finally, Matlab software is used to analyze the simulation model.The results illustrate the basic characteristics of the proposed model.
Key words
electric vehicle; virtual time-of-use tariff; peak shaving; charging and discharging optimization
近年来电动汽车数量迅速增加, 到2025年, 所有已销售的电动汽车规模的渗透率将达到10%[1-3]。然而, 电动汽车的充放电行为与传统的以汽油燃料为动力的汽车有所不同。由于汽油汽车发展时间比较长, 自身所需的基础设施(如加油站等)已非常完善, 同时汽油汽车的可使用时长、单次加油可行驶里程数等也比电动汽车更长。然而, 电动汽车目前还没有很完善的基础配套设施, 因此需要对电动汽车的充放电进行合理安排, 以保障用户使用电动汽车的便捷性和可靠性[4-8]。
以往电动汽车进行充放电时所采用的方法大多为无序充电, 其背景环境是电动汽车数量不多, 在整个配电网能够承受范围内可以自由地进行充放电。但随着电动汽车数量的急剧增加, 大量电动汽车同时接入配电网进行无序充电, 势必会给配电网的安全运行带来负面影响, 因此需要合理地调控电动汽车的充放电行为, 以达到削峰填谷的目的[9-10]。
本文提出了一种基于虚拟电价的电动汽车有序充电方法。在电动汽车入网后, 利用虚拟电价完成对电动汽车充放电的初步调度, 再用动态分时电价确定功率可调的电动汽车充放电功率。该方法不仅可以使配电网与用户达到共赢, 而且具有卓越的削峰填谷作用。
1 虚拟电价与动态分时电价机制
本文在静态电价的基础上[4], 提出了基于虚拟电价的电动汽车有序充电的方法。与静态电价相比, 虚拟电价最明显的特点就是能够实时地反映出供需关系。根据这一特点, 可以设计合理的策略来确定每一辆电动汽车的充放电计划。虚拟电价并不适用于实际的充放电成本计算, 所以只在供电侧使用虚拟电价, 完成电动汽车充放电计划的制定。
将时间进行离散化处理, 一天24 h分割为J个时段, 每段时间为Δt。虚拟电价与负荷信息的关系为
| $ {\gamma _l}(L_{\rm{a}}^l(k),\widehat {L_{\rm{a}}^l(k)},k) = \\ \left\{\begin{array}{c}\varphi_{0}+\varphi_{1} L_{\mathrm{a}}^{l}(k)+\varphi_{2}\left[\widehat {L_{\rm{a}}^l(k)}-\Phi_{R, 1}\right]^{+} , \\ k \Delta t \leqslant T_{\mathrm{in}, l} \\ \varphi_{0}+\varphi_{1} L_{\mathrm{a}}^{l}(k)+\varphi_{2}\left[\widehat {L_{\rm{a}}^l(k)}-\Phi_{R, 2}\right]^{+} , \\ k \Delta t>T_{\mathrm{in}, l}\end{array}\right.$ | (1) |
| $ \varphi_{j}=\frac{p_{\mathrm{ri}, R, j}}{\Phi_{R, j}} $ | (2) |
| $L_{\mathrm{a}}^{l}(k)=L_{\mathrm{B}}(k)+L_{\mathrm{EV}}^{l}(k)$ | (3) |
式中:
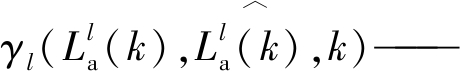 电动汽车l接入时, k时段的虚拟电价;
电动汽车l接入时, k时段的虚拟电价;
φ0, φ1, φ2——虚拟电价调整系数;
pri, R, j, ΦR, j——参考电价与参考负荷值, R∈(0, J], j=1, 2;
| $ \left[\widehat {L_{\rm{a}}^l(k)}-\Phi_{R, j}\right]^{+}=\max \left\{0, \widehat {L_{\rm{a}}^l(k)}-\Phi_{R, j}\right\} $ |
 电动汽车l接入时k时段配电网的总负荷信息;
电动汽车l接入时k时段配电网的总负荷信息;
LB(k)——基本负荷;
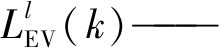 电动汽车l接入时, 已经制定完充放电计划的车辆总负荷。
电动汽车l接入时, 已经制定完充放电计划的车辆总负荷。
在运用虚拟电价完成负荷网侧的电价调控后, 还需要通过由静态电价发展出的动态分时电价机制, 完成在用户侧的预期目标[4]。此处的动态分时电价是经过预处理的, 首先设置最高电价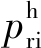 和最低电价
和最低电价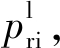 全天的动态电价pri(k)在最高与最低电价之间浮动, 以便与虚拟电价达成匹配。在匹配的过程中, 通过让电动汽车用户在电价低谷时充电, 在电价高峰时放电, 完成预期的削峰填谷的优化, 并减少电动汽车用户的充电费用。
全天的动态电价pri(k)在最高与最低电价之间浮动, 以便与虚拟电价达成匹配。在匹配的过程中, 通过让电动汽车用户在电价低谷时充电, 在电价高峰时放电, 完成预期的削峰填谷的优化, 并减少电动汽车用户的充电费用。
综上所述, 电动汽车的整个充放电优化过程是由虚拟电价机制和动态分时电价机制两个部分组成。虚拟电价机制是从供电侧考虑, 将虚拟电价作为一个理论指标, 进行削峰填谷的负荷优化; 动态分时电价机制是从用电侧考虑, 采取浮动式电价匹配虚拟电价, 让用户避开负荷高峰时段充电, 减少用户的充电成本。综合两者的优点, 能够更加完美地解决电动汽车的充放电问题, 不仅能够吸引用户参与, 也能保证策略的实施程度。
2 电动汽车优化调度模型
将预期能够介入负荷配电网的电动汽车数量设为集合N, 在任何情况下, 实际的电动汽车数量n一定不会多于集合N的数量, 记作n
 |N|。在实际应用中, 每个车主都有自己的用车特点, 将电动汽车l主要的行车参数组成一个集合, 表示为
|N|。在实际应用中, 每个车主都有自己的用车特点, 将电动汽车l主要的行车参数组成一个集合, 表示为
| $X_{l}=\left[T_{\mathrm{in}, l}, T_{\mathrm{out}, l}, S_{0, l}, S_{\mathrm{E}, l}, C_{\mathrm{s}, l}, P_{\mathrm{c}, l}, P_{\mathrm{d}, l}\right]$ | (4) |
式中:Tin, l, Tout, l——电动汽车实际开始充电和实际结束充电的时间;
S0, l, SE, l——电动汽车初始的荷电状态与充完电离开时预期的荷电状态, S0, l, SE, l∈[0, 1];
Cs, l——电池总容量;
Pc, l, Pd, l——电动汽车额定充放电功率。
假设一辆电动汽车l接入电网进行充电的时长为Tpe, l=Tout, l-Tin, l, 将所有电动汽车的充电时长Tpe, l组成一个集合, 并按照从小到大的顺序进行排列, 用Tm, l表示。同时, 为了能够显示出时段集合对电动汽车电池的可操作性, 加入新变量
| $ f_{m, l}(k)=\left\{\begin{array}{lc} 1 & k \in T_{m, l} \\ 0 & \text {其 他} \end{array}\right. $ | (5) |
在电动汽车入网模式下, 设置电动汽车与配电网之间的关系为pl(k)。当pl(k) > 0时, 表示电动汽车正在充电; 当pl(k) < 0时, 表示电动汽车正在放电; 当pl(k)=0时, 表示电动汽车正在进行浮充, 即电动汽车不工作, 但由于其内部自身的局部耗电性, 会造成轻微的电量损耗, 此时配电网会有一个微小电流为电动汽车充电, 与其自身损耗基本持平, 使得汽车达到稳压状态, 可以随时投入工作。
在整个Tpe, l时段中, 电动汽车的实际充放电功率可表示为
| $P_{l}(k)=p_{l}(k) f_{m, l}(k)$ | (6) |
式中:Pl(k)——整个充放电过程的优化变量, 满足-Pd, l≤Pl(k)≤Pc, l。
在关于电动汽车l的充放电时段问题、充放电状态问题以及与配电网之间的功率交换问题基本解决后, 电动汽车l的充放电计划也就完成了, 可用公式表示为
| $P_{l}=\left[P_{l}\left(T_{m, l}^{1}\right), P_{l}\left(T_{m, l}^{2}\right), P_{l}\left(T_{m, l}^{3}\right), \cdots, P_{l}\left(T_{m, l}^{N_{l}}\right)\right]$ | (7) |
其中, 对于 表示在时段集合Tm, l中, 对应的第i个时段的电动汽车的充放电功率, 将电动汽车l的所有充电时段集合在一起, 就完成了电动汽车l的整体充放电计划。
表示在时段集合Tm, l中, 对应的第i个时段的电动汽车的充放电功率, 将电动汽车l的所有充电时段集合在一起, 就完成了电动汽车l的整体充放电计划。
在本文中, 所有的电池模型均设置为锂电池模型, 并根据其相关特性在建模前进行一定的简化处理。假设电池的充放电是以恒定功率进行的, 并且其自放电率忽略不计, 可得到电池的荷电状态与充放电时间基本呈线性关系, 公式为
| $S_{l}(k)=S_{l}(k-1)+P_{l}(k) \eta\left(P_{l}(k)\right) \frac{\Delta t}{C_{\mathrm{s}, l}}$ | (8) |
式中:Sl(k), Sl(k-1)——电动汽车l在k和k-1个时段时的电池状态;
η(Pl(k))——电池自身的功率转换效率。
在整个电动汽车的使用成本中, 锂电池占比很大, 其大致由以下3部分组成:
| $U_{l}=\left(c_{\mathrm{cd}, l} \mid \eta_{\mathrm{c}}=\eta_{\mathrm{d}}=1\right)+c_{\mathrm{bat}, l}+c_{\operatorname{los}, l}$ | (9) |
式中:ccd, l|ηc=ηd=1——在电池充电效率ηc和放电效率ηd均为1的理想状态下产生的充放电费用;
cbat, l——锂电池的自身寿命损耗成本;
closs, l——电能损失, 即电池在与电网进行功率交换时产生的必然损失。
电池寿命损耗cbat, l的产生原因是电动汽车频繁地参加入网服务, 每次的充放电过程都会对电池造成损伤。电池的损耗折算到成本侧进行建模分析可得
| $ c_{\mathrm{bat}, l}=c_{\mathrm{bat}, l}^{\mathrm{D}}+c_{\mathrm{bat}, l}^{\mathrm{F}} $ | (10) |
式中:
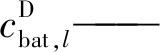 放电次数过多导致的退化成本, 简称放电成本;
放电次数过多导致的退化成本, 简称放电成本;
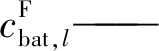 由充放电时产生的功率波动对电池造成的损耗成本, 简称功率波动成本。
由充放电时产生的功率波动对电池造成的损耗成本, 简称功率波动成本。
在进行量化处理时, 计算公式为
| $ c_{\mathrm{bat}, l}^{\mathrm{D}}=\varphi_{\mathrm{d}, l} E_{\mathrm{dis}, l}=\frac{c_{\mathrm{b}} C_{\mathrm{s}, l}+c_{\mathrm{L}}}{B_{\mathrm{c}l} C_{\mathrm{s}, l} D_{\mathrm{OD}}} E_{\mathrm{dis}, l} $ | (11) |
| $ c_{\mathrm{bat}, l}^{\mathrm{F}}=\varepsilon_{\mathrm{f}} \sum\limits_{i=2}^{N_{l}}\left[P_{l}\left(T_{m, l}^{i}\right)-P_{l}\left(T_{m, l}^{i-1}\right)\right]^{2} $ | (12) |
式中:φd, l——每千瓦时放电量对应的电池的退化成本参数;
cb——每千瓦时电池容量的购买成本;
cL——更换电池费用成本;
Bcl——在某个放电深度下电池的使用循环次数;
DOD——放电深度;
Edis, l——电动汽车参与入网服务的总时间内所有的放电量;
εf——损耗成本系数。
在整体电能转换过程中, 电网侧实际提供的电能与车主实际需求的电能之间存在一部分差值, 称为电能损失, 可表示为
Eloss, l=Eabso, l-Einj, l-Eexp, l=
| $\begin{aligned} E_{\text {loss }, l}=& E_{\text {abso }, l}-E_{\text {inj }, l}-E_{\text {exp }, l}=\\ & E_{\exp , l}\left(\frac{1}{\eta_{\mathrm{c}}}-1\right)+E_{\text {dis }, l}\left(\frac{1}{\eta_{\mathrm{c}}}-\eta_{\mathrm{d}}\right) \end{aligned}$ | (13) |
从各个时段的电能流动角度来看, 电能损失可分为充电损失和放电损失, 因此电能损失也可表示为
| $ \begin{aligned} E_{\text {loss }, l}=& \left[E_{\text {abso }, l}-\left(E_{\text {dis }, l}+E_{\text {exp }, l}\right)\right]+\\ & \left(E_{\text {dis }, l}-E_{\text {inj }, l}\right) \end{aligned} $ | (14) |
其中, [Eabso, l-(Edis, l+Eexp, l)]为充电损失; (Edis, l-Einj, l)为放电损失, 两个式子展开后结果相同, 印证了结论的准确性。所以电能损失产生的费用为
| $ c_{\text {loss }, l}=\sum\limits_{k \in T_{m, l}} E_{\text {loss }, l}(k) p_{\text {ri }, l}(k) $ | (15) |
为了使电动汽车充放电成本最少[10], 综合电动汽车的充放电模型和锂电池模型, 构建基于虚拟电价的电动汽车优化调度模型为:
| $\min V_{l}=\sum\limits_{k \in T_{m, l}}\left\{P_{l}(k) \gamma_{l}\left(L_{\mathrm{a}}^{l}(k), \widehat {L_{\rm{a}}^l(k)},k), k\right) \Delta t\right\}$ | (16) |
| $ \mathrm{s.t.} S_{\min } \leqslant S_{l}(k) \leqslant S_{\max }$ | (17) |
| $S_{0, l}+\sum\limits_{k \in T_{m, l}} \Delta t \frac{P_{l}(k)}{C_{\mathrm{s}, l}} \geqslant S_{\mathrm{E}, l}$ | (18) |
| $\left\{\begin{array}{ll}L_{\mathrm{a}}^{l}(k) \leqslant K_{\mathrm{T}} A_{\mathrm{T}} \quad k=T_{m, l}^{1} \\ \widehat {L_{\rm{a}}^l(k)} \leqslant K_{\mathrm{T}} A_{\mathrm{T}} \quad k=T_{m, l}^{2}, T_{m, l}^{3}, T_{m, l}^{4}, \cdots, T_{m, l}^{N_{l}}\end{array}\right.$ | (19) |
| $T_{\mathrm{pe}, l}>T_{\mathrm{c}, l} \quad l=1,2,3, \cdots, n$ | (20) |
| $T_{\mathrm{c}, l}=\frac{\left(S_{\mathrm{E}, l}-S_{0, l}\right) C_{\mathrm{s}, l}}{P_{\mathrm{c}, l} \eta_{\mathrm{c}}}$ | (21) |
式中:Vl——电动汽车的虚拟充放电成本;
KT——变压器效率;
AT——变压器额定容量;
Tc, l——电动汽车在充电时, 为了达到车主所期望的荷电状态所需要的最短时间。
通过上述公式, 最终完成了整个电动汽车的优化调度。
3 仿真分析与验证
本文使用MATLAB软件进行模型仿真, 采取小波分析模型、模糊聚类模型以及遗传算法模型3种模型。
假设接入变压器下只带基本负荷以及与电动汽车有关的集群负荷, 基本负荷即是除电动汽车外所有负荷的集合。由于后面将进行无序充电的仿真, 故不考虑变压器的容量, 假定在任何情况下均不会过负荷。
设置的整个仿真所需要的电动汽车基本参数如表 1所示。
表 1
电动汽车相关参数
| 电动汽车数量/辆 | 电池的容量/kWh | 额定充电功率/kW | 充电效率 |
| 50 | 60 | 7 | 0.92 |
| 额定放电功率/kW | 放电效率 | 初始荷电状态边界 | 最终荷电状态边界 |
| 7 | 0.92 | 0.9 | 0.1 |
为了更好地模拟实际情况, 根据居民区的基本平均负荷信息特征, 尽可能地将虚拟电价与居民日常峰谷电价设定为同一水平的金额比例。本文设置电价相关参数如表 2所示。
表 2
电价相关参数
| φ0 | ΦR, 1 | ΦR, 2 | Bcl/ 千次 |
εf/ [分·(kWh)-1] |
| -0.2 | 405 | 76 | 3 | 0.5 |
| 高峰电价 | 低谷电价 | 电池容量购买成本cb | ||
| [元·(kWh)-1] | ||||
| 1.5 | 0.37 | 1 800 | ||
由于某个特定区域内电动汽车集群的任何充放电行为特征以及出行行为特征都具有一定的概率特性, 为了避免突发变量, 或特定区域与整体区域的某些条件不符, 参考北京交通出行调查结果[11], 设置电动汽车出行使用参数如下:电动汽车离开时间期望值为7:45, 标准差为1 h; 电动汽车返回时间期望值为19:00, 标准差为1 h; 返回时电池荷电状态期望值为0.6, 标准差为0.1。
假设上述所有参数均服从正态分布, 满足本文需求。设置电动汽车充放电起始时间、终止时间以及电池的起始荷电状态、终止荷电状态等参数均相互独立, 不交叉。
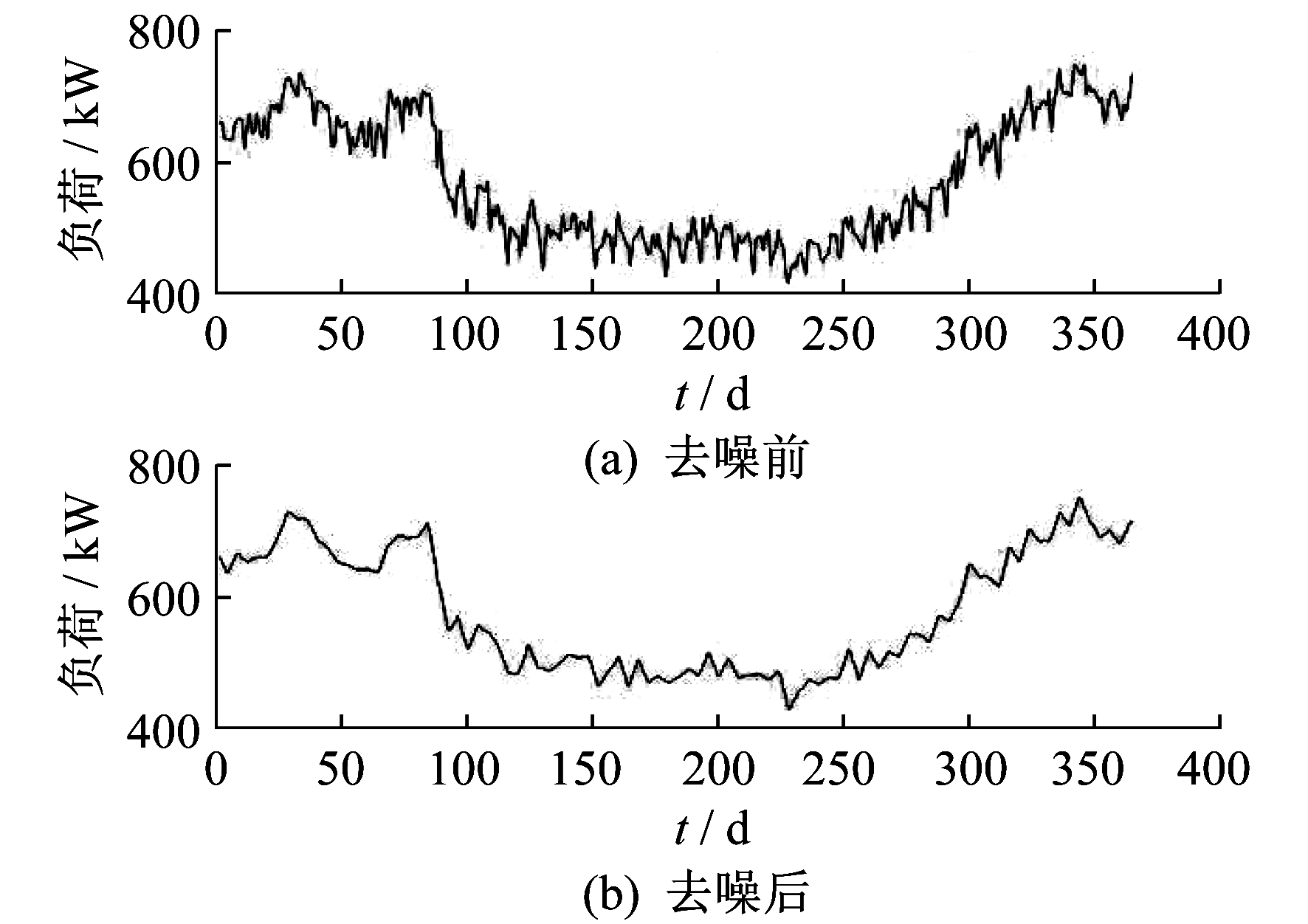
3.1 小波分析去噪
本文利用小波分析模型消除突变量对整体负荷信息的影响, 将全年的负荷值代入小波分析模型, 得到小波去噪后的负荷信息, 如图 1所示。
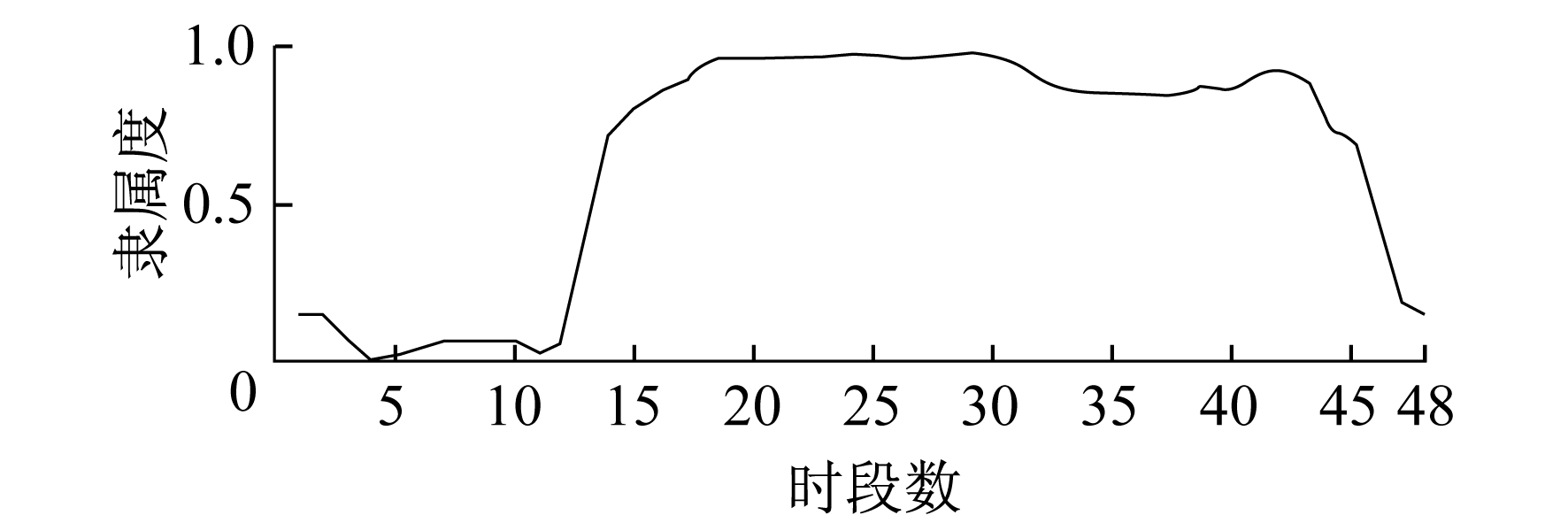
3.2 模糊聚类
3.3 遗传算法
利用遗传算法求解基于电价的电动汽车优化调度模型, 仿真中设置自适应交叉概率为0.8, 子代变异概率为0.2, 总体种群数为100, 迭代次数为100次。
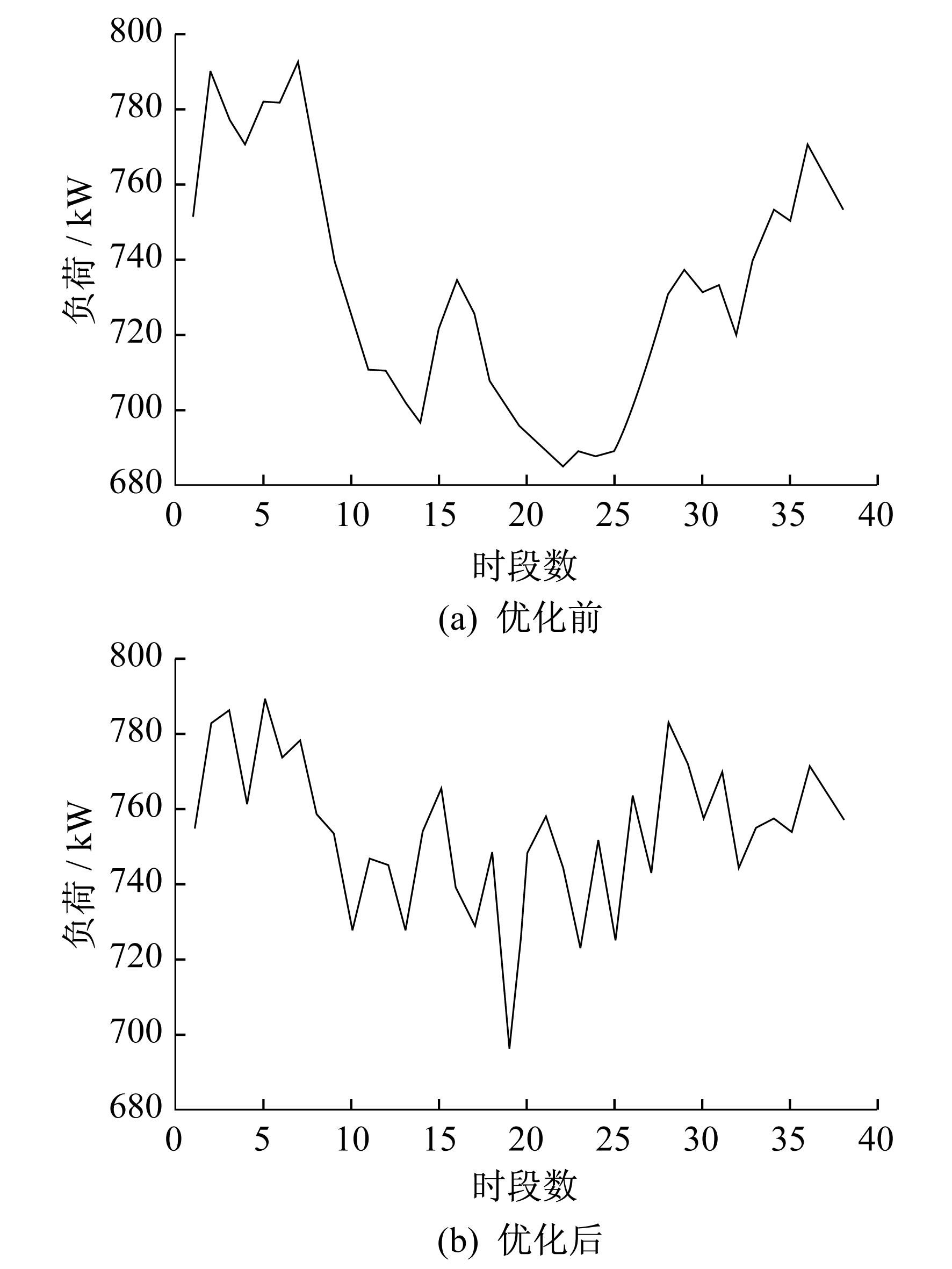
优化前后的负荷-时段曲线如图 3所示。由图 3可以看出, 优化后负荷的最大值和最小值之间的差距缩小, 并且在中间浮动范围内, 负荷值向中心靠拢, 减小了负荷波动差。
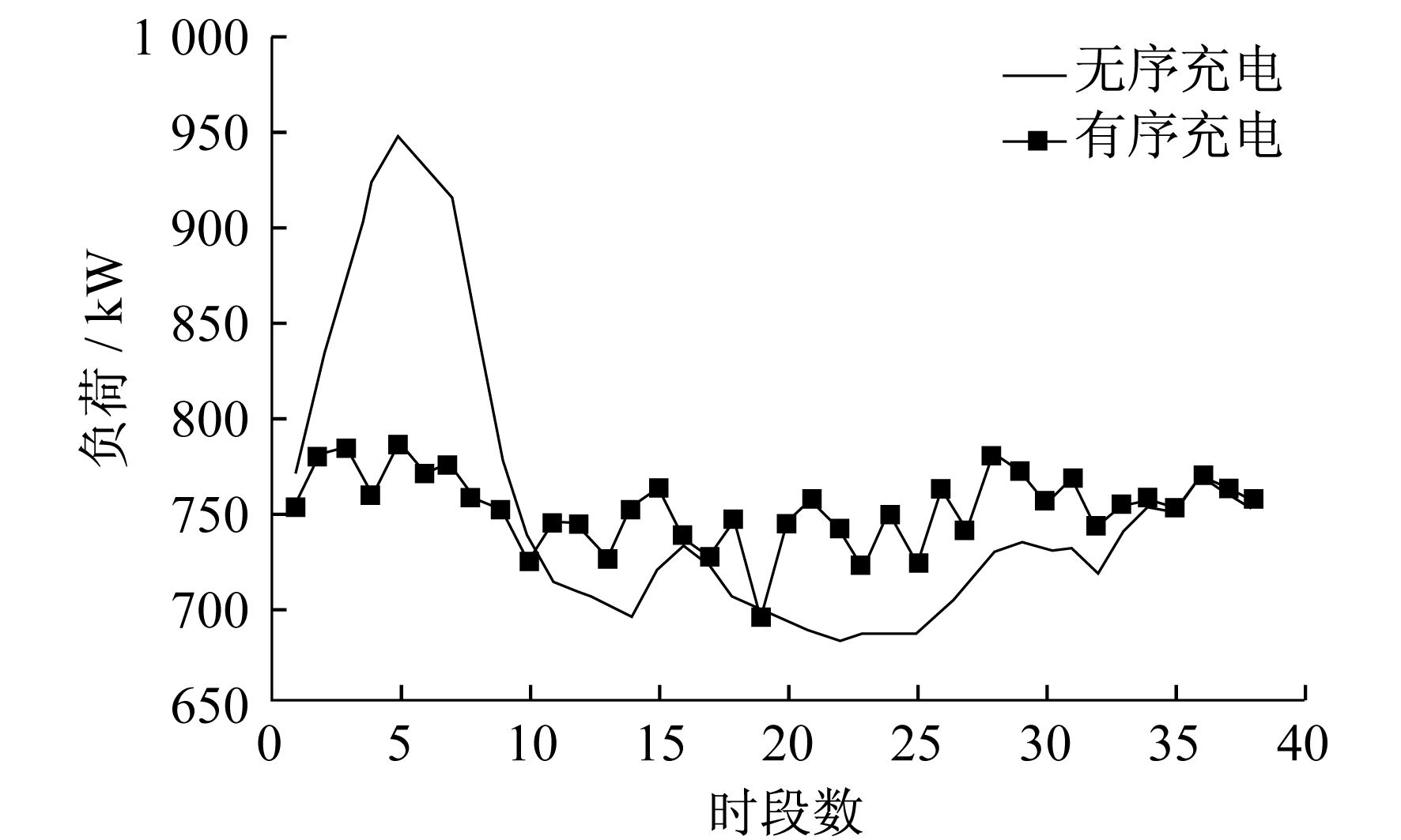
图 4为无序充电与有序充电的日负荷对比曲线。由图 4可以看出, 有序充电将负荷直接转移到低谷处, 消除了同一时段大量充放电负荷对配电网产生满载甚至是过载的影响, 非常有效地达到了削峰填谷的目的, 减小了配电网满载带来的危险。
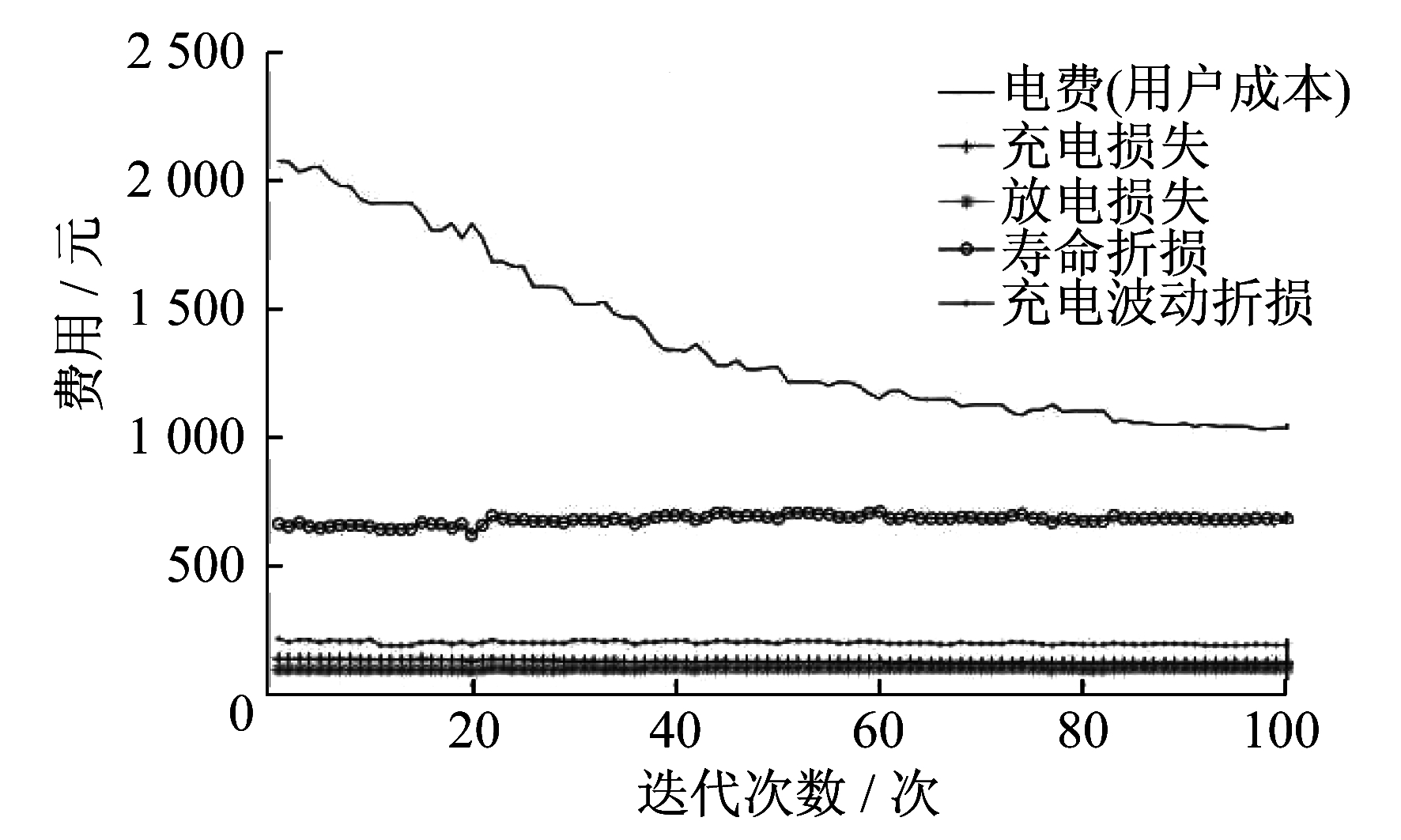
基于虚拟电价电动汽车的优化调度, 各项成本曲线如图 5所示。由图 5可知, 50辆车的总体充电费用能保持在1 000元左右, 平均每一辆车充电成本为20元。
4 结语
本文提出了基于虚拟电价的电动汽车充放电优化调度方法。通过MATLAB仿真分析可知, 采用的优化调度方法能够有效地实现负荷侧的削峰填谷, 在用户侧降低充电费用和电池的损耗成本。
参考文献
-
[1]RASLAVICIUS L, AZZOPARDI B, KERSYS A, et al. Electric vehicles challenges and opportunities: lithuanian review[J]. Renewable and Sustainable Energy Reviews, 2015, 42: 786-800. DOI:10.1016/j.rser.2014.10.076
-
[2]HE Y F, VENKATESH B, GUAN L. Optimal scheduling for charging and discharging of electric vehicles[J]. IEEE Transactions on Smart Grid, 2012, 3(3): 1095-1105. DOI:10.1109/TSG.2011.2173507
-
[3]电动汽车接入电网的影响与利用[J]. 中国电机工程学报, 2012, 32(4): 1-10.
-
[4]基于动态分时电价的电动汽车充电站有序充电策略[J]. 中国电机工程学报, 2014, 34(22): 3638-3646.
-
[5]基于实时电价的多目标电动汽车控制策略[J]. 上海电力学院学报, 2016, 32(5): 485-489.
-
[6]电动汽车充放电对电力系统的影响综述[J]. 电力信息与通信技术, 2016, 14(5): 55-59.
-
[7]电动汽车协调充放电对电网的影响[J]. 上海电力学院学报, 2015, 31(1): 7-10.
-
[8]QIAN K J, ZHOU C K, ALLAN M, et al. Modeling of load demand due to EV battery charging in distribution system[J]. IEEE Transactions on Power Systems, 2011, 26(2): 802-810. DOI:10.1109/TPWRS.2010.2057456
-
[9]电动汽车参与V2G的最优峰谷电价研究[J]. 中国电机工程学报, 2013, 33(31): 15-25.
-
[10]大规模电动汽车充放电优化控制及容量效益分析[J]. 电力系统自动化, 2012, 36(10): 19-26.
-
[11]北京交通研究中心. 2011年北京交通发展年度报告[EB/OL]. [2018-02-06]. http://www.bjtrc.org.cn/.