|
|
|
发布时间: 2019-08-10 |
|
|
|
|
收稿日期: 2018-04-18
基金项目: 上海绿色能源并网工程技术研究中心资助项目(13DZ2251900)
中图法分类号: TM464
文献标识码: A
文章编号: 1006-4729(2019)04-0333-06
|
摘要
多逆变器并网运行存在稀释效应, 影响孤岛检测的速度和精度。对多逆变器并网运行系统进行了孤岛检测稀释效应分析, 并采用模糊控制的方法对其进行优化处理, 削减稀释效应, 加快孤岛检测速度, 提高检测精度。采用MATLAB/Simulink进行了试验仿真, 结果表明, 优化后的方法能够快速实现孤岛检测, 减小稀释效应。
关键词
孤岛检测; 多逆变器并网; 稀释效应; 模糊控制
Abstract
Multi-inverter grid-connected operation and dilution effect, smaller island detection speed and accuracy are studied.The multi-inverter grid-connected operation system islanding dilution effect is analyzed, and fuzzy control method is used to optimize its treatment to reduce the dilution effect, speed up the island detection speed and improve the detection accuracy.The experimental results show that the optimized method can realize the island detection quickly and reduce the dilution effect.
Key words
islanding detection; multi-inverter grid connection; dilution effect; fuzzy control
随着新能源的迅速发展, 分布式能源的利用比重显著增加。孤岛检测是分布式能源并网运行的重要环节。逆变器孤岛运行是指在公共电网中, 由于故障或者维修而停止向负载供电时, 分布式电源没有及时检测出公共电网处于停电状态, 仍继续向负载供电, 长时间孤岛运行状态将会对电气设备产生影响, 对检修人员造成人身伤害。因此, 孤岛检测是逆变器并网运行中不能缺少的环节。
目前孤岛检测方法主要有3类:被动检测法(Passive Islanding Detection Method, P-IDM)、主动检测法(Active Islanding Detection Method, A-IDM)和远程通信检测法(Rumor Communication Islanding Detection Method, RC-IDM)。P-IDM通过检测电路中某些电气量(如公共点电压、电网频率、逆变器输出电流等)的值是否超出正常运行的输出阈值范围来判断是否发生孤岛[1-2]。A-IDM是通过向电网注入扰动信号, 在电网正常运行时, 电路电气量被大电网钳制而不产生改变; 若孤岛发生, 电路电气量将受到注入信号的影响而发生偏移, 通过多个周期的扰动逐渐偏离正常输出阈值范围, 最终超出阈值的上限或下限, 从而检测出孤岛的发生[3]。A-IDM能够在较短时间内检测出孤岛, 检测盲区较小, 但是对系统电能质量影响较大[4]。RC-IDM采用信息传送的方式, 将检测的信号传递给逆变器进行判断是否发生孤岛, 虽精确度高, 对电能质量没有影响, 但是需要借助通信技术, 成本高, 不适合大规模的使用。
随着智能算法的迅速发展, 孤岛检测利用智能算法进行快速检测成为趋势。主要的智能算法有模糊控制法、神经网络控制法、支持向量机控制法、经验模态分解法等。目前, 许多学者将模糊控制算法应用于工程控制, 算法成熟。本文提出了一种基于模糊控制改进的主动频率偏移法, 用于多逆变器并网运行的孤岛检测。
1 主动频率偏移法的工作特性
1.1 Sandia频率偏移法
Sandia频率偏移(Sandia Frequency Shift, SFS)法孤岛检测是通过并网逆变器向电网注入有微小畸变的正弦电流, 在电网和逆变器断开形成孤岛后, 公共耦合点(Point of Common Coupling, PCC)的电压频率受逆变器输出电流的影响, 跟随其向上或者向下偏移, 直至超出设定的阈值, 从而检测出孤岛的发生[5]。以PCC的电压频率向上移动为例, 逆变器输出电流如图 1中虚线波形所示。电网断开后, PCC处电压频率不受电网频率的钳制, 而受注入系统扰动波形的影响, PCC处电压较额定电压的频率大, 经过正反馈后逐渐增大, 直至设定的阈值, 实现孤岛检测的功能。
图 1中死区宽度的大小可由斩波系数表示, 斩波系数越大, 逆变器输出电流频率越大, 其作用越明显。
传统的SFS法的斩波系数为
| $C_{\mathrm{f}}=C_{\mathrm{f} 0}+k\left(f-f_{\mathrm{g}}\right)=C_{\mathrm{f} 0}+k \delta_{f}$ | (1) |
式中:Cf0——初始斩波系数;
k——正反馈系数;
f——PCC的电压频率;
fg——电网电压的额定频率;
δf——频率偏差, δf=f-fg。
因此, SFS法引入的扰动相移角为
| $ \theta_{\mathrm{SFS}}=\frac{\pi\left[C_{\mathrm{f} 0}+k\left(f-f_{\mathrm{g}}\right)\right]}{2} $ | (2) |
负载的相位角为
| $ \theta_{\text {load }}=-\arctan \left[Q_{\mathrm{f}}\left(\frac{f_{0}}{f}-\frac{f}{f_{0}}\right)\right] $ | (3) |
式中:Qf——负载的品质因数;
f0——负载的谐振频率。
要使SFS法能够检测出孤岛的发生, 必须满足SFS的相位偏移角变化率大于负载相角的变化率, 即满足
| $ \left.\frac{\mathrm{d} \theta_{\text {load }}}{\mathrm{d} f}\right|_{f=f_{0}} \leqslant\left.\frac{\mathrm{d} \theta_{\mathrm{SFS}}}{\mathrm{d} f}\right|_{f=f_{\mathrm{g}}} $ | (4) |
将式(2)和式(3)代入式(4)中, 可以化简得
| $ k \geqslant \frac{4 Q_{\mathrm{f}}}{\pi f_{\mathrm{g}}} $ | (5) |
由于负载品质因数满足Qf≤2.5, 因此可求得反馈系数满足k≥0.064。通过增大k值的大小可以有效地减小孤岛检测的盲区, 但是不能无限的增大, k值过大时会导致加入的扰动角过大, 引入的谐波含量增大。由此可见, 选择的参数要依据实际电路决定。
当发生孤岛时, f和f0之间的关系式为
| $ \left\{\begin{array}{l} \frac{\mathrm{d} \theta_{\text {load }}(f)}{\mathrm{d} f} \geqslant \frac{\mathrm{d} \theta_{\mathrm{SFS}}}{\mathrm{d} f} \\ \theta_{\text {load }}(f)=\arctan \left[Q_{\mathrm{f}}\left(\frac{f}{f_{0}}-\frac{f_{0}}{f}\right)\right]=\theta_{\mathrm{SFS}} \end{array}\right. $ | (6) |
由式(6)中等式约束条件可求得盲区边界曲线表达式为
| $ f_{0}=\frac{f}{2 Q_{\mathrm{f}}}\left[-\tan \theta_{\mathrm{SFS}}+\sqrt{\tan ^{2} \theta_{\mathrm{SFS}}+4 Q_{\mathrm{f}}^{2}}\right] $ | (7) |
式(7)中, 49.5≤f≤50.5, θSFS由式(2)代入式(7)得到。由此可以画出取不同k值时的盲区曲线。
1.2 滑模频率偏移法
滑模频率偏移(Slide-mode Shift, SMS)法对逆变器输出电流施加一个偏差角[6-7], 即实现相位的偏移。扰动偏差角是PCC频率和电网频率的函数。逆变器输出电流的表达式为
| $i_{\mathrm{SMS}}=I_{\mathrm{SMS}} \sin \left(2 \pi f t+\theta_{\mathrm{SMS}}\right)$ | (8) |
施加的扰动偏差角可表示为
| $ \theta_{\mathrm{SMS}}=\frac{2 \pi}{360} \theta_{\mathrm{m}} \sin \left(\frac{\pi}{2} \frac{f-f_{\mathrm{g}}}{f_{\mathrm{m}}-f_{\mathrm{g}}}\right) $ | (9) |
式中:θm——扰动偏差角的最大偏移量;
fm——扰动偏移角最大值时对应的频率。
逆变器并网运行时, 公共点电压频率被电网钳制为fg; 当电网断开, 即发生孤岛时, 公共点频率受到逆变器输出电流频率的影响, 使发生孤岛时逆变器输出电流对PCC进行扰动, 从而使公共点频率超出阈值的上限或下限。要实现孤岛检测, 即要满足
| $ \left.\frac{\mathrm{d} \theta_{\text {load }}}{\mathrm{d} f}\right|_{f=f_{\mathrm{g}}} \leqslant\left.\frac{\mathrm{d} \theta_{\mathrm{SMS}}}{\mathrm{d} f}\right|_{f=f_{\mathrm{g}}} $ | (10) |
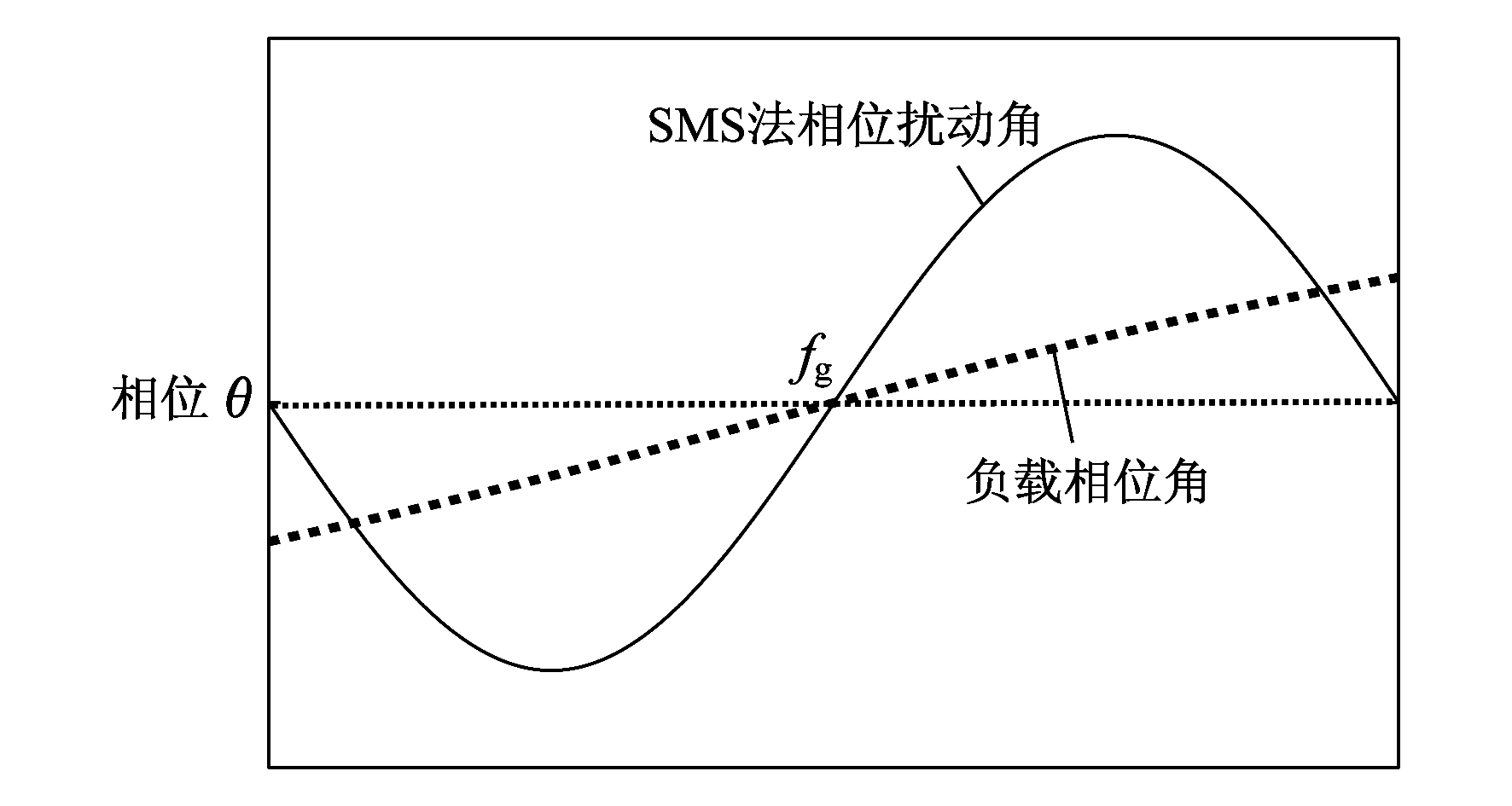
图 2为SMS法相伴扰动角和负载相位角曲线示意。
从图 2可以看出, 在f=50 Hz附近时, SMS曲线的斜率大于负载的斜率, PCC频率受逆变器输出电流的影响而发生偏移。当电网频率高于电网额定频率时, 施加的相位扰动角大于零, 通过正反馈的作用时PCC的电压不断增大, 直至大于频率阈值的上限; 当电网频率低于电网额定频率时, 施加的相位扰动角小于零, 通过反馈作用时PCC的电压不断减小, 直至小于频率阈值的下限。
SMS法能够加快孤岛检测的速度, 孤岛检测盲区较小, 但是加入的相位扰动角会影响电网输出的电能质量。在负载的品质因数较高时, 负载曲线的斜率大于SMS法的曲线斜率, 扰动角的引入不足以让公共点频率超出阈值范围, 导致孤岛检测失败。
2 SFS法和SMS法结合在多逆变器并网系统中稀释效应分析
在多逆变器并网运行系统中, 各逆变器分别注入一个扰动信号, 各信号通过叠加将会产生稀释效应[8-10], 导致扰动信号的幅度减小, 影响检测的速度和精度。
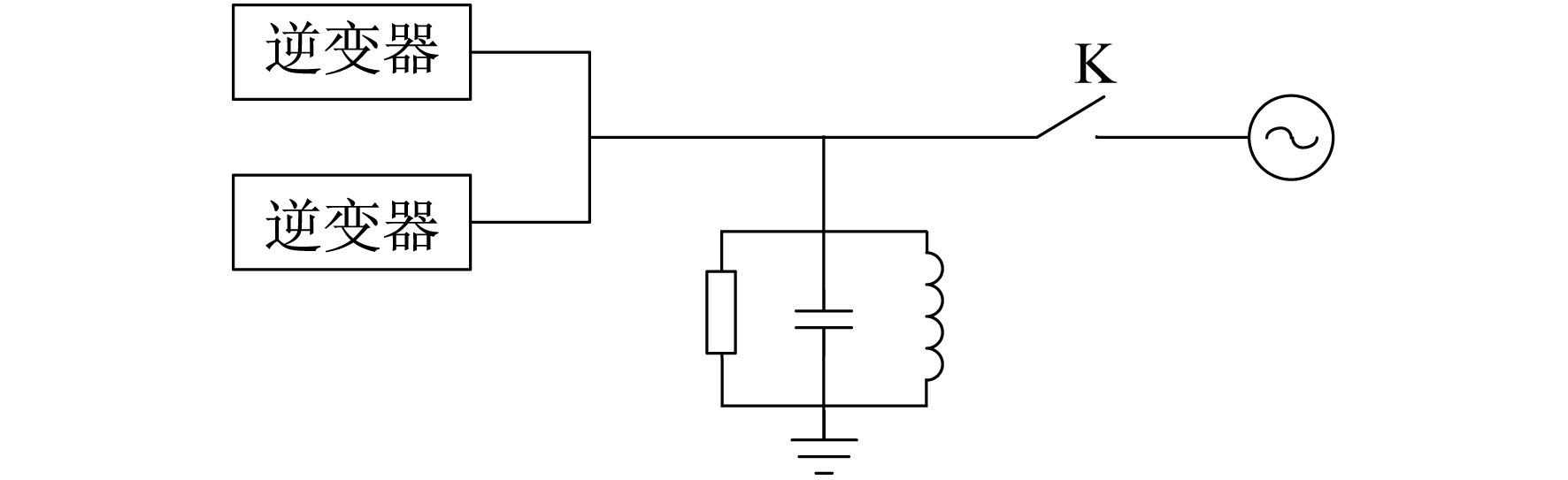
图 3为两逆变器并网运行示意。
图 3中, 两逆变器中一台采用SFS法, 另一台采用SMS法, 现对其进行稀释效应分析。
假设采用SFS法的逆变器输出电流是采用SMS法逆变器输出电流的β倍, 因此两逆变器的输出电流分别为
| $ i_{\mathrm{SFS}}=\sqrt{2} \beta I_{\mathrm{SMS}} \sin \left(2 \pi f t+\theta_{\mathrm{SFS}}\right) $ | (11) |
| $i_{\mathrm{SMS}}=\sqrt{2} I_{\mathrm{SMS}} \sin \left(2 \pi f t+\theta_{\mathrm{SMS}}\right)$ | (12) |
两逆变器并网运行时PCC的输出电流为
| $i_{\mathrm{INV}}=i_{\mathrm{SFS}}+i_{\mathrm{SMS}}= \\ \sqrt{2} \beta I_{\mathrm{SMS}} \sin \left(2 \pi f t+\theta_{\mathrm{SFS}}\right)+ \\ \sqrt{2} I_{\mathrm{SMS}} \sin \left(2 \pi f t+\theta_{\mathrm{SMS}}\right)= \\ \sqrt{2} I_{\mathrm{INV}} \sin \left(2 \pi f t+\theta_{\mathrm{INV}}\right)$ | (13) |
| $I_{\mathrm{INV}}=I_{\mathrm{SMS}} \sqrt{1+\beta^{2}+2 \beta \cos \left(\theta_{\mathrm{SFS}}+\theta_{\mathrm{SMS}}\right)}$ | (14) |
| $\theta_{\mathrm{INV}}=\tan ^{-1}\left(\frac{\tan ^{2} \alpha \cdot \sin \theta_{\mathrm{SFS}}+\sin \theta_{\mathrm{SMS}}}{\tan ^{2} \alpha \cdot \cos \theta_{\mathrm{SFS}}+\cos \theta_{\mathrm{SMS}}}\right)$ | (15) |
式中:
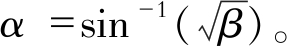
由式(15)可知, 逆变器输出电流相位角满足
| $\min \left(\theta_{\mathrm{SFS}}, \theta_{\mathrm{SMS}}\right) \leqslant \theta_{\mathrm{INV}} \leqslant \max \left(\theta_{\mathrm{SFS}}, \theta_{\mathrm{SMS}}\right)$ | (16) |
由式(16)可知, 由于稀释效应, 逆变器输出电流的相位角小于两种方法中的最大值, 因此检测速度减慢。
3 基于模糊控制的多逆变器并网孤岛检测方法
3.1 SFS法系数k的模糊控制优化
电网断电后, 在未知负载特性的情况下, 采用SFS法时, 在k的取值范围中及时选取适合当前负载的k值是较为困难的, 同时根据以往的理论分析及仿真结果来看, 逆变器电压的频率偏移量和频率偏移率会受到外部扰动的干扰。模糊控制器适用于非线性、时变、滞后系统的控制, 不必对被控制对象建立完整的数学模型, 是一种容易控制和掌握的较为理想的非线性控制器, 具有较佳的鲁棒性、适应性和容错性。此外, 采用模糊控制器可选取合理的k值。
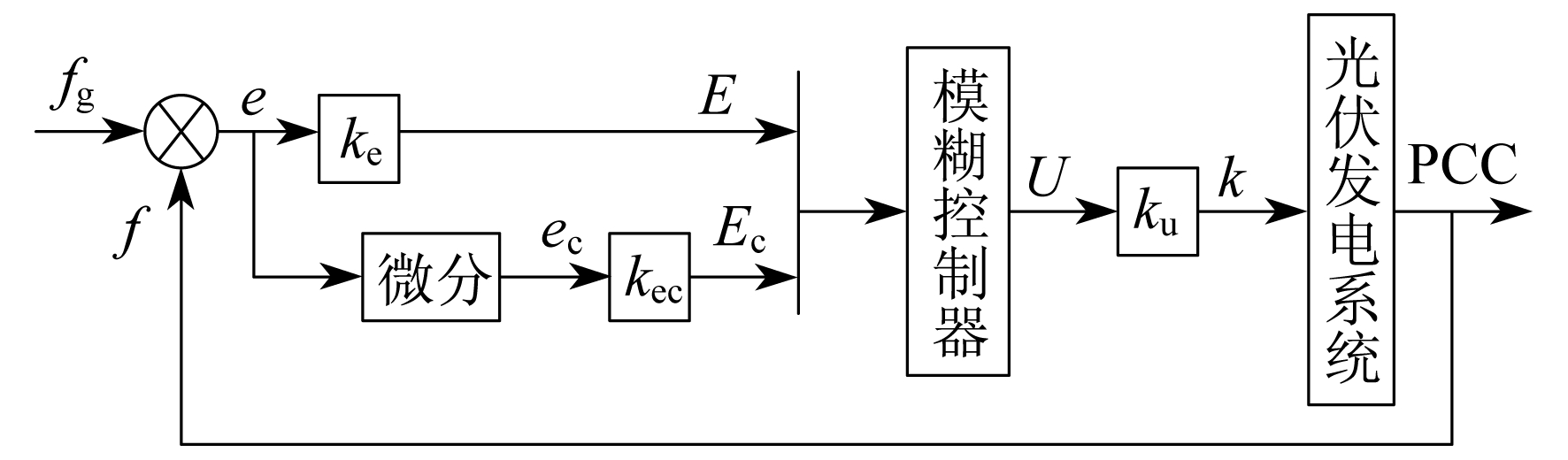
逆变器离网后形成孤岛运行状态, 负载特性未知, 选取特定的k值较为困难, 因此选取一个二维模糊控制器。图 4为二维模糊控制器的框图。
图 4中, e为逆变器电压频率fuinv与电网额定电压f0的差值。ec为e的变化率, 这两者作为控制器的输入项; 控制器输出项为反馈系数k; ke和kec为输入因子; ku为输出因子。选取PCC电压频率fupcc与电网电压频率fg的差值e和e的微分ec作为模糊控制的输入量, 反馈系数k作为模糊控制的输出量, ke, kec, ku作为模糊控制器的量化因子。
3.2 SFS法系数k的模糊规则
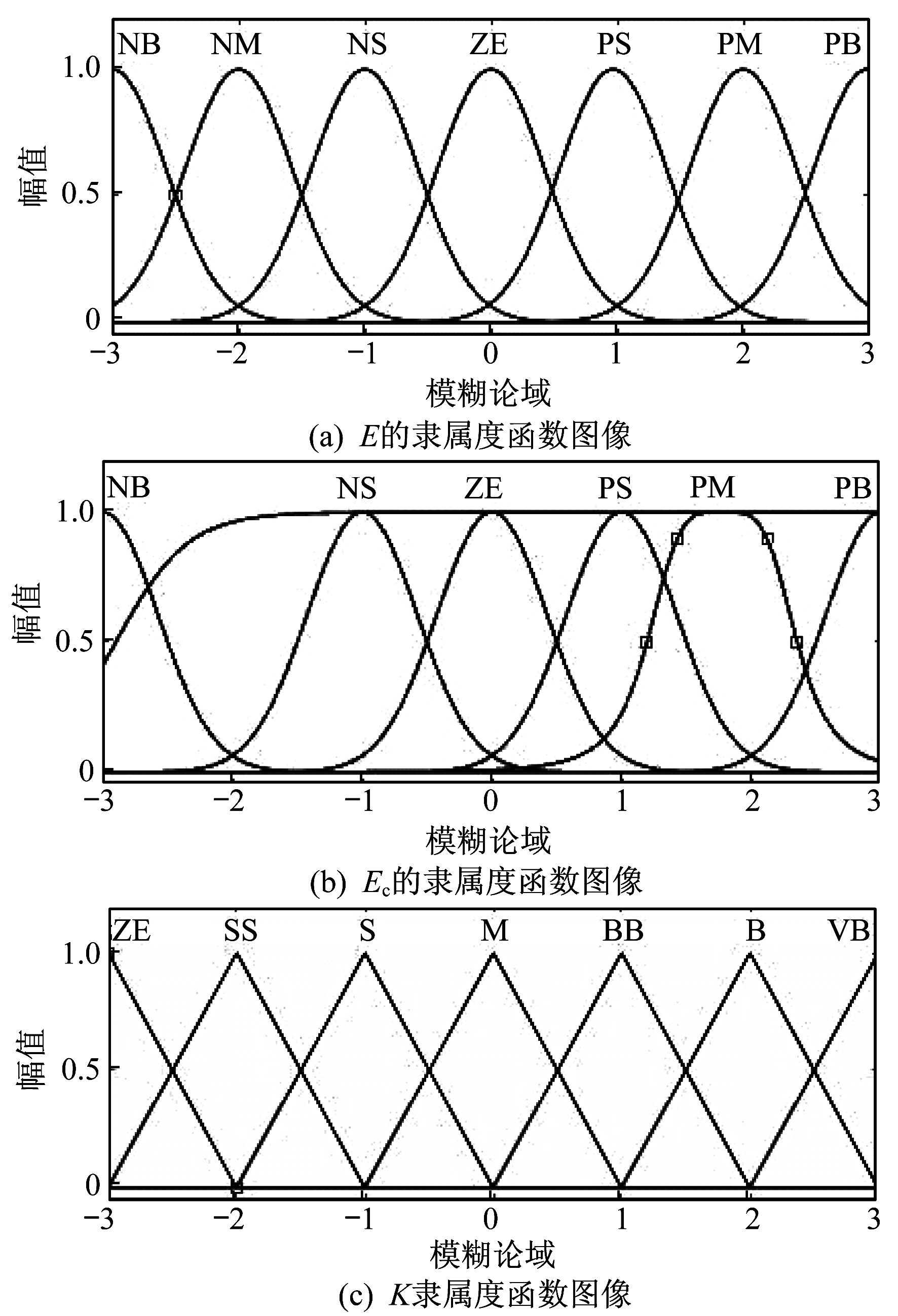
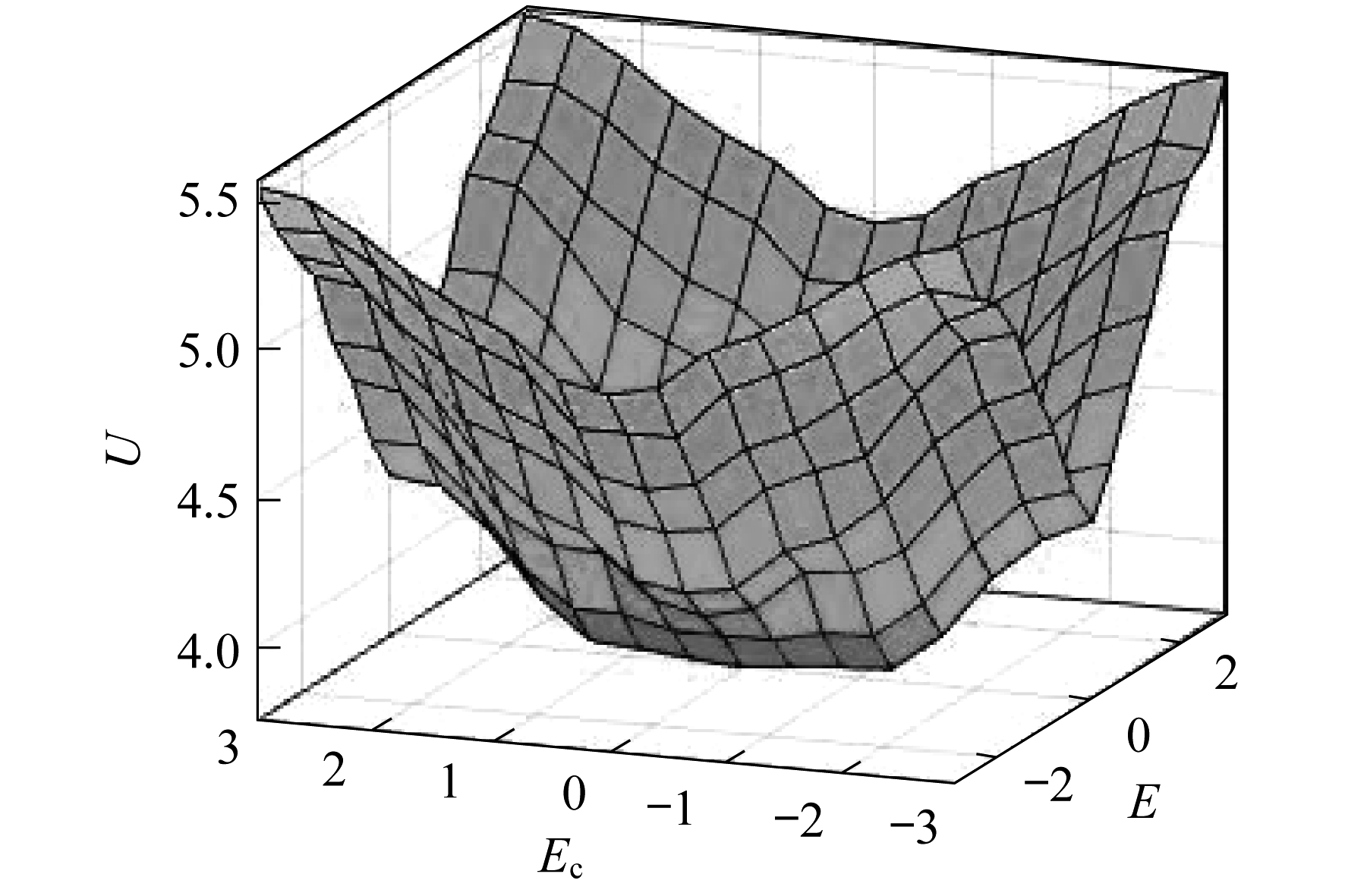
由于负载特性未知, 频率差值e可能为正, 也可能为负, 因此选取e∈[-0.5, 0.5], ec∈[-50, 50], e和ec的模糊论域为[-3, 3], 其对应的模糊子集E=Ec={NB, NM, NS, ZE, PS, PM, PB}。反馈系数k的论域为[3, 6], 其对应的模糊子集U={VS, S, SS, M, BB, B, VB}, E, Ec, K的隶属度函数如图 5所示。量化因子ke=6, kec=0.08, ku=3。
其对应的模糊控制规则表如表 1所示, 模糊规则表的Surface图如图 6所示。
表 1
模糊控制规则
| U | E | |||||||
| NB | NM | NS | ZE | PS | PM | PB | ||
| Ec | NB | VB | VB | BB | SS | BB | VB | VB |
| NM | VB | B | M | SS | M | B | VB | |
| NS | VB | B | SS | S | SS | B | VB | |
| ZE | VB | BB | SS | VS | SS | BB | VB | |
| PS | VB | B | SS | S | SS | B | VB | |
| PM | VB | B | M | SS | M | B | VB | |
| PB | VB | VB | BB | SS | BB | VB | VB | |
根据模糊关系对应输出模糊集合, 再由模糊集合得到模糊子集, 将模糊子集经加权平均法转化为清晰的输出量, 输出量与量化因子ku的乘积即为反馈系数k, 经模糊处理后的系数k能够适应系统的特性, 选择合适的k值, 可以实现快速孤岛检测。
4 试验仿真
4.1 采用SFS法和SMS法的单逆变器并网孤岛检测结果
在单逆变器并网运行系统中, 分别采用SFS法和SMS法进行仿真试验, 以验证两种方法在单逆变器并网运行系统中的有效性。
在单逆变器运行情况下采用SFS孤岛检测法, 其参数选择如表 2所示。
表 2
采用SFS法孤岛检测的参数选择
| 名称 | 参数选择 |
| SFS法 | $C_{f 0}=0.02, k=0.08$ |
| 系统参数 | $u_{\text {inv }}=400 \mathrm{V}, u_{\text {grid }}=220 \mathrm{V}, f_{\mathrm{g}}=50 \mathrm{Hz}$ |
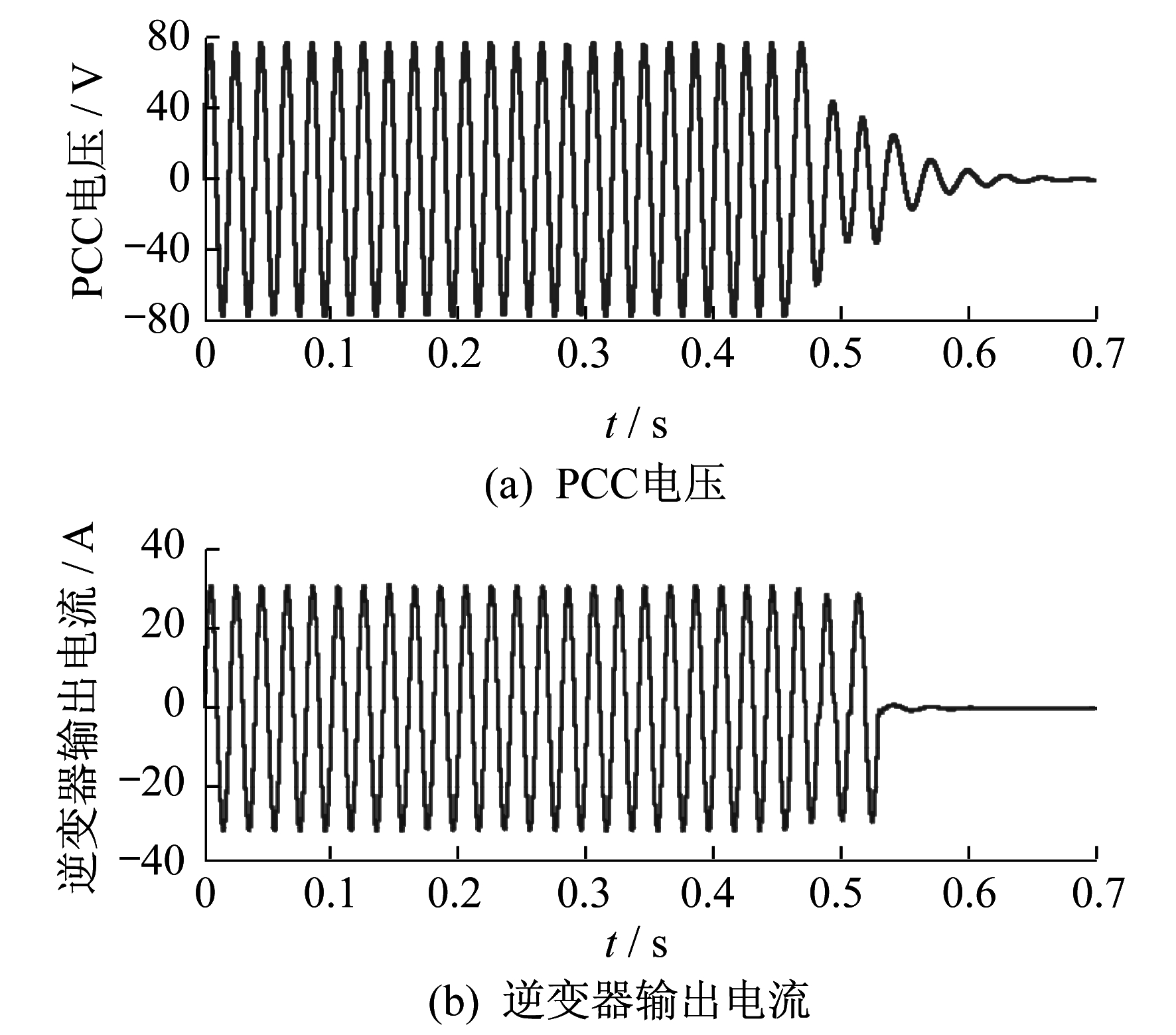
在单逆变器运行系统中采用SFS法进行扰动试验, 检测孤岛状态。在MATLAB中的仿真结果如图 7所示。图 7中, 在0.4 s发生孤岛, 系统检测出发生孤岛, 发出信号中断逆变器输出电流, 在t=0.58 s时逆变器输出电流降为零, t=0.65 s时PCC的电压降为零。
在单逆变器运行系统中采用SMS法进行孤岛检测, 其参数选择如表 3所示。
表 3
采用SMS法孤岛检测的参数选择
| 名称 | 参数选择 |
| SMS法 | $\theta_{\mathrm{m}}=12^{\circ}, f_{\mathrm{m}}-f_{\mathrm{g}}=3 \mathrm{Hz}$ |
| 系统参数 | $u_{\mathrm{inv}}=400 \mathrm{V}, u_{\mathrm{grid}}=220 \mathrm{V}, f_{\mathrm{g}}=50 \mathrm{Hz}$ |
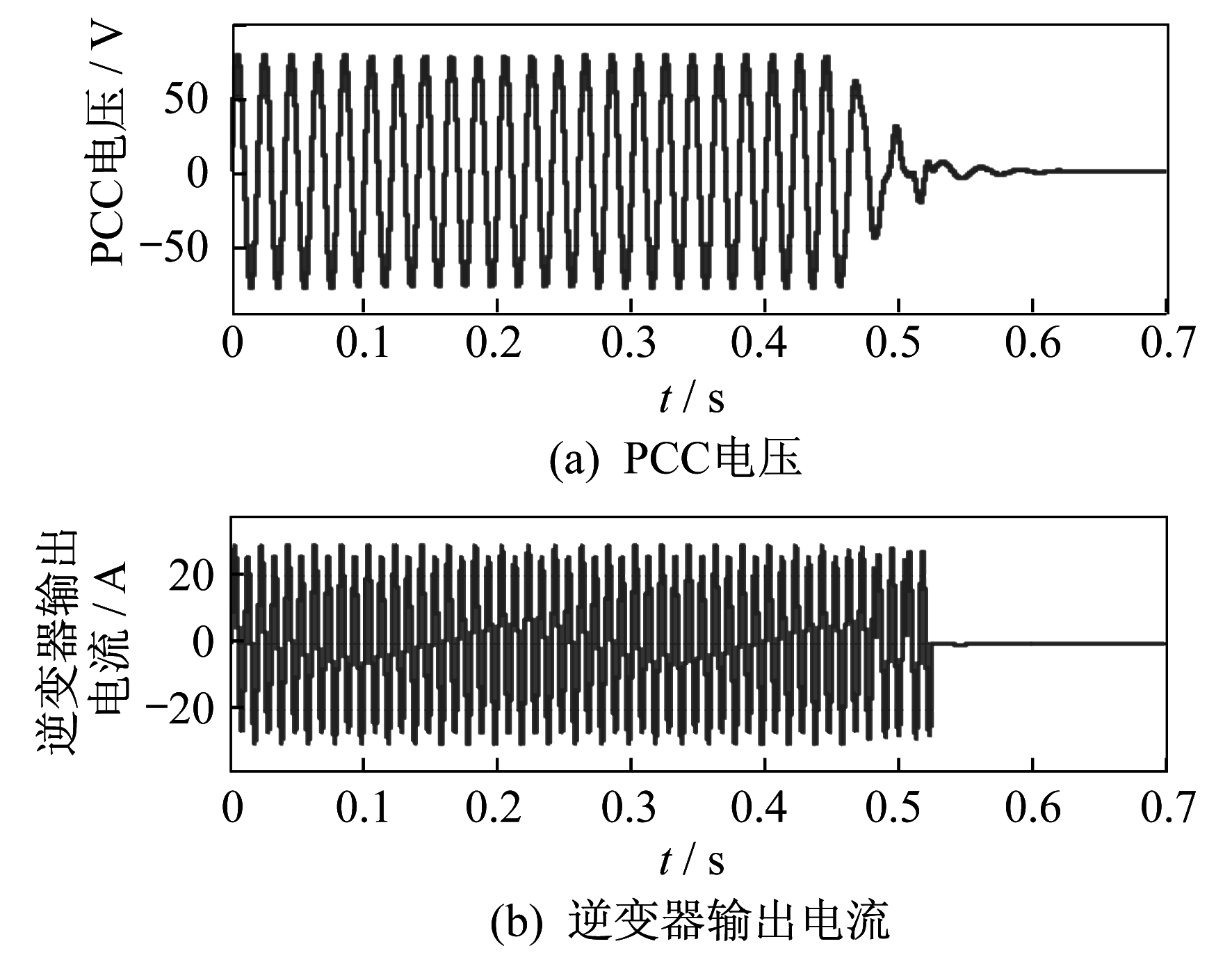
在单逆变器运行系统中采用SMS法进行扰动试验, 检测孤岛状态, 在MATLAB中的仿真结果如图 8所示。图 8中, 在0.4 s发生孤岛, 系统检测到发生孤岛, 发出信号中断逆变器输出电流, 在t=0.53 s时逆变器输出电流降为零, 在t=0.62 s时PCC的电压降为零。
仿真结果表明, 采用SFS法和SMS法都可以有效地实现单逆变器并网运行的孤岛检测, 满足国标GB/T 19939—2005要求在2 s内检测出孤岛运行状态的要求[14]。
4.2 采用SFS法和SMS法结合的多逆变器并网孤岛检测结果
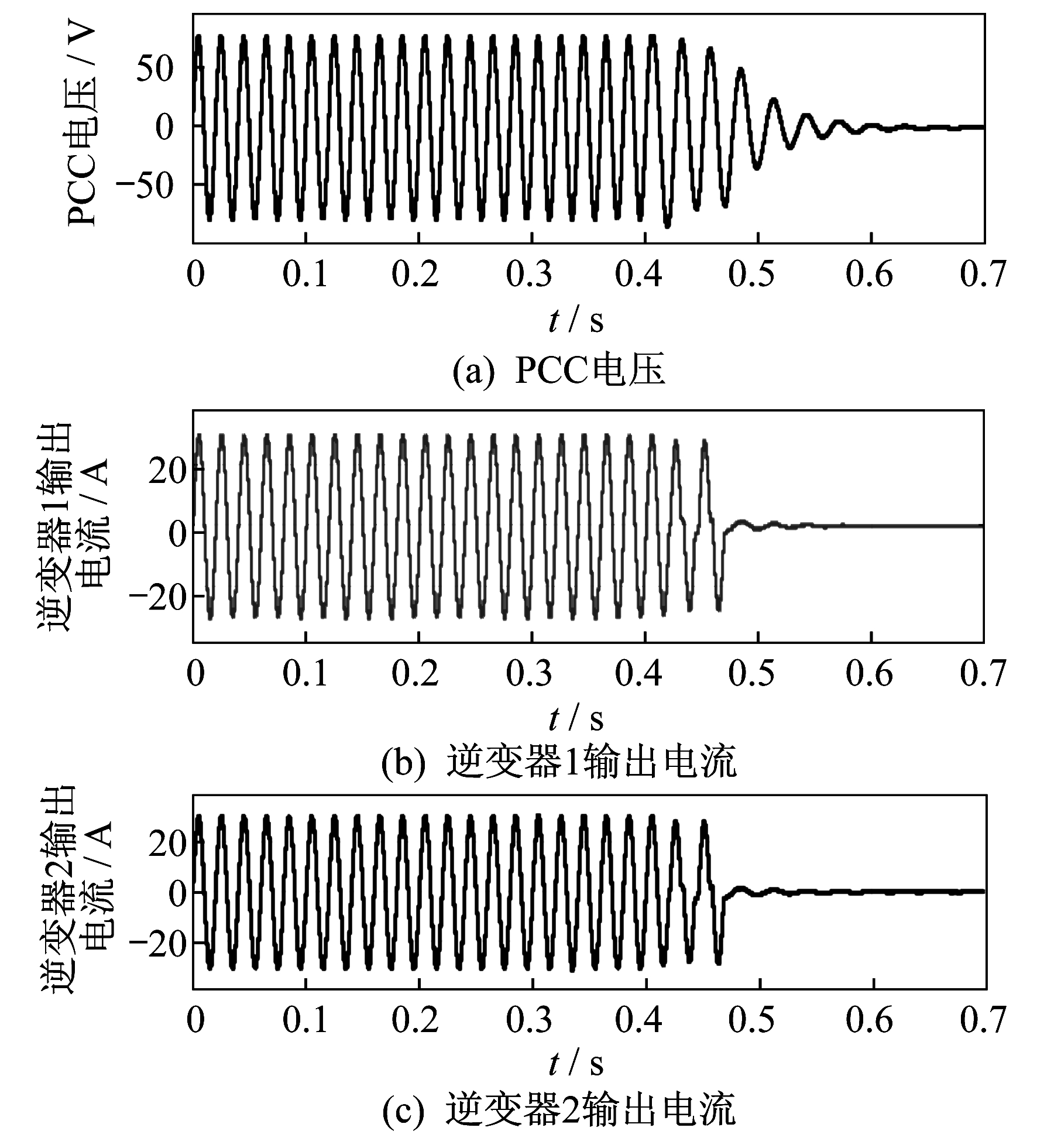
在多逆变器并网运行系统中, 采用传统SFS法与SMS法相结合进行扰动试验。两种方法所取参数如表 4所示, 仿真结果如图 9所示。
表 4
采用SFS法和SMS法孤岛检测的参数选择
| 方法 | 参数选择 |
| $\mathrm{SFS}法$ | $C_{\mathrm{fD}}=0.02, k=0.08$ |
| $\mathrm{SMS}法$ | $\theta_{\mathrm{m}}=12^{\circ}, f_{\mathrm{m}}-f_{\mathrm{g}}=3 \mathrm{Hz}$ |
图 9中, 在0.4 s发生孤岛, 系统检测到发生孤岛, 发出信号中断逆变器输出电流, 在t=0.6 s时逆变器输出电流降为零, 检测到孤岛发生, 并发出指令使逆变器停机, 在t=0.65 s时PCC的电压降为零。
表 5为不同并网类型孤岛检测时间比较。
表 5
不同并网类型孤岛检测时间比较
| 并网类型 | 方法 | 检测时间/s |
| 单逆变器 | SFS法 | 0.18 |
| SMS法 | 0.13 | |
| 多逆变器 | SFS法和SMS法结合 | 0.20 |
由表 5可知, 由于存在稀释效应, 采用SFS和SMS两种方法在多逆变器并网运行孤岛检测时比在单逆变器中分别采用SFS法和SMS法的检测速度要慢。
4.3 采用模糊控制法改进的多逆变器并网孤岛检测结果
由上述分析可知, 在多逆变器并网运行时, 采用传统的SFS法和SMS法结合能够在2 s内检测出孤岛状态。下面采用模糊控制优化的方法进行仿真, 其试验结果如图 10所示。图 10中, 在0.4 s发生孤岛, 系统检测到发生孤岛, 发出信号中断逆变器输出电流, 在t=0.55 s时逆变器输出电流降为零, 检测到孤岛发生, 并发出指令使逆变器停机, 在t=0.62 s时PCC的电压降为零, 满足国标GB/T 19939—2005光伏系统在2 s内检测出孤岛的要求。
由此可知, 相比传统的SFS法和SMS法结合的孤岛检测法, 采用模糊控制改进后的方法能够加快2.5个周期的检测速度, 对逆变器输出电流的谐波影响较小, 电网电能质量得到了提高。
5 结语
本文对逆变器并网运行系统进行了孤岛控制稀释效应分析, 并采用了模糊控制法对SFS法中的参数k进行了优化处理, 通过MATLAB/Simulink仿真结果表明, 采用模糊控制算法, 能够有效地减小稀释效应, 加快了检测速度, 提高了电网电能质量。
参考文献
-
[1]基于典型故障类型的分布式光伏并网对电压稳定性的影响[J]. 上海电力学院学报, 2016, 32(5): 478-484.
-
[2]分布式电源孤岛效应检测方法研究[J]. 科学技术创新, 2018(2): 13-14. DOI:10.3969/j.issn.1673-1328.2018.02.007
-
[3]基于无功电流控制的并网逆变器孤岛检测[J]. 电工技术学报, 2017, 32(16): 294-300.
-
[4]YAFAOUI A, WU B, KOURO S. Improved active frequency drift anti-islanding detection method for grid connected photovoltaic systems[J]. IEEE Transactions on Power Electronics, 2012, 27(5): 2367-2375. DOI:10.1109/TPEL.2011.2171997
-
[5]应用于微电网光伏并网逆变器的孤岛检测[J]. 电工技术, 2017(2): 121-123.
-
[6]正反馈主动移频式孤岛检测算法的改进[J]. 可再生能源, 2017, 35(12): 1821-1827. DOI:10.3969/j.issn.1671-5292.2017.12.014
-
[7]三种频率偏移孤岛检测方法的性能比较[J]. 电网技术, 2016, 40(3): 964-971.
-
[8]基于准Z源逆变器的光伏发电系统的双滑模变结构控制[J]. 上海电力学院学报, 2017, 33(5): 459-465.
-
[9]主动移频式孤岛检测法产生稀释效应机理的分析[J]. 电力系统保护与控制, 2013, 41(4): 84-90. DOI:10.7667/j.issn.1674-3415.2013.04.015
-
[10]适用于多台逆变器并联运行的孤岛检测方法[J]. 电力科学与工程, 2018, 34(3): 51-56. DOI:10.3969/j.ISSN.1672-0792.2018.03.009
-
[11]CAO D, WANG Y, SUN Z, et al. Novel islanding detection method for distributed PV systems with multi-inverters[J]. Journal of Power Electronics, 2016, 16(3): 1141-1151. DOI:10.6113/JPE.2016.16.3.1141
-
[12]HAMZEH M, RASHIDIRAD N, SHESHYEKANI K, et al. A new islanding detection scheme for multiple inverter-based DG systems[J]. IEEE Transactions on Energy Conversion, 2016, 31(3): 1002-1011. DOI:10.1109/TEC.2016.2558631
-
[13]一种基于模糊控制的改进主动式孤岛检测法[J]. 电气传动, 2017, 47(5): 71-74.
-
[14]光伏防孤岛保护检测标准及试验影响因素分析[J]. 电网技术, 2015, 39(4): 924-931.