|
|
|
发布时间: 2019-08-10 |
|
|
|
|
收稿日期: 2018-04-18
基金项目: 国家电网公司科技项目(52090016002M); 上海市科学技术委员会地方能力建设计划基金(16020500900)
中图法分类号: TM769
文献标识码: A
文章编号: 1006-4729(2019)04-0327-06
|
摘要
迭代自组织数据分析算法(ISODATA)是一种基于统计模式识别的非监督学习动态聚类算法。针对当前各算法初始聚类数取值困难、容易陷入局部最优等问题, 介绍了ISODATA的原理和实现步骤, 并将此算法应用于负荷分类中。在MATLAB中结合具体日负荷曲线样本进行聚类分析, 结果证明聚类效果较好。将ISODATA与各种传统聚类方法进行了对比实验, 比较各种算法的聚类效果、预定聚类数目对算法结果的影响, 以及初始聚类中心的选择对结果的影响。对比结果证明, 此方法适用于负荷分类的研究。
关键词
迭代自组织数据分析算法; 聚类; 日负荷曲线; 曲线识别; 大数据; 数据挖掘
Abstract
Interative self-organization data analysis algorithm(ISODATA) is a kind of unsupervised learning dynamic clustering algorithm based on statistical pattern recognition.The principle and process of the ISODATA are introduced in detail.This algorithm is applied in load classification, combined with specific daily load curve samples in matlab for cluster analysis.ISODATA is compared with traditional clustering methods in the results of algorithm clustering and the effects of the clustering center are better.The result is compared with the traditional clustering effect of various clustering methods and proves to be relatively more accurate, which confirms this verified the applicability of method in the study of the load curve classification.
Key words
iterative self-organizing data analysis algorithm; clustering; daily load curve; curve identification; big data; data mining
电力系统的负荷波动十分频繁, 负荷种类多种多样, 不同地理位置、时段、种类的负荷都对应着不同的负荷曲线, 负荷曲线具有连续性和周期性的特征。按照行业负荷分类的惯例, 传统负荷主要被分为工业、农业、商业、城乡居民及其他负荷, 不同类别的日负荷曲线区分明显。但是随着电力系统的发展, 一些新兴产业的兴起, 传统的划分方式过于粗糙, 已经不能满足人们的需求, 更加细致、准确、实用的数据挖掘技术不断地被提出和应用。掌握电力系统的负荷特性和负荷组成, 建立结构合理、参数准确的综合负荷模型, 对电力系统平稳、安全的运行具有重大意义。
随着大数据时代的来临, 越来越多的数据挖掘技术应用到各行各业中, 数据挖掘技术是人工智能和数据库技术相结合的产物, 聚类方法是数据挖掘技术的一个重要分支[1]。聚类方法是用各类算法将样本数据根据某一相似的特性进行区分, 同一类中保证数据的相似性, 不同类之间保证数据的差异性。电力负荷曲线聚类的研究是配电网大数据的基石, 负荷数据预处理、异常用电行为分析、需求侧管理、用电用户划分等多种数据挖掘技术都需要用到这一技术。因此, 有必要对电力负荷曲线聚类进行研究。
聚类方法有很多种, 一是划分法, 如K-means算法。文献[2]主要针对K-means算法的缺陷进行了研究和改良, 综合提出了最适合电力负荷数据特征的优化方法, 而不是将单一的方法进行叠加。这种方法简单、时间复杂度和空间复杂度较低, 但是聚类结果受到随机初始化中心点的影响很大。二是层次法, 是将样本数据进行逐层分解。文献[3]基于Ward层次聚类算法, 提出了C-Ward算法, 省略了对数据样本点进行预先划分的步骤。这类算法可解释性好, 但是时间复杂度高。三是基于密度的方法, 其核心思想是只要邻近区域内的样本密度超过某个阈值, 就会不停地聚类, 最典型的的算法是DBSCAN算法。文献[4]利用密度梯度算法进行负荷分类的研究, 选取不同类的边界点的分布情况作为特征。这类算法对噪声的抵抗性较强, 可以解决各种形状的聚类问题, 但处理高维样本数据的能力比较薄弱。四是基于模型的方法, 即寻找数据对既定模型的最佳拟合模型, 使同一类的数据隶属于同一种概率分布, 最典型的是神经网络法。文献[5]以负荷的组成情况为依据来进行分类, 同时应用神经网络和C-均值聚类算法, 将获得的聚类数目和各类中心点作为C-均值算法的初始值进一步聚类, 具有较强的实用性和有效性。
为了解决大多数聚类算法对初始聚类个数的设置难问题和对初始聚类中心选取过于敏感的问题, 本文探讨了迭代自组织数据分析算法(Iterative Self-organizing Data Analysis Algorithm, ISODATA)在负荷分类中的应用, 主要研究该算法与以上主流聚类算法在负荷分类应用方面相比的优缺点。
1 ISODATA概述
ISODATA作为一种软性聚类的方法, 是在样本对象初始特征不明显的情况下, 在迭代的过程中逐渐逼近事物最本质的特征。这种机器学习的过程与人类认知事物的方式类似, 聚类方法相对科学。其关键步骤在于聚类的合并和分裂运算, 通过多个阈值进行限制, 类间距离过小将其合并, 同类样本距离过大将其分裂, 从而达到预期的聚类效果。
由于在很多情况下, 各种聚类算法的参数无法准确设定, 就使得ISODATA在参数调试完成前往往得不到理想的结果, 因此对该算法控制参数的调试过程比较繁琐[6-10]。但是, 当参数调整准确以后, 得到的结果往往优于传统的聚类方法。这是因为该算法加入了人的想法作为限制条件, 从而使得聚类结果更加“人性化”。对于某一类的数据, 例如针对负荷曲线的聚类, 调试参数的过程只需一次, 之后对于同一类型的其他样本可以直接适用, 同样简单、快捷。因此, ISODATA在负荷曲线分类中的实用性很强[11-14]。
ISODATA在运行前需要输入的参数主要有:预估的聚成类别数K; 每个聚类样本含有最少的样本数量θN; 每个聚类中样本标准差的阈值θS, 即分裂系数, 如果大于此数, 此聚类需进行分裂; 各聚类中心之间距离的阈值θC, 即合并系数, 如果小于此数, 两个聚类进行合并; 进行迭代的总次数I。
在对上述参数进行设置后, ISODATA大体分为以下7个步骤。
步骤1 输入N个样本数据{xi=1, 2, 3, …, N}, 随机选出NC个初始聚类中心{z1, z2, z3, …, zNC}。
步骤2 将N个样本数据分给最近的聚类Sj, 样本与聚类中心的距离采用欧式距离。假如 则x∈Sj。
则x∈Sj。
步骤3 如果Sj中的样本数目Sj < θN, 则取消该样本子集。
步骤4 修正各聚类中心Zj, 修正公式为
| $z_{j}=\frac{1}{N_{j}} \sum\limits_{x \in S_{j}} x, \quad j=1,2,3, \cdots, N_{\mathrm{C}}$ | (1) |
步骤5 判断是否进行分裂运算, 一般以下3种情况需要进行分裂处理。NC≤K/2, 即最终聚类数小于当时给定值的1/2;同时不满足迭代运算次数是偶数次或NC≥2K; 一个聚类中样本距离标准差向量最大值σjmax > θS。每次分裂形成的新的聚类中心表达式为
| $Z_{1}=Z_{i}+f_{\text {actor }} \times \sigma_{j \max }$ | (3) |
| $Z_{2}=Z_{i}-f_{\text {actor }} \times \sigma_{j \max }$ | (4) |
步骤6 判断合并运算, 计算各类之间的距离Dij, 若Dij < θC, 或者某类中样本个数小于规定θN, 则进行合并操作。新的聚类中心为
| $Z_{k}=\frac{1}{N_{i}+N_{j}}\left(N_{i} \times Z_{i}+N_{j} \times Z_{j}\right)$ | (5) |
步骤7 重复迭代, 直至达到迭代次数。
2 聚类评价指标
通常从两个方面评价一个非监督聚类算法的有效性:一是紧密度, 即每类中的样本数据应尽可能地相似; 二是分离度, 即不同聚类之间数据的差异性应尽可能地大。常用的评价方法有外部评价法、内部评价法和相对评价法。本次实验采用聚类完成时得到的各聚类中心向量, 计算内平方和WSS和外平方和BSS作为聚类效果的评价指标。对于有m条样本, n个特征点的负荷组成情况, WSS和BSS的表达式为
| $ W_{\mathrm{SS}}=\sum\limits_{i=1}^{m} d\left(\boldsymbol{p}_{i}, \boldsymbol{q}^{(i)}\right)^{2} $ | (6) |
| $B_{\mathrm{SS}}=\sum\limits_{k=1}^{m}\left|Z_{k}\right| d\left(\boldsymbol{Q}, \boldsymbol{q}_{k}\right)^{2}$ | (7) |
| $C_{\mathrm{HI}}=\frac{B_{\mathrm{SS}}}{W_{\mathrm{SS}}}$ | (8) |
式中:pi——聚类i的中心向量, pi=(pi1, pi2, pi3, …, pin);
q(i)——隶属于聚类i的样本数据,
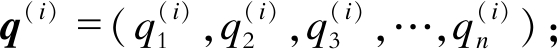
Zk——第k聚类中样本的个数;
Q——所有样本数据中心的特征向量, Q=(Q1, Q2, Q3, …, Qn);
qk——第k类样本中心的特征向量, qk=(qk1, qk2, qk3, …, qkn)。
WSS和BSS分别体现了同一聚类中数据的相似程度和不同聚类之间数据的差异程度。显然, WSS的值越小, 同一类中数据的相似度越高; BSS的值越大, 不同类之间数据的差异性越大。总之, CHI指数越大, 聚类效果越好。
3 算例分析
根据系统测量到的用户负荷数据, 选取电网中437个用户的日负荷曲线(即用户有功功率的使用情况)作为待分类样本, 取一天当中24个时刻点的负荷情况作为一条负荷曲线的特征点。在对数据进行归一化处理的基础上进行分类, 以抵消数值差别过大带来的影响。记第i时刻的负荷为Ph(h=1, 2, 3, …24), 负荷最大值为Pmax, Xh=Ph/Pmax, Xh即为归一化后的负荷曲线在h时刻的值。
采用ISODATA(M1)对以上样本曲线进行聚类, 并与当前主流聚类算法进行比较, 验证其在负荷分类中的可行性。参与对比的算法分别有传统的K-means算法(M2)、层次聚类算法(M3)、模糊C-均值算法(M4)、自组织映射神经网络算法(M5)等。本次实验将主要从聚类效果、聚类数目的取值影响和初始中心向量的选取影响来对比ISODATA和各聚类算法。
3.1 ISODATA聚类效果展示
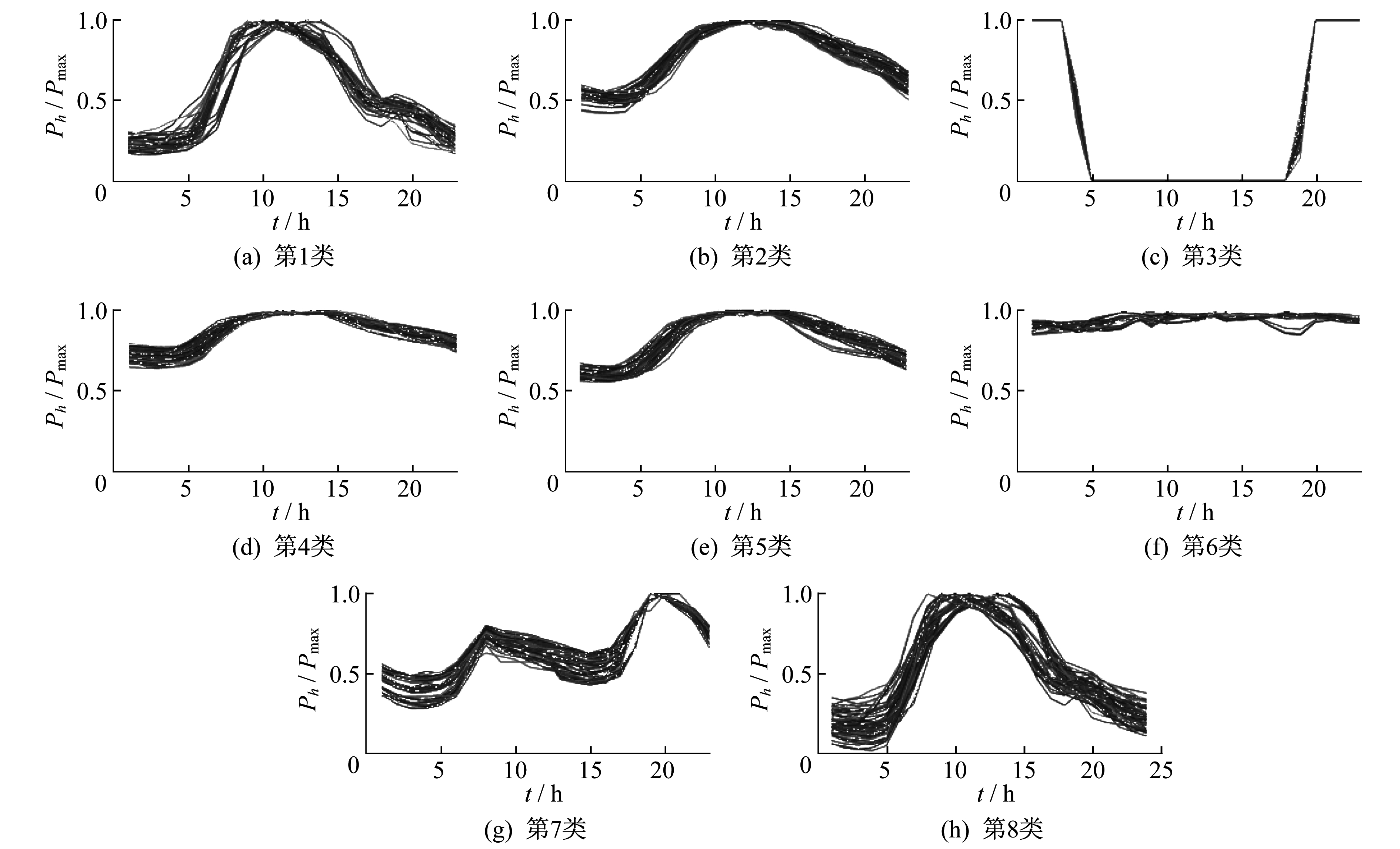
本次聚类仿真在MATLAB软件中进行, 经过多次调试, 效果较为理想的参数如下:迭代次数为100次; 预期聚类数为8个; 类与类之间的最小距离为0.2;每个聚类中最小样本数为10个; 最大样本距离分布的标准差为0.1。聚类结果如图 1所示。
图 1中的曲线为日负荷曲线, 即当天该负荷的有功功率消耗情况。日负荷曲线样本被分为8类, 各类样本数量分别为34, 78, 19, 83, 73, 30, 52, 68。聚类效果较好, 不同类之间区别分明, 具有很好的参考价值。除了第3类和第7类比较特殊外, 大多数负荷曲线都在中午12时达到顶峰; 第1和第2类是学校、办公室等场所, 白天办公时间用电负荷较高, 晚上逐渐降低; 第4和第5类属于医院等负荷, 负荷曲线较为平缓, 波动较小; 第6类一般属于昼夜不停运作的大型工厂负荷, 机器一天24 h高强度运作, 几乎没有波动; 第7类属于KTV等夜间娱乐行业, 在晚上8时左右达到用电高峰。了解负荷特性的变化规律, 对于电力部门进行负荷分类、预测、调度, 以及制定电价有很好的借鉴意义。
3.2 5种算法的聚类评价指数比较
采用相同的数据样本, 在同样聚成8类的情况下, 根据式(6)、式(7)、式(8)得到5种算法的聚类评价指标, 如表 1所示。
表 1
5种聚类算法的评价指标结果
| 算法 | BSS | WSS | CHI |
| M1 | 449.40 | 15.76 | 28.53 |
| M2 | 450.60 | 14.60 | 30.86 |
| M3 | 449.30 | 15.83 | 28.38 |
| M4 | 451.32 | 17.93 | 25.17 |
| M5 | 449.40 | 15.77 | 28.50 |
由表 1可以看出, 5种聚类算法的聚类效果比较接近。其中, ISODATA的聚类效果比层次聚类算法、模糊C-均值算法以及自组织映射神经网络算法要好。但是, ISODATA的3项评价指标均不及传统K-means算法。这是因为K-means算法完全是以类间距离最小为准则而编写的, 并没有其他限制性因素, 而ISODATA考虑了人的“想法”, 按照人们的预期添加了多种限制条件。虽然ISODATA的评价指数不及K-means算法, 但它得到了更符合人们要求的聚类结果。例如, 用户不希望聚成的某一类中样本数量过少, 又不希望其中样本差异过大, 就可以通过聚类前的输入参数进行限制, 从而更具有实用价值。
3.3 预定聚类数对ISODATA结果的影响
若保持437条日负荷曲线数据样本不变, 设定目标聚类数K(K=2, 3, 4…, 10), 观察目标聚类数K对各聚类算法最终聚类数K′的影响。实验结果如表 2所示。
表 2
预定聚类数对各算法最终聚类数的影响
| K | K′ | ||
| M1 | M2 | M5 | |
| 2 | 7 | 2 | 2 |
| 3 | 7 | 3 | 3 |
| 4 | 7 | 4 | 4 |
| 5 | 7 | 5 | 5 |
| 6 | 7 | 6 | 5 |
| 7 | 7 | 7 | 6 |
| 8 | 8 | 8 | 7 |
| 9 | 9 | 9 | 7 |
| 10 | 9 | 10 | 7 |
从表 2可以看出, ISODATA和自组织神经网络算法的最终聚类数与初始聚类数不同, 传统K-means算法的最终聚类数没有发生改变。经过多次实验, 针对此次样本数据, 所有聚类算法的最优类别数普遍为7, 8, 9。ISODATA在K=2时, 就能自动聚成7类; 在K > 9时, 能够自动聚成9类, 鲁棒性极强, 具有自动调节最优类别数的能力。神经网络法在K≥8时, 全部聚成7类, 对初始聚类数也有一定的调节能力; 但在K≤7时, 调节能力不明显。传统K-means算法则是完全依据初始聚类数进行聚类。对于聚类数不明的复杂电力大数据样本来说, ISODATA具有很好的改良聚类效果的能力。
3.4 初始聚类中心的选择对ISODATA的影响
大多数聚类算法的初始聚类中心都是随机生成或者随机选取的, 这就导致了有的算法可能会因为初始聚类中心选择不当而陷入局部最优。为了验证初始聚类中心的选择是否会对ISODATA造成影响, 在样本数据和所有参数都不变的情况下, 每次在437条数据样本中随机选取8条作为初始聚类中心, 实验10次, 以观察聚类结果是否会发生变化, 并与其他聚类算法相比较。比较结果如表 3所示。
表 3
初始聚类中心变化时各种聚类算法的CHI指标对比情况
| 次数 | M1 | M2 | M3 | M4 |
| 2 | 28.53 | 30.86 | 28.38 | 30.62 |
| 3 | 28.53 | 30.86 | 28.38 | 28.12 |
| 4 | 28.53 | 30.86 | 28.38 | 27.51 |
| 5 | 28.53 | 30.86 | 28.38 | 27.51 |
| 6 | 28.53 | 30.86 | 28.38 | 28.12 |
| 7 | 28.53 | 30.86 | 28.38 | 28.12 |
| 8 | 28.53 | 30.86 | 28.38 | 30.62 |
| 9 | 28.53 | 30.86 | 28.38 | 22.71 |
| 10 | 28.53 | 30.86 | 28.38 | 27.51 |
从表 3可以看出, 初始聚类中心的变化对模糊C-均值算法的影响较大。模糊C-均值算法的CHI值波动范围很大, 最低只有22.71, 最高为30.62, 仅次于传统K-means算法的30.86;而ISODATA几乎完全不受初始聚类中心的影响, 不用考虑陷入局部最优带来的误差, 算法稳定性较高。
根据以上对比实验可以得出以下结论:传统K-means聚类算法的初始点选择不稳定, 引起了聚类结果的不稳定; 层次聚类算法虽然不需要确定分类数, 但是一旦进行分裂或者合并, 就不能修正, 聚类质量受到限制; 模糊C-均值算法对初始聚类中心比较敏感, 需要人为确定聚类数, 容易陷入局部最优解; 自组织映射神经网络算法与实际大脑处理有很强的理论联系, 但处理时间较长, 需要进一步研究使其适应大型数据库; ISODATA不受初始聚类中心的影响, 运算时间远小于自组织映射神经网络算法, 经过多次合并分裂后, 聚类准确率也处于较高水平, 完全适用于电力负荷曲线的分类研究。
4 结语
在大数据时代的背景下, 面对海量的电能质量监测数据, 准确、快捷的数据挖掘技术成为处理数据的有效手段。本文介绍了ISODATA的原理和实现步骤, 并将此算法应用到日负荷曲线的分类中, 聚类结果较为理想。与当前主流的聚类算法进行对比, 得到了不同算法的聚类效果对比情况、聚类数K值和初始聚类中心的选取等方面对聚类结果产生的影响。此算法在聚类之前需要对各种参数进行设置, 在传统算法上新增了分裂和合并两个步骤, 从而大大减少了聚类算法的盲目性, 但也使得算法更加复杂。尽管参数的选择需要多次尝试, 但是当参数调整好后, 就完全能够应用于处理同类的样本分类问题, 同时解决了未知样本聚类数取值难的问题。今后, ISODATA的主要研究方向为如何快速、准确地进行参数设置, 以节约时间成本。
参考文献
-
[1]黄雯.数据挖掘算法及其应用研究[D].北京: 北京邮电大学, 2013.
-
[2]肖琪.基于优化K-means算法的电力负荷分类研究[D].大连: 大连理工大学, 2015.
-
[3]基于约束动态更新的半监督层次聚类算法[J]. 自动化学报, 2015, 41(7): 1253-1263.
-
[4]杨振.密度梯度算法在负荷动特性分类与综合中的研究与应用[D].长沙: 湖南大学, 2009.
-
[5]SOM神经网络和C-均值法在负荷分类中的应用[J]. 电力系统及其自动化学报, 2011, 23(4): 36-39. DOI:10.3969/j.issn.1003-8930.2011.04.007
-
[6]仲伟宽.数据挖掘技术在负荷特性分析中的应用[D].南京: 东南大学, 2006.
-
[7]基于自适应模糊C均值算法的电力负荷分类研究[J]. 电力系统保护与控制, 2010, 38(16): 112-115.
-
[8]基于自组织映射神经网络的电力用户负荷曲线聚类[J]. 电力系统自动化, 2008, 32(15): 66-70. DOI:10.3321/j.issn:1000-1026.2008.15.015
-
[9]张忠华.电力系统负荷分类研究[D].天津: 天津大学, 2007.
-
[10]基于改进的ISODATA算法的大样本数据聚类方法研究[J]. 内蒙古农业大学学报, 2013, 34(1): 133-137.
-
[11]K-means和ISODATA聚类算法的比较研究[J]. 江西理工大学学报, 2012, 33(1): 78-82.
-
[12]数据挖掘及其在电能质量分析中的应用[J]. 电力系统及其自动化学报, 2009, 21(5): 51-55. DOI:10.3969/j.issn.1003-8930.2009.05.010
-
[13]大数据时代的信息安全[J]. 上海电力学院学报, 2013, 29(6): 599-603.
-
[14]改进的K-means算法在电厂煤质分析中的应用[J]. 上海电力学院学报, 2015, 31(6): 585-588.