|
|
|
发布时间: 2019-08-10 |
|
|
|
|
收稿日期: 2018-04-18
基金项目: 国家自然科学基金(51607110)
中图法分类号: TM72
文献标识码: A
文章编号: 1006-4729(2019)04-0321-06
|
摘要
基于电路理论, 建立了双发射结构磁谐振式无线电能传输(WPT)系统的等效互感模型。与单发射结构相比, 双发射结构可以提高负载接收功率和传输效率, 而且随着发射线圈与接收线圈之间耦合系数的降低, 双发射结构的优势更加明显。结合数值仿真试验, 对比得出当两种结构的接收线圈发生横向偏移与角度偏转时, 负载功率和传输效率的比值分别可达2.8和1.39以上, 验证了理论分析的正确性。最后, 进一步分析了两种结构在欠耦合、临界耦合、过耦合3种区域的传输效率, 发现双发射结构可以增加系统的纵向传输距离, 且在临界耦合区域内可以有效扩大系统的横向传输范围。
关键词
无线电能传输; 双发射线圈; 耦合系数; 传输效率; 传输方向
Abstract
Firstly, the mutual inductance equation of the double transmitters(DT) structure is established, which theoretically demonstrates that the structure can significantly improve the received power(RP) and transmission efficiency(TE).Especially, the lower coupling coefficient, the more obvious advantage of the double transmitters structure.And then combined with numerical simulation, the ratio of RP and TE are more than 2.8 and 1.39 respectively when the receiving coil of two structures has horizontal movement and angular deflection, which verifies the theoretical analysis.Finally, the TE of two structures in three regions (over-coupled, critical-coupled and under-coupled)is analyzed, and the results show that DT structure can increase the longitudinal distance and under the critical-coupled region, it also can expand the lateral transmission range.
Key words
wireless power transmission; double transmitters; coupling coefficient; transmission efficiency; transmission direction
近年来无线电能传输(Wireless Power Transmission, WPT)技术得到了迅速发展, 已经在无线充电汽车[1]、医疗、采矿等领域得到了广泛应用。目前, 主流的WPT技术主要有磁感应耦合式、磁耦合谐振式、微波辐射式和激光方式4种。其中磁耦合谐振式无线能量传输(Wireless Power Transfer Via Magnetic Resonance Coupling, WPT/MRC)是近年来无线能量传输领域新提出的一种技术方案, 相比于其他WPT方法, 具有传输距离适中、传输功率大和传输效率高等优点, 已成为当前研究的热点[2]。
WPT/MRC技术的研究主要体现在如何提高传输效率、传输功率以及扩大传输距离3个方面[3]。目前, 国内外文献主要通过对中继谐振线圈、采用新型线圈材料以及利用多发射端/多接收端结构进行设计等方法来增加传输距离, 提高传输功率和传输效率, 使其具有更好的传输性能。
在谐振线圈应用方面, 文献[4]提出, 当发射线圈和中继线圈垂直放置时可以改变功率传输路径; 文献[5]讨论了中继谐振器摆放方位的优化策略; 文献[6]指出, 随着中继线圈个数的增加, 系统的可用带宽变宽, 且通带边缘变得更加陡峭, 有利于抵抗电磁干扰。
新材料制作的发射线圈和接收线圈因其具有高耦合系数、低阻抗损耗、高传输效率等优点, 目前被广泛应用于WPT系统中。文献[7]提出了基于近场超材料超透镜的中继谐振结构, 通过试验验证了利用超材料提高传输效率的可行性; 文献[8]提出采用铁氧体材料制成平板型磁芯, 加入发射和接收线圈中, 可以更好地约束周围磁场, 减少漏磁, 提高传输性能, 而且加入该磁芯后, 允许发射和接收线圈之间有一定的角度偏差, 增加了系统供电的灵活性。
在多发射端/多接收端结构方面, 文献[5]提出, 将带有90°馈电的十字交叉线圈结构作为发射线圈, 即可实现全方位的无线能量传输, 但该方法受到实际尺寸要求的限制; 文献[9-11]通过控制两个垂直放置的发射线圈的电流相位或电源类型, 来获得一个较稳定的中心磁场区域, 从而保证了传输效率的稳定; 文献[12]分析了双发射结构, 从磁场分布的角度验证了该结构可以扩大系统的传输距离; 文献[13]提出的四线圈激励的无线电能传输系统, 不仅增加了传输距离, 而且减弱了传输方向的敏感度。上述传输结构的可行性已经在试验中得到了验证。但是目前对接收线圈位置发生变化时如何改变系统能量传输方向的具体理论分析和量化的研究还很少。
本文以最基本的双发射线圈结构作为研究对象, 对比单发射线圈结构, 分析其优越性以及在不同区域传输效率的变化情况, 以期为多发射线圈结构的传输方向提供参考。
1 模型建立与理论分析
1.1 系统模型建立
目前, 用于WPT系统的数学建模分析方法主要有耦合模理论(Coupled-Mode Theory, CMT)[14]和等效电路法[15]两种。前者多用于微波射频领域, 从能量角度阐述了系统能量传输的工作原理, 但在分析系统模型的实际物理参数时, 难以得出详细的结果, 无法精确描述系统性能。后者采用等效电路方法建立互感模型, 能够较为精确地描述谐振耦合系统中各种物理参数对系统传输功率和传输效率的影响。相关文献已证明耦合模模型与电路理论模型在计算系统稳态参数(负载功率和传输效率)时具有等效性[16]。本文采用电路互感理论对双发射WPT系统进行建模分析。
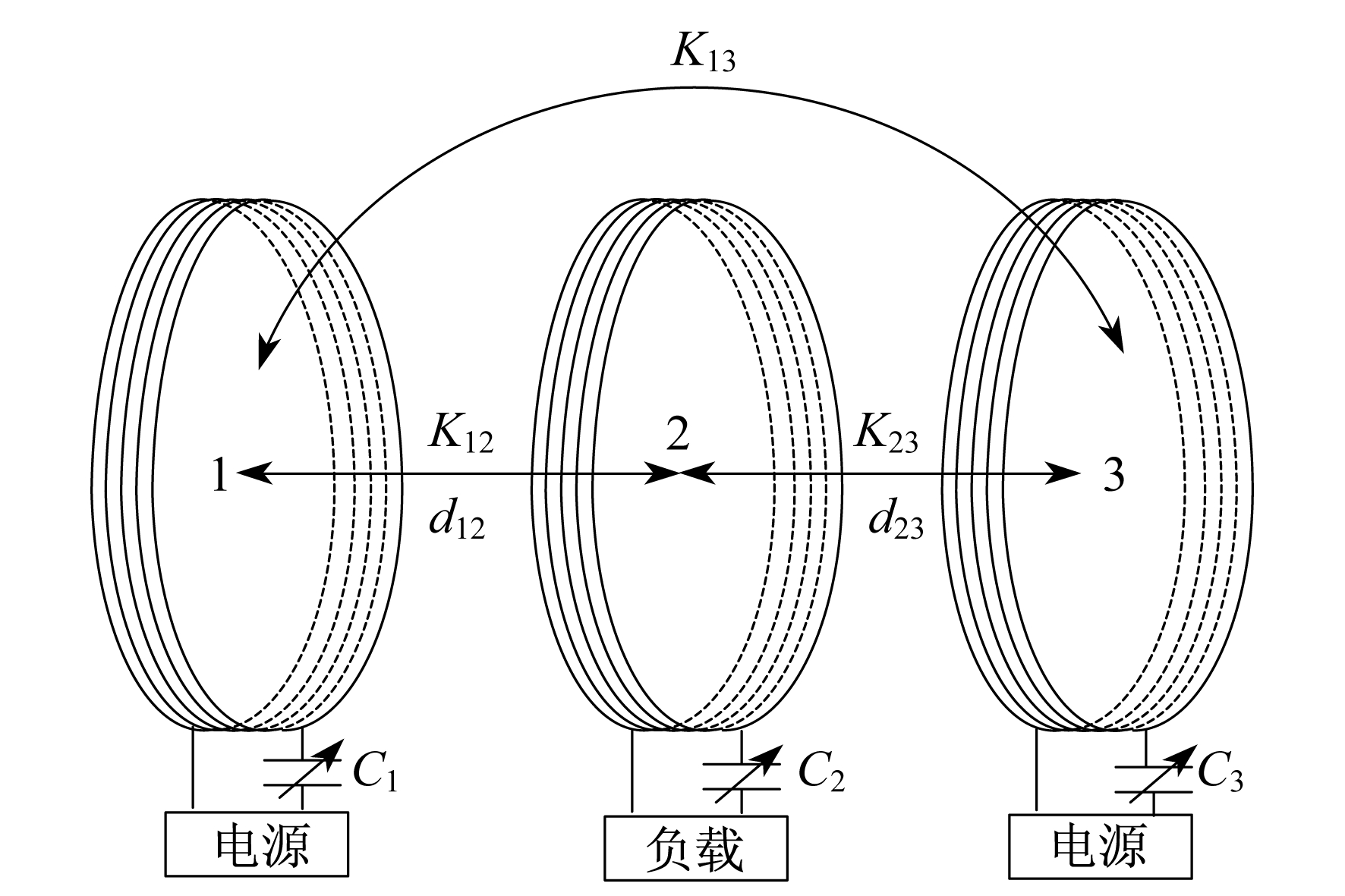
图 1为双发射WPT系统结构图。图 1中, C1, C2, C3为发射线圈和接收线圈的等效电容; K13为两发射线圈之间的耦合系数; K12和K23为发射线圈和接收线圈之间的耦合系数; d12和d23为发射线圈与接收线圈之间的偏移距离。
系统由高频电源、发射线圈和接收线圈、可调电容、负载组成, 双发射线圈与接收线圈平行同轴放置。发射端与接收端均由谐振频率相同的多匝线圈组成, 且线圈间通过谐振耦合实现空间磁场能量的无线传输。
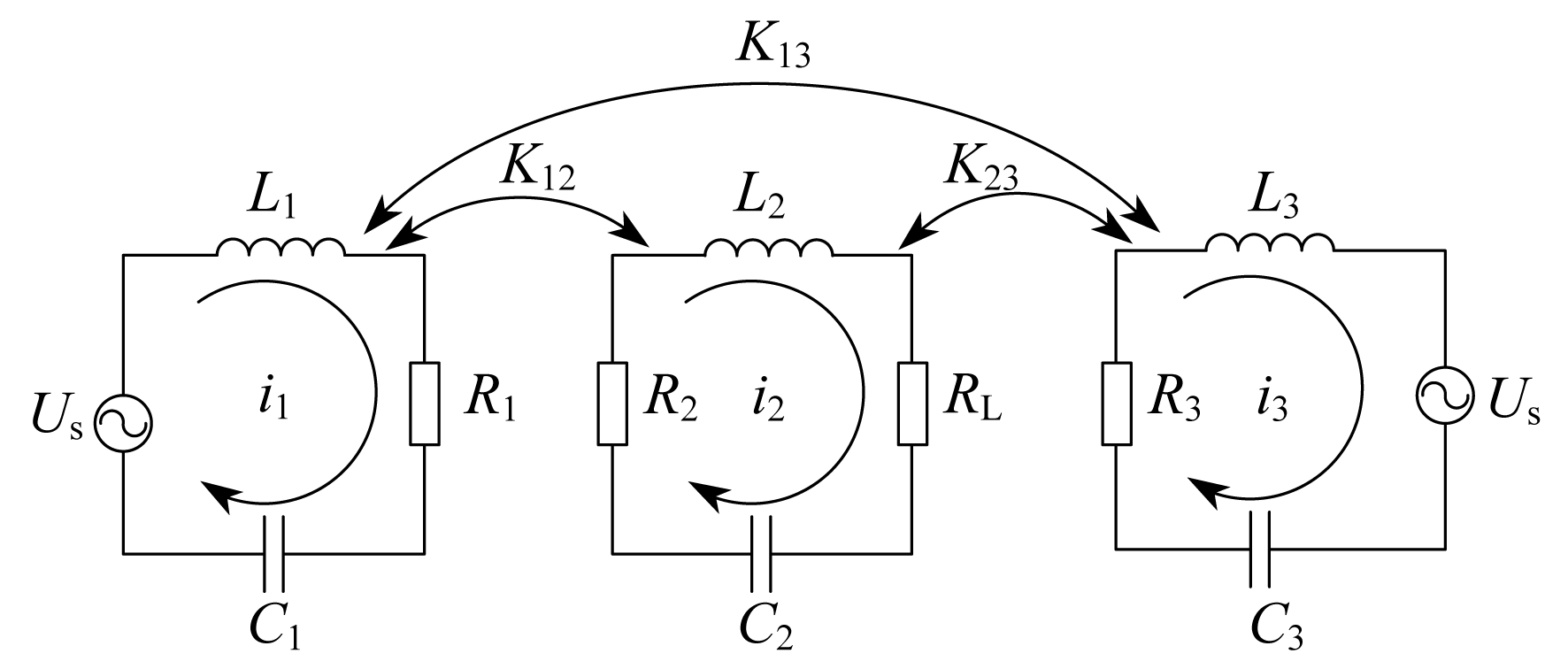
系统等效电路模型如图 2所示。图 2中, 发射线圈连接高频电源Us, 接收线圈连接负载RL。R1和R3分别为两个发射线圈的等效电阻(包括电源内阻和线圈在高频下的等效电阻), R2为接收线圈的等效电阻; L1, L3, L2分别为发射线圈和接收线圈的等效电感; i1, i3, i2分别为流过发射线圈和接收线圈的电流; K13是两发射线圈之间的耦合系数, K12和K23均为发射线圈和接收线圈之间的耦合系数。当两发射线圈之间的距离远大于线圈的半径时, 耦合系数K13可以忽略不计, 即K13≈0(以下模型中直接省略了K13)。C1, C3, C2分别为发射线圈和接收线圈的等效电容(包括寄生电容和补偿电容), 满足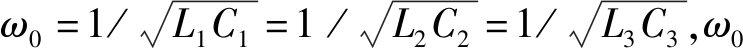 为系统谐振角频率。双发射线圈与接收线圈的尺寸和结构相同, 可默认双发射线圈与接收线圈的等效参数及谐振频率保持一致。
为系统谐振角频率。双发射线圈与接收线圈的尺寸和结构相同, 可默认双发射线圈与接收线圈的等效参数及谐振频率保持一致。
1.2 系统接收功率与传输效率分析
设流过发射线圈和接收线圈的电流分别为i1, i3, i2, 方向如图 2所示。根据基尔霍夫电压定律(KVL)可建立互连电路方程为
| $ \left\{\begin{array}{c} \left(R_{1}+\mathrm{j} \omega L_{1}+\frac{1}{\mathrm{j} \omega C_{1}}\right) \dot{I}_{1}+\mathrm{j} \omega M_{12} \dot{I}_{2}=\dot{U}_{\mathrm{s}} \\ \left(R_{3}+\mathrm{j} \omega L_{3}+\frac{1}{\mathrm{j} \omega C_{3}}\right) \dot{I}_{3}+\mathrm{j} \omega M_{23} \dot{I}_{2}=\dot{U}_{\mathrm{s}} \\ \left(R_{2}+R_{L}+\mathrm{j} \omega L_{2}+\frac{1}{\mathrm{j} \omega C_{2}}\right) \dot{I}_{2}+\mathrm{j} \omega M_{12} \dot{I}_{1}+ \\ \mathrm{j} \omega M_{23} \dot{I}_{3}=0 \end{array}\right. $ | (1) |
式中:M12, M23——发射线圈与接收线圈之间的互感。
当系统工作在谐振状态时(即ω=ω0), 存在jωL1+1/jωC1=0。由式(1)可求出发射线圈和接收线圈的等效电流为
| $\left\{ \begin{array}{l} \dot{I}_{1}=\frac{\dot{U}_{\mathrm{s}}}{R_{1}+\frac{\omega^{2} M_{12}^{2}}{\left(R_{2}+R_{L}\right) \frac{R_{1}}{R_{1}+R_{3}}}} \\ \dot{I}_{3}=\frac{\dot{U}_{\mathrm{s}}}{R_{3}+\frac{\omega^{2} M_{23}^{2}}{\left(R_{2}+R_{L}\right) \frac{R_{3}}{R_{1}+R_{3}}}} \\ \dot{I}_{2}=-\frac{\mathrm{j} \omega M_{12}\left(R_{1}+R_{3}\right) \dot{U}_{\mathrm{s}}}{R_{1} R_{3}\left(R_{2}+R_{L}\right)+\left(R_{1}+R_{3}\right) \omega^{2} M_{12}^{2}} \end{array} \right.$ | (2) |
电源的输入功率Pin和负载的输出功率Pout分别为
| $\begin{aligned} P_{\text {in }} &=\operatorname{Re}\left[\dot{U}_{\mathrm{s}} \boldsymbol{I}_{1}+\dot{U}_{\mathrm{s}} \boldsymbol{I}_{3}\right] \\ & P_{\text {out }}=\left|\dot{I}_{2}\right|^{2} R_{L} \end{aligned}$ | (3) |
则系统传输效率ηm为
| $ \eta_{\mathrm{m}}=\frac{P_{\mathrm{out}}}{P_{\mathrm{in}}} $ | (4) |
将式(2)代入式(3)、式(4)可得负载的输出功率和系统传输效率的具体表达式为
| $ P_{\text {out }}=\frac{\omega^{2} K_{12}^{2} L_{1} L_{2} U_{\mathrm{s}}^{2} R_{L}}{\left[R_{\mathrm{m}}\left(R_{2}+R_{L}\right)+\omega^{2} K_{12}^{2} L_{1} L_{2}\right]^{2}} $ | (5) |
| $\eta_{\mathrm{m}}=\frac{1}{1+\frac{Q_{L}}{Q_{2}}\left[1+\frac{1}{\xi_{\mathrm{m}}^{2}}\left(1+\frac{Q_{2}}{Q_{L}}\right)^{2}\right]}$ | (6) |
其中:
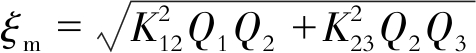
Rm=R1/(1+R1/R3)
式中:Kij——耦合系数,
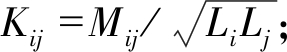
Qi——线圈的品质因素, Qi=ωLi/Ri;
QL——负载的品质因素, QL=ωL2/RL。
为便于比较, 这里一并给出典型单发射系统的接收功率与传输效率表达式。图 1中, 当只存在发射线圈1和接收线圈2时, 系统即为单发射结构, 其负载功率Ps和传输效率ηs分别为
| $ P_{\mathrm{s}}=\frac{\omega^{2} K_{12}^{2} L_{1} L_{2} U_{\mathrm{s}}^{2} R_{L}}{\left[R_{1}\left(R_{2}+R_{L}\right)+\omega^{2} K_{12}^{2} L_{1} L_{2}\right]^{2}} $ | (7) |
| $\eta_{\mathrm{s}}=\frac{1}{1+\frac{Q_{L}}{Q_{2}}\left[1+\frac{1}{\xi_{\mathrm{s}}^{2}}\left(1+\frac{Q_{2}}{Q_{L}}\right)^{2}\right]}$ | (8) |
其中:
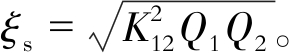
分别比较单发射和双发射两种结构系统的负载接收功率与传输效率。由式(5)和式(7)可以得出双发射结构与单发射结构负载功率的比值为
| $ \sqrt{\frac{P_{\text {out }}}{P_{\mathrm{s}}}}=1+\frac{\left(R_{1}-R_{\mathrm{m}}\right)\left(R_{2}+R_{L}\right)}{R_{\mathrm{m}}\left(R_{2}+R_{L}\right)+\omega^{2} K_{12}^{2} L_{1} L_{2}} $ | (9) |
比较式(5)和式(9)可以看出, 发射线圈的内阻R1 > 0, R3 > 0, 所以R1/R3 > 0, Rout < R1, 即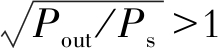 成立。因此, 相同情况下双发射结构负载所获得的功率大于单发射结构。
成立。因此, 相同情况下双发射结构负载所获得的功率大于单发射结构。
由式(6)和式(8)可以得出双发射结构与单发射结构传输效率的比值为
| $\frac{\eta_{\mathrm{m}}}{\eta_{\mathrm{s}}}=\frac{\left(Q_{2}+Q_{L}\right) \xi_{\mathrm{s}}^{2} \xi_{\mathrm{m}}^{2}+Q_{L}\left(1+\frac{Q_{2}}{Q_{L}}\right)^{2} \xi_{\mathrm{m}}^{2}}{\left(Q_{2}+Q_{L}\right) \xi_{\mathrm{s}}^{2} \xi_{\mathrm{m}}^{2}+Q_{L}\left(1+\frac{Q_{2}}{Q_{L}}\right)^{2} \xi_{\mathrm{s}}^{2}}$ | (10) |
当发射线圈和接收线圈的参数一致且接收线圈与两发射线圈的相对位置对称时, 存在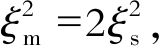 故式(10)可以化简为
故式(10)可以化简为
| $ \frac{\eta_{\mathrm{m}}}{\eta_{\mathrm{s}}}=1+\frac{Q_{L}\left(1+\frac{Q_{2}}{Q_{L}}\right)^{2}}{2\left(Q_{2}+Q_{L}\right) \xi_{\mathrm{s}}^{2}+Q_{L}\left(1+\frac{Q_{2}}{Q_{L}}\right)^{2}} $ | (11) |
发射线圈和接收线圈的品质因数Q2 > 0, Q3 > 0且K12≥0(发射线圈与接收线圈距离过大时取到等号), 因此,
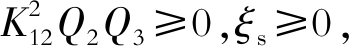 即(ηm/ηs) > 1成立。由式(9)和式(11)的证明可知, 较单发射线圈结构, 双发射线圈结构能提高系统的传输功率和传输效率。
即(ηm/ηs) > 1成立。由式(9)和式(11)的证明可知, 较单发射线圈结构, 双发射线圈结构能提高系统的传输功率和传输效率。
当系统耦合系数K12发生变化时, 线圈阻抗R和品质因数Q基本保持不变。由式(9)可知, 当发射线圈与接收线圈之间的耦合系数K12减小时,
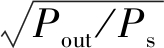 的值变大, 即Pout/Ps变大; 由式(11)可知, 随着K12的减小,
的值变大, 即Pout/Ps变大; 由式(11)可知, 随着K12的减小,
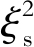 降低, ηout/ηs增大。说明当线圈之间的耦合系数越低时, 双发射结构提升负载功率和传输效率的优势越明显, 也间接证明了其能量传输范围更大。
降低, ηout/ηs增大。说明当线圈之间的耦合系数越低时, 双发射结构提升负载功率和传输效率的优势越明显, 也间接证明了其能量传输范围更大。
因此, 在系统耦合系数较低时, 可利用双发射线圈结构代替单发射线圈结构, 以提高系统的负载功率和传输效率。负载功率与传输效率的大小是由多种因素决定的, 其中线圈之间的相对位置是主要因素之一。本文主要探讨接线线圈发生横向偏移和角度偏转两种情况下负载功率与传输效率的大小。
2 模型计算与特性分析
采用上述电路理论模型来分析计算磁耦合谐振式WPT系统发射线圈和接收线圈之间耦合系数的变化规律、系统的传输效率以及不同传输区域的特性, 同时, 利用有限元法数值分析软件HFSS对电路模型进行计算和验证。
2.1 耦合系数特性分析
首先建立无线电能传输模型。发射线圈和接收线圈均采用平面螺旋线圈结构, 且尺寸和其他参数均保持一致。其中, 线宽w=1 mm, 匝数n=6, 线间距g=5 mm, 最大半径r=9.25 cm, 线圈电感L=15.76 μH, 电容C=3.547 pF, 线圈接口处串联电容C=50 pF, 使系统谐振频率设计在14.5 MHz。发射线圈与接收线圈上分别设置集中端口, 且端口阻抗设置为50 Ω, 发射线圈与接收线圈同轴且水平距离为12 cm, 电源频率与系统谐振频率相同。
双发射系统中接收线圈从0 cm逐渐偏移到7 cm时耦合系数K的理论值[17-18]与仿真计算值的变化情况如表 1所示。表 1中, d表示接收线圈水平偏移的距离。
表 1
接收线圈水平偏移时的耦合系数
| d/cm | K | d/cm | K | |||
| 仿真值 (10-2) |
理论值 (10-2) |
仿真值 (10-2) |
理论值 (10-2) |
|||
| 0 | 8.09 | 7.84 | 4 | 6.83 | 6.49 | |
| 1 | 7.90 | 7.62 | 5 | 6.31 | 6.03 | |
| 2 | 7.65 | 7.28 | 6 | 5.69 | 5.46 | |
| 3 | 7.29 | 6.91 | 7 | 5.03 | 4.66 | |
接收线圈的偏转角度θ从0°到90°逐渐偏转, 每隔10°记录一次数据, 得到耦合系数的理论值与仿真计算值如表 2所示。
表 2
接收线圈轴向偏转时的耦合系数
| θ/(°) | K | θ/(°) | K | |||
| 仿真值 (10-2) |
理论值 (10-2) |
仿真值 (10-2) |
理论值 (10-2) |
|||
| 0 | 8.09 | 7.84 | 50 | 7.53 | 6.25 | |
| 10 | 8.04 | 7.52 | 60 | 6.64 | 5.89 | |
| 20 | 7.99 | 7.21 | 70 | 4.90 | 4.08 | |
| 30 | 8.05 | 6.96 | 80 | 2.62 | 1.99 | |
| 40 | 7.95 | 6.74 | 90 | 0 | 0 | |
对于双发射结构, 不论接收线圈发生水平偏移还是角度偏转, 其与两个发射线圈的相对位置保持不变, 始终满足K12=K23。
由表 1和表 2可以看出, 在误差允许范围内, 理论值与数值计算结果基本一致, 验证了本文所建立模型的正确性。由表 1可知, 偏移距离越大, 耦合系数的下降就越快, 偏移1 cm时K仅下降2.35%, 但偏移7 cm时, K下降了37.82%。由表 2可知, 接收线圈偏转角度θ≤40°时, K的下降率保持在1.56%以内, 变化不大; 当θ > 40°时, K最低下降了6.9%;当θ为90°时, K为零, 此时系统耦合最低, 传输效率最低。
2.2 系统传输效率分析
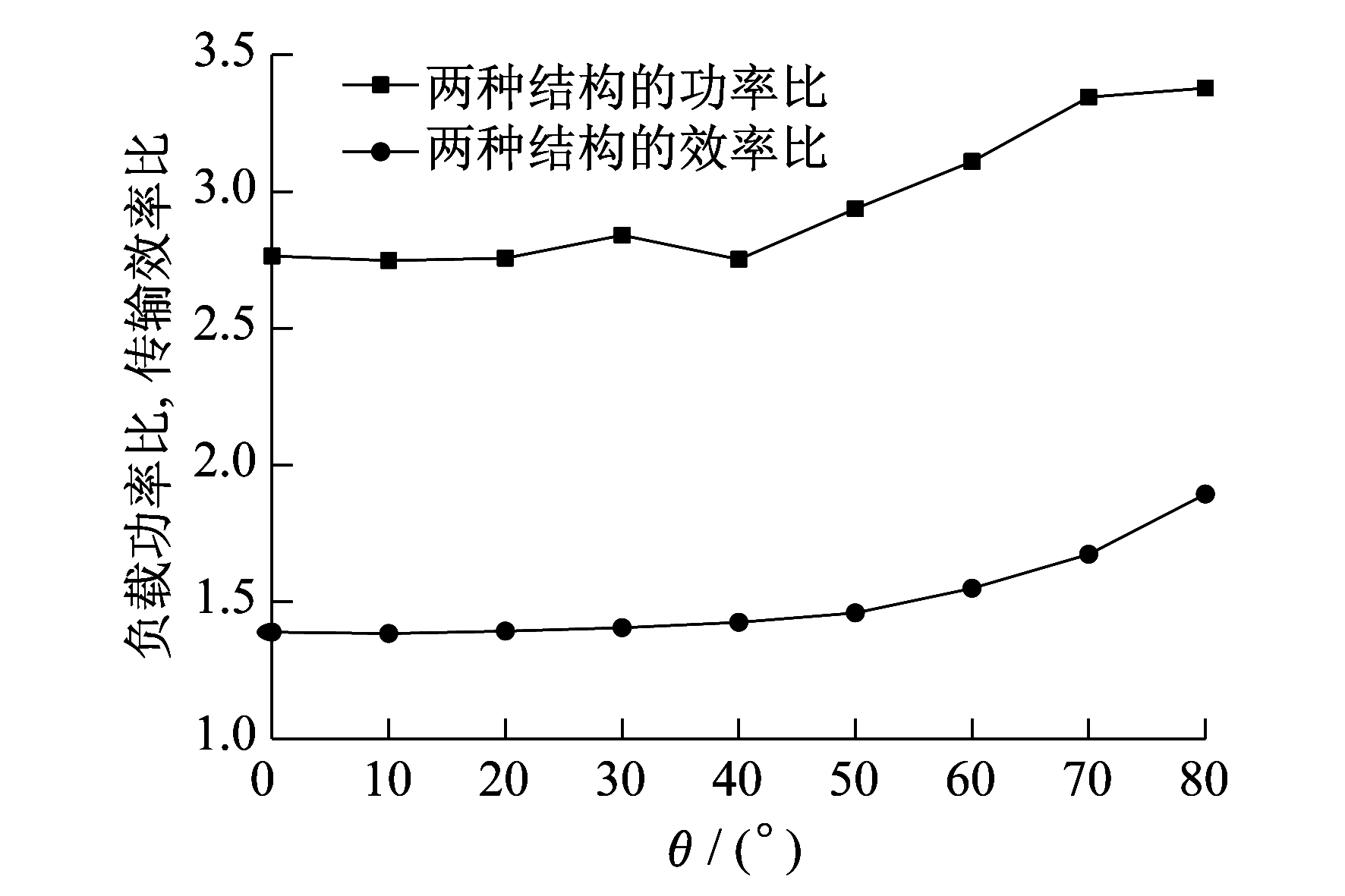
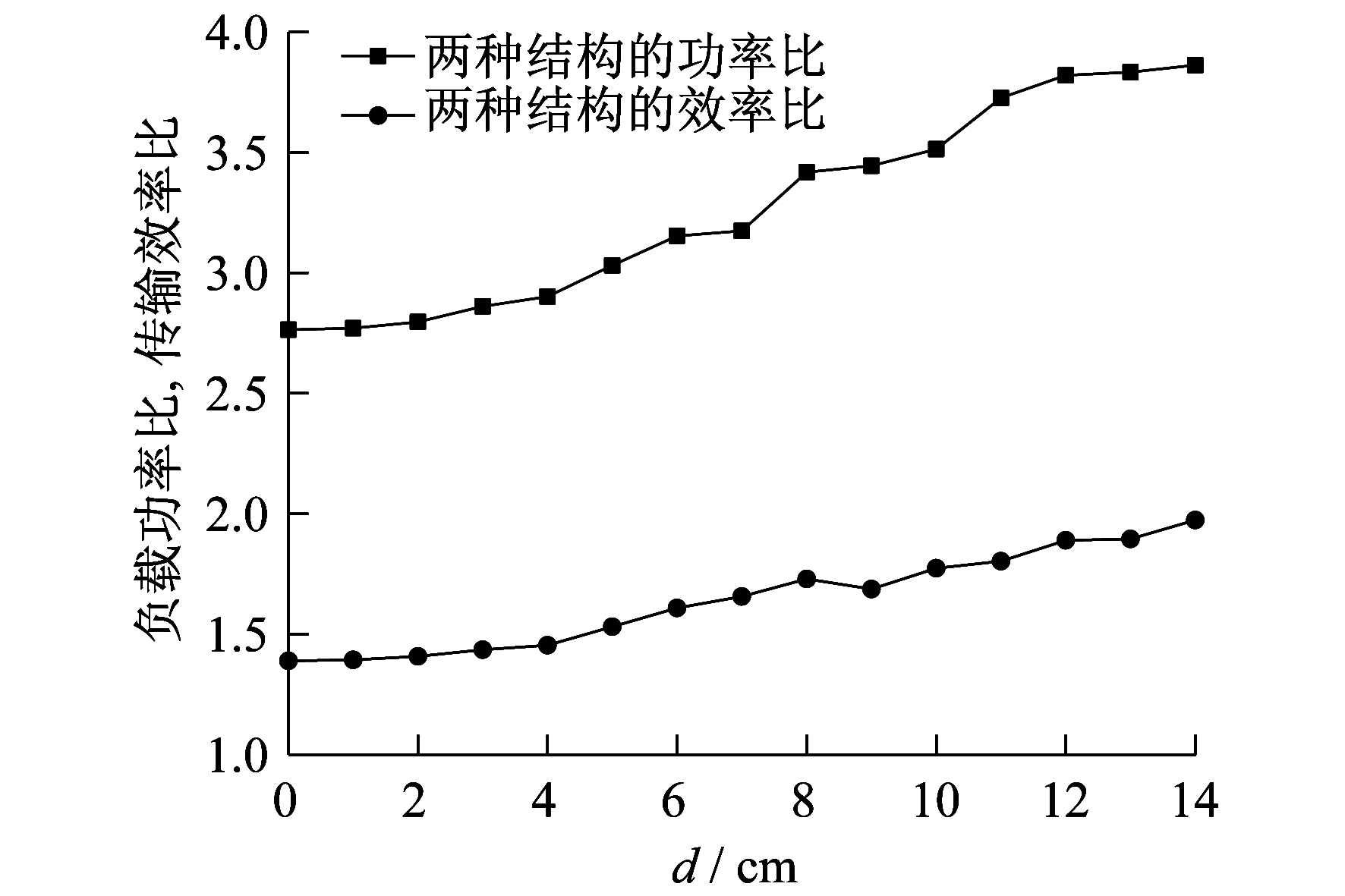
分别计算单发射线圈结构和双发射线圈结构的接收线圈在横向偏移和角度偏转情况下的负载功率与传输效率并对应求比值, 得到的曲线如图 3和图 4所示。其中, 接收线圈偏转到90°时, 两种结构获得的功率和效率都为零, 即此时发射线圈和接收线圈之间的耦合系数为零, 所以图 3只给出了0°到80°的比值。
由图 3可知, 当接收线圈从0°逐渐偏转到50°时, 双发射线圈结构负载获得的功率约是单发射线圈结构负载功率的2.8倍; 在60°偏转到90°的过程中, 功率差距逐渐加大, 偏转至90°时功率比值达到3.3。相较于功率比的变化而言, 效率比的变化较为平缓, 其中在0°~40°之内, 效率比保持在1.39左右, 随着线圈偏转角度的增加, 效率比逐渐增大到1.89。由图 4可知, 随着线圈偏移距离的逐渐增加, 两种结构的传输效率比增大较缓慢, 而负载功率比增大显著; 当线圈偏移距离达到14 cm时, 两种结构获得的功率差距最大, 比值达到3.86。
随着偏移距离和偏转角度的增加, 系统功率比和效率比均逐渐增加。对比图 3和图 4可知, 线圈偏移距离对系统功率比的影响大于线圈角度偏转的影响, 但效率比基本相同。由此可以看出, 当发射线圈与接收线圈之间的耦合系数变化且功率比和效率比均为正数时, 说明双发射线圈结构的负载功率和传输效率都优于单发射线圈结构。结合表 1和表 2的分析可知, 随着线圈间耦合系数的降低, 功率与效率的比值越大, 双发射线圈结构的优势就越明显。
3 系统传输区域分析
对于磁耦合谐振式无线电能传输系统, 双发射无线电能传输结构可根据线圈间的距离变化将系统耦合区域划分为欠耦合、临界耦合和过耦合3种区域[19-20](仅考虑两发射线圈是关于接收线圈的对称结构)。为了更全面地了解双发射线圈结构与单发射线圈结构的传输特性, 对两种结构在上述3种区域中的传输特性进行了分析。
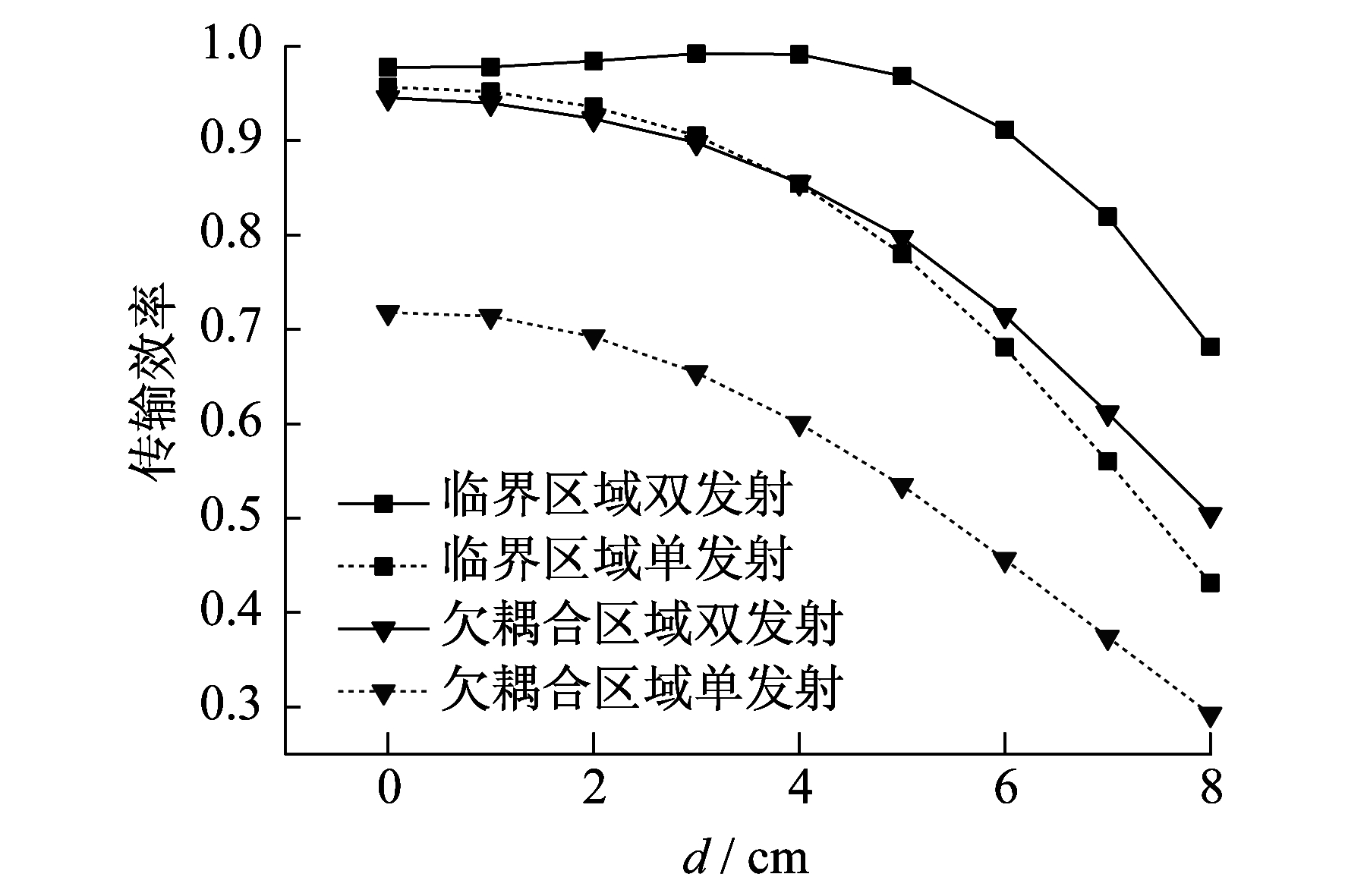
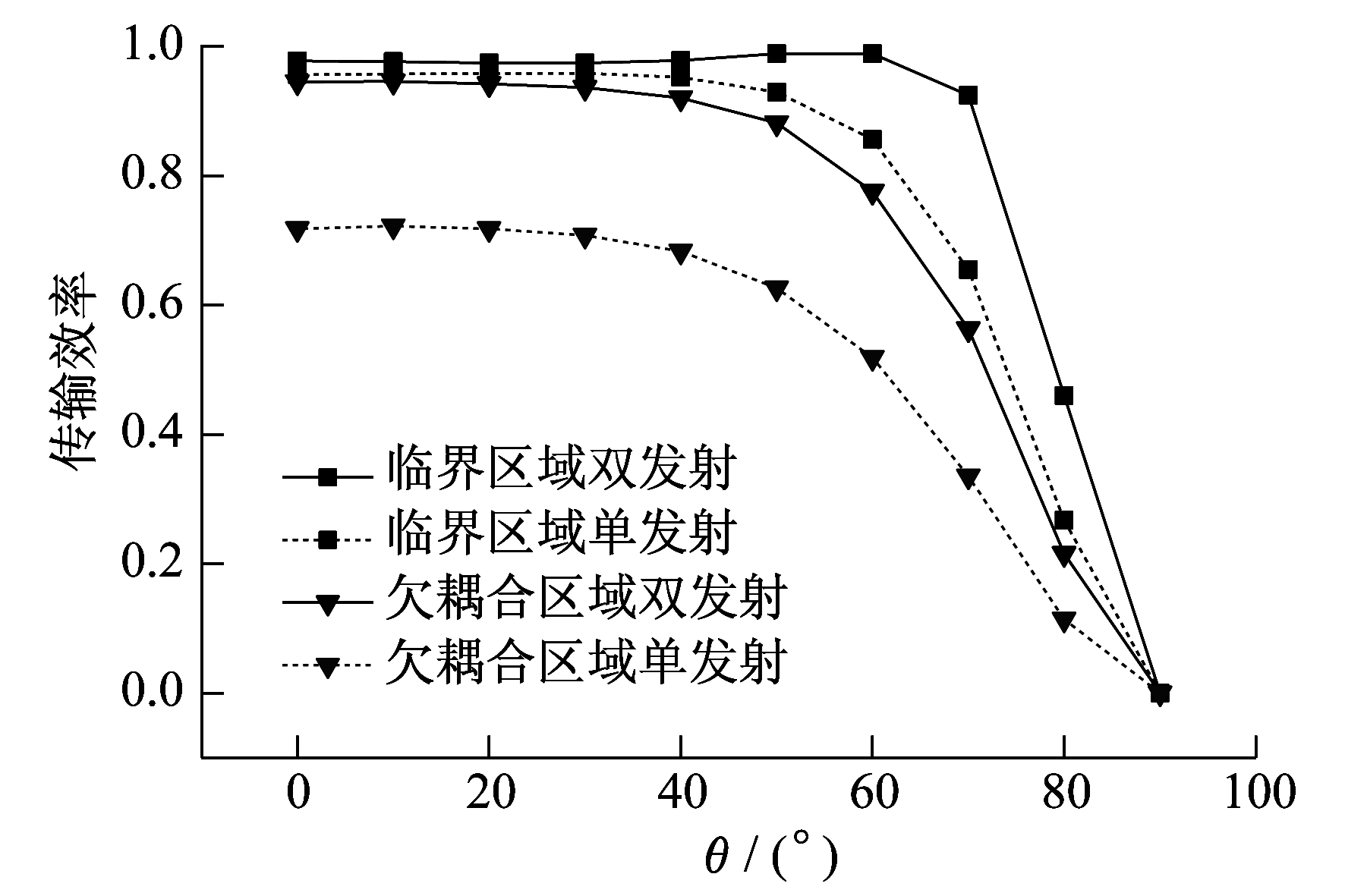
图 5和图 6分别为系统处于欠耦合(d13=d23=14 cm)和临界耦合(d13=d23=11 cm)状态下, 两种结构接收线圈发生横向偏移和角度偏转时的传输效率曲线。
由图 5和图 6可知, 在临界耦合区域内, 当双发射线圈结构的接收线圈偏移0~6 cm或偏转0°~70°时, 传输效率都保持在0.9以上; 而对于单发射结构, 相同效率只允许发生0~3 cm的偏移距离或0°~50°的偏转角度。这说明双发射结构可以有效扩大系统的横向传输范围, 同时也提高了传输方向的灵活性。
相比临界耦合区域中的传输效率, 在欠耦合区域中, 接收线圈发生偏移或偏转时, 双发射结构的平均效率分别降低0.14和0.16, 单发射结构的平均效率分别下降0.29和0.34。由此可见, 随着接收线圈偏移距离和偏转角度的增加, 双发射结构的传输稳定性更好。
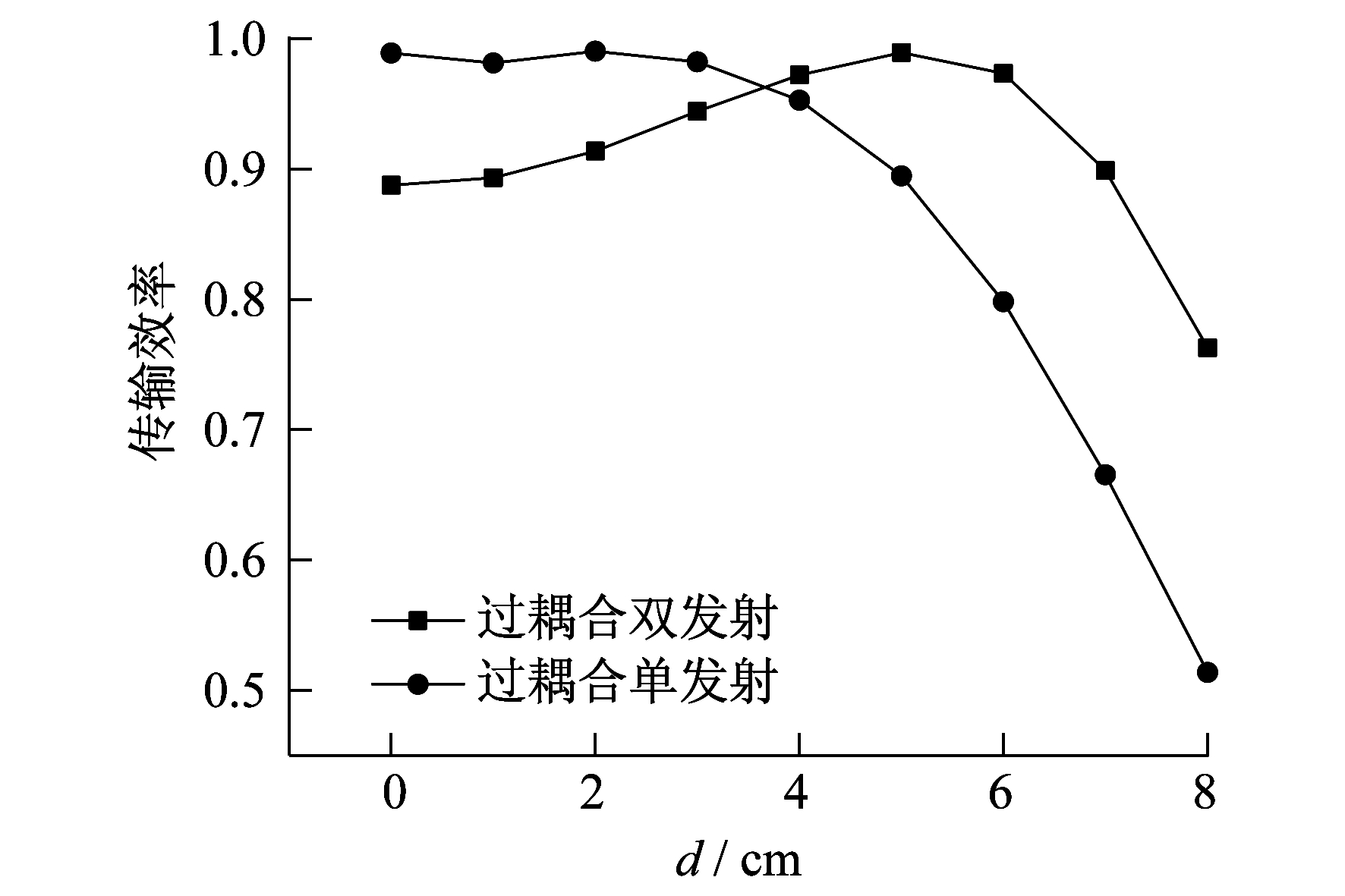
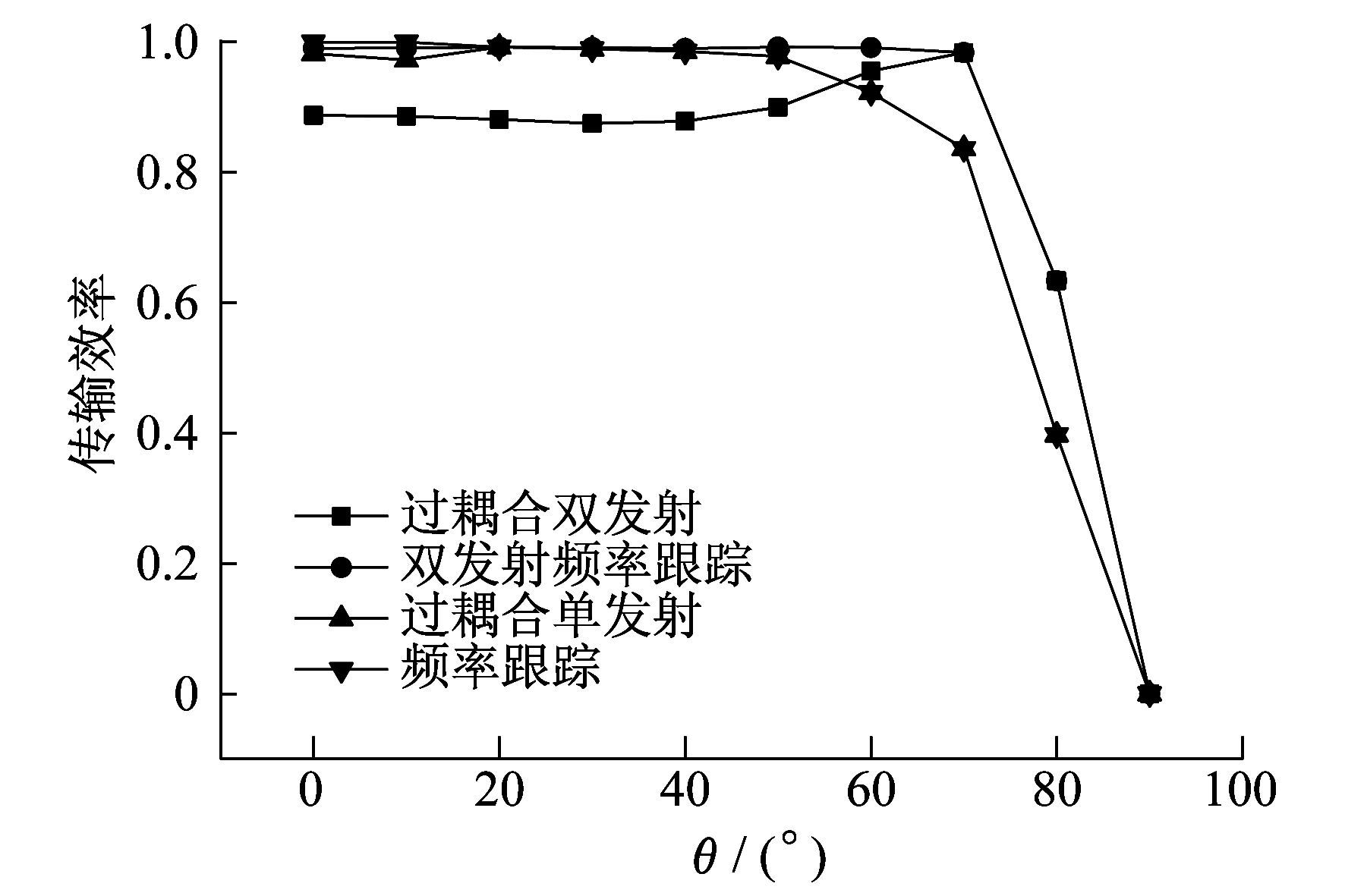
图 7和图 8分别为过耦合区域(d13=d23=9 cm)中, 两种结构的传输效率变化情况。
由图 7和图 8可知, 当接收线圈发生偏移或者偏转时, 双发射线圈结构的效率都是先增大后减小, 且当偏移距离和偏转角度分别小于3.7 cm和58°时, 单发射线圈的传输效率高于双发射线圈的传输效率; 当大于3.7 cm和58°时, 单发射线圈的传输效率低于双发射线圈的传输效率。
4 结论
本文采用等效电路方法建立了双发射结构磁谐振式无线电能传输系统的互感模型, 对系统的耦合系数特性、传输效率以及传输区域特性进行了分析, 并与常规单发射结构进行了比较, 结论如下:
(1) 相比单发射结构, 双发射结构可以提高系统的负载接收功率和传输效率, 而且随着耦合系数的降低, 双发射结构的优势更加明显;
(2) 双发射结构可以增大系统的纵向传输距离;
(3) 临界耦合区域内, 双发射结构可以有效扩大系统的横向传输范围, 传输方向性更加灵活。
参考文献
-
[1]考虑环境温度的电动汽车充电负荷预测[J]. 上海电力学院学报, 2017, 33(2): 138-144.
-
[2]无线电能传输技术的研究现状与应用[J]. 中国电机工程学报, 2015, 35(10): 2584-2600.
-
[3]无线电能传输技术研究与应用综述[J]. 电工技术学报, 2013, 28(10): 1-11. DOI:10.3969/j.issn.1000-6753.2013.10.001
-
[4]ZHANG F, HACKWORTH S A, FU W, et al. Relay effect of wireless power transfer using strongly coupled magnetic resonances[J]. IEEE Transactions on Magnetics, 2011, 47(5): 1478-1481. DOI:10.1109/TMAG.2010.2087010
-
[5]ZHANG F, LIU J, MAO Z, et al. Mid-range wireless power transfer and its application to body sensor networks[J]. Open Journal of Applied Sciences, 2012, 2(1): 35-46. DOI:10.4236/ojapps.2012.21004
-
[6]吕玥珑.磁耦合谐振式无线能量传输特性研究[D].哈尔滨: 哈尔滨工业大学, 2014.
-
[7]URZHUMOV Y, SMITH D R. Metamaterial-enhanced coupling between magnetic dipoles for efficient wireless power transfer[J]. Physical Review B Condensed Matter, 2011, 83(20): 99-105.
-
[8]车邦军.基于扫描磁场的全向无线能量传输方法研究[D].哈尔滨: 哈尔滨工业大学, 2014.
-
[9]UCHIDA A, SHIMOKAWA S, KAWANO H, et al. Phase and intensity control of multiple coil currents in resonant magnetic coupling[C]// Microwave Workshop Series on Innovative Wireless Power Transmission: Technologies, Systems, and Applications, IEEE, Kyoto, Japan, 2012: 53-56.
-
[10]UCHIDA A, SHIMOKAWA S, KAWANO H, et al. Phase and intensity control of multiple coil currents in mid-range wireless power transfer[J]. IET Microwaves Antennas & Propagation, 2014, 8(7): 498-505.
-
[11]ISHIZAKI T, NOJIRI S, ISHIDA T, et al. 3-D free-access WPT system for charging movable terminals[C]//Microwave Workshop Series on Innovative Wireless Power Transmission: Technologies, Systems, and Applications, IEEE, Kyoto, Japan, 2012: 219-222.
-
[12]LEE K, CHO D H. Diversity analysis of multiple transmitters in wireless power transfer system[J]. IEEE Transactions on Magnetics, 2013, 49(6): 2946-2952. DOI:10.1109/TMAG.2012.2234132
-
[13]四线圈激励共振式无线电能传输系统及其研究分析[J]. 电力系统自动化, 2015(16): 108-114. DOI:10.7500/AEPS20141225006
-
[14]HAUS H A, HUANG W. Coupled-mode theory[J]. Proceedings of the IEEE, 1991, 79(10): 1505-1518. DOI:10.1109/5.104225
-
[15]PATEL R, RAGHUWANSHI M M, JAISWAL A N. Modifying genetic algorithm with species and sexual selection by using K-means algorithm[C]//IEEE International. Advance Computing Conference, Patiala, India, 2009: 114-119.
-
[16]磁耦合谐振系统中的两种模型对比探究[J]. 电工技术学报, 2013(增刊2): 13-17.
-
[17]磁耦合谐振式无线电能传输系统存在干扰因素下的频率特性研究[J]. 电工电能新技术, 2015, 34(4): 24-30. DOI:10.3969/j.issn.1003-3076.2015.04.005
-
[18]ZHAO J, HUANG X, WANG W. Wireless power transfer with two-dimensional resonators[J]. IEEE Transactions on Magnetics, 2014, 50(1): 1-4.
-
[19]XUE M, YANG Q. Research of frequency characteristics in wireless power transfer system via magnetic resonance coupling under interference factors[J]. Adv Technol Electr Eng Energy, 2015, 34(4): 24-30.
-
[20]XIA N, TIAN M, LIAN H, et al. Analysis of effective transmission distance of double transmitters in magnetic coupled resonant WPT system[C]//International Conference on Intelligent Computing for Sustainable Energy and Environment, Nanjing, China, 2017: 686-694.