|
|
|
发布时间: 2019-08-10 |
|
|
|
|
收稿日期: 2018-04-18
中图法分类号: TM93;TM312
文献标识码: A
文章编号: 1006-4729(2019)04-0315-06
|
摘要
针对低压微电网分层控制系统, 提出了一种基于ZigBee通信网络的半实物仿真方案。利用MATLAB/Simulink构建了低压微电网系统模型及其二层控制架构, 其中二层控制架构的通信网络由ZigBee实物节点搭建。整个仿真系统可以保证分布式能源(DGs)的有功按比例输出。ZigBee实物节点之间采用点对点通信方式, 并结合Simulink串口模块和MATLAB的S函数编程实现了实际控制信号的传递。实验结果验证了所构建的半实物仿真方案的可行性和有效性。
关键词
低压微电网; 分层控制; ZigBee装置; 半实物仿真
Abstract
Aiming at the hierarchical control system of low-voltage microgrid, a semi-physical simulation scheme over ZigBee communication network is proposed.The low-voltage microgrid system model and its two-layer control architecture are constructed by using MATLAB/Simulink, in which the communication network of the two-layer control structure is constructed by ZigBee physical node.The simulation system can guarantee the active power of distributed generations(DGs) output proportional.The communication between ZigBee physical nodes is point to point, witch is combined with the Simulink serial module and S-function of Matlab programming to achieve the transmission of the actual control signal.Finally, the experimental results verify the feasibility and effectiveness of the constructed semi-physical simulation.
Key words
low-voltage microgrid; hierarchical control; ZigBee device; semi-physical simulation
微电网是分布式能源(Distributed Generations, DGs)组网的最有效形式, 既能并网运行, 也能独立运行[1-2]。在低压微电网中, DGs常采用有功功率-幅值(P-V)和无功功率-频率(Q-f)的阻性下垂控制方式[3]。由于输电线路的阻抗不同, 使得DGs间有功功率输出不能按预定比例精确输出, 同时微电网系统的电能质量存在偏差, 所以微电网控制系统一般采用分层控制来实现功率分配策略和电能质量补偿[4]。
依据通信形式的不同, 微电网系统控制策略包括集中控制[5]、分散控制[6]和分布式控制[7-8]3种。集中控制是通过收集各个DGs的本地信息, 经过中心控制器来实现对微电网系统的整体控制, 但其通信量较大。分散控制中, 各个DGs依据本地信息实现自我控制, 无需通信网络, 但有时难以实现系统级的调节。分布式控制只需DGs间建立稀疏通信网络, 就能够实现对微电网系统的控制, 不但减少了通信量, 而且提高了通信的可靠性和安全性, 在微电网中的应用越来越广泛, 其通常采用多智能体方式来实现[9-10]。
由于多智能体类嵌入式设备的应用, 使得微电网系统向智能化发展, 电力网络和信息网络的交互机理变得日益复杂, 被称为信息物理系统(Cyber-physical System, CPS)[11]。微电网系统由物理系统(一次系统)和控制系统(二次系统)两部分构成, 对应电力CPS中的物理系统和信息系统(其中信息系统又分为信息处理和信息通信两部分)[12]。文献[13]提出了一种采用有限状态机(Finite Stste Machine, FSM)和混合逻辑动态模型(Mixed Logical Dynamical, MLD)两种混合系统模型对电网进行一次、二次系统建模, 然而缺少具体的仿真和应用案例。文献[14]在CPS的基础上, 设计了基于MATLAB/Simulink的电力系统和通信仿真软件OPNET的主从式电力CPS协同仿真平台, 都是基于软件实现电力CPS仿真。本文基于MATLAB/Simulink构建了低压微电网系统, 并将实际物理ZigBee通信网络用于系统通信, 构建半实物仿真。该半实物仿真对电力CPS的研究具有一定的借鉴意义。
1 低压微电网系统
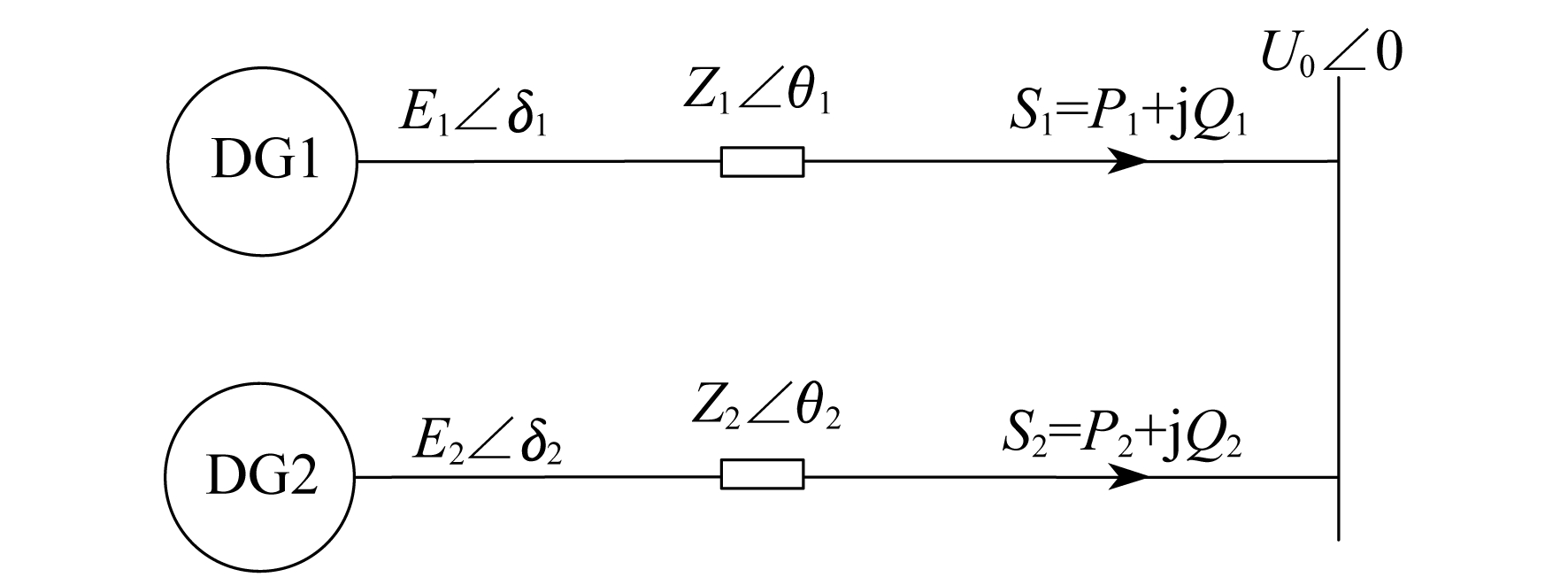
图 1为低压微电网中两个并联DG功率传输的简化图。DG1与DG2同理, 以DG1为例, E1∠δ1是DG1的逆变器经滤波后得到的线路始端电压, E1为电压有效值, δ1为电压相位, 通常情况下功角差δ1很小, 即sin δ1≈δ1, cos δ1≈1; U0为母线电压有效值, 电压相位为0; Z1∠θ1=R1+jX1为DG1与母线间的线路阻抗。
在低压微电网中线路阻抗主要呈现阻性[3], Z1≈R1, θ1≈0°。S1=P1+jQ1为线路传输的末端单相复功率, P1和Q1分别表示有功功率和无功功率, 公式为
| $P_{1}=\frac{E_{1}}{Z_{1}}\left[\left(E_{1}-U_{0} \cos \delta_{1}\right) \cos \theta_{1}\right. \\ \left.+U_{0} \sin \delta_{1} \sin \theta_{1}\right] \approx \frac{E_{1}\left(E_{1}-U_{0}\right)}{R_{1}}$ | (1) |
| $Q_{1}=\frac{E_{1}}{Z_{1}}\left[\left(E_{1}-U_{0} \cos \delta_{1}\right) \sin \theta_{1}-\right. \\ \left.U_{0} \sin \delta_{1} \cos \theta_{1}\right] \approx-\frac{E_{1} U_{0}}{R_{1}} \delta_{1}$ | (2) |
DG1采用P-V和Q-f下垂控制[2], 公式为
| $E_{\mathrm{refl}}=E_{\mathrm{N} 1}+m_{\mathrm{p} 1}\left(P_{\mathrm{N} 1}-P_{\mathrm{R} 1}\right)$ | (3) |
| $f_{\mathrm{ref1}}=f_{\mathrm{N} 1}+m_{\mathrm{q} 1} Q_{\mathrm{R} 1}$ | (4) |
式中:Eref1, fref1——DG1下垂控制得到的电压参考值和频率参考值;
mp1, mq1——DG1的P-V和Q-f下垂系数;
EN1, fN1——DG1的额定电压值和额定频率值;
PN1——DG1的额定有功功率值;
PR1, QR1——DG1输出的实际有功功率和无功功率。
运用文献[15]中的功率分配方法对低压微电网系统中DGs的输出功率和微电网系统的电能质量进行调节。引入二层控制对DGs输出的有功功率进行调节, 通过获取两条母线上的电压信息, 求取全网平均电压Uavg, 利用下式对DGs进行PI调节
| $ \Delta E_{\mathrm{p}}=\left(k_{\mathrm{p}}+\frac{k_{\mathrm{i}}}{s}\right)\left(E_{\mathrm{ref}}-U_{\mathrm{avg}}\right) $ | (5) |
式中:ΔEp——本地控制电压偏差调节量;
kp, ki——PI控制器的调节参数。
同时, 保证母线电压和频率质量, 对偏差进行PI调节
| $ \Delta E_{\mathrm{v}}=\left(k_{\mathrm{vp}}+\frac{k_{\mathrm{vi}}}{s}\right)\left(E_{\mathrm{N}}-U_{\mathrm{avg}}\right) $ | (6) |
| $\Delta f=\left(k_{\mathrm{fp}}+\frac{k_{\mathrm{fi}}}{s}\right)\left(f_{\mathrm{N}}-f_{\mathrm{avg}}\right)$ | (7) |
式中:ΔEv, Δf——DGs二层控制电压偏差调节量和频率偏差调节量;
kvp, kvi——电压控制器的PI调节参数;
kfp, kfi——频率控制器的PI调节参数;
favg——全网的平均频率。
DGs二层控制输出的两个调节量为ΔE=ΔEp+ΔEv和Δf。
2 ZigBee通信网络
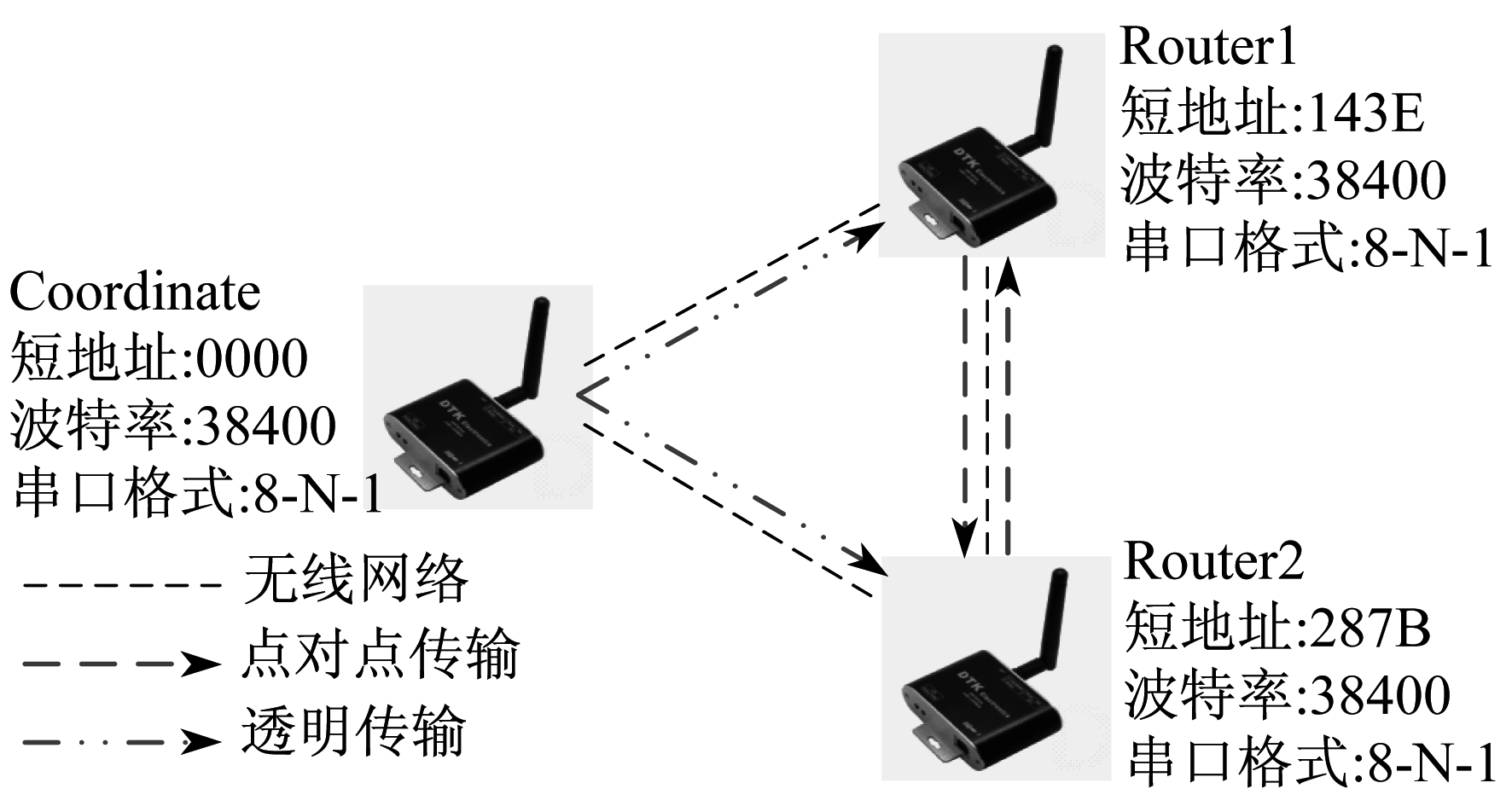
ZigBee是无线通信技术的一种, 具有自组织、低成本等特点[16-17]。本文采用中鼎泰克电子生产的型号为DRF2618A的ZigBee装置, 数据传输模式如图 2所示。图 2中, 3个ZigBee装置构成了通信网络, 其中一个ZigBee通信装置为协调器(Coordinate), 短地址为0000, 波特率为38 400 bps, 串口格式中数据位为8位, 无奇偶校验位, 停止位为1, 另外两个ZigBee通信装置为路由器(Router), 短地址分别为143E和287B, 其他参数与协调器设置相同。
ZigBee装置的数据传输方式分为透明传输模式和点对点传输模式。透明传输模式下, 协调器发出的数据全部透明传输到路由器, 所有路由器都可收到; 某个路由器发出的数据, 透明传输到协调器, 只有协调器收到。点对点传输模式下, 协调器发送数据给某个特定的路由器; 某个路由器发送数据给某个特定的路由器。
本文采用两个路由器点对点互传的方式。发送指令的格式为:数据传送指令(0xFD)+数据长度+目标地址+数据(最多32Bytes)。如果Router1发送的指令为:FD 04 28 7B 01 02 03 04, 则Router2接收到的数据为:FD 04 00 01 01 02 03 04 14 3E, 其中FD表示数据传输指令, 04表示数据区的长度为4个字节, 28 7B表示目标短地址, 01 02 03 04表示数据, 14 3E表示发送方的短地址, 即数据来源地址。
3 半实物仿真平台的搭建
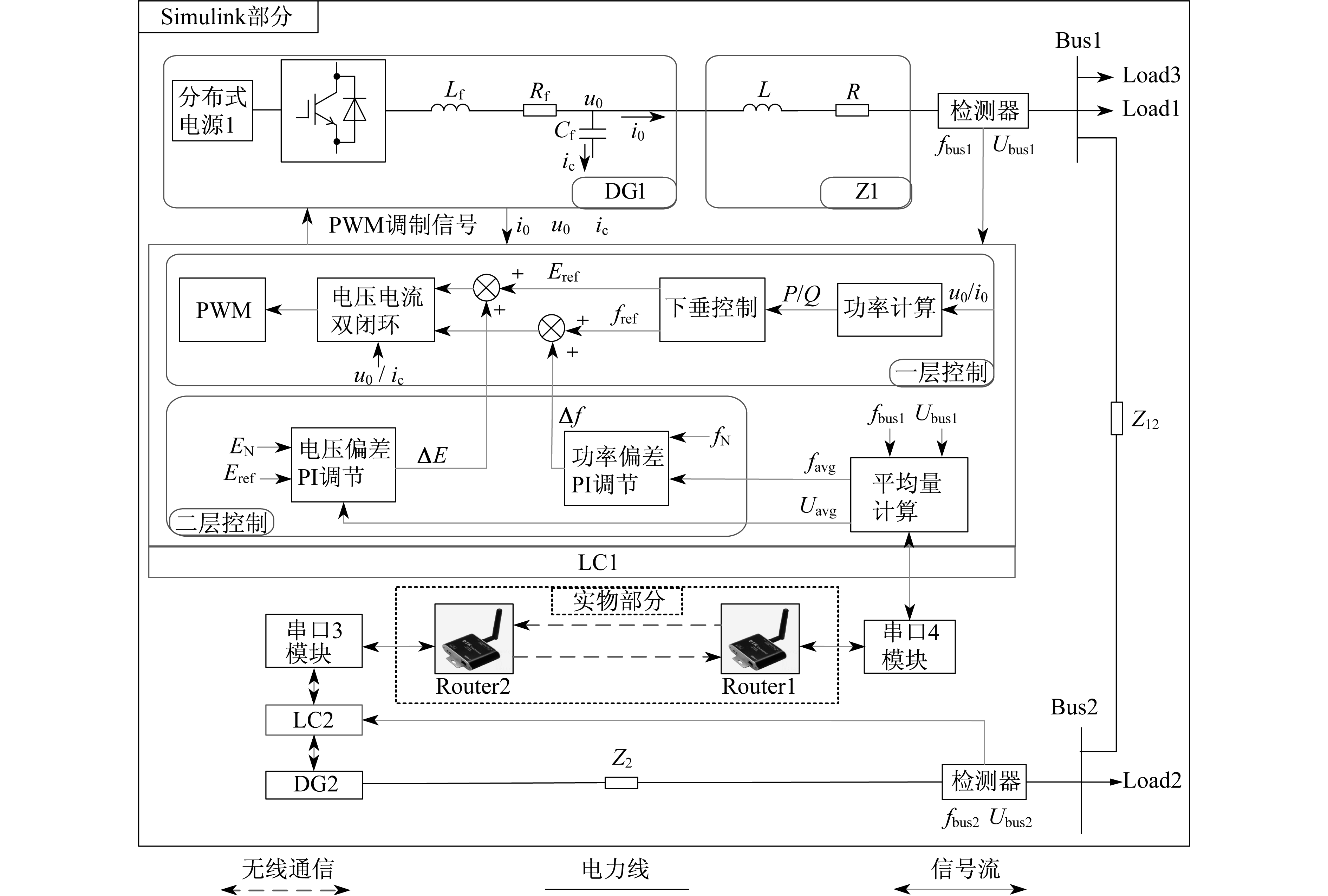
半实物仿真原理图包括软件部分和实物部分, 如图 3所示。利用仿真软件MATLAB/Simulink搭建低压微电网系统:微电网由2个DG组成, 每个DG都有一个本地控制器(Local Controller, LC), LC中包含一层控制、二层控制和平均量计算3个功能, 其中一层控制由功率计算、下垂控制、电压电流双闭环控制和脉冲宽度调制(Pulse Width Modulation, PWM)控制4部分组成。软件与硬件通过串口进行通信, 采用Simulink仪器控制工具箱(Instrument Control Toolbox)中的Serial Configuration, Serial Send和Serial Receive模块组[18]实现驱动。Serial Configuration模块用于配置串行口串口号、数据传输的波特率、数据位数、奇偶校验模式等参数; Serial Send模块用于向串口发送二进制数据; Serial Receice模块用于串口的数据接收。本文将PC的串口3与Router2连接, 串口4与Router1连接, ZigBee装置通过无线通信网络连接。
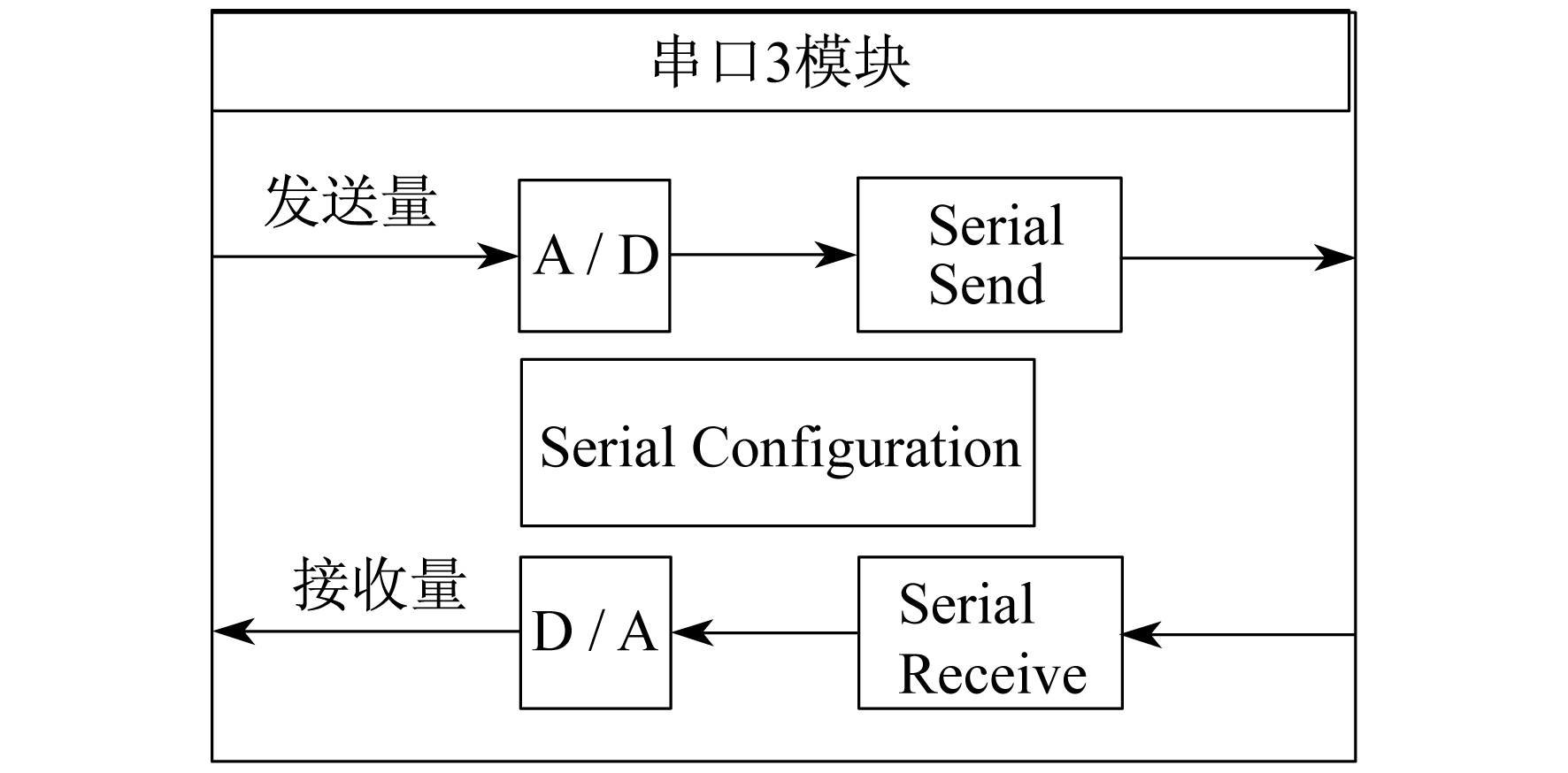
串口3模块示意图如图 4所示。模块Serial Configuration用于配置串行口通信协议。串行口通信协议设定与所连的ZigBee装置参数设置相同, 串行口相关参数设置见表 1。
表 1
串行口参数示意
| 串行口 | 波特率/bps | 数据位 | 停止位 | 奇偶校验位 |
| Com4 | 38400 | 8 | 1 | 无 |
| Com3 | 38400 | 8 | 1 | 无 |
由于ZigBee装置间数据传送为数字量, 在数据传送之前对其进行模数(A/D)转换, 接收成功后再次进行模数(D/A)转换, 采用S-Function编程实现。微电网系统交换的信息为母线电压值和频率值, 设置A/D转换中电压值和频率值分别对应数据发送的第5和第6字节以及第7和第8字节的十六进制数据。设精度值为0000~F000, S-Function相关程序如下:
function sys=mdlOutputs(t, x, u)
global temp1;
global temp2;
temp1=fix(u(1)×65535/400);
temp2=fix(u(2)×65535/60);
output1=[fix(temp1/256), mod(temp1, 256)];
output2=[fix(temp2/256), mod(temp2, 256)];
if abs(round(t/0.001)-t/0.001) < 1e-8
sys =[253 4 20 62 output1 output2];
else
sys =[];
end
其中, 全局变量temp1和temp2分别代表电压值和频率值, 构建的低压微电网系统的电压值变动范围为0~400 V, 频率值波动范围为0~60 Hz。将电压和频率转换为精度值65 535条件下的数值后, 通过高低位分离转化为十六进制数, 通过if语句每隔0.001 s将控制命令发送给串口连接的ZigBee装置。
设置D/A转换中电压值和频率值分别对应数据接收的第5和第6字节以及第7和第8字节的十六进制数据。其S-Function相关程序如下:
function sys=mdlOutputs(t, x, u)
global temp1;
global temp2;
temp1=u(5)*256+u(6);
temp2=u(7)*256+u(8);
output1=temp1*400/65535;
output2=temp2*60/65535;
sys =[output1 output2];
其中, 全局变量temp1和temp2分别代表电压值和频率值, 从串口连接的ZigBee装置接收数据, 分别取第5和第6字节以及第7和第8字节的高低位合成十六位的电压值和电流值, 再通过数据转化为十进制的电压值和电流值, 然后传送到LC中。串口4模块的设定情况同理。
图 5为综合实验仿真环境图。通过软件MATLAB与实物ZigBee装置构建起半实物仿真平台, 能更好地模拟实际情况, 相比于传统数值仿真更具真实性和说服力。
4 实验仿真
低压微电网系统含2个DG, 2个母线Bus和3个负荷, 系统参数如表 2和表 3所示。
表 2
DG模型参数
| DG | mp/ [V·(kW)-1] |
mq/ [Hz·(kW)-1] |
PN/ kW |
Qmax/ kW |
| 1 | 1.50 | 1.25e-2 | 10 | 40 |
| 2 | 0.75 | 1.25e-2 | 20 | 40 |
表 3
线路和负荷参数
| 负荷 | 参数值/kW | 阻抗 | 参数值/Ω |
| Load1 | 15+j10 | Z1 | 0.3+j0.063 |
| Load2 | 10+j15 | Z2 | 0.2+j0.031 |
| Load3 | 8+j8 | Z12 | 0.04+j0.0063 |
其中:Z1和Z2分别为DG1和DG2与相应母线Bus1和Bus2之间的线路阻抗; Z12为母线Bus1和母线Bus2间的连接阻抗; Load1和Load2为母线Bus1上的连接负荷, Load3为母线Bus2上的连接负荷; 两个DG额定有功功率比设置为PN1:PN2=1:2, 两个DG最大允许输出无功功率比为Qmax1:Qmax2=1:1。额定电压设置为EN=311 V(相电压峰值), 额定频率设置为fN=50 Hz。设置仿真实验的时间为2 s, 在0~0.5 s运行时不加入二层控制, 在0.5~1 s运行时加入二层控制, 在1~1.5 s运行时切除负荷Load3, 在1.5~2 s运行时重新加入负荷Load3。
实验仿真有3种情况:第1种为结合ZigBee装置的半实物仿真; 第2种为完全采用Simulink建模仿真; 第3种为在第2种情况中考虑传递延时1 ms(与半实物仿真中S-Function编程时每隔1 ms输出相对应)。
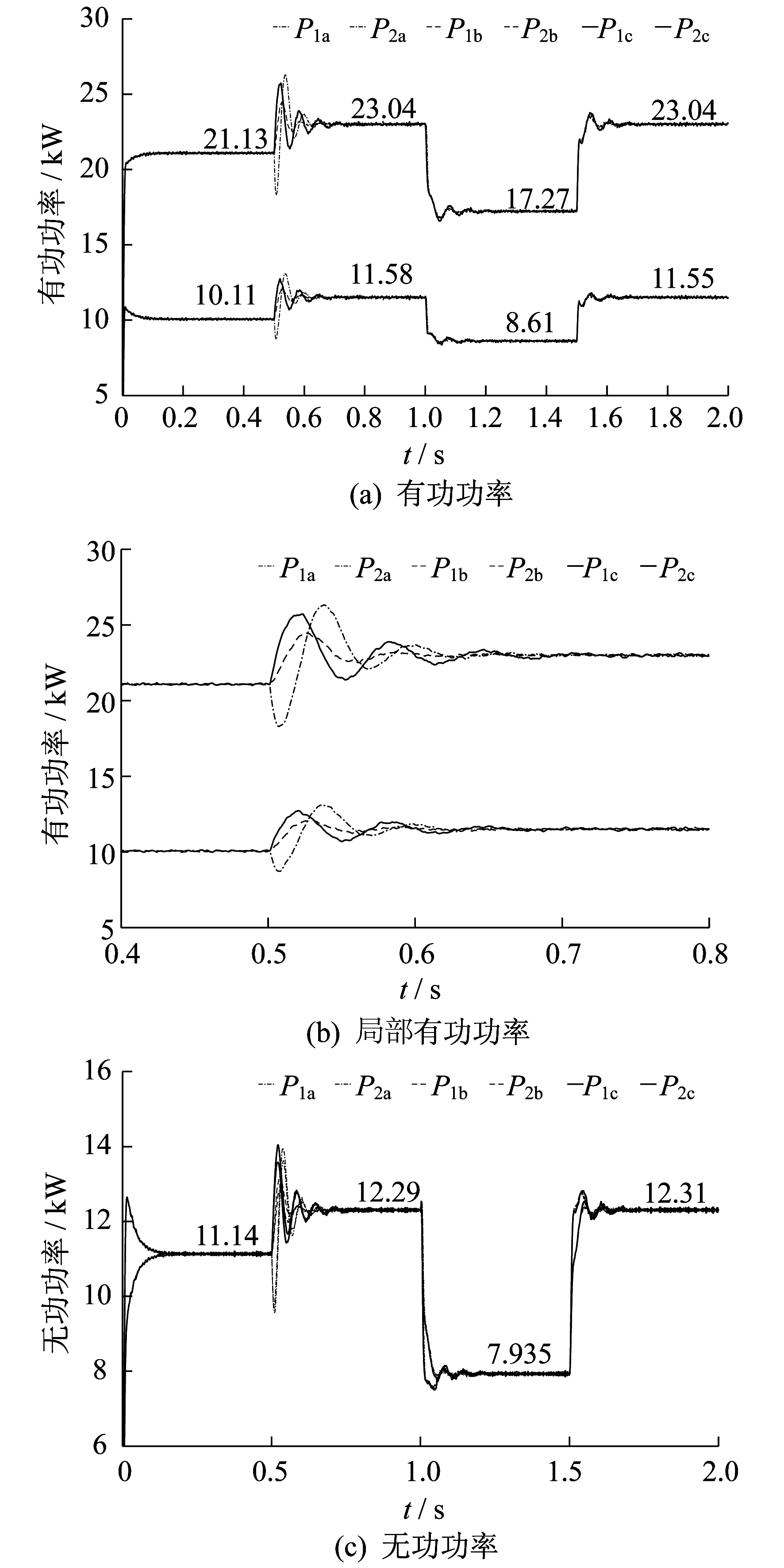
实验仿真结果如图 6所示。图 6中, 实线P1c和P2c为结合ZigBee装置的半实物仿真实验时两个DG输出的有功功率; P1a和P2a为完全采用Simulink建模仿真时两个DG输出的有功功率; P1b和P2b为完全采用Simulink建模仿真, 并考虑传递延时1 ms时两个DG输出的有功功率。图 6(c)中变量为对应的无功功率。
由图 6(a)可以看出, 在t=0~0.5 s时两个DG的输出有功功率P1i:P2i(i=a, b, c)接近1:2;在t=0.5~1 s时两个DG的输出有功功率P1i:P2i=1:2;经过切除负荷和重新接入负荷过程后, 两个DG的输出有功功率依旧保持P1i:P2i=1:2。
由图 6(b)可以看出, 结合ZigBee装置的半实物仿真与完全采用Simulink建模仿真时, 在0.5 s启动二层控制实现DG输出有功功率成比例分配过程中都经过了一定的波动后达到稳定。
由图 6(c)可以看出, 两个DG输出的无功功率在未加入二层控制前相等, 在加入二层控制后也相等且均有所提高, 在切除负荷后仍相等, 并且接入负荷后恢复为之前的值。
从以上实验结果可以看出, 在完全采用Simulink建模仿真(第2种情况)时, 二层控制能有效控制DGs的有功功率按比例输出。在加入实际ZigBee节点后(第1种情况), 二层控制也能有效控制DGs的有功功率按比例输出。然而加入实际ZigBee节点后, 需要考虑ZigBee网络存在的网络延时对微电网系统的影响, 本文设置1 ms的时间来保证ZigBee有足够时间进行数据传输。第3种情况是为了模拟完全采用Simulink建模仿真时, 1 ms的传递延时对微电网控制系统的影响, 同时与第1种情况形成对比, 以验证该半实物仿真的正确性。因此, 采用该半实物仿真能够从实际角度验证延时对微电网控制系统的影响。
5 结语
本文结合ZigBee装置和MATLAB/Simulink构建了低压微电网系统的半实物仿真方案。低压微电网系统中考虑两个DG的情况, 通过二层控制使得DG输出有功功率按比例分配, 用ZigBee实物装置进行电压和频率信息交换, 最后通过实验验证了半实物仿真方案的可行性和有效性。
然而本文所构建的微电网系统半实物仿真方案, 只是将信息通信部分实物化, 信息控制部分在软件Simulink中实现。在未来的研究中, 将考虑扩展控制器的半实物仿真, 同时增加DG的种类、数量及信息通信节点数, 并加入控制算法。
参考文献
-
[1]KUMAR M, SRIVASTAVA S C, SINGH S N. Control strategies of a DC microgrid for grid connected and islanded operations[J]. IEEE Transactions on Smart Grid, 2015, 6(4): 1588-1601. DOI:10.1109/TSG.2015.2394490
-
[2]基于模糊下垂控制的微电网分层协调控制策略研究[J]. 上海电力学院学报, 2017, 33(3): 211-215.
-
[3]一种低压微电网中的分布式电压控制算法[J]. 电力系统保护与控制, 2014, 42(20): 75-80. DOI:10.7667/j.issn.1674-3415.2014.20.013
-
[4]CHE L, SHAHIDEHPOUR M, ALABDULWAHAB A. Hierarchical coordination of a community microgrid with AC and DC microgrid[J]. IEEE Transactions on Smart Grid, 2015, 6(6): 3042-3051. DOI:10.1109/TSG.2015.2398853
-
[5]含多分布式电源独立微电网的混合控制策略[J]. 电力系统自动化, 2015, 39(11): 103-109. DOI:10.7500/AEPS20140518002
-
[6]无需互联通信的直流微电网事实功率协调控制策略[J]. 电网技术, 2015, 39(12): 3449-3456.
-
[7]YAZDANIAN M, MEHRIZI-SANI A. Distributed control techniques in microgrids[J]. IEEE Transactions on Smart Grid, 2014, 5(6): 2091-2909.
-
[8]BOLOGNANI S, ZAMPIERI S. A distributed control strategy for reactive power compensation in smart microgrid[J]. IEEE Transactions on Automatic Control, 2013, 58(11): 2818-2833. DOI:10.1109/TAC.2013.2270317
-
[9]基于非线性多智能体系统的微网分布式功率控制方法[J]. 中国电机工程学报, 2014, 34(25): 4277-4286.
-
[10]LI Q, CHEN F X, CHEN M Y. Agent-based decentralized control method for islanded microgrids[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 637-649.
-
[11]电网信息物理系统的关键技术及其进展[J]. 中国电机工程学报, 2015, 35(14): 3522-3531.
-
[12]电力系统信息物理融合建模与综合安全评估:驱动力与研究构想[J]. 中国电机工程学报, 2016, 36(6): 1481-1489.
-
[13]电网信息物理系统的混合系统建模方法研究[J]. 中国电机工程学报, 2016, 36(6): 1464-1470.
-
[14]融合时间同步策略的主从式信息物理系统协同仿真平台实现[J]. 电力系统自动化, 2017, 40(10): 9-15. DOI:10.7500/AEPS20160923005
-
[15]基于ZigBee通信网络的低压微电网分布式功率控制[J]. 电力系统保护与控制, 2018, 46(7): 115-122. DOI:10.7667/PSPC170431
-
[16]基于ZigBee和3G的远程监测系统的设计[J]. 计算机测量与控制, 2014, 22(10): 3171-3173. DOI:10.3969/j.issn.1671-4598.2014.10.028
-
[17]基于ZigBee技术的输电线路覆冰在线监测[J]. 上海电力学院学报, 2017, 33(6): 568-572.
-
[18]基于Simulink串口通信模块及数据采集卡构建半实物仿真系统[J]. 工业控制计算机, 2017, 30(2): 23-25. DOI:10.3969/j.issn.1001-182X.2017.02.011