在简单的工业控制中, PID控制器的使用可以达到良好的控制效果, 而在某些复杂且精度要求较高的系统中, 单单是PID控制已经不能满足要求了。分数阶PID比整数阶多了两个参数, 对于微分和积分的控制更加灵敏。通过对这两个参数的调整改变, 其控制范围更广, 也更精确。本文结合粒子群算法和分数阶PID控制器, 以自动调压系统为控制对象, 使控制效果比经典的PID控制器更佳, 更令人满意。

文献[1]详细介绍了分数阶微分方程的相关理论。相比较而言, 我国进入这一方面的研究起步较晚, 相关的著作^[2]于2007年出版。文献[3-5]以鲁棒性为切入点, 深入地研究了分数阶控制器, 得出了CRONE控制策略。文献[6]对比经典的PID控制器, 表明分数阶PID控制器最大的特点在于可调参数的个数增至5个, 原来3个参数(比例参数K_p, 积分参数K_i, 微分参数K_d)依然保留, 但微分和积分的阶次不再固定为1, 而是变成了非整数。由于可调参数的增多, 相应的控制范围也会扩大, 且精度也会有所增加, 其一般格式记为积分阶次和微分阶次, 而整数阶可以看作是它的一种特殊情况。

目前对分数阶控制的研究时间并不长, 相关文献数量也不多, 且多数研究仅针对某种固定的被控系统, 不具有普遍性。文献[7-11]设计出了应用于分数阶受控系统的分数阶PID控制器的方法; 文献[12]设计出了应用于某一种特定类型的整数阶系统的方法; 文献[13]研究了线性时不变分数阶系统的鲁棒稳定性问题; 文献[14-15]设计了极点阶数搜索法, 用于参数整定, 可以达到被控系统期望的要求。由此可见, 提出一种具有一定普遍性的设计方法, 使分数阶被控系统与整数阶被控系统的被控效果达到要求十分必要。

自动电压调节器主要由基本调节装置和辅助装置两部分组成。其中, 基本调节装置负责完成基本的功能, 包括电压测量单元、综合放大单元、电压整定单元、无功补偿单元等。为了便于后续的仿真和分析, 可以近似忽略系统中非线性的因素以及发电机自身的饱和影响。因此, 简单来说, 自动电压调节(Automatic Valtage Regulation, AVR)系统可被视为一个简单的反馈控制系统, 控制的对象是发电机, 控制器为励磁调节器, 执行环节通过励磁机实现。

励磁系统中常用的放大器主要有旋转放大器、磁放大器或是近代的电子式放大器。其传递函数为

$ \frac{V_{\mathrm{R}}(s)}{V_{\mathrm{e}}(s)}=\frac{K_{\mathrm{A}}}{1+\tau_{\mathrm{A}} s} $

(1)

式中:K_A——放大器增益系数, 取值范围为10~400;

τ_A——放大器时间常数, 取值范围为0.02~0.1 s。

励磁机的类型有很多, 而且相对复杂。为了方便搭建仿真模型, 本文采取最简单的线性化模型。其传递函数为

$ \frac{V_{\mathrm{F}}(s)}{V_{\mathrm{R}}(s)}=\frac{K_{\mathrm{E}}}{1+\tau_{\mathrm{E}} s} $

(2)

式(2)忽略了饱和以及其他非线性的一些影响, 励磁机增益系数K_E取值一般在10~400;时间常数τ_E的变化范围为0.5~1.0 s。

同步发电机的端电压受其负载的影响, 线性化后的简单模型可以大致反映出发电机机端电压和场电压之间的函数关系。其传递函数为

$ \frac{V_{t}(s)}{V_{\mathrm{F}}(s)}=\frac{K_{\mathrm{G}}}{1+\tau_{\mathrm{G}} s} $

(3)

式(3)中的发电机增益系数K_G和时间常数τ_G的大小都与负载的大小有关, 从全载到空载的过程中, K_G的值也会随之变化, 变化范围为0.7~1; τ_G的变化范围为1.0~2.0 s。

电压由电压互感器测得, 再经桥式整流。这一过程可以由一个简单的传递函数表示出来, 即

$ \frac{V_{\mathrm{S}}(s)}{V_{t}(s)}=\frac{K_{\mathrm{R}}}{1+\tau_{\mathrm{R}} s} $

(4)

式(4)中的传感器时间常数τ_R的值很小, 一般在0.01~0.06 s。

作为一种广泛而又成熟的控制方式, 经典的PID控制技术在励磁系统中的使用十分普遍。其控制方式主要分为比例、微分和积分控制3个部分, 每个部分又对应一个可调参数, 通过改变参数的大小, 进而达到控制的目的。PID控制器的结构简单且实践经验丰富, 能够达到一定的静态和动态稳定的要求, 其传递函数为

$ C(s)=K_{\mathrm{P}}+\frac{K_{\mathrm{i}}}{s}+K_{\mathrm{d}} s $

(5)

将PID控制加入系统中, 得到基于PID控制的线形AVR系统框图, 如图 1所示。

Oustaloup近似化方法是目前应用广泛且效果良好的近似化方法, 能够通过滤波器来拟合分数阶微积分算子, 因此常被用于分数阶控制器CRONE中。本文也采用Oustaloup近似化方法, 是因该方法可以通过MATLAB来实现, 简单易行, 而且效果基本满意。

Oustaloup方法是针对如下分数阶微分算子的近似方法

$ H(s)=\left(\frac{s}{\omega_{\mathrm{u}}}\right)^{\alpha}, \alpha \in R^{+} $

(6)

选择给定的频率段为[ω_A, ω_B], 用

$ C_{0} \frac{1+\frac{s}{\omega_{\mathrm{b}}}}{1+\frac{s}{\omega_{\mathrm{h}}}} $

(7)

来代替s/ω_u, 其中

$ \left(\omega_{\mathrm{b}} \omega_{\mathrm{h}}\right)^{\frac{1}{2}}=\omega_{\mathrm{\mu}}, \omega_{\mathrm{b}} \lt \omega_{\mathrm{A}}, \omega_{\mathrm{h}} \gt \omega_{\mathrm{B}} $

(8)

并且

$ C_{0}=\frac{\omega_{\mathrm{b}}}{\omega_{\mathrm{u}}}=\frac{\omega_{\mathrm{u}}}{\omega_{\mathrm{h}}} $

(9)

则传递函数可表示为

$H(s)=C\left(\frac{1+\frac{s}{\omega_{\mathrm{b}}}}{1+\frac{s}{\omega_{\mathrm{h}}}}\right)^{\alpha}$

(10)

其中, 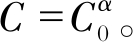将传递函数写成零极点形式

$H(s)=\lim _{n \rightarrow \infty} \hat{H}(s)$

(11)

其中

$ \hat{H}(s)=\left(\frac{\omega_{\mathrm{u}}}{\omega_{\mathrm{h}}}\right)^{\alpha} \prod\limits_{k=-N}^{N} \frac{1+\frac{s}{\omega_{k}^{\prime}}}{1+\frac{s}{\omega_{k}}} $

(12)

可得

$ \omega_{k}^{\prime}=\omega_{\mathrm{b}}\left(\frac{\omega_{\mathrm{h}}}{\omega_{\mathrm{b}}}\right)^{\frac{k+N+\frac{1}{2}(1-\alpha)}{2 N+1}} $

(13)

$\omega_{k}=\omega_{\mathrm{b}}\left(\frac{\omega_{\mathrm{h}}}{\omega_{\mathrm{b}}}\right)^{\frac{k+N+\frac{1}{2}(1+\alpha)}{2 N+1}}$

(14)

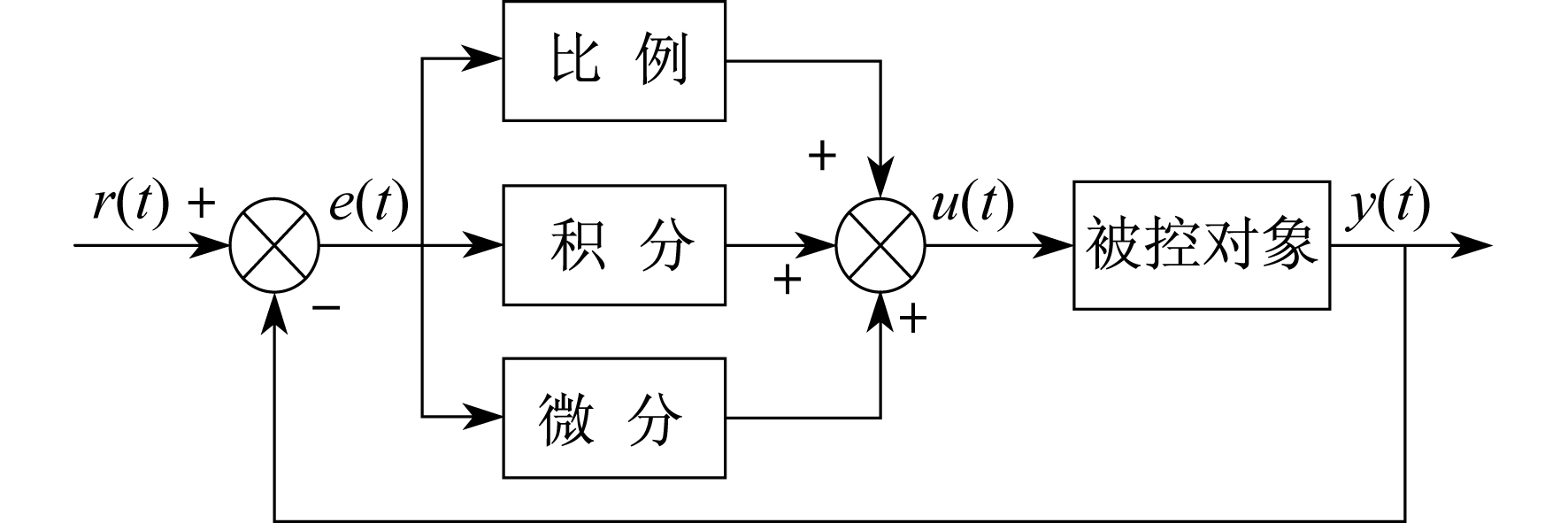
连续PID控制器系统框图如图 2所示。由图 2可知, 整数阶PID控制器是通过对误差信号e(t)进行比例、积分和微分运算, 其结果的加权, 得到控制器的输出u(t)。该值则为控制器对象的控制值。

整数阶PID控制器的数学表达为

$u(t)=K_{\mathrm{p}} e(t)+K_{\mathrm{i}} \int_{0}^{t} e(t) \mathrm{d} t+K_{\mathrm{d}} \frac{\mathrm{d} e(t)}{\mathrm{d} t}$

(15)

式中:u(t)——控制器的输出;

e(t)——控制器输入。

整数阶PID控制器的传递函数为

$ C(s)=\frac{U(s)}{E(s)}=K_{\mathrm{p}}+\frac{K_{\mathrm{i}}}{s}+K_{\mathrm{d}} s $

(16)

离散形式的PID控制器为

$ \begin{aligned} u(k)=& K_{\mathrm{p}} e(k)+K_{\mathrm{i}} \sum_{j=0}^{k} e(j) T+\\ & K_{\mathrm{d}} \frac{e(k)-e(k-1)}{T} \end{aligned} $

(17)

式中:k——采样序号;

T——采样周期。

典型的分数阶PID控制器的结构框图如图 3所示。

与整数阶PID控制器相似, 分数阶PI^λD^μ控制器的微分方程为

$u(t)=K_{\mathrm{p}} e(t)+K_{\mathrm{i}} D^{-\lambda} e(t)+K_{\mathrm{d}} D^{\mu} e(t)$

(18)

式中:λ, μ——控制器的积分阶次和微分阶次, λ > 0, μ > 0, 为任意实数。

分数阶PID控制器的传递函数为

$ C(s)=\frac{U(s)}{E(s)}=K_{\mathrm{p}}+\frac{K_{\mathrm{i}}}{s^{\lambda}}+K_{\mathrm{d}} s^{\mu} $

(19)

当λ和μ取不同值时, 分数阶PID控制器具有不同的形式。

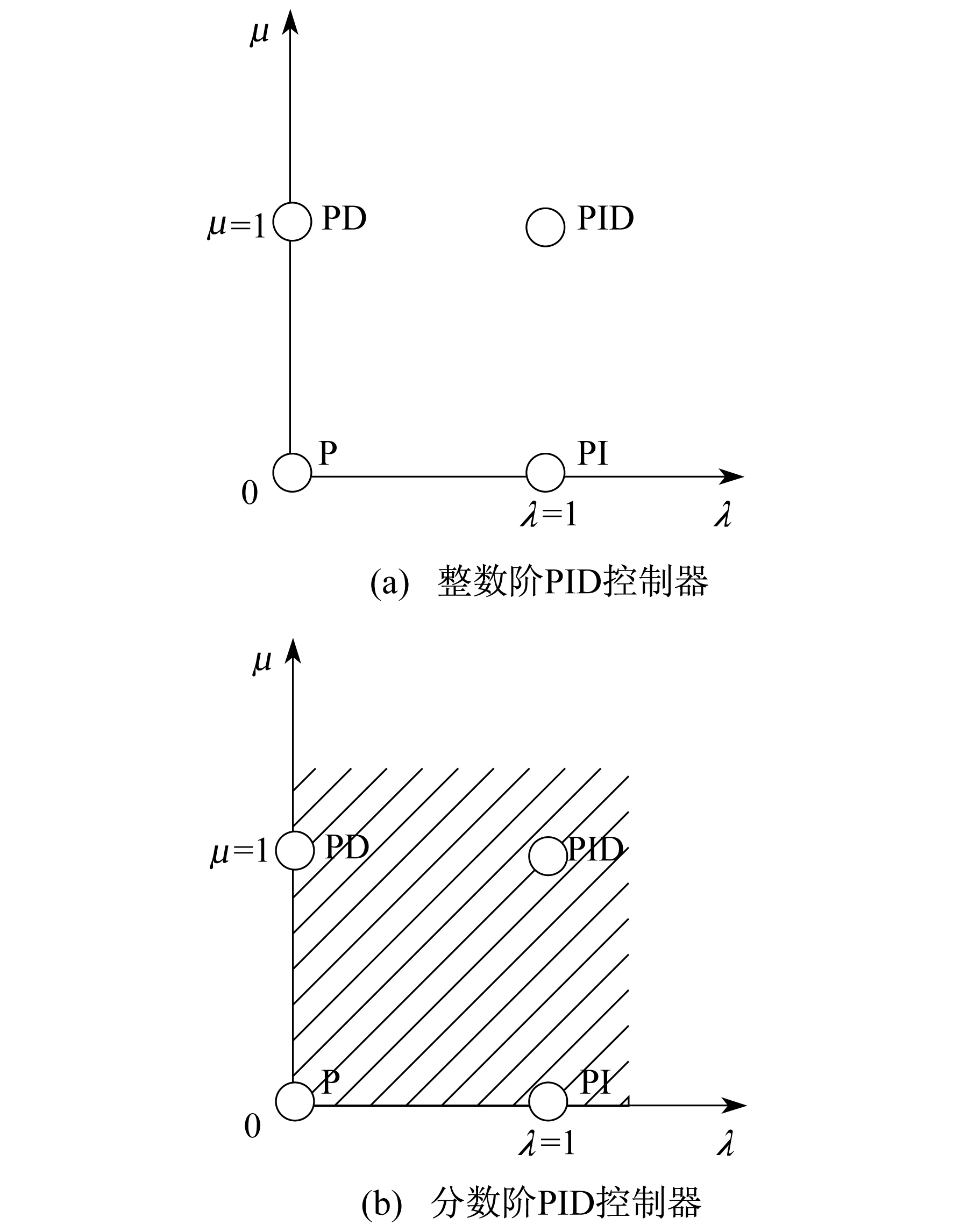
整数阶PID控制器和分数阶PID控制器的取值范围对比如图 4所示。

由图 4可知:当λ=0, μ=0时, 得比例控制器C(s)=K_p; 当λ=1, μ=0时, 得整数阶PI控制器C(s)=K_p+K_is^-1; 当λ=0, μ=1时, 得整数阶PD控制器C(s)=K_p+K_ds; 当λ=1, μ=1时, 得整数阶PID控制器C(s)=K_p+K_is^-1+K_ds; 当λ=0, μ > 0时, 得分数阶PD^μ控制器C(s)=K_p+K_ds^μ; 当λ > 0, μ=0时, 得到分数阶PI^λ控制器C(s)=K_p+K_is^-λ。

由此可见, 分数阶的范围更广, 涵盖了整数阶, 因此分数阶的优势非常明显, 其阶次可以改成分数, 这样就变得非常灵活, 理论上比整数阶具有更好的控制效果。但多了两个参数, 处理起来也会复杂一些, 需要寻找特定的方式来处理。

分数阶PID设计的主要难点是分数阶微积分模块的建立。若模块完成了建立, 那么就可以利用传递函数搭建模型, 其中就会用到分数阶微积分模块。本文选择控制系统中常用的ITAE评估值, 将其在模型中搭建起来。至此, 基本的模型便搭建完成, 可以利用程序对其实现调用。

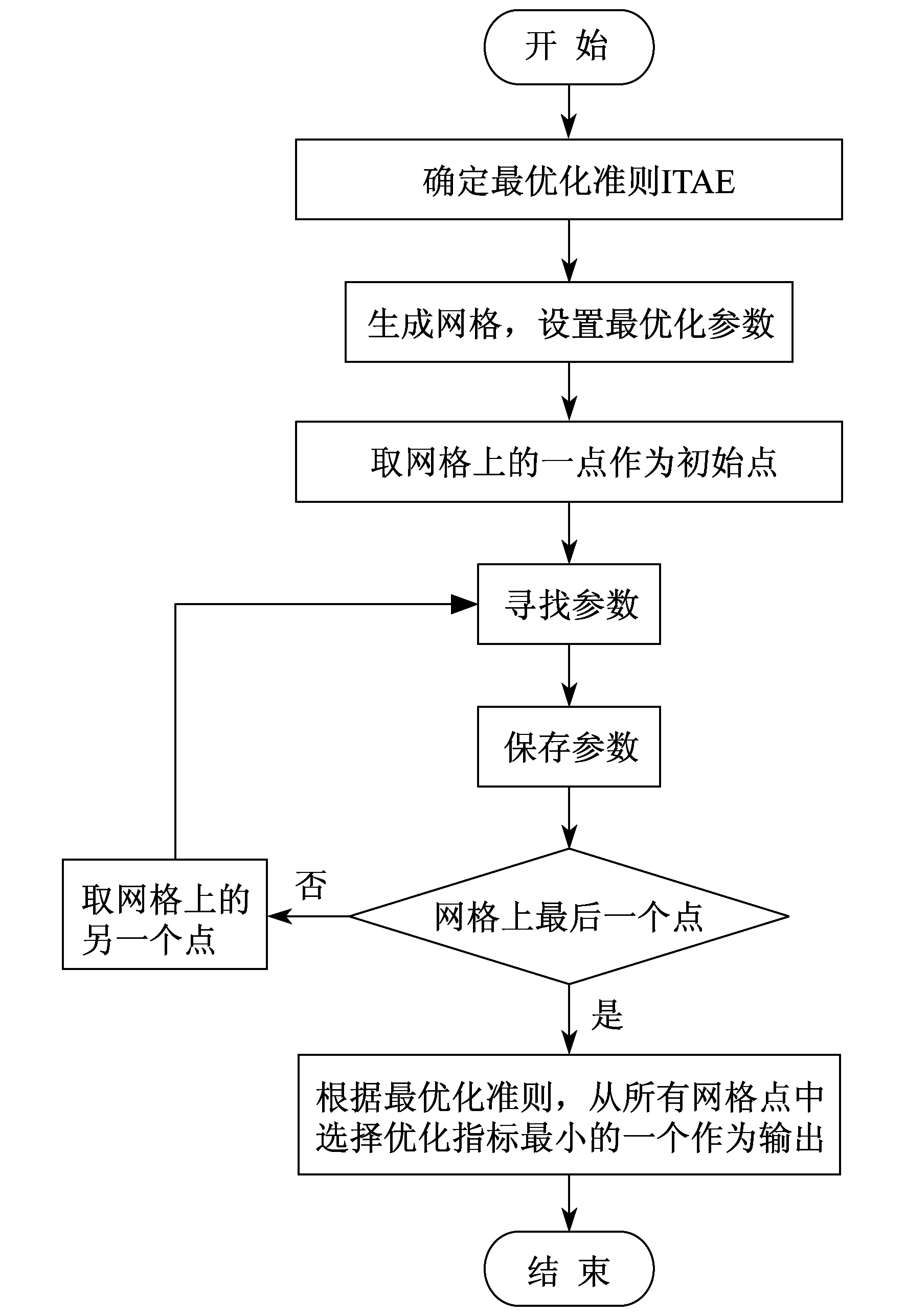
相关文献介绍了一种确定分数阶阶次的方法, 即网格寻优法。其基本原理是设置一张“网”, 该网的横纵坐标给定了[0, 1]的范围, 每条平行横纵轴线上相邻点的距离也是给定的, 可以是[0, 1]内的任意值, 称为步距。很显然, 步距越小, 搜索的精度就越高, 而相应的所花时间就越长。最后, 会得出很多的评估值, 而评估值越小, 参数越好, 容易得出最小评估值, 此时所对应的阶次便是最优结果。此外, 一般初值的选择采用随机初始化, 为了使结果更加精确, 可以多设置一些初代粒子。

整个设计流程如图 5所示。

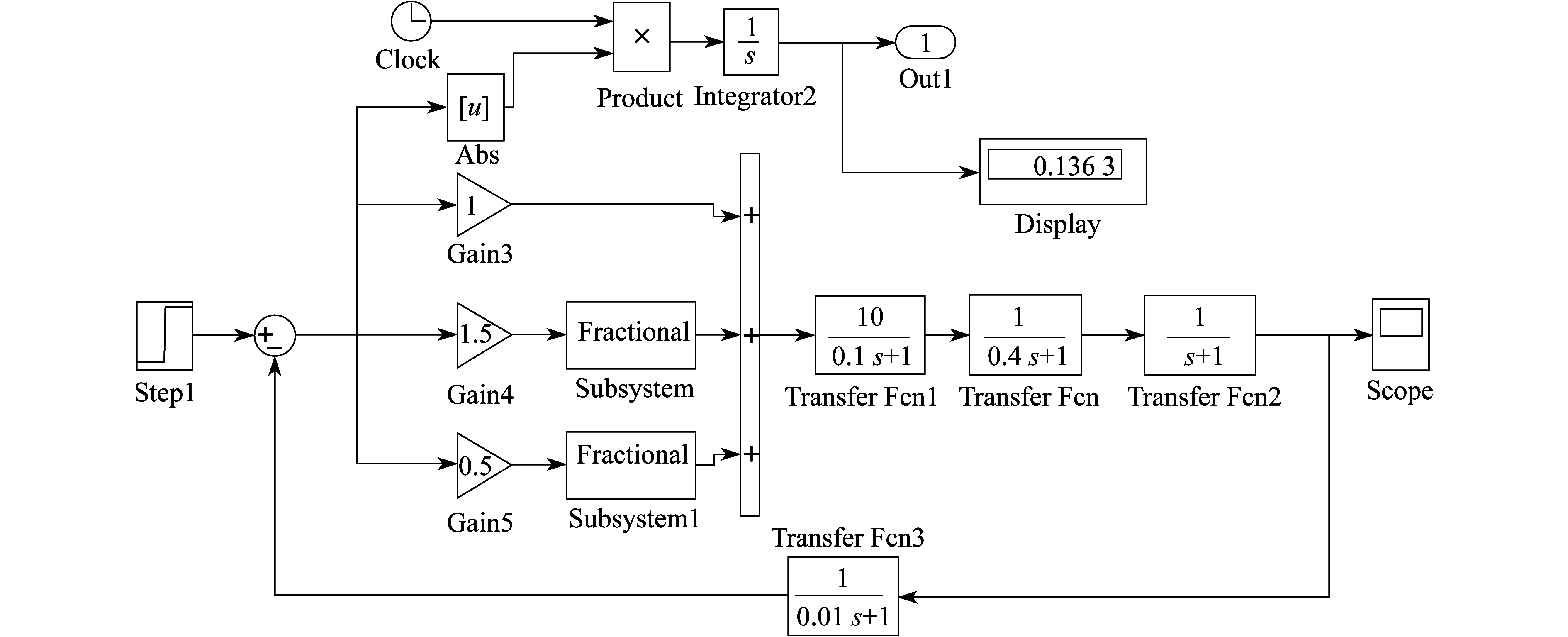
采用分数阶PID控制器来控制AVR系统, 其Simulink模型搭建如图 6所示。

微积分模块设置近似频率范围为[0.000 1 10 000], 而滤波器的阶次选择为4。需要注意的是, 因为滤波器近似化是按照微分算子设置的, 所以选择阶次的值时, 积分阶次应该设置为负值, 微分阶次为正值。

无PID控制的AVR系统Simulink优化模型和仿真结果如图 7和图 8所示。

在进行整数阶和分数阶PID控制前, 先观察无PID控制情况下的AVR系统的阶跃响应, 如图 8所示。由图 8可以看出, 在阶跃响应的情况下, 整个系统最后虽是收敛的, 但速度和震荡的幅度都满足不了系统的要求, 可见控制作用必不可少。

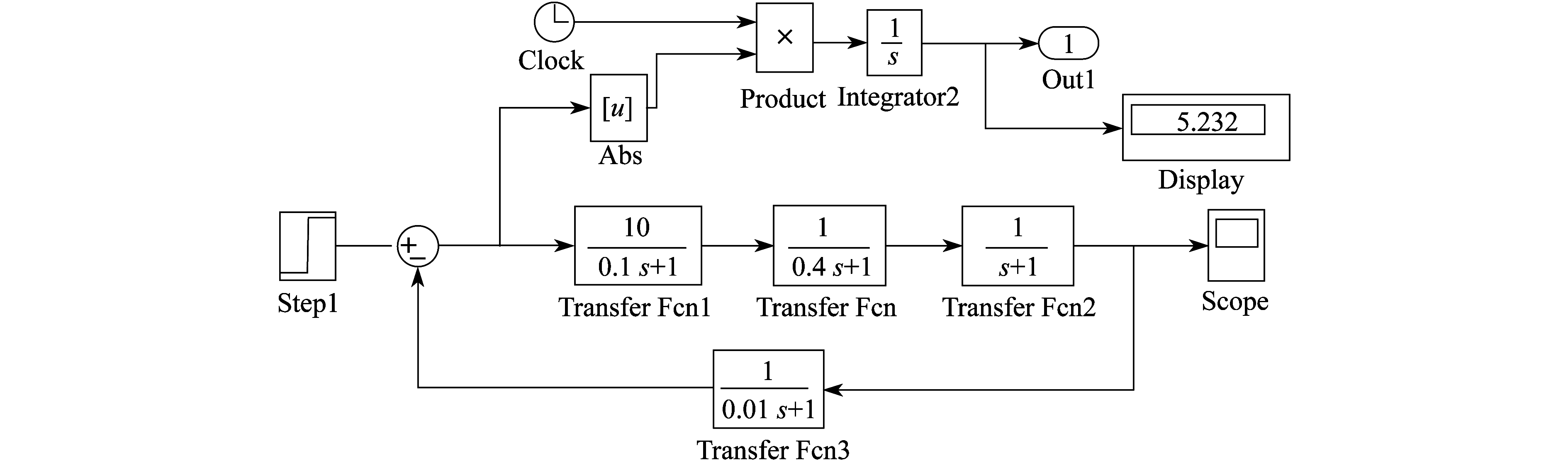
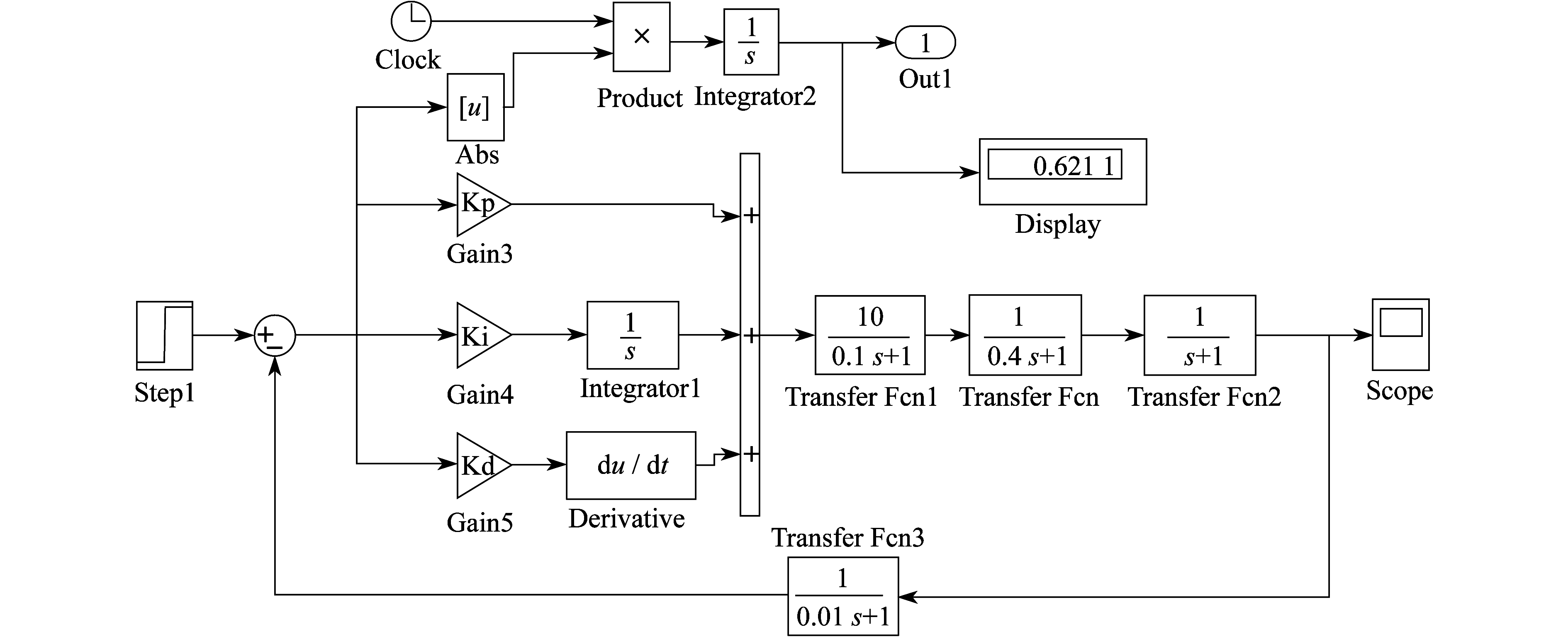
整数阶和分数阶PID控制下的AVR系统Simulink优化模型如图 9和图 10所示。

为了与分数阶PID控制器进行比较, 先对系统进行了整数PID控制, 其中的参数K_p, K_i, K_d的寻找应用了粒子群算法, 最后得到的PID传递函数为

$ G(s)=1.6971+\frac{1.2431}{s}+0.58613 s $

(20)

这种情况下的ITAE评估值为0.621 1。由于使用了粒子群算法, 所以优化作用非常明显。

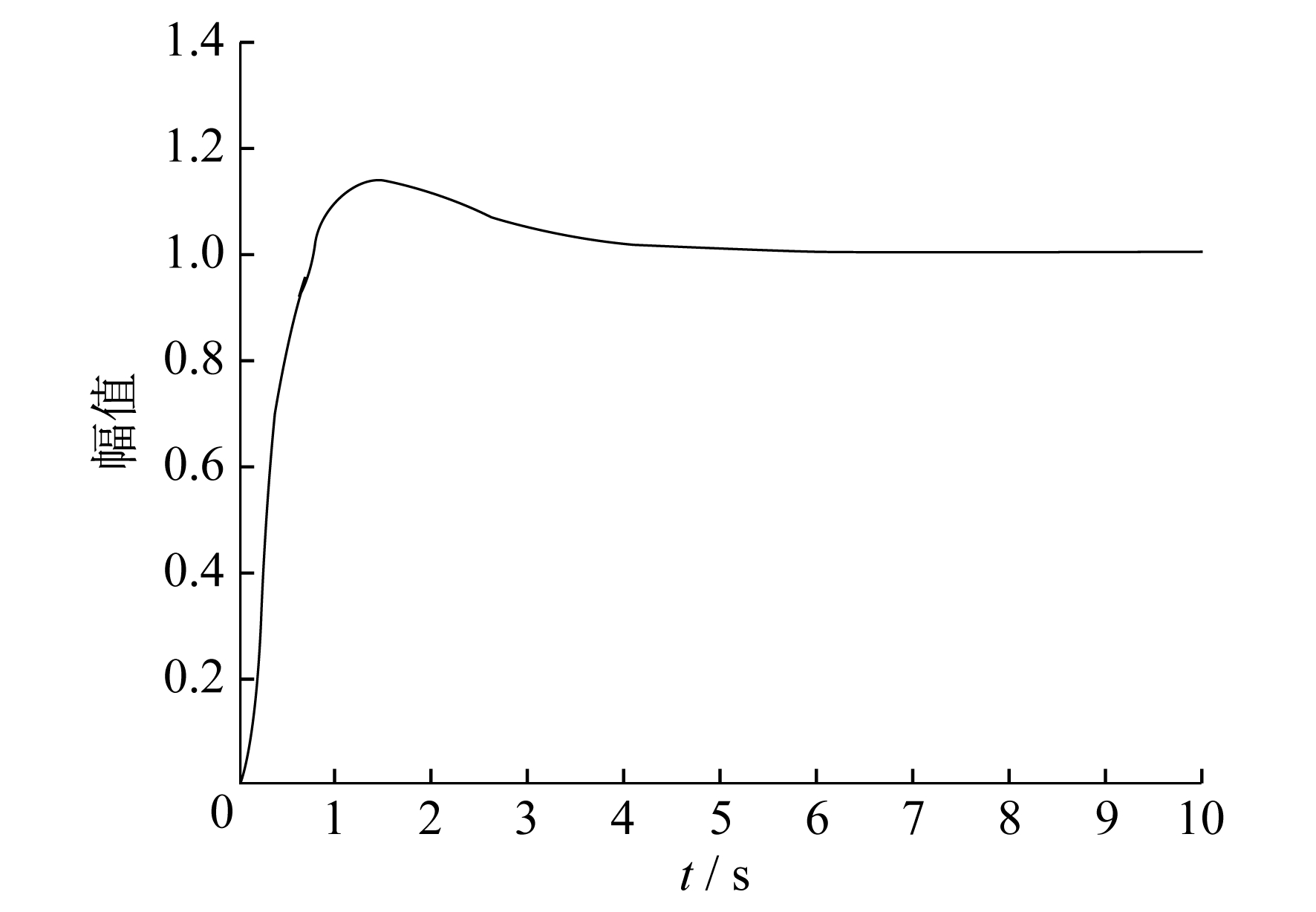
以该组PID参数进行阶跃响应后得到的响应曲线如图 11所示。

对比图 8和图 11可以看出, 加装了粒子群算法找寻参数后的整数阶PID控制器与无PID控制器的系统相比有了极大的提高, 能够较快且波动较少地到达稳定, 但仍存在稳定时间过长的问题, 无法满足电力系统对电压迅速稳定的要求。

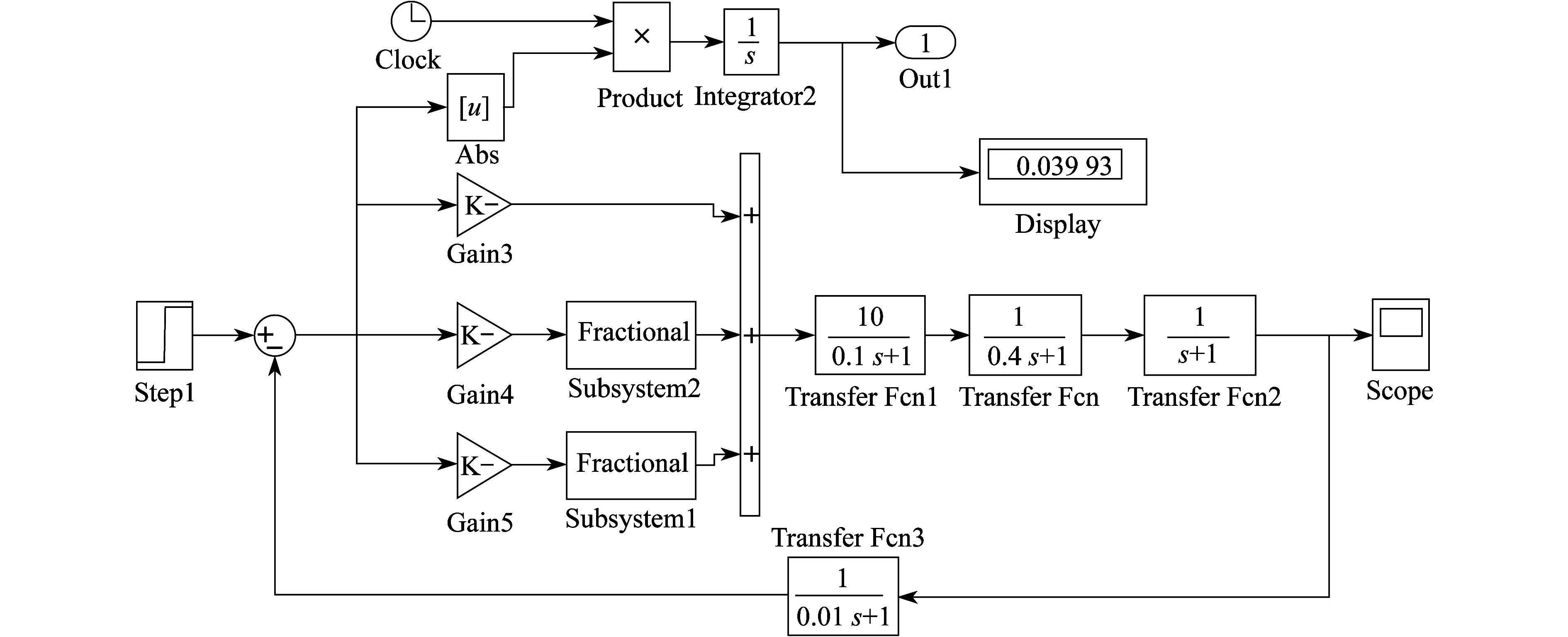
阶跃信号下的AVR系统仿真, 分数阶PID控制下的Simulink优化模型的仿真结果如图 12所示。

本文采取了简化方法, 最后得到的分数阶PID传递函数为

$ G(s)=1.6971+\frac{1.2431}{s^{0.997735}}+0.58613 s $

(21)

虽然最后寻找到的阶次非常接近于1, 但其评估值可以用来说明问题。分数阶PID控制下的系统评估值为0.039 93, 较整数阶PID控制器有了相当大的改善。从图 12可以看出, 虽然超调量比整数阶的大了一点, 但在稳定时间方面有了很大的改善。

这里需要说明的是, 上文提到的采用网格化方法, 即依次将[0, 1]范围内的积分阶次λ和微分阶次μ代入模型进行仿真, 再将得到的评估值进行比较, 以此得到最优的阶次。但运行实践表明, 该方式需要较长的运行时间, 因需对网格化模型中的每一个点进行一次寻优:若所涉的步距过小, 则分数阶PID控制器的优势不能明显地体现出来; 若步距过大, 则会进一步增加运行仿真的时间。为了满足实际需要, 本文进行了改进:以整数阶PID控制器的3个整定参数作为分数阶PID控制器的K_p, K_i, K_d的值, 并在进行分数阶控制器寻优时, 以λ=1和μ=1作为初始点。

介绍了Oustaloup逼近方法, 并搭建了Simulink模型, 再进行子系统封装, 使其实现了对分数阶微分方程处理的功能, 从而可以轻松地对分数阶AVR系统搭建Simulink仿真模型。比较分析了改进后的分数阶控制器与优化的整数阶控制器, 评估值的大小以及响应曲线都表明, 前者在后者的基础上又有了一定的提高。利用网格化法整定参数所需要的时间较长, 而本文提出的改进方法, 尽管在效果上不如逐点搜寻, 但大大缩短了时间。