|
|
|
发布时间: 2019-08-10 |
|
|
|
|
收稿日期: 2018-04-18
基金项目: 上海绿色能源并网工程技术研究中心资助项目(13DZ2251900);国家自然科学基金青年科学基金(51807114)
中图法分类号: TM732
文献标识码: A
文章编号: 1006-4729(2019)04-0301-07
|
摘要
针对上海地区受电比例逐年增大所带来的低谷调峰困难问题, 提出了一种分时电价下电动汽车有序充电参与低谷调峰的策略。在上海电网原有峰谷电价的基础上, 制定了合理的分时电价体系。以系统运行成本最低为目标, 建立了含电动汽车有序充电的低谷调峰优化模型。根据上海电网实际算例, 采用优化软件Lingo进行求解, 验证了该策略的有效性和可行性。
关键词
低谷调峰; 电动汽车; 分时电价; 有序充电
Abstract
Aiming at the difficulty of peak regulation in valley time in Shanghai brought about by the power receiving proportion which increases year by year, a strategy of peak regulation in valley time is proposed based on orderly charging of electric vehicles at the time-of-use price.On the basis of Shanghai power grid's original peak valley electricity price, a reasonable time-of-use price system is formulated.An optimization model of peak regulation in valley time is established which contains orderly charging of electric vehicles aiming at the lowest operating cost of the system.According to the actual example in Shanghai power grid, the commercial optimization software Lingo is used to solve the model, verifying the effectiveness and feasibility of the strategy.
Key words
peak regulation in valley time; electric vehicles; time-of-use price; orderly charging
近年来, 随着经济和社会的快速发展, 国民用电负荷持续增大, 用电负荷峰谷差逐年增大, 在一些以火电和核电为主要机组类型的电网出现了突出的低谷调峰容量不足的问题[1]。在负荷低谷时段, 部分火力发电机组运行在极不经济区, 甚至被迫通过日启停进行调峰[2]。然而在非工作日, 电力负荷小, 若通过启停机组进行调峰, 在第二日工作日负荷上来后, 由于受到机组自身参数的约束而不能快速地达到需要的出力, 因而给电力系统的经济性和可靠性带来了很大的影响。
随着电动汽车规模和数量的不断增长, 电动汽车作为移动储能单元参与电网的调度, 通过车电联动(Vehicle-to-grid, V2G)的方式, 可以实现电网的经济可靠运行。上海市经济和信息化委员会发布消息称, 上海新能源汽车推广突破10万辆; 据上海市车辆登记部门提供的最新数据, 2016年全年上海上牌新能源汽车共计4.506万辆; 2013年至2016年累计推广新能源汽车10.272 6万辆。截止到2017年底, 我国新能源汽车的保有量已达172.9万辆, 纯电动汽车接近150万辆。但是大量的电动汽车的无序充电, 不仅不能解决电网低谷备用不足的问题, 反而会造成峰上加峰的现象。
在电动汽车参与电网调度方面, 已有学者进行了相关研究。文献[3]以电动汽车放电量最大化为目标, 通过放电竞价的方法使部分电动汽车用户在负荷高峰期对电网放电, 从而达到削峰的目的。文献[4]在实时电价机制下, 以电动汽车群接入电网后负荷曲线峰谷差最小及电动汽车车主收益最大为优化目标, 建立了电动汽车控制模型, 得到了电动汽车与电网的交互功率曲线。文献[5]在分时电价的基础上, 建立了负荷波动最小和用户费用最低的多目标调度模型, 在减小负荷峰谷差的同时提高了用户的经济性。文献[6]建立了风电与电动汽车协同并网的调度模型, 用蒙特卡罗模拟法模拟出定量电动汽车不同V2G模式下的充放电功率, 达到了消纳风电、减小负荷波动的目的。上述文献针对的都是电动汽车参与电网削减高峰负荷, 而对于电网低谷调峰问题所做的研究较少。本文针对上海电网低谷备用不足的问题, 在分时电价的基础上, 提出了一种基于电动汽车有序充电的电网低谷调峰优化模型, 通过电价的引导使电动汽车用户能够在负荷低谷期间进行充电, 减小负荷峰谷差, 从而减轻电网低谷调峰的压力。
1 电动汽车无序充电
小区电动汽车充电负荷与接入小区时的初始荷电状态量、接入时间段密切相关, 而两者又与用户的出行规律息息相关, 换句话说, 用户的出行特征是研究小区电动汽车充电负荷的基础。用户的出行链是指私家车从家中出发, 经过各种活动之后, 再次回到家中的一系列出行[7]。出行链包含每次出行的行驶里程、到达时刻、停车时长, 以及离开时刻等出行特征。
1.1 电动汽车出行链
在不受控的情况下, 电动汽车用户通常是早上离开家里出发去上班, 随后迎来电动汽车的停车高峰; 在下午或夜晚返回家中, 迎来电动汽车的驶离高峰[8]。电动汽车早上受到上班时间的限制, 途中的逗留时间很短, 大概只有10~20 min, 下午时间较宽裕, 车主会因为休闲娱乐、购物吃饭等一些事务, 在回家途中产生相对较长的逗留时间[9]。
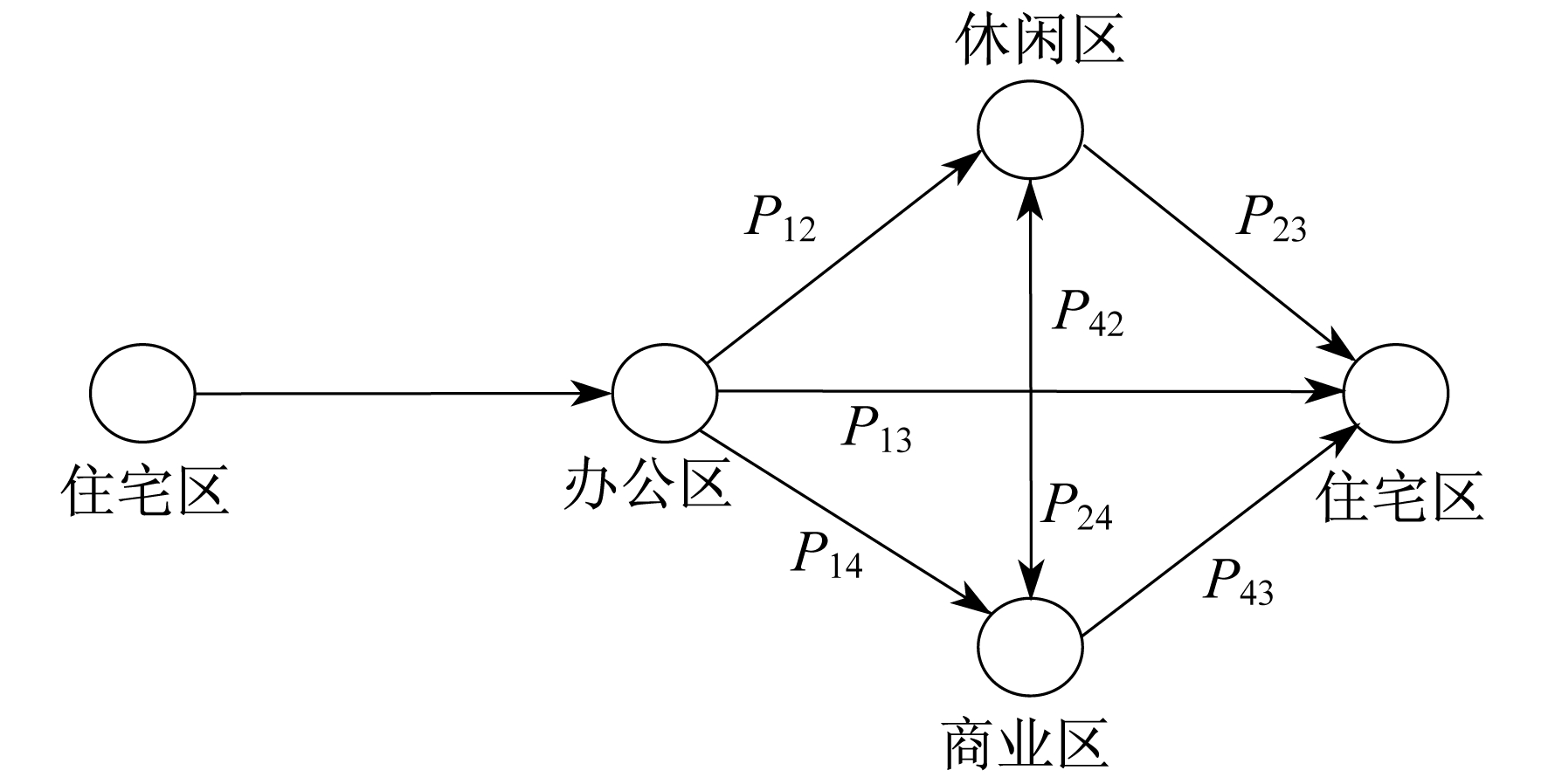
图 1为一般情况下工作日私家电动汽车的出行链。图 1中, P12, P13, P14分别为车主从办公区行驶去往休闲区、住宅区和商业区的地点转移概率; P23和P24分别为车主从休闲区去往住宅区和商业区的地点转移概率; P43和P42分别为车主从商业区去往住宅区和休闲区的地点转移概率。
电动汽车用户一般早上从家出发去公司上班, 下班后会出现回家、休闲娱乐和购物吃饭3种行为。根据马尔科夫理论, 车辆去往下一个地点的概率由当前地点的行驶需求决定[10]。出行链是指从初始地出发, 经过若干次出行之后, 再次回到初始地的整个出行过程[11]。由此可见, 不受控的电动汽车在充电行为上存在强烈的随机性。
(1) 必要性活动的出行链 必要性活动以上班为主要活动, 上班或下班途中会发生生活购物、文化娱乐等一些停留。从调查数据来看, 绝大部分用户一天的出行次数在4次以内, 少数用户的出行次数在5~6次。
(2) 非必要性活动的出行链 非必要性活动的出行情况比较随机, 主要是以文化娱乐、生活购物为主要活动, 同时探亲访友、看病探病和私人办事等其他事情也会放在非必要性活动的出行链中完成。
1.2 电动汽车出行特征
1.2.1 行驶里程的概率密度分布
研究显示, 对各种不同出行目的的行驶里程dx, i进行拟合, 发现其均服从对数正态分布。
| $f\left(d_{x, i}\right)=\frac{1}{d_{x, i} \sigma_{d_{x, i}} \sqrt{2 \pi}} \exp \left(-\frac{\left[\ln \left(d_{x, i}\right)-\mu_{d_{x, i}}\right]^{2}}{2 \sigma_{d_{x, i}}^{2}}\right)$ | (1) |
如果用户的日行驶总里程为d, 第i次出行的行驶里程为dx, i, 则满足以下关系式
| $ d=\sum\limits_{i=1}^{N} d_{x, i} $ | (2) |
1.2.2 出行途中停车时间的概率密度分布
1.2.3 电动汽车最后返回时刻的概率密度分布
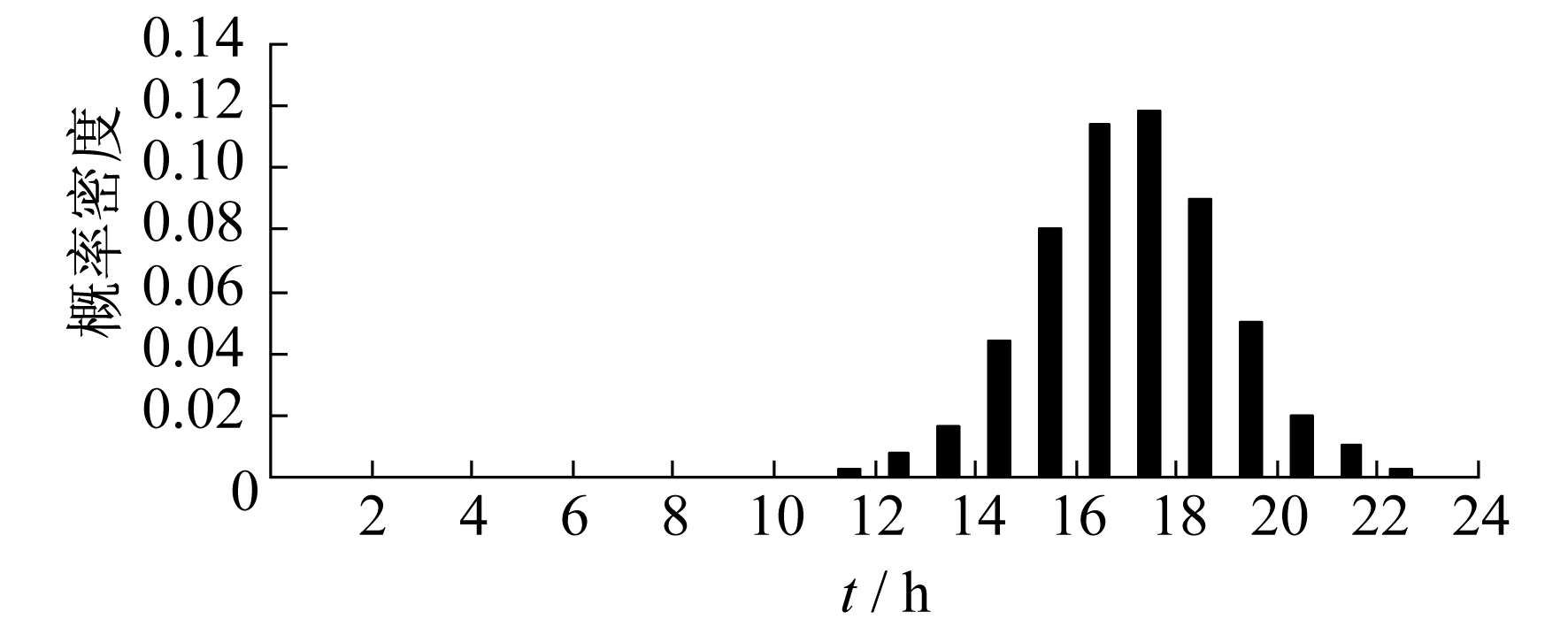
电动汽车的返回时刻tc也即电动汽车的起始充电时间(假设用户在电动汽车返家时立即对其充电)满足如下概率密度函数
| $ f\left(t_{\mathrm{c}}\right)=\left\{\begin{array}{c} \frac{1}{\sigma_{t_{\mathrm{c}}} \sqrt{2 \pi}} \exp \left(-\frac{\left(t_{\mathrm{c}}-\mu_{t_{\mathrm{c}}}\right)^{2}}{2 \sigma_{t_{\mathrm{c}}}^{2}}\right) \\ \mu_{t_{\mathrm{c}}}-12 \lt t \leqslant 24 \\ \frac{1}{\sigma_{t_{c}}} \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{\left(t_{c}+24-\mu_{t_{c}}\right)^{2}}{2 \sigma_{t_{c}}^{2}}\right) \\ 0 \lt t \leqslant \mu_{t_{\mathrm{c}}-12} \end{array}\right. $ | (4) |
起始充电时间的概率分布如图 2所示。
1.3 无序充电下电动汽车的充电负荷
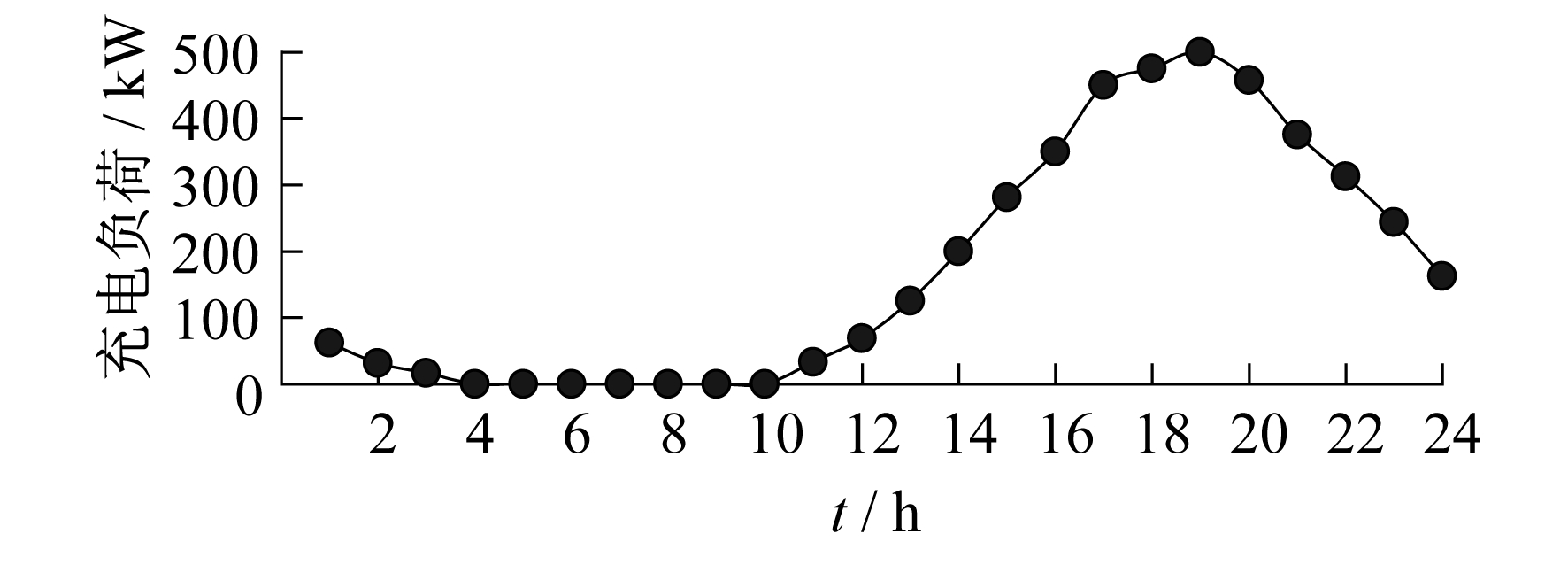
从上述电动汽车的出行链和出行特征的分析可知, 电动汽车的行为模式存在较大的随机性, 且与实际生活中发生的事情具有强烈的关联性, 导致电动汽车的充电行为产生较大的不确定性。由于电动汽车充电行为的不确定性, 其无序充电方式下的充电负荷也不具有规律性。本文选取500辆电动汽车, 假设电动汽车充电功率恒为3 kW, 采用蒙特卡洛算法计算得到这500辆电动汽车的充电负荷如图 3所示。
从图 3可以看出, 一般电动汽车从10:00~11:00开始充电, 这是电动汽车早晨到达公司后进行的充电行为; 在18:00~19:00充电负荷达到了高峰, 这是因为这一时段大部分电动汽车到家后进行充电。由此可知, 电动汽车用户的无序充电行为将会造成大量电动汽车在负荷高峰时段充电, 导致局域电网出现峰上加峰的现象。这样既不利于电网的稳定、经济运行, 同时又导致机组设备的急剧运行和频繁启停, 降低了设备的寿命。因此, 建立一种合理的需求侧响应机制, 引导电动汽车有序的充电行为显得尤为重要。
2 电动汽车有序充电控制
2.1 电动汽车有序充电概念
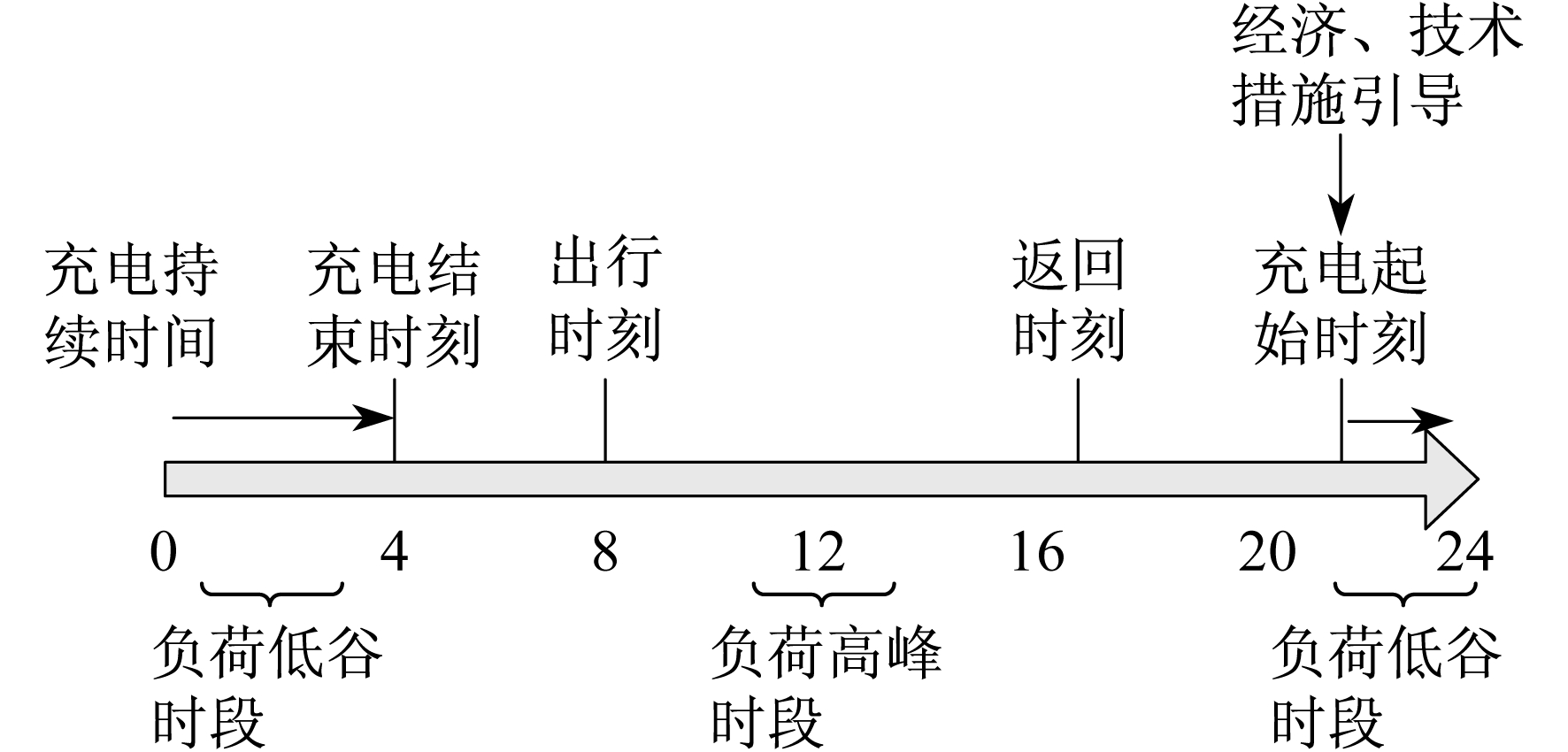
针对大规模电动汽车接入电网后对电网影响的定量评估及以减少负面影响为目标的充电控制策略研究, 已成为人们关注的热点问题, 而有序充电的概念随之产生。一般电动汽车有序充电的示意图如图 4所示。从电网的角度来说, 电动汽车有序充电是指在满足电动汽车充电需求的前提下, 运用实际有效的经济或技术措施来引导、控制电动汽车的充电行为, 尽可能地减小对电网负荷的影响, 减少了发电装机容量的建设, 以保证电动汽车与电网的协调互动发展[13]。
在需求侧响应的机制下, 可以采用电价或者激励的方式改变电动汽车用户的出行习惯和充电行为, 引导用户进行有序充电。合理的电价体系不仅能够促使电动汽车用户有序充电、降低对电网负荷的冲击, 还能有效地提高电网的经济性。一般的电价机制有峰谷电价、尖峰电价和实时电价, 其中最常用的是峰谷分时电价。
2.2 基于分时电价的电动汽车有序充电
一般情况下, 未受控的电动汽车充电在时空分布特性上展现出随机性。大量的电动汽车无序充电会导致电网峰上加峰, 给电网调峰带来较大的影响。作为一种电网常规的需求侧响应手段, 电网分时电价是将每日中的时段根据用电高峰分为峰、谷、平3个区间段, 每个区间段给定不同的电价水平, 以引导和鼓励居民参与电网削峰填谷。由于上海电网的峰谷分时区间与电网真实低谷区间有出入, 因此在上海电网原有居民峰谷分时电价的基础上, 本文将一天24 h分为峰、谷、超低谷3个区间段, 对应的时间段分别为6:00~22:00, 22:00~2:00, 2:00~6:00, 在不同区间段给予不同的电价水平, 用以鼓励电动汽车用户更好地参与低谷调峰。
根据此充电电价, 用户可以自己设置电动汽车的起始充电时间。如2:00开始为负荷超低谷时段, 在此电价影响下, 用户可以设置起始充电时间为2:00。大规模私家电动汽车按照此电价引导能够在电网超低谷时段进行充电, 不仅可以减轻电网的低谷调峰压力, 而且能够减少用户的用电费用。
2.3 电动汽车有序充电负荷模型
如今, 电动汽车的动力电池主要有铅酸电池、镍氢电池和锂电池, 其中锂电池凭借能量密度高、循环使用寿命长等优点成为电动汽车动力电池的主流。私家电动汽车的充电方式一般为恒流-恒压充电方式, 但恒压充电过程相对于恒流充电过程非常短暂, 只占其1%。因此, 本文研究的电动汽车电池对象为只考虑恒流充电方式的锂电池。假设每位用户返家时电动汽车的剩余电量(State of Charge, SOC)为Ssoc, i, 每辆电动汽车电池容量为Scap, i, 充电功率为pEV, i, 则电动汽车在参与低谷调峰时充电总功率为
| $ P_{\mathrm{EV}}=\sum\limits_{j=1}^{N} p_{\mathrm{EV}, i} $ | (5) |
每辆电动汽车的充电持续时间为
| $ T_{\mathrm{EV}, i}=\frac{\left(1-S_{\mathrm{soc}, i}\right) S_{\mathrm{cap}, i}}{p_{\mathrm{EV}, i}} $ | (6) |
据相关调查可知, 目前上海主流电动汽车的电池容量平均在20~30 kWh, 每辆电动汽车在慢充方式下的平均充电功率在2~4 kWh。
3 基于电动汽车有序充电的电网低谷调峰优化模型
为了有效缓解上海电网低谷调峰问题, 本文建立了以系统运行成本最低为目标函数的电网低谷调峰优化模型。
3.1 目标函数
| $\min F=\min \left(C_{\text {power }}+C_{\text {out }}+C_{\text {wind }}\right)$ | (7) |
式中:F——系统运行总成本;
Cpower——系统火电机组运行成本;
Cout——外来电的购电成本, 上海电网以购电合同的形式与其他区域签订每年的购置电量, 故外购电的购电成本可作为常数考虑;
Cwind——风电机组运行成本。
| $\begin{aligned} C_{\text {power }}=& \sum\limits_{t=1}^{T} \sum\limits_{i=1}^{N}\left[f_{i}\left(P_{i, t}\right)+S_{i, t}\left(1-u_{i, t-1}\right)+\right.\\ &\left.E_{i, t}\right] \cdot u_{i, t} \end{aligned}$ | (8) |
| $f_{i}\left(P_{i, t}\right)=A_{i}\left(P_{i, t}\right)^{2}+B_{i}\left(P_{i, t}\right)+C_{i}$ | (9) |
| $S_{i}\left(z_{i,(t-1)}\right)=k_{i}+B_{i}\left(1-\exp \frac{-z_{i,(t-1)}}{q_{i}}\right)$ | (10) |
式中:T——调度周期内的总时间段;
N——系统中总的机组数量;
Pi, t——第i台机组在第t时间段内的有功出力;
fi(Pi, t)——机组i在t时刻的发电成本;
Si, t——机组i在t时刻的启动成本, 启动成本与机组连续停运的时间长短有关;
ui, t——第i台机组在时间段t时刻的状态, ui, t=1为运行状态, ui, t=0为停运状态;
Ei, t——机组i由于自身阀点效应所带来的煤耗;
Ai, Bi, Ci——机组i的燃料费用系数;
zi, (t-1)——第i台机组在t-1时段已经连续停运的时间;
ki, Bi, hi——发电机组自身的启动参数;
qi——第i台机组的启动成本。
实际的火电机组在发电过程中由于汽轮机的进气阀突然打开时产生的拔丝现象, 导致机组耗量特性曲线向上凸起, 所带来的成本为
| $E_{i, t}\left(P_{i, t}\right)=\left|g_{i} \sin \left[h_{i}\left(P_{i \min }-P_{i, t}\right)\right]\right|$ | (11) |
式中:gi, hi——机组i的阀点效应系数, 由机组自身确定。
3.2 约束条件
3.2.1 系统约束
(1) 功率平衡约束是指电网中所有发电机组在任一时间段的总发电量要与系统总负荷以及网络损耗之和相等, 即
| $ \sum\limits_{i=1}^{N} u_{i, t} P_{i, t}=P_{\mathrm{D}, t}+P_{\mathrm{EV}, t}+P_{\operatorname{loss}, t} $ | (12) |
式中:PD, t——系统在t时段的负荷;
Ploss, t——系统在t时段的网络损耗。
(2) 系统旋转备用约束为
| $ \sum\limits_{i=1}^{N} u_{i, t} P_{i \max }-P_{\mathrm{D}, t} \geqslant P_{\mathrm{R}, t} $ | (13) |
式中:Pi max——机组i的最大输出功率;
PR, t——系统正负旋转备用容量, 取系统负荷的10%。
3.2.2 机组约束
(1) 机组出力上下限约束为
| $u_{i, t} P_{i \min } \leqslant P_{i, t} \leqslant u_{i, t} P_{i \max }$ | (14) |
式中:Pi min——机组i的最小输出功率。
(2) 机组爬坡约束。在实际运行中, 由于机组的物理限制, 机组有功出力的变化受其自身的爬坡限制。在一个时间间隔内, 增加和减少机组的有功出力必须限制在一定的范围内。
| $P_{i, t}-P_{i, t-1} \leqslant 60 U_{i}$ | (15) |
| $P_{i, t-1}-P_{i, t} \leqslant 60 D_{i}$ | (16) |
式中:Ui, Di——机组i的上行爬坡率和下行爬坡率。
(3) 机组最小启停时间约束为
| $ \left(u_{i, t-1}-u_{i, t}\right)\left(T_{i, t-1}-T_{i}^{\mathrm{off}}\right) \geqslant 0 $ | (17) |
| $ \left(u_{i, t}-u_{i, t-1}\right)\left(-T_{i, t-1}-T_{i}^{\mathrm{on}}\right) \geqslant 0 $ | (18) |
式中:
 机组i允许的最小连续停机时间和最小连续开机时间。
机组i允许的最小连续停机时间和最小连续开机时间。
3.2.3 电动汽车充电约束
电动汽车充电功率约束为
| $P_{\mathrm{EV}, \min } \leqslant p_{\mathrm{EV}, i} \leqslant P_{\mathrm{EV}, \max }$ | (19) |
式中:PEV, min, PEV, max——电动汽车最小和最大充电功率。
4 算例分析
4.1 算例数据
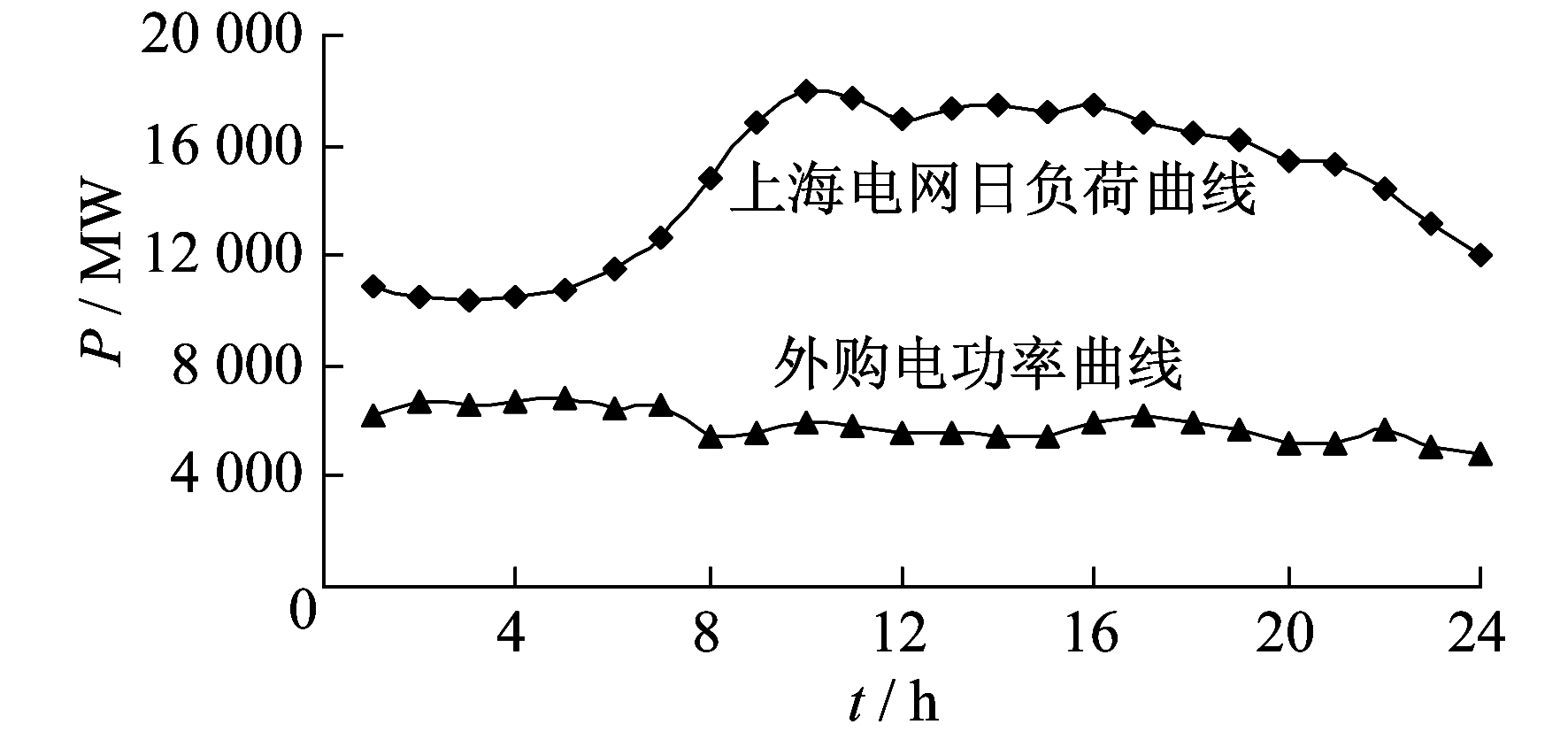
本文根据上海2015年典型日负荷情况, 采用上述电网低谷调峰优化模型, 分析其低谷调峰的能力。算例系统为上海电网实际系统, 参与调峰的机组为上海51台火电机组, 小型电厂、自备电厂和风电机组不参与调峰。所用典型日负荷曲线以及在该日最小开机方式下的出力曲线如图 5所示。
从图 5可以看出, 在1:00~6:00, 电网负荷处于低谷, 此时的外来电达到负荷的50%~60%, 呈现较为严峻的低谷负备用不足问题。此外, 受制于电压稳定裕度, 上海电网规定了对应负荷水平下的最小开机方式, 故这部分机组不能调停, 给上海电网的低谷调峰工作带来较大的困难。
私家电动汽车的日返家时间与返家时的SOC分别满足N(19.5, 1.52)和N(0.6, 0.12)的正态分布。本文假定每辆电动汽车的电池容量为25 kWh, 每辆电动汽车在恒流充电方式下的充电功率为3 kW。
此外, 本文在上海电网原有峰谷电价的基础上, 重新划分峰平谷3个时段, 各个时段制定不同的电价水平。修改后的各个时段电价是向附近私家电动汽车用户以问卷的形式获得, 并选取平均值。具体充电电价如表 1所示。
表 1
上海电网峰谷电价和电动汽车充电电价(元·kWh-1)
| 时间段 | 上海电网原峰谷电价 | 电动汽车充电电价 |
| 6:00~22:00 | 0.617 | 0.85 |
| 22:00~2:00 | 0.307 | 0.45 |
| 2:00~6:00 | 0.307 | 0.25 |
4.2 结果分析
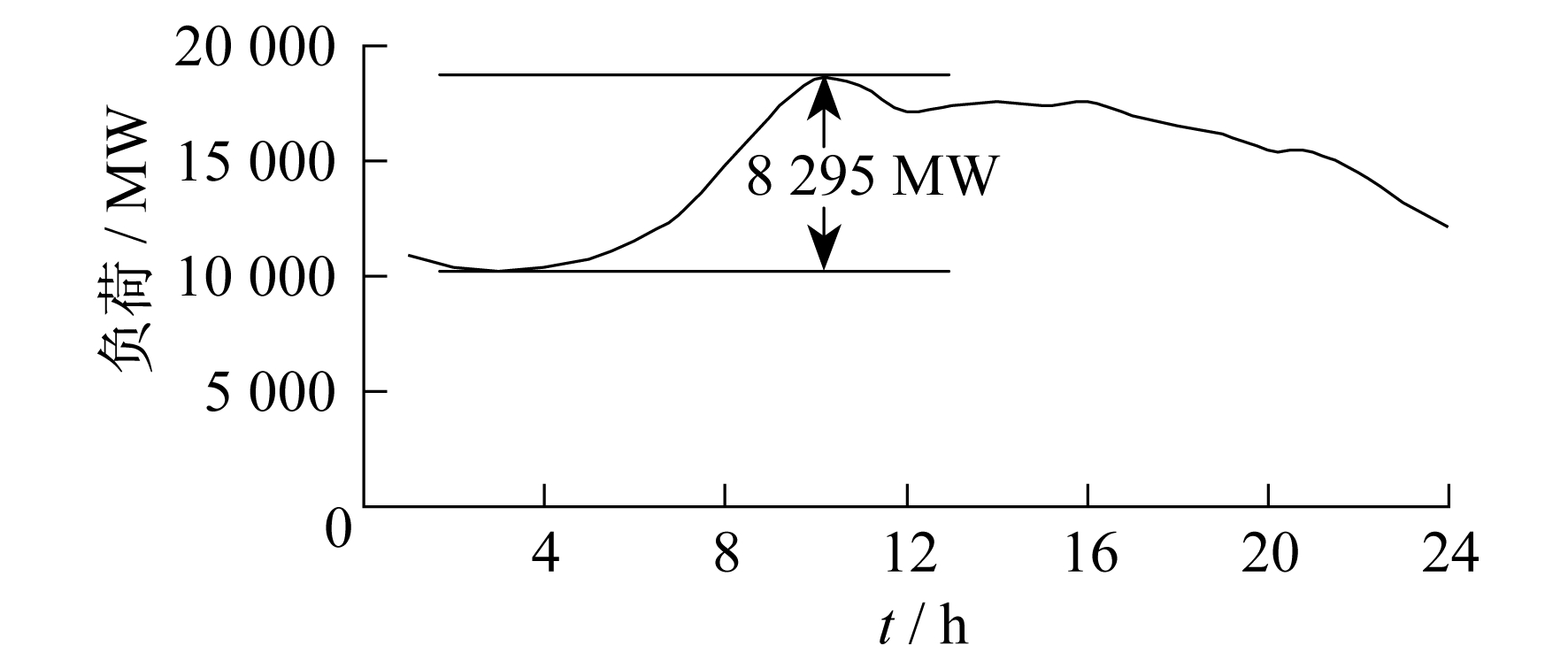
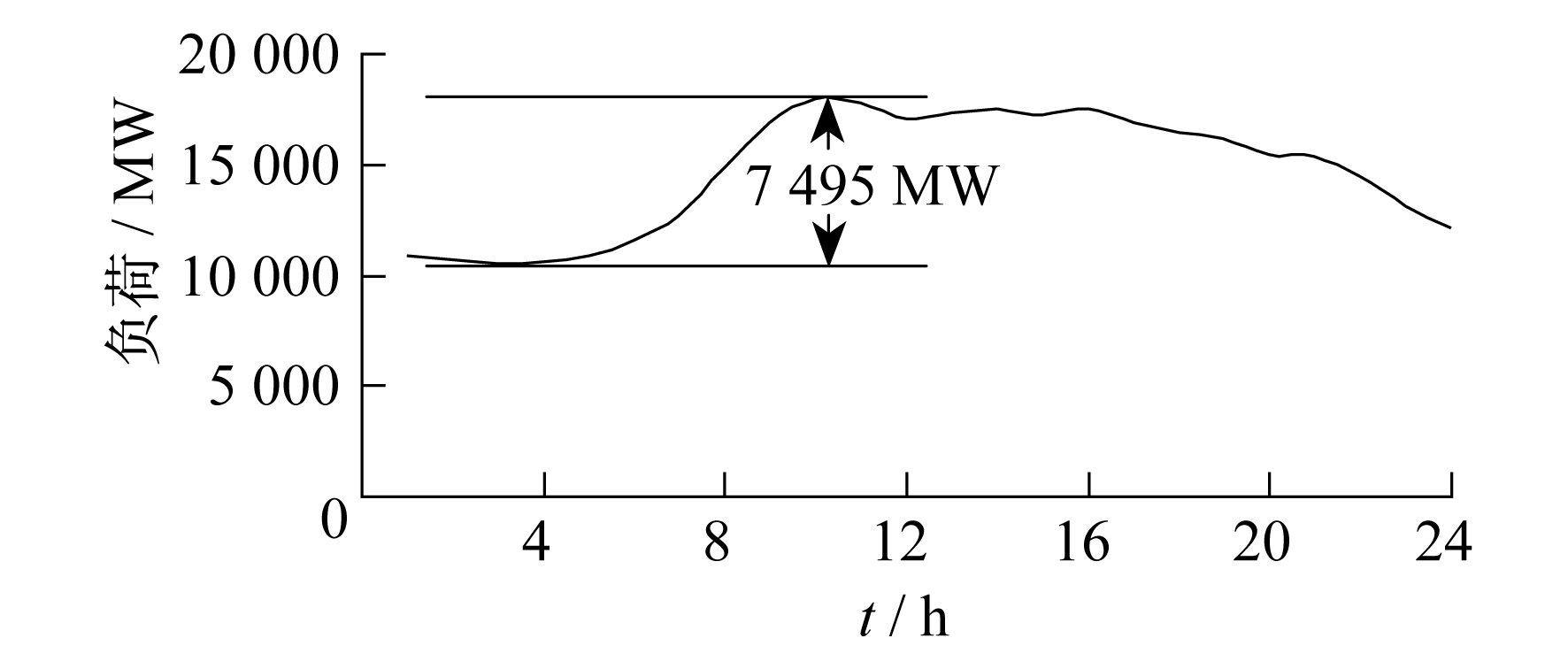
采用非线性优化软件Lingo求解低谷调峰优化模型。以电动汽车不参与低谷调峰, 即电动汽车为无序充电方式为方案1;以5万辆电动汽车参与低谷调峰, 即假定有5万辆电动汽车用户将起始充电时间设定在低谷期间为方案2。方案1与方案2的负荷曲线以及日最大峰谷差如图 6和图 7所示。
对比图 6和图 7可以发现, 在无序充电方式下, 由于电动汽车的自发性, 考虑到用户的出行链和出行特征, 可能会造成大量电动汽车在负荷高峰时段充电, 从而导致局域电网出现峰上加峰的现象。这既不利于电网的稳定、经济运行, 又会导致机组设备的急剧运行和频繁启停, 降低了设备的寿命。在适当的分时电价引导下, 让部分电动汽车用户在夜间低谷时段充电, 从而将一部分高峰负荷转移到了低谷, 在一定程度上减小了日负荷峰谷差, 减轻了电网低谷调峰的压力。
方案1与方案2的系统运行总成本、低谷调峰情况以及用户充电费用如表 2所示。
表 2
两套方案的系统运行成本及低谷调峰情况对比
| 方案 | 系统运行 总成本/ 万元 |
日最高负荷 | 日最低负荷 | 日负荷 峰谷差 率/% |
日平均充 电费用/ (元· 辆-1) |
| MW | |||||
| 1 | 5 120.82 | 17 974.54 | 10 329.40 | 42.53 | 3.019 |
| 2 | 5 012.77 | 17 974.54 | 10 479.40 | 41.69 | 1.756 |
由表 2可知, 与方案1相比, 方案2在调度周期内的系统运行总成本从5 120.82万元减小为5 012.77万元, 减少了2.11%, 这是因为在低谷期间电动汽车进行充电, 部分机组不需要停运来进行调峰, 免去了该部分机组的启停费用。日负荷峰谷差率从42.53%降到了41.69%, 在一定程度上减轻了电网低谷调峰的压力。此外, 方案2平均每辆电动汽车的充电费用比方案1减少了1.263元, 使得用户的满意度在一定程度上有所提升。
在此基础上, 电动汽车参与数量分别选取1万辆、5万辆、10万辆、50万辆、100万辆, 采用Lingo优化软件进行求解, 得到不同规模电动汽车参与下电网运行成本以及低谷时段填谷容量如表 3所示。
表 3
不同规模电动汽车参与下电网成本和填谷容量
| 电动汽车数量/ 万辆 |
电网运行成本/ 万元 |
低谷时段填谷 容量/MWh |
日负荷峰谷 差率/% |
| 1 | 5 123.08 | 87 | 42.03 |
| 5 | 5 012.78 | 439 | 41.69 |
| 10 | 4 975.29 | 921 | 39.77 |
| 50 | 4 856.61 | 4 705 | 37.39 |
| 100 | 4 905.01 | 9 618 | 37.18 |
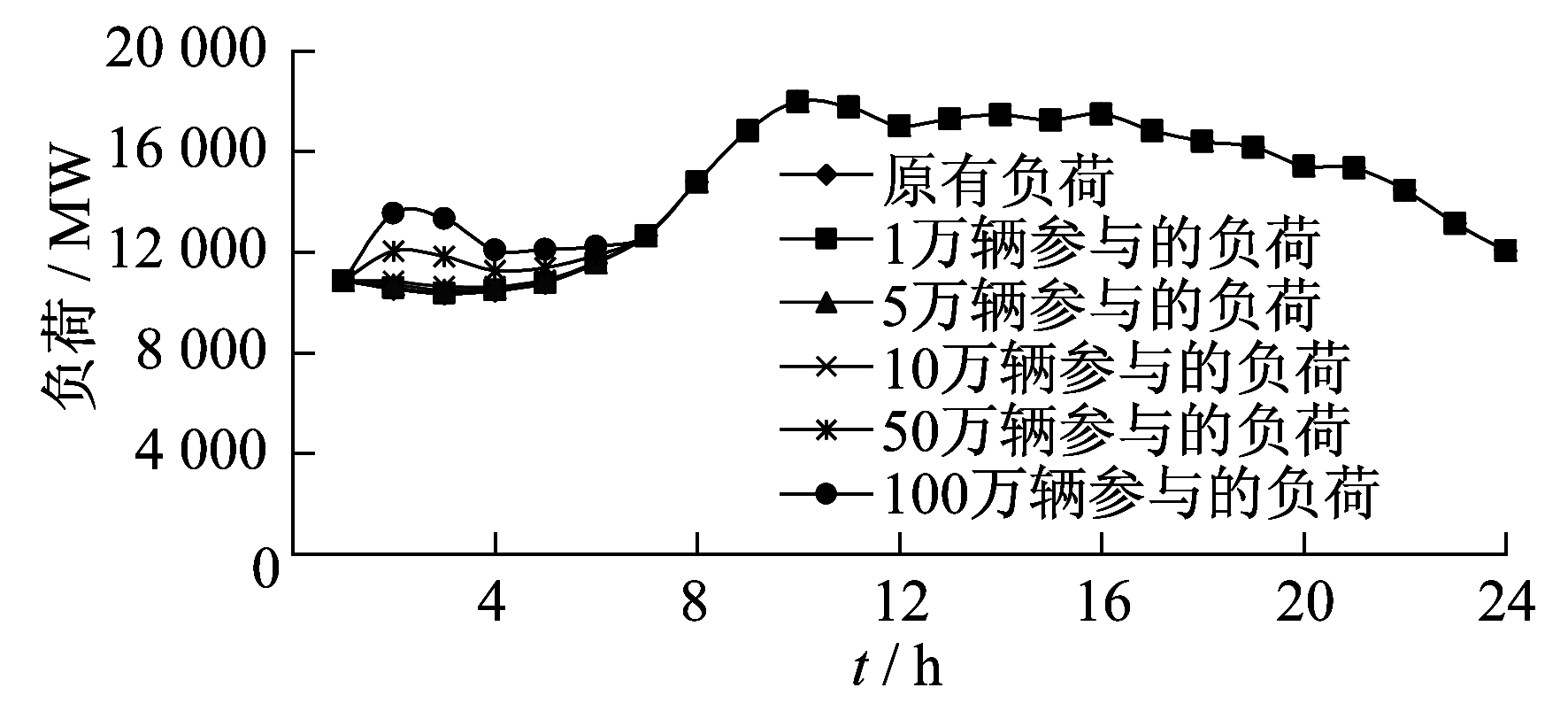
不同规模电动汽车参与低谷调峰后的负荷曲线如图 8所示。
由图 8可知, 随着参与低谷调峰的电动汽车数量的增加, 系统运行的总成本基本呈线性化减少, 低谷时段的填谷容量呈倍率增加趋势, 同时日负荷峰谷差率也不断缩小。当电动汽车的规模达到100万辆时, 虽然在低谷期间的填谷容量增加, 但对应的系统运行总成本却比50万辆时有所提高, 且其日负荷峰谷差率较之未有明显的降低。原因是当100万辆电动汽车在低谷期间同时接入电网时, 由于规模数量过大, 在低谷期间造成了一个小的用电高峰, 从而导致系统在应对此用电高峰时需要一定的成本。为此, 若要让大规模电动汽车更好地参与低谷调峰工作, 需要更好的需求侧管理机制, 在减小电网运行成本的同时, 也能将负荷峰谷差率降至更低的水平。
5 结语
本文建立了电动汽车参与的以系统运行成本最低为目标函数的低谷调峰优化模型。根据负荷的高峰和低谷出现的时段, 将一天分成峰、谷、平3个时间段, 不同时段制定不同的电价水平。在分时电价下, 电动汽车有序充电能较好地缓解低谷期间容量不足的问题, 同时也可以减少用户的充电成本。此外, 大量电动汽车参与分时电价响应, 能够有效地解决低谷调峰问题。
参考文献
-
[1]调峰市场效用分析与低谷调峰市场设计[J]. 电力系统自动化, 2013, 37(21): 134-138. DOI:10.7500/AEPS20130425013
-
[2]华东电网调峰资源统筹利用研究[J]. 华东电力, 2009(5): 708-711. DOI:10.3969/j.issn.1001-9529.2009.05.007
-
[3]基于需求侧放电竞价的电动汽车充放电调度研究[J]. 电网技术, 2016, 40(4): 1140-1146.
-
[4]基于实时电价的多目标电动汽车控制策略[J]. 上海电力学院学报, 2016, 32(5): 485-489.
-
[5]基于分时电价的电动汽车充放电多目标优化调度[J]. 电网技术, 2014, 38(11): 2972-2977.
-
[6]风电与电动汽车协同并网调度环境及经济模型[J]. 上海电力学院学报, 2017, 33(2): 113-118.
-
[7]基于出行链随机模拟的电动汽车充电需求分析[J]. 电网技术, 2015, 39(6): 1477-1484.
-
[8]张钧.城市机动车车辆停放特性分析与停车需求预测研究[D].南京: 东南大学, 2007.
-
[9]考虑时空分布的电动汽车充电负荷预测方法[J]. 电力系统自动化, 2014, 38(10): 13-20.
-
[10]GRAHN P, MUNKHAMMAR J. PHEV home charging model based on residential activity patterns[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2507-2515. DOI:10.1109/TPWRS.2012.2230193
-
[11]LUAN K, JUN Z C. Research on commuter's choice behavior between travel mode and tripchain[J]. Journal of Highway and Transportation Research and Development, 2010, 27(6): 107-111.
-
[12]基于MNL模型的私人小汽车出行时间选择研究[J]. 交通标准化, 2011(1): 63-67. DOI:10.3869/j.issn.1002-4786.2011.01.007
-
[13]充电站内电动汽车有序充电策略[J]. 电力系统自动化, 2012, 36(11): 38-43.