|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-05-22
中图法分类号: TM621.2
文献标识码: A
文章编号: 1006-4729(2019)05-0419-08
|
摘要
针对电厂耗煤量具有不确定性的特点及传统Elman神经网络利用梯度下降训练网络参数易陷于局部最优的缺点, 基于人工蜂群(ABC)算法, 提出了一种改进蜜源更新方式和跟随蜂选择引领蜂方式的改进ABC优化算法, 结合进煤量、存煤量和发电量, 建立了Elman神经网络电厂耗煤量短期预测模型(IABC-Elman)。实际算例表明, 基于IABC-Elman电厂耗煤量短期预测模型结果能达到耗煤量短期预测的标准, 与传统神经网络相比具有更高的预测精度。
关键词
电网经济调度; 耗煤量预测; Elman神经网络; 人工蜂群算法
Abstract
Due to the uncertainty of coal consumption in power plants and the shortcomings of traditional Elman neural network using gradient descent training network parameters to be trapped in local optimum, an improved artificial bee colony (ABC) is proposed to update the honey source and follow the bee.The optimization algorithm of artificial bee colony that leads the new method of bee is selected, and the short-term prediction model of coal consumption of Elman neural network power plant (IABC-Elman) is established by combining coal intake, coal storage and power generation.The actual example shows that the short-term prediction model of power plant based on IABC-Elman neural network can achieve the short-term prediction of coal consumption, and has higher prediction accuracy than traditional neural network.
Key words
grid economic dispatch; coal consumption prediction; Elman neural network; Artificial Bee Colony algorithm
在我国电网运行体系下, 调度部门依据电厂上报数据计算各时间段内所能够达到的最大发电水平从而制定发电计划[1]。任何不满足调度部门计划的发电行为, 都会导致电网的非正常运行, 甚至造成重大电力事故。为避免此类情况的发生, 调度部门需依据电厂上报的进煤量、煤炭消耗量、煤炭库存量, 计算并掌握电厂的真实发电能力, 合理地安排发电计划, 以确保整个电网的安全有序运行[2]。
相关研究人员对耗煤量预测进行了大量研究。文献[3]发现, 在时间序列上, 发电量与耗煤量之间存在线性相关关系, 应用最小二乘法、一元线性回归分析, 得出了某发电企业的预测耗煤量一元线性模型, 实现了对耗煤量的预测; 文献[4]提出了基于时序分解的用电负荷分析与预测, 为耗煤量预测提供了一种时序分解的方法; 文献[5]提出了基于人工蜂群(Artificial Bee Colony, ABC)-支持向量机(Support Vector Machine, SVM)的燃气轮机故障诊断研究, 为ABC优化算法与SVM结合提供了思路; 文献[6]结合粒子群算法对蜜源位置进行了更新, 提出了一种改进ABC(IABC)算法, 可以更快地得到新的最优解。
上述预测方法虽然取得不错的效果, 但文献[3]方法过于局限, 只有极少电厂可以根据一元线性回归的方法准确得到耗煤量预测值。电厂耗煤量具有变化性及大数值不稳定, 且时间上也未必连续的特点; 文献[4]提出的时序分解方法不适用于耗煤量预测。文献[6]改进的ABC算法过于复杂, 迭代时间较长, 且较标准ABC算法提升不大。由于Elman神经网络根据反向传播(Back Propagation, BP)网络的随机梯度下降反向传播算法进行训练时, 容易出现收敛速度慢、易陷入局部最小的缺点, 以及ABC算法虽然具有全局搜索能力强、收敛快速等优点, 但标准ABC算法蜜源更新处于一种自由选择的状态, 导致更新速度慢, 在迭代过程中容易产生“超强个体”的问题, 本文采用改进ABC算法, 对Elman神经网络连接权值、阈值进行优化, 提出了一种IABC-Elman电厂耗煤量短期预测模型。采用重庆某电厂2 003组历史数据, 随机选取1 996组数据作为训练样本训练模型, 剩余数据作为测试样本对模型进行周期为7天的短期耗煤量预测验证。实验结果表明, 与Elman神经网络、BP神经网络、广义回归神经网络(General Regression Neural Network, GRNN)相比, IABC-Elman模型具有更高的预测精度。
1 火电厂耗煤量影响因素分析
影响火电厂耗煤量的因素主要有电厂存煤量、进煤量及发电量。它们之间的关系如下:
| $C_{\mathrm{s}}=C_{1}+C_{\mathrm{i}}-C_{1+1}$ | (1) |
| $E=f\left(C_{1}\right)$ | (2) |
式中:Cs——火电厂日耗煤量;
Cl——火电厂存煤量;
Ci——火电厂日进煤量;
Cl+1——火电厂的次日存煤量;
E——火电厂日发电量;
f(x)——耗煤量特性函数。
影响进煤量的因素较多, 主要有以下3点:
(1) 电煤供应 煤炭供应包含国内煤炭开采总量与国外进口煤炭总量之和[7];
(2) 电煤运输 目前, 电煤运输的主要方式为铁路和水路运输[8];
(3) 煤炭价格 实际生产活动中, 火电厂购煤量一方面由发电量决定, 另一方面考虑收益, 电厂在煤价较低时增加购煤量, 煤价较高时减少购煤量, 以满足调度分配的发电需求。
火电厂存煤量大小可以决定电厂是否有能力按最大的发电水平发电, 也将直接影响电网调度部门能否准确分配发电任务。此外, 电厂存煤量也是调度部门评估电厂发电能力并及时作出调度的重要依据。根据式(2), 火电厂承担的发电任务与耗煤量是函数关系, 即发电量是耗煤量的体现。在实际生产中, 为满足未来一段时间的发电需求, 火电厂应该及时按量补充煤炭存储量, 所以火电厂的耗煤量在一定程度上会影响进煤量, 从而对存煤量产生作用[9]。
2 Elman神经网络简介
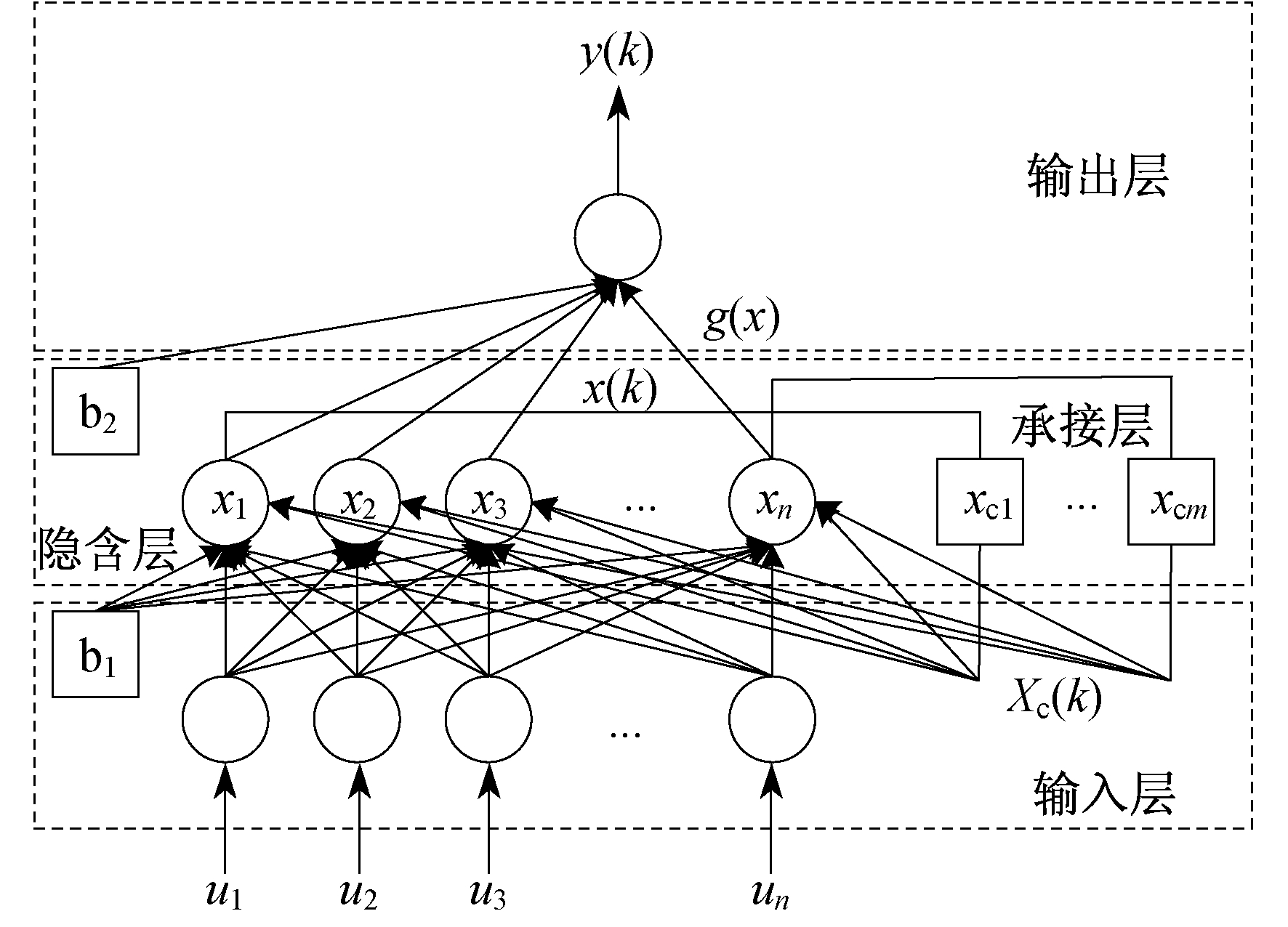
Elman神经网络在前馈式网络的隐含层中增加一个承接层, 以达到记忆的目的。它能直接反应动态过程系统的特性[10]。Elman神经网络结构如图 1所示。
输入层有信号传输作用, 输出层有线性加权作用; 隐含层的传递函数采用线性或非线性函数, 承接层的作用是记忆隐含层单元前一刻的输出值并返回给网络的输入, 作为一个一步延时算子, 使网络具有动态记忆功能。
Elman神经网络的数学模型为
| $\boldsymbol{x}(k)=f\left[\boldsymbol{w}^{1} \boldsymbol{x}_{\mathrm{c}}(k)+\boldsymbol{w}^{2} \boldsymbol{u}(n-1)\right]$ | (3) |
| $\boldsymbol{x}_{\mathrm{c}}(k)=\alpha \boldsymbol{x}_{\mathrm{c}}(k-1)+\boldsymbol{x}(k-1)$ | (4) |
| $\boldsymbol{y}(k)=g\left[\boldsymbol{w}^{3} \boldsymbol{x}(k)\right]$ | (5) |
式中:x(k), x(k-1)——隐含层输出向量;
xc(k), xc(k-1)——承接层输出向量;
w1, w2, w3——输入层-隐含层、承接层-隐含层、隐含层-输出层权值矩阵;
u(n)——n维输入向量;
y(k)——m维输出向量;
f(x), g(x)——隐含层与输出层神经元之间的传递函数;
α——自连接反馈增益因子, 0≤α≤1。
α, w1, w2, w3决定了Elman神经网络的结构, 通过合理取值可以得到较好的模型结构。设第k步系统实际输出向量为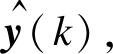 则在时间段(0, T)内, Elman网络误差指标函数为
则在时间段(0, T)内, Elman网络误差指标函数为
| $ \begin{aligned} E(k)=& \frac{1}{2} \sum_{k=1}^{n}[\boldsymbol{y}(k)-\hat{\boldsymbol{y}}(k)]^{\mathrm{T}} \cdot \\ & [\boldsymbol{y}(k)-\hat{\boldsymbol{y}}(k)] \end{aligned} $ | (6) |
经多次迭代调整连接权值, 并将其代入式(3)~式(5)中得到网络输入误差, 再次进行迭代训练, 直到误差满足精度为止。
3 ABC算法及其改进
3.1 ABC算法
ABC算法是一种生物仿生算法, 由蜜源、引领蜂、跟随蜂和侦察蜂等要素组成。引领蜂和跟随蜂各占蜂群总数的50%, 每一个蜜源仅有一只引领蜂开采。模型定义蜜蜂最基本的两种行为模式:一是引领蜂找到一处花蜜含量丰富的蜜源, 则会引领其他蜜蜂跟随到达此处进行采蜜活动; 二是当该处蜜源所含花蜜较少时, 放弃该蜜源[11]。
ABC算法的核心思想是:设有N个蜜源{x1, x2, x3, …, xN}, 每个蜜源xi(i=1, 2, 3, …, N)都是一个d维向量; 设定蜜蜂总循环搜索次数为Nmcn, 每个蜜源可重复开采次数为Nlimit。蜂群的初始化:随机产生N个不同蜜源, 即有N个解, 分别计算蜜源适应度并将其由大到小排列, 种群前50%作为引领蜂, 后50%作为跟随蜂和侦察蜂。引领蜂在蜜源邻域进行搜索, 由式(7)产生新蜜源, 将新旧蜜源对比, 保留花蜜较为丰富的蜜源。
| $V_{i j}=x_{i j}+r_{i j}\left(x_{i j}-x_{k j}\right)$ | (7) |
式中:Vij——在xij附近产生的新位置;
k, j——通过随机公式产生的随机数, k≠j;
rij——随机因子, rij∈[-1, 1], rij使新位置约束在xij附近。
在寻找到新的蜜源后进入跟随阶段。在跟随阶段中, 跟随蜂根据引领蜂的“8”字舞所传递的蜜源信息[12], 依据式(8)选择引领蜂, 然后在蜜源邻域依据式(7)生成一个新蜜源, 并比较两个蜜源的优劣, 保留质量较好的蜜源。
| $ P_{i}=\frac{F_{\mathrm{fit}(i)}}{\sum\limits_{i=1}^{N} F_{\mathrm{fit}(i)}}, i=1,2,3, \cdots, N $ | (8) |
式中:Pi——跟随蜂选择引领蜂的概率;
Ffit(i)——第i个解的适应度。
当引领蜂连续经过Nlimit次循环后蜜源的丰富度没有更新时, 则放弃该蜜源, 成为侦察蜂。
3.2 ABC算法存在的缺陷
ABC算法主要存在的问题有二。一是蜜源搜索采用在邻域内搜索新蜜源, 并与初始化蜜源进行对比, 择优选择最佳蜜源的方法。在通过这种策略寻找新蜜源时, 因采用一个介于[-1, 1]的随机因子来控制邻域区间, 因此在对新蜜源位置进行更新时, 会导致蜜源位置选择处于一种自由选择的“盲目”状态[13], 最终导致算法无法对邻域范围进行全面搜索, 使得在前期寻找最优蜜源位置时可选范围狭小, 整个ABC算法极易陷入局部最优解。二是跟随蜂根据赌轮盘法选择引领蜂的方式。在标准ABC中, 跟随蜂根据式(7)所产生的蜜源位置, 根据式(8)进行适应度值的计算, 蜜源的适应度值越大, 与之对应的引领蜂被选择的概率就会越大。但在实际应用中, 在选择压力过小时, 迭代过程中会产生概率P接近1的蜜蜂, 称为超常蜜蜂。这些超常蜜蜂因为竞争力极为强大而控制选择过程, 使ABC算法的全局搜索能力迅速下降; 反之, 如果种群内个体的适应度值相差不大, 则很容易忽视优秀个体, 在一定程度上会影响算法的收敛速度, 增加运算时间。
针对ABC算法存在的问题, 本文提出了一种改进蜜源更新方式和跟随蜂选择引领蜂方式的改进ABC算法。
3.3 改进蜜源更新方式
在ABC算法中, 引领蜂和跟随蜂将最初发现的蜜源与后续在邻域搜索到的新蜜源进行比较, 选取最优蜜源, 并通过随机因子的取值来控制邻域搜索区间。但通过随机因子搜索邻域的方法并不能有效保证随算法循环次数的增加而使搜索范围与蜜源数目相符合, 极易使蜜源位置陷入局部最优解, 寻优速度变慢, 最终导致最优蜜源位置不准确。本文提出了一种更加合理的比例因子φij。
| $ \phi_{i j}=\left\{\begin{array}{l} \mu_{1}+\mathrm{e}^{\mu_{2}}, \text { rand } \lt 0.5 \\ -\mu_{1}-\mathrm{e}^{\mu_{2}}, \text { 其 他 } \end{array}\right. $ | (9) |
| $ \left\{\begin{array}{l} \mu_{1}=\frac{\operatorname{rand}(0,1) \times N_{\text {cycle}}}{N_{\text {maxcycle}}} \\ \mu_{2}=-\frac{N_{\text {cycle}}}{N_{\text {maxcycle}}} \end{array}\right. $ | (10) |
| $V_{i j}=x_{i j}+\phi_{i j}\left(x_{i j}-x_{k j}\right)$ | (11) |
式中:Ncycle, Nmaxcycle——迭代次数和最大迭代次数。
改进ABC算法中, 按式(11)进行蜜源位置更新, 比例因子φij会随进化过程自适应变化。式(10)中, 在算法初期, 当Ncycle是一个较小的值时, 根据式(10), μ1和μ2为较大值, φij也会得到一个较大值。如果搜索范围足够大, 足够大的比例因子扩大搜索邻域, 算法对新蜜源的选择性就会更大, 使群内个体更快更多地向较优个体进化, 避免算法易陷入局部最优。随迭代次数的增加, 进化到一定程度后, Ncycle成为一个较大值时, 根据式(10), μ1和μ2为较小值, 则会得到一个较小的比例因子, 由此实现了在后期有效缩小邻域搜索范围, 提高算法后期搜索效率的目的。实验结果表明:与随机因子相比, 在寻找当前蜜源搜索邻域范围内, 采用比例因子可以更快更准确地寻找到更加优质的新蜜源, 提高了算法的优化性能。
3.4 改进跟随蜂选择引领蜂方式
ABC算法中, 引领蜂找到蜜源后回到蜂巢, 同时跟随蜂根据式(7)判断引领蜂所寻蜜源的丰富程度, 即适应度, 蜜源越丰富适应度值越大, 被跟随蜂选中的概率Pi就越大; 反之, “贫瘠”蜜源被跟随蜂选中的概率Pi就越小。
针对ABC中产生超常个体强大竞争力进而影响选择过程的问题, 同时在适应度相差不大的条件下易忽视优秀个体的状况, 本文改进了跟随蜂选择引领蜂的方式, 采用式(12)进行优秀个体选择, 即
| $ P_{i}=0.9+\frac{f_{i}}{\max f_{\text {fit }}} \times 0.1 $ | (12) |
式中:fi——第i位置蜜源的适应度值;
max ffit——当前迭代次数下适应度最大值。
采用新概率计算方法能有效地减小算法的复杂程度, 大大缩短运行时间, 同时也可以避免因算法本身产生超常个体影响选择的问题。
经过改进蜜源更新方式以及改进跟随蜂跟随引领蜂的选择方式得到的算法称为改进人工蜂群算法。具体的求解步骤如下。
(1) 算法初始化。初始化蜂群大小S, 最大迭代次数Nmaxcycle, 统计数值B, 限制参数Nlimit, 数据维度等值。
(2) 寻找蜜源阶段(引领蜂阶段)。引领蜂由式(11)在初始蜜源邻域范围搜索新蜜源, 当新蜜源的丰富程度优于当前蜜源的丰富程度时, 新蜜源替换旧蜜源, 同时B加1。
(3) 由式(12)得到跟随蜂跟随引领蜂的概率, 从而进行选择。
(4) 采蜜阶段(跟随蜂阶段)。跟随蜂确定蜜源并在蜜源内寻找新的蜜源。当所寻蜜源优于当前蜜源时, 则蜜源位置进行更新, 否则B加1。
(5) 循环迭代过程中, 若蜜源位置始终未更新, 而未更新数值B到达某一限值时, 即Nlimit对应的引领蜂变为侦查蜂, 继续搜寻新蜜源。
(6) 分析并记录最优解。
(7) 继续进行运算。当迭代数达到Nmaxcycle时, 算法结束。
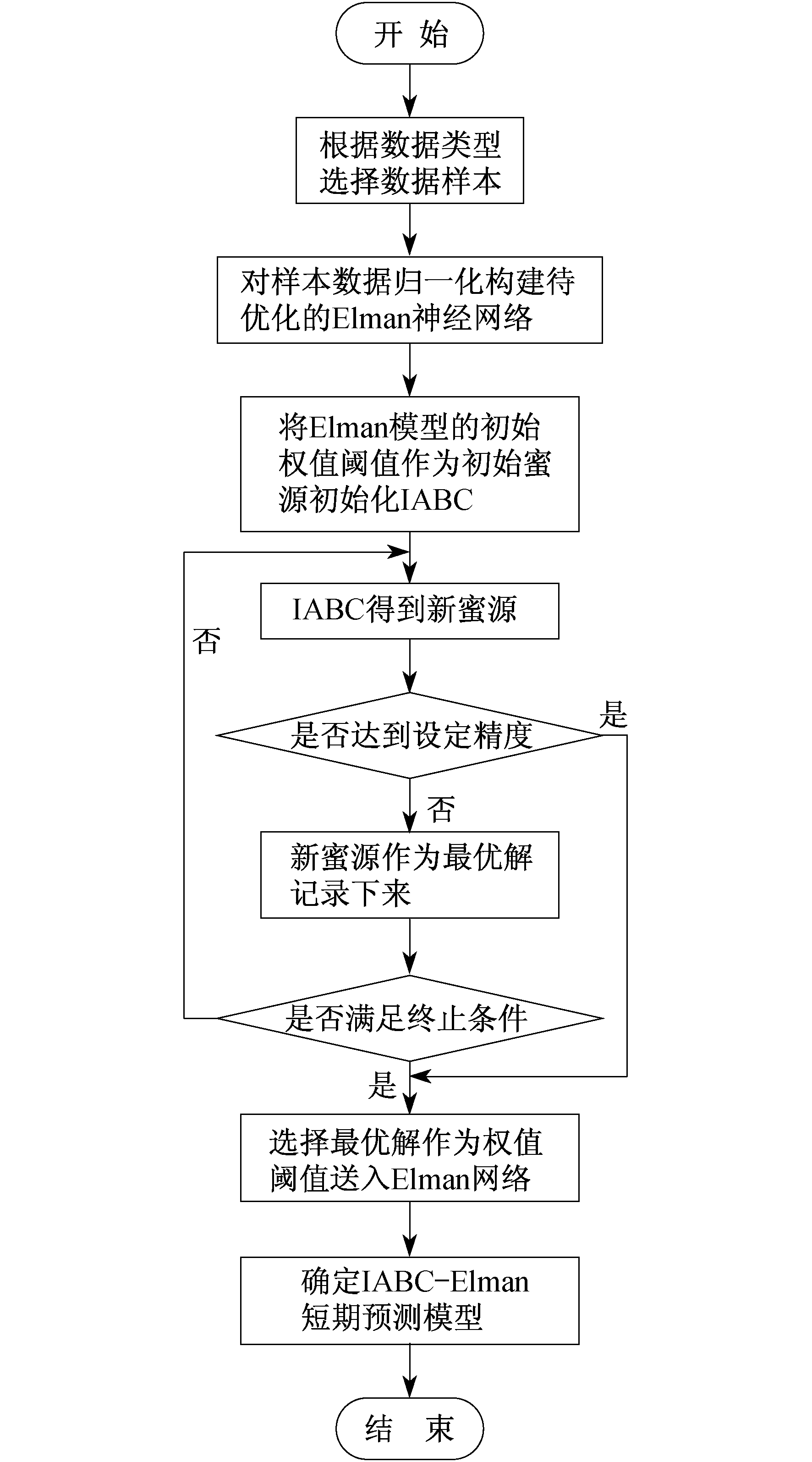
IABC基本流程图如图 2所示, 左边框图部分是改进部分。
4 改进ABC算法优化Elman算法流程
Elman网络训练方式与同BP网络训练方法基本相同:利用随机梯度下降反向传播算法进行训练, 存在收敛速度慢, 易陷于局部最优值, 且神经网络最终结果、整体性能与初始参数有密切关系。Elman网络的初始参数均为随机生成。为进一步提高Elman网络的泛化性能, 避免迭代训练过程中陷入局部极值点, 利用改进ABC算法对网络初始权值阈值进行优化, 构建IABC-Elman短期预测模型。
IABC-Elman算法流程如下。
(1) 根据数据类型划分进煤量、存煤量和厂发电量组成训练集样本。
(2) 建立Elman神经网络。
(3) 将Elman网络初始化的权值阈值数据重构作为初始蜂群。ABC算法参数包括:蜂群大小(S)、引领蜂数量(Ne)、跟随蜂数量(No)、解的个数(Ns)、极限值(Nlimit)、最大迭代次数(Nmaxcycle)。引领蜂的数量与跟随蜂的数量相等, 且满足以下关系
| $S=2 N_{\mathrm{s}}=N_{\mathrm{e}}+N_{\mathrm{o}}$ | (13) |
设初始蜜源Xi(i=1, 2, 3, …NS), 每一个蜜源都是D维向量, Xi代表流程(1)中初步建立的Elman网络的权值阈值。
(4) 计算每个蜜源(解)的适应度为
| $ f\left(\boldsymbol{X}_{i}\right)=\left\{\begin{array}{l} 1, E_{\mathrm{MSE}_{i}}=0 \\ \frac{1}{1+E_{\mathrm{MSE}_{i}}}, E_{\mathrm{MSE}_{i}} \gt 0 \end{array}\right. $ | (14) |
式中, EMSEi为Elman的第i个解的均方误差; f(Xi)越大, 表明适应度越高, f(Xi)=1是最理想状态。
(5) 引领蜂根据式(11)在初始解邻域范围内进行新解搜索。若新解适应度值大于原解, 则用新解代替原解(即贪婪学习法[12]), 否则B加1。
(6) 根据改进的跟随蜂选择引领蜂计算得到蜜源的收益率, 然后从现有解的邻域寻找新解。
(7) 若有解更新次数已经超过算法设定的Nlimit值, 即该解蜜源贫瘠, 不能继续优化, 则引领蜂遗弃该蜜源, 由式(12)产生新解来代替它, 同时记录最优解。
(8) 若迭代次数大于Nmaxcycle, 则结束训练, 返回步骤(7)。
(9) 将最优解数据结构重构为Elman网络的权值阈值结构, 作为Elman网络的最优权值阈值建立优化模型。
5 实例分析
IABC-Elman神经网络耗煤量短期预测模型流程如图 3所示。本文采用MATLAB软件验证IABC-Elman神经网络耗煤量短期预测模型的有效性。数据来自重庆某电厂2013年1月1日至2018年6月26日采集的进煤量、存煤量、耗煤量及发电量历史数据。训练样本为原始的2 003组数据中随机选取的1 996组数据, 时间、进煤量、存煤量及厂发电量作为输入, 耗煤量作为输出训练Elman耗煤量预测模型, 1 997~2 003的7组随机数据为测试数据。训练样本中的缺失数据和异常数据采用临近日期相同类型数据的加权平均计算结果代替原有坏数据。
由于季节不同对用电量的影响也不同, 使得不同季节耗煤量亦不尽相同, 所以在将训练数据送入模型训练之前, 需要根据四季用电的高峰时段将样本数据进行聚类以提高模型的预测精度[14]。通过聚类, 将1 996组数据分为4类。
表 1为根据四季用电量不同聚类得到的部分夏季训练样本。
表 1
部分IABC-Elman模型训练样本
| 日期 | 进煤量/104t | 存煤量/105t | 厂发电量/107kWh | 耗煤量/104t |
| 2013-06-29 | 1.63 | 6.817 | 1.329 | 0.63 |
| 2014-07-21 | 1.59 | 6.475 | 1.441 | 0.66 |
| 2015-07-19 | 1.78 | 6.935 | 1.480 | 0.60 |
| 2016-06-13 | 1.21 | 6.981 | 1.498 | 0.75 |
| 2017-06-14 | 1.58 | 6.382 | 1.446 | 0.63 |
| 2017-06-17 | 1.71 | 6.717 | 1.361 | 0.54 |
| 2017-08-23 | 1.96 | 6.600 | 1.645 | 0.71 |
根据修改蜜源更新方法及选择蜂跟随引领蜂的选择方式编写改进ABC算法; 根据图 3所示的IABC算法优化Elman连接权值阈值; 神经网络激励函数的隐含层函数f(x)采用sigmoid函数, 输出层g(x)函数采用线性函数。隐含层神经元个数的确定是一个较复杂的问题:隐含层神经元个数设置过少, 网络获取样本信息能力较差, 造成网络学习不够成熟, 不足以概括和体现样本规律; 若神经元个数设置过多, 则会将数据非规律性函数关系记录下来, 导致网络过度拟合, 且网络训练的时间会更长[15]。
隐含层神经元个数经验公式为
| $ J=\sqrt{m+n}+c $ | (15) |
式中:m——输入层节点数;
n——输出层节点数;
c——常数, c=1, 2, 3, …, 10。
根据确定的输入输出结构可以得模型隐含层神经元个数范围为3~12。
本文将模型预测输出与期望输出差值的均方差定义为精度[16], 在相同训练次数下, 隐含层神经元个数为3时, 最好精度为0.084 9;隐含层神经元个数为6时, 最好精度为0.024 1;隐含层神经元个数为8时, 最好精度为0.043 6;隐含层神经元个数为9时, 最好精度为0.021 3;隐含层神经元个数为12时, 最好精度为0.040 7。当隐含层神经元个数超过8时也能够达到设定目标, 但增加神经元个数并没有使网络性能得到明显改善。最终本文确定隐含层神经元个数为6;最大训练次数均取3 000次, 初始学习速率为0.001。为评估各模型耗煤量短期预测的预测精度, 选取平均绝对误差、最大绝对误差、平均相对误差、均方根误差和均方误差(Mean Square Error, MSE)作为评价指标。
将表 1中的预测输入数据分别输入IABC-Elman神经网络、Elman神经网络、GRNN和BP神经网络, 取相同的最大训练次数、隐含层神经元个数以及相同的学习率, 基于4种网络的煤量短期预测输出结果如图 4所示。
由图 4可知, IABC-Elman网络的预测值与实际值曲线之间的距离最小, 可以跟随实际数据的变化趋势。在误差曲线中也可以看出, IABC-Elman的误差曲线在[-0.1, 0.05]之间, 是4种方法中最小的。
4种神经网络的评价结果比较如表 2所示。
表 2
4种神经网络评价结果比较
| 神经 网络 |
均方根 误差 |
均方 误差 |
平均 绝对 误差 |
最大 绝对 误差 |
平均 相对 误差 |
| % | |||||
| IABC-Elman | 0.163 | 0.026 | 1.470 | 4.521 | 5.260 |
| Elman | 0.181 | 0.033 | 4.981 | 1.261 | 7.911 |
| BP | 0.195 | 0.038 | 7.154 | 1.648 | 11.206 |
| GRNN | 0.184 | 0.034 | 5.973 | 1.680 | 9.642 |
由表 2可以看出, 基于IABC-Elman神经网络的耗煤量短期预测结果要明显优于Elman网络、BP网络和GRNN网络。主要原因是初始Elman神经网络的连接权值阈值(输入层-隐含层、隐含层-输出层), 在原有ABC的基础上, 改进了蜜源更新方式的蜜源更新公式和跟随蜂选择引领蜂的选择概率公式, 避免了原有ABC算法易陷入局部最大值以及算法后期跟随蜂选择压力过大的问题, 最终得到了优化的权值阈值。
6 结语
神经网络具有自学习、自组织较好的容错性以及优良的非线性逼近能力, 对电厂耗煤量非线性数据有很好的处理能力。针对电厂耗煤量短期预测提出了IABC-Elman耗煤量短期预测模型。实验结果表明, 在相同网络参数设置下, IABC-Elman短期耗煤量预测模型的均方根误差, 均方误差, 平均绝对误差均低于Elman, BP, GRNN等神经网络预测模型; 在综合考虑进煤量、存煤量及发电量的影响因素下, 对耗煤量的预测精度较高。
参考文献
-
[1]中华人民共和国国务院.电网调度管理条例[Z/OL]. (1993-11-01)[2019-03-04]. http://baike.baidu.com/item/电网调度管理条例/7972891?fr=aladdin.
-
[2]制度变迁、市场选择与我国电力工业体制改革[J]. 经济论坛, 2013(19): 35-39.
-
[3]基于最小二乘法的时间序列短期发电量预测[J]. 电力系统及其自动化学报, 2005, 17(1): 23-26. DOI:10.3969/j.issn.1003-8930.2005.01.006
-
[4]基于多时段综合相似日的光伏发电功率预测[J]. 电源技术, 2017, 41(1): 103-106. DOI:10.3969/j.issn.1002-087X.2017.01.033
-
[5]基于人工蜂群算法优化支持向量机的燃气轮机故障诊断[J]. 热能工程, 2018(9): 39-43.
-
[6]基于改进蜂群算法的机器人路径规划[J]. 计算机系统应用, 2017, 33(4): 341-345.
-
[7]电力供应链的电煤库存研究[J]. 电网技术, 2012, 36(12): 242-249.
-
[8]中国煤炭运输现状发展趋势与对策研究[J]. 铁道经济研究, 2016(3): 38-41.
-
[9]中国煤炭资源供应格局演变及流动路径分析[J]. 地域研究与开发, 2012(2): 9-14. DOI:10.3969/j.issn.1003-2363.2012.02.003
-
[10]MOGHANLOO F N, YAZDIZADEH A, FOMANI A P J. A new modified elman neural network with stable learning algorithm for identification of nonlinear systems[M]. Berlin Heidelberg: Springer International Publishing, 2015: 171-193.
-
[11]ZHONG S, DONG Y F, SAROSH A. Artificial bee colony algorithm for parametric optimization of space attitude tracking controller[M]. Berlin: Foundations and Pract-ical Applications of Cognitive Systems and Information Processing, Springer Berlin Heidelber, 2016: 501-510.
-
[12]基于人工蜂群算法的支持向量机优化[J]. 天津大学学报, 2011(9): 803-809.
-
[13]基于ABC算法改进AEA算法的研究及其应用[J]. 控制工程, 2018, 21(6): 858-862.
-
[14]数据挖掘常用聚类算法研究[J]. 控制与策略, 2018, 10(16): 3710-3712.
-
[15]电力系统超短期负荷预测算法及应用[J]. 上海电力学院学报, 2013, 29(1): 9-12.
-
[16]基于气象因子的Elman神经网络短期负荷预测[J]. 电力系统及其自动化学报, 2017, 17(1): 23-26.