|
|
|
发布时间: 2019-10-10 |
|
|
|
|
收稿日期: 2019-04-02
中图法分类号: X928.7;O38
文献标识码: A
文章编号: 1006-4729(2019)05-0413-06
|
摘要
在传统的蒸气云爆炸(Vapor Cloud Explosion, VCE)参数预测的TNO(The Netherlands Organization)多能法中, 引入基于模糊逻辑的方法确定爆炸强度等级, 提出了基于模糊逻辑的蒸气云爆炸参数预测框架算法(Fuzzy Logic Prediction Framework Algorithm for Vapor Cloud Explosion Parameters, VCEP-FLPFA)。在定义爆炸强度等级隶属度函数时, 充分使用专家经验、爆炸历史数据等知识。基于文献数据及经验信息, 给出了VCEP-FLPFA的一种实现策略, 并以某LPG储配中心为例, 对该算法的具体应用进行了说明。
关键词
蒸气云爆炸; TNO多能法; 模糊逻辑; 爆炸强度
Abstract
A novel fuzzy logic prediction framework algorithm for vapor cloud explosion parameters (VCEP-FLPFA) is presented, which introduces a fuzzy method to describe explosion strength class number based on the traditional TNO (The Netherlands Organization) multi-energy method.The fuzzy membership degree functions for ignition energy and obstruction and parallel plane confinement are defined based on expert experience and VCE historical data etc.A specific method for VCEP-FLPFA is provided.The LPG storage and distribution center is taken as an example to illustrate the application of the algorithm.
Key words
vapor cloud explosion; TNO multi-energy method; Fuzzy logic; explosion strength
蒸气云爆炸(Vapor Cloud Explosion, VCE)是工业厂区存在的主要安全危险之一。近半个世纪以来, 国内外已发生多起由VCE引起的重大事故, 造成严重的人员伤亡和财产损失[1-2]。
对VCE参数预测方法的研究, 国内外专家学者提出了诸多方法, 如三硝基甲苯(TNT)当量模型、TNO(The Netherlands Organization)、TNO多能法、沸腾液体扩展蒸气爆炸(Boiling Liquid Expanding Vapor Explosion, BLEVE)、计算流体动力学(Computational Fluid Dynamics, CFD)等。其中, TNO多能法因其使用简便而被广泛应用[3-8], 也被写入中华人民共和国安全生产行业标准《化工企业定量风险评价导则》(AQ/T 3046—2013)等相关标准中。TNO多能法中, 爆炸强度被划分为10个等级(标识为1~10), “1”代表强度最弱, “10”代表强度最强[7]。针对不同强度等级的爆炸, TNO多能法定义了对应的预测静态侧向压力曲线、动态侧向压力曲线、爆炸波持续时间及波形。爆炸强度等级确定的合理性, 直接决定了爆炸参数的预测是否合理。若爆炸强度等级设定过高, 则预测出的爆炸参数偏高, 导致基于此预测结果所开展的工程设计偏于保守, 造成不必要的建设投资浪费; 反之, 若爆炸强度等级设定过低, 则预测出的爆炸参数偏低, 导致基于此预测结果所开展的工程设计存在系统安全风险。
KINSELLA K G[10]提出了VCE超压参数的快速预测方法, 根据专家经验对点燃能强度、障碍物阻塞程度、受限程度进行定性判定, 再结合其提出的爆炸强度等级索引表, 确定爆炸强度等级。
本文引入模糊逻辑方法, 定量定性地确定点燃能强度、障碍物阻塞程度、受限程度, 以更方便有效地使用专家经验、爆炸历史数据等知识, 为此提出了基于模糊逻辑的蒸气云爆炸参数预测框架算法(Fuzzy Logic Prediction Framework Algorithm for Vapor Cloud Explosion Parameters, VCEP-FLPFA), 合理确定爆炸强度等级及其隶属度, 并基于此信息合理预测静态侧向压力、动态侧向压力、爆炸波持续时间及波形, 以及人员伤害半径等相关信息。基于文献数据及经验信息, 本文给出了预测框架方法的一种具体实现方法, 并以文献[11-12]的LPG储配中心为例, 说明预测方法的具体应用。
1 VCEP-FLPFA描述
模糊逻辑是通过模仿人的思维方式来表示和分析不确定、不精确信息的方法和工具, 用于表达界限不清晰的定性知识与经验。它借助于隶属度函数概念, 区分模糊集合, 处理模糊关系, 模拟人脑实施规则型推理。模糊推理过程包括输入模糊化、模糊规则库、模糊推理、解模糊化输出等[13]。
1.1 系统输入及模糊化
本文参照文献[10]中KINSELLA K G的定义, 将点燃能强度、障碍物阻塞程度、受限程度的模糊变量定义如下。
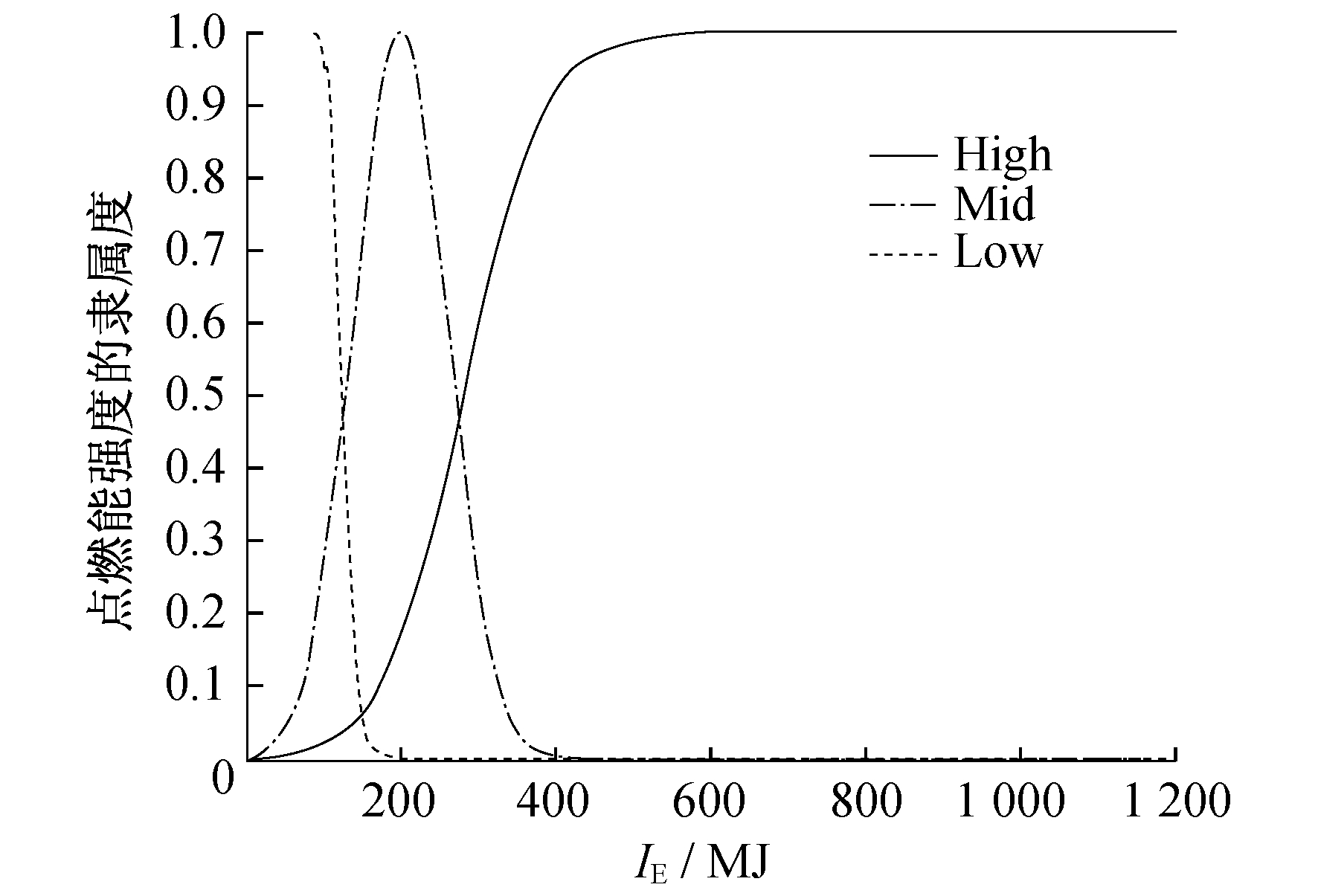
(1) 点燃能强度 点燃能强度模糊变量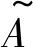 取值为:High, Mid, Low。工业现场存在的静电、电闸调电、电机起动引起的火花, 以及高温物体表面都可作为点火源引发VCE。这种工业现场存在的点火源被称为弱点火源, 点火能量一般小于100 MJ[14], 点燃能强度为Low。相应地, 雷管、受限蒸气云等被称为强点火源, 点火能量一般大于1 000 MJ, 点燃能强度为High。基于此专家经验, 可定义
取值为:High, Mid, Low。工业现场存在的静电、电闸调电、电机起动引起的火花, 以及高温物体表面都可作为点火源引发VCE。这种工业现场存在的点火源被称为弱点火源, 点火能量一般小于100 MJ[14], 点燃能强度为Low。相应地, 雷管、受限蒸气云等被称为强点火源, 点火能量一般大于1 000 MJ, 点燃能强度为High。基于此专家经验, 可定义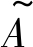 的隶属度函数, 记为
的隶属度函数, 记为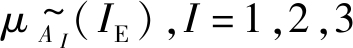 分别代表模糊值High, Mid, Low的隶属度函数, 其中IE为点燃能。
分别代表模糊值High, Mid, Low的隶属度函数, 其中IE为点燃能。
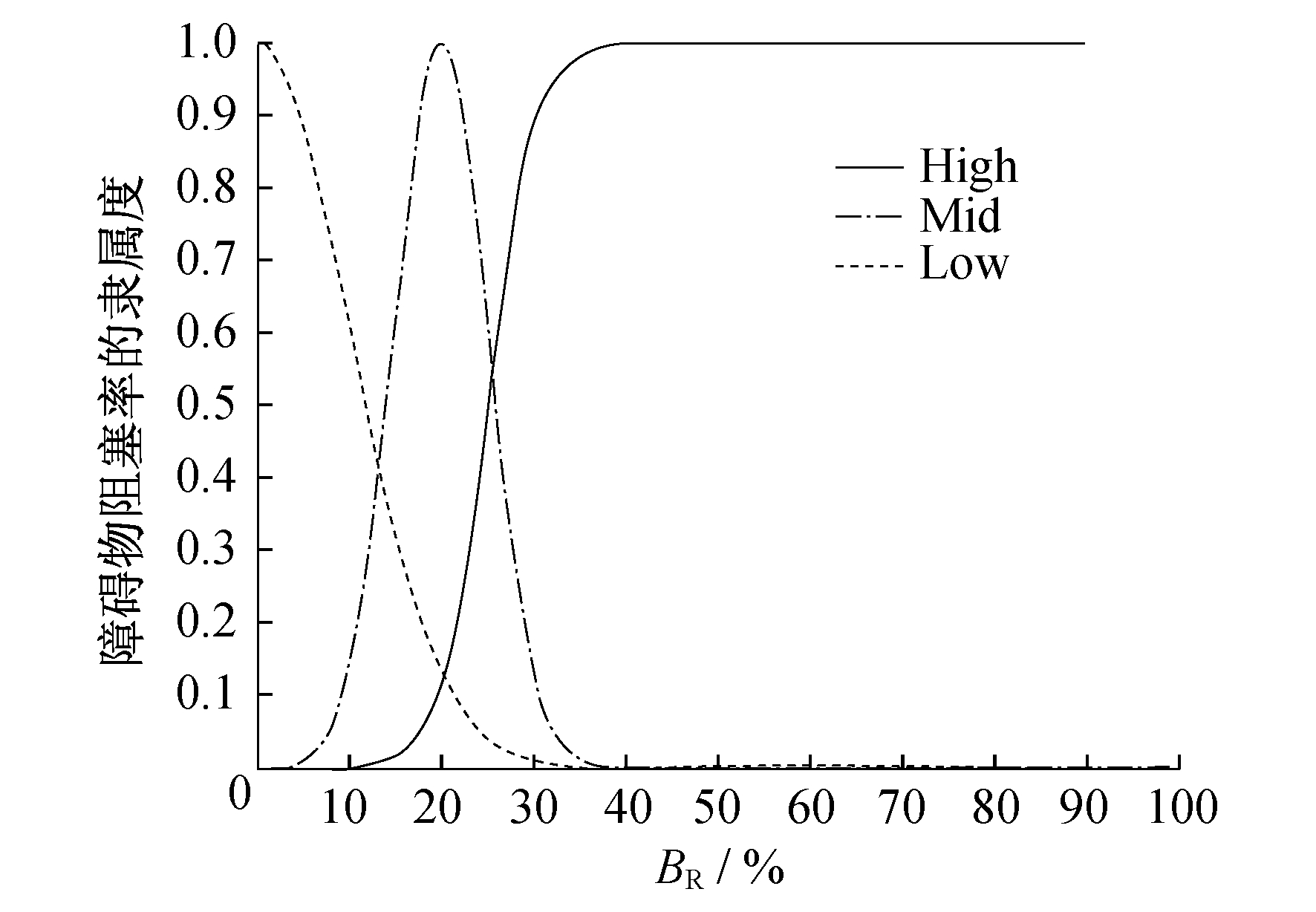
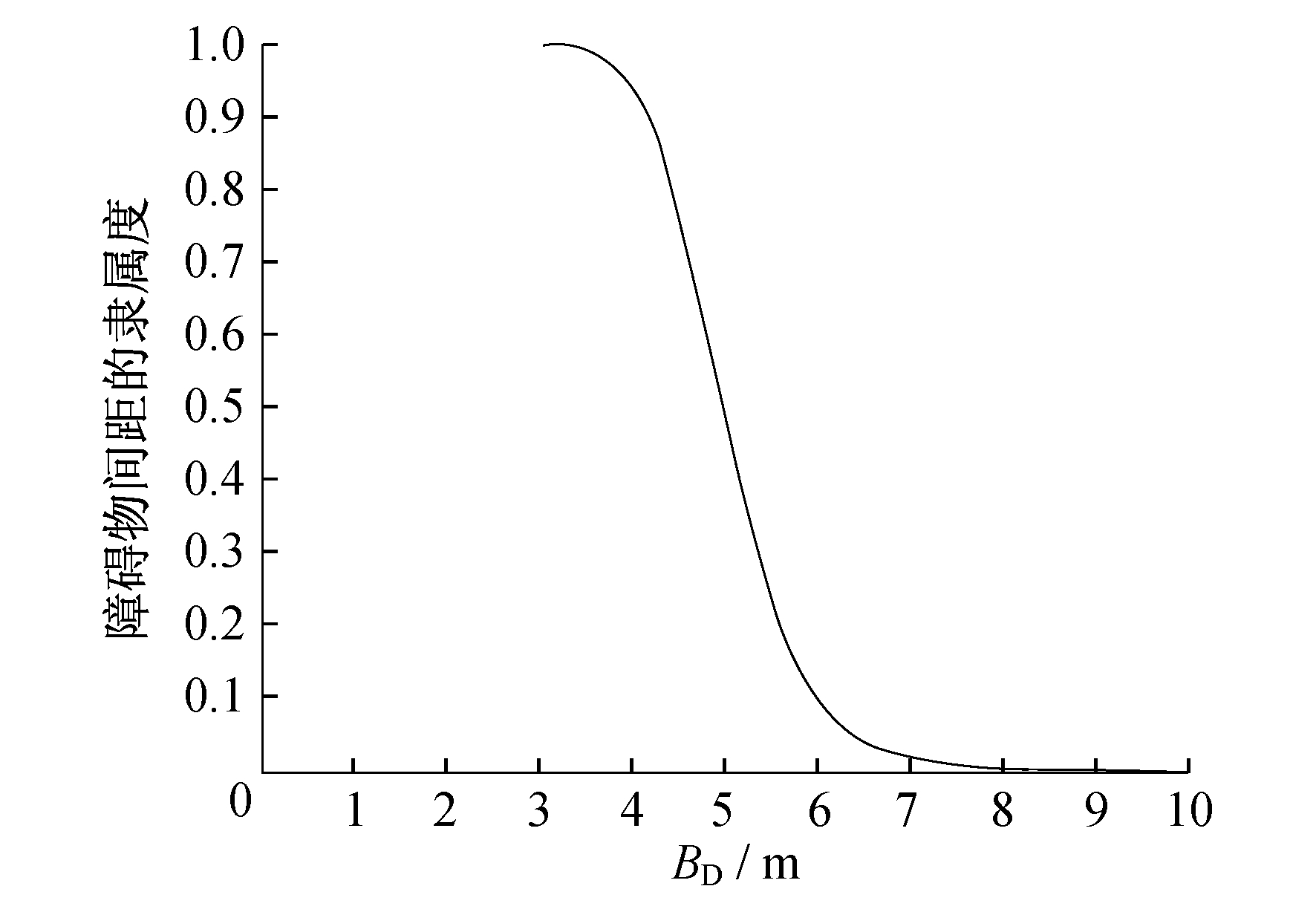
(2) 障碍物阻塞程度 障碍物阻塞程度模糊变量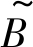 取值为:High, Mid, Low。障碍物阻塞率≥30%且障碍物间距小于≤3 m, 则障碍物阻塞程度为High; 障碍物阻塞率 < 30%或障碍物间距 > 3 m, 则障碍物阻塞程度为Mid; 没有障碍物, 则障碍物阻塞程度为Low。基于此专家经验, 可定义
取值为:High, Mid, Low。障碍物阻塞率≥30%且障碍物间距小于≤3 m, 则障碍物阻塞程度为High; 障碍物阻塞率 < 30%或障碍物间距 > 3 m, 则障碍物阻塞程度为Mid; 没有障碍物, 则障碍物阻塞程度为Low。基于此专家经验, 可定义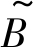 的隶属度函数, 记为
的隶属度函数, 记为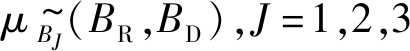 分别代表模糊值High, Mid, Low的隶属度函数, 其中BR和BD分别为障碍物阻塞率和障碍物间距。
分别代表模糊值High, Mid, Low的隶属度函数, 其中BR和BD分别为障碍物阻塞率和障碍物间距。
(3) 受限程度 受限程度模糊变量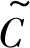 取值为:High, Low。蒸气云或部分蒸气云, 被两面或三面平面墙或障碍物限制, 则受限程度为High; 蒸气云除受地面限制外, 没有其他限制面, 则受限程度为Low。蒸气云受限程度除了与是否存在限制平面有关外, 还与限制平面之间的距离有关。限制平面间距越小, 则受限程度越大, 产生的爆炸强度越大。基于此专家经验, 可定义
取值为:High, Low。蒸气云或部分蒸气云, 被两面或三面平面墙或障碍物限制, 则受限程度为High; 蒸气云除受地面限制外, 没有其他限制面, 则受限程度为Low。蒸气云受限程度除了与是否存在限制平面有关外, 还与限制平面之间的距离有关。限制平面间距越小, 则受限程度越大, 产生的爆炸强度越大。基于此专家经验, 可定义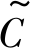 的隶属度函数, 记为
的隶属度函数, 记为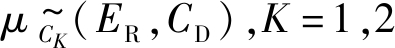 分别代表模糊值High和Low的隶属度函数, 其中ER和CD分别为VCE半径、限制平面之间的距离。
分别代表模糊值High和Low的隶属度函数, 其中ER和CD分别为VCE半径、限制平面之间的距离。
1.2 输出模糊化
系统输出为爆炸强度等级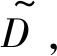 取值为:
取值为:
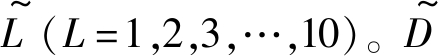 的隶属度函数为
的隶属度函数为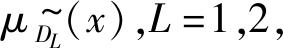 3, …, 10分别代表模糊值
3, …, 10分别代表模糊值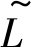 的隶属度函数。
的隶属度函数。
1.3 模糊规则库
KINSELLA K G提出的爆炸强度等级索引表如表 1所示。
表 1
爆炸强度等级索引
| 爆炸强度类别 | 点燃能强度 | 障碍物阻塞程度 | 受限程度 | TNO爆炸强度等级 | ||||||
| Low | High | High | Mid | Low | Yes | No | ||||
| 1 | × | × | × | 7~10 | ||||||
| 2 | × | × | × | 7~10 | ||||||
| 3 | × | × | × | 5~7 | ||||||
| 4 | × | × | × | 5~7 | ||||||
| 5 | × | × | × | 4~6 | ||||||
| 6 | × | × | × | 4~6 | ||||||
| 7 | × | × | × | 4~5 | ||||||
| 8 | × | × | × | 4~5 | ||||||
| 9 | × | × | × | 3~5 | ||||||
| 10 | × | × | × | 2~3 | ||||||
| 11 | × | × | × | 1~2 | ||||||
| 12 | × | × | × | 1 | ||||||
参照表 1编制模糊规则库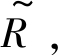 定义
定义
| $\tilde{R}: \tilde{A} \times \tilde{B} \times \tilde{C} \rightarrow \tilde{D}$ |
1.4 模糊推理
模糊推理定义为
| $\tilde{D}=\tilde{A} \times \tilde{B} \times \tilde{C} 。\tilde{R}$ |
1.5 解模糊化
根据模糊推理结果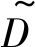 确定爆炸强度等级的隶属度, 并依据所定义的解模糊化方法(如最大隶属度取最大值方法、面积中心法等)确定爆炸强度等级。
确定爆炸强度等级的隶属度, 并依据所定义的解模糊化方法(如最大隶属度取最大值方法、面积中心法等)确定爆炸强度等级。
2 VCEP-FLPFA的一种实现方法
2.1 定义隶属度函数
2.1.1 点燃能强度的隶属度函数
其隶属度函数为
| $ \mu_{A_{1}}^{\sim}\left(I_{\mathrm{E}}\right)=\frac{1}{1+\mathrm{e}^{-10^{(-1.7)} \times\left(I_{\mathrm{E}}-280\right)}} $ | (1) |
| $ \mu_{A_{2}}^{\sim}\left(I_{\mathrm{E}}\right)=\mathrm{e}^{\frac{-\left(I_{\mathrm{E}}-200\right)^{2}}{2 \times 60^{2}}} $ | (2) |
| $ \mu_{A_{3}}^{\sim}\left(I_{\mathrm{E}}\right)=\frac{1}{1+\left|\frac{\mathrm{I}_{\mathrm{E}}-25}{100}\right|^{12}} $ | (3) |
点燃能强度的隶属度函数曲线如图 1所示。
2.1.2 障碍物阻塞程度的隶属度函数
此处定义障碍物阻塞程度的隶属度为障碍物阻塞率隶属度与间距隶属度的乘积, 记为
| $\begin{aligned} \mu_{{B_{J}}}^{\sim}\left(B_{\mathrm{R}}, B_{\mathrm{D}}\right) &=\mu_{{B_{J}}}^{\sim}\left(B_{\mathrm{R}}\right) \cdot \mu_{{B_{J}}}^{\sim}\left(B_{\mathrm{D}}\right) \\ & J=1,2,3 \end{aligned}$ | (4) |
| $\mu_{B_{1}}^{\sim}\left(B_{\mathrm{R}}\right)=\frac{1}{1+\mathrm{e}^{-0.4 \times\left(B_{\mathrm{R}}-25\right)}}$ | (5) |
| $\mu_{B_{2}}^{\sim}\left(B_{\mathrm{R}}\right)=\mathrm{e}^{\frac{-\left(B_{\mathrm{R}}-20\right) ^{2}}{2 \times 5^{2}}}$ | (6) |
| $\mu_{B_{3}}^{\sim}\left(B_{\mathrm{R}}\right)=\mathrm{e}^{\frac{-\left(B_{\mathrm{R}}\right)^{2}}{2 \times 10^{2}}}$ | (7) |
| $\mu_{B_{J}}^{\sim}\left(B_{\mathrm{D}}\right)=\frac{1}{1+\left(\frac{B_{\mathrm{D}}}{5}\right)^{12}}, J=1,2,3$ | (8) |
2.1.3 受限程度的隶属度函数
| $ \mu_{C_{K}}^{\sim}\left(E_{\mathrm{R}}, C_{\mathrm{D}}\right), K=1,2 $ | (9) |
| $ \mu_{C_{1}}^{\sim}\left(E_{\mathrm{R}}, C_{\mathrm{D}}\right)=\frac{1}{1+\left(\frac{\frac{C_{\mathrm{D}}}{E_{\mathrm{R}}}}{5}\right)^{6}} $ | (10) |
| $ \mu_{C_{2}}^{\sim}\left(E_{\mathrm{R}}, C_{\mathrm{D}}\right)=\frac{1}{1+\mathrm{e}^{-1.5}\left(\frac{C_{\mathrm{D}}}{E_{\mathrm{R}}-6}\right)} $ | (11) |
受限程度的隶属度函数曲线如图 4所示。
2.2 定义模糊系统输出
模糊系统输出为爆炸强度等级, 此处定义爆炸强度等级为精确量, 即为L=1, 2, 3, …, 10。
2.3 定义模糊规则库
本文定义的模糊规则库如表 2所示。
表 2
模糊规则库
| 点燃能强度 | 障碍物阻塞程度 | 受限程度 | 爆炸 强度 等级 |
|||||||
| High | Mid | Low | High | Mid | Low | High | Low | |||
| × | × | × | 10 | |||||||
| × | × | × | 9 | |||||||
| × | × | × | 8 | |||||||
| × | × | × | 7 | |||||||
| × | × | × | 6 | |||||||
| × | × | × | 5 | |||||||
| × | × | × | 8 | |||||||
| × | × | × | 7 | |||||||
| × | × | × | 6 | |||||||
| × | × | × | 5 | |||||||
| × | × | × | 5 | |||||||
| × | × | × | 4 | |||||||
| × | × | × | 6 | |||||||
| × | × | × | 5 | |||||||
| × | × | × | 4 | |||||||
| × | × | × | 3 | |||||||
| × | × | × | 2 | |||||||
| × | × | × | 1 | |||||||
模糊规则库可描述为
| $\mathrm{IF} \widetilde{A_{I}}$ and $\widetilde{B_{J}}$ and $\widetilde{C_{K}}, \mathrm{THEN} \;D_{M}$ |
式中:I=1, 2, 3;
J=1, 2, 3;
K=1, 2;
M=1, 2, 3, …, 18;
DM=1, 2, 3, …, 10。
2.4 模糊推理
针对具体的输入IE, BR, BD, ER, CD, 模糊推理结果为爆炸强度等级DM的可能性μ(DM)。其定义如下
| $ \begin{aligned} \mu\left(D_{M}\right)=& \mu_{A_{I}}^{\sim}\left(I_{\mathrm{E}}\right) \cdot \mu_{B_{J}}^{\sim}\left(B_{\mathrm{R}}, B_{\mathrm{D}}\right) \\ & \mu_{C_{K}}^{\sim}\left(E_{\mathrm{R}}, C_{\mathrm{D}}\right) \end{aligned} $ | (12) |
2.5 解模糊化
现以预测爆炸静态侧向超压为例, 说明具体的解模糊化方法。类似的方法也可以预测动态峰值压力和正向持续时间。
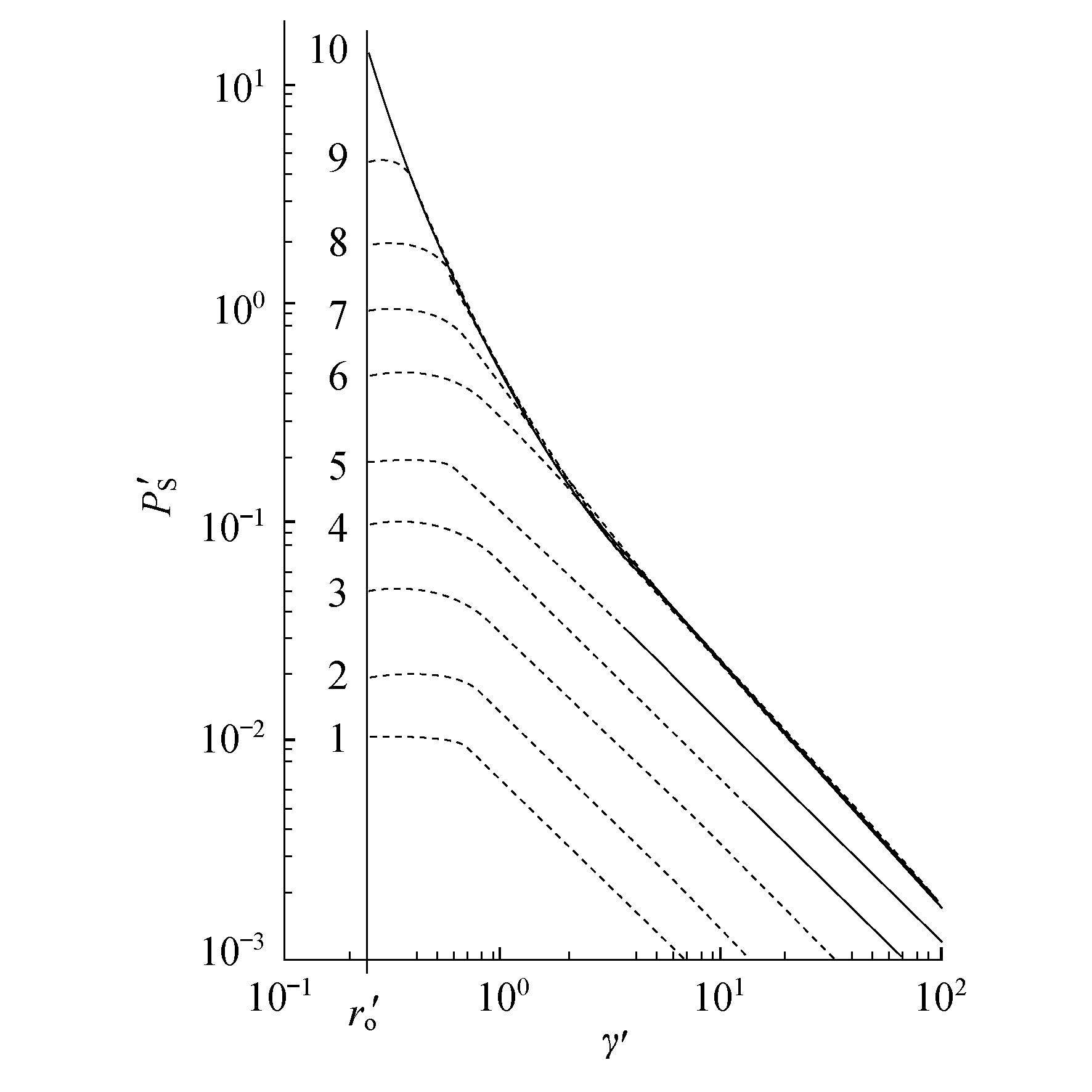
TNO多能法针对爆炸强度等级给出了对应无量纲距离γ′的无量纲静态侧向超压值P′S曲线, 具体如图 5所示[5]。
其中, 无量纲距离的计算公式为
| $ \gamma^{\prime}=z\left(\frac{P_{0}}{E}\right)^{\frac{1}{3}} $ | (13) |
式中:z——感兴趣的地点与爆炸中心的距离, m;
P0——当地大气压, 一般取1.0×105 Pa;
E——爆炸源能量, MJ。
由图 5可以获得无量纲静态侧向超压值P′S, 则静态侧向超压值的计算公式为
| $P_{\mathrm{s}}=P_{\mathrm{s}}^{\prime} P_{0}$ | (14) |
文献[14]给出了无量纲静态侧向超压值的拟合函数关系式, 记为P′SL(γ′), L=1, 2, 3, …, 10。如爆炸强度等级7的拟合函数为
| $ P_{\mathrm{S}_{7}}^{\prime}\left(\gamma^{\prime}\right)=\left\{\begin{array}{l} 1, \gamma^{\prime} \leqslant 0.4 \\ -1.002\;6 \gamma^{\prime}+1.428\;792 \\ 0.4 \lt \gamma^{\prime} \leqslant 0.843\;299 \\ \frac{0.464\;1838}{\left(\gamma^{\prime}\right)^{1.411\;65}}, 0.843\;299 \lt \gamma^{\prime} \leqslant \\ 3.6315644 \\ \frac{0.298\;902\;8}{\left(\gamma^{\prime}\right)^{1.100\;35}}, 3.631\;564\;4 \lt \gamma^{\prime} \leqslant 100 \\ 0.001, \gamma^{\prime} \gt 100 \end{array}\right. $ | (15) |
基于模糊逻辑的无量纲静态侧向超压预测值计算公式为
| $ P_{\mathrm{S}}^{\prime}=\frac{\sum\limits_{M=1}^{18} \mu\left(D_{M}\right) \cdot P_{\mathrm{S}_{D_{M}}}^{\prime}\left(\gamma^{\prime}\right)}{\sum\limits_{M=1}^{18} \mu\left(D_{M}\right)} $ | (16) |
3 应用实例
3.1 VCEP-FLPFA计算
3.1.1 计算障碍物体积和自由空间体积
3.1.2 计算蒸气云尺寸
LPG储罐的供气管路泄漏, 泄漏的液化石油气流到储罐下面, 蒸发形成的液化石油气与空气的混合物弥漫在储罐之间。假定蒸发液化石油气的重量为4 750 kg, 在环境温度为15 ℃时, 液化石油气在混合气体中的当量体积百分比为4%, 当量密度为1.86 kg/m3。
蒸气云体积:Vc=(100/4)×(4 750/1.86)=63 844 m3。
爆炸半径:[(3/2π)×63 844]1/3=31.24 m。
由于自由空间的体积Vgr=83 882 m3大于蒸气云体积Vc, 所以Vgr值减小为与Vc值相等, 即Vgr=Vc=63 844 m3。从而, 非障碍区域的蒸气云体积为零。
液化石油气与空气混合物的当量燃烧热为3.46 MJ/m3, 从而爆炸源能量E=3.46×106×63 844=220.9 GJ。
3.1.3 计算爆炸强度等级的隶属度
系统输入参数如下:点燃源为弥漫在储罐下的液化石油气, 即受限蒸气云, 假定点燃能IE=1 000 MJ; 障碍物阻塞率BR=16 000/99 882=16.02%;障碍物间距BD=1.5 m; VCE半径ER=31.24 m; 限制平面之间的距离CD=2.0 m。
根据本文提出的VCEP-FLPFA, 计算出隶属度排在前3位的爆炸强度等级分别是8, 6, 10, 对应的隶属度为:μ(8)=0.728 3; μ(6)=0.277 2; μ(10)=0.026 8。
3.1.4 计算爆炸静态侧向超压值
假定感兴趣的区域距离爆炸中心z为385 m, 则
| $ \gamma^{\prime}=z\left(\frac{P_{0}}{E}\right)^{\frac{1}{3}}=385 \times\left(\frac{1.0 \times 10^{5}}{220.9 \times 10^{9}}\right)^{\frac{1}{3}}=2.956\;2 $ |
代入文献[14]给出的无量纲静态侧向超压值的拟合函数关系式, 得
| $ P_{S}^{\prime}= $ |
| $ \frac{\mu(8) \cdot \mathrm{P}_{8}^{\prime}\left(\gamma^{\prime}\right)+\mu(6) \cdot \mathrm{P}_{6}^{\prime}\left(\gamma^{\prime}\right)+\mu(10) \cdot \mathrm{P}_{10}^{\prime}\left(\gamma^{\prime}\right)}{\mu(8)+\mu(6)+\mu(10)}= 0.095\;51$ |
从而,
| $ P_{\mathrm{s}}=P_{\mathrm{S}}^{\prime} P_{0}=9\;551(\mathrm{Pa}) $ |
3.2 传统的TNO计算
在建筑防爆设计中, 为了确保安全, 往往人为地确定爆炸强度等级为10, 则
| $ P_{\mathrm{s}}=P_{10}^{\prime} P_{0}=12348(\mathrm{Pa}) $ |
3.3 计算结果对比及分析
在VCEP-FLPFA中, 引入专家经验, 其预测的爆炸静态侧向超压值更为合理。与VCEP-FLPFA相比, 传统的TNO计算方法预测的爆炸静态侧向超压值高出约25%, 这将会导致建筑防爆设计过于保守, 大大增加建筑防爆设施的成本。
4 结语
本文在传统TNO多能法的基础上, 引入了基于模糊逻辑的人工智能技术手段, 所提出的VCEP-FLPFA可以更有效地使用专家经验、爆炸历史数据等知识, 预测结果更合理, 可为建筑防爆规划与设计提供可靠的科学数据。本文提出的方法具有通用性, 随着人们对VCE研究的深入, 可进一步优化本文提出的隶属度函数、爆炸强度等级经验表, 或者提出更为合理的隶属度函数、爆炸强度等级索引表, 以更有效地预测VCE参数。
参考文献
-
[1]WIEKEMA B J. Vapour cloud explosions-an analysis based on accidents. Part I[J]. Hazardous Materials, 1984, 55(8): 295-311.
-
[2]PRITCHARD D K. A review of methods for predicting blast damage from vapour cloud explosions[J]. Loss Prevention in the Process Industries, 1989, 2(4): 187-193. DOI:10.1016/0950-4230(89)80032-4
-
[3]MERCX W P M, VAN DEN BERG A C. Methods for the calculation of physical effects(the yellow book)[M]. Netherlands: TNO, 1997.
-
[4]MERCX W P M, VAN DEN BERG A C, HAYHURST C J, et al. Developments in vapour cloud explosion blast modeling[J]. Hazardous Materials, 2000, 71(1/2/3): 301-319.
-
[5]VAN DEN BERG A C. BLAST-a 1-D variable flame speed blast simulation code using a 'Flux-Corrected Transport' algorithm, Prins Maurits Laboratory TNO report no. PML 1980-162[R]. Netherlands: PML, 1980.
-
[6]WIEKEMA B J. Vapour cloud explosion model[J]. Hazardous Materials, 1980, 51(3): 221-232.
-
[7]ROBERTS A F, PRITCHARD D K. Blast effects from unconfined vapour cloud explosions[J]. Occupational Accidents, 1982, 3(4): 231-247. DOI:10.1016/0376-6349(82)90001-3
-
[8]VAN DEN BERG A C. The Multi-Energy method-A framework for vapour cloud explosion blast prediction, Prins Maurits Laboratory TNO report no. PML 1984-C-72[R]. Netherlands: PML, 1984.
-
[9]全国安全生产标准化技术委员会化学品分技术委员会.化工企业定量风险评价导则: AQ/T 3046—2013[S].北京: 煤炭工业出版社, 2013.
-
[10]KINSELLA K G. A rapid assessment methodology for the prediction of vapour cloud explosion over pressure[C]//Pro-ceedings of the International Conference and Exhibition on Safety, Health and Loss Prevention in the Oil, Chemical and Process Industries. Singapore: Butterworth-Heinemann, 1993: 200-211.
-
[11]PIETERSEN C M, CENDEJAS HUERTA S. Analysis of the LPG incident in San Juan Ixhuatepec, Mexico City, 19 November 1984, TNO report ref. 85-0222[R]. Netherlands: TNO, 1985.
-
[12]VAN DEN BOSCH C J H, WETERINGS R A P M. Methods for the calculation of physical effects due to releases of hazardous materials(liquids and gases). Yellow Book CPR 14E[M]. 2nd Edition. Hague: Gevaarlijke Stoffen, 2005.
-
[13]赵德齐.模糊数学[M].北京: 中央民族大学出版社, 1995.
-
[14]DNV. DNV SAFETI V6.4 on-line help document[CP/CD]. Norway: DNV, 2004.